Resumo
Ensinar como mecanismos causais ou modelos estatísticos funcionam nem sempre é algo simples, especialmente quando estes não podem ser facilmente exemplificados. O objetivo deste artigo é mostrar como Simulações de Monte Carlo (SMC) podem ser usadas para superar dificuldades como estas. Após fazermos uma breve introdução ao método, mostramos como utilizá-lo, a fim de ilustrar fenômenos de difícil mensuração ou conceitos abstratos; além disso, também mostramos como ele pode ser empregado para explicar intuitivamente a influência das violações de pressupostos sobre os resultados de alguns modelos estatísticos frequentemente utilizados na Ciência Política. Por fim, oferecemos um passo a passo para reproduzir nossos exemplos utilizando o software R, além de um simples aplicativo virtual (Shiny app) com estes exemplos, de modo a ser adaptado para uso em sala de aula.
Palavras-chave:
método de Monte Carlo; Ciência Política; metodologia política
Abstract
Teaching how causal mechanisms or statistical models work is often a difficult endeavor, even more so when there are no obvious ways to exemplify what is being taught. In this article, we show how Monte Carlo Simulations (SMC) can be employed in Political Science classes to overcome these problems. After a brief introduction to the method, we discuss practical application of simulations that can be used to shed light on abstract concepts and phenomena that are hard to measure. Additionally, we give examples of how simulations help to explain intuitively what consequences the misuse of statistical models might entail. Finally, we also provide step-by-step instructions to reproduce our examples using R and a web application (Shiny app) that can be easily adapted for teaching purposes.
Keywords:
Monte Carlo methods; Political Science; political methodology
Introdução
Ensinar como certas teorias ou modelos estatísticos funcionam nem sempre é algo simples, especialmente quando estes não podem ser facilmente exemplificados. Este é o caso de várias aulas de metodologia, em que o professor vê-se na difícil tarefa de explicar de forma clara por que certas ferramentas são adequadas em algumas situações, e não em outras, ou por que o uso inadequado de uma técnica produz resultados inválidos. Também é o caso de discussões em que fenômenos abstratos e variáveis de difícil mensuração, como ideologia e preferências, são objetos de análise. Embora pareçam bastante específicas, situações como estas são recorrentes em aulas de Ciências Sociais e cursos afins, ainda que não exista consenso, ou sequer literatura específica, sobre estes problemas na perspectiva do ensino de Ciência Política no Brasil - o que apenas ajuda a reforçar o diagnóstico traçado há mais de dez anos por Soares (2005SOARES, G. A. D. O calcanhar metodológico da Ciência Política no Brasil.Sociologia, Problemas e Práticas, n. 48, p. 27-52, 2005.) sobre o calcanhar metodológico da Ciência Política brasileira.2 2 Exceções, que tratam do ensino de métodos para a Ciência Política, podem ser encontrados em Barberia, Godoy e Barboza (2014b), Figueiredo Filho e Silva Jr. (2010), Figueiredo Filho, Silva Jr. e Rocha (2012), Figueiredo Filho et al. (2013) e Silva e Guarnieri (2014). Para um panorama recente sobre o ensino de métodos, ver Barberia, Godoy e Barboza (2014a).
Neste artigo, procuramos contribuir para esta ainda incipiente literatura, oferecendo um método simples para lidar com problemas como os relatados anteriormente. Nosso objetivo é mostrar como Simulações de Monte Carlo (SMC, daqui para frente) podem ser adaptadas como recurso didático para ilustrar conteúdos complexos e/ou abstratos. O principal aspecto desta abordagem, conforme argumentamos na próxima seção, é a possibilidade que ela nos oferece de simular amostras de acordo com um Processo Gerador de Dados (PGD) controlado, ou seja, de criar mundos artificiais totalmente manipuláveis pelos usuários. Em vez de nos levar a pensar principalmente no modelo estatístico que deve ser aplicado para cada tipo de dado, as SMC invertem essa perspectiva, colocando em primeiro lugar o exame dos mecanismos que produzem determinado fenômeno de acordo com alguma expectativa teórica. Essa inversão de perspectiva é o que torna intuitivo o aprendizado metodológico por meio de SMC (Carsey e Harden, 2015CARSEY, T. M.; HARDEN, J. J. Can you repeat that please? Using Monte Carlo simulation in graduate quantitative research methods classes. Journal of Political Science Education, v. 11, n. 1, p. 94-107, 2015.).
Após oferecermos um breve passo a passo de como planejar uma simulação e apresentar alguns critérios para julgar sua adequação e qualidade, ilustramos o potencial da abordagem com dois exemplos adaptados para uso em sala de aula. Primeiro, apresentamos uma simulação de um processo legislativo básico, em que os votos dos legisladores em cada votação são gerados aleatoriamente e as regras de maioria necessária para aprovação e as preferências dos legisladores podem ser modificadas previamente. Por meio deste simples exemplo, os alunos aprendem de uma maneira visual como pequenas modificações nas regras do processo legislativo, ou na polarização ideológica de um congresso, podem provocar problemas de paralisia decisória. De modo geral, discutimos também como este exemplo permite ilustrar uma vantagem na aplicação didática das SMC: possibilitar uma compreensão mais concreta de aspectos normalmente difíceis de serem isolados ou observados no mundo real (Mooney, 1997MOONEY, C. Z. Monte Carlo simulation. Thousand Oaks: Sage Publications, 1997.).
No segundo exemplo, mostramos como empregar o método para explicar intuitivamente a influência das violações de pressupostos sobre os resultados de um dos modelos estatísticos mais empregados na Ciência Política: a regressão linear por Mínimos Quadrados Ordinários (MQO). Como alguns alunos frequentemente sentem dificuldade ao estudar estatística, ou sentem-se intimidados pela matemática envolvida na formalização dos modelos, argumentamos que uma forma de superar estas dificuldades é oferecer uma intuição de como funciona o modelo em questão em situações hipotéticas. Para isso, a título de exemplo, simulamos duas variáveis estabelecendo vários graus de correlação entre si, e criamos outra variável dependente a partir destas; em seguida, mostramos como a omissão de uma daquelas variáveis constitutivas enviesa as estimativas de modelos lineares de acordo com a correlação entre o termo omitido e o incluído (ou seja, quanto maior a correlação, maior o viés na estimativa), algo central nos debates metodológicos nas Ciências Sociais (Angrist e Pischke, 2008ANGRIST, J. D.; PISCHKE, J. Mostly harmless econometrics: an empiricist's companion. Princeton: Princeton University Press, 2008.). Seguindo estas ilustrações, discutimos essas aplicações e oferecemos algumas ilustrações mais aplicadas de SMC para a pesquisa, o que amplia o potencial de aplicação da ferramenta. Por fim, apresentamos onde e como encontrar o código usado aqui com comentários, a fim de que seja possível reproduzir nossos exemplos utilizando um software livre para computação estatística, o R,3 3 O R é um ambiente de programação estatístico, e pode ser baixado de forma gratuita pela internet. além de um aplicativo virtual de simples manuseio - Shiny app -, que pode ser adaptado para uso em sala de aula.
Dessa forma, nossa expectativa com este artigo é auxiliar principalmente docentes na apresentação em sala de aula de conteúdos complexos e/ou abstratos de forma mais intuitiva. Adicionalmente, esperamos realçar duas das principais vantagens do uso de SMC como ferramenta didática, que discutimos na conclusão deste artigo: de um lado, o uso de simulações permite reduzir o tempo gasto pelo professor com a discussão conceitual; de outro, os alunos conseguem assimilar melhor o conhecimento requerido na área, além de aprenderem como desenhar suas próprias simulações, sejam elas didáticas, sejam aplicadas à pesquisa (Carsey e Harden, 2015CARSEY, T. M.; HARDEN, J. J. Can you repeat that please? Using Monte Carlo simulation in graduate quantitative research methods classes. Journal of Political Science Education, v. 11, n. 1, p. 94-107, 2015.). Dito de outro modo, nosso objetivo central é oferecer uma ferramenta simples para auxiliar na formação de estudantes e pesquisadores em Ciência Política. Também na conclusão, retomamos este ponto para discutir a ainda pouca disponibilidade de técnicas de ensino na disciplina, o que ressalta a importância da nossa contribuição e a dificuldade de testar comparativamente a eficácia de cada uma.4 4 Agradecemos a um dos pareceristas anônimos pela sugestão de melhor elaborar esses pontos.
Antes de adentrar propriamente na apresentação dos aspectos técnicos da SMC e na sua aplicação à Ciência Política, é importante destacar que o seu uso com o objetivo de facilitar o processo de ensino-aprendizagem já é explorado por outras áreas do conhecimento técnico-científico: na Química, para ensino de luminescência, cinética (Winnischofer et al., 2010WINNISCHOFER, H. et al. Simulação Monte Carlo no ensino de luminescência e cinética de decaimento de estados excitados. Química Nova, v. 33, n. 1, p. 225-228, 2010.); na Metrologia, para avaliação de incerteza na medição (Donatelli e Konrath, 2005DONATELLI, G. D.; KONRATH, A. C. Simulação de Monte Carlo na avaliação de incertezas de medição. Revista de Ciência &Tecnologia, v. 13, n. 25/26, p. 5-15, 2005.); simulação de eventos discretos para o ensino de Engenharia de Produção (Molina, Marins e Montevechi, 2010MOLINA, C. E. C.; MARINS, F. A. S.; MONTEVECHI, J. A. B. Proposta de utilização da simulação a eventos discretos no ensino da engenharia de produção. Revista P&D em Engenharia de Produção, v. 8, n. 1, p. 11-15, 2010.); na Física, para o ensino de mecanismo de transferência de calor (Dionisio e Spalding, 2014DIONISIO, G.; SPALDING, L. E. S. Método computacional de Monte Carlo adaptado como recurso didático para o estudo dos mecanismos de transferência de calor. In: SIMPÓSIO NACIONAL DE ENSINO DE CIÊNCIA E TECNOLOGIA, 4., 2014, Ponta Grossa. Disponível em: <Disponível em: http://sinect.com.br/anais2014/anais2014/artigos/ensino-de-fisica/01408122365.pdf
>. Acesso em: 14 jun. 2016.
http://sinect.com.br/anais2014/anais2014...
). Esses são alguns exemplos da variedade de usos da SMC para o ensino de teoria e conceitos abstratos, que mostram que a técnica já é usada de forma consistente há algum tempo no ensino de várias ciências. Nas próximas seções vamos explorar essa ferramenta para o ensino de Ciência Política e para o ensino de técnicas quantitativas de análise de dados como MQO.
Monte Carlo: uma breve introdução
Segundo uma definição de manual, SMC é um processo em que são criadas N variáveis aleatórias com o objetivo de examinar suas propriedades de forma agregada (Mooney, 1997MOONEY, C. Z. Monte Carlo simulation. Thousand Oaks: Sage Publications, 1997.; Prado, 1999PRADO, D. Teoria das filas e da simulação. 2. ed. Belo Horizonte: Editora de Desenvolvimento Gerencial, 1999.). Em termos mais claros, o método consiste em simular repetidas amostras aleatórias segundo algum tipo de distribuição pré-especificada (isto é, um PGD), para que, em seguida, seja possível analisar conjuntamente o resultado obtido a partir de cada uma destas amostras.
Um simples jogo de cara ou coroa exemplifica esse tipo de simulação: a distribuição teórica da variável de interesse - resultado do lançamento de uma moeda - é binomial, isto é, só podemos obter um resultado discreto de um universo de dois resultados possíveis após o lançamento de uma moeda não viciada - cara ou coroa. Neste caso, poderíamos lançar a mesma moeda 100 vezes (100 simulações) e registrar o resultado do lançamento. Depois, poderíamos calcular algum resultado de interesse; por exemplo, a probabilidade de o resultado de um lançamento qualquer ter sido cara. Embora simples, este exercício ajuda-nos a entender a principal característica de uma SMC: a geração de amostras aleatórias (em nosso caso, do lançamento de moedas) repetidas várias vezes segundo algum modelo de probabilidade e a análise posterior dos resultados dos eventos de interesse.
Em vez de coletar dados, formular uma hipótese e testá-la, portanto, as simulações permitem-nos gerar dados estipulando como eles devem se comportar. Podemos, por exemplo, simular um determinado fenômeno, como os votos de um partido, ou como os resultados agregados variam conforme alteramos o PGD (como o partido concentra seus votos, qual a probabilidade de uma moeda retornar cara, ou qual o grau de associação entre duas ou mais variáveis).
Por conta da possibilidade de controlar o número de simulações e as características das variáveis simuladas, uma das potencialidades do método é justamente emular um experimento em seu formato tradicional. Ao repetir o processo de geração de dados e utilizar aleatoriedade para investigar como pequenas variações alteram ou não um resultado, é possível examinar como pequenas mudanças na implementação de uma simulação afetam seus resultados (Axelrod, 1997AXELROD, R. Advancing the art of simulation in the social sciences. In: CONTE, R.; HEGSELMANN, R.; TERNA, P. (Eds.). Simulating social phenomena. Heidelberg: Springer, 1997.; Mooney, 1997MOONEY, C. Z. Monte Carlo simulation. Thousand Oaks: Sage Publications, 1997.). Estes experimentos ideais servem justamente para investigar questões que, de outro modo, seriam difíceis de serem respondidas empiricamente devido à necessidade de uma massiva coleta de dados que correspondam às situações possíveis de ocorrência de determinado fenômeno, além de permitirem uma ampla gama de aplicações, como testes de modelos estatísticos, testes de hipóteses, entre outros. Como diz Axelrod (1997, p. 24) em seu artigo seminal sobre simulações nas Ciências Sociais, “simulation is a way of doing thought experiments. While the assumptions may be simple, the consequences may not be at all obvious”. Ao utilizarmos SMC, portanto, podemos examinar uma série de questões que, de outro modo, seriam difíceis de serem examinadas somente a partir da investigação empírica.
Substantivamente, a ideia de fazer várias simulações e analisar seus resultados baseia-se em um teorema bastante conhecido no campo da inferência estatística clássica: o teorema do limite central (Grinstead e Snell, 2012GRINSTEAD, C.; SNELL, J. Introduction to probability. Rhode Island: American Mathematical Society, 2012.). Dito de forma condensada, este teorema propõe que, se gerarmos um número suficientemente grande de amostras aleatórias e calcularmos alguma estatística a partir delas (média, mediana etc.), o valor médio destas estatísticas indicará o valor real desse parâmetro na população. Um exemplo muito simples ajuda a clarificar esse ponto: podemos sortear dez pessoas dentro da população total do Brasil e mensurar a altura média da população a partir desta amostra. Basicamente, o teorema do limite central nos diz que, se repetirmos esse procedimento várias vezes, a média dos resultados de todas as médias amostrais convergirá para o valor real da média de altura no Brasil - mesmo que dez indivíduos seja, de modo geral, um número muito pequeno.
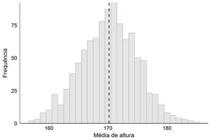
O gráfico 1 ilustra o exemplo anterior, em que estipulamos que a distribuição da altura da população brasileira segue uma distribuição normal, com média de 170 cm e desvio-padrão de 15 cm; a partir destes valores, simulamos 1.000 amostras contendo dez pessoas e calculamos a média de altura destas amostras; por fim, criamos um histograma desta distribuição para verificar os resultados, que, como pode ser visto, estão todos ao redor da média estipulada. Como ficará claro na próxima seção, este método pode ser generalizado para inúmeras outras situações, inclusive muito mais complexas.
Ingredientes para construir uma SMC
Antes de nos determos nas aplicações de SMC para o ensino de Ciência Política, é preciso compreender como uma simulação é construída. De acordo com Carsey e Harden (2015CARSEY, T. M.; HARDEN, J. J. Can you repeat that please? Using Monte Carlo simulation in graduate quantitative research methods classes. Journal of Political Science Education, v. 11, n. 1, p. 94-107, 2015.) e Mooney (1997MOONEY, C. Z. Monte Carlo simulation. Thousand Oaks: Sage Publications, 1997.), toda simulação tem três componentes,5 5 Na verdade, tanto Carsey e Harden (2015) quanto Mooney (1997) reportam cinco itens, mas dois deles podem ser condensados sem perda de generalidade. ou ingredientes, básicos: 1) um processo gerador de dados (PGD); 2) a simulação de N amostras a partir deste processo; e 3) a análise dos resultados agregados - e, sendo o caso, a redefinição do PGD e consequente repetição do processo. Discutimos esses aspectos em ordem, mostrando, etapa por etapa, como o exemplo anterior foi construído sobre a altura média da população brasileira.
Passo 1 - Definindo um PGD
Um PGD nada mais é do que a forma como definimos como um fenômeno será gerado. Em estudos eleitorais, por exemplo, poderíamos dizer que a votação de um candidato pode ser expressa da seguinte forma:
Simplificadamente, esse modelo pode ser pensado como uma regressão linear por mínimos quadrados, em que as variáveis à direita são os fatores que acreditamos influir na votação de um candidato i. Em uma SMC, precisamos definir previamente esse processo, e, a partir dele, simular as amostras. Um candidato pode ter qualidades pessoais igual a 9, em um indicador sintético hipotético que varie segundo uma escala de 0 a 10, e gastar R$ 10 mil em sua campanha. Essas informações, consideradas de acordo com os parâmetros do modelo que definirmos, lhe renderá Y i votos. Dependendo de como construirmos o PGD, podemos estabelecer que cada ponto a mais no indicador de qualidades pessoais gera, em média, 1.000 votos (β 1 = 1.000), e que cada real a mais gasto na campanha gera dez votos (β 2 = 10). Assim, nosso candidato hipotético teria (1.000 * 9) + (10 * 10.000) = 109.000 votos. A partir disso, podemos simular diversos outros candidatos, com qualidades pessoais e gastos de campanhas gerados aleatoriamente a partir de alguma distribuição teórica de probabilidades - como a normal, por exemplo.
No caso do exemplo oferecido na seção anterior, sobre a altura média dos brasileiros, nosso PGD é bastante simples: especificamos uma média de altura fictícia da população brasileira (170 cm) e seu desvio-padrão (15 cm). Nossos dois parâmetros de simulação, neste caso, são essas duas estatísticas, que, em conjunto, indicam que estipulamos a distribuição de altura dos brasileiros como seguindo uma distribuição normal (variável contínua), em que as alturas das pessoas variam de forma simetricamente decrescente em torno da média de 170 cm - que é exatamente o que o gráfico 1 reporta. De qualquer modo, cabe reforçar que este PGD que estipulamos é completamente modificável, significando que podemos estipular quaisquer valores de altura média e desvio-padrão na população. Parte da força de SMC reside justamente nessa possibilidade de poder alterar completamente o PGD de acordo com as necessidades da investigação.
Uma das principais vantagens desse método, portanto, é forçar o pesquisador a pensar de modo detido em como um fenômeno é gerado, isto é, deixar de pensar no modelo estatístico usado para testar uma hipótese, e, em vez de procurar entender como a natureza produz determinado fenômeno, procurar a melhor ferramenta para analisá-lo (Carsey e Harden, 2015CARSEY, T. M.; HARDEN, J. J. Can you repeat that please? Using Monte Carlo simulation in graduate quantitative research methods classes. Journal of Political Science Education, v. 11, n. 1, p. 94-107, 2015.). De forma semelhante, esse modo de analisar um fenômeno simplifica o entendimento dos modelos de hipóteses, já que permite entender como mínimas alterações no PGD alteram os resultados obtidos.
Passo 2 - Simulando amostras aleatórias
O segundo passo em uma SMC é a geração de um número suficientemente grande de amostras a partir do PGD definido no passo 1. Aqui, o objetivo é extrair um número de amostras aleatórias que nos permitam analisar os resultados agregados com precisão. Neste sentido, o número de amostras simuladas é o componente central dessa etapa: por um lado, se forem simuladas poucas amostras, teremos maiores dificuldades de distinguir o que é acerto do que é erro aleatório (poder estatístico); por outro lado, simular muitas amostras normalmente consome bastante tempo e recursos de processamento. Com os processadores que temos hoje e as facilidades de alguns softwares e linguagens de programação, este último aspecto normalmente não é um problema em simulações mais simples, que envolvem calcular alguma estatística básica, como a média; porém, quando se trata da estimação de modelos mais complexos, este é um aspecto que deve ser levado em consideração. Contudo, como regra geral, considera-se normalmente que algo entre 1.000 e 10.000 simulações seja suficiente para a maioria dos problemas - no exemplo utilizado na seção anterior, geramos 1.000 amostras de dez pessoas.
Passo 3 - Analisando os resultados
Nesta etapa, o objetivo é analisar as amostras geradas anteriormente de forma agregada. Enquanto examinamos o resultado de uma regressão multivariada por meio de uma série de estatísticas (coeficientes, p-valores, ajuste, resíduos) em uma simulação, normalmente estamos interessados em uma única estatística: ou a distribuição dos coeficientes de uma das variáveis em um modelo, ou a distribuição dos p-valores, ou a distribuição dos ajustes etc. Isto significa que, em geral, o foco das simulações está em saber como determinada estatística comporta-se quando é aplicada a uma amostra aleatória gerada a partir de um dado PGD. De todo modo, nada impede que seja analisada mais de uma estatística dos dados gerados, embora isto dependa, essencialmente, do objetivo a ser alcançado com a simulação.
No exemplo sobre a altura da população brasileira, estávamos interessados em saber se, na média, 1.000 amostras de dez pessoas seriam capazes de nos indicar a média real da altura da população como um todo. Conforme é possível verificar, algumas amostras apresentaram valores menores ou maiores do que o esperado - algo normal, dado que uma amostra com dez indivíduos é pequena em relação ao tamanho da população, e qualquer ocorrência de um valor extremo em relação ao parâmetro esperado afeta o resultado da estatística; ao ampliar o número de amostras, contudo, o valor médio obtido de todas elas se aproxima daquele estipulado de antemão, 170 cm.
O quadro 1 resume as etapas à formulação de uma SMC discutidas até aqui.
Programando SMC
Com todas essas etapas concluídas - definição do PGD, estipulação do número e da estatística examinada nas amostras -, é necessário programar a simulação. Até o início dos anos 1990, utilizar computadores nem sempre era a opção principal neste aspecto. Para fazer um dos estudos mais citados com uso de simulação nas Ciências Sociais até hoje, Schelling (1969SCHELLING, T. C. Models of segregation. The American Economic Review, v. 59, n. 2, p. 488-493, 1969.) utilizou apenas moedas para gerar suas amostras aleatórias. Hoje, a principal opção recomendada pelos livros-texto sobre simulações - incluídas as simulações baseadas em agentes - é a solução computacional por meio de linguagens de programação. Como o foco deste artigo está em mostrar o potencial didático de SMC, não nos deteremos na discussão sobre o melhor software ou linguagem de programação para este objetivo. Nossa opção neste artigo é pelo ambiente de programação R, que tem cada vez mais usuários na Ciência Política e é uma linguagem que apresenta uma série de vantagens para aplicação em análises estatísticas.
Assim como outras linguagens de programação, o R dispõe de funções de controle de fluxo e algumas funções nativas para gerar variáveis aleatórias que são indispensáveis em uma simulação. Entre as mais utilizadas, rnorm e rbinom podem ser empregadas para criar variáveis aleatórias contínuas com distribuição normal e binomial, respectivamente, e permitem ao usuário especificar algumas de suas propriedades, como média, desvio-padrão e probabilidade de ocorrência de um evento. Outra característica que torna vantajoso o uso do R para simulações é a vetorização, que permite realizar uma série de operações de forma mais rápida do que em outras linguagens de programação. Estas e outras características do R, bem como uma introdução à linguagem e ao ambiente de programação (em português), são apresentadas detalhadamente em Aquino (2014AQUINO, J. A. R para cientistas sociais. Ilhéus: Editus, 2014.).
Como avaliar se uma simulação é bem-sucedida?
Tratando do método de modo mais amplo, Axelrod (1997AXELROD, R. Advancing the art of simulation in the social sciences. In: CONTE, R.; HEGSELMANN, R.; TERNA, P. (Eds.). Simulating social phenomena. Heidelberg: Springer, 1997.) sugere três critérios para avaliarmos uma simulação: 1) validade; 2) usabilidade; e 3) extensibilidade. O primeiro aspecto diz respeito ao que podemos entender como validade interna da simulação: ela realmente dá conta de simular o fenômeno ou amostras de interesse? Ou, de outro modo, algum erro não detectado na construção do modelo (ou erro de implementação) influíram nos resultados obtidos? Caso algum procedimento técnico na programação de uma simulação contenha erros, estes possivelmente gerarão problemas de validade.
O segundo aspecto é a usabilidade da simulação. Quando construímos um modelo, ele deve ser compreensível, fácil de ser reproduzido e adaptado por outros usuários. Inclusive, parte do uso de simulações como recurso didático passa pela replicação de alguns modelos mais simples, para que, posteriormente, sejam adaptados ou reformulados pelos usuários. Portanto, na medida em que não é clara a implementação de uma simulação, ela traz prejuízos à usabilidade. Por fim, o terceiro item a ser avaliado é a extensibilidade, que diz respeito à capacidade de generalização e adaptação da simulação para aplicações em outras questões ou atividades.
Exemplos de SMC
Nesta seção, ilustramos o potencial das SMC como recurso didático no ensino de Ciência Política, por meio de dois exemplos. O primeiro é mais substantivo, tratando de como alterações em procedimentos legislativos e nas preferências dos legisladores podem afetar drasticamente a quantidade de proposições que um congresso é capaz de aprovar. O segundo exemplo, de caráter metodológico, ilustra como violações dos pressupostos de uma regressão linear por mínimos quadrados podem enviesar as estimativas obtidas por meio dele. A ideia geral é mostrar que simulações podem ser usadas para ensinar conteúdos abstratos e complexos de forma fácil e intuitiva. Ou seja, em vez de passar aos alunos um guia de ferramentas estatísticas com recomendações sobre seus usos, ou um livro-texto repleto de definições conceituais, por meio de simulações, é possível perceber como pequenas mudanças institucionais podem produzir enormes efeitos agregados (primeiro exemplo), bem como visualizar as consequências práticas do uso inadequado de determinada técnica (segundo exemplo).
Simulando um processo legislativo simples
Embora pareça algo não problemático à primeira vista, aprovar uma lei em um congresso moderno, como os existentes em países democráticos, é um processo complexo (Cox, 2000COX, G. W. On the effects of legislative rules. Legislative Studies Quarterly, v. 25, n. 2, p. 169-192, 2000.). Em primeiro lugar, porque normalmente existem diversas proposições aguardando para serem apreciadas - o que, já de saída, implica decidir coletivamente quando cada uma delas será votada. Em segundo lugar, porque os temas de cada votação devem ser discutidos pelos legisladores (ao menos em congressos minimamente democráticos), momento reservado para que se produza informação sobre suas consequências e discussões sobre seus potenciais benefícios, o que toma tempo. Por último, estas proposições são finalmente votadas; e, aqui também, a questão da maioria utilizada para aprová-la necessariamente pode influenciar o resultado final de cada votação.
Todos esses problemas coordenativos fazem parte do conhecimento comum na Ciência Política sobre como congressos funcionam e sobre como determinadas regras e instituições ajudam na superação deles. Em aulas de introdução ao tema, contudo, a discussão sobre esses pontos pode acabar não sendo tão clara, já que questões como preferências, funções de utilidade e efeitos das regras normalmente são abstratas o suficiente para produzir dúvidas em alguns alunos. Uma forma de contornar isto é utilizar o SMC para simular um processo legislativo, com um determinado número de legisladores e de proposições que são votadas por meio de diferentes regras. No caso, o exemplo que se segue trata apenas deste último aspecto, mas é fácil generalizá-lo para abarcar outros.
O primeiro passo aqui é criar nosso PGD a fim de simular um plenário. Conforme dito anteriormente, o que é necessário para isto é estipular quais variáveis entrarão na simulação e como elas serão distribuídas. Para esse exemplo, nossa unidade natural é o legislador, que, de forma simplificada, tem duas opções: votar sim ou não. Podemos definir um conjunto de legisladores (unidades) indexados por i que votam j proposições de forma binária (1 para sim, 0 para não). Deste modo, nossa variável de interesse assume uma distribuição binomial, e estabelecemos que a probabilidade de um legislador qualquer votar sim é 0.5.6 6 Para um exemplo de simulação de processo legislativo em que os legisladores votam como se fosse um lançamento de moeda (probabilidade de votar sim igual a 0.5), ver Saiegh (2009).
Para exemplificar como as maiorias requeridas para aprovação afetam a probabilidade de que uma proposição legislativa qualquer seja aceita, realizamos duas simulações: na primeira, empregamos o critério de unanimidade, segundo o qual só são aprovadas proposições endossadas por todos os legisladores no plenário; na segunda, utilizamos o critério de maioria simples, isto é, pelo qual 50% + 1 dos legisladores são suficientes para aprovar uma proposição. Em cada caso, 1.000 proposições são votadas por cinco legisladores. Abaixo, segue um resumo da simulação, de acordo com os passos discutidos anteriormente:
-
PGD: cinco legisladores votam proposições de forma binária (sim ou não) com probabilidade de votar sim igual a 0.5;
-
Número de simulações: 1.000 (para cada regra de maioria);
-
Estatística de interesse: proporção de proposições aprovadas em cada regra de maioria (unanimidade ou maioria simples).
Os resultados desse exercício seguem no gráfico 2. De forma resumida, o efeito da regra de aprovação utilizada em um plenário em que os deputados decidem seus votos de forma aleatória é enorme: enquanto com regra majoritária quase metade das proposições votadas são aprovadas, em um legislativo que adota regra de unanimidade apenas uma ínfima parcela das proposições o são. Intuitivamente este resultado faz sentido, já que todos os legisladores individualmente possuem poder de veto, o que reduz drasticamente o espaço possível de mudanças no status quo (Tsebelis, 2002TSEBELIS, G. Veto players: how political institutions work. Princeton: Princeton University Press , 2002.).
Simulação de um processo legislativo com diferentes regras de maioria (1.000 votações com cinco legisladores)
Embora esses resultados sejam extremos, como parte da aplicação é possível utilizar outras regras de maioria, proposições, legisladores e, inclusive, alterar as preferências destes legisladores, o que definiria de antemão a probabilidade de votarem de um modo ou de outro. Com as mesmas ferramentas, portanto, diversos aspectos de um processo legislativo podem ser explorados. Na sequência, ilustramos uma dessas variações do exemplo anterior: alterar a forma com que os legisladores votam, isto é, suas preferências.
Para essa simulação, adaptamos o modelo anterior em alguns pontos. Em primeiro lugar, mantendo a regra de maioria simples, incorporamos mais cinco legisladores à simulação, totalizando dez deles; além disso, distribuímos estes legisladores em dois grupos (isto é, partidos), cinco para cada. Em segundo lugar, alteramos a forma com que os legisladores de um mesmo partido votam: legisladores de um partido (o partido A, digamos) geralmente votam favoravelmente às proposições; legisladores do outro partido (o partido B, digamos), ao contrário, têm preferências geralmente contrárias às do partido A. Para complementar a simulação, também incorporamos variações na polarização destas preferências: em um caso, membros do partido A têm probabilidade 0.6 de votar favoravelmente qualquer matéria, enquanto os membros do partido B têm 0.4, o que dá uma diferença de preferências de 0.2; assim, variaremos essas distâncias de 0 (os dois partidos tendem a votar de igual maneira) até 1 (os dois partidos votam de forma diametralmente oposta).
O resumo dessa simulação consta a seguir. Note, também, que, com um número par de legisladores, uma proposição só é aprovada se ao menos metade mais um formar uma maioria - no caso de dois partidos com o mesmo número de legisladores, isto pode significar que ao menos um deles precisa desertar, ou seja, votar de forma contrária à preferência da maioria do seu partido.
-
PGD: dez legisladores, cinco em cada partido, votam proposições de forma binária (sim ou não), e a probabilidade de que qualquer um destes vote sim é diferente em cada partido (a distância desta probabilidade entre partidos será manipulada de 0, quando os partidos têm a mesma preferência, até 1);
-
Número de simulações: 10.000 (para cada intervalo na distância de preferências entre os partidos);
-
Estatística de interesse: proporção de proposições aprovadas.
Simulação de um processo legislativo com regra de maioria simples e diferentes graus de polarização entre dois partidos
Como dá para perceber a partir da visualização do gráfico 3, na maioria dos casos o grau de polarização entre dois partidos não chega a afetar a probabilidade de uma dada proposição ser aprovada em uma votação por maioria. Mas, a partir do ponto em que esta polarização atinge patamares extremos (quando ela é maior que 0.8 em uma escala de 0 a 1), a produtividade do legislativo cai subitamente. Ao menos para fins ilustrativos, isto mostra que nem sempre polarização ideológica é um problema em um processo legislativo: frequentemente, existe algum grau de manobra para que se aprove uma matéria. No caso do exemplo, em um congresso exatamente dividido entre dois partidos, inteiramente autônomo e ditado apenas pela ideologia dos seus membros, só um caso extremo de polarização provocaria uma paralisia decisória total. Nos demais cenários, ao menos algumas proposições sempre seriam aprovadas.
Simulando regressões lineares com variáveis omitidas
Em nosso segundo exemplo, ilustramos como uma violação bastante comum no uso de modelos de regressão pode enviesar as estimativas obtidas por meio dele: o problema da variável omitida. Conforme alertam os manuais de metodologia (Angrist e Pischke, 2008ANGRIST, J. D.; PISCHKE, J. Mostly harmless econometrics: an empiricist's companion. Princeton: Princeton University Press, 2008.), omitir uma variável correlacionada com o termo de erro gera diferentes graus de viés nos coeficientes de uma ou mais variáveis incluídas, embora a magnitude e o sentido deste viés normalmente não possam ser detectados de antemão. O problema com essa definição é a dificuldade de explicar a razão disto aos alunos. Variações da explicação, como dizer que outras variáveis absorvem o impacto da variável omitida ou derivar a prova formal de que a omissão tem potencial de enviesamento, nem sempre são particularmente úteis e facilmente assimiláveis. Como o foco de curso de Ciências Sociais e afins normalmente não está no treinamento formal requerido para compreender métodos quantitativos, SMC permitem-nos ilustrar, na prática e de forma gráfica, o que acontece quando um ou mais pressupostos da regressão são violados, contornado dificuldades de compreensão.
Para esse exemplo, aproveitamo-nos de um tipo muito simples de omissão de variável de um modelo linear, a fim de mostrar claramente esse efeito. Basicamente, o procedimento consiste em simular duas variáveis com algum grau de correlação entre elas, com o objetivo de gerar uma terceira variável, que servirá como variável dependente do modelo a ser estimado. Como as duas variáveis foram usadas para criar a dependente, necessariamente (de acordo com os pressupostos do modelo) servirão para explicar a variação desta. Contudo, ao omitirmos uma delas, as estimativas que obtivermos serão enviesadas.
O PGD nesse exemplo consiste no seguinte. Primeiro, criamos duas variáveis contínuas, X e Z, com distribuição normal e N = 100. Por definição, criamos estas duas variáveis com correlação de Pearson de 0.5. A partir destas duas variáveis, criamos uma variável dependente (Y) também contínua, segundo o modelo:
onde β 0 representa o intercepto do modelo (o valor que Y i deve ter quando X i e Z i são iguais a 0), que definimos como igual a 1; β 1 e β 2 também foram estabelecidos como 1; e ε i é um termo de erro com distribuição normal, média 0 e desvio-padrão de 1. Cada uma das simulações neste exercício, portanto, criará aleatoriamente três variáveis que, em conjunto, serão utilizadas para determinar o valor de Y i . Nosso objetivo aqui, deste modo, é estimar um modelo linear para cada uma destas simulações apenas com a variável X como variável independente, isto é, omitindo Z. Neste exemplo, rodamos 1.000 simulações. O desenho desta simulação segue abaixo:
-
PGD: três variáveis contínuas com distribuição normal, média 0 e desvio-padrão de 1; X i e Z i têm correlação de 0.5 entre elas; uma quarta variável é criada a partir das outras Y i , e é igual a 1 + 1 * X i + 1 * Z i + ε i ;
-
Simulações: 1.000;
-
Estatística de interesse: o coeficiente estimado da variável X quando Z é omitida.
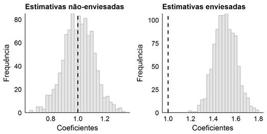
Os resultados desse segundo exercício seguem no gráfico 4. Como é possível observar, nas regressões estimadas que não incluíram a variável Z, a estimativa média do coeficiente de X obtida ficou longe do valor estipulado para β 1 de 1. Ao contrário, incluindo Z na especificação do modelo, o coeficiente aproxima-se, na média, do valor definido. Além disso, este exemplo fornece outra pista aos alunos sobre a direção e a magnitude do viés de variável omitida: tendo definido a correlação entre X e Z de 0,5, a estimativa média do efeito de X sobre Y quando omitimos Z foi 0.5 maior do que o esperado. A repetição da simulação com correlação entre X e Z de -0.5 e 0.3, como fizemos no gráfico 5, mostra que, também nestes casos, a correlação entre o termo omitido e o incluído tem impacto direto nas estimativas que obtemos ao estimar modelos lineares. Em resumo, o viés será de magnitude igual à correlação entre a variável omitida e a incluída.
Simulação de viés de variável omitida com diferentes níveis de correlação (1.000 regressões)
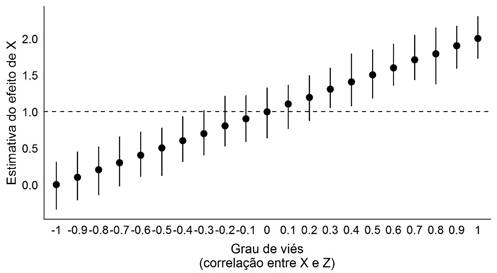
Para ilustrar melhor esse ponto, podemos ir além e simular todos os graus possíveis de correção entre X e Z, o que vai de -1 a 1. O gráfico 6 realiza este exercício. Nele, cada ponto com linhas representa uma simulação de 1.000 regressões lineares com o termo Z, que é endógeno a X, omitido do modelo; a linha horizontal tracejada, por sua vez, representa o valor real de X, que é enviesado de acordo com o grau de correlação entre X e Z, conforme indicado no eixo X do gráfico. Novamente, fica claro que o grau de viés do estimador de X depende da correlação entre ele e Z: quando a correlação entre eles é negativa (lado esquerdo do gráfico), o modelo subestima o efeito de X; entretanto, quando a correlação entre o termo omitido e o incluído é positiva, o efeito é superestimado. Apenas no caso em que não existe correlação entre X e Z, no meio do eixo X, é que o efeito retornado não sofre de viés.
Simulação de viés de variável omitida com diferentes níveis de correlação (1.000 regressões para cada)
De forma geral, esse exercício de simulação exemplifica, de forma gráfica, sem muitos detalhes, o efeito prático que a violação de um pressuposto de um modelo linear pode ter. Assim como no exemplo anterior, esta simulação também pode ser facilmente adaptada para examinar outras questões, como a inclusão de outras variáveis, uso de outros modelos e teste de outros pressupostos.
Outros exemplos da pesquisa em Ciência Política
Embora nosso foco aqui recaia sobre o ensino de Ciência Política, aplicações derivadas de SMC vêm crescendo na pesquisa em Ciência Política (Carroll et al., 2009CARROLL, R. et al. Measuring bias and uncertainty in DW-NOMINATE ideal point estimates via the parametric bootstrap.Political Analysis, v. 17, n. 3, p. 261-275, 2009.; Carter e Signorino, 2010CARTER, D. B.; SIGNORINO, C. S. Back to the future: modeling time dependence in binary data.Political Analysis , v. 18, n. 3, p. 271-292, 2010.; King et al., 2001KING, G. et al. Analyzing incomplete political science data: an alternative algorithm for multiple imputation. American Political Science Review, v. 95, n. 1, p. 49-69, 2001.; Keele e Kelly, 2006KEELE, L.; KELLY, N. J. Dynamic models for dynamic theories: the ins and outs of lagged dependent variables.Political Analysis , v. 14, n. 2, p. 186-205, 2006.; Martin e Quinn, 2002; Jackman, 2000JACKMAN, S. Estimation and inference via Bayesian simulation: an introduction to Markov chain Monte Carlo.American Journal of Political Science, v. 44, n. 2, p. 375-404, 2000.). Diferentemente dos exemplos que mostramos anteriormente, nestes casos geralmente utiliza-se simulação com objetivos mais concretos, tais como: testar a sensibilidade da especificação de um modelo (Carter e Signorino, 2010; Martin e Quinn, 2002; Quinn, 2004), estimar intervalos de confiança (Carroll et al., 2009), lidar com observações extremas, missings e outliers (King et al., 2001), realizar testes não paramétricos (Groseclose, 1994GROSECLOSE, T. Testing committee composition hypotheses for the US Congress.The Journal of Politics, v. 56, n. 2, p. 440-458, 1994.), entre outros. Por serem fáceis de serem operacionalizadas, estas aplicações podem ser empregadas complementarmente com finalidades didáticas, incentivando os alunos a replicarem, ou a desenvolverem, simulações para situações concretas de pesquisa.
O uso mais frequente do método envolve utilizar SMC para obter noção da incerteza de uma estimativa. Alguns testes ou modelos quantitativos frequentemente impossibilitam o cálculo paramétrico de intervalos de confiança, tipicamente em desenhos de pesquisa multiníveis ou hierárquicos, em que existem observações aninhadas em diferentes estratos ou grupos - seja pelo tamanho reduzido do N dentro dos grupos, seja pela relação hierarquizada das observações, ou, ainda, por causa de inadequação dos pressupostos necessários para estimar um dado modelo. Nestes casos, uma adaptação da lógica de SMC ajuda a corrigir esse problema. Basicamente, a solução para isto consiste em criar diversas subamostras da amostra original, de acordo com alguns parâmetros pré-especificados - geralmente, número e tamanho das amostras -, o que denominamos de bootstrap (Carroll et al., 2009CARROLL, R. et al. Measuring bias and uncertainty in DW-NOMINATE ideal point estimates via the parametric bootstrap.Political Analysis, v. 17, n. 3, p. 261-275, 2009.; Freedman, 2009FREEDMAN, D. A. Statistical models: theory and practice. Cambridge: Cambridge University Press, 2009.).
Para mencionar um exemplo mais conhecido, Stokes et al. (2013STOKES, S. C. et al. Brokers, voters, and clientelism: the puzzle of distributive politics. Cambridge: Cambridge University Press , 2013.) utilizam essa estratégia para estudar o clientelismo na Argentina a partir de dados de survey. Especificamente, os autores aplicaram um questionário em uma amostra representativa de políticos locais, estratificados em algumas regiões, para saber deles suas estratégias distributivas de campanha - entre outros, se eles distribuíam ou não incentivos seletivos aos seus eleitores, quais eleitores eles visavam, como monitoravam o voto deles. Em um segundo momento, foi criada uma amostra adicional de cabos eleitorais (punteros) indicados pelos próprios entrevistados. Como as respostas dadas por estes últimos tendem a ser correlacionadas com as dos políticos locais, simplesmente calcular intervalos de confiança como se esta fosse uma amostra simples ou estratificada poderia subestimar a incerteza das estimativas (Stokes et al., 2013, p. 261-278).
Para contornar isto, Stokes et al. (2013STOKES, S. C. et al. Brokers, voters, and clientelism: the puzzle of distributive politics. Cambridge: Cambridge University Press , 2013.) implementam um método não paramétrico de cálculo do intervalo de confiança que guarda semelhança com um SMC - o bootstrap (Freedman, 2009FREEDMAN, D. A. Statistical models: theory and practice. Cambridge: Cambridge University Press, 2009.). Primeiro, foram sorteados N municípios (metade de todos os presentes na base) entre as regiões para compor um primeiro nível amostral; segundo, partindo desta amostra de municípios, alguns políticos locais foram sorteados dentro de cada município incluído na amostra; por fim, alguns cabos eleitorais dentro de cada cluster de políticos foram sorteados. No geral, portanto, cada amostra utilizada no bootstrap possui três estratos, ou clusters, e os elementos nos níveis menores só são incluídos na amostra se o estrato ao qual eles pertencem for sorteado em uma etapa prévia da composição da amostra. Repetindo este procedimento 1.000 vezes, as estimativas de incerteza de cada estatística de interesse foram calculadas - livres de qualquer pressuposto.
Exemplos como esse não se encaixam em um tipo clássico de SMC, já que não existe um PGD - afinal, os dados empregados, em todos os casos, são observacionais. Ainda assim, por fazer uso de repetidos sorteios de uma amostra, com número de observações e de simulações estipulados previamente, e da análise agregada dos resultados (no caso, a distribuição das estimativas em cada amostra sorteada), o processo não paramétrico de cálculo de intervalo de confiança, bem como o uso de simulações para testar a sensibilidade de um modelo ou método, partilham alguns princípios em comum com uma SMC. E, uma vez mais, técnicas como estas podem ser mais facilmente ensinadas e aplicadas quando partimos de uma simulação em um formato mais tradicional como base.
Código usado nos exemplos
Os exemplos que oferecemos neste artigo são apenas algumas das possíveis aplicações de SMC no ensino de Ciência Política. De qualquer forma, eles podem servir como modelos mais gerais para a criação de outras aplicações. No exemplo do processo legislativo, por exemplo, outros tipos de regra de maioria podem ser utilizados para analisar seus efeitos sobre a produção legislativa, e, de forma semelhante, não é difícil adaptar esse exemplo para o funcionamento de comissões legislativas, em que um grupo menor de legisladores vota uma proposição antes de ela ir à votação no plenário. Já no exemplo sobre variável omitida, nada impede que se testem outros pressupostos de uma regressão linear, bem como de outros tipos de modelos.
Para facilitar a adoção de simulações como essas, o código para replicar nossos exemplos está disponível na internet, e pode ser adaptado para abarcar outras aplicações.7 7 O website da aplicação virtual (Shiny app) contém os exemplos usados neste artigo, todos implementados de forma dinâmica, e estão disponíveis em: <http://denissonsilva.com/simulacao>. Além disso, também disponibilizamos um aplicativo virtual que já implementa todos os exemplos discutidos de forma simples e intuitiva: para usá-los, basta um navegador e conexão com a internet.
Conclusão
Neste artigo, procuramos mostrar como a SMC pode ser usada em aulas de Ciência Política. Conforme os exemplos oferecidos procuraram mostrar, simulações tornam palpáveis conteúdos abstratos, permitindo aos alunos visualizar graficamente fenômenos complexos, a exemplo do funcionamento de um processo legislativo. Além disso, os alunos conseguem adquirir intuição sobre como funcionam modelos estatísticos e melhor compreensão sobre processos geradores de dados, conforme o exemplo sobre variáveis omitidas procurou mostrar. Nesse espaço final, também cabe discutir, além de algumas vantagens das simulações não abordadas anteriormente, dificuldades inerentes ao uso da técnica e do teste de técnicas didáticas na área de ensino de Ciência Política, de forma mais ampla.
Algo que merece destaque aqui é que não procuramos testar empiricamente os efeitos sobre o aprendizado do uso de simulações no ensino de Ciência Política. Na verdade, nosso esforço principal foi introduzir o uso de simulações como recurso didático para, então, discutir os detalhes técnicos de como implementá-las em salas de aula. Neste sentido, procuramos aumentar o repertório de técnicas de ensino na disciplina, chamando a atenção para algumas vantagens inerentes ao método: conforme discutimos, ele é visual, intuitivo, permite a participação ativa dos alunos e é totalmente adaptável. De qualquer forma, reconhecemos que este é apenas um primeiro passo em uma agenda de pesquisa sobre a eficácia de métodos e técnicas de ensino em Ciência Política no país - mas, para ela avançar, também é preciso lidar com diversas questões ainda pouco abordadas na literatura.
Uma delas é a carência de estudos na área. Diferentemente da tradição de outras disciplinas, como exemplificado na introdução, possuímos raríssimos trabalhos de sistematização de diferentes técnicas de ensino, bem como trabalhos que as testem empiricamente;8 8 O trabalho de Barberia, Godoy e Barboza (2014a), já mencionado, constitui exceção. isto, claro, reflete em parte a pouca atenção que a área, como um todo, dedicava até pouco tempo ao ensino de métodos. Neste sentido, carecemos de um corpo suficientemente robusto de técnicas e modelos de ensino que nos permitam estudá-los comparativamente.
Contudo, apenas importar resultados empíricos dos efeitos de técnicas de ensino da literatura internacional pode não ser a solução para esse problema. Alunos de Ciência Política no Brasil possuem formações na graduação diferentes daquelas obtidas no exterior, geralmente com menor ênfase em matemática, estatística e programação; e com maior ênfase em filosofia e epistemologia. Isto implica que ferramentas que funcionam em outros contextos podem não funcionar aqui. Tanto pela nossa experiência usando simulações em sala de aula quanto pela experiência de outros pesquisadores (Carsey e Harden, 2015CARSEY, T. M.; HARDEN, J. J. Can you repeat that please? Using Monte Carlo simulation in graduate quantitative research methods classes. Journal of Political Science Education, v. 11, n. 1, p. 94-107, 2015.), consideramos que as SMC têm potencial de contornar o geralmente baixo grau de familiaridade de alunos das Ciências Sociais com formulações matemáticas e métodos quantitativos.
Realizar experimentos em sala de aula, em formatos semelhantes ao de experimentos de laboratório comuns na Ciência Política internacional (Carsey e Harden, 2015CARSEY, T. M.; HARDEN, J. J. Can you repeat that please? Using Monte Carlo simulation in graduate quantitative research methods classes. Journal of Political Science Education, v. 11, n. 1, p. 94-107, 2015.), também não é algo tão simples, tanto logística quanto eticamente, no Brasil. Os efeitos do tratamento (isto é, aplicar ou não uma determinada técnica de ensino em um grupo de alunos e não em outros) podem ter efeitos duradouros sobre suas trajetórias - efeitos frequentemente não antecipáveis. Turmas de graduação e pós-graduação, por sua vez, possuem poucos indivíduos, grades curriculares e composição diferentes umas das outras: é fácil perceber que alunos egressos de cursos de graduação em Ciência Política ou Políticas Públicas possuem treinamento diferente daquele recebido por alunos de Ciências Sociais ou Relações Internacionais, para ficar apenas com um exemplo. Tudo isto, em suma, dificulta o teste empírico de técnicas de ensino e a generalização dos seus resultados, e não podemos ignorar esses problemas se quisermos avançar nessa discussão.
Não queremos sugerir com isso simplesmente um abandono da avaliação de técnicas de ensino na Ciência Política, nem da área de ensino, apenas chamar a atenção para a existência de diversas questões não discutidas suficientemente sobre o tema. Deste ponto de vista, acreditamos serem válidos os esforços de desenvolvimento e adaptação de técnicas, de discussão sobre o funcionamento delas, e, por fim, o estudo comparado dos resultados de cada um, em um esforço para avaliar seus desempenhos. No nosso caso, retomando o que expusemos ao longo do texto, SMC enquadram-se nesse cenário como uma ferramenta de ensino adicional, com características potencialmente positivas para complementar, ou mesmo substituir, aulas expositivas tradicionais.
O uso de SMC em sala de aula pode ser entendido como um esforço para tornar o aprendizado mais dinâmico. Neste sentido, essas simulações guardam semelhanças com outros tipos de simulações, como jogos em sala de aula, que vêm sendo cada vez mais adotadas na Ciência Política (Frederking, 2005FREDERKING, B. Simulations and student learning. Journal of Political Science Education , v. 1, n. 3, p. 385-393, 2005.). Exemplos destas vão desde jogos para simular transições democráticas, em que são atribuídos papéis aos alunos em uma negociação hipotética, até simulações de processos eleitorais. Porém, enquanto que, de forma geral, estas simulações ativas têm o potencial de engajar alunos ativamente no aprendizado, normalmente ocupam muito tempo e demandam um planejamento de aula bastante detalhado. Neste ponto, SMC representam um meio-termo entre uma aula tradicional expositiva e estas com simulações ativas, ou seja, ao mesmo tempo em que utilizam a ideia de criar um mundo fictício totalmente manipulável, SMC podem ser visualizadas graficamente, reproduzidas e adaptadas facilmente (especialmente quando programadas em linguagens como R ou Python).
Outra vantagem de SMC é que elas podem ser usadas em aulas de metodologia, em que a simples exposição do conteúdo, desprovida de exemplos, normalmente é pouco eficaz e extremamente exaustiva. Em vez de fazer um inventário de situações nas quais cada técnica estatística discutida deve ser aplicada, o uso de SMC põe o foco em desenvolver uma percepção visual sobre como cada uma destas técnicas funciona e sob quais pressupostos. Exercícios complementares, também baseados em simulações, podem então ser desenvolvidos e aplicados em sala de aula, permitindo aos alunos explorar outros exemplos e refazer cada simulação inúmeras vezes.
Como esperamos ter ficado claro a partir do que foi exposto, nosso objetivo principal foi incentivar o uso de novos métodos didáticos, e também sua aplicação na pesquisa. No mínimo, acreditamos que docentes podem complementar suas aulas com simulações; no limite, a depender de seus resultados, decidir dar maior ou menor espaço a ela. Chegando a este ponto, em que tenhamos experiências semelhantes em mais lugares e em diferentes momentos, será possível empreender uma avaliação mais detida da técnica - tanto do ponto de vista docente quanto dos discentes. Esperamos, enfim, que esse esforço ganhe terreno na Ciência Política e nas Ciências Sociais, de forma geral, para que, no futuro, seja possível analisar o impacto desta - e o de outras técnicas de aprendizagem de forma comparada.
Referências
- ANGRIST, J. D.; PISCHKE, J. Mostly harmless econometrics: an empiricist's companion Princeton: Princeton University Press, 2008.
- AQUINO, J. A. R para cientistas sociais Ilhéus: Editus, 2014.
- AXELROD, R. Advancing the art of simulation in the social sciences. In: CONTE, R.; HEGSELMANN, R.; TERNA, P. (Eds.). Simulating social phenomena Heidelberg: Springer, 1997.
- BARBERIA, L. G.; GODOY, S. R.; BARBOZA, D. P. Novas perspectivas sobre o ‘calcanhar metodológico’: o ensino de métodos de pesquisa em Ciência Política no Brasil.Revista Teoria & Sociedade, v. 22, n. 2, p. 156-184, 2014a.
- ______; ______; ______. Inovação no ensino de métodos quantitativos em Ciência Política: aplicação de modelo baseado em atividades.Agenda Política, v. 2, n. 2, p. 152-179, 2014b.
- CARROLL, R. et al Measuring bias and uncertainty in DW-NOMINATE ideal point estimates via the parametric bootstrap.Political Analysis, v. 17, n. 3, p. 261-275, 2009.
- CARTER, D. B.; SIGNORINO, C. S. Back to the future: modeling time dependence in binary data.Political Analysis , v. 18, n. 3, p. 271-292, 2010.
- CARSEY, T. M.; HARDEN, J. J. Can you repeat that please? Using Monte Carlo simulation in graduate quantitative research methods classes. Journal of Political Science Education, v. 11, n. 1, p. 94-107, 2015.
- COX, G. W. On the effects of legislative rules. Legislative Studies Quarterly, v. 25, n. 2, p. 169-192, 2000.
- DONATELLI, G. D.; KONRATH, A. C. Simulação de Monte Carlo na avaliação de incertezas de medição. Revista de Ciência &Tecnologia, v. 13, n. 25/26, p. 5-15, 2005.
- DIONISIO, G.; SPALDING, L. E. S. Método computacional de Monte Carlo adaptado como recurso didático para o estudo dos mecanismos de transferência de calor. In: SIMPÓSIO NACIONAL DE ENSINO DE CIÊNCIA E TECNOLOGIA, 4., 2014, Ponta Grossa. Disponível em: <Disponível em: http://sinect.com.br/anais2014/anais2014/artigos/ensino-de-fisica/01408122365.pdf >. Acesso em: 14 jun. 2016.
» http://sinect.com.br/anais2014/anais2014/artigos/ensino-de-fisica/01408122365.pdf - FIGUEIREDO FILHO, D. B. et al When is statistical significance not significant?Brazilian Political Science Review, v. 7, n. 1, p. 31-55, 2013.
- FIGUEIREDO FILHO, D. B.; SILVA JR., J. A. Visão além do alcance: uma introdução à análise fatorial.Opinião Pública, v. 16, n. 1, p. 160-185, 2010.
- FIGUEIREDO FILHO, D. B.; SILVA JR., J. A.; ROCHA, E. C. Classificando regimes políticos utilizando análise de conglomerados.Opinião Pública , v. 18, n. 1, p. 109-128, 2012.
- FREDERKING, B. Simulations and student learning. Journal of Political Science Education , v. 1, n. 3, p. 385-393, 2005.
- FREEDMAN, D. A. Statistical models: theory and practice Cambridge: Cambridge University Press, 2009.
- GRINSTEAD, C.; SNELL, J. Introduction to probability Rhode Island: American Mathematical Society, 2012.
- GROSECLOSE, T. Testing committee composition hypotheses for the US Congress.The Journal of Politics, v. 56, n. 2, p. 440-458, 1994.
- JACKMAN, S. Estimation and inference via Bayesian simulation: an introduction to Markov chain Monte Carlo.American Journal of Political Science, v. 44, n. 2, p. 375-404, 2000.
- KEELE, L.; KELLY, N. J. Dynamic models for dynamic theories: the ins and outs of lagged dependent variables.Political Analysis , v. 14, n. 2, p. 186-205, 2006.
- KING, G. et al Analyzing incomplete political science data: an alternative algorithm for multiple imputation. American Political Science Review, v. 95, n. 1, p. 49-69, 2001.
- MARTIN, A. D.; QUINN, K. M. Dynamic ideal point estimation via Markov chain Monte Carlo for the US Supreme Court, 1953-1999.Political Analysis , v. 10, n. 2, p. 134-153, 2000.
- MOLINA, C. E. C.; MARINS, F. A. S.; MONTEVECHI, J. A. B. Proposta de utilização da simulação a eventos discretos no ensino da engenharia de produção. Revista P&D em Engenharia de Produção, v. 8, n. 1, p. 11-15, 2010.
- MOONEY, C. Z. Monte Carlo simulation Thousand Oaks: Sage Publications, 1997.
- PRADO, D. Teoria das filas e da simulação 2. ed. Belo Horizonte: Editora de Desenvolvimento Gerencial, 1999.
- QUINN, K. M. Bayesian factor analysis for mixed ordinal and continuous responses. Political Analysis , v. 12, n. 4, p. 338-353, 2004.
- SAIEGH, S. M. Political prowess or “Lady Luck”? Evaluating chief executives’ legislative success rates. The Journal of Politics , v. 71, n. 4, p. 1342-1356, 2009.
- SCHELLING, T. C. Models of segregation. The American Economic Review, v. 59, n. 2, p. 488-493, 1969.
- SILVA, G. P.; GUARNIERI, F. H. Comments on when is statistical significance not significant?Brazilian Political Science Review , v. 8, n. 2, p. 133-136, 2014.
- SOARES, G. A. D. O calcanhar metodológico da Ciência Política no Brasil.Sociologia, Problemas e Práticas, n. 48, p. 27-52, 2005.
- STOKES, S. C. et al Brokers, voters, and clientelism: the puzzle of distributive politics Cambridge: Cambridge University Press , 2013.
- TSEBELIS, G. Veto players: how political institutions work Princeton: Princeton University Press , 2002.
- WINNISCHOFER, H. et al Simulação Monte Carlo no ensino de luminescência e cinética de decaimento de estados excitados. Química Nova, v. 33, n. 1, p. 225-228, 2010.
-
1
Uma versão preliminar deste artigo beneficiou-se de valiosas sugestões de Dawisson Belém Lopes e demais participantes do Grupo de Trabalho (GT) de Ensino e Pesquisa do X Encontro da Associação Brasileira de Ciência Política (ABCP), em Belo Horizonte. Agradecemos também aos pareceristas anônimos da Revista Brasileira de Ciência Política pelas críticas e sugestões, que contribuíram para melhorar substantivamente esta versão final. O código para replicação dos resultados reportados pode ser encontrado em: <https://github.com/meirelesff/monte_carlo_rbcp>. Versões interativas virtuais com os exemplos usados também pode ser encontrada em: <http://denissonsilva.com/simulacao>.
-
2
Exceções, que tratam do ensino de métodos para a Ciência Política, podem ser encontrados em Barberia, Godoy e Barboza (2014b), Figueiredo Filho e Silva Jr. (2010), Figueiredo Filho, Silva Jr. e Rocha (2012), Figueiredo Filho et al. (2013) e Silva e Guarnieri (2014). Para um panorama recente sobre o ensino de métodos, ver Barberia, Godoy e Barboza (2014a).
-
3
O R é um ambiente de programação estatístico, e pode ser baixado de forma gratuita pela internet.
-
4
Agradecemos a um dos pareceristas anônimos pela sugestão de melhor elaborar esses pontos.
-
5
Na verdade, tanto Carsey e Harden (2015) quanto Mooney (1997) reportam cinco itens, mas dois deles podem ser condensados sem perda de generalidade.
-
6
Para um exemplo de simulação de processo legislativo em que os legisladores votam como se fosse um lançamento de moeda (probabilidade de votar sim igual a 0.5), ver Saiegh (2009).
-
7
O website da aplicação virtual (Shiny app) contém os exemplos usados neste artigo, todos implementados de forma dinâmica, e estão disponíveis em: <http://denissonsilva.com/simulacao>.
-
8
O trabalho de Barberia, Godoy e Barboza (2014a), já mencionado, constitui exceção.
Datas de Publicação
-
Publicação nesta coleção
Dez 2017
Histórico
-
Recebido
13 Abr 2017 -
Aceito
30 Maio 2017








 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Elaboração própria.
Elaboração própria.
 Elaboração própria.
Elaboração própria.
 Elaboração própria.
Elaboração própria.
 Elaboração própria.
Elaboração própria.
 Elaboração própria.
Elaboração própria.
 Elaboração própria.
Elaboração própria.
