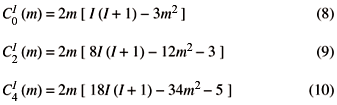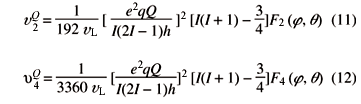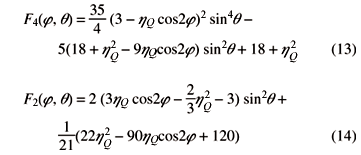Multiple - quantum magic - angle spinning NMR: a new technique for probing quadrupolar nuclei in solids

Abstracts

We have recently described a new technique capable of recording high resolution NMR spectra of half - integer quadrupolar nuclei in solid samples, based on the combined use of magic - angle - spinning (MAS) and multiple - quantum (MQ) spectroscopy¹. This review summarizes the basic theoretical aspects underlying this high resolution MQMAS NMR experiment, emphasizing as well practical aspects involved in the optimization of its signal - to - noise. We also describe the features of MQMAS spectral lineshapes, and exemplify these with a number of applications on various quadrupolar nuclei. Also discussed is the occurrence of unusual spinning sideband patterns along the multiple - quantum domain; additional references to ongoing progress in the area that has appeared in the recent literature are also presented.

solid state NMR; quadrupolar nuclei; resolution enhancement; 2D NMR spectroscopy

Recentemente descrevemos um nova técnica capaz de obter espectros de RMN de alta resolução de núcleos quadrupolares com spins múltiplos de 1/2 no estado sólido, baseada no uso combinado de rotação no ângulo mágico (MAS) e espectroscopia múltipla quântica¹ (MQ). Esta revisão descreve aspectos da teoria básica que suporta o experimento de RMN MQMAS de alta resolução e também enfatiza aspectos práticos envolvidos na otimização de sua relação sinal/ruído. Descrevemos também características da forma das linhas espectrais da MQMAS exemplificando com algumas aplicações para vários núcleos quadrupolares.É discutido também a ocorrência de padrões não usuais de bandas laterais ao longo do domínio múltiplo quântico; referências adicionais, que surgiram na literatura recentemente sobre o progresso desta técnica, são também apresentadas.

Review

Multiple - Quantum Magic - Angle Spinning NMR: A New Technique for Probing Quadrupolar Nuclei in Solids

Ales Medek, and Lucio Frydman ^*

Department of Chemistry (M/C 111), University of Illinois at Chicago, 845 W. Taylor St., Chicago, IL 60607 - 7061

Recentemente descrevemos um nova técnica capaz de obter espectros de RMN de alta resolução de núcleos quadrupolares com spins múltiplos de 1/2 no estado sólido, baseada no uso combinado de rotação no ângulo mágico (MAS) e espectroscopia múltipla quântica¹ (MQ). Esta revisão descreve aspectos da teoria básica que suporta o experimento de RMN MQMAS de alta resolução e também enfatiza aspectos práticos envolvidos na otimização de sua relação sinal/ruído. Descrevemos também características da forma das linhas espectrais da MQMAS exemplificando com algumas aplicações para vários núcleos quadrupolares.É discutido também a ocorrência de padrões não usuais de bandas laterais ao longo do domínio múltiplo quântico; referências adicionais, que surgiram na literatura recentemente sobre o progresso desta técnica, são também apresentadas.

We have recently described a new technique capable of recording high resolution NMR spectra of half - integer quadrupolar nuclei in solid samples, based on the combined use of magic - angle - spinning (MAS) and multiple - quantum (MQ) spectroscopy¹. This review summarizes the basic theoretical aspects underlying this high resolution MQMAS NMR experiment, emphasizing as well practical aspects involved in the optimization of its signal - to - noise. We also describe the features of MQMAS spectral lineshapes, and exemplify these with a number of applications on various quadrupolar nuclei. Also discussed is the occurrence of unusual spinning sideband patterns along the multiple - quantum domain; additional references to ongoing progress in the area that has appeared in the recent literature are also presented.

Keywords: solid state NMR, quadrupolar nuclei, resolution enhancement, 2D NMR spectroscopy

Introduction

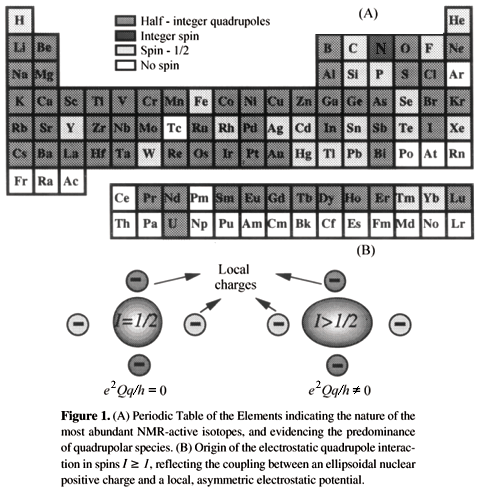
A majority of all magnetically active nuclides in the Periodic Table possess half - integer spin numbers higher than 1 (I = 3/2, 5/2, 7/2 and 9/2; Fig. 1)². This implies that unlike their more common spin -1/2 counterparts such as ¹H and ¹³C, which interact exclusively with either external or internal magnetic fields, such higher half - integer nuclei will possess quadrupole moments and thus also interact with the electric field gradients (EFG) originated from asymmetries in the charge distribution of the surrounding lattice³. Depending on the degree of distortion in this local charge distribution the resulting quadrupole couplings can be large, sometimes even comparable or exceeding the Zeeman coupling between the nuclear magnetic moment and the external magnetic field B₀. However in a majority of cases (including all the ones that we will consider here) quadrupolar couplings can be treated as perturbations to the main Zeeman interaction due to the relatively small size of their coupling constants e²Q/h with respect to the Larmor frequency u_L. The resulting quadrupole couplings are then, to first order, orientation - dependent and proportional to the square of the z component of the angular momentum m, where -I < m < I. In the case of moderately strong (»MHz) quadrupole coupling constants this implies that all the allowed Dm = ±1 transitions will in powdered samples be broadened beyond the NMR detection limit, except for the central -1/2 « 1/2 transition. Consequently most solid state NMR studies of half - integer quadrupolar nuclei have focused on these central transitions that are devoid to first order from quadrupole effects, and therefore much sharper than the rest (Fig. 2).

In spite of their evidently easier detection, central transition quadrupolar NMR spectra do not generally render sharp resonances from powdered samples due to the presence of residual second - order quadrupolar broadenings. Such higher order effects - proportional to the square of the internal perturbation divided by the main Zeeman interaction - are usually negligibly small (»1 Hz) in cases of shielding or dipolar couplings but will affect central transitions of half - integer quadrupoles to a considerable extent, and easily broaden their resonances into the tens or hundreds of kHz. Despite this inherent limitation, knowledge of the quadrupolar and shielding parameters characterizing quadrupolar sites provides such valuable information about the local electronic environments that the acquisition of these broadened central transition NMR spectra has been one of the mainstays of solid state NMR spectroscopy⁴. Interest in these solid state NMR investigations has also been fueled by the widespread occurrence of quadrupolar nuclei in many technologically important materials such as minerals, ceramics, glasses, semiconductors and catalysts^5-7. Owing to the naturally solid constitution of these samples solution NMR studies provide limited amount of information about these (often insoluble) materials, a problem that is further aggravated by the severe signal broadening observed in liquids due to quadrupolar relaxation.

Unfortunately, spectral crowding between second-order broadened inequivalent powder patterns usually prevents the analysis of spectra from quadrupolar nuclei in stationary powders if more than a few sites are present. The importance of a technique for improving the resolution of these solid state NMR line shapes is thus easy to appreciate. As is the case of spin -1/2 an important step toward this goal of high resolution was the introduction of variable - and magic - angle spinning (MAS) NMR methods^8-11. Nevertheless, although fast MAS can in principle remove completely the chemical shielding and dipole-dipole interactions (which behave as first-order anisotropies) and thereby eliminate their spectral broadenings, there is little 'magic' to this choice of spinning angle when it comes to dealing with second - order effects like those originated from large quadrupolar couplings. This complication, whose origins are further discussed below, became one of the most important limitations of solid state quadrupolar NMR and of its applications to the study of complex powdered systems.

A deeper understanding on the origins of the limitations faced by sample spinning towards the removal of quadrupolar broadenings was achieved about a decade ago, and lead to the development of two ingenious averaging procedures which finally achieved the long - sought goal of bringing high resolution NMR to quadrupolar nuclei: dynamic angle spinning (DAS) and double rotation (DOR)^12-15. The solution offered by these two techniques was to simultaneously average the first - and second - order broadenings by removing the constraint of spinning about a single axis, subjecting the sample instead to a more complex time-dependent trajectory with respect to the external magnetic field. This, however, was achieved at the expense of either a mechanical switching of the spinning angle incompatible with short relaxation times or strong homonuclear couplings (DAS), or by simultaneously spinning two rotors positioned inside one another (DOR). In 1995 we described an alternative approach for removing the first - and second - order based on the use of multiple-quantum (MQ) spectroscopy, which in combination with conventional MAS could achieve a refocusing similar to that occurring in DAS. This technique became known as multiple quantum magic angle spinning (MQMAS)¹, and due to its simple implementation it has quickly become a method of choice for studies of quadrupolar nuclei in powdered samples. This article summarizes the basic theoretical and practical aspects of MQMAS, and reviews some of its current applications to half integer quadrupoles.

MQMAS Removal of the Anisotropies

Just as their spin -1/2 counterparts, quadrupolar nuclei possess magnetic moments with which they interact with the external magnetic field as well as with the local fields generated by the chemical shielding and the magnetic moments of other nuclei. Apart from these magnetic couplings, however, nuclei with I > 1/2 are distinguished by a non - spherical shape (Fig. 1), associated to a nuclear quadrupole moment and capable of coupling with the surrounding electric field gradients. Like all spin interactions this coupling can be described quantum - mechanically by a Hamiltonian, depending on a quadrupolar coupling constant C_Q = e²qQ/4I(2I - 1)h, on an asymmetry parameter h_Q, and on nuclear spin operators. Although analyzing the effects of an arbitrary quadrupolar Hamiltonian H_Q in the presence of the Zeeman coupling is a complex task not always susceptible to an analytical treatment, this description can be simplified by considering H_Q only as a perturbation to the Larmor precession (as is usually done with other spin interactions). To first order the quadrupolar Hamiltonian can then be written as:

where A₂₀ is an orientation-dependent polynomial known as an irreducible second-rank spherical tensor element, depending on the relative orientation (Euler angles) between the EFG tensor of a particular crystallite and the Zeeman field B₀. This is the same type of orientation dependence characterizing other first-order effects like the chemical shielding, and in principle it is susceptible to averaging by conventional MAS. Important to notice is the Î_z² dependence of these first-order effects, which explains the fact that the central -1/2 « +1/2 transition (as well as, in principle, any other symmetric -m « + m transition within the manifold) will be devoid of their influence (Fig. 2).

In spite of this simple picture and due to the large magnitudes of the quadrupolar couplings usually encountered, second-order corrections to the energy levels need also be considered in the spectral calculation. Standard perturbation theory predicts that these effects will be represented by the Hamiltonian

The derivation of this correction term involves considering the square of the quadrupolar interaction scaled by Zeeman interaction, hence leading to the C_Q²/u_L dependence. It also leads to a geometric dependence involving products of second - rank spherical tensor elements (as opposed to the {A_2n}_{n= -2 - 2} themselves, cf. Eq. (1)); since each of these elements is quadratic in the cosines/sines of the Euler angles, a more complex orientation dependence than that of the first-order effects can be expected. Finally, the fact that H_Q⁽²⁾ comes from squaring the quadrupolar interaction implies that even though the H_Q's center of mass is zero, H_Q⁽²⁾-derived lineshapes will be affected by a net isotropic quadrupolar shift

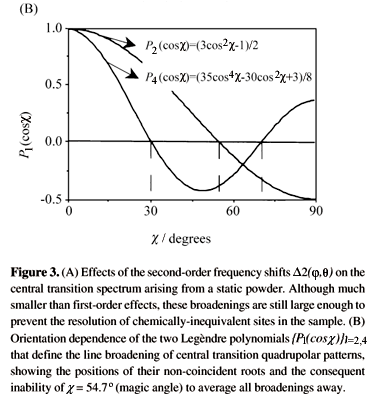
All these features as well as analyses on how second - order quadrupolar effects influence the line shapes arising from static central transition spectra have been extensively discussed in the literature⁴; they are illustrated in Fig. 3A for a particular condition⁴.

Although thanks to the presence of isotropic quadrupolar shifts a new site separation factor will be active in these spectra, the anisotropy of H_Q⁽²⁾ implies that sites in a powder will have severely broadened central transition line shapes. As in the case of spin-1/2 fast spinning of the sample at an angle c with respect to B₀ is an alternative for narrowing these powder patterns. Disregarding the anisotropic dipolar or chemical shift contributions and allowing only for an isotropic chemical shielding u^CS_iso, the transition frequencies that will result for any symmetric -m « +mtransition upon subjecting H_Q⁽²⁾ to fast sample spinning can be written as¹⁶

where we have stressed both the spinning-angle c as well as the quantum-number m dependencies, originating from the {A_2n} and Î_z operators in Eq. (2) respectively. In this frequency expression (j, q) are powder angles orienting a given crystalline with respect to the rotor frame, the effects of the sample spinning are reflected in the second- and fourth-order Legèndre polynomials

and the choice of transition order (e.g. m= -1/2« m = 1/2) is summarized by zero-, second- and fourth-rank coefficients

depending on the spin I and order m of the transition (Table 1). For the sake of completeness we also list the second- and fourth-rank angular-dependent frequencies responsible for the observed line broadenings u₂^Q(q, j), u₄^Q(q, j),

with F₂,(j, q) and F₄,(j, q) defined as:

Eq. (4) differs in one fundamental respect from its non-quadrupolar analogs: whereas shielding and dipolar anisotropies are solely scaled by P₂(cosc) and therefore susceptible to averaging by MAS, the second-order nature of H_Q⁽²⁾ introduces a new, P₄(cosc), term. This again is a consequence of the quadratic dependence of H_Q⁽²⁾ on the {A_2n} elements. Although the individual P₂ and P₄ polynomials that scale the spectral broadenings can be zeroed at particular choices of the spinning axis (Fig. 3B), no single c value can remove simultaneously the u₂^Q(q,j), u₄^Q(q,j) anisotropies.

The DAS experiment remedies this fundamental limitation by carrying out a 2D NMR acquisition during whose evolution times (t_1, t₂), the sample undergoes spinning about two different angles (c_1, c₂). Then, if one monitors the central transition and selects the spinning angles and evolution times to simultaneously fulfill the refocusing conditions

a purely isotropic evolution will be detected. This isotropic echo is free from any orientation - dependent frequency contribution, and consequently its Fourier transformation will yield a high resolution spectrum. An alternative to the acquisition of such signals originates in the observation that from a formal point of view, the spinning angle c and the choice of transition order m play a similar role in defining the evolution frequency of spins: the former will scale it according to the {P_l(cosc)}_{l = 0 - 4} polynomials, the latter according to the {C_l^I(m)}_{l = 0 - 4} coefficients. Then, instead of fixing m at 1/2 and using c as a degree of freedom, it is possible to propose a 2D experiment whereby for a fixed spinning angle c the spins evolve during initial and final times under the effects of two different transition orders m₁and m₂. If conditions are chosen so as to fulfill the averaging

a purely isotropic signal will be detected which can in turn be transformed into a high resolution spectrum. Although a range of c are compatible with Eqs. (17) and (18) the most convenient choice of spinning angle is c_m = 54.7°, since under these MAS conditions the hitherto neglected chemical shift and dipolar anisotropies will also be effectively averaged away by the spinning. Furthermore, under MAS the condition posed by Eq. (17) is no longer relevant and only fourth-rank anisotropies need to be refocused; this in turn implies that under MAS the powder patterns arising from any +m « -m symmetric transition within the spin manifold will be proportional to one another (Fig. 4). At this point also the selection rules for NMR (Dm = ±1) need to be considered, which restrict the coherence order which is directly observed during t₂ to m₂ = 1/2 – the central single – quantum transition. As for the choice of m₁ this will in principle be dictated by the spin number (e.g., for I = 3/2 only m₁ = 3/2 is available); however, also the sign of m₁ which determines the sense of evolution during t₁ is under experimental control by standard phase cycling procedures¹⁷. It is then always possible to choose the correct t₁ evolution sense, regardless of the relative sign of the C₄^I(m₁), C₄(1/2) coefficients, that will lead to the refocusing of the fourth - rank anisotropies. According to Eq. (18) such high - resolution echo will form at

The appearance of such long - lived echoes at this particular (t₁, t₂) combination is, at least for tuning purposes, the most basic test of the MQMAS performance. Its formation is illustrated in Fig. 5A for a ²³Na MQMAS experiment on sodium oxalate (m₁ = 3/2); fast decaying anisotropic evolutions are evident along both the triple- and single-quantum domains (t₁, t₂), as is the refocusing of the decay along the ideal t₂ = (7/9)t₁ slope predicted in Eq. (19). Due of the fact that the 3Q and 1Q anisotropies correlated in this experiment are proportional to one another, the conventional 2D Fourier processing of these data leads to sharp parallel spectral ridges tilted by a slope of 7/9; projection of such raw data onto either the 3Q or 1Q axes will not yield a 1D high resolution spectrum regardless of the axis chosen (Fig. 5B). Something similar happens in the DAS experiment, where scaled mirror-imaged powder patterns arise for the various pairs of complementary angles.As in the latter case it is convenient and practical to transform the tilted MQMAS powder patterns into a format that can yield a high resolution trace; this can be done by a shearing transformation in the mixed (t₁,u₂)-domain, which leads to line shapes whose projection onto one of the spectral axes only possesses isotropic components: u₁' = u₁ + u₂½C₄^I(m₁) ½/ C₄^I(1/2). Alternative procedures can be employed for retrieving a high resolution MQMAS quadrupolar spectrum^41,44, but this is probably the easiest way of obtaining purely isotropic 1D MQMAS line shapes. In fact peaks in such traces can be considerably sharp, sometimes even narrower than their solution-state counterparts due to the absence in the solid state of severe transverse relaxation effects.

In the specific example of a triple- to single-quantum correlation (e.g., ²³Na in sodium oxalate, I = 3/2) the two frequencies resulting after the shearing of the 2D correlation NMR spectrum will be given by

The isotropic frequency u₁' can be directly extracted from the position of the sharp centerband along the sheared 3Q domain. Since the center of mass of the u₄^Q(j, q) term for randomly distributed powders is zero (Eq. (12)), a center of mass calculation of the anisotropic line shape along u₂ ends up reflecting only the sum of the two isotropic components

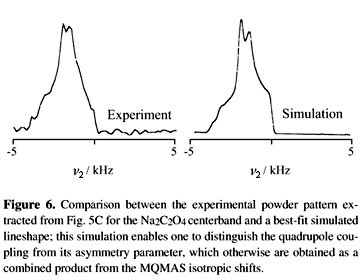
Eqs. (20) and (22) define a simple set of two equations with two unknowns enabling one to discriminate between the isotropic chemical u_iso^CS and quadrupolar shifts u₀^Q, values which were previously attainable from model free analysis only by repeating NMR measurements at multiple fields. Moreover, once the isotropic quadrupolar shift has been determined Eq. (3) can be used for guiding the iterative fitting of the anisotropic lineshape resulting along the u₂ axis, which is in fact equivalent to the regular MAS spectrum expected for the now u₁-resolved chemical site. As expected this lineshape is characterized by two parameters: the quadrupolar coupling constant e²qQ/h and the asymmetry parameter h_Q. Since both of these parameters are related by Eq. (3), fitting the resulting line shapes is just a function of one independent parameter that needs to be optimized; Fig. 6 illustrates the result of such fitting procedure. This fitting procedure can then be applied for each of the inequivalent sites resolved in the 2D MQMAS NMR spectrum. Moreover, it can also be extended to analyses of line shapes from disordered materials such as glasses where natural distributions of isotropic shieldings or quadrupolar couplings occur.

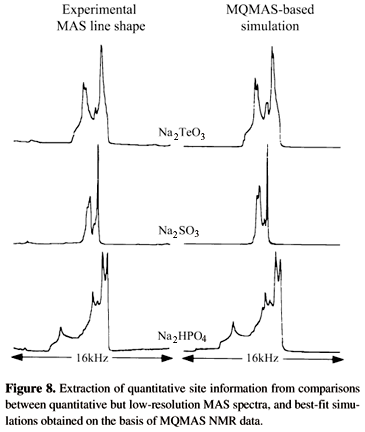
Further comparisons between static, MAS and MQMAS acquisitions are presented in Fig. 7¹⁶; from these, the superior resolving power of the 2D NMR technique becomes evident. Although the dependence of the MQ excitation and MQ ®1Q conversion steps on the quadrupolar coupling parameters, further discussed in the following paragraph, precludes a direct quantification of the individual sites in the analyte via simple peak integration, acquisition of a separate 1D MAS NMR spectrum (which can be carried out quantitatively) can help to solve this issue. Indeed all the parameters characterizing the nuclear couplings can be directly extracted from the MQMAS experiment, leaving only a small number of intensity factors to be established from the now easy to analyze MAS NMR spectrum (Fig. 8). As further mentioned below, a number of alternative and more sophisticated quantification protocols based solely on the analysis of 2D MQMAS NMR spectra have also been recently proposed.

The MQMAS NMR Experiment: Basic Sequence Considerations

The previous paragraph discussed the theoretical bases of the MQMAS technique and showed how a spectral analysis of the resulting 2D NMR line shapes can lead to all the parameters defining the quadrupolar plus the isotropic chemical shift interactions for each inequivalent site in the sample. This Section addresses a more practical MQMAS aspect: the optimization of the experimental parameters so as to achieve maximum transfer efficiencies for both the MQ excitation and the MQ-to-SQ conversion processes, and thereby the highest possible S/N.

Several pulse sequences have already been proposed to implement the MQMAS acquisition, and it is very likely that new and improved protocols will continue arising in the near future. In this paragraph we will mainly focus on a simple, yet robust two-pulse irradiation scheme (Fig. 9A). This two-pulse MQMAS experiment involves an initial pulse which is used to pump high order MQ coherences from the initial z-polarization, and a second strong pulse that is used to convert the evolving MQ states into observable 1Q magnetizations. This two-pulse sequence was initially proposed by Vega and Pines for performing double quantum ²H-NMR spectroscopy, and was subsequently extended to half-integer quadrupolar nuclei experiments^18-21. It represents a good compromise between high S/N, acceptable line shapes and experimental simplicity, and sheds light on the basic physics involved in many of the variants proposed towards the acquisition of MQMAS NMR data. A full and exact analysis on the nature of this sequence would require analyzing the dependence of the spins behavior on a large number of parameters including the spin number I, the coupling parameters (e²qQ/h, h_Q, u^CS_iso), the spinning rate u_r and the transverse radiofrequency (rf) field u₁. An exact solution considering all these experimental variables requires a complex propagation of the spin density matrix which although feasible would tend to mask the basic features of the experiment; a simpler analytical treatment taking into account only the first-order term of the quadrupolar Hamiltonian and the rf irradiation is therefore here summarized. It has been shown that unless very large shielding effects, very weak rf fields or inordinately high spinning rates are considered, a very good approximation to the behavior of the two-pulse sequence can be obtained in this manner. Specifically, this treatment assumes that during irradiation the relevant Hamiltonian is simply

implying that sample rotation, second-order effects, etc. can be neglected during the rf pulse, thanks in part to the latter's short duration. Nuclear spins initially in a thermodynamic equilibrium state parallel to the z-axis, (i.e.,) will be excited by this irradiation and yield, among other states, the desired 3Q coherences. This excitation process can be conveniently described by fictitious spin -1/2 operators which for a spin I = 3/2 define a triple - quantum subspace in terms of Î_x^1-4, Î_y^1-4, and Î_z^1-4matrices. Then, for the common range of irradiation fields u₁ and of quadrupolar coupling constants e²qQ/h met in most experiments, an analytical solution can be derived by transforming H_irr into the eigenbase of the Î_x operator^20,22. It can then be shown that the main process of interest in the 3Q excitation can be expressed as

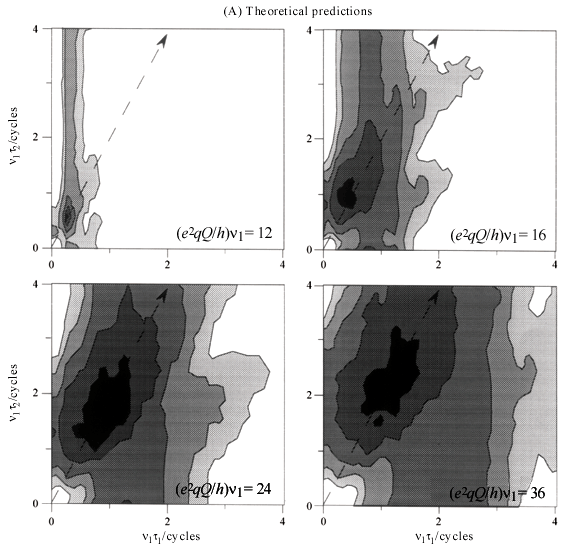
Although this prediction of a single nutation frequency for the triple-quantum coherence buildup is just an approximation resulting from perturbation theory it is quite a good one, as illustrated by the obviously sinusoidal behavior of the single crystal curves presented in Fig. 10A and calculated without relying on such perturbative approximation. The nutation curves for a powder can then be computed as simple weighted superpositions of these single crystal nutation patterns for all possible (j,q) angle, leading to the curves in Fig. 10B. These theoretical predictions are in turn fully corroborated by MQMAS NMR experiments, which over a range of (e²qQ/h)/u₁ ratios and for short excitation pulses t_exc exhibit powder excitation curves possessing a monotonic growth with a local maximum around u₁t_exc= 0.8 cycles. This value can be used as suitable starting pulse width when trying to set up a determination on a sample with unknown coupling parameters.

A similar theoretical approach can be employed to optimize the triple- to single-quantum conversion process brought about by the second pulse of the MQMAS pulse sequence. The central transition single-quantum signal to be observed can then be represented by the pair of fictitious spin -1/2 operators Î_x^2-3, Î_y^2-3. Assuming an arbitrary initial triple-quantum state Î_a^1-4, the effect of the conversion pulse can then be described by

These (S_i)_{i = 1 - 4} coefficients are sinusoidal functions depending on the coupling parameters and on the length t_convof the second pulse. By contrast to the excitation case, however, there is no leader among these nutation terms leading to interference among them and to a poor conversion efficiency even for the single crystal case, which rapidly decreases with increasing (e²qQ/h)/u₁ ratios. Still even for powder samples, a maximum at u₁t_conv ~0.2 cycles can be localized corresponding to a transient coherent superposition of the individual single crystal signals. The closeness between these theoretical predictions of the conversion curve and MQMAS observation on modelsample (Fig. 11)¹⁶ justifies again our use of the simplified time-independent H_irr model. Furthermore, the fact that the optimum pulses end up being much shorter than the duration of one typical rotor cycle provides another justification for the time - independent model assumed in this paragraph. More complete discussions on the optimization of the basic two-pulse MQMAS sequence for different spin numbers and conditions can be found elsewhere^16,23,24. It should be remembered, however, that these "optimal" pulse values are just good initial starting points, susceptible to considerable S/N improvement by even small variations in their timing. Before setting up a complete 2D MQMAS NMR acquisition it is therefore convenient to monitor the t₂ echo for a particular and fixed t₁ value (usually equal to a small integer multiple of rotor periods due to the intense effects of MQMAS sidebands, see below), and then vary the individual pulse width parameters around the suggested values until the strongest MQ signal has been detected. Only with these optimum values it is worth devoting the amount of spectrometer time that is required for the acquisition of a complete 2D MQMAS NMR spectrum.

Additional Pulse Sequence Considerations

In addition to the simple two-pulse sequence discussed in the preceding paragraph, a number of alternative schemes for the acquisition of 2D MQMAS data have been recently discussed. An ingenious approach introduced by Griffin and coworkers exploits the concept of rotationally induced adiabatic coherence transfers (RIACT) under the effect of spin-locking fields²⁵, along the lines initially introduced by Vega in connection to spin-locked quadrupolar states²⁶. This procedure relies on the sample spinning for achieving the excitation or conversion of the MQ coherences; this removes to some extent the dependence of the MQMAS signal on the quadrupolar coupling constant and thereby renders the experiment more quantitative. These gains, however, are usually achieved at the expense of an overall loss in S/N and increased sensitivities to off-resonance effects (e.g., spreads in isotropic shifts or chemical shift anisotropies).

Another pulse sequence alternative (Fig. 9B) stems from a systematic analysis on the performance that a two-pulse unit of the form

could exhibit toward the excitation of triple-quantum coherences²⁷. Using both theoretical and numerical optimizations based on density matrix propagations of the type described above the effects brought about by this sequence on varying the pulse widths, relative irradiation phases and interpulse delays, were explored. In the absence of chemical shifts these five - dimensional numeric searches consistently revealed that excitation sequences involving D = 0, f = p/2 (equivalent to a single x-y composite pulse) and t₁» 2t₂,will yield the largest triple-quantum coherences. Although the exact spins behavior was slightly dependent on the (e²qQ/h)/u₁ ratio (Fig. 12A), an efficient MQ excitation was observed in this manner over a range of conditions in the neighborhood of u₁t₁ = 0.4 cycles, u₁t₂ = 0.8 cycles. The 3Q intensities afforded by these optimized x-y composite pulses were approximately 30% higher than those resulting from conventional single-pulse excitations; representative experimental results confirming the superior performance of these composite pulse schemes are shown in Fig. 12B²⁷.

In addition to these sequences based on the use of square rf pulses, a series of recent papers has focused on the application of shaped pulses to MQMAS. A promising shaped-pulse proposition involves replacing the square conversion pulse in the two-pulse sequence by an amplitude modulated one⁴⁷.This modulation will effectively split the on-resonance pulse into symmetric off - resonance components, thereby increasing the efficiency of the 3Q ® 1Q conversion step which involves manipulating the outlying satellite transitions (Fig. 9C). In spin -3/2 MQMAS experiments of simple model compounds, enhancement of over 300% have recently been reported with this simple procedure. A closely related approach involves using double-frequency-swept chirp pulses that enhancing the MQ conversion step by sweeping through the off-resonance satellite transitions⁴⁸.Yet another elegant and simple way to improve the MQMAS S/N has been proposed by Nielsen and coworkers²⁸, who take advantage of a Carr-Purcell-Meiboom-Gill echo train during the acquisition period to generate multiple 1Q signals in a single scan.

Most of these pulse sequence developments focused on optimizing the MQMAS S/N in the presence of small or negligible off-resonance irradiations, therefore disregarding the potential influence from large isotropic or anisotropic chemical shifts. This is usually a very good approximation if alkali metals or light main group elements are involved due to their relatively small shielding contributions (< 0.1 u₁), but for the case of heavier elements the large magnitudes of their chemical shift scales may severely interfere with the excitation of the MQ coherences. In some situations extreme shielding effects may prevent the acquisition of MQMAS signals altogether, even when dealing with sites possessing small quadrupole couplings. These chemical shielding offsets effects can be compensated in part by preparing the MQ coherences via amplitude - modulated x - x profiles, as illustrated in Fig. 13 with ⁵⁹Co MQMAS NMR spectra of a synthetic [Co(tetraphenylporphyrin-bismethyl-imidazole)]BF₄ complex known to possess a large (»3000 ppm) chemical shift anisotropy²⁷. Still, even under these optimal conditions the overall MQMAS signal is usually poorer than that observed in the absence of large chemical shifts.

Fine structure of the MQMAS NMR line shapes

In addition to a successful refocusing of the anisotropic interactions, retrieving high quality half-integer quadrupolar line shapes by MQMAS demands dealing with a number of peculiarities related to the two-dimensional nature of this experiment. Here we briefly address two such effects and their influence on the structure of the MQMAS peaks patterns: the presence of mixed-phase peak distortions, and the unusual spinning sideband observed along the indirectly-detected domain of the 2D spectrum.

The first of these effects comes from the well-known limitations of 2D FFT to obtain purely absorptive bidimensional lineshapes when monitoring spins precessing with only one sense of t₁ and t₂ time evolutions¹⁷. Avoiding the dispersive artifacts that arise in these peaks requires some form of time-reversal, involving either the formation of a spin-echo, the acquisition of separate echo/anti-echo or cosine/sine MQ-modulated signals (corresponding to different combinations of +t₁ and -t₁ evolutions), or the simultaneous acquisition of echo+antiecho amplitude-modulated signals followed by their disentanglement via techniques such as time-proportional phase incrementation (TPPI) or off-resonance irradiation (strongly discouraged for this experiment due to the reasons mentioned in the previous paragraph). Since MQMAS, particularly when carried out on crystalline materials, is actually an echo experiment (Eq. (19)), these mixed phase artifacts are usually not too severe. But when dealing with poor echo - formers such as glasses, or when requiring highly-resolved purely-absorptive line shapes, the acquisition of echo and anti-echo signals with identical intensities for all crystallites needs to be carried out. In many instances such acquisitions cannot be implemented using the conventional two-pulse MQMAS sequence due to the fact that the efficiencies with which the last pulse transfers +MQ and -MQ coherences to 1Q magnetizations are different. In the fictitious spin -1/2 terminology introduced to describe this conversion pulse (Eq. (25)), this reflects the observation that regardless of the t_conv pulse width chosen it is not possible to make identical the efficiencies of the Î_x^1-4® Î_x^2-3 and Î_y^1-4® Î_y^2-3 transfers. Yet as known from solution NMR, this problem can be alleviated by introducing an intermediate step where MQ coherences are momentarily stored along the z-axis and only then made into observable 1Q magnetizations. The resulting z-filter approach²⁹ ends up using a 0 ® ± 3(t₁) ® 0 ® -1(t₂) coherence transfer scheme, thereby requiring the addition of an extra pulse into the MQMAS sequence and sacrificing part of the signal. On the other hand, the advantage of this z-filter lies in the fact that since efficiencies for +3(t₁) ® 0 ® -1(t₂) and -3(t₁) ® 0 ® -1(t₂) can now be made equal, purely absorptive 2D peaks result.

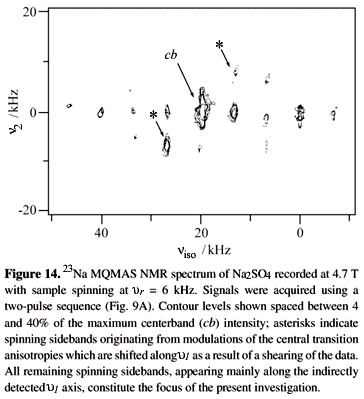
A second feature characterizing MQMAS NMR spectra and which up to now was ignored for the sake of simplicity, is the occurrence of extensive spinning sidebands along the indirectly detected MQ frequency domain. These can be observed in many of the presented spectra, and are illustrated again in Fig. 14. These sidebands behave like their conventional spin -1/2 counterparts in that they are positive and appear at multiples of the rotor frequency with decreasing intensities as the spinning speed is increased; their origin, however, does not necessarily relate to the usual spinning-induced time modulation of chemical shift, dipolar or second-order quadrupolar interactions. Indeed these MQMAS spinning sidebands can span a significantly larger frequency range than those corresponding to the static linewidths of these nuclear interactions, and possible explanations based on magnified MQ chemical shielding or dipolar couplings can be ruled out since strong sidebands appear even for samples exhibiting small coupling interactions. Instead, these indirect-domain sidebands are a consequence of the orientation dependencies associated with the nutation pulses used for MQ excitation and MQ detection, which are in turn rendered time-dependent due to the presence of MAS. A rigorous analysis of such problem requires introducing into the effects of the two - pulse MQMAS sequence the explicit time-dependent oscillations of the first-order quadrupolar frequencies during t₁:

where the A_i and B_i terms describe the dependence of the instantaneous quadrupolar frequency on the angles (j,q) connecting the principal axis system of the electric field gradient tensor with the rotor fixed frame³⁰. When inserted in Eqs. (23) and (24), the t₁-dependent eigenvalues adopted by u_Q during the excitation and conversion pulses result in potentially intense spinning sidebands along the MQ dimension even in the absence of shielding, dipolar or second - order quadrupolar anisotropies. An analytical solution for the MQMAS signal can be derived as explained in connection to Eq. (24) by expanding the eigenvalues of H_irr in powers of u₁/u_Q; this perturbative approach simplifies significantly the problem while still rendering almost identical results to these given by exact numerical calculations and MQMAS experimental spinning sideband intensities (Fig. 15). Unfortunately, since these rotational sideband intensities are mainly a function of e²qQ/h and h_Q and since the previously described analyses of the MQMAS frequency patterns can easily yield these internal coupling parameters, simulating these indirect-domain spinning sideband patterns only yields redundant information.

Concluding Remarks

This presentation summarized some of the basic features of 2D MQMAS NMR as it applies to the acquisition of high resolution spectra from half-integer quadrupolar nuclei. The technique appears to be a powerful yet experimentally simple tool capable of resolving inequivalent chemical sites for a large number of quadrupolar isotopes; it can be used to distinguish isotropic chemical from isotropic quadrupolar shifts, as well as to pinpoint the individual quadrupolar coupling parameters e²Qq/h and h_Q. Combination of MQMAS with simple MAS also enables a quantification of the relative contents of the various chemical species present. A number of interesting spin-physics manipulations have also been triggered by this experiment; unfortunately, many of these phenomena have only been briefly discussed in this presentation and some have not even been mentioned yet. Particularly exciting among the latter are the prospects of using pulsed field gradients in MQMAS acquisitions³¹, of further optimizing MQMAS on moderate field spectrometers³², and of including MQMAS as a partial step in more complex heteronuclear correlation schemes to establish connectivities between quadrupolar and spin-1/2 nuclei^33-36. Additional papers dealing with the technique's assessment, further improvements,and applications to solid state studies of technologically – or biologically– important quadrupolar samples, have also appeared in the recent literature^{16,23-25,27-29,31-80}. It is interesting to notice how much enthusiasm has been triggered by this new approach, which in essence is just the combination of MAS with a 2D sequence based on the application of a pair of rf pulses. Notwithstanding its simplicity and perhaps because of it, it is likely that additional MQMAS-related developments will continue to emerge throughout the coming years.

Acknowledgments

Throughout the development of much of the material described in this paper we were enriched by valuable collaborations, particularly with Ms. Laura Marinelli, Dr. John S. Harwood, Dr. P.K. Madhu and Prof. S. Vega. The research described in this work was supported by the US National Science Foundation through grants DMR - 9806810 and CHE - 9841790 (Creativity Extension Award). L.F. is a Camille Dreyfus Teacher - Scholar (1996-2001), University of Illinois Junior Scholar (1997-2000), Alfred P. Sloan Fellow (1997-2000).

Received: March 29, 1999

• 1.Frydman, L.; Harwood, J.S. J. Am. Chem. Soc. 1995, 117, 5367.
• 2.Harris, R.K.; Mann, B.E. NMR and the Periodic Table; Academic Press: New York, 1970.
• 3.Slichter, C.P. Principles of Nuclear Magnetic Resonance; 3rd ed.; Springer-Verlag: New York, 1990.
• 4.Freude, D.; Haase, J. NMR Basic Principles and Progress 1993, 29, 1.
• 5.Maciel, G.E. Science 1984, 226, 282.
• 6.Oldfield, E.; Kirkpatrick, R.J. Science 1985, 227, 1537.
• 7.Turner, G.L.; Kirkpatrick, R.J.; Risbud, S.H.; Oldfield, E. Am. Ceram. Soc. Bull. 1987, 66, 656.
• 8.Andrew, E.R.; Bradbury, A.; Eades, R.G. Nature 1958, 182, 1659.
• 9.Lowe, I.J. Phys. Rev. Lett. 1959, 2, 285.
• 10.Schaefer, J.; Stejskal, E.O. J. Am. Chem. Soc. 1976, 98, 1031.
• 11.Maricq, M.M.; Waugh, J.S. JCP 1979, 70, 3300.
• 12.Llor, A.; Virlet, J. Chem. Phys. Lett. 1988, 152, 248.
• 13.Chmelka, B.F.; Mueller, K.T.; Pines, A.; Stebbins, J.; Wu, Y.; Zwanziger, J.W. Nature 1989, 339, 42.
• 14.Mueller, K.T.; Sun, B.Q.; Chingas, G.C.; Zwanziger, J.W.; Terao, T.; Pines, A. J. Magn. Res. 1990, 86, 470.
• 15.Wooten, E.W.; Muller, K.T.; Pines, A. Acc. ; Chem. Res. 1992, 25, 209.
• 16.Medek, A.; Harwood, J.S.; Frydman, L. J. Am. Chem. Soc. 1995, 117, 12779.
• 17.Ernst, R.R.; Bodenhausen, G.; Wokaun, A. Principles of Nuclear Magnetic Resonance in One and Two Dimensions; Clarendon: Oxford, 1987.
• 18.Wokaun, A.; Ernst, R.R. J. Chem. Phys. 1977, 67, 1752.
• 19.Vega, S. J. Chem. Phys. 1978, 68, 5518.
• 20.Vega, S.; Naor, Y.J. J. Chem. Phys. 1981, 75, 75.
• 21.Nielsen, N.C.; Bildsře, H.; Jakobsen, H.J. Chem. Phys. Lett. 1992, 191, 205.
• 22.Jannsen, R.; Veeman, W.S.; J. Chem. Soc., Faraday Trans. 1988, 84, 3747.
• 23.Amoureux, J.P.; Fernandez, C.; Frydman, L. Chem. Phys. Lett. 1996, 259, 347.
• 24.Amoureux, J.P.; Fernandez, C. Solid State NMR 1998, 10, 211.
• 25.Wu, G.; Rovnyak, D.; Griffin, R.G. J. Am. Chem. Soc. 1996, 118, 9326.
• 26.Vega, S. J. Magn. Res. 1992, 96, 50.
• 27.Marinelli, L.; Medek, A.; Frydman, L. J. Magn. Res. 1998, 132, 88.
• 28.Vosegaard, T.; Larsen, F.H.; Jakobsen, H.J.; Ellis, P.D.; Nielsen, N.C. J. Am. Chem. Soc. 1997, 119, 9055.
• 29.Amoureux, J.P.; Fernandez, C.; Steuemagel, S. J. Magn. Reson. A 1996, 123, 116.
• 30.Marinelli, L.; Frydman, L. Chem. Phys. Lett. 1997, 275, 188.
• 31.Fyfe, C. A.; Skibsted, J.; Grondey, G.; Meyer, H. Chem. Phys. Lett. 1997, 281, 44.
• 32.Hanaya, M.; Harris, R.K. J. Phys. Chem. 1997, 101, 6903.
• 33.Fernandez, C.; Delevoye, L.; Amoureux, J.P.; Lang, D.P.; Pruski, M. J. Am. Chem. Soc. 1997, 119, 6858.
• 34.Wang, S.H.; Paul, S.M.D.; Bull, L.M. J. Magn. Res. 1997, 125, 364.
• 35.Steuernagel, S. Solid State NMR 1998, 11, 197.
• 36.Ashbrook, S.E.; Brown, S.P.; Wimperis, S. Chem. Phys. Lett. 1998, 288, 509.
• 37.Massiot, D.; Touzo, B.; Trumeau, D.; Coutures, J.P.; Virlet, J.; Florian, P.; Grandinetti, P.J. Solid State NMR 1996, 6, 73.
• 38.Fernandez, C.; Amoureux, J.P. Solid State NMR 1996, 5, 315.
• 39.Wu, G.; Rovnyak, D.; Sun, B.; Griffin, R.G. Chem. Phys. Lett. 1996, 249, 210.
• 40.Samoson, A. J. Magn. Reson. A 1996, 121, 209.
• 41.Brown, S.P.; Heyes, S.J.; Wimperis, S. J. Magn. Reson. A 1996, 119, 280.
• 42.Massiot, D. J. Magn. Reson. A 1996, 122, 240.
• 43.Duer, M.J.; Stourton, C. J. Magn. Reson. 1997, 124, 189.
• 44.Brown, S.P.; Wimperis, S. J. Magn. Reson. 1997, 124, 279.
• 45.Ding, S.; McDowell, C.A. Chem. Phys. Lett. 1997, 270, 81.
• 46.Wang, S. H.; Xu, Z.; Baltisberger, J.H.; Bull, L.M.; Stebbins, J.F.; Pines, A. Solid State NMR 1997, 8, 1.
• 47.Madhu, P.K.; Goldbourt, A.; Frydman, L.; Vega, S. Chem. Phys. Lett. 1999, 307, 41.
• 48.Kentgens, A.P.M.; Verhagen, R. Chem. Phys. Lett. 1999, 300, 429.
• 49.Duer, M.J. Chem. Phys. Lett. 1997, 277, 167.
• 50.Amoureux, J.P.; Lang, D.P.; Pruski, M.; Fernandez, C. J. Magn. Reson. 1998, 131, 170.
• 51.Pruski, M.; Lang, D.P.; Fernandez, C.; Amoureux, J. P. Solid State NMR 1997, 7, 327.
• 52.Fernandez, C.; Lang, D. P.; Amoureux, J. P.; Pruski, M. J. Am. Chem. Soc. 1997, 120, 2672.
• 53.Lacassagne, V.; Florian, P.; Montouillout, V.; Gervais, C.; Babonneau, F.; Massiot, D. Magn. Reson. Chem. 1998, 36, 956.
• 54.Ding, S.; McDowell, C.A. J. Magn. Res. 1998, 135, 61.
• 55.Charpeutier, T.; Fermon, C.; Virlet, J. J. Chem. Phys. 1998, 109, 3116.
• 56.Man, P.P. Phys Rev. B 1998, 58, 2764.
• 57.Sarv, P.; Fernandez, C.; Amoureux, J.P.; Keskinken, K. J. Phys. Chem. 1996, 100, 19223.
• 58.Fernandez, C.; Amoureux, J.P. Chem. Phys. Lett. 1995, 242, 449.
• 59.Kraus, H.; Prins, R.; Kentgents, A.P.N. J. Phys. Chem. 1996, 100, 16336.
• 60.Fernandez, C.; Amoureux, J.P.; Chezeau, J.M.; Delmotte, L.; Kessler, H. Microporous Materials 1996, 6, 331.
• 61.Peeters, M.P.J.; Kentgens, A.P.M. Solid State NMR 1997, 9, 203.
• 62.Hunger, M.; Sarv, P.; Samoson, A. Solid State NMR 1997, 9, 115.
• 63.Hanaya, M.; Harris, R.K. Solid State NMR 1997, 8, 147.
• 64.Dirken, P.J.; Kohn, S.C.; Smith, M.E.; Eck, E.R.H. Chem. Phys. Lett. 1997, 266, 568.
• 65.Hwang, S.J.; Fernandez, C.; Amoureux, J.P.; Cho, J.; Martin, S.W.; Pruski, M. Solid State NMR 1997, 8, 109.
• 66.Sarv, P.; Wichterlova, B.; Cejka, J. J. Phys. Chem. B 1998, 102, 1372.
• 67.Amoureux, J.P.; Bauer, F.; Ernst, H.; Fernandez, C.; Freude, D.; Michel, D.; Pingel, U.T. Chem. Phys. Lett. 1998, 285, 10.
• 68.Hwang, S.J.; Fernandez, C.; Amoureux, J.P.; Han, J.W.; Cho, J.; Martin, S. W.; Pruski, M. J. Am. Chem. Soc. 1998, 120, 7337.
• 69.Wu, G.; Rovnayk, D.; Huang, P.C.; Griffin, R.G. Chem. Phys. Lett. 1997, 277, 79.
• 70.Rocha, J.; Esculcas, A.P.; Fernandez, C.; Amoureux, J.P. J. Phys. Chem. 1998, 100, 17889.
• 71.Fernandez, C.; Amoureux, J.P.; Delmotte, L.; Kessler, H. Microporous Materials 1996, 6, 125.
• 72.Rocha, J.; Lin, Z.; Fernandez, C.; Amoureux, J.P. Chem. Comm. 1996, 22, 2513.
• 73.Rocha, J.; Lourenco, J.P.; Ribeiro, M.F.; Fernandez, C.; Amoureux, J.P. Zeolites 1997, 19, 156.
• 74.Ganapathy, S.; Das, T.K.; Vetrivel, R.; Ray, S.S.; Sen, T.; Sivasanker, S.; Delevoye, L.; Fernandez, C.; Amoureux, J.P. J. Am. Chem. Soc. 1998, 120, 4752.
• 75.Iwamoto, R.; Fernandez, C.; Amoureux, J.P.; Grimblot, J. J. Phys. Chem. B 1998, 102, 4342.
• 76.Xu, Z.; Stebbins, J.F. Solid State NMR 1998, 11, 243.
• 77.Fyfe, C.A.; Altenschildesche, H.M.Z.; Skibsted, J. Inorg. Chem. 1999, 38, 84.
• 78.Hu, K. N.; Hwang, L.P. Solid State NMR 1998, 12, 211.
• 79.Charpeutier, T.; Virlet, J. Solid State NMR 1998, 12, 227.
• 80.Jansen, S.R.; Hintzen, H.T. Metselaar, R.; J.W.Dehaan; Vandeven, L.J.M. Kentgens, A.P.M. Nachtegaal, G.H. J. Phys. Chem. B 1998, 102, 5969.

Publication Dates

• Publication in this collection
  21 June 2001
• Date of issue
  Aug 1999

History

• Received
  29 Mar 1999