Abstracts
The application of sophisticated chemometrics techniques to large datasets has been made possible by continuing technological improvements in off-the-shelf computers. Recently, such improvements have been mainly achieved by the introduction of multi-core processors. However, the efficient use of multi-core hardware requires the development of software that properly address parallel computing. This paper is concerned with the implementation of parallelism using the Matlab Parallel Computing Toolbox, which requires only simple modifications to existing chemometrics code in order to exploit the benefits of multi-core processing. By using this software tool, it is shown that parallel implementations may provide substantial computational gains. In particular, the present study considers the problem of variable selection employing the successive projections algorithm and the genetic algorithm, as well as the use of cross-validation in partial least squares. For demonstration, two analytical applications are presented: determination of protein in wheat by near-infrared reflectance spectrometry and classification of edible vegetable oils by square-wave voltammetry. By using the proposed parallel computing implementations, computational gains of up to 204% were obtained.
parallel computation; successive projections algorithm; genetic algorithm; partial least squares; voltammetric analysis; near-infrared spectrometric analysis
A aplicação de técnicas quimiométricas sofisticadas a grandes conjuntos de dados tem se tornado possível devido aos contínuos aprimoramentos tecnológicos em computadores comerciais. Recentemente, tais aprimoramentos têm sido obtidos principalmente através da introdução de processadores com múltiplos núcleos. Contudo, o uso eficiente de hardware com múltiplos núcleos requer o desenvolvimento de software apropriado para computação paralela. Este artigo trata da implementação de paralelismo empregando o Matlab Parallel Computing Toolbox, que requer somente pequenas modificações em códigos quimiométricos já existentes de modo a explorar os benefícios do processamento em múltiplos núcleos. Empregando essa ferramenta de software, mostra-se que implementações paralelas podem proporcionar expressivos ganhos computacionais. Em particular, considera-se o problema de seleção de variáveis empregando o algoritmo das projeções sucessivas e o algoritmo genético, bem como o uso de validação cruzada em mínimos quadrados parciais. Para ilustração, duas aplicações analíticas são apresentadas: determinação de proteína em trigo por espectrometria de reflectância no infravermelho próximo e classificação de óleos vegetais comestíveis por voltametria de onda quadrada. Empregando as implementações propostas para computação paralela, ganhos computacionais de até 204% foram obtidos.
ARTICLE
Multi-core computation in chemometrics: case studies of voltammetric and NIR spectrometric analyses
Anderson da Silva SoaresI; Roberto K. H. GalvãoII; Mário César U. AraújoIII,* * e-mail: laqa@quimica.ufpb.br ; Sófacles F. C. SoaresIII; Luiz Alberto PintoII,IV
IDivisão de Ciência da Computação and Divisão de Engenharia Eletrônica, Instituto Tecnológico de Aeronáutica, 12228-900 São José dos Campos-SP, Brazil
IIDivisão de Engenharia Eletrônica, Instituto Tecnológico de Aeronáutica, 12228-900 São José dos Campos-SP, Brazil
IIIDepartamento de Química, CCEN, Universidade Federal da Paraíba, CP 5093, 58051-970 João Pessoa-PB, Brazil
IVCoordenadoria de Engenharia de Controle e Automação, Instituto Federal do Espírito Santo, 29164-231 Serra-ES, Brazil
ABSTRACT
The application of sophisticated chemometrics techniques to large datasets has been made possible by continuing technological improvements in off-the-shelf computers. Recently, such improvements have been mainly achieved by the introduction of multi-core processors. However, the efficient use of multi-core hardware requires the development of software that properly address parallel computing. This paper is concerned with the implementation of parallelism using the Matlab Parallel Computing Toolbox, which requires only simple modifications to existing chemometrics code in order to exploit the benefits of multi-core processing. By using this software tool, it is shown that parallel implementations may provide substantial computational gains. In particular, the present study considers the problem of variable selection employing the successive projections algorithm and the genetic algorithm, as well as the use of cross-validation in partial least squares. For demonstration, two analytical applications are presented: determination of protein in wheat by near-infrared reflectance spectrometry and classification of edible vegetable oils by square-wave voltammetry. By using the proposed parallel computing implementations, computational gains of up to 204% were obtained.
Keywords: parallel computation, successive projections algorithm, genetic algorithm, partial least squares, voltammetric analysis, near-infrared spectrometric analysis
RESUMO
A aplicação de técnicas quimiométricas sofisticadas a grandes conjuntos de dados tem se tornado possível devido aos contínuos aprimoramentos tecnológicos em computadores comerciais. Recentemente, tais aprimoramentos têm sido obtidos principalmente através da introdução de processadores com múltiplos núcleos. Contudo, o uso eficiente de hardware com múltiplos núcleos requer o desenvolvimento de software apropriado para computação paralela. Este artigo trata da implementação de paralelismo empregando o Matlab Parallel Computing Toolbox, que requer somente pequenas modificações em códigos quimiométricos já existentes de modo a explorar os benefícios do processamento em múltiplos núcleos. Empregando essa ferramenta de software, mostra-se que implementações paralelas podem proporcionar expressivos ganhos computacionais. Em particular, considera-se o problema de seleção de variáveis empregando o algoritmo das projeções sucessivas e o algoritmo genético, bem como o uso de validação cruzada em mínimos quadrados parciais. Para ilustração, duas aplicações analíticas são apresentadas: determinação de proteína em trigo por espectrometria de reflectância no infravermelho próximo e classificação de óleos vegetais comestíveis por voltametria de onda quadrada. Empregando as implementações propostas para computação paralela, ganhos computacionais de até 204% foram obtidos.
Introduction
Modern techniques and instrumentation provide ever-growing amounts of data (in terms of variables and samples) that need to be processed for analytical purposes. Hyphenated methods1 and laser-induced plasma breakdown spectroscopy,2 for instance, generate a considerable number of measurements for each sample. One may also cite near-infrared (NIR) spectrometric analysis of complex matrices such as agricultural products and fuels, which may require large sample sets for multivariate calibration.3 In such applications, the computational effort involved in chemometrics data processing is not negligible.
It may be argued that this growing demand of chemometrics has been compensated by improvements in the performance of commercial computers. In fact, early concerns related to the engineering limits of complexity and speed in microprocessor units have been circumvented by the deployment of multi-core processors.4 However, the efficient use of such multi-core hardware requires the development of software that properly address parallel computing.5,6 Therefore, the chemometrics practitioner must be prepared to deal with this new reality.
In recent years, there has been increasing interest in the study, design, and analysis of parallel algorithms.7-9 Parallelization can significantly improve performance in applications that involve many repetitions of a given task or long tasks comprising several simpler operations. The main idea is to divide a problem into smaller problems that can be solved simultaneously. In a multi-core platform, such smaller problems may be assigned to different cores, in order to make full use of the available computing capabilities.
In this context, a recent paper10 presented an implementation of leave-one-out cross-validation in multi-core processors using the message passing interface (MPI) library in a C++ compiler. However, the proposed implementation requires the expert use of low-level C++ features, which may be too cumbersome to most chemometricians. In this sense, it would be of value to exploit multi-core processing in a simpler, high-level software platform such as Matlab, which has become a popular tool in chemometrics.11-14
The present paper is concerned with the implementation of parallelism using the Matlab Parallel Computing Toolbox,15 which requires only simple modifications to existing code in order to exploit the benefits of multi-core processing. By using this software tool, parallel implementations are presented for three computationally intensive chemometric procedures, namely the selection of variables using the successive projections algorithm (SPA)16-27 and the genetic algorithm (GA),16-18,22,24,26,28,29 and the use of leave-one-out cross-validation30-32 for model order selection in partial least squares (PLS).30,31,33-35 Computational improvements in multivariate calibration and classification tasks are demonstrated. The multivariate calibration case study involves near-infrared determination of protein content in a publicly available data set of wheat samples. The classification study concerns the discrimination of four types of edible vegetable oils by square-wave voltammetry.
Background and Theory
Parallel computing in Matlab
The Parallel Computing Toolbox (PCT) of Matlab was designed to facilitate the implementation of parallel algorithms for multi-core computation. In what follows, the use of the toolbox will be illustrated by a simple numerical example. Consider the two scripts presented below, where "m" is defined by the user.
Script 1: creation of a random square matrix
Script 2: pseudo-inverse calculations
Script 1 creates a random (m × m) matrix X. Script 2 uses the Matlab pinv function for calculation of the Moore-Penrose36 pseudoinverse of m matrices of dimensionsm × m . For simplicity of presentation, the pseudoinverse matrices are not stored, as this example will be mainly concerned with the time required to complete the calculations. The overall computational effort involved in script 2 may be considerable for large m. However, the script is amenable to parallelization, as the pseudoinverse calculations for different matrices (i.e., different values of index i in script 2) can be carried out independently.
Two main PCT functions can be used in this case, namely "parfor" and "createTask". However, the parfor function has many programming restrictions that hinder its application and may also compromise the gains in computational performance.15 For these reasons, the createTask function is adopted in the present work.
The parallelization of script 2 can be implemented by using scripts 3 and 4 presented below.
Script 3: parallelization of script 2
Script 4: auxiliary function for parallelization of script 2
The two tasks (TASK(1) and TASK(2)) created in script 3 split the calculations into two threads. The first thread carries out the pseudoinverse calculations for the first m/2 matrices (i ranging from 1 to m/2 in script 2) and the second thread carries out the pseudoinverse calculations for the last m/2 matrices (i ranging from m/2 + 1 to m in script 2). If m is an odd number, m/2 is rounded to the nearest integer (round(m/2)). It is worth noting that script 3 can be easily modified to use more than two threads. In the case of four threads, for example, each one would carry out the calculations for m/4 matrices (1 to m/4, m/4 + 1 to m/2, m/2 + 1 to 3m/4 and 3m/4 + 1 to m), as shown below.
Script 3 with four threads
Figure 1 presents the results obtained by using the quad-core (four cores) apparatus described in the "Computational Setup" section. Parameter m (number of pseudoinverse calculations) was varied from 100 to 1300. The calculations were carried out with no paralellization, as well as with two and four threads. As it can be seen, for large values of m the time required for completion can be made smaller by using parallelization. However, such an improvement in performance is not attained for small values of m (smaller than 400 in this example), as the creation of multiple threads involves an overhead that may be comparatively significant in tasks of small complexity.
As a general rule, further gains in performance are not expected if the number of threads is increased beyond the number of processor cores.8 In fact, after threads have been assigned to each and every core, there will remain no idle cores and the full capability of the processor will be engaged in the computation task. However, new technologies may introduce exceptions to this rule. The Intel Core i7 quad-core processor, for example, is capable of hyper-threading, which allows each core to process up to two threads simultaneously.9 As a result, the processor may be used as an eight-core device for parallelization purposes.
Parallelization of the successive projections algorithm
The successive projections algorithm (SPA) was originally designed to minimize multicollinearity problems in multiple linear regression (MLR).16,18 Subsequently, the algorithm was extended to deal with classification problems using linear discriminant analysis (LDA).22,23,26,27 In what follows, the regression and classification versions of SPA will be termed SPA-MLR and SPA-LDA, respectively.
SPA comprises two main phases.21,24 Phase 1 consists of projection operations carried out on the matrix of instrumental responses X (N × K). These projections are used to generate chains of variables in which the elements are selected to display the least collinearity with the previous ones. One chain is initialized from each of the K variables, thus resulting in a total of K chains.
In SPA-MLR, all objects are mean-centered prior to the projection operators. Due to the loss of one degree of freedom involved in this procedure, each chain may have up to (N - 1) variables. In SPA-LDA, the objects are centered on the mean of their respective classes. Therefore, if there are C classes involved in the problem, each chain may have up to (N - C) variables.
In Phase 2, candidate subsets of variables are extracted from each of the K chains generated in Phase 1. These subsets are then evaluated according to a suitable performance index. Usually, the performance index is calculated in a separate validation set, in order to avoid overfitting problems. In SPA-MLR the performance index is typically the root-mean-square error obtained when the MLR model is applied to the validation set.21,24 In SPA-LDA the performance index is related to the average risk of misclassification. Such a risk is calculated by evaluating the Mahalanobis distance of the validation samples with respect to their true class, as well as to the closest wrong class.22 Finally, a backward elimination procedure is employed in SPA-MLR (Phase 3) to improve the parsimony of the model.21,24 An equivalent procedure has not yet been developed for SPA-LDA.
Although all phases of SPA can be parallelized, Phase 2 is the actual bottleneck for the overall computational efficiency of the algorithm, as will be shown in the Results section. Therefore, the parallelization study will be restricted to Phase 2 in both SPA-MLR and SPA-LDA. For this purpose, it is sufficient to create separate threads to process different chains of variables, as illustrated in Figure 2.
Parallelization of the genetic algorithm
Genetic algorithms are stochastic search techniques inspired on natural selection mechanisms.24,28,29 In the present work, a genetic algorithm (GA) is employed to select variables for multivariate calibration using MLR (GA-MLR) and classification using LDA (GA-LDA). A standard GA formulation using binary chromosomes is adopted. Each of the K available variables is associated to a position in the chromosome, which is termed a gene. The gene values can be either 1 (variable is included in the model) or 0 (variable is not included in the model).
In order to apply natural selection rules, a fitness value needs to be assigned to each chromosome in the population.24,28,29 As in SPA, the fitness is evaluated in a separate validation set, in order to avoid overfitting problems. In GA-MLR, the fitness is calculated as the inverse of the root-mean-square error of the MLR model in the validation set. In GA-LDA, the fitness is calculated as the inverse of the average risk of misclassification, defined as in SPA-LDA. The probability of a given individual being selected for the mating pool is proportional to its fitness (roulette method). One-point crossover and mutation operators are employed with probabilities of 60% and 10%, respectively. The population size is kept constant, with each generation being completely replaced by its descendants. However, the best individual is automatically transferred to the next generation (elitism) to avoid the loss of good solutions. The GA is carried out for 50 generations with 4000 chromosomes each.
In both GA-MLR and GA-LDA, parallelization can be achieved by creating separate threads to evaluate the fitness of different chromosomes, as illustrated in Figure 2.
Paralellization of cross-validation in partial least squares
Partial least squares (PLS) is a generalization of multiple linear regression, in which the relationship between the instrumental responses (matrix X) and the properties of interest (matrix Y) is modelled in terms of latent variables.33 In PLS, such variables correspond to directions in the multivariate space which maximize the explained variance of both the X and Y data. If the Y data consist of a single variable (that is, if matrix Y has one column), the PLS algorithm is known as PLS1. If the Y data comprise more than one variable (that is, if matrix Y has several columns), the algorithm is known as PLS2.
Although PLS was originally developed as a multivariate calibration algorithm, it can be applied to classification problems by using a convenient representation of the class indexes.31 If the problem involves C classes, the class index for each object can be encoded in a y-vector with (C - 1) elements equal to zero and a single element equal to one. The position of this element in the y-vector denotes the class index of the object under consideration. In this case, the Y matrix will have C columns and the PLS2 algorithm can be employed. When the resulting model is applied to the classification of a new object, the class index can be obtained as the position of the largest element in the predicted y-vector.
Choosing an appropriate number of latent variables is a key aspect in PLS modelling. The number of variables should be large enough to capture the relevant sources of data variation. However, if too many variables are employed, data overfitting problems may occur and the predictive ability of the resulting model may be compromised. In this context, cross-validation is a commonly used procedure to choose the model order in PLS.30,31,33-35 Cross-validation consists of dividing the data into groups, and then building separate models by removing one of the groups at a time. In the "leave-one-out" procedure, each group consists of a single object. Each model is then used to predict the Y-values in the removed group. At the end, the prediction errors of all models are collected to calculate a performance index such as the root-mean-square error of cross-validation (RMSECV). The number of latent variables can be chosen in order to minimize the RMSECV value. Alternatively, a statistical criterion can be adopted to choose a smaller number of latent variables, for which the RMSECV value is not significantly larger than its minimum value.37
In the cross-validation procedure, the construction of each separate PLS model can be carried out independently. Therefore, a parallel implementation can be easily developed, as illustrated in Figure 2.
Experimental
Wheat data set for multivariate calibration
The data set for the multivariate calibration study consists of 775 VIS-NIR spectra of whole-kernel wheat samples, which were used as shoot-out data in the 2008 International Diffuse Reflectance Conference (http://www.idrc-chambersburg.org/shootout.html). Protein content was chosen as the property of interest. The spectra were acquired in the range 400-2500 nm with a resolution of 2 nm. In the present work, only the NIR region in the range 1100-2500 nm was employed. In order to remove undesirable baseline features, first derivative spectra were calculated by using a Savitzky-Golay filter with a 2nd order polynomial and an 11-point window.30
The Kennard-Stone (KS) algorithm38-39 was applied to the resulting spectra to divide the data into calibration, validation and prediction sets with 389, 193 and 193 samples, respectively. The validation set was employed to guide the selection of variables in SPA-MLR and GA-MLR. The prediction set was only employed in the final performance assessment of the resulting MLR models. In the PLS study, the calibration and validation sets were joined into a single modelling set, which was used in the leave-one-out cross-validation procedure. The number of latent variables was selected on the basis of the cross-validation error by using the F-test criterion of Haaland and Thomas with α = 0.25 as suggested elsewhere.37,40 The prediction set was only employed in the final evaluation of the PLS1 model.
Edible vegetable oils data set for classification
The data set for the classification study consists of 114 voltammograms of edible vegetable oil samples obtained in a previous work,23 in which optimized experimental conditions were reported. Each voltammogram comprises 800 variables (potentials) in the cathodic range down to - 0.9 V. The data set includes canola, sunflower, corn and soybean oils, some of which were stored for several months past the expiry date. These "expired" samples were gathered into a single group for classification purposes. Therefore, the problem involves five classes (canola, sunflower, corn, soybean and expired), as in the previous work.23
The KS algorithm was applied to the voltammograms to divide the data into training, validation and test sets with 59, 23 and 32 samples, respectively. The validation set was employed to guide the selection of variables in SPA-LDA and GA-LDA. The test set was only employed in the final performance assessment of the resulting LDA models. In the PLS study, the class indexes were encoded in a binary Y matrix with five columns in order to use the PLS2 algorithm. Moreover, the training and validation sets were joined into a single modelling set, which was used in the leave-one-out cross-validation procedure. As in the multivariate calibration case, the number of latent variables was selected on the basis of the cross-validation error by using the F-test criterion of Haaland and Thomas with α = 0.25. The test set was only employed in the final evaluation of the PLS2 model.
Computational setup
All calculations were carried out by using a desktop computer with an Intel® Core 2 quad-core processor (2.3 GHz) and 4 GB of RAM memory. Matlab 7.0 and Parallel Computing Toolbox 4.1 were employed throughout. Average and standard deviation values for computation times were obtained by running each chemometric algorithm three times.
Results and Discussion
Wheat data set
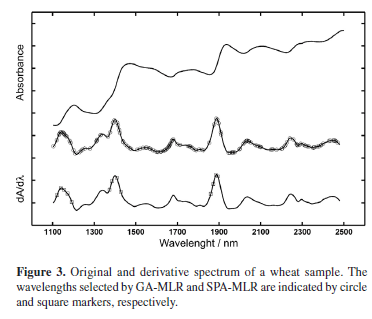
Table 1 presents the results obtained by applying the resulting SPA-MLR, GA-MLR and PLS1 models to the prediction set of wheat samples. As it can be seen, there is good correlation between the predicted and reference values and the root-mean-square error of prediction (RMSEP) is small as compared to the range of protein content in the samples. Table 1 also shows the number of variables employed in each model (wavelengths in SPA-MLR, GA-MLR and latent variables in PLS1). It is worth noting that SPA-MLR is more parsimonious than GA-MLR with respect to the number of spectral variables included in the model. The variables selected by SPA-MLR and GA-MLR are indicated in Figure 3.
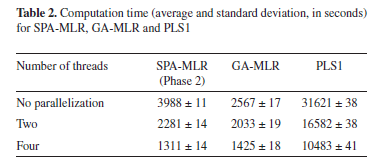
Table 2 presents the computation time required to obtain the SPA-MLR, GA-MLR and PLS1 models. As it can be seen, the use of parallel processing results in a significant decrease in computation time with respect to the standard implementation (no parallelization). By using four threads, computational gains of 204%, 80% and 202% were obtained for SPA-MLR, GA-MLR and PLS1, respectively. Such percentages were calculated by considering the speed of calculations, which is inversely related to the computation time.
As it can be seen, greater gains were achieved for SPA-MLR and PLS1, as compared to GA-MLR. The reason for such a difference may be explained as follows. The computational cost involved in the evaluation of each chromosome in GA-MLR depends on the number of variables encoded in that chromosome (i.e. the number of 1-valued genes). In fact, the fitness calculation procedure requires the calibration of an MLR model, which is more complex if more variables are employed. Therefore, since the population comprises chromosomes with different numbers of encoded variables, the distribution of workload among the processor cores (illustrated in Figure 2) is not well-balanced, which results in a non-optimal use of the available computational resources.41 In such a situation, some cores may remain idle while the others are still busy with the fitness calculations.
It is worth noting that the times required by Phase 1 and 3 of SPA-MLR (54 s and 1 s, respectively) are small as compared to Phase 2. Therefore, no parallelization schemes were developed for these phases.
Edible vegetable oils data set
SPA-LDA and GA-LDA selected 10 and 12 variables (potential values in the voltammograms), respectively, whereas the PLS2 model employed 14 latent variables. By applying the resulting models to the test set, all samples were correctly classified. It is worth noting that SPA again resulted in a slightly more parsimonious model as compared to GA. The potential values selected by SPA-LDA and GA-LDA are indicated in Figure 4.
Table 3 presents the computation time required by SPA-LDA, GA-LDA and PLS2 algorithms. As in the previous application, the time required by Phase 1 of SPA-LDA (7.2 s) is small as compared to Phase 2. It is worth noting that a final variable elimination procedure (which corresponds to Phase 3 in SPA-MLR) is not employed in SPA-LDA. Again, the use of parallel processing provided a significant decrease in computation time. By using four threads, computational gains of 126%, 77% and 110% were obtained for SPA-LDA, GA-LDA and PLS2, respectively.
Conclusions
This paper discussed the potential benefits of exploiting parallel computing for chemometrics calculations in multi-core hardware platforms. As shown in a numerical example, such benefits can be obtained by introducing simple modifications to existing Matlab code. Case studies involving the successive projections algorithm and the genetic algorithm for variable selection, as well as partial least squares with cross-validation were presented. For this purpose, datasets of NIR spectra for multivariate calibration and voltammograms for classification were employed. In these applications, computational gains of up to 204% were obtained by using the proposed implementation for parallel computing.
The modern chemometrician will have to be prepared to exploit the full capabilities of multi-core processors. In this context, the appropriate use of parallel computing plays an important role, as shown in this paper. It is worth noting that sample-wise parallelization can also be easily implemented in applications such as data compression,42 noise removal,43 and spectral library search.44 In such cases, multiple threads can be used to process different samples simultaneously. Future works could also be concerned with the development of parallelization schemes for specific parts of chemometric algorithms, such as the sorting and selection of chromosomes according to the fitness function in GA.
Acknowledgments
This work was supported by FAPESP (Grant 2006/58850-6 and Doctorate Scholarship 2007/57803-7), CAPES (MSc Scholarship and PROCAD Grant 0081/05-1) and CNPq (Research Fellowships and Instituto Nacional de Ciência e Tecnologia Analítica Avançada). The authors also thank Dr. Francisco Fernandes Gambarra-Neto for providing the voltammograms of the edible vegetable oil data set.
Submitted: August 25, 2009
Published online: May 11, 2010
FAPESP has sponsored the publication of this article.
- 1. Schoenmakers, P.; Ann. Rev. Anal. Chem. 2009, 2, 333
- 2. Pasquini, C.; Cortez, J.; Silva, L. M. C; Gonzaga, F. B.; J. Braz. Chem. Soc. 2007, 18, 463.
- 3. Pasquini, C.; J. Braz. Chem. Soc. 2003, 14, 198.
- 4. Geer, D.; Computer 2005, 38, 11.
- 5. James, D.; Margaret, M.; Proceedings of the 33rd Annual International Symposium on Computer Architecture, 2006, pp. 78-88.
- 6. Hughes, C.; Hughes, T.; Professional Multicore Programming: Design and Implementation for C++ Developers, Wiley: India, 2008.
- 7. Buttari, A.; Langou, J.; Kurzak, J.; Dongarra, J.; Paral. Comput. 2009, 35, 38.
- 8. Akhter, S.; Roberts, J.; Multi-core Programming: Increasing Performance Through Software Multi-threading, Intel Press, 2006.
- 9. Kaivola, R.; Ghughal, R.; Narasimhan, N.; Telfer, A.; Whittemore, J.; Pandav, S.; Slobodová, A.; Taylor , C.; Frolov, V.; Reeber, E.; Naik, A.; Lect. Notes Comp. Sci. 2009, 5643, 414.
- 10. Zhang, Z. M.; Liang, Y. Z.; Xu Q. S.; Chemom. Intell. Lab. Syst. 2009, 96, 94.
- 11. Daszykowski, M.; Serneels, S.; Kaczmarek, K.; Chemom. Intell. Lab. Syst. 2007, 85, 269.
- 12. Jaumot, J.; Gargallo, R.; de Juan, A.; Chemom. Intell. Lab. Syst. 2005, 76, 101.
- 13. Chau, F. T.; Chung, W. H; J. Chem. Educ. 1995, 72, A84.
- 14. Ohaver, T. C.; Chemom. Intell. Lab. Syst. 1989, 6, 95.
- 15. Parallel Computing Toolbox 4.1User's Guide, The Mathworks: Natick, MA, 2008.
- 16. Araújo, M. C. U.; Saldanha, T. C. B.; Galvão, R. K. H.; Yoneyama, T.; Chame, H. C.; Visani, V.; Chemom. Intell. Lab. Syst. 2001, 57, 65.
- 17. Dantas Filho, H. A.; Souza, E. S. O. N.; Visani, V.; Barros, S. R. R. C.; Saldanha, T. C. B.; Araújo, M. C. U.; Galvão, R. K. H.; J. Braz. Chem. Soc. 2005, 16, 58.
- 18. Galvão, R. K. H.; Pimentel, M. F.; Araújo, M. C. U.; Yoneyama, T.; Visani, V.; Anal. Chim. Acta 2001, 443, 107.
- 19. Honorato, F. A.; Galvão, R. K. H.; Pimentel, M. F.; Barros Neto, B.; Araújo, M. C. U.; Carvalho, F. R.; Chemom. Intell. Lab. Syst. 2005, 76, 65.
- 20. Dantas Filho, H. A.; Galvão, R. K. H.; Araújo, M. C. U.; Silva, E. C.; Saldanha, T. C. B.; José, G. E.; Pasquini, C.; Raimundo Jr., I. M.; Rohwedder, J. J. R.; Chemom. Intell. Lab. Syst. 2004, 72, 83.
- 21. Galvão, R. K. H.; Araújo, M. C. U.; Fragoso, W. D.; Silva, E. C.; José, G. E.; Soares, S. F. C.; Paiva, H. M.; Chemom. Intell. Lab. Syst. 2008, 92, 83.
- 22. Pontes, M. J. C.; Galvão, R. K. H.; Araújo, M. C. U.; Moreira, P. N. T.; Pessoa Neto, O. D.; José, G. E.; Saldanha, T. C. B.; Chemom. Intell. Lab. Syst. 2005, 78, 11.
- 23. Gambarra Neto, F. F.; Marino, G.; Araújo, M. C. U.; Galvão, R. K. H.; Pontes, M. J. C.; Medeiros, E. P.; Lima, R. S.; Talanta 2009, 77, 1660.
- 24. Galvão, R. K. H.; Araújo, M. C. U. In Comprehensive Chemometrics: Chemical and Biochemical Data Analysis; Brown, S.; Tauler, R.; Walczak, B., eds.; Elsevier: Oxford, 2009.
- 25. Galvão, R. K. H.; Araújo, M. C. U.; Silva, E. C.; José, G. E.; Soares, S. F. C.; Paiva, H. M.; J. Braz. Chem. Soc 2007, 18, 1580.
- 26. Pontes, M. J. C.; Cortez, J. ; Galvão, R. K. H.; Pasquini, C.; Araújo, M. C. U.; Coelho, R. M.; Chiba, M. K.; Abreu, M. F.; Madari, B. E.; Anal. Chim. Acta 2009, 642, 12.
- 27. Moreira, E. D. T.; Pontes, M. J. C.; Galvão, R. K. H.; Araújo, M. C. U.; Talanta 2009, 79, 1260.
- 28. Jouan-Rimbaud, D.; Massart, D. L.; Leardi, R.; Noord, O. E.; Anal. Chem. 1995, 67, 4295.
- 29. Leardi, R.; J. Chemom. 2001, 15, 559.
- 30. Beebe, K. R.; Pell, R. J.; Seasholtz, B.; Chemometrics-A Pratical Guide, Wiley: New York, 1998.
- 31. Massart, D. L.; Vandeginste, B. G. M.; Buydens, L. M. C.; Jong, S.; Lewi, P. J.; Smeyers-Verbeke, J.; Handbook of Chemometrics and Qualimetrics, Elsevier Science: Amsterdam, 1997.
- 32. Cawley, G. C.; Talbot, N. L. C.; Pattern Recogn. 2003, 36, 2585.
- 33. Wold, S.; Sjöström, M; Eriksson, L.; Chemom. Intell. Lab. Syst. 2001, 58, 109.
- 34. Wakeling, I. N.; Morris, J. J.; J. Chemom. 1993, 7, 291.
- 35. Clark, M.; Cramer III, R. D.; Quant. Struct.-Act. Relat. 1993, 12, 137.
- 36. Cramer, R.; Kiltz, E.; Padró, C.; Lect. Notes Comput. Sci. 2007, 4622, 613.
- 37. Haaland, D. M.; Thomas, E. V.; Anal. Chem 1988, 60, 1193.
- 38. Kennard, R.W.; Stone L. A.; Technom. 1969, 11, 137.
- 39. Kanduc, K. R.; Zupan, J.; Majcen N.; Chemom. Intell. Lab. Syst. 2003, 65, 221.
- 40. Li, B. X.; Wang, D. M.; Xu, C. L.; Zhang, Z. J.; Microchim. Acta 2005, 149, 205.
- 41. Zomaya, A. Y.; Teh, Y. H.; IEEE Trans. Parallel Distrib. Syst. 2001, 12, 899.
- 42. Cobas, J. C.; Tahoces, P. G., Fernández, I. I.; Martín-Pastor, M.; Chemom. Intell. Lab. Syst. 2008, 91, 141.
- 43. Galvão, R. K. H.; Dantas Filho, H. A.; Martins, M. N.; Araújo, M. C. U; Pasquini, C.; Anal. Chim. Acta 2007, 581, 159.
- 44. Loudermilk, J. B.; Himmelsbach, D. S.; Barton, F. E.; Appl. Spectrosc. 2008, 62, 661.
Publication Dates
-
Publication in this collection
10 Sept 2010 -
Date of issue
2010
History
-
Received
25 Aug 2009 -
Accepted
11 May 2010