Resumos
Este artigo usa modelos lineares e não lineares de Índice de Difusão para prever, um período à frente, a taxa de crescimento trimestral do PIB agrícola brasileiro. Esses modelos são compostos de fatores comuns que permitem redução significativa do número de variáveis explicativas originais. Os resultados de eficiência preditiva apontam para uma superioridade das previsões geradas pelos modelos de Índice de Difusão sobre os modelos ARMA. Entre os modelos de Índice de Difusão, o modelo não linear com efeito threshold superou os resultados do modelo linear e do modelo AR.
PIB agrícola; modelos de Índice de Difusão; previsão; não linearidades
This article uses linear and nonlinear diffusion index models to forecast, one step ahead, the quarterly growth rate of Brazilian Agricultural GDP. These models are composed by common factor which allow a significant reduction in the number of the original explanatory variables. After comparing the forecasts of these two models between themselves and with the ones generated by an AR model, used as benchmark, one comes to the conclusion that among the diffusion index models, the nonlinear model with a threshold effect presents a small improvement, in terms of predictive efficiency, in relation to the linear and the AR models.
agricultural GDP; Diffusion Index Model; forecast; nonlinearities
ECONOMIA E SOCIEDADE BRASILEIRAS
Modelos de índice de difusão para prever a taxa de crescimento do PIB agrícola brasileiro
Roberto Tatiwa FerreiraI; José Nilo de Oliveira JúniorII; Ivan CastelarIII
IProf. do Depto. de Economia Aplicada/CAEN/UFC
IIProf. do Departamento de Economia UFPA Pós-Graduação em Economia
IIIProf. do Depto. de Economia Aplicada/UFC
RESUMO
Este artigo usa modelos lineares e não lineares de Índice de Difusão para prever, um período à frente, a taxa de crescimento trimestral do PIB agrícola brasileiro. Esses modelos são compostos de fatores comuns que permitem redução significativa do número de variáveis explicativas originais. Os resultados de eficiência preditiva apontam para uma superioridade das previsões geradas pelos modelos de Índice de Difusão sobre os modelos ARMA. Entre os modelos de Índice de Difusão, o modelo não linear com efeito threshold superou os resultados do modelo linear e do modelo AR.
Palavras-chave: PIB agrícola, modelos de Índice de Difusão, previsão, não linearidades.
Classificação JEL: C530, Q190.
ABSTRACT
This article uses linear and nonlinear diffusion index models to forecast, one step ahead, the quarterly growth rate of Brazilian Agricultural GDP. These models are composed by common factor which allow a significant reduction in the number of the original explanatory variables. After comparing the forecasts of these two models between themselves and with the ones generated by an AR model, used as benchmark, one comes to the conclusion that among the diffusion index models, the nonlinear model with a threshold effect presents a small improvement, in terms of predictive efficiency, in relation to the linear and the AR models.
Key words: agricultural GDP, Diffusion Index Model, forecast, nonlinearities.
JEL Classification: C530, Q190.
1_ Introdução
Ao longo dos últimos 20 anos, a expansão do agronegócio tem sido marcante, caracterizando-se por cadeias produtivas cada vez mais integradas e por uma profissionalização crescente e intensiva do agricultor. Os anos da década de 1990, em particular, representaram um momento de profundas transformações da economia brasileira. O novo ambiente econômico, marcado pela estabilidade monetária e maior abertura da economia, proporcionou novas oportunidades de investimento e competição dos produtos brasileiros nos mercados interno e externo (Freitas; Spolador, 2006).
Segundo Gasques e Villa Verde (2003), a agricultura brasileira, no início da década de 1990, foi atingida por uma mudança do comportamento do poder central quanto aos programas que atendiam ao setor. O Programa de Abastecimento, por exemplo, que na década de 1980 representava 70% das aplicações federais, já na década seguinte não chegou a 30%. A maior causa da redução de recursos para a agricultura foi a política de estabilização adotada a partir de março de 1990, na qual o controle monetário e fiscal foram os pontos centrais. Essa mudança na política econômica alterou substancialmente a forma de financiamento da agricultura pelo setor público.
Os referidos autores mostram ainda que, no início da década de 1990, ocorreu um esvaziamento das políticas de curto prazo, as quais concentraram na década anterior quase todo o esforço de política agrícola. Para algumas políticas como as do trigo, açúcar e álcool, a saída do governo teve pontos positivos em face da economia que isso representou e das distorções que aquelas políticas provocaram ao longo dos anos. Para outras políticas, porém, como crédito rural, preços mínimos e estoques reguladores, a ausência do governo trouxe problemas que se refletiram diretamente no volume de produção, nos investimentos e, principalmente, na estabilização de preços e na renda.
A partir de 1994, com a implementação do Plano Real e com as mudanças que o acompanharam, principalmente no câmbio, o setor agrícola passou a experimentar um momento mais favorável. No entanto, uma queda dos preços internacionais anulou parcialmente o estímulo derivado da mudança cambial de 1999; mas, em compensação, uma fase de alta desses preços, a partir de 2002, reforçou o estímulo cambial, resultando em grande dinamismo, em especial nos últimos três anos agrícolas (2001/2002, 2002/2003 e 2003/2004). Verificou-se também que a volatilidade dos preços internacionais deu lugar, a partir do segundo semestre de 2004 até o inicio de 2006, a uma fase de baixos preços agrícolas no mercado internacional, o que implicou adversidades para o setor (Brandão et al., 2005).
Constata-se também que a expansão agrícola recente caracterizou-se por um aumento de nada menos do que 22,8% da área plantada com grãos, ao longo de apenas três anos agrícolas (2001/2002, 2002/2003 e 2003/2004). Tal expansão recente difere radicalmente do padrão que prevaleceu durante toda a década de 1990, no qual a área total com lavouras permaneceu constante, e todo o aumento da produção agrícola vegetal adveio de aumentos da produtividade da terra. Essa referida expansão de área se deu principalmente na soja, que cresceu, somente nesses três anos agrícolas, 39,8% nas Regiões Sul e Sudeste, e nada menos do que 66,1% na Região Centro-Oeste. Vale ressaltar que a rápida expansão de área plantada se deu muito mais pela conversão de pastagens do que pela abertura de novas áreas seja no cerrado, seja na floresta amazônica.
Dadas todas essas transformações que o setor agrícola enfrentou durante a década de 1990 e início da década de 2000, sobretudo no que diz respeito à magnitude do produto agrícola, a elaboração de um modelo econométrico para prever a taxa de crescimento do PIB agrícola brasileiro deve conter variáveis que permitam capturar os efeitos do setor externo, das condições de oferta e demanda dos bens e serviços agrícolas, bem como do lado nominal da economia brasileira.
Por outro lado, a literatura especializada vem chamando a atenção para a importância da parcimônia no processo de previsão, ou seja, quanto maior o número de coeficientes no modelo, maior a incerteza sobre os parâmetros estimados; isso pode trazer graves consequências para a eficiência da previsão. Desta forma, vários modelos têm sido propostos para evitar esse problema.
Os modelos fatoriais para séries de tempo têm sido uma dessas opções. Um deles é o modelo de Índice de Difusão, proposto por Stock e Watson (1998), que tem como ideia central o fato de que toda a informação incluída em um grande número de variáveis pode ser resumida num pequeno número de fatores comuns entre elas.
Além da parcimônia, os modelos de previsão enfrentam outras questões, sendo uma das principais a perda de eficiência quando há quebras estruturais na variável a ser prevista (Clements; Hendry, 1998). Como alternativa aos modelos lineares, nessa situação, há várias especificações não lineares que se propõem a tratar tais mudanças.
Uma delas é o modelo do tipo threshold proposto inicialmente por Tong (1983) e aprimorado por Hansen (2000), na qual um modelo não linear permite um conjunto de valores diferentes para os seus parâmetros, de acordo com possíveis alterações nos regimes econômicos. Já o modelo de Índice de Difusão com efeito threshold proposto por Tatiwa (2005), além de trazer a ideia do modelo de Índice de Difusão, incorpora a possível existência de mais de um regime econômico, como proposto pelo modelo threshold. Assim, como o PIB é uma variável sujeita a ciclos de negócios, esse tipo de modelo poderia gerar melhores previsões do que o modelo de fatores lineares. No entanto, em termos de resultados empíricos, nada garante, a priori, a superioridade das previsões do modelo não linear sobre o linear.
O objetivo principal deste trabalho, portanto, consiste em verificar se os modelos de Índice de Difusão linear e o com efeito threshold geram previsões para a taxa de crescimento trimestral do PIB agrícola brasileiro, com menor erro do que os modelos de séries temporais do tipo ARIMA, os quais se consagraram, entre outras características desejáveis, em virtude dos seus desempenhos preditivos.
Deste modo, foram utilizados dados trimestrais do PIB agrícola brasileiro mais um conjunto de 83 variáveis macroeconômicas, representando o setor externo e o lado real e nominal da economia brasileira, além de dez variáveis climáticas. O período que engloba as variáveis inicia-se no primeiro trimestre de 1990 e termina no primeiro trimestre de 2005. Reservou-se uma parte da amostra total, do primeiro trimestre de 2004 até o primeiro trimestre de 2005, para realizar previsões ex-post, as quais permitem a comparação com os valores realizados.
Além desta seção, este trabalho se compõe de mais quatro outras seções. A seção 2 trata da revisão da literatura. A seção 3 descreve a metodologia utilizada, e a seção 4 detalha os resultados encontrados. Finalmente, a seção 5 resume as conclusões.
2_ Revisão da literatura
Na literatura sobre previsões, não há resultados consensuais sobre a comparação da eficiência preditiva entre os modelos não lineares e os modelos lineares. A revisão bibliográfica sobre esse assunto indica que resultados a favor dos modelos não lineares devem ser mais bem analisados. Como ilustração, os principais estudos nessa área são discutidos a seguir.
As aplicações empíricas encontradas em Clements e Krolzig (1998) e Clements e Smith (1999) evidenciam que os modelos lineares são eficientes em suas previsões. Por outro lado, Clements, Frances e Smith (1999) encontraram fraca evidência para o PIB dos Estados Unidos de que o modelo TAR fornece melhor previsão comparada ao modelo AR.
Dijk e Siliverstovs (2003), utilizando modelos lineares e não lineares para prever a taxa de crescimento da produção industrial para o grupo de países do G7, corroboram a ideia de que o modelo não linear apresenta melhores resultados do que o modelo linear, no que concerne às incertezas contidas nas séries de tempo.
Já Boero e Marrocu (2002) concluíram que as previsões para a taxa de câmbio nominal dos Estados Unidos do modelo Smooth-TAR (STAR) não superam as previsões do modelo AR. Neste mesmo sentido, Diebold e Nason (1990) enumeraram várias razões que justificam a melhor performance obtida pelos modelos lineares em comparação aos não lineares. Uma delas é que a aparente não linearidade detectada pelos testes para linearidade é devida a outliers ou a quebras estruturais, o que diminui o desempenho da previsão.
Para o Brasil, Chauvet (2001) e Chauvet, Lima e Vasquez (2002) mostraram que os modelos não lineares fornecem resultados mais eficazes para previsão das taxas de crescimento do produto brasileiro do que os modelos lineares.
No que se refere ao uso de modelos de Índice de Difusão para gerar previsões, os resultados têm se mostrado favoráveis à sua utilização. Stock e Watson (1998) empregaram esse tipo de modelo para prever a taxa de crescimento do PIB e a inflação dos EUA. A performance preditiva dos modelos de Índice de Difusão foi superior à obtida pelos modelos AR, VAR e de rede neurais.
Tatiwa, Bierens e Castelar (2005), ao realizarem previsões para a taxa de crescimento do PIB brasileiro, utilizando modelos de Índice de Difusão lineares e não lineares, concluíram que as previsões feitas por tais modelos foram superiores às previsões geradas por um modelo do tipo AR.
3_ Metodologia
A metodologia que será descrita nas subseções seguintes vai detalhar os modelos lineares e não lineares que foram usados para fazer as previsões, um passo à frente da taxa de crescimento do produto agrícola.
3.1_ Modelo de Índice de Difusão (DI)
Seguindo Stock e Watson (1998), os modelos de fatores, ou de Índice de Difusão, são modelos com variáveis latentes. Isso significa que algumas variáveis são não observáveis. Se f representa r dessas variáveis e x é um vetor de k variáveis observadas, com r < k, a análise do modelo de fatores expressa a matriz de dados X(T x K) como uma combinação linear de vetores linearmente desconhecidos, usualmente chamados de "fatores comuns", mais um fator específico. Para i = 1, ..., k, pode-se representá-lo da seguinte forma:
onde cada f acima é o escore do fator. Cada vetor coluna com esses escores é um fator comum; cada λ é o peso do fator, e cada e representa um fator específico. A definição usual de fatores comuns é que eles são funções lineares de variáveis conhecidas, contribuindo para a variância comum de todas as variáveis. Por outro lado, o fator específico contribui somente para a variância da variável que está sendo explicada.
Outro modo de expressar o sistema (1), para um dado período de tempo T = t, é:
ou simplesmente,
onde, xt = [x1t, ..., xkt]' é um vetor (k x 1), Λ é uma matriz (k x r) de pesos dos fatores, Ft = [f1, ..., fr]' é um vetor (r x 1), et= [e1t, ..., ekt]' é um vetor (k x 1) de erros, e r < k. Assumindo que essas partes comuns não são correlacionadas com a parte específica, que também não são correlacionadas no tempo e que F'F = FF' = Ir, pode-se mostrar1
1
Assumindo o bom comportamento dos dados, para poder aplicar a lei fraca dos grandes números de Khinchine. Uma condição que garante a identificação dos fatores comuns e dos específicos refere-se aos autovalores das matrizes F e L, os quais devem ser distintos para que a identificação ocorra. Entretanto, para aplicações com um grande número de variáveis na matriz de dados
xt e algumas condições de estacionariedade, torna essa condição desnecessária (Forni; Hallin; Lippi; Reichlin, 2000).
que p lim(1 / n)XX ' = Σ = ΛΛ' + Ψ, e logo var(xi) =  .
.
Portanto, todas as k variáveis na matriz X são representadas por uma combinação linear de r fatores comuns, mais o fator específico, e esses r fatores comuns e seus pesos são suficientes para explicar a estrutura de variância comum de todas as k variáveis. Considerando yt+1 como a previsão um passo à frente da taxa de crescimento do PIB agrícola brasileiro, os modelos usados neste trabalho são da forma:
onde t = 1, ..., T e α(L) e β(L) são polinômios do operador de defasagens de dimensões q1 e q2, respectivamente. Observe-se que há (q1 + q2) x k parâmetros em (3). Quando k é muito grande, a estimação desses parâmetros pode ser muito imprecisa.
Assumindo que
e também que (yt + 1, xt) possuem uma representação de fator dinâmico, com  (
( < k) fatores dinâmicos, Stock e Watson (2002) refinaram a equação (3)2
2
Esta próxima suposição implica que
E (
yt
+1 \
β
t,
yt,
Xt,
β
t-1,
t,
yt
-1,
Xt
-1, ...) depende somente de
Ft.
da seguinte forma:
< k) fatores dinâmicos, Stock e Watson (2002) refinaram a equação (3)2
2
Esta próxima suposição implica que
E (
yt
+1 \
β
t,
yt,
Xt,
β
t-1,
t,
yt
-1,
Xt
-1, ...) depende somente de
Ft.
da seguinte forma:
nas quais, λ(L) = I + B1(L) + ... + Bp(Lp), Bi é uma matriz (k ×  ) e ft é um vetor de fatores (
) e ft é um vetor de fatores ( × 1). Então, o modelo fatorial pode absorver um grande número de observações contidas nas k variáveis em um pequeno número de fatores r. Modelando todas as defasagens polinomiais, Stock e Watson (1998) desenvolveram uma representação estática da equação (4), ou seja,
× 1). Então, o modelo fatorial pode absorver um grande número de observações contidas nas k variáveis em um pequeno número de fatores r. Modelando todas as defasagens polinomiais, Stock e Watson (1998) desenvolveram uma representação estática da equação (4), ou seja,
3.2_ Modelo de Índice de Difusão com efeito "threshold" (TARDI)
Os modelos que utilizam o efeito threshold têm sido usados em estudos empíricos macroeconômicos na tentativa de capturar fases de expansões e recessões nos ciclos de negócio ou em qualquer outra situação que requeira uma divisão induzida da amostra para regimes diferentes. O modelo TARDI, proposto por Tatiwa (2005), une o modelo de Índice de Difusão, descrito na seção anterior, com o modelo threshold proposto por Hansen (1996, 1997 e 2000).
A ideia central do modelo é utilizar as propriedades do modelo linear de fatores (DI), decorrentes da utilização da técnica de componentes principais, com a característica não linear do modelo threshold, que captura a presença de diferentes regimes encontrados na série de tempo.
Desta forma, o modelo de Índice de Difusão com efeito threshold pode ser expresso da seguinte forma:
onde gt1 é a variável threshold e I(.) é uma função indicadora. Fazendo,  ,
,  para j=1,2,
para j=1,2,  ,
,  , zt(γ) = (ztI (gt–1< γ) ztI (gt–1 > γ))' e θ = (π1π2)'; então, a equação (7) pode ser escrita da seguinte forma:
, zt(γ) = (ztI (gt–1< γ) ztI (gt–1 > γ))' e θ = (π1π2)'; então, a equação (7) pode ser escrita da seguinte forma:
3.3_ Estimação, teste e previsão
3.3.1_ Estimação do modelo de Índice de Difusão (DI)
O procedimento de estimação3
3
Foi utilizada uma rotina adaptada de Stock e Watson (1998) para estimar o modelo DI e fazer as previsões e outra rotina adaptada de Hansen (1997) para o mesmo propósito no modelo TARDI.
para o modelo de Índice de Difusão autorregressivo, baseado nas equações (6) e (2), é composto de dois passos. Primeiro se estimam os valores na equação (2), com base nos dados observados de xt, através da técnica de componentes principais. Como essa técnica é muito sensível à variabilidade dos dados, foram usados valores padronizados de xt. Desta forma4
4
Para mais detalhes sobre o processo de estimação do modelo de Índice de Difusão por componentes principais, ver Stock e Watson (1998).
, as estimativas dos fatores  t são os autovetores associados com os n maiores autovalores da matriz padronizada
t são os autovetores associados com os n maiores autovalores da matriz padronizada  , onde
, onde  é um vetor (T x 1).
é um vetor (T x 1).
Como tais fatores são estimados por meio de componentes principais, isso significa que o primeiro fator é o autovetor associado com o mais alto autovalor e ele pode ser entendido como uma combinação linear de dados observados que explicam a maior parte da variância dos dados. Seguindo essa lógica, o segundo fator é o autovetor associado com o segundo maior autovalor e, portanto, explana a parte da variância que não é explicada pelo primeiro fator, e assim por diante. Além disso, outra característica importante da solução por componentes principais é a rotação que garante que cada um desses fatores será linearmente independente dos outros, evitando-se, assim, qualquer grau de colinearidade que possa existir entre os regressores.
No segundo passo, yt+1 é regredido sobre uma constante,  t e yt para obter
t e yt para obter  ,
, e
e  na equação (6). Esses dois passos para o desenvolvimento do método de estimação foram adotados em Stock e Watson (1998, 2002).5
5
Stock e Watson (1998) mostraram que os fatores estimados são uniformemente consistentes e que esses estimadores são consistentes mesmo quando existe variação no tempo em L. E ainda mostraram que, se
r é desconhecido e se
m > r, se pode alcançar um Erro de Previsão eficiente.
na equação (6). Esses dois passos para o desenvolvimento do método de estimação foram adotados em Stock e Watson (1998, 2002).5
5
Stock e Watson (1998) mostraram que os fatores estimados são uniformemente consistentes e que esses estimadores são consistentes mesmo quando existe variação no tempo em L. E ainda mostraram que, se
r é desconhecido e se
m > r, se pode alcançar um Erro de Previsão eficiente.
3.3.2_ Estimação do modelo de Índice de Difusão com efeito "threshold" (TARDI)
A estimação do modelo TARDI será baseada em Hansen (1997). As variáveis adotadas na função gt–1foram curtas e longas diferenças do logaritmo do PIB, i.e., gt–1 ={In(pibt–1 / pibt–2), In(pibt–2 / pibt–3), In(pibt–3 / pibt–4), In(pibt–4 / pibt–5), In(pibt–1 / pibt–3), In(pibt–1 / pibt–4), In(pibt–1 / pibt–5)}. Desde que, nesse caso, a equação de regressão é não linear e descontínua, a estimação dos parâmetros θ e γ será obtida através de mínimos quadrados condicional sequencial. Seja γ = gt–1 e  , onde o estimador de MQ de γ pode ser encontrado pela investigação dos valores de Γ, que minimizam os resíduos da regressão de yt em zt(γ). Ou seja:
, onde o estimador de MQ de γ pode ser encontrado pela investigação dos valores de Γ, que minimizam os resíduos da regressão de yt em zt(γ). Ou seja:
onde,
Após obter  , o estimador de Mínimos Quadrados de θ, esse é computado como
, o estimador de Mínimos Quadrados de θ, esse é computado como  =
=  (
( ).
).
Para saber se o modelo linear captura todas as sequências não lineares das séries de tempo, pode-se utilizar o teste descrito em Hansen (1996, 1997, 2000) para testar a hipótese nula H0 : π1 = π2 (regimes econômicos idênticos) utilizando como hipótese alternativa H1 : π1≠ π2 (regimes econômicos diferentes), através de um teste de Wald robusto com relação à heterocedasticidade. Ou seja,
Na equação acima, R=[ I -I],  ,
,  e
e  . A estatística de Wald apresentada na equação (13) não possui distribuição padrão. Para se obter os valores críticos dessa estatística, utilizou-se o procedimento de bootstrap apresentado em Hansen (2000), o qual fornece o p-valor assintótico dessa estatística de teste.
. A estatística de Wald apresentada na equação (13) não possui distribuição padrão. Para se obter os valores críticos dessa estatística, utilizou-se o procedimento de bootstrap apresentado em Hansen (2000), o qual fornece o p-valor assintótico dessa estatística de teste.
3.3.3_ Previsão
A equação geral usada para o modelo DI, para fazer previsão um passo à frente, é dada por:
 onde
onde  e
e  . Como em Stock e Watson (2002), o modelo DI utiliza somente fatores correntes no processo de previsão. O modelo DI-AR é o modelo DI mais as defasagens da variável dependente; o modelo DI-LAG refere-se ao modelo DI mais fatores defasados, e o modelo DI-AR-LAG apresenta defasagens da variável dependente, bem como dos fatores. O número de defasagens, nos modelos que as utilizaram, foi escolhido mediante o critério de informação Bayesiano (BIC).
. Como em Stock e Watson (2002), o modelo DI utiliza somente fatores correntes no processo de previsão. O modelo DI-AR é o modelo DI mais as defasagens da variável dependente; o modelo DI-LAG refere-se ao modelo DI mais fatores defasados, e o modelo DI-AR-LAG apresenta defasagens da variável dependente, bem como dos fatores. O número de defasagens, nos modelos que as utilizaram, foi escolhido mediante o critério de informação Bayesiano (BIC).
Nos modelos DI-BIC, DIAR-BIC, DILAG-BIC e DIARLAG-BIC, tanto o número de variáveis defasadas como o número de fatores a ser utilizado em cada um desses modelos foram definidos pelo BIC.
Já para o modelo TARDI a previsão de um passo à frente segue a seguinte equação:
4_ Resultados empíricos
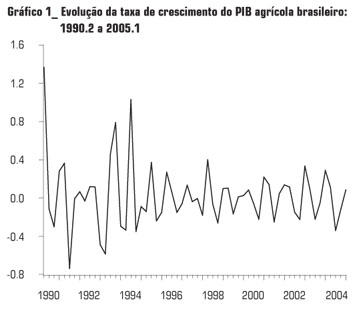
Os valores trimestrais do PIB agrícola brasileiro no período entre 1990.01 a 2005.01, em unidades de mil reais, foram deflacionados pelo IGP-DI com base no primeiro trimestre de 2005.6 6 Dados coletados na base de dados do Instituto de Pesquisa Econômica Aplicada (IPEADATA). Depois, aplicou-se o log neperiano e, em seguida, a primeira diferença na variável já deflacionada, obtendo-se a taxa de crescimento trimestral do PIB agrícola brasileiro, cuja evolução temporal é representada no gráfico abaixo.
Os modelos foram estimados no período 1990.2 a 2003.4, e previsões de um passo à frente foram realizadas no período 2004.1 a 2005.1. Depois de estimados, previsões desses modelos foram geradas, e os seus respectivos erros quadráticos médios de previsão (EQM) foram calculados. O erro de previsão é obtido pela diferença entre o valor observado e o previsto. O EQM é o valor médio calculado a partir desses erros elevados ao quadrado. Portanto, quanto menor for o EQM de um modelo, menores são os seus erros de previsão em média.
Na próxima seção, os resultados sobre o processo de estimação e previsão dos modelos são apresentados. Em relação ao processo de seleção dos modelos, optou-se por estimar várias alternativas, com diferentes configurações e combinações de defasagens e números de fatores, e selecionou-se o modelo com menor erro quadrático médio de previsão (EQM).
4.1_ Resultados do modelo ARMA
Previsões de modelos ARMA(p,q), p={0,1,2,3,4} e q={0,1,2,3,4} foram geradas. Em termos de desempenho preditivo, o modelo selecionado foi um modelo com apenas a segunda defasagem da variável dependente denominado de AR2. A equação abaixo apresenta as estimativas dos parâmetros desse modelo, bem como os seus respectivos desvios padrões.
Esse modelo apresentou um erro quadrático médio de previsão (EQM) de 0.02 e servirá como base de comparação (benchmark) para os demais modelos de Índice de Difusão. A medida de eficiência preditiva dos modelos usados neste estudo é a proporção7 7 Esta medida é utilizada como padrão nesse tipo de literatura; ver, por exemplo, Stock e Watson (1998). do erro quadrático médio de previsão (MSFE) com relação ao modelo AR2.
4.2_ Resultados do modelo de Índice de Difusão (DI)
Os modelos DI foram estimados com até cinco fatores e com até quatro defasagens para os fatores e para a parte autorregressiva do modelo; i.e, defasagens da variável dependente. Vale lembrar que, para a estimação desses fatores, 83 variáveis8 8 As variáveis econômicas utilizadas para estimação do modelo (DI) tiveram como fonte o Instituto Brasileiro de Geografia e Estatística (IBGE) e foram coletadas na base de dados do Instituto de Pesquisa Econômica Aplicada (IPEA), entre o primeiro trimestre de 1990 e o primeiro trimestre de 2005. Mais informações sobre as transformações utilizadas, ver Apêndice I do trabalho. macroeconômicas representando o setor externo, o lado real e nominal da economia brasileira e dez variáveis climáticas9 9 As variáveis climáticas correspondem às médias pluviométricas dos Estados de maior representação territorial de cada região brasileira. Essas foram coletadas no Instituto de Pesquisa Espaciais (INPE), entre o primeiro trimestre de 1990 e o primeiro trimestre de 2005. foram utilizadas.
No que se refere à eficiência preditiva dos modelos DI, o melhor modelo foi aquele sem defasagens e com quatro fatores,10 10 A escolha do melhor modelo foi feita em termos de eficiência preditiva. o qual apresenta um erro quadrático médio de previsão de 0.018. Portanto, esse modelo, denominado de DI(4), melhorou as previsões do modelo AR2 em 10%.11 11 Este valor é encontrado fazendo-se o seguinte procedimento: . A próxima equação apresenta as estimativas dos parâmetros do DI(4) e seus respectivos desvios padrões.
Tais resultados, de maneira geral, corroboram aqueles encontrados por Tatiwa, Bierens e Castelar (2005), para a taxa de crescimento do PIB brasileiro, no sentido de que o modelo DI prevê melhor se comparado ao modelo AR. No referido trabalho, o modelo DI com três fatores obteve uma previsão cerca de 36% melhor do que o AR(1).
O Gráfico 2 apresenta os valores reais e os valores das previsões da taxa de crescimento do PIB agrícola dos modelos DI e AR2. Pode-se verificar que ambos os modelos preveem de forma satisfatória a direção da variável em análise.
Como foi explicado anteriormente, o número de defasagens e de fatores utilizados nos modelos DI-BIC, DIAR-BIC, DILAG-BIC e DIARLAG-BIC foram definidos pelo critério de informação de Schwarz (BIC). Segundo esse critério, não se devem utilizar defasagens e fatores nesses modelos. Isso significa que os resultados dos modelos DI-AR, DI-LAG e o modelo DI-AR-LAG são os mesmos, uma vez que nenhuma defasagem e nenhum fator foram utilizados.
Desta forma, tais modelos também apresentaram o mesmo resultado para o erro quadrático médio de previsão, que foi de 0.046. Valor muito superior ao do melhor modelo de Índice de Difusão o DI(4). Em outras palavras, o uso desse critério de informação para a especificação de um modelo de Índice de Difusão não é recomendado para o problema em análise.
4.3_ Resultados do modelo de Índice de Difusão com efeito "threshold" (TARDI)
Várias especificações alternativas do TARDI, modelos com um a cinco fatores e com quatro defasagens da variável dependente,12 12 Em termos da eq(15) q 1={1,2,3,4} e q 2={1,2,3,4,5}. foram utilizadas para gerar previsões da taxa de crescimento trimestral do PIB agrícola brasileiro.
No que se refere à eficiência preditiva, o modelo com os dois primeiros fatores, com a segunda defasagem da variável dependente e com  como a variável threshold, foi o que apresentou o menor EQM entre essa classe de modelos e entre todos os modelos testados neste estudo. O EQM desse modelo foi de 0.016, 20% menor do que os gerados pelo AR2, e algo em torno de 11% menor do que o modelo linear de Índice de Difusão. Abaixo são apresentados os principais resultados do processo de estimação desse modelo.
como a variável threshold, foi o que apresentou o menor EQM entre essa classe de modelos e entre todos os modelos testados neste estudo. O EQM desse modelo foi de 0.016, 20% menor do que os gerados pelo AR2, e algo em torno de 11% menor do que o modelo linear de Índice de Difusão. Abaixo são apresentados os principais resultados do processo de estimação desse modelo.
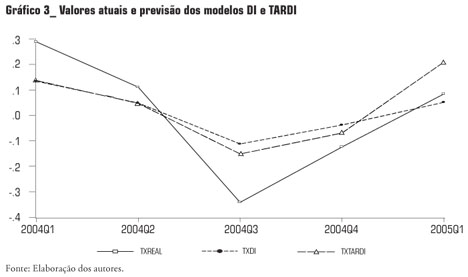
A Tabela 1 apresenta os valores reais e previstos pelos modelos que apresentaram menor EQM dentro de sua categoria, e o Gráfico 3 apresenta os valores reais e previstos pelos modelos DI(4) e TARDI.
Ao se aplicar o teste de linearidade versus efeito threshold na estrutura similar ao TARDI descrito no parágrafo anterior, mudando apenas as variáveis de efeito limiar, obtêm-se os resultados apresentados na Tabela 2.
Os p-valores sugerem que existe um efeito threshold significante a um nível de 1%, quando é considerada a diferença curta de In(pibt-1 / pibt-2), bem como quando se considera a diferença longa de In(pibt-1 / pibt-3).
No entanto, será considerado, daqui para diante, apenas o modelo TARDI que utiliza a diferença curta de In(pibt-1 / pibt-2), pois esse foi o que apresentou os melhores resultados na previsão.
Vale salientar que o teste de não linearidade remanescente mostrou que não se pode rejeitar a hipótese de linearidade. Desta forma, os dois regimes do modelo TARDI são suficientes para capturar a parte não linear das séries de tempo em questão.
O Gráfico 1, exibido no início desta seção, revela a possível presença de outliers em 1990.2, 1991.3, 1993.4 e 1994.3. A rotina de detecção desse tipo de valor no SPSS13 13 Statistical Package for the Social Sciences. O procedimento de detecção de outliers utilizado é aplicado diretamente na série analisada sem a necessidade de estabelecer a distribuição inicial dessa e seu resultado não se altera se diferentes modelos forem utilizados, o que é o caso neste estudo. De forma mais específica, neste procedimento a amostra é separada em três quartis (q 1, q 2 e q 3) que definem quatro subintervalos, cada um com 25% da amostra total. Depois são obtidos um valor mínimo (vmin) = q 1 1.5(q 3- q 1) e um valor máximo (vmax) = q 3 + 1.5(q 3- q 1). Uma observação é considerada um outlier, na hipótese de o seu valor ultrapassar um desses limites. corrobora a inspeção visual dos trimestres 1991.3 e 1993.4. Desta forma, os modelos foram novamente reestimados com variáveis binárias para capturar possíveis efeitos dos outliers.14 14 Foram estimados modelos ARMA, DI e TARDI com variáveis binárias para 1991.3 e 1993.4. No caso dos modelos TARDI, as variáveis binárias foram centralizadas em torno de sua média para evitar uma possível coluna de valores nulos na matriz de dados após divisões da amostra realizadas nesse tipo de modelo. Neste processo, os períodos de estimação e previsão permaneceram os mesmos.
A inclusão das variáveis binárias não altera a seleção das demais características em relação às especificações dos modelos para realizar previsões. Como exemplo, considere os modelos ARMA utilizados neste estudo. A especificação com apenas a segunda defasagem da própria variável, que é denominada de AR2 neste estudo, foi a que gerou menor EQM entre as demais especificações ARMA, tanto nos casos com a inclusão de variáveis binárias quanto nos casos sem essas.
Entretanto, quando comparadas às especificações dos melhores modelos, com e sem variáveis binárias, verificou-se que os modelos estimados sem essas variáveis geraram menores EQMS em relação às suas respectivas especificações que incluíram essas variáveis. A Tabela 3 apresenta os valores previstos e os EQMs dos modelos estimados com tratamento para outliers, utilizando as variáveis binárias para 1991.3 e 1993.4, que geraram menores EQMs dentro de seus respectivos tipos de modelo.
5_ Conclusões
O objetivo central deste trabalho foi o de identificar um modelo econométrico capaz de gerar previsões para a taxa de crescimento trimestral do PIB agrícola brasileiro mais eficientes do que as produzidas pelos modelos ARIMA. Para isso, modelos lineares e não lineares de Índice de Difusão (DI) foram utilizados.
Entre a classe de modelos ARMA(p,q), o modelo que continha apenas a segunda defasagem da variável dependente, denominado de AR2, foi o que gerou o menor erro quadrático médio de previsão (EQM), em torno de 0.02, apresentando as previsões mais eficientes entre as várias alternativas utilizadas (p=q={1,2,3,4}).
No que se refere ao desempenho dos modelos lineares de Índice de Difusão o que apresentou o menor EQM foi o modelo com quatro fatores denominado de DI(4). O EQM do DI(4) foi de 0.018, melhorando as previsões geradas pelo modelo AR2 em 10%. A possibilidade de a variável em análise apresentar ciclos econômicos foi considerada explicitamente neste estudo através da utilização de um modelo de Índice de Difusão com efeito threshold, denominado de TARDI.
O modelo TARDI com dois fatores, com a segunda defasagem da variável dependente e com In(pibt-1 / pibt-2) desempenhando o papel da variável threshold, foi o modelo que apresentou o menor EQM, apenas 0.016, entre todos os modelos testados neste estudo. Isso melhorou em 20% as previsões produzidas pelo AR2 e algo em torno de 11% em relação às previsões realizadas pelo modelo DI(4).
Os resultados referentes à eficiência preditiva dos modelos de Índice de Difusão corroboram os encontrados em Stock e Watson (1994), Tatiwa (2005) e por Tatiwa, Bierens e Castelar (2005). A possibilidade de utilizar um grande conjunto de informações, contidas em índices construídos com base em 83 variáveis macroeconômicas e 10 variáveis climáticas, e mesmo assim apresentar uma estrutura parcimoniosa em termos de parâmetros, pode explicar o bom desempenho dos modelos de Índice de Difusão para prever um passo à frente a taxa de crescimento do PIB agrícola brasileiro.
Artigo recebido em outubro de 2007;
aprovado em novembro de 2010.
E-mail de contato dos autoresrtf2@uol.com.br, joseniloojr@yahoo.com.br, lume1250@yahoo.com.br
- BOERO, G.; MARROCU, E. The performance of setar models : A regime conditional evaluation of point, interval and density forecasts The Warwick Economics Research Paper Series (TWERPS) 663, University of Warwick, Department of Economics, 2002
- BRANDÃO, Antonio S. P.; RESENDE, Gervásio C.; MARQUES, Roberta, W. C. Crescimento agrícola no período 1999-2004, explosão da área plantada com soja e meio ambiente no Brasil. Texto para Discussão do IPEA, nş 1.062, Rio de Janeiro, 2005. 30 p.
- CHAUVET, M. A monthly indicator of Brazilian GDP. Brazilian Economic Journal (Revista Brasileira de Economia), v. 21, 2001.
- CHAUVET, M.; LIMA E. C. R.; VASQUEZ, B. Forecasting Brazilian output in the presence of breaks: A comparison of linear and nonlinear models. Working Paper 2002-28 Series of The Federal Reserve Bank of Atlanta, 2002.
- CLEMENTS, M.P.; FRANCES, P.H.; SMITH, J. On setar non-linearity and forecasting. Erasmus School of Economics Research Paper EL9414-/A, 1999.
- CLEMENTS, M. P.; HENDRY, D. F. Forecasting economic time series United Kingdom: Cambridge University Press, 1998.
- CLEMENTS, M. P.; KROLZIG, H. M. A comparison of the forecast performance of Markov-switching and Threshold Autoregressive Models of US GNP. Econometrics Journal, n. 1, p. 47-75, 1998.
- CLEMENTS, M. P.; SMITH, J. A Monte Carlo study of the forecasting performance of empirical SETAR Models. Journal of Applied Econometrics, n. 14, p. 123-41, 1999.
- DIEBOLD, F. X.; NASON, J. A. Nonparametric exchange rate prediction. Journal of International Economics, n. 28, p. 315-332, 1990.
- DIJK, V. D.; SILIVERSTOVS, B. Forecasting industrial production with linear, nonlinear, and structural change models. Econometric Institute Report, n. 16, 2003.
- FORNI, M.; HALLIN, M.; LIPPI, M.; REICHLIN, L. The generalized dynamic-factor model: Identification and estimation. The Review of Economics and Statistics, v. 82, n. 4, p. 540-554, 2000.
- FREITAS, Rogério E.; SPOLADOR, Humberto F. S. Os termos de troca para a soja na agricultura brasileira. Texto para Discussão do IPEA, n. 1.239, Brasília, nov. 2006.
- GASQUES, J. G.; VILLA VERDE, C. M. Gastos públicos na agricultura, evolução e mudanças Texto para Discussão, n. 948, IPEA, p. 1-31, abr. 2003.
- HANSEN, B. E. Inference when a nuisance parameter is not identified under the null hypothesis. Econometrica, 64(2):41330, 1996.
- HANSEN, B. E. Inference in TAR Models. Studies in nonlinear dynamics and econometrics, v. 2, n. 1, 1997.
- HANSEN, B. E. Sample splitting and threshold estimation. Econometrica, v. 68, n. 3, p. 575-603, 2000.
- HANSEN, B. E. Evidence on structural instability in macroeconomics time series Technical Working Paper 164, National Bureau of Economic Research, 1994.
- HANSEN, B. E. Diffusion indexes Technical Working Paper 6702, National Bureau of Economic Research, 1998.
- HANSEN, B. E. Macroeconomic forecasting using diffusion indexes. Journal of Business & Economic Statistics, v. 20, n. 2, p. 147-162, 2002.
- TATIWA, R. F. Forecasting Quarterly Brazilian GDP growth rate with linear and nonlinear diffusion index models. 2005. 83p. Tese (Doutorado em Economia) CAEN - Universidade Federal do Ceará, 2005.
- TATIWA, R. F.; BIERENS, H.; CASTELAR, I. Forecasting Quarterly Brazilian GDP growth rate with linear and nonlinear diffusion index models. Revista Economia SELECTA, v. 6, n. 3, p. 205-229, 2005.
- TONG, H. Threshold Models in Non-Linear Time Series Analysis: Lecture Notes in Statistics 21 Springer-Verlag, Berlin, 1983
Apêndice I

 .
. Datas de Publicação
-
Publicação nesta coleção
20 Jul 2012 -
Data do Fascículo
Abr 2012
Histórico
-
Recebido
Out 2007 -
Aceito
Nov 2007