Resumen
La finalidad de este artículo es presentar algunas reflexiones teóricas y metodológicas que hemos incorporado al diseño un curso-laboratorio de Cálculo Diferencial, basadas en las configuraciones actuales de los procesos de aprendizaje y de enseñanza de esta asignatura. Del planteamiento y experimentación del curso surge como conclusión que la enseñanza actual del Cálculo exige la búsqueda y aprovechamiento de las experiencias de la nueva sociedad, la cual está rodeada de diferentes artefactos digitales que permiten rescatar el movimiento como núcleo conceptual de cálculo.
Palabras-clave:
Cálculo Diferencial; Procesos matemáticos; Mediación digital; Actividades interdisciplinarias
Abstract
The aim of this article is to present some theoretical and methodological reflections we have incorporated into the design of a lab-course called Differential Calculus, which is based on the current settings of the processes of learning and teaching of this subject. The approach and experimentation of the subject emerges as a conclusion that the current Calculus teaching requires finding and exploiting the experience of a new society, which is surrounded by different digital gadgets that allow the restoration of the movement as conceptual core of calculus.
Keywords:
Differential Calculus; Mathematical processes; Digital mediation; Interdisciplinary activities
1 Introducción
Reconocemos, en primera instancia, que el estudio de la variación y el cambio ha sido parte del desarrollo mismo de la cognición humana y que el Cálculo Diferencial nace de la necesidad de resolver problemas de variación, acumulación y tendencia. En los cursos de Cálculo de varias universidades –generalmente basados en los libros de texto –, los problemas de cambio y variación se presentan como ejemplos después de mostrar la teoría. Coincidimos con Moreno (2005)MORENO, M. El papel de la didáctica en la enseñanza del cálculo: evolución, estado actual y retos futuros. In: SIMPOSIO DE LA SOCIEDAD ESPAÑOLA DE INVESTIGACIÓN EN EDUCACIÓN, 9., 2005, Córdoba. Anales…Córdoba: Universidad de Córdoba, 2005. p. 81-96., quien menciona que tradicionalmente estos cursos se desarrollan a partir de la teoría, la cual necesitó del trabajo de una comunidad de matemáticos durante varios siglos; esto ha conllevado a que se pierda la esencia de ésta y que se olvide que surgió de la necesidad de resolver problemas de la vida cotidiana y de las ciencias.
La problemática aquí expuesta, se localiza en lo que han identificado algunos investigadores como pensamiento matemático avanzado; en esta línea, como lo reporta Dreyfus (1991)DREYFUS, T. Advanced mathematical thinking processes. In: Tall, D. (Ed.). Advanced mathematical thinking. Dordrecht: Kluwer Academic Publisher, 1991. p. 25-41., se ha generado conocimiento alrededor de los procesos cognitivos en los cursos de matemáticas universitarias. Por otro lado, han surgido estudios históricos y epistemológicos de los contenidos matemáticos, específicamente de conceptos de análisis, cálculo y álgebra, así como estudios didácticos en los que se aterrizan las reflexiones cognitivas en los currículos de estas asignaturas. Así también, y con mayor auge en los últimos años, emergen investigaciones asociadas al papel que juegan las tecnologías digitales en la enseñanza y aprendizaje de las matemáticas universitarias.
En este documento presentamos resultados de una investigación1 1 Proyecto 1341. Caracterización de las habilidades básicas del Pensamiento Variacional que son necesarias para la comprensión del Cálculo Diferencial. Vicerrectoría de Investigación y Extensión de la Universidad Industrial de Santander. , aún en curso, que ha tenido como objetivo: caracterizar las habilidades básicas del Pensamiento Variacional que son necesarias para la comprensión del Cálculo Diferencial. Los resultados obtenidos, más que ser afirmaciones contundentes, se consolidan en una serie de reflexiones teóricas y metodológicas que emergen del estudio y análisis de varias de las investigaciones realizadas en el campo. Estas reflexiones, a su vez, emergen del diseño e implementación de un curso-laboratorio de Cálculo Diferencial mediado por un software matemático interactivo alrededor de problemas de cambio, variación, interdependencia, aproximación y tendencia para tratar los conceptos de función, límites y derivada. Éste – a diferencia de un curso tradicional, en el que predomina el carácter estático de las representaciones de los objetos matemáticos y su objetivo principal apunta a estudiar los conceptos formalizados y aprender algoritmos para, posteriormente, aplicarlos – enfatiza en el desarrollo del pensamiento variacional, a partir de un enfoque de resolución de problemas en el que se espera que el estudiante sea quien construya las nociones asociadas a la variación (FIALLO; PARADA, 2014FIALLO, J.; PARADA, S. Curso de pre-cálculo apoyado en el uso de geogebra para el desarrollo del pensamiento variacional. Revista Científica, Bogotá, v. 20, p. 56-71, 2014.).
Las actividades del curso emergen de una comunidad de práctica de educadores matemáticos que siguen el modelo de reflexión y acción de Parada (2011)PARADA, S. Reflexión y acción en comunidades de práctica: un modelo de desarrollo profesional. 2011. 309 f. Tesis (Doctorado en Matemática Educativa) – Centro de Investigación y Estudios Avanzados del Instituto Politécnico Nacional, México D. F., 2011., éste se ha puesto en escena durante cuatro semestres consecutivos y ha beneficiado alrededor de 1075 estudiantes.
2 ¿Qué y cómo se constituye el estudio de la variación?
Importantes publicaciones dan cuenta de diferentes acercamientos metodológicos, éstos asociados al análisis del currículo como los de Vinner (1991)VINNER, S. The role of denitions in the teaching and learning of mathematics. In: Tall. D. (Ed.). Advanced Mathematical Thinking. Dordrecht: Kluwer Academic Publishers, 1991. p. 65-81. y Artigue (1997)ARTIGUE, M. La integración de calculadoras gráficas y formales en la enseñanza de las matemáticas en el bachillerato. In: REUNIÓN LATINOAMERICANA DE MATEMÁTICA EDUCATIVA, 11, 1997, Bogotá. Anales… Bogotá: Grupo Editorial Iberoamérica S. A, 1997. en los cuales se rescata la importancia de aprovechar las intuiciones de los estudiantes para la construcción de nociones del pensamiento matemático avanzado. En otros trabajos el foco recae en el estudio de los errores y dificultades de los estudiantes para comprender dichas nociones tal como lo reportan Artigue y Ervynck (1993)Artigue, M., and Ervynck, G. (1993). Proceedings of Working Group 3 on Student's Difficulties in Calculus, ICME-7, Québec, Canada., entre otros.
Comprender la variación implica explicar cómo se relacionan las magnitudes variables en un problema particular, así como medir y analizar cómo cambian estas magnitudes. Por ejemplo, desde los niveles de educación básica pueden analizarse los cambios en la temperatura, peso, posición, población, velocidad, entre otros. Los estudios sobre los fenómenos que cambian, han sido una poderosa motivación del hombre para construir modelos matemáticos, los cuales se han representado con ecuaciones que relacionan variables. Sin embargo, los estudiantes cuando interactúan con la noción de variación tienen serias dificultades, pues como lo señala Nemirovsky (1992)NEMIROVSKY, R. Students’ Tendency to Assume Resemblances between a Function and Its Derivative. Reports-Research/Technical, Massachusetts, v. 143, 1992. Disponible en: <http://edres.org/eric/ED351193.htm>. Acceso en: 15, mar. 2014.
http://edres.org/eric/ED351193.htm...
dicha interacción es compleja ya que involucra coordinación de muchas piezas diferentes de conocimiento y la resolución de problemas de este tipo implica usar técnicas no variacionales como las de semejanza. Al respecto, el autor enfatiza en la importancia de que los estudiantes analicen las funciones de forma local y global. Son las actividades de aprendizaje las que posibilitan que un sujeto empiece a recurrir a acercamientos alternativos, que les permiten conocer la información que proporciona la gráfica de una función y relacionarla con la gráfica de su derivada. A dicha forma de trabajo le llama acercamiento variacional.
En los Estándares Curriculares de Matemáticas de Colombia (MEN, 2006) se expone que el pensamiento variacional tiene que ver con el reconocimiento, la percepción, la identificación y la caracterización de la variación y el cambio en diferentes contextos, así como con su descripción, modelación y representación en distintos sistemas o registros simbólicos, ya sean verbales, icónicos, gráficos o algebraicos. Se menciona que este pensamiento cumple un papel preponderante en la resolución de problemas sustentados en el estudio de la variación y el cambio, y en la modelación de procesos de la vida cotidiana, las ciencias naturales y sociales y las matemáticas mismas.
Concordamos con estas precisiones, dado que enfatiza en la resolución de problemas que involucran el reconocimiento, la percepción, la identificación y la caracterización de la variación y el cambio en diferentes contextos; lo que implica relacionar magnitudes variables en sus diferentes representaciones. Cuando los estudiantes ingresan a la educación superior, su pensamiento variacional requiere, a su vez, de una madurez de sus pensamientos métrico, numérico, geométrico e incluso aleatorio, ya que la actividad matemática que se espera que éstos realicen requiere entrelazar los objetos matemáticos propios de cada pensamiento (datos, números, medidas, espacios y formas), los cuales requieren engranarse para desarrollar los procesos matemáticos necesarios para la resolución de problemas (engranaje entendido como el mecanismo utilizado para transmitir potencia y dinamismo de un proceso a otro y desarrollar la actividad matemática propia del pensamiento variacional).
Lo que esperamos es que la movilización de los objetos matemáticos de dicho engranaje se dinamicen funcionalmente, potenciando la comprensión y construcción del conocimiento matemático y el desarrollo del pensamiento variacional, logrando aplicarlo de forma variada, crítica, reflexiva en diferentes situaciones y contextos. Dicha dinamización implica el desarrollo de procesos generales del pensamiento matemático en el dominio específico de los diferentes tipos de pensamiento.
En el diseño del curso-laboratorio de Cálculo Diferencial (contexto de nuestra investigación) se hace uso de los artefactos digitales con las que contamos hoy; para él se plantearon actividades creadas desde y para un medio dinámico-digital, las cuales hemos empleado en la fase experimental del curso. Las representaciones visuales son mucho más flexibles. Por ejemplo, se puede trazar la recta tangente a la gráfica de una función en un punto y luego desplazarla a lo largo de la misma, de manera que se adapte a las características de la curva en cada punto (creciente, decreciente, punto de inflexión, máximo, mínimo, etcétera). Poder hacerlo genera en el estudiante el sentimiento de estar trabajando con objetos concretos que puede manejar a través de las nuevas representaciones digitales.
3 Una estructura curricular para la era digital
En las últimas décadas, han surgido considerables contribuciones sobre cómo y cuándo usar las tecnologías digitales para aproximarse significativamente a los objetos del cálculo, entre ellos se rescatan importantes aportes de Cuevas y Pluvinage (2003)CUEVAS, C.; PLUVINAGE, F. Les projets d'action pratique, éléments d'une ingénierie d'eseigments des mathématiques. Annales de didactique et sciences cognitives, Paris, v. 8, p. 273-392, 2003., Kaput, Blanton y Moreno (2008)KAPUT, J.; BLANTON, M.; MORENO, L. Algebra from a symbolization point of view. In: KAPUT, J.; CARRAHER, D.; BLATNTON, M. (Ed.). Algebra in the early grades. Mahwah NJ: Lawrence Erlbaum Associates, 2008. p. 19-56., Hitt (2014)HITT, F. Nuevas tendencias en la enseñanza del cálculo: la derivada en ambientes TICE. Revista AMIUTEM, Ciudad Guzmán, Jalisco, v. 2, n 2, p. 1-19, 2014, Machin y Rivero (2002)MACHIN, M.; RIVERO, D. Students’ attitudes towards Mathematics and computers when using derive in the learning of calculus concepts. The International Journal of Computer Algebra in Maths Education, Plymouth, v. 9, n. 4, p. 259-283, 2002., Tall (1995)TALL, D. Cognitive Growth in Elementary and Advanced Mathematical Thinking. Plenary lecture, In: PSYCHOLOGY OF MATHEMATICS EDUCATION, 19., 1995, Recife. Proceedings… Recife: Universidade Federal de Pernambuco, 1995. p. 161-175., Guin y Trouche (1999)GUIN, D.; TROUCHE, L. The complex process of converting tools into mathematical instruments: the case of calculators. International Journal of Computers for Mathematical Learning, Netherlands, v. 3, p. 195-227, 1999, Moreno (2014)MORENO, L. Educación Matemática: del signo al pixel. Colombia: Universidad Industrial de Santander, 2014., entre muchos otros, quienes preponderan la necesidad de incorporar las tecnologías en la enseñanza y aprendizaje de las nociones del cálculo y del álgebra, pues éstas le aportan herramientas para visualizar, manipular, explorar, conjeturar dinámicamente los objetos matemáticos.
La cognición humana cambia, en particular porque cambian los mecanismos de mediación y en consecuencia son más los artefactos culturales que pueden ser internalizados. Hoy en día, con la perspectiva histórica que se tiene, se puede extraer mayores beneficios que los que estaban al alcance de los estudiantes de entonces.
3.1 Núcleos conceptuales
El diseño curricular del curso-laboratorio que aquí mencionamos pretende, desde un enfoque de resolución de problemas, aportar al desarrollo de los procesos matemáticos de comunicación, representación, proposición, comparación y ejercitación de procedimientos, y razonamiento y demostración, para la comprensión de los conceptos de función, límites y derivadas, agrupados en los núcleos conceptuales que describimos a continuación.
El cambio como núcleo conceptual del Cálculo surge de resolver problemas en los que se requiere identificar y usar variables, no como una letra que representa un número o el valor desconocido en una ecuación, sino las variables como cantidades mesurables, que cambian cuando las situaciones en que ocurren cambian. Al respecto, Steen (1998)STEEN, L. La enseñanza agradable de las matemáticas. México: Limusa, 1998. plantea que, en general, las variables no tienen trascendencia en sí mismas sino cuando se relaciona con otras variables, por lo que plantea que los estudiantes deberían reconocer la variación directa, inversa, acelerada, convergente, cíclica y escalonada.
Todas estas variaciones se pueden representar en movimiento a través de una simulación en un medio digital como GeoGebra, que permite visualizar los variantes e invariantes, para poder analizar y comprender las propiedades que caracterizan a cada una de ellas. Este acercamiento a la variación involucra el concepto de función como la generalización de la interdependencia entre magnitudes variables.
El estudio de problemas de aproximación nos lleva a los conceptos de límites y derivadas. A través del problema de hallar la velocidad instantánea o de hallar la pendiente de la recta tangente, llegamos al concepto de límite por aproximaciones o el estudio de los infinitesimales. Al respecto, Aleksandrov et al. (1994)ALEKSANDROV, A. D. et al. La matemática: su contenido, métodos y significado. Madrid: Alianza Editoral, 1994. exponen que el método del límite consiste en determinar el valor exacto de una magnitud, determinando primero, no la magnitud sino realizando una serie de aproximaciones a ella, cada una de las cuales es más precisa que la anterior. Del examen de esa cadena de aproximaciones se determina unívocamente el valor exacto de la magnitud. Por este método, que es en esencia profundamente dialéctico, se obtiene una constante fija como resultado de un movimiento.
La tendencia como núcleo conceptual surge cuando se usa la derivada para introducir el concepto de límite de una función. Así, la tendencia, como lo mencionan García, Serrano y Díaz (2002)GARCÍA, G.; SERRANO, C.; DÍAZ, H. La aproximación: una noción básica en el cálculo: un estudio en la educación básica. Bogotá: Universidad Pedagógica Nacional, 2002. exige una visualización de tipo numérico de los procesos infinitos de aproximación como un todo, lo que permite aceptar cierta regularidad en las aproximaciones obtenidas en el proceso para intuir un resultado final.
3.2 Procesos matemáticos en el estudio de la variación
Azcárate y Camacho (2003)AZCÁRATE, C.; CAMACHO, M. Sobre la investigación en Didáctica del Análisis Matemático. Boletín de la Asociación Matemática Venezolana, Caracas, v. 10, n. 2, p. 135-149, 2003. resaltan algunos procesos matemáticos que están inmersos en el pensamiento matemático avanzado, entre ellos: la abstracción, el análisis, la categorización, la conjeturación, la generalización, la síntesis, la definición, la demostración, la formalización. Además, reconoce que desde otro orden deben considerarse habilidades para representar, conceptualizar, inducir y visualizar.
En los siguientes apartados presentamos la caracterización y ejemplificación de los procesos y habilidades con los cuales hemos fundamentado, teórica y metodológicamente, el curso-laboratorio del que emergen las reflexiones aquí expuestas. Aunque los presentamos por secciones, no debemos interpretarlos de manera independiente ni disyunta, por el contrario todos los procesos son dependientes y complementarios entre sí.
3.2.1 Proceso de comunicación
Todo individuo necesita construir, interpretar y conectar varias representaciones de ideas, hacer observaciones y conjeturas, formular preguntas, y producir argumentos persuasivos y convincentes. La comunicación matemática tiene que ver con los modos de interpretación que los estudiantes le dan a un objeto matemático, haciendo uso de su lenguaje cotidiano para expresar sus ideas respecto a él. Específicamente en un curso de Cálculo Diferencial, un estudiante necesitará comunicar ideas relacionadas con el cambio, la variación, la interdependencia, la aproximación y la tendencia para tratar los conceptos de función, límites y derivada. En Rojas, Suárez y Parada (2014)ROJAS, S.; SUÁREZ, S.; PARADA, S. Presaberes matemáticos con los que ingresan estudiantes a la universidad. In: ACTA LATINOAMERICANA DE MATEMÁTICA EDUCATIVA ALME, 27., 2014, México D. F. Anales… México D. F.: Comité Latinoamericano de Matemática Educativa A. C., 2014. p. 1169-1176. se caracterizan los procesos comunicativos y, aquí, las describimos específicamente asociadas a la variación; así: i) Interpretar, consiste en dar sentido a la estructura de un problema; así como entender o leer demostraciones, definiciones, gráficos, mapas o esquemas matemáticos en los que se planteen o describan argumentos de un objeto matemático; ii) Explicar, implica exponer la descripción del objeto de conocimiento con palabras claras o ejemplos, expresando el porqué de un proceso, con la finalidad de hacer inteligible a otro ese objeto de conocimiento. Los artefactos digitales actuales aportan herramientas para expresar significados visuales que complementan las representaciones convencionales; iii) No es posible convencer sin dar a comprender, lo que implica Justificar y argumentar. Argumentar consiste en convencer o defender una idea o los resultados obtenidos por medio de razones relevantes; va acompañada del uso adecuado del lenguaje y del discurso matemático.
En lo que sigue, presentamos un diseño de clase del curso-laboratorio para ilustrar los procesos y habilidades que consideramos necesitan potenciarse para la comprensión de las nociones básicas del Cálculo Diferencial. El diseño de clase llamado Cuerdas vibrantes tiene una estructura interdisciplinaria (entre la matemática, la música y la física) mediada por las tecnologías digitales. La actividad se inspira en la propuesta planteada por Conde (2013)CONDE, A. La unidad relativa como vínculo cognitivo entre el tiempo musical y las fracciones. 2013. 192 f. Tesis (Doctorado en Matemática Educativa) – Centro de Investigación y Estudios Avanzados del Instituto Politécnico Nacional, México D.F., 2013., en el que se dota a objetos matemáticos de significado desde el contexto musical. Éste diseño permite dar significado a un fenómeno natural que no puede interpretarse desde una sola disciplina y es el caso de la medición de frecuencias de los sonidos musicales, pues además de involucrarse las notas musicales (Do, re, mi, fa, sol, la, si, do), se requiere de las matemáticas para comprender la medida de los fraccionamientos de la cuerda vibrante y de la física para dar significado al fenómeno acústico producido por dichas particiones. Junto con el diseño del curso-laboratorio, también se exhibirán algunos episodios de la puesta en escena del mismo (los episodios se recuperan de la segunda experimentación del curso con un grupo 30 estudiantes de nuevo ingreso a la universidad inscritos a programas de ingenierías y ciencias básicas).
En la Figura 1 exponemos un fragmento histórico sobre los vínculos entre las matemáticas (esta se presenta como actividad inicial de la sesión de trabajo), la música y su evolución formal en el mundo occidental. Iniciar desde estos hechos históricos revela a los estudiantes una conexión entre éstas disciplinas que tal vez él no conocía. Por otra parte, la simulación del monocordio, descrito en el fragmento histórico, ofrece al estudiante una representación visual que consiste en las particiones de una cuerda y sus relaciones fraccionarias entre ellas y una representación sonora correspondiente a la asignación de una frecuencia sonora a cada partición de la cuerda. La simulación y la manipulación de la misma, induce a los estudiantes a dar una interpretación del fenómeno en estudio. Dicha interpretación está determinada por la percepción visual del estudiante que opera en aprehender algunos rasgos sobresalientes de los objetos. Rasgos que necesariamente conducen a un conjunto de procesos mentales que tienen lugar entre la recepción visual del objeto y la construcción de su representación mental.
Entre tanto, la percepción auditiva que ocurre simultáneamente con la recepción del sonido a través de los oídos, implica el desciframiento (reconocer, discriminar e interpretar) de estímulos auditivos asociándolos a experiencias previas (McADAMS, 1993McADAMS, S. Recognition of sound sources and events. In: McADAMS, S.; BIGAND, E. (Ed.). Thinking in Sound: the Cognitive Psychology of Human Audition. Oxford: Oxford University Press, 1993. p. 146-198.). Es decir, se apela a la representación mental en forma de memoria auditiva para establecer relaciones y dar sentido a los sonidos percibidos. Esperamos que al escuchar los sonidos musicales con atención puedan interpretar las diferencias entre las frecuencias sonoras.
Hasta aquí, consideramos necesario y suficiente que los estudiantes realicen interpretaciones aparentemente separadas del mismo fenómeno. En este momento nos interesa estimular la memoria auditiva que se desarrolla en gran parte por la repetición de estímulos auditivos que se perfeccionan y fortalecen a través de la atención.
En la actividad de la Figura 2 se presenta una simulación con dos representaciones visuales y una sonora. La simulación ilustra la construcción de la escala musical con sus expresiones fraccionarias y su representación en un plano cartesiano.
Con esta actividad buscamos extender la interpretación de los estudiantes sobre el fenómeno percibido para generar sus explicaciones de forma oral, escrita o corporal de la variación inversa que existe entre las dos magnitudes: a menor longitud de la cuerda-mayor la frecuencia.
Continuando con nuestra ilustración, consideramos que la justificación y la argumentación pueden apoyarse en las representaciones usadas hasta el momento. Por ejemplo, para justificar la variación inversa que existe entre las dos magnitudes: a menor longitud de la cuerda, mayor la frecuencia. Independientemente de los conocimientos musicales del estudiante, el oído tiene la posibilidad de distinguir características particulares que diferencia un sonido de otro. Estas características particulares se denominan cualidades del sonido. El argumento del estudiante puede ser la explicación sobre los cambios de las longitudes de la cuerda que se hacen cada vez más pequeños, entonces se produce un efecto en los sonidos que los hacen cada vez más agudos. Es decir, establece una diferencia entre sonidos graves y agudos, dependiendo de la longitud de la cuerda. Ahora, si cuenta con conocimientos de la física su argumento será más técnico, podría decir, que en la actualidad las notas musicales no se definen a partir de la longitud de un objeto vibrante, sino a partir de las frecuencias de vibración de la onda sonora emitida por el objeto.
Estudiante. 1Se mueve más (hace alusión al movimiento de la cuerda de menor longitud respecto a la anterior de mayor longitud)Profesor¿Por qué se mueve más?Estudiante. 1Porque mayor frecuencia genera mayor vibración
3.2.2 Proceso de formulación, comparación y ejercitación de procedimientos
Los procedimientos se refieren a las actuaciones, destrezas, estrategias, métodos, técnicas, usos y aplicaciones diversas que un estudiante realiza para resolver problemas de manera cada más hábil e independiente. En general, este proceso en la solución de problemas de variación y cambio requiere de habilidades para: i) Dominar los sistemas numéricos, sus operaciones y estructuras, en la resolución de problemas de Cálculo Diferencial, se espera que los estudiantes dominen el campo de los números reales y sus operaciones, además que establezcan y justifiquen relaciones entre diferentes notaciones de números reales para decidir sobre su uso en una situación dada; ii) Calcular magnitudes utilizando diferentes procesos e instrumentos, para ello se necesita la comprensión y familiarización con las unidades, procesos e instrumentos comunes usados en la toma de medidas de las magnitudes más usuales como longitud, tiempo, velocidad, aceleración, amplitud, capacidad, peso y superficie. Además de la aplicación de las técnicas y fórmulas apropiadas para la resolución de problemas de variación y cambio; iii) Construir modelos geométricos de los objetos matemáticos para expresar la variación, aquí esperamos que el estudiante manipule o realice representaciones de objetos bidimensionales o tridimensionales en el plano; emplee procedimientos de tipo gráfico que suponen expresar una imagen visual de un concepto o relación variacional; describa y modele fenómenos periódicos del mundo real usando relaciones y funciones; y iv) Identificar, relacionar y establecer propiedades entre las magnitudes variables de una situación, esta habilidad se ve reflejada cuando los estudiantes pueden modelar situaciones de cambio a través de las funciones, gráficas y tablas; comprender y hallar razones de cambio; analizar las relaciones y propiedades entre las expresiones algebraicas y gráficas y analizar los procesos infinitos que subyacen en las notaciones decimales.
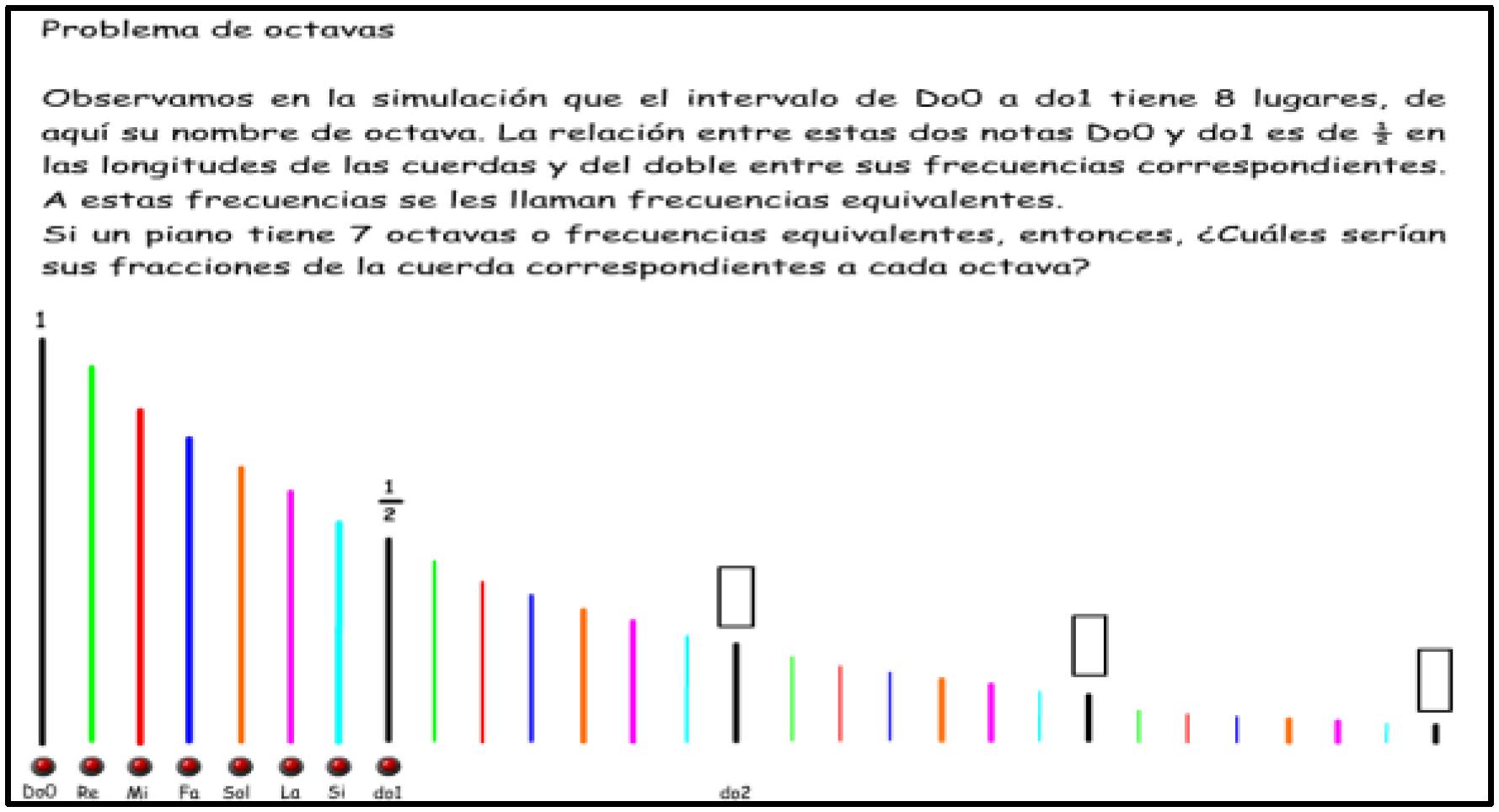
Continuando con nuestro ejemplo, para resolver el problema de octavas que se presenta en la Figura 3, les proponemos a los estudiantes que realicen cálculos numéricos a lápiz y papel. Anunciamos que los estudiantes hallen la secuencia aplicando el operador (½ de) y con esto conseguimos que ellos encuentren algunos términos de la sucesión.
Es importante orientar esta actividad para que el estudiante no pierda de vista que cada fraccionamiento hace más pequeña la magnitud, pues algunos de ellos llegan a la universidad con la dificultad de extender las propiedades de los números naturales a los números racionales expresados como fracciones (concibe el numerador y el denominado como números independientes). El problema planteado aparentemente es sencillo para estudiantes universitarios, sin embargo, además de lograr reforzar presaberes asociados a las fracciones, posibilita abordar las nociones de variación que hemos mencionado.
Estudiante 2La longitud está reduciéndose (referencia a la Figura 3) y cada octava es la mitad de la primera, entonces ésta es una octava (señala do2) y cuando llego a la segunda octava (al do1). Entonces ésta (do1) va a ser la mitad de la anterior (do2) y así.
 . De esta forman se puede generar una sucesión de octavas. No obstante, para este escrito la orientación del problema coincide con la generación de octavas desde una cuerda vibrante, sus fraccionamientos y sus sonidos asociados. La relación entre dichas magnitudes se evidencia en la siguiente explicación:
. De esta forman se puede generar una sucesión de octavas. No obstante, para este escrito la orientación del problema coincide con la generación de octavas desde una cuerda vibrante, sus fraccionamientos y sus sonidos asociados. La relación entre dichas magnitudes se evidencia en la siguiente explicación:  , esta expresión la podemos ilustrar con los datos de la
, esta expresión la podemos ilustrar con los datos de la De la explicación verbal y la representación de la Figura 4 del estudiante, podríamos inferir que éste modela los fraccionamientos de la cuerda a través de gráficas e identifica una magnitud invariante (1/2) cuya iteración genera un patrón.
Otro aspecto que indagamos con las preguntas de la Figura 5 es que los estudiantes realicen predicciones sobre el fenómeno acústico, soportadas en sus ideas intuitivas conducentes a reflexiones como: ¿hasta qué momento podríamos fraccionar la cuerda?, ¿el sonido producido por esa última partición podría ser percibida por el oído humano?, ¿sigue existiendo sonido aunque no sean percibidos por los seres humanos? etc. Estas reflexiones podrían dar claridad a los estudiantes sobre los dominios de las disciplinas implicadas. Es decir, desde el contexto musical los sonidos percibidos por el ser humano son los que tienen sentido musical.
Estudiante 2Si tengo menor longitud la frecuencia es mayor, pero si tengo mayor longitud la frecuencia es menor, tanto la c como la d son válidas (c y d incisos de la Figura 5). Si nos guiamos por el gráfico, vamos de mayor a menor, pero si yo lo tomo de derecha a izquierda, entonces sería de menor a mayor, ya aumenta la longitud, la frecuencia va a ser menor, es la d.Estudiante. 3Pero teniendo en cuenta la simulación, la respuesta es la c.
Desde nuestro punto de vista, las posturas de los Estudiantes 2 y 3 son válidas. Los dos estudiantes comparan las longitudes de las particiones de la cuerda con sus frecuencias sonoras, lo que permite reconocer la interdependencia entre éstas. La interdependencia experimentada en la simulación aporta a los estudiantes una la sensación física de variación por medios sonoros, en los que se perciben los cambios de los sonidos asignados a los fraccionamientos de la cuerda. La física desde el estudio del fenómeno vibratorio, da cuenta de la existencia de frecuencias sonoras aunque no sean percibidas por nosotros y ante la imposibilidad física de fraccionamiento de la cuerda la matemática permite modelar el fenómeno inicialmente percibido por los sentidos.
El propósito de la actividad siguiente es sondear sobre ¿cuál sería la última fracción de la cuerda que podrimos hallar? Para ello proponemos hacer una extensión numérica (mínimo de 15 términos) en una tabla y con dichos datos construir la gráfica en el plano cartesiano a lápiz y papel. Aquí, deseamos que los estudiantes construyan una idea intuitiva sobre la no existencia de una última fracción. Al respecto se evidencia que los estudiantes encuentran por medio de aproximaciones numéricas una tendencia cuando el proceso se vuelve infinito para encontrar la última fracción. Pero, como se muestra en la siguiente discusión, algunos estudiantes aun no pueden concluir sobre la no existencia del último elemento, situación que podría atribuirse a las restricciones del lápiz y papel.
Profesor¿Llega a cero?Estudiante 4No, no llega a ceroProfesor¿Por qué?Estudiante 5Porque es infinitoEstudiante 5Nunca va a ser cero.Profesor¿Cuál sería el último valor?Estudiante 5Uno sobre infinito
En este caso, el Estudiante 5 podría realizar un número limitado de cálculos aritméticos por las restricciones físicas del papel. Sin embargo, él intuye que esta búsqueda del último elemento requiere de un proceso de divisiones sucesivas conducentes a un proceso infinito en el campo de las matemáticas. Aquí, creemos importante el uso del software porque los estudiantes confrontan y corroboran sus representaciones a lápiz y papel con sus correspondientes representación dinámica. Esto les posibilita a ellos visualizar el comportamiento de los fraccionamientos de la cuerda vibrante, relacionar variables e inferir la tendencia. Además de confirmar sus conjeturas cimentadas en la actividad a lápiz y papel sobre el tratamiento de un proceso infinito al realizar iteraciones infinitas.
Estudiante 6Entre más fracciones haga más pequeña va a ser la cuerda. Pero nunca va a llegar a cero, nunca va a tocar a cero. Matemáticamente la cuerda la voy a poder dividir infinitas veces.Profesor¿cómo sabe?, ahí se ve que toca (Figura 6).Estudiante 6Es que la fracción es muy pequeña, pero no toca a cero. Puedo seguir acercando muchísimo más, eso quiere decir que la fracción es mínima.
Por lo general, hallar la expresión a partir de una tabla o gráfica, es complejo para los estudiantes ya que tradicionalmente en la matemática escolar se privilegia la conversión de la expresión o tabla a la gráfica, y pocas veces el proceso inverso como lo planteamos en la pregunta ¿cuál es la expresión algebraica que permite construir la gráfica que modela el fenómeno de fraccionamientos de la cuerda?
Profesor¿16 cómo se podría expresar en potencias?Estudiante 72*2=4*2=8*2=16Profesor¿Cuántas veces multiplicó por 2?Estudiante 74, entonces 2 a la n, sería el número de veces que se encuentran acá (señala en la tabla la fila 18). Entonces ½ a la ésta celda (Figura 7).Estudiante 8Yo encontré una forma más fácil, dividí el resultado en dos, en dos….Profesor¿Cuál sería la centésima fracción? (pregunta para los estudiantes 7 y 8)Estudiante 7½ elevado a la 100.
3.2.3 Proceso de representación
Queremos llamar la atención acerca de los orígenes de este cálculo [Cálculo Diferencial e Integral] que fueron principalmente los nuevos problemas de la mecánica y los viejos problemas de la geometría, consistentes estos últimos en la determinación de tangentes a una curva dada y en el cálculo de áreas y volúmenes.
En el caso de la cognición matemática, las funciones de mediación las desempeñan básicamente los sistemas de representación aritméticos, geométricos, algebraicos, métricos, gráficos, analíticos, gestuales etc. Sin dichos sistemas no hay acceso posible a los objetos matemáticos. Aún más, no solo no hay acceso sino que dichos objetos no tienen una existencia previa, independiente de sus representaciones (MORENO, 2014MORENO, L. Educación Matemática: del signo al pixel. Colombia: Universidad Industrial de Santander, 2014.). Las representaciones dinámicas por un software de matemática interactiva se filman, se exploran mediante el movimiento lo cual permite al estudiante una nueva interpretación y abrir la puerta a nuevas estrategias de exploración y justificación de un problema matemático.
Las habilidades consideradas dentro del proceso de representación son: i) Construir representaciones de los objetos matemáticos (no necesariamente las usuales), los estudiantes necesitan desarrollar la capacidad de crear representaciones para organizar, registrar y comunicar ideas matemáticas. La modelación y la simulación de un problema de variación y cambio en un medio digital, permite visualizar las variantes e invariantes del problema, permite ver qué variables y relaciones entre variables son importantes, ver atributos (lineal, periódico, simétrico, continuo, uniforme); ii) Interpretar diferentes representaciones de los objetos matemáticos, los estudiantes pueden ver en una gráfica o modelar con las manos el comportamiento tendencial de las gráficas (crecimiento, decrecimiento, máximos, mínimos), interpretar la derivada como la pendiente de la recta tangente; en una tabla encontrar patrones y regularidades numéricas, analizar la aproximación y la tendencia, comprender la derivada como razón de cambio; y utilizar las fórmula algebraica para realizar estudios analíticos y demostrar la validez de los resultados empíricos obtenidos por aproximación; iii) Reconocer, relacionar y conectar las diferentes representaciones de un mismo objeto matemático a través de sus invariantes, a través del reconocimiento de los variantes e invariantes, los estudiantes pueden relacionar y conectar las diferentes representaciones gráficas bidimensionales y tridimensionales, algebraicas, numéricas y geométricas del mismo objeto matemático. Lo que posibilita establecer modelos matemáticos de distintos niveles de complejidad, a partir de los cuales se pueden hacer predicciones, utilizar procedimientos numéricos, geométricos y analíticos, obtener resultados y verificar que tan razonable son éstos respecto a las condiciones iniciales del problema.
Por las características particulares de la integración interdisciplinar de este curso-laboratorio, recurrimos a artefactos computacionales que permiten crear conexiones entre percepciones y representaciones estáticas y dinámicas de los objetos matemático-musicales. En concordancia con las formas de percibir los objetos matemático-musicales se han construido simulaciones en Flash Macromedia CS32 2 Lenguaje de programación orientado a objetos Adobe Flash Macromedia CS3 , en la cual se asigna frecuencias sonoras a las longitudes de las particiones de una cuerda vibrante, lo que da sentido a las nociones integradas desde las disciplinas involucradas. En esta actividad se potencializa el uso del software para extender de forma numérica y gráfica de procesos iterativos que con lápiz y papel difícilmente pueden lograrse.
Evidenciamos en el desarrollo del curso-laboratorio que los estudiantes usan la simulación del problema de octavas, como extensor en la construcción de sus propias representaciones. Dicha representación se basa en ideas intuitivas sobre el efecto físico de fenómeno sonoro percibido. Aunque el problema no implica complejidad, los estudiantes, en su mayoría, prefieren construir la representación a lápiz y papel para dar solución aritmética al problema. También se pudo observar que para los estudiantes fue difícil determinar en las representaciones a lápiz y papel las variables en el plano, pero la mediación del software (con sus representaciones dinámicas) les permitió explorar y verificar sus conjeturas.
La habilidad de interpretación de representaciones se posibilita con actividades que permitan la constante articulación de las representaciones que dan significado al objeto. En la actividad interdisciplinaria que venimos mostrando, además de las representaciones visuales se ofrece a los estudiantes una representación auditiva de los objetos matemáticos, que puede dar significado a la variación inversa experimentada por ellos en un fenómeno sonoro. Las experiencias de los estudiantes permiten discriminar, comprender y tomar decisiones relacionadas a los usos de objetos matemático-musicales en ciertas situaciones requeridas.
Las relaciones y conexiones de las representaciones permiten transitar a los estudiantes por significados asociados a ellas. Es decir, desde la simulación del monocordio se introduce un primer significado de la fracción como parte-todo que se experimenta al dividir el todo o la unidad, estableciendo una relación entre dos magnitudes definidas. De igual forma, se establece un significado de medida al establecer comparaciones entre longitudes de las fracciones de la cuerda vibrante. No obstante, en el planteamiento del problema de octavas se propone la división entre partes iguales precisada mediante las iteraciones del operador matemático (1/2 de…), que también da significado de la fracción como operador. Consideramos que el proceso iterativo le aplica movimiento a la representación, la cual produce una sensación de variación observada en las representaciones pictóricas y percibidas acústicamente, lo cual significa dotarlo de significado sensorial.
3.2.4 Proceso de razonamiento y demostración
La búsqueda de solución a los problemas de la mecánica y de la geometría, llevaron a varios de los grandes matemáticos a la búsqueda de patrones, regularidades y generalización a través de la observación, experimentación e intuición, para que posteriormente otros grandes matemáticos organizaran y sistematizaran las ideas en torno a definiciones, axiomas y teoremas. Varios de los conceptos trabajados en los inicios del cálculo fueron asumidos como verdaderos porque validaban las ideas y conjeturas planteadas por la intuición, la experimentación y la inducción. Sin embargo, a partir de la axiomatización de las ideas del cálculo y la época de las matemáticas modernas, la intuición y la inducción pasaron a un segundo plano, dando paso a un exagerado énfasis en el rigor, que conllevó a la tensión entre el razonamiento intuitivo, inductivo y el deductivo con las debidas consecuencias en la enseñanza de las matemáticas (MORENO, 2014MORENO, L. Educación Matemática: del signo al pixel. Colombia: Universidad Industrial de Santander, 2014.).
Por otro lado, desde la didáctica de las matemáticas se ha planteado que el papel de una demostración no es solamente mostrar la validez del mismo, sino también mostrar las razones de esa validez. Una demostración debería permitir comprender el teorema, no solamente decir qué es verdadero sino, también, decir por qué es verdadero. Teniendo en cuenta lo anterior y la metodología del curso-laboratorio consideramos que las habilidades requeridas en el proceso de razonar sobre fenómenos de variación corresponden a: i) Conjeturar, implica que el estudiante continuamente esté planteando hipótesis como producto de la exploración, visualización, experimentación, análisis, descubrimiento, generalización y deducción de relaciones, propiedades y regularidades de las funciones, límites y derivadas y sus diferentes representaciones; ii) Demostrar, incluye todos los argumentos planteados por los estudiantes para explicar, verificar, justificar o validar con miras a convencerse a sí mismo y a los demás de la veracidad de una afirmación matemática. Esta caracterización de demostración permite considerar varios tipos de demostración, producto de un razonamiento intuitivo, inductivo, deductivo o abductivo (FIALLO, 2011FIALLO, J. Estudio del proceso de demostración en el aprendizaje de las Razones Trigonométricas en un ambiente de Geometría Dinámica. 2011. 267 f. Tesis (Doctorado en Didáctica de las Matemáticas) – Universidad de Valencia, Valencia, España, 2011.).
Estudiante 9Cuando los fraccionamientos de la cuerda es infinito, el software coloca la fracción en cero, pero realmente no es cero, es una aproximación que hace el programa a cero porque es un valor muy pequeño (Figura 8)
Esta hipótesis también es confirmada por medio de interacciones con la representación gráfica de los términos numéricos, particularmente, con el uso de la herramienta Zoom de Acercamiento, el estudiante observará que la curva se aproxima tanto como se quiera al eje x, pero que ésta no toca al eje x en algún punto.
Aquí, la noción de tendencia se hace evidente: a iteraciones infinitas de la sucesión, esta tiende a cero. Sin dar definiciones, por medio de ideas intuitivas estamos promoviendo la comprensión de la noción de Límite de una sucesión.
4 Reflexiones finales
En el desarrollo del escrito, hemos procurado mostrar con una experiencia (aplicación de una actividad interdisciplinar), la forma en que se puede integrar la tecnología alrededor de la resolución de un problema que articula las nociones de variación, cambio, aproximación y tendencia, permitiéndoles a los estudiantes desarrollar habilidades de los procesos matemáticos y comprender el concepto de función como interdependencia entre dos magnitudes variables, como una gráfica o una tabla que asigna a cada magnitud independiente un único valor.
Los estudiantes pueden llegar a la expresión algebraica de la función, analizando el patrón en la tabla hecha a lápiz y papel (si usa la representación fraccionaria en lugar de la representación decimal), o en la tabla interactiva de la hoja de cálculo por la necesidad de buscar una generalización. Otro concepto que surge de manera natural por la resolución del problema en la hoja de cálculo y las preguntas planteadas en la actividad, es la del infinito potencial y actual. Si el estudiante usa el redondeo de dos cifras decimales que trae por defecto el software, éste muestra a partir de la séptima fila una lista de ceros, lo que debe ser aprovechado por el profesor para cuestionar y crear la necesidad de aumentar el redondeo y discutir si realmente podemos decir que en el infinito la sucesión es cero. Estas acciones nos conducen a las ideas de aproximación y tendencia, articuladoras del concepto de límite.
Consideramos que las experiencias de los estudiantes a partir de ideas intuitivas, les aportan elementos suficientes para argumentar y verificar ideas matemáticas. En este sentido, los estudiantes pueden dar una explicación y una argumentación a la afirmación: n aumenta, la imagen de  , teniendo claridad de las nociones implícitas de dicha afirmación ya trabajadas durante el desarrollo del curso-laboratorio. La imagen y la tabla dinámica le ayudan al estudiante a encontrar argumentos como que a medida que
, teniendo claridad de las nociones implícitas de dicha afirmación ya trabajadas durante el desarrollo del curso-laboratorio. La imagen y la tabla dinámica le ayudan al estudiante a encontrar argumentos como que a medida que  se acerca a cero, pero no atraviesa el eje x porque ésta nunca es negativa; o que la fracción siempre se hace más pequeña porque el denominador de la fracción es cada vez más grande, pero nunca llega a ser cero.
se acerca a cero, pero no atraviesa el eje x porque ésta nunca es negativa; o que la fracción siempre se hace más pequeña porque el denominador de la fracción es cada vez más grande, pero nunca llega a ser cero.
Mediante esta experiencia, damos cuenta de habilidades de cada uno de los procesos matemáticos asociados al desarrollo del Pensamiento Variacional las cuales son necesarias para la comprensión del Cálculo Diferencial; consideramos entonces que este trabajo se constituye un aporte para la educación matemática, específicamente al pensamiento matemático avanzado, pues puede orientar la formación de profesores universitarios y la reflexión curricular sobre los cursos de Cálculo Diferencial en los que se aprovechen los situaciones interdisciplinarias.
Un valor agregado de este curso-laboratorio en el contexto interdisciplinar, es que además de las representaciones semióticas requeridas por la naturaleza de los objetos matemáticos, podríamos lograr dar un significado auditivo a un objeto matemático, en este caso de la variación. Si los estudiantes interactúan con dichas representaciones de la escala musical, asociadas a la estructura fraccionaria y extendida a procesos iterativos infinitos, están asignando un evento sonoro como forma de representación e identificación de las relaciones de variación existente entre los fraccionamientos de la longitud de la cuerda y su frecuencia correspondiente.
El diseño e implementación del curso-laboratorio se ha constituido en el producto y objeto de reflexión de una comunidad de práctica de educadores matemáticos que enseñan Cálculo, y nos invita a continuar contribuyendo en la línea del pensamiento matemático avanzado, pues como se muestra en Moreno (2015)MORENO, D. Procesos de interpretación y acción de profesores que participan en una comunidad de práctica en la que se realiza el diseño curricular de un curso de precálculo. 2015. 170 f. (Tesis de maestría en educación matemática) – Universidad Industrial de Santander, Colombia, 2015., el trabajo colaborativo en comunidad posibilita un aprendizaje significativo, como una amalgama perfecta entre teoría, innovación y experiencia.
-
1
Proyecto 1341. Caracterización de las habilidades básicas del Pensamiento Variacional que son necesarias para la comprensión del Cálculo Diferencial. Vicerrectoría de Investigación y Extensión de la Universidad Industrial de Santander.
-
2
Lenguaje de programación orientado a objetos Adobe Flash Macromedia CS3
Referencias
- ALEKSANDROV, A. D. et al. La matemática: su contenido, métodos y significado. Madrid: Alianza Editoral, 1994.
- ARTIGUE, M. La integración de calculadoras gráficas y formales en la enseñanza de las matemáticas en el bachillerato. In: REUNIÓN LATINOAMERICANA DE MATEMÁTICA EDUCATIVA, 11, 1997, Bogotá. Anales… Bogotá: Grupo Editorial Iberoamérica S. A, 1997.
- Artigue, M., and Ervynck, G. (1993). Proceedings of Working Group 3 on Student's Difficulties in Calculus, ICME-7, Québec, Canada.
- ARTIGUE, M.; ERVYNCK, G. Eds. Proceedings of Working Group 3 on Student's Difficulties in Calculus Québec: International Congress on Mathematical Education, 7, 1993,
- AZCÁRATE, C.; CAMACHO, M. Sobre la investigación en Didáctica del Análisis Matemático. Boletín de la Asociación Matemática Venezolana, Caracas, v. 10, n. 2, p. 135-149, 2003.
- COLOMBIA. Ministerio de Educación Nacional. Estándares básicos de competencias en lenguaje, matemáticas, ciencias y ciudadanas. Bogotá, 2006.
- CONDE, A. La unidad relativa como vínculo cognitivo entre el tiempo musical y las fracciones. 2013. 192 f. Tesis (Doctorado en Matemática Educativa) – Centro de Investigación y Estudios Avanzados del Instituto Politécnico Nacional, México D.F., 2013.
- CUEVAS, C.; PLUVINAGE, F. Les projets d'action pratique, éléments d'une ingénierie d'eseigments des mathématiques. Annales de didactique et sciences cognitives, Paris, v. 8, p. 273-392, 2003.
- DREYFUS, T. Advanced mathematical thinking processes. In: Tall, D. (Ed.). Advanced mathematical thinking. Dordrecht: Kluwer Academic Publisher, 1991. p. 25-41.
- FIALLO, J. Estudio del proceso de demostración en el aprendizaje de las Razones Trigonométricas en un ambiente de Geometría Dinámica 2011. 267 f. Tesis (Doctorado en Didáctica de las Matemáticas) – Universidad de Valencia, Valencia, España, 2011.
- FIALLO, J.; PARADA, S. Curso de pre-cálculo apoyado en el uso de geogebra para el desarrollo del pensamiento variacional. Revista Científica, Bogotá, v. 20, p. 56-71, 2014.
- GARCÍA, G.; SERRANO, C.; DÍAZ, H. La aproximación: una noción básica en el cálculo: un estudio en la educación básica. Bogotá: Universidad Pedagógica Nacional, 2002.
- GUIN, D.; TROUCHE, L. The complex process of converting tools into mathematical instruments: the case of calculators. International Journal of Computers for Mathematical Learning, Netherlands, v. 3, p. 195-227, 1999
- HITT, F. Nuevas tendencias en la enseñanza del cálculo: la derivada en ambientes TICE. Revista AMIUTEM, Ciudad Guzmán, Jalisco, v. 2, n 2, p. 1-19, 2014
- KAPUT, J.; BLANTON, M.; MORENO, L. Algebra from a symbolization point of view. In: KAPUT, J.; CARRAHER, D.; BLATNTON, M. (Ed.). Algebra in the early grades Mahwah NJ: Lawrence Erlbaum Associates, 2008. p. 19-56.
- MACHIN, M.; RIVERO, D. Students’ attitudes towards Mathematics and computers when using derive in the learning of calculus concepts. The International Journal of Computer Algebra in Maths Education, Plymouth, v. 9, n. 4, p. 259-283, 2002.
- McADAMS, S. Recognition of sound sources and events. In: McADAMS, S.; BIGAND, E. (Ed.). Thinking in Sound: the Cognitive Psychology of Human Audition. Oxford: Oxford University Press, 1993. p. 146-198.
- MORENO, D. Procesos de interpretación y acción de profesores que participan en una comunidad de práctica en la que se realiza el diseño curricular de un curso de precálculo. 2015. 170 f. (Tesis de maestría en educación matemática) – Universidad Industrial de Santander, Colombia, 2015.
- MORENO, L. Educación Matemática: del signo al pixel. Colombia: Universidad Industrial de Santander, 2014.
- MORENO, M. El papel de la didáctica en la enseñanza del cálculo: evolución, estado actual y retos futuros. In: SIMPOSIO DE LA SOCIEDAD ESPAÑOLA DE INVESTIGACIÓN EN EDUCACIÓN, 9., 2005, Córdoba. Anales…Córdoba: Universidad de Córdoba, 2005. p. 81-96.
- NEMIROVSKY, R. Students’ Tendency to Assume Resemblances between a Function and Its Derivative. Reports-Research/Technical, Massachusetts, v. 143, 1992. Disponible en: <http://edres.org/eric/ED351193.htm>. Acceso en: 15, mar. 2014.
» http://edres.org/eric/ED351193.htm - PARADA, S. Reflexión y acción en comunidades de práctica: un modelo de desarrollo profesional. 2011. 309 f. Tesis (Doctorado en Matemática Educativa) – Centro de Investigación y Estudios Avanzados del Instituto Politécnico Nacional, México D. F., 2011.
- ROJAS, S.; SUÁREZ, S.; PARADA, S. Presaberes matemáticos con los que ingresan estudiantes a la universidad. In: ACTA LATINOAMERICANA DE MATEMÁTICA EDUCATIVA ALME, 27., 2014, México D. F. Anales… México D. F.: Comité Latinoamericano de Matemática Educativa A. C., 2014. p. 1169-1176.
- STEEN, L. La enseñanza agradable de las matemáticas. México: Limusa, 1998.
- TALL, D. Cognitive Growth in Elementary and Advanced Mathematical Thinking. Plenary lecture, In: PSYCHOLOGY OF MATHEMATICS EDUCATION, 19., 1995, Recife. Proceedings… Recife: Universidade Federal de Pernambuco, 1995. p. 161-175.
- VINNER, S. The role of denitions in the teaching and learning of mathematics. In: Tall. D. (Ed.). Advanced Mathematical Thinking Dordrecht: Kluwer Academic Publishers, 1991. p. 65-81.
Fechas de Publicación
-
Publicación en esta colección
Sep-Dec 2016
Histórico
-
Recibido
Abr 2015 -
Acepto
Ene 2016


 Fuente: Construcción propia
Fuente: Construcción propia
 Fuente: Construcción propia
Fuente: Construcción propia
 Fuente: Creación y simulación propia
Fuente: Creación y simulación propia
 Fuente: Trabajo escrito de un estudiante
Fuente: Trabajo escrito de un estudiante
 Fuente: Preguntas generadoras propuestas en el curso-laboratorio
Fuente: Preguntas generadoras propuestas en el curso-laboratorio
 Fuente: Trabajo de los estudiantes en la computadora
Fuente: Trabajo de los estudiantes en la computadora
 Fuente: Construcción de los estudiantes de la tabla
Fuente: Construcción de los estudiantes de la tabla
 Fuente: Construcciones gráfica y tabular de los estudiantes
Fuente: Construcciones gráfica y tabular de los estudiantes