Resumos
Neste artigo propomos um modelo de otimização inteira mista para o problema de dimensionamento e seqüenciamento dos lotes de produção em fábricas de refrigerantes de pequeno porte, com tempos e custos de set up de produção dependentes do seqüenciamento dos lotes. O modelo considera o estágio de envase como sendo o gargalo da produção da planta, o que é comum em fábricas de pequeno porte com uma única linha de envase, e restrições de lote mínimo do estágio de xaroparia. Variações da heurística relax and fix são propostas e comparadas na solução de exemplares do modelo, gerados com dados reais de uma fábrica localizada no interior do Estado de São Paulo. Os resultados mostram que as abordagens são capazes de gerar soluções melhores do que as utilizadas pela empresa.
Programação inteira mista; programação da produção; modelos integrados de dimensionamento e seqüenciamento da produção
In this paper we propose a mixed integer programming model to the lot sizing and sequencing problem of a soft drink plant with sequence-dependent set up costs and times. The model considers that the bottling stage is the production bottleneck, which is common in small plants with only one production line, and minimum lot size constrains of the syrup stage. Variations of the relax and fix heuristic are proposed and compared. A computational study with instances generated based on real data from a plant situated in the State of São Paulo-Brazil is also presented. The results show that the approaches are capable to produce better solutions than the ones from the company.
Mixed integer programming; production scheduling; lot sizing and sequencing models
Um modelo de otimização inteira mista e heurísticas relax and fix para a programação da produção de fábricas de refrigerantes de pequeno porte
A mixed integer programming model and relax and fix heuristics for the production scheduling of small scale soft drink plants
Deisemara FerreiraI; Reinaldo MorabitoI; Socorro RangelII
IUFSCar
IIUNESP
RESUMO
Neste artigo propomos um modelo de otimização inteira mista para o problema de dimensionamento e seqüenciamento dos lotes de produção em fábricas de refrigerantes de pequeno porte, com tempos e custos de set up de produção dependentes do seqüenciamento dos lotes. O modelo considera o estágio de envase como sendo o gargalo da produção da planta, o que é comum em fábricas de pequeno porte com uma única linha de envase, e restrições de lote mínimo do estágio de xaroparia. Variações da heurística relax and fix são propostas e comparadas na solução de exemplares do modelo, gerados com dados reais de uma fábrica localizada no interior do Estado de São Paulo. Os resultados mostram que as abordagens são capazes de gerar soluções melhores do que as utilizadas pela empresa.
Palavras-chave: Programação inteira mista, programação da produção, modelos integrados de dimensionamento e seqüenciamento da produção.
ABSTRACT
In this paper we propose a mixed integer programming model to the lot sizing and sequencing problem of a soft drink plant with sequence-dependent set up costs and times. The model considers that the bottling stage is the production bottleneck, which is common in small plants with only one production line, and minimum lot size constrains of the syrup stage. Variations of the relax and fix heuristic are proposed and compared. A computational study with instances generated based on real data from a plant situated in the State of São Paulo-Brazil is also presented. The results show that the approaches are capable to produce better solutions than the ones from the company.
Key words: Mixed integer programming, production scheduling, lot sizing and sequencing models.
INTRODUÇÃO
Atualmente o Brasil produz mais de 13 bilhões de litros de refrigerantes por ano, ficando abaixo somente dos EUA e do México. Dados da ABIR Associação Brasileira das Indústrias de Refrigerantes e de Bebidas Não Alcoólicas mostram que o setor de refrigerantes fechou o ano de 2006 com crescimento de 4,75% em relação a 2005 (ABIR, 2007). Apesar do aumento das vendas, o consumo per capita no Brasil continua relativamente pequeno se comparado a países da Europa, e está em 12º lugar no ranking mundial de consumo de refrigerante, mas, segundo a ABIR, tem potencial para crescimento devido ao clima quente e propício para a ingestão de bebidas.
Um dos fatores que favoreceu o aumento do consumo de refrigerantes nos últimos anos foi a criação da embalagem de plástico descartável PET (Polietileno Tereftalato), que hoje corresponde a aproximadamente 80% das vendas, das quais 70% são de PET 2 litros. A embalagem PET dispensa a logística reversa de recolhimento de vasilhames, facilita o consumo residencial, na medida em que os consumidores não têm mais que investir, transportar e armazenar o vasilhame de vidro, além de não limitar o consumo ao número de vasilhames que o consumidor possui. A sistemática de engarrafamento também não exige altos investimentos do fabricante, por permitir repasse imediato do custo de embalagem, o que favoreceu a abertura de novas fábricas regionais, cujos produtos são conhecidos como tubaínas. Comercializadas a preços menores, as tubaínas conquistaram os consumidores de menor poder aquisitivo e colaboraram para o aumento no consumo de bebidas desde 1994 (Neit, 2004). Hoje, as fábricas regionais competem em preço e qualidade com grandes indústrias de bebidas. Em 2006, essas empresas foram responsáveis, juntas, por 25,6% de participação do mercado nacional (ABIR, 2007), o que representa uma porcentagem significativa considerando a dimensão do volume de produção nacional. Dados da Associação dos Fabricantes de Refrigerantes Regionais do Brasil (AFREBRAS, 2007) indicam a existência de 238 fábricas regionais, responsáveis por 118 marcas. Algumas destas empresas atuam no mercado há mais de 50 anos.
Basicamente, os refrigerantes, e outras bebidas como chás e sucos, são produzidos em dois estágios. No primeiro a matéria-prima principal, que é o xarope, é preparada. No segundo estágio a bebida pronta, xarope adicionado a água e gás carbônico, é então envasada. Um dos desafios constantes para o departamento de planejamento e controle da produção nas fábricas de bebidas é a determinação de um programa de produção eficiente. A programação da produção de bebidas envolve vários fatores, tais como: tempo disponível para produção, disponibilidade de insumos, demanda a ser atendida, tempos de troca dependentes do seqüenciamento da produção e ainda a sincronia entre os estágios de envase de bebida e preparo do xarope a ser envasado. Sendo que este último é um fator que tem um peso grande na utilização da capacidade e nos custos. Em fábricas de pequeno porte esta dificuldade é ainda maior, pois em geral não possuem nenhum tipo de ferramenta computacional específica de apoio para a elaboração da programação da produção e que permita avaliações rápidas e efetivas de diferentes cenários de produção.
A cada troca de itens na produção de bebidas é necessária uma limpeza da linha de envase e/ou ajustes da linha de envase em relação ao tamanho dos vasilhames e sabor da bebida. O tempo de preparo (set up) da linha de envase para a produção é dependente da seqüência de produção. Além das linhas de envase, os tanques também passam por uma limpeza antes do próximo xarope ser preparado, e o tempo desta limpeza também é dependente da seqüência de produção. Por exemplo, o tempo de preparo e limpeza entre a produção de uma bebida normal e uma bebida dietética é bem maior do que o tempo de preparo e limpeza na seqüência inversa, isto é, a produção de uma bebida dietética seguida da produção de uma bebida normal. Como o preparo pode ser demorado e custoso, e pode gerar desperdícios de tempo e custos de produção, é fundamental que ele seja considerado na programação da produção. Boa parte das empresas de bebidas resolve o problema do dimensionamento e seqüenciamento dos lotes de produção em duas etapas. Em uma primeira etapa é determinada a dimensão dos lotes, levando em consideração as demandas dos produtos, disponibilidades de insumos, capacidade de produção, etc. Em uma etapa subseqüente, a seqüência dos lotes determinados é definida em cada linha de envase e cada tanque considerando os tempos disponíveis, tempos de troca e outros fatores que influenciam no seqüenciamento da produção.
Na literatura podem ser encontrados estudos que modelam matematicamente apenas o dimensionamento dos lotes (e.g., Kuik et al., 1994; França et al., 1999; Toledo; Armentano, 2006; Brahimi et al., 2006); estudos que modelam apenas o seqüenciamento da produção (e.g., Manne, 1960; Pinedo, 1995; Cheng et al., 2004), e também estudos que integram em um mesmo modelo matemático o dimensionamento e o seqüenciamento dos lotes (e.g., Fleischmann, 1990; Drexl; Kimms, 1997; Clark; Clark, 2000; Karimi et al., 2003). Entre os estudos que integram o dimensionamento e o seqüenciamento de lotes, um trabalho interessante é o de Fleischmann e Meyr (1997). Eles apresentam o modelo GLSP (General Lot-sizing and Scheduling Problem), onde os períodos de produção (macroperíodos) são divididos em períodos menores (subperíodos ou número de preparos do período). As variáveis de preparo e produção indicam a produção e a troca de itens em cada subperíodo. O número máximo de subperíodos de cada período é definido pelo usuário, e em cada subperíodo pode haver a produção de no máximo um item. Fleischmann e Meyr (1997) desenvolveram um algoritmo de busca local para resolver exemplares do modelo GLSP. A extensão do modelo GLSP para o caso multi-máquinas com tempos de troca dependentes da seqüência, modelo GLSPPL, foi feita em Meyr (2002). Estes modelos de otimização inteira mista são difíceis de ser resolvidos, mesmo aqueles que considerem apenas o dimensionamento de lotes. Alguns deles pertencem à classe de problemas NP-difícil (Bitran; Yanasse, 1982; Meyr, 2002).
O modelo integrado de dimensionamento e seqüenciamento da produção foi aplicado em alguns estudos de caso no Brasil (e.g., Araújo et al., 2004; Toso; Morabito, 2005; Luche; Morabito, 2005). Em Araújo et al. (2004) é tratado um problema de programação de ligas de metal em fornos para produção de diferentes tipos de peças numa fundição. Toso e Morabito (2005) modelam e propõem abordagens de solução para o problema da programação da produção de fábricas de ração animal, e Luche e Morabito (2005) tratam de um problema de programação da produção de grãos eletrofundidos. Poucos trabalhos na literatura tratam especificamente do planejamento e programação da produção de bebidas. Clark (2003) e Rangel e Ferreira (2003) desenvolvem modelos para tratar apenas do dimensionamento de lotes neste setor. Gutiérrez e Pizzolato (2004) modelam o dimensionamento e seqüenciamento de lotes de uma fábrica de bebidas. Este trabalho considera um problema onde as taxas de produção e demandas são consideradas constantes nos períodos, o problema é resolvido para uma única máquina, e os tempos de set up são médias dos tempos dependentes da seqüência. Os atrasos não são permitidos e o processo de xaroparia não é considerado no modelo.
Mais recentemente, em Toledo (2005) e Toledo et al. (2007a) foi proposto um modelo de programação matemática inteira mista, Modelo PIDLPP, baseado no modelo GLSP, para o dimensionamento e seqüenciamento da produção de bebidas. O modelo considera M máquinas, J bebidas, L xaropes, dois estágios de produção (envase e xaroparia) e a sincronia entre eles, que é um aspecto importante em fábricas de médio e grande porte. Devido à complexidade e dimensão do modelo (o modelo envolve cerca de 65 famílias de restrições), em Toledo (2005) e Toledo et al. (2007b) também foi proposta uma abordagem de solução por meio de heurísticas e meta-heurísticas.
No presente trabalho propomos um modelo matemático, também baseado no modelo GLSP, porém mais simples do que o modelo PIDLPP para o problema de dimensionamento e seqüenciamento da produção de refrigerantes em fábricas de pequeno porte. Um estudo de caso foi realizado em uma fábrica localizada no interior do Estado de São Paulo, com apenas uma linha de envase e vários tanques para preparo do xarope. O modelo proposto, denominado Modelo P1E1M Um Estágio Uma Máquina, representa situações em que o gargalo de produção é a linha de envase. Na próxima seção deste artigo é descrito resumidamente o processo de produção de refrigerantes de acordo com a realidade da fábrica estudada. O modelo matemático e o método de solução baseado em heurísticas relax and fix são apresentados logo a seguir. Os resultados computacionais da aplicação da abordagem em exemplares realistas são apresentados e analisados em "Estudo Computacional". Finalmente, são discutidas as conclusões e perspectivas para pesquisa futura.
PRODUÇÃO DE REFRIGERANTES
De forma geral, a produção de bebidas é composta por quatro estágios: tratamento de água, preparo dos xaropes, envase e empacotamento. O preparo do xarope possui duas etapas. Na primeira etapa os ingredientes são pesados, em quantidades denominadas kits, e previamente misturados. Após esta etapa o composto é enviado para um tanque de preparo, onde é adicionado açúcar líquido ou adoçante (para os sabores diet). Esta mistura é agitada por hélices que tornam o xarope uma mistura homogênea. Para que este composto seja bem misturado pelas hélices, é necessária uma quantidade mínima de xarope no tanque, suficiente para cobrir as hélices.
Na linha de envase, os vasilhames de plástico (garrafas PET) que entram são lavados e em seguida passam por uma máquina (enchedora) que os enche com a bebida pronta. A enchedora é ligada ao proporcionador, que mistura o xarope a uma determinada quantidade de água, resultando então a bebida pronta (vide Figura 1). Depois de enchidos, os vasilhames seguem pela esteira onde são fechados, rotulados, empacotados, paletizados e então levados para o estoque. Uma vez que os vasilhames são colocados na esteira, eles só podem ser retirados dela ao final do processo, quando são então transferidos para o depósito (Rangel; Ferreira, 2003). A linha de envase recebe xarope de apenas um tanque por vez, como é ilustrado pelo Tanque 1 da Figura 1, e possui apenas uma entrada e uma saída de vasilhames.
Toda vez que um novo sabor de refrigerante e/ou novo tamanho de vasilhame for utilizado, as máquinas precisam de um tempo de preparação (limpeza e/ou ajuste do maquinário). Esta preparação depende da seqüência da produção. Se após a produção de um refrigerante normal se produzir um refrigerante dietético, a limpeza da linha de envase passa por mais etapas do que na ordem contrária, o que consome mais tempo e pode gerar mais custos do que se fosse feita a ordem inversa. O modelo matemático proposto na próxima seção considera o estágio de envase em uma linha de produção com tempos e custos de troca de bebidas dependentes do seqüenciamento da produção, e restrições de lotes mínimos de xaropes.
MODELAGEM PROPOSTA E MÉTODO DE SOLUÇÃO
Propomos neste trabalho um modelo de otimização inteira mista, Modelo Um Estágio Uma Máquina (P1E1M), para auxiliar nas decisões do planejamento e controle da produção em fábricas de bebidas de pequeno porte onde o gargalo está no envase. O modelo pretende resolver as questões de quanto e em que ordem as bebidas devem ser produzidas na linha de envase para atender a demanda dos períodos do horizonte de planejamento, considerando restrições de capacidade e de insumos disponíveis. São também considerados tempos e custos de troca de bebidas dependentes do seqüenciamento. O modelo é do tipo big bucket, onde vários produtos (itens) podem ser produzidos por período. Para incluir o seqüenciamento no modelo, os períodos (macroperíodos) são divididos em períodos menores (subperíodos) (Fleischmann; Meyr, 1997). Nos sub-períodos é permitida a produção de apenas um item, isto é, uma bebida de determinado sabor e embalagem. O número máximo de subperíodos é definido pelo usuário, mas o tamanho dos subperíodos é determinado pelo modelo, pois é o tamanho do lote que será produzido, conforme descrição do modelo a seguir.
Modelagem do problema um estágio uma máquina P1E1M
O modelo P1E1M utiliza os conjuntos de índices, parâmetros e variáveis definidos a seguir.
Índices:
i, j (1,..., J) = itens;
t (1,..., T) = períodos;
s (1,..., N) = subperíodos;
l (1,..., L) = sabor dos xaropes;
St= conjunto dos subperíodos do período t;
a = conjunto de todas as bebidas a serem produzidas;
b = conjunto de todos os xaropes disponíveis;
gl = conjunto de todas as bebidas que utilizam o xarope l.
Os parâmetros e variáveis abaixo com o sobrescrito I se referem ao estágio I (xaroparia) do processo de produção e os com o sobrescrito II se referem ao estágio II (envase).
Parâmetros
J = número total de bebidas;
T = número total de períodos;
N = número total de subperíodos;
L = número total de xaropes (sabores);
djt = demanda da bebida j no período t;
hj = custo de estocar uma unidade da bebida j;
gj = custo de atrasar a entrega de uma unidade da bebida j;
 = custo de fazer a troca da bebida i para j;
= custo de fazer a troca da bebida i para j;
 = quantidade consumida de tempo para fazer a troca da bebida i para j na linha de envase;
= quantidade consumida de tempo para fazer a troca da bebida i para j na linha de envase;
 = quantidade consumida de tempo para a produção de uma unidade da bebida j;
= quantidade consumida de tempo para a produção de uma unidade da bebida j;
 = capacidade de tempo disponível da linha de envase no período t;
= capacidade de tempo disponível da linha de envase no período t;
K I = capacidade disponível da xaroparia;
 = quantidade mínima de xarope l a ser preparada em um tanque;
= quantidade mínima de xarope l a ser preparada em um tanque;
rlj = quantidade consumida de xarope l para produção de uma unidade da bebida j;
 = estoque inicial da bebida j;
= estoque inicial da bebida j;
 = 0, quantidade em atraso da bebida j no início do horizonte de planejamento.
= 0, quantidade em atraso da bebida j no início do horizonte de planejamento.
Variáveis:
 = quantidade de estoque da bebida j no período t;
= quantidade de estoque da bebida j no período t;
 = quantidade em atraso da bebida j no período t;
= quantidade em atraso da bebida j no período t;
 = quantidade de produção da bebida j no subperíodo s;
= quantidade de produção da bebida j no subperíodo s;
O modelo proposto é dado a seguir.
Sujeito a:
Estágio II (Envase)
Estágio I (Xaroparia)
O critério de otimização (1) é minimizar os custos de estoque, atraso e troca. A restrição (2) diz respeito ao balanceamento de estoque. Como a variável de produção está definida em termos dos subperíodos do período t, é necessário somar a produção em todos subperíodos s Î St. A restrição (3) garante que o tempo de produção mais o tempo gasto para as trocas de bebidas não excede a capacidade disponível da linha de envase no período t. A restrição (4) garante que só haverá produção caso a linha de envase esteja preparada ( =1). A restrição (5) estabelece que a linha de envase sempre esteja preparada para produzir exatamente uma bebida por subperíodo. A restrição (6) controla a troca de bebidas. Pode ocorrer apenas uma troca por subperíodo, restrição (7). Note que as variáveis
=1). A restrição (5) estabelece que a linha de envase sempre esteja preparada para produzir exatamente uma bebida por subperíodo. A restrição (6) controla a troca de bebidas. Pode ocorrer apenas uma troca por subperíodo, restrição (7). Note que as variáveis  são reais. As restrições (5) e (6) e a minimização dos custos de troca de bebidas garantem que essas variáveis assumam apenas os valores 0 ou 1 em uma solução ótima.
são reais. As restrições (5) e (6) e a minimização dos custos de troca de bebidas garantem que essas variáveis assumam apenas os valores 0 ou 1 em uma solução ótima.
Cada lote de bebida produzida consome uma determinada quantidade de xarope a ser preparada nos tanques, e que deve estar disponível no início do sub-período do envase. Como foi apresentado em "Producão de Refrigerantes", este preparo tem exigências de lotes mínimos para que resulte em uma mistura homogênea. A restrição (8) garante o preparo deste lote mínimo de xarope. Note que o termo  é a demanda de xarope, ou seja, é a quantidade de xarope l a ser preparada em um tanque no subperíodo s. Este termo substitui a utilização de uma variável
é a demanda de xarope, ou seja, é a quantidade de xarope l a ser preparada em um tanque no subperíodo s. Este termo substitui a utilização de uma variável  específica para designar o lote do xarope l no sub-período s. A restrição (9) refere-se ao domínio das variáveis do modelo.
específica para designar o lote do xarope l no sub-período s. A restrição (9) refere-se ao domínio das variáveis do modelo.
O modelo P1E1M se difere do modelo GLSPPL de Meyr (2002) pela inclusão de atrasos na produção, variáveis de preparo de um segundo estágio de produção e a limitação do número de trocas nos subperíodos, restrição (7).
O modelo P1E1M, (1)-(9), é difícil de ser resolvido otimamente nos casos práticos, mesmo considerando fábricas de pequeno porte. Para tratá-lo é utilizada uma heurística que relaxa um grupo de variáveis inteiras e, após a solução do modelo relaxado, fixa um subconjunto de variáveis. Esta heurística é conhecida na literatura como heurística relax and fix e é descrita na próxima seção.
Heurística Relax and Fix
A solução do modelo P1E1M usando sistemas de otimização de última geração não se mostrou satisfatória e indicou a necessidade do desenvolvimento de métodos de solução específicos. Uma abordagem de solução baseada em métodos exatos é a heurística relax and fix (Wolsey, 1998). Essa abordagem tem sido usada na solução de diversos tipos de problemas de forma pura ou híbrida. Nesta heurística, o conjunto de variáveis inteiras de um problema de otimização inteira mista é particionado em P conjuntos disjuntos, Qi, i = 1,..., P, de diferentes importâncias. O número P de conjuntos determina o número de iterações da heurística. Em uma iteração n, apenas as variáveis do conjunto Qn são definidas como inteiras, as demais variáveis inteiras são relaxadas. O submodelo resultante é então resolvido. Se o submodelo é inviável, pare. Não é possível encontrar uma solução viável para o problema original com as variáveis dos conjuntos Qi, i = 1,..., (n - 1), fixas nos valores atuais. Se o submodelo for viável, as variáveis do conjunto Qn, ou parte delas, são fixadas em seu valor corrente, e o processo se repete para os demais conjuntos. Há necessidade ainda da definição de um critério para fixação das variáveis. A característica fundamental dessa heurística é a solução de submodelos menores que o original a cada iteração. A partição do conjunto de variáveis e o critério de seleção das variáveis a serem fixadas têm grande influência na dificuldade de solução dos submodelos.
No trabalho de Federgruen et al. (2007) é apresentada uma heurística de intervalos progressivos, onde a heurística relax and fix é tida como um caso particular. O autor considera que na heurística relax and fix não há fixação de variáveis contínuas, o que dá o máximo de flexibilidade na obtenção de soluções viáveis. O caso extremo de menor flexibilidade é a fixação de todas as variáveis contínuas da iteração. Estas duas heurísticas são denominadas respectivamente por Heurística de Horizonte Expandido e Heurística de Particionamento Estrito.
Na heurística relax and fix usual as variáveis são agrupadas por período e apenas as variáveis inteiras são fixadas a cada iteração. No trabalho de Dillenberger et al. (1994), este critério de agrupamento das variáveis foi aplicado para a solução de um modelo de dimensionamento de lotes multimáquinas, multiitens e multiperíodos. O número de iterações da heurística é dado então pelo número de períodos do modelo. Em Kelly e Mann (2004), um problema de engenharia química é resolvido, e as variáveis a serem fixadas são agrupadas de acordo com os processos de produção pelos quais os itens passam.
Escudero e Salmeron (2005) comparam variações de heurísticas relax and fix na solução de um modelo de seqüenciamento de projetos. As estratégias diferem entre si pela forma como a partição do conjunto de variáveis é feita. A partição é definida por um parâmetro k que determina o número de iterações da heurística, e por um valor cjt, denominado valor da variável, que é atribuído à variável xjt. O valor cjt é ordenado de forma decrescente, tal que sendo n =  | Tj | o número de variáveis de decisão,
| Tj | o número de variáveis de decisão,  >,...,>
>,...,>  . Supondo que n' seja o número de variáveis inteiras que se deseja por iteração, pode-se definir k =
. Supondo que n' seja o número de variáveis inteiras que se deseja por iteração, pode-se definir k =  . O valor cjtpode ser, por exemplo, o peso que a variável tem na função objetivo, assim as variáveis de custo mais alto são escolhidas primeiro.
. O valor cjtpode ser, por exemplo, o peso que a variável tem na função objetivo, assim as variáveis de custo mais alto são escolhidas primeiro.
A heurística relax and fix também é utilizada de forma híbrida em meta-heurísticas como a Busca Tabu (vide Pedroso, 2004; Pedroso; Kubo, 2005). Ela pode ser utilizada tanto para fornecer uma solução inicial para a Busca Tabu, quanto para a reconstrução de soluções. Em Pedroso e Kubo (2005) a heurística relax and fix é usada na solução de um modelo de dimensionamento de lotes capacitado com tempos e custos de set up e variáveis de atraso. Os autores propõem uma heurística relax and fix denominada relax-and-fix-one-product. Como o nome sugere, nela as variáveis inteiras de cada iteração são selecionadas por item, um de cada vez, além de serem agrupadas por período e máquina. A vantagem é resolver submodelos menores, uma vez que alguns modelos de dimensionamento de lotes monomáquina, monoperíodo e multiitens ainda são difíceis de serem resolvidos.
Em Toledo (2005) a heurística relax and fix foi aplicada na solução de um problema de dimensionamento e seqüenciamento da produção de bebidas. O modelo está classificado como um modelo capacitado, multimáquinas, multiitens, multiperíodos, dois níveis, com tempos e custos de set up dependentes da seqüência. Nesta aplicação a heurística não apresentou resultados satisfatórios. O maior exemplar resolvido possui 258 variáveis binárias, 1.390 contínuas e 924 restrições. Para fixar as variáveis o algoritmo percorre e fixa primeiro cada lote de produção da linha de envase, depois o lote de xarope, isto do último período para o primeiro.
No presente trabalho, que também trata de um problema de dimensionamento e seqüenciamento da produção de bebidas, exploramos a utilização da heurística relax and fix na solução do modelo P1E1M. A heurística relax and fix é proposta considerando diversos tipos de partição do conjunto de variáveis, e vários critérios para a fixação de variáveis. Foram testadas oito variações da estratégia relax and fix, descritas na Tabela 1. A primeira coluna da tabela indica o nome da estratégia, a segunda coluna mostra os critérios de partição do conjunto de variáveis, a terceira coluna indica quais variáveis são fixadas. As variáveis apresentadas na tabela são as mesmas usadas na descrição do modelo P1E1M, no entanto, os índices foram omitidos para facilitar a leitura.
As cinco primeiras estratégias têm o critério de partição de variáveis usual, ou seja, por período. As estratégias variam, então, pela forma como as variáveis são fixadas. Este critério supõe que os submodelos devem ter uma dimensão que favoreça a tomada de decisões dentro do horizonte de planejamento, sem que seja necessário trabalhar com o modelo completo. O objetivo foi avaliar a influência destas variáveis na solução dos submodelos. Considerando as estratégias G1.1 e G1.2, note que, ao fixar a variável yII, apenas se escolhe para qual bebida a linha de envase estará preparada ou não. A variável yI, além de definir o preparo no tanque, define também a produção ou não do lote, sendo que o tamanho deste lote pode variar entre o máximo e o mínimo estabelecidos pelas restrições (8). A estratégia G1.2 é tão flexível quanto G1.1, mas fixa explicitamente as variáveis de troca. Isto reduz o tamanho dos submodelos, tanto no número de variáveis quanto no número de restrições que podem ser eliminadas por rotinas de pré-processamento, geralmente incluídas nos sistemas de resolução de última geração. A fixação do lote ocorre apenas pela fixação da variável xII, estratégia G1.3. A estratégia G1.4, por fixar apenas as variáveis de períodos onde há produção, é mais flexível que as anteriores. Além de reajustes nos tamanhos dos lotes, ela permite que nos subperíodos ociosos sejam produzidos novos lotes de qualquer item em iterações futuras. Uma tentativa de melhorar a estratégia G1.4 é reavaliar os subperíodos que ficaram ociosos, e não tiveram variáveis fixadas em iterações anteriores, e fixar suas variáveis caso eles deixem de ser ociosos. Nesta estratégia, G1.5, a cada iteração os submodelos se tornam menos flexíveis do que os submodelos da estratégia G1.4. No entanto, o tamanho destes submodelos diminui à medida que novas fixações são realizadas.
As próximas três estratégias definem submodelos bem menores, pois as partições das variáveis são dadas por alguns subperíodos, e assim as decisões de dimensionamento e seqüenciamento dos lotes podem ser muito ruins a longo prazo. No entanto, nos testes realizados, todos os submodelos são resolvidos até a otimalidade. Na estratégia G2.2, busca-se melhorar a qualidade das soluções, uma vez que todos os períodos terão variáveis de um subperíodo fixadas. A estratégia G2.3 considera dois subperíodos de cada período, o primeiro e o último subperíodo. Ao considerar o último subperíodo de cada período busca-se evitar que os últimos subperíodos de cada período sejam sobrecarregados.
A cada iteração da heurística relax and fix é resolvido um problema de otimização inteira mista. Em geral são usados métodos exatos incluídos em sistemas de otimização (e.g., o método branch and cut). Apesar dos modelos resultantes da fixação de algumas variáveis serem menores que o modelo original, a dificuldade de solução pode se manter. Portanto, foi estabelecido um critério de parada de tal forma que o tempo total da heurística não ultrapassasse 3 horas. Se a solução ótima do submodelo resolvido a cada iteração não for obtida dentro do limite máximo de tempo de processamento, o método branch and cut é interrompido e a melhor solução obtida é avaliada para fixação das variáveis.
ESTUDO COMPUTACIONAL
Para desenvolver este trabalho, foram realizadas visitas a uma fábrica de refrigerantes de pequeno porte para o entendimento do problema e a coleta de dados. Os dados coletados na fábrica são referentes à produção: demandas de produtos, tempos de troca de bebidas nas linhas de envase, capacidade das linhas e tanques, entre outros dados necessários para resolver o problema. Foram realizadas várias visitas para se conseguir todos os dados necessários para um estudo computacional com dados reais. O modelo P1E1M (1)-(9) e as estratégias relax and fix G1.1, G1.2, ..., G2.3 foram implementados na linguagem de modelagem AMPL 100 (Fourer et al., 1993) acoplado ao sistema de otimização CPLEX versão 10.0 (ILOG, 2006). Os testes foram realizados em um computador com processador Pentium 4, 1.0 Gb de RAM, 3.2 Ghz. A seguir são descritos os exemplares gerados e os resultados obtidos.
Exemplar da fábrica
A fábrica possui apenas uma linha de envase e produz 27 tipos de refrigerantes, variando entre sabor e tamanho. No total são 10 sabores (xaropes) diferentes, preparados em vários tanques na xaroparia. O planejamento da produção é feito para cinco períodos, cada período representa uma semana diferente; o horizonte de planejamento é então de um mês de produção (i.e., 30 ou 31 dias envolvendo cinco semanas diferentes). O número de subperíodos é determinado pelo número máximo de trocas na semana, que neste caso é 24. Desta maneira cada período possui 24 subperíodos, exceto o primeiro período, que é composto por dois dias de trabalho (referentes aos dois primeiros dias do mês) e possui oito subperíodos, no total são 104 subperíodos. Mais detalhes deste exemplar podem ser encontrados em Ferreira (2006). Os outros dados coletados e utilizados nos testes foram distorcidos para preservar interesses da empresa, por exigência explícita da mesma.
Também por motivos de confidencialidade, informações como custos não foram disponibilizadas. Assim, os custos foram estimados a partir dos valores comercializados para os consumidores. Por exemplo, o custo de estoque de uma bebida foi simplesmente considerado como sendo um percentual informado do custo de produção, levando-se em conta a taxa de juros de mercado no período de análise. Este custo representa um custo de oportunidade associado ao valor de estoque no período. Como a empresa não forneceu os custos de produção das bebidas, estes custos foram estimados da seguinte maneira: a partir do preço de venda da bebida informado, foi simplesmente descontada deste valor a margem de contribuição ao lucro informada da bebida. O custo de atraso de uma bebida foi estimado como sendo o custo de produção da bebida mais a margem de contribuição ao lucro que se obteria se ela tivesse sido vendida, ou seja, o preço de venda informado da bebida. Note que, se o produto for produzido e vendido no período seguinte, a empresa recupera a venda perdida. O custo de troca da bebida i para a bebida j na linha de envase foi estimado como sendo um custo de oportunidade, isto é, a margem de contribuição ao lucro que se deixou de obter com a parada da linha de envase para a troca (margem de contribuição ao lucro da bebida j)*(quantas unidades de bebida j poderiam ter sido produzidas durante este tempo de troca).
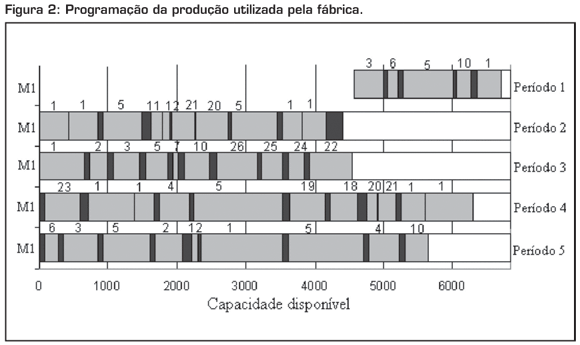
Este exemplar possui 82.796 variáveis (3.848 variáveis binárias e 78.948 variáveis contínuas) e 80.404 restrições. Ele foi resolvido inicialmente pelo pacote de otimização CPLEX 10 com os parâmetros de solução padrões (default), e sua solução foi comparada à solução fornecida pela empresa. O tempo de solução foi limitado em três horas de processamento, que é um tempo considerado razoável para a empresa, uma vez que na prática o tempo para determinação da programação da produção é de três horas ou mais. A Figura 2 ilustra a programação da produção da linha de envase utilizada pela fábrica nos cinco períodos (semanas). O eixo horizontal representa a capacidade disponível da linha, 6.840 minutos (apenas o primeiro período tem capacidade menor, 2.280 minutos). O eixo vertical é a programação da linha de envase em cada período. Os retângulos em cinza são os lotes de cada bebida, e os retângulos pretos são os tempos de troca. A bebida envasada é indicada pelo número logo acima do lote. Note que algumas das 27 bebidas produzidas pela fábrica não foram demandadas no horizonte de planejamento deste exemplar e, portanto, não foram programadas para produção.
A Tabela 2, a seguir, apresenta os custos desta solução fornecida pela empresa e os resultados obtidos com as estratégias do CPLEX. Tendo em vista que a solução fornecida pelo default CPLEX, CPLEX-1, foi pior que a solução da empresa, um teste modificando o parâmetro de geração de planos de corte do CPLEX foi realizado. Nesse teste, CPLEX-2, a geração de todos os tipos de planos de corte implementados no CPLEX (Gomory, cobertura, fluxo, clique, etc.) foi desligada. Pela Tabela 2 nota-se que a estratégia CPLEX-2 fornece uma solução menos custosa do ponto de vista de estoque e troca do que a solução da empresa, e não contém atrasos. Note que a redução de custo em relação à solução da empresa é significativa (cerca de 37 %). A última coluna da tabela apresenta o gap da solução em relação ao limitante inferior, fornecido pelo CPLEX.
Outros Exemplares
Para analisar o desempenho das estratégias de solução, outros exemplares foram gerados a partir do exemplar anterior (Ex.1). A Tabela 3 resume as modificações realizadas para a geração dos exemplares. Estas variações nos exemplares permitem que cenários diferentes sejam analisados, em que a capacidade produtiva é mais apertada, ou as relações entre os custos de estoque, troca e atraso são modificadas. Note que os exemplares têm o mesmo tamanho do exemplar da fábrica (modelos com milhares de variáveis e restrições). A Tabela 4 apresenta o resultado da solução encontrada para cada um dos exemplares dentro do limite de tempo computacional de três horas. Abaixo de cada solução é apresentado o gap de otimalidade da solução.
A estratégia CPLEX-2 é melhor nos cinco exemplares (destacada em negrito). Porém o gap destas soluções ainda é alto, indicando a dificuldade de solução dos exemplares. Para tentar melhorar a solução do modelo P1E1M, foram testadas as estratégias relax and fix propostas na seção "Modelagem proposta e método de solução", combinadas com a estratégia CPLEX-2, ou seja, os submodelos em cada iteração são resolvidos sem a geração de planos de corte. A Tabela 5 apresenta o valor das soluções obtidas. O menor custo obtido para cada exemplar é apresentado em negrito. Note que, exceto para o exemplar 1, para todos os exemplares as estratégias relax and fix são capazes de gerar soluções melhores do que a estratégia CPLEX-2 sozinha. Em alguns casos essas diferenças são significativas em termos percentuais.
No caso do exemplar 1, é possível comparar sua solução com a solução da empresa, que é de 189.369,43 unidades monetárias. Apesar dos gaps de otimalidade continuarem altos, todos maiores que 90%, nota-se pela Tabela 5 que quatro das oito estratégias relax and fix testadas, estratégias G1.1, G1.2, G1.4 e G1.5, forneceram soluções competitivas em relação à solução da empresa, sendo que a melhor solução, fornecida pela estratégia G1.2, é cerca de 29 % menos custosa que a solução da empresa. Em média, quatro das oito estratégias testadas foram melhores que a estratégia CPLEX-2, sendo que a estratégia G1.2 obteve a maior redução, cerca de 14,4 %. Em relação aos demais exemplares, ocorreu uma variação no desempenho das estratégias. As estratégias G1.1 e G1.2 podem ser consideradas as estratégias relax and fix com os melhores desempenhos, por terem obtido a melhor solução para dois dos cinco exemplares e as melhores médias (Tabela 5). A Tabela 6 apresenta o valor médio dos custos de estoque, atraso e troca de cada estratégia calculados para os cinco exemplares. Os valores em negrito são os menores valores de custos obtidos.
Avaliando as estratégias em relação aos custos de estoque, o desempenho delas é muito parecido. Apenas a estratégia G1.3 tem um custo médio de estoque menor que 3.000. As estratégias CPLEX-2, G1.4 e G1.5 se destacam pelos menores custos de atraso, sendo que a estratégia G1.5 possui os menores valores de todas as soluções. Avaliando estas estratégias em relação aos custos de troca, a estratégia G1.4 é a melhor. As estratégias G1.1 e G1.2 possuem custos de atraso maiores que as estratégias CPLEX-2, G1.4 e G1.5, porém os custos de troca são menores.
CONSIDERAÇÕES FINAIS
Neste trabalho foi proposto um modelo de otimização inteira mista para auxiliar no processo de tomada de decisões da programação da produção em fábricas de refrigerantes de pequeno porte, em que o gargalo de produção está na linha de envase. O modelo mostrou-se útil na representação do problema, e foi capaz de gerar soluções melhores que a fornecida pela fábrica. No entanto, a sua resolução mostrou as limitações dos sistemas de otimização de última geração disponíveis atualmente, e a necessidade de se buscar métodos específicos de solução.
Diversas variações da heurística relax and fix foram testadas para resolver o modelo P1E1M. Analisando os resultados obtidos, as estratégias relax and fix forneceram cinco soluções melhores que a solução da empresa, e a melhor solução tem uma redução de aproximadamente 37% do custo total. Mais quatro cenários de produção foram testados e as estratégias relax and fix também foram aplicadas na solução desses exemplares. As estratégias G1.1 e G1.2 obtiveram as melhores soluções para dois dos cinco exemplares testados, e as melhores médias de todos os exemplares. Em Ferreira et al. (2007) são propostas extensões desta abordagem de solução para o caso de fábricas de refrigerantes maiores, com várias linhas de envase, em que o gargalo de produção pode estar tanto no envase quanto na xaroparia, e por isso o seqüenciamento dos xaropes nos tanques e a sincronia entre os estágios de xaroparia e envase precisam ser considerados.
O seqüenciamento dos itens associado ao modelo P1E1M é obtido através da divisão de um período em sub-períodos. Uma proposta alternativa é o uso de modelos baseados no Problema do Caixeiro Viajante Assimétrico para obter o seqüenciamento dos itens em cada período do problema de dimensionamento de lotes. Recentemente, Toso et al. (2007) exploraram essa abordagem na solução de um problema integrado de dimensionamento e seqüenciamento de lotes em fábricas de nutrição animal. Um tópico interessante para pesquisa futura é testar esta abordagem no problema de programação da produção em fábricas de refrigerantes.
Agradecimentos
Agradecemos aos dois revisores anônimos pelos úteis comentários e sugestões, e à FAPESP (processo 04/00462-5) e ao CNPq (processos 473001/2004-7, 522973/95-4) pelo apoio financeiro.
Artigo recebido em 03/04/2007
Aprovado para publicação em 25/10/2007
Sobre os autores
Deisemara Ferreira
E-mail: deise@dep.ufscar.br
Reinaldo Morábito
E-mail: morabito@ufscar.br
Universidade Federal de São Carlos Departamento de Engenharia de Produção
End.: Caixa Postal: 676 São Carlos SP CEP 13565-905
Tel: (16) 3351-8237, r. 9216, Fax: (16) 3351-8240
Socorro Rangel
UNESP Campus São José do Rio Preto Dep. de Ciências de Computação e Estatística
End.: Rua Cristovão Colombo, 2265 São José do Rio Preto SP CEP 15054-000
Tel.: (17) 3221-2233; Fax: (17) 3221-2203
E-mail: socorro@ibilce.unesp.br
- ABIR, Associação Brasileira das Indústrias de Refrigerantes e de Bebidas Não Alcoólicas; Dados de Mercado. Disponível em: <http://www.abir.gov.br>. Acesso em: 1ş fev. 2007.
- ABIR, Associação Brasileira das Indústrias de Refrigerantes e de Bebidas Não Alcoólicas. Obesidade. De quem é a culpa? Arquivos de notícias ABIR, 2005. Disponível em: <http://www.abir.org.br/article.php3?id_article=362>. Acesso em: 1º out. 2006.
- AFREBRAS, Associação dos Fabricantes de Refrigerantes do Brasil. Dados de Mercado. Disponível em: <http://www.afrebras.org.br/associados.htm>. Acesso em: 24 mar. 2007.
- ARAÚJO, S. A.; ARENALES, M. N.; CLARK, A. R. Dimensionamento de lotes e programação do forno numa fundição de pequeno porte. Gestão & Produção, v. 11, n. 2, p. 165-176, 2004.
- BITRAN, G. R.; YANASSE, H. H. Computational Complexity of the Lot Size Problem. Management Science, v. 28, n. 10, p. 1174-1186, 1982.
- BRAHIMI, N.; DAUZEREPERES, S.; NAJID, N. M.; NORDLI, A. Single item lot sizing problems. European Journal of Operational Research, v. 168, p. 1-16, 2006.
- CHENG, T. C. E.; DING, Q.; LIN, B. M. T. A concise survey of scheduling with time-dependent processing time. European Journal of Operational Research, v. 152, p. 1-13, 2004.
- CLARK, A. R.; CLARK, S. J. Rolling-horizon lot-sizing when set-up times are sequence-dependent. International Journal of Production Research, v. 38, p. 2287-2307, 2000.
- CLARK, A. R. Hybrid heuristics for planning lot setups and sizes. Computers & Industrial Engineering, v. 45, p. 545-562, 2003.
- DILLENBERGER, C.; ESCUDERO, L. F.; WU ZHANG, A. W. On practical resource allocation for production planning and scheduling with period overlapping setups. European Journal of Operational Research, v. 75, p. 275-286, 1994.
- DREXL, A.; KIMMS A. Lot Sizing and Scheduling Survey and Extensions, European Journal of Operational Research. v. 99, p. 221-235, 1997.
- ESCUDERO, L. F.; SALMERON J., On a Fix-and-Relax framework for a Class of Project Scheduling Problems. Annals of Operations Research, v. 140, p. 163-188, 2005.
- FEDERGRUEN, A.;, MEISSNER, J.; TZUR, M. Progressive interval heuristics for multi-item capacitated lot sizing problems. Operations Research, v. 55, n. 3, p. 490-502, 2007.
- FERREIRA, D., Abordagens para o Problema Integrado de Dimensionamento e Sequenciamento de Lotes da Produção de Bebidas. Tese de Doutorado, Universidade Federal de São Carlos, Departamento de Engenharia de Produção, Dezembro, 2006.
- FERREIRA, D.; MORABITO, R.; RANGEL, M. S. Abordagens de solução para o problema integrado de dimensionamento e seqüenciamento de lotes de produção de bebidas com dois estágios e múltiplas máquinas. Submetido para publicação, 2007.
- FLEISCHMANN, B. The Discrete Lot-sizing and Scheduling Problem European Journal of Operational Research, v. 44, p. 337-348, 1990.
- FLEISCHMANN, B.; MEYR H. The General Lotsizing and Scheduling Problem. OR Spektrum, v. 19, p. 11-21, 1997.
- FRANÇA, P. M.; ARMENTANO, V. A.; TOLEDO, F. M. B. A network flow model for capacitated lot sizing problem. Omega-International Journal Of Management Science, v. 27, n. 2, p. 275-284, 1999.
- FOURER, R.; GAY, M. D.; KERNIGHAN, B.W. AMPL A Modeling Language for Mathematical Programming, Danvers, Massachusetts: The Scientific Press, 1993.
- GUTIÉRREZ, J. C.; PIZZOLATO, N. D., Desenvolvimento e aplicação de um modelo heurístico para a programação de lotes econômicos de produção (ELSP) com tempos e custos de setup dependentes da seqüência. Anais do XXXVI SBPO, São João Del Rei, MG, novembro, 2004.
- ILOG Using the CPLEX Callable Library, Copyright, ILOG, 2006.
- KARIMI, B.; GHOMI, S. M. T. F.; WILSON, J. M. The capacitated lot sizing problem: a review of models and algorithms. Omega International Journal of Management Science, v. 31, n. 5, p. 365-378, 2003.
- KELLY, J. D.; MANN, J. L., Flowsheet decomposition heuristic for scheduling: a relax and fix method. Computers & Chemical Engineering, v. 28, n. 11, p. 2193-2200, 2004.
- KUIK, R.; SALOMON, M.; WASSENHOVE, L. Batching Decisions: Structure and Models. European Journal of Operational Research, v. 75, p. 234-263, 1994.
- LUCHE, J. R.; MORABITO, R. Otimização na programação da produção de grãos eletrofundidos: Um estudo de caso. Gestão & Produção, v. 12, n. 1, p. 135-149, 2005.
- MANNE, A. S., On the job-shop scheduling problem. Operations Research, v. 8, p. 219-223, 1960.
- MEYR, H. Simultaneous Lotsizing and Scheduling by Combining Local Search with Dual Reoptimization. European Journal of Operational Research, v. 120, p. 311-326, 2000.
- MEYR, H. Simultaneous lotsizing and scheduling on parallel production lines, European Journal of Operational Research, v. 39, p. 277-292, 2002.
- NEIT, Núcleo de Economia Industrial e da Tecnologia. Panorama Setorial: Indústria de Bebidas. Boletim, n. 4, maio de 2004.
- PEDROSO, J. P. Tabu Search for mixed integer programming, Technical Report Series DCC-2004-02, LIACC, Universidade do Porto, 2004.
- PEDROSO, J. P.; KUBO, M. Hybrid Tabu Search for lot sizing problems. In Blesa M., Blum C., Roli A., e Sampels, M. (editores), Lecture Notes in Computer Science Springer Berlin/Heidelberg, v. 3636, p. 66-77, 2005.
- PINEDO, M. Scheduling Theory, Algorithms and Systems Prentice Hall, 1995.
- RANGEL, M. S.; FERREIRA, D. Um Modelo de Dimensionamento de Lotes para uma fábrica de refrigerantes. TEMA - Tendências em Matemática Aplicada e Computacional, v. 4, n. 2, p. 237-246, 2003.
- TOLEDO, C. F. M. Problema Conjunto de Dimensionamento de Lotes e Programação da Produção. Tese de Doutorado, Universidade Estadual de Campinas, Faculdade de Engenharia Elétrica e Computação, Setembro, 2005.
- TOLEDO, C. F. M.; FRANÇA, P. M.; MORABITO, R.; KIMMS, A. Um modelo de otimização para o problema integrado de dimensionamento de lotes e programação da produção em fábricas de refrigerantes. Pesquisa Operacional, v. 27, n. 1, p. 155-186, 2007a.
- TOLEDO, C. F. M.; FRANÇA, P. M.; MORABITO, R.; KIMMS, A. A Multi-Population Genetic Algorithm to Solve the Synchronized and Integrated Two-Level Lot Sizing and Scheduling Problem". Aceito para publicação no International Journal of Production Research, 2007b.
- TOLEDO, F. M. B.; ARMENTANO, V. A. A Lagrangian-based heuristic for the capacitated lot-sizing problem in parallel machines. European Journal of Operational Research, v. 175, p. 1070-1083, 2006.
- TOSO, E. A. V.; MORABITO, R. Otimização no dimensionamento e seqüenciamento de lotes de produção: estudo de caso numa fábrica de rações. Gestão & Produção, v. 12, n. 2, p. 203-217, 2005.
- TOSO, E. A. V.; MORABITO, R.; CLARK, A. R. Abordagens ATSP com Eliminação de Sub-rotas para o Problema de Dimensionamento e Seqüenciamento de Lotes de Produção de Ração Animal. Submetido para publicação, 2007.
- WOLSEY, L. A. Integer Programming John Wiley & Sons, 1998.
Datas de Publicação
-
Publicação nesta coleção
10 Jun 2008 -
Data do Fascículo
2008
Histórico
-
Recebido
03 Abr 2007 -
Aceito
25 Out 2007