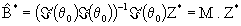Resúmenes
En muchas aplicaciones agrícolas o biológicas, se ajustan modelos basados en funciones de producción Yi = (Xi, <FONT FACE="Symbol">q</font>) + e para un conjunto de variables predictoras Xj j = 1,. . . , k y un vector parámetros <FONT FACE="Symbol">q</font>. En este trabajo se presenta una alternativa para detectar observaciones influyentes, cuando la función de producción es univariada y la estimación de los parámetros se realiza por el método de Gauss - Newton.
función de producción; observacione influyente
Models of production functions Yi = (Xi , <FONT FACE="Symbol">q</font>) + e, with explanatory variables xj , j=1,..., k and a parameter vector <FONT FACE="Symbol">q</font> are used in agricultural and biological areas. In the present work we present an alternative to detect influent observations, when the production function is univariate and the Gauss-Newton method is used to estimate the parameters.
production function; influent observation
Em muitas aplicações agrícolas ou bilógicas, ajustam-se modelos baseados em funções de produção Yi = (Xi, <FONT FACE="Symbol">q</font>) + e, para um conjunto de variáveis preditoras xj , j=1,..., k e um vetor de parâmetros <FONT FACE="Symbol">q</font>. Neste estudo apresenta-se uma alternativa para detectar observações influentes, quando a função de produção é univariada e a estimação dos parâmetros é executada através do método de Gauss-Newton.
funções de produção; observações influentes
UNA ALTERNATIVA PARA DETECTAR OBSERVACIONES INFLUYENTES EN FUNCIONES DE PRODUCCIÓN UNIVARIADAS1 1 Este trabajo tuvo apoyo financiero de COLCIENCIAS - COLOMBIA.
L.F. RINCÓN2; L.A. LÓPEZ2; A.F. IEMMA3
2Depto. de Matemáticas y Estadísticas-UN - Santa Fe de Bogotá, Colombia.
3Depto. de Matemática e Estatística-ESALQ/USP, C.P. 9, CEP: 13418-900 - Piracicaba, SP.
RESUMEN: En muchas aplicaciones agrícolas o biológicas, se ajustan modelos basados en funciones de producción Yi = (Xi, q) + e para un conjunto de variables predictoras Xj j = 1,. . . , k y un vector parámetros q. En este trabajo se presenta una alternativa para detectar observaciones influyentes, cuando la función de producción es univariada y la estimación de los parámetros se realiza por el método de Gauss - Newton.
Descriptores: función de producción, observacione influyente
UMA ALTERNATIVA PARA DETECTAR OBSERVAÇÕES
INFLUENTES EM FUNÇÕES UNIVARIADAS DE PRODUÇÃO
RESUMO: Em muitas aplicações agrícolas ou bilógicas, ajustam-se modelos baseados em funções de produção Yi = (Xi, q) + e, para um conjunto de variáveis preditoras xj , j=1,..., k e um vetor de parâmetros q. Neste estudo apresenta-se uma alternativa para detectar observações influentes, quando a função de produção é univariada e a estimação dos parâmetros é executada através do método de Gauss-Newton.
Descritores: funções de produção, observações influentes
AN ALTERNATIVE FOR THE DETECTION OF INFLUENT
OBSERVATIONS IN UNIVARIATE PRODUCTION FUNCTIONS
ABSTRACT: Models of production functions Yi = (Xi , q) + e, with explanatory variables xj , j=1,..., k and a parameter vector q are used in agricultural and biological areas. In the present work we present an alternative to detect influent observations, when the production function is univariate and the Gauss-Newton method is used to estimate the parameters.
Key Words: production function, influent observation
INTRODUCCIÓN
En un estudio con funciones de producción aplicadas a problemas agrícolas, pecuarios o a ciencias biológicas en general, frecuentemente se ajusta modelos no lineales para describir el comportamiento de la variables Yi en función de un conjunto de k variables predictoras X = (Xi1,...,Xik) i = 1,...,n.
En el caso de tener una sola variable de predicción, se puede caracterizar la ecuación de regresión por el modelo no lineal univariado
donde f (Xi, q) es una función de respuesta conocida, q un vector p-dimensional de parámetros desconocidos, y ei el error aleatorio, como puede verse en Gallant (1987) y Rivas et al (1993).
Para obtener la estimación de los parámetros en el modelo (1), generalmente se hace uso de procedimientos basados en métodos iterativos.
En este trabajo, se uso el método de Gauss - Newton para la estimación de los parámetros, por la facilidad de los cálculos y la rapidez de convergencia de los estimadores. Para la aplicación del método de estimación, se debe tener en cuenta los siguientes pasos:
1 - Se determina un vector q0 de valores iniciales para los parámetros, y se calcula
f (Xi, q0 ), i=1, 2,....., n
2 - Se define el campo vectorial
3 - Se propone el modelo lineal
(2)
donde
es la matriz Jacobiana de F de orden n x p calculada en q0, es decir, la i-ésima fila de tiene como elementos las derivadas parciales
Cuando es de rango completo la estimación mínimos cuadrados
siendo
(3)
Del modelo (2), se obtiene la estimación, la cual será tomada como segundo valor inicial para el proceso iterativo, que se repite hasta satisfacer un criterio de convergencia preestablecido.
MÉTODO PARA DETECTAR OBSERVACIONES INFLUYENTES
Dado el modelo no lineal univariado (1) con f (xi, q) una función de respuesta conocida, q un vector p-dimensional de parámetros desconocidos, y ei el error experimental; al aplicar el método de estimación de Gauss - Newton descrito en la sección anterior, la estimación 
al final de la primera iteración para cada parámetro estimado corresponde a la expresión:
(4)
Donde qj0 es el valor inicial propuesto para la estimación del parámetro qj y mij los elementos de la j-ésima columna de la matriz M definida en (3).
Al introducir una modificación 
en la primera observación de la forma:
para el nuevo modelo 
y nuevamente por mínimos cuadrados se sigue que:
teniendo como resultado al final de la primera iteración, que la influencia de g1 en los parámetros estimados esta dada por:
Donde mjl son los elementos de la primera columna de la matriz M, 
es la estimación del j-ésimo parámetro en el modelo modificado y 
es la estimación del j-ésimo parámetro en el modelo original.
Si la modificación se hace en la i-ésima observación para algún i =1 , . . ., n definiendo:
para 
la diferencia en las estimaciones del j-ésimo parámetro al modificar la i-ésima observación se obtiene a partir de la expresión:
(5)
con mji el elemento de la j-ésima fila e i-ésimo columna de la matriz M.
De (5) se define la estadística DFBeta 
que cuantifica al final de la primera interacción, el efecto en la estimación de los parámetros al eliminar la i-ésima observación en el modelo (1)
M*i representa la i-ésima columna de la matriz M y 
es la constante de ajuste que define la estadística DFBeta(i) para el modelo (2). Esta constante se obtiene en forma sencilla usando la metodología de Rincón (1995) a partir de la expresión:
con
ILUSTRACIÓN DEL MÉTODO
En Quintero (1994), se presentan los siguientes datos relacionados con la ganancia promedio de peso de 27 novillos, los cuales se observaron durante ocho periodos distintos de tiempo:
Para este conjunto de datos, se analizaron diferentes modelos, los cuales buscaban explicar la ganancia de peso medio de los novillos, en función del tiempo. Para estos datos se presenta el análisis buscando detectar observaciones influyentes en el modelo que mejor se ajusto a los datos, este fue:
(6)
Donde Pi representa el peso promedio de los 27 novillos en el tiempo ti , 
es el vector de parámetros, y ei el error experimental, el cual se asume que se distribuye 
, el modelo (6) también fue usado por Menchaca (1990) en un estudio de crecimiento.
Se usó como vector de valores iniciales q0 = (63.594093, 0.003672, -0.000002) obtenido de las estimaciones mínimos cuadrados cuando se uso el modelo transformado 
con este valor inicial de q0 y usando la metodología propuesta en Rincón (1995) para detectar observaciones influyentes en modelos de regresión; se ajusto el modelo:
(7)
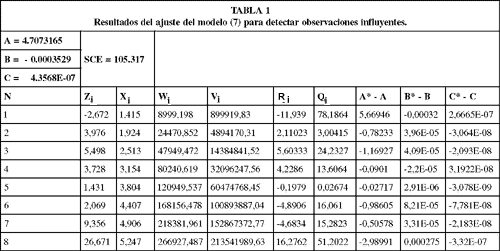
Obteniendo los resultados que se presentan en la tabla No. 1, en donde:
Ri son las constantes de ajuste 
para cada observación y A* - A, B* - B, C* - C son las componentes de la estadística DFBeta(i).
Qi : Mide el aporte de cada observación al error.
De los resultados de la tabla 1 es posible concluir que la 1a observación merece especial atención, puesto que es la que mayor error aporta al modelo (Q1 = 78.1864) y además es la más influyente en la estimación de los parámetros.
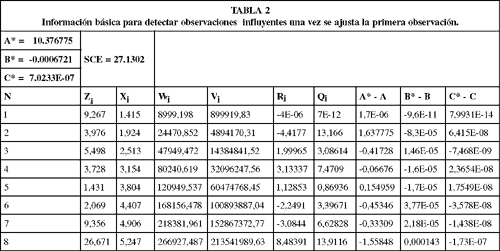
Una vez detectado la observación influyente se procedió a ajustar los datos. Los resultados de este ajuste se presentan la tabla 2. Se debe tener en cuenta que 
, es decir, el modelo ajustado con la modificación 
verificándose que:
los cuales coinciden con los obtenidos al ajustar el modelo después de eliminar la 1a observación.
Obteniendo finalmente un buen ajuste del modelo cuando se tiene el siguiente conjunto de parámetros q = qo + (10.3767; - 0.00067; 7.023 x 10-7) = (73.9707; 0.003; 0.0000019).
Los parámetros obtenidos ajustando la primera observación son bastante aproximados, a los encontrados cuando se remueve la observación influyente como puede observarse en la salida numero 3 del anexo anexo , las cuales son una buena aproximación a las estimaciones logradas después de la primera iteración realizada en SAS en él modulo NLIN.
En el anexo
anexo
se presenta el programa cuando se uso del procedimiento NLIN del paquete estadístico SAS usando como método de estimación el procedimiento de Gauss - Newton. Además se muestran: en la salida 1. los resultados de la estimación para el modelo (2) con los datos originales; en la salida 2. los resultados de la estimación modificando la primera observación con su constante de ajuste 
, es decir, con 
, y finalmente en la salida 3. Los resultados de la estimación eliminando la 1a observación, donde se verifica que DFBeta (i) esta bien definida y que las estimaciones logradas después de la primera iteración con el método de Gauss - Newton se aproximan bastante bien a las obtenidas con el método descrito en la sección 2.
ANEXO
Programa para SAS procedimiento NLIN
data edad;
input t p @@;
cards ;
100 87.32 200 126.33 300 165.33 400 204.33
500 243.33 600 282.33 700 321.33 800 360.34
;
proc print;
run;
proc nlin iter=25 convergence=1.0E-13 ;
parms a=63.594093 b=0.003672 c=-0.000002 ;
model p=a*exp(b*t+c*t*t) ;
der.a=exp(b*t+c*t*t) ;
der.b=a*t*exp(b*t+c*t*t) ;
der.c=a*t*t*exp(b*t+c*t*t) ;
output out=salida p=Pajus residual=res ;
proc print;
run;
SALIDA 1.
Non-Linear Least Squares Iterative Phase
Dependent Variable P Method: Gauss-Newton
NOTE: Convergence criterion met.
Non-Linear Least Squares Summary Statistics Dependent Variable P
Parameter Estimate Asymptotic Asymptotic 95 %
Std. Error Confidence Interval
SALIDA 2.
Non-Linear Least Squares Iterative Phase
Dependent Variable P Method: Gauss-Newton
Non-Linear Least Squares Summary Statistics Dependent Variable P
Parameter Estimate Asymptotic Asymptotic 95%
Std. Error Confidence Interval
SALIDA 3.
Non-Linear Least Squares Iterative Phase
Dependent Variable P Method: Gauss-Newton
NOTE: Convergence criterion met.
Non-Linear Least Squares Summary Statistics Dependent Variable P
457061.62900
Parameter Estimate Asymptotic Asymptotic 95%
Std. Error Confidence Interval
Recebido para publicação em 05.07.96
Aceito para publicação em 28.11.97
- GALLANT, R. Nonlinear Statistical Models. New York, John Wiley. 1987.
- MENCHACA. M. A. Modelo de crecimiento en peso de bovinos. Revista Cubana de Ciencia Agrícola. Instituto de Ciencia Animal. v.25, p.125, 1990.
- RIVAS, G.; LÓPEZ, L. A., y VELASCO, A. Regresión no lineal. Revista Colombiana de Estadística. v.27, p.89, 1993.
- QUINTERO, R. Ajuste de modelos no lineales para la ganancia de peso en bovinos. Tesis de grado, Universidad Nacional de Colombia. 1994.
- RINCÓN, L. F. An alternative to calculate the Qk Statistic in Simple Linear Regresión Models. Resumos, Actas 4a Escola de Modelos de Regressăo. Aguas de Săo Pedro, Brasil. 1995.
anexo
Fechas de Publicación
-
Publicación en esta colección
04 Feb 1999 -
Fecha del número
Mayo 1998
Histórico
-
Recibido
05 Jul 1996 -
Acepto
28 Nov 1997
