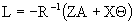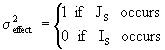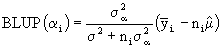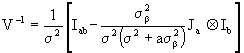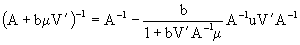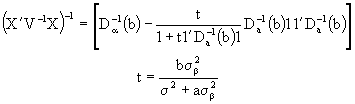ON THE ESTIMATION AND PREDICTION IN MIXED LINEAR MODELS¹

 

L.A. LÓPEZ²; A.F. IEMMA^3
2Depto. de Matemáticas y Estadística-UN - Santa Fé de Bogotá, Colombia.
³Depto. de Matemática e Estatística-ESALQ/USP, C.P. 9, CEP: 13418-900 - Piracicaba, SP.

 

 

SUMMARY: Beginning with the classical Gauss-Markov Linear Model for mixed effects and using the technique of the Lagrange multipliers to obtain an alternative method for the estimation of linear predictors. A structural method is also discussed in order to obtain the variance and covariance matrixes and their inverses.
Key Words: linear model, mixes effect, predictor, estimator

 

SOBRE A ESTIMAÇÃO E PREDICÇÃO EM MODELOS LINEARES MIXTOS

RESUMO: Através do modelo linear clássico de Gausss-Markov caracterizado como modelo de efeitos mistos, aplicou-se a tecnologia dos multiplicadores de Lagrange para obter um método alternativo de estimação de preditores lineares. Além disso, é proposto um critério estrutural simples para a obtenção das matrizes de variâncias, covariâncias e de suas inversas.
Descritores: modelos lineares, efeitos mistos, preditores, estimadores

 

 

INTRODUCTION

In many experimental situations one or more factors can be associated to sampling processes, while other factor combinations are associated to fixed effects, which is the characteristic of the mixed models. Such situations are common in experiments with living beings.

According to Scheffe (1959), this type of models were studied by Fisher in 1916, who called them "Component of Variance Models" with great repercusion in quantitative genetic studies. Since then this type of models have been widespread in many scientific disciplines. With Henderson (1953) there was a greated advance in the components of variance analysis with unbalanced data structures. Motivated by the several aplications, many investicators have contributed for the development of new techniques and procedures of estimation of components of variance, being of outstanding value the contributions of Hartley & Rao (1967) who developed a maximum likelihood method, Reml, Rao (1972) and Lamotte (1973), who presented the well know Minque Method.

In studies of this type of models, it is important to emphatize the following fundamental aspects:

i) Estimation of the fixed effects. ii) Estimation of the random effects. iii) Estimation of the components of variance.

In the sequence of the present work the fixed effect models aproache the balanced and unbalanced data structures, developing the theoretical basic results for the aspects (i) and (ii).

The general structures of the best linear umbiased estimator, BLUE, and the best linear umbiased predictors, BLUP, are obtained by generalized least squares, nevertheless an alternative method is presented to estimate the linear predictors using the Lagrange multiplier technic.

In order to ilustrate the theoretical results, explicit forms are presented for the BLUE and BLUP in a model with one or two classification ways and in a complete randomized block design with cell mean structure.

 

MATHEMATICAL MODEL OF VARIANCE STRUCTURE

In this section a mathematical model is presented associated with the fixed-effect models and the basic assumptions for expected values and variances.

Let the model

with

Y: Observations vector of Nx1 dimensions;
X: Known matrix associated with the fixed effects of NxK dimensions, with rank (X) £ min (N, K);
b: Unknown vector associated with the fixed effects of Kx1 dimensions.
U: Vector associated with the randomized effects of qx1 dimensions:

and

U: Randomized vector q_ix1 dimensions; i=1,..., s.
Z: Is usually an incidence matrix associated with the randomized effects of Nxq dimensions in general observable:

Z_i: Observable matrix of Nxq_i; i= 1, ..., s
e: Unobservable vector of Nx1 dimensions,
Satisfying:

i) if U₀ = e, then we can rewrite the U vectors with E (U_i) = 0 for every i=1, ..., s.
and
it is clear that and ; for i=1,....s

ii)         (2.3)

where: Direct sum of matrices.

iii)      (2.4)

 

ESTIMATORS OF THE FIXED AND RANDOM EFFECTS

The principal interest in the estimation process of models (2.1) is concentrated in the best Lineal Umbiased Estimators (BLUE), which is associated to the fixed effect and the Best Linear Umbiased Predictor (BLUP), associated with the random effects.

If in (2.1) we assume that with R a positive definite matrix, there exists an ortogonal matrix such than: premultiplying (2.1) by A, we arrive to a model of the form: with .

Minimizing the expression:

and making it equal to zero (0) the partial derivates are:

From equation (2) in (3.2) we obtain:

substituting (3.3) in equation (1) of (3.2), and from Henderson and Searle (1981) we have:

substituting (3.4) en (3.3), the solution is

Theorem. If the matrix associated to the fixed effects is a nonsingular matrix, we have:

wich is a complet colum rank matrix (3.5) and is equivalent to the sollution of Ordinary Least Squares.

Proof. Premultiplying (3.6) by X, we have XB=VX, then premultiplying it by V^-1, post-multiplying by B^-1 and transposing the matrix we have:

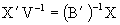
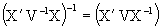
post-multiplying (3.8) by X'V^-1Y, then and the equivalence is immediatly

 

CHARACTERIZATION OF THE LINEAR PREDICTORS

Let a linear function of the fixed and random parameters of the model L'Y, known as the predictor be:

the right side of this equation is known as the Predictant Form (4.1) and it follows this, according to Zyskind (1974), Iemma (1987) and Iemma & Palm (1992). In order to estimate the linear predictors, the variance of the prediction error is minimized.

Var(N' b+M' U - L' Y) = M' DM + L' VL - M' DZL - L' ZDM

subject to the contition

In the process of minimizing Lopez (1992), using the Lagrange´s Multiplicators Technic, obtained the function to minimize:

deriving with respect to the parameters (L,l), the system of equations looked for is:

 

where and  V=ZDZ' + R

It´s also observed that:

or and also

Replacing (4.5) and (4.6) in (4.4), the new system of equation is:

for equation (1) in (4.7) follows that:

substituting in (2) and (3) from the same system of equations the next generated system is:

applying the partitioned invertion matrix rule to (4.9), and having in mind (4.8) we have:

In Hendersson (1984), it´s proved that if K=ZD then substituting in (4.10) and by (3.3) we have finally that

from wich we can conclude that the observation´s Linear Predictor depends on the fixed and random effects, estimated in the model .

 

HOW TO OBTAIN V AND V^-1

In this section, a synthesis of López (1989) work is presented. He introduced a methodology to construct the V matrix associateed with the model (2.1) and it´s inverse (V^-1), with emphasis in balanced models like V = ZDZ'+R when, then rewriting where can be expressed as the Kronecker Products of identity matrices of order S. (I_S) and squares of elements (J_S). If the response variable can be written as:   I=1,...,I  J=1,...J;...;   T=1,...T, that is, a model where t-variation effecs can be identified with p the number of subindices associated to the response variable, we have 2^p partitions of Kronecker Products of matrices I_S and J_S, that is,

the Indicator Function is defined as:

then (5.1) can be written as:

characterizing the arrangement vector (5.2) as a vector associated to the variance´s random effecfts it is contructed as of by the next criterium:

In this form (2.3) can be written as:

with a suitable permutation of (5.1), and a suitable permutation of the depending upon the way the model is structured.

If , from López (1989), we have

where

As defined by Searle & Henderson (1979) when the structure of the data is unbalanced and the factor is fitted to a hierarchical model. A procedure to obtain the inverse of the variance components is found in López (1989, 1992).

 

APLICATIONS

In this section explicit forms of BLUE and BLUP are presented in models with one or two classification ways.

Aplication 1. Let the model

with from (5.1) in this case:

and

form (5.3) and (5.4); an them

from (3.5) BLUE (m) = and from (3.3)

if in (6.1) we have an unbalenced structure that is if i=1,...,a; i=1,...,n_i

and

Aplication 2. Consider a design of unbalanced blocks described by the model

and and if also a reparame-trization is done in the fixed effects that X is a complete rank matrix, or when we have a cell mean model, then:

to invert (6.3) we recall the results of Henderson & Searle (1981) where

then

then

In general, with balanced structures, if the matrix associated to the fixed effects is of complete column rank (reparametrized or cell means) the BLUE, will not depend on the random affects.

 

REFERENCES

HARTHEY, H.O.; RAO, J. Maximum likelihooh estimation for the mixed analysis of variance model. Biometrika, v.54, p.93-108, 1967.         [ Links ]

HENDERSON, C. R. Estimation of variance and covariance components. Biometrics, v.49, p.226-257, 1953.         [ Links ]

HENDERSON, H.V; SEARLE, S.R. On deriving the inverse of some of matrices. Siam Revew. p.53-60, 1981.         [ Links ]

IEMMA, A.F. Modelos lineares: Uma introdução para profissionais na pesquisa agropecuária. Londrina: Universidade Estadual de Londrina, Departamento de Matemática Aplicada, 1987, 2263p.         [ Links ]

IEMMA, A.F.; PALM, R. Matrices inverses généralisées et leur utilisation dans le modele lineaire. Gembloux: Faculte des Sciences Agronomiques, 1992. 25p. (Notes de Statistique et d´informatique, 1).         [ Links ]

LAMOTTE, L.R., Quadratic estimations of variance components. Biometrics, v.29, p.317-330, 1973.         [ Links ]

LÓPEZ PÉREZ, L.A., Estimação e predicao nos modelos mistos não balanceados. Piracicaba, 1992. 85p. Tese (Doutorado) - Escola Superior de Agricultura Luis de Queiroz, Universidade de São Paulo.         [ Links ]

LÓPEZ PÉREZ, L.A., Cálculo de la matriz inversa de componentes de varianza en estructuras desbalanceadas. Revista Colombiana de Estadística, v.19, p.113-124, 1989.         [ Links ]

PETERSON, H.; THOMPSON, R. Recovery of covariance components. Journal of Multivariate Analysis, v.42, p.583-545, 1971.         [ Links ]

RAO, C.R. Estimation of variance and covariance components in linear models. Journal of the American Statistical Association, v.69, p.112-115, 1972.         [ Links ]

SCHEFFE, H. Analysis of variance, New York: John Wiley, 1976.         [ Links ]

SEARLE, S.R; HENDERSON, H.V. Disperson matrices for variance components models. Journal of the American Statistical Association, v.34, p.465-470, 1979.         [ Links ]

ZYSKIND, G. General theory of linear hypothesis. Iowa State University Press, 1974.         [ Links ]

 

 

Recebido para publicação em 05.07.96
Aceito para publicação em 28.11.97

 

 

¹This work is sponsored by COLCIENCIAS Colombia.