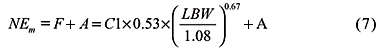Abstracts
Mathematical models can be used to improve performance, reduce cost of production, and reduce nutrient excretion by accounting for more of the variation in predicting requirements and feed utilization in each unique production situation. Mathematical models can be classified into five or more categories based on their nature and behavior. Determining the appropriate level of aggregation of equations is a major problem in formulating models. The most critical step is to describe the purpose of the model and then to determine the appropriate mix of empirical and mechanistic representations of physiological functions, given development and evaluation dataset availability, inputs typically available and the benefits versus the risks of use associated with increased sensitivity. We discussed five major feeding systems used around the world. They share common concepts of energy and nutrient requirement and supply by feeds, but differ in structure and application of the concepts. Animal models are used for a variety of purposes, including the simple description of observations, prediction of responses to management, and explanation of biological mechanisms. Depending upon the objectives, a number of different approaches may be used, including classical algebraic equations, predictive empirical relationships, and dynamic, mechanistic models. The latter offer the best opportunity to make full use of the growing body of knowledge regarding animal biology. Continuing development of these types of models and computer technology and software for their implementation holds great promise for improvements in the effectiveness with which fundamental knowledge of animal function can be applied to improve animal agriculture and reduce its impact on the environment.
cattle; feeding; nutrient; requirement; supply
Modelos matemáticos podem ser utilizados para melhorar a performance, reduzir os custos de produção, e minimizar a exceção de nutrientes através de melhores estimativas da exigência e utilização de alimentos em vários cenários produtivos. Modelos matemáticos podem ser classificados em cinco ou mais categorias dependendo da sua natureza. Um dos maiores problemas na construção de modelos matemáticos é o nível de agregação das equações. Os passos mais importantes são o estabelecimento do propósito do modelo, determinação da melhor combinação de equações empíricas e teóricas para representar das funções fisiológicas dado a disponibilidade de banco de dados, informações tipicamente encontradas a nível de campo, e os benefícios e riscos associados com o uso do modelo na produção animal. Nesse artigo são discutidos cinco sistemas de alimentação padrão de ruminantes mais utilizados atualmente. Eles compartilham de conceitos de exigência e disponibilidade de energia e nutrientes, mas diferem na estrutura e como esses conceitos são abordados. Modelos animais podem ser utilizados para vários propósitos, entre eles uma simples descrição de observações, estimativa de respostas à diferentes manejos, e caracterização de mecanismos biológicos. Dependendo dos objetivos, várias alternativas podem ser utilizadas na construção do modelo matemático, entre elas, equações algébricas simples, equações de relação puramente estatísticas, ou até modelos mecanicistas e dinâmicos. Esse último favorece o uso da quantidade crescente de informações cientificas relacionadas à biologia animal. O desenvolvimento contínuo desses tipos de modelos juntamente com as inovações computacionais e de softwares permitem avanços na forma de uso dos conhecimentos fundamentais de nutrição animal de forma que a produção animal possa ser melhor explorada ao mesmo tempo reduzindo-se o impacto ambiental.
alimentação; exigência; gado; nutriente; suprimento
REVIEW
Mathematical models in ruminant nutrition
Modelos matemáticos na nutrição de ruminantes
Luís Orlindo TedeschiI, * * Corresponding author < lot1@cornell.edu> ; Danny Gene FoxI; Roberto Daniel SainzII; Luís Gustavo BarioniIII; Sérgio Raposo de MedeirosIV; Celso BoinV
ICornell University - Department of Animal Science, 14850 - Ithaca, NY - USA
IIUniversity of California - Department of Animal Science, 95616 - Davis, CA - USA
IIIEmbrapa Cerrados, BR 020 km 18 - 73310-970 - Planaltina, DF - Brasil
IVEmbrapa Gado de Corte, BR 262 km 4 - 79002-970 - Campo Grande, MS - Brasil
VUSP/ESALQ - Depto. de Zootecnia, C.P. 09 - 13416-900 - Piracicaba, SP - Brasil
ABSTRACT
Mathematical models can be used to improve performance, reduce cost of production, and reduce nutrient excretion by accounting for more of the variation in predicting requirements and feed utilization in each unique production situation. Mathematical models can be classified into five or more categories based on their nature and behavior. Determining the appropriate level of aggregation of equations is a major problem in formulating models. The most critical step is to describe the purpose of the model and then to determine the appropriate mix of empirical and mechanistic representations of physiological functions, given development and evaluation dataset availability, inputs typically available and the benefits versus the risks of use associated with increased sensitivity. We discussed five major feeding systems used around the world. They share common concepts of energy and nutrient requirement and supply by feeds, but differ in structure and application of the concepts. Animal models are used for a variety of purposes, including the simple description of observations, prediction of responses to management, and explanation of biological mechanisms. Depending upon the objectives, a number of different approaches may be used, including classical algebraic equations, predictive empirical relationships, and dynamic, mechanistic models. The latter offer the best opportunity to make full use of the growing body of knowledge regarding animal biology. Continuing development of these types of models and computer technology and software for their implementation holds great promise for improvements in the effectiveness with which fundamental knowledge of animal function can be applied to improve animal agriculture and reduce its impact on the environment.
Key words: cattle, feeding, nutrient, requirement, supply
RESUMO
Modelos matemáticos podem ser utilizados para melhorar a performance, reduzir os custos de produção, e minimizar a exceção de nutrientes através de melhores estimativas da exigência e utilização de alimentos em vários cenários produtivos. Modelos matemáticos podem ser classificados em cinco ou mais categorias dependendo da sua natureza. Um dos maiores problemas na construção de modelos matemáticos é o nível de agregação das equações. Os passos mais importantes são o estabelecimento do propósito do modelo, determinação da melhor combinação de equações empíricas e teóricas para representar das funções fisiológicas dado a disponibilidade de banco de dados, informações tipicamente encontradas a nível de campo, e os benefícios e riscos associados com o uso do modelo na produção animal. Nesse artigo são discutidos cinco sistemas de alimentação padrão de ruminantes mais utilizados atualmente. Eles compartilham de conceitos de exigência e disponibilidade de energia e nutrientes, mas diferem na estrutura e como esses conceitos são abordados. Modelos animais podem ser utilizados para vários propósitos, entre eles uma simples descrição de observações, estimativa de respostas à diferentes manejos, e caracterização de mecanismos biológicos. Dependendo dos objetivos, várias alternativas podem ser utilizadas na construção do modelo matemático, entre elas, equações algébricas simples, equações de relação puramente estatísticas, ou até modelos mecanicistas e dinâmicos. Esse último favorece o uso da quantidade crescente de informações cientificas relacionadas à biologia animal. O desenvolvimento contínuo desses tipos de modelos juntamente com as inovações computacionais e de softwares permitem avanços na forma de uso dos conhecimentos fundamentais de nutrição animal de forma que a produção animal possa ser melhor explorada ao mesmo tempo reduzindo-se o impacto ambiental.
Palavras-chave: alimentação, exigência, gado, nutriente, suprimento
INTRODUCTION
Mathematical models can be used to improve performance, reduce cost of production, and reduce nutrient excretion by accounting for more of the variation in predicting requirements and feed utilization in each unique production situation. However, the use of models to assist in production decisions is limited by the information (model inputs) that is typically available on the farm. The purpose of this review is to discuss the development of nutrition models for predicting requirements and feed utilization by cattle in formulating accurate rations and feeding systems in each production situation.
Using models to predict requirements and supply of energy and nutrients
Mathematical models can be used to integrate our knowledge of feed, intake, and digestion and passage rates upon feed energy values, escape of dietary protein, and microbial growth efficiency. They can be valuable tools for estimating animal requirements and nutrients derived from feeds in each unique farm production scenario, and thus can have an important role in providing information that can be used in the decision-making process to enhance the feeding system.
A cattle nutrition model is defined as an integrated set of equations and transfer coefficients that describe their various physiological functions (Gill et al., 1989). Included in cattle models are predictions of tissue requirements (maintenance, growth, pregnancy, lactation and tissue reserves) and supply of nutrients (dry matter intake, feed carbohydrate and protein fraction pool sizes and their characteristic digestion and passage rates, microbial growth, intestinal digestion and metabolism of absorbed nutrients). The purpose of a simulation model is to describe mathematically the response of each compartment or several connected compartments to a variable or combination of variables. Mathematical models can be categorized (France & Thornley, 1984; Haefner, 1996) as:
Static vs. Dynamic; dynamic models incorporate time explicitly whereas static models do not,
Empirical vs. Mechanistic; empirical models provide a best fit to data obtained at the prediction level (e.g., body weight) whereas mechanistic models incorporate concepts about the underlying biology and data from lower levels of aggregation (e.g. cellular function),
Stochastic vs. Deterministic; deterministic models always give the same solution to a given set of inputs whereas stochastic models include probabilistic element(s), giving a distribution of outputs to a given set of inputs,
Continuous vs. Discrete; continuous models represent time continuously (time may take on any value) while in discrete models time is an integer only, and
Spatially Homogeneous vs. Heterogeneous; spatially homogeneous models have an explicit representation of space (e.g. objects have a position in space) whereas in spatially heterogeneous models space is not essential (e.g. population dynamics, enzyme kinetics).
The mathematical representation and prediction of animal function has been a widespread endeavor in biology and a wide range of approaches has been proposed. Objectives in modeling animal performance may include:
Description of past observations,
Prediction of outcomes of different management strat egies, and/or
Explanation of mechanisms.
Each of these objectives requires a different approach. Descriptive and predictive models are usually static and empirical, whereas explanatory or mechanistic models require a dynamic approach. Dynamic models are usually represented by differential equations, which may be solved analytically or numerically.
A mathematical model is considered mechanistic when it simulates behavior of a function through elements at a lower level of aggregation. Completely mechanistic models do not exist (Gill et al., 1989). A limitation is the ability to account for the fact that most biological responses are integrated and nonlinear and change over time (dynamic) (Sauvant, 1991). Dynamic models are rarely used for application in formulating rations on farms because of limitations in information over the whole range of possible conditions that is typically available to drive such mathematical models and the inability to evaluate all of the functions. In most feeding systems, the prediction of metabolism of nutrients is not as advanced as the prediction of ruminal fermentation, because of the complex metabolic pathways connecting the numerous tissue and metabolic compartments, the multiple nutrient interactions, and the sophisticated metabolic regulations (hormones, enzymes), which drive the partitioning of absorbed nutrients (homeorhesis and homeostasis) (Sauvant, 1991). Therefore, most animal nutrition models used for formulating diets on farms use a combination of mechanistic and empirical approaches, are generally steady state and static, and use statistical representations of data that represent the aggregated response of whole compartments.
Determining the appropriate level of aggregation of equations (closeness to the cellular level) is a major problem in formulating models. The most critical step is to describe the objective of the model and then to determine the appropriate mix of empirical and mechanistic representations of physiological functions, given development and evaluation dataset availability, inputs typically available and the benefits versus the risks of use associated with increased sensitivity. Since many inputs cannot be absolutely quantified with information typically available on farms, these models must allow inputs from each situation to be adjusted in a logical way until predicted and observed performance (daily gain, milk amount and composition, and body condition score changes) agree (also known as calibration). Then, responses to changes in management and feeds can be more accurately predicted by accounting for effects on ruminal fermentation, intestinal digestion, metabolizability of energy and amino acids, and product amount and composition.
Models commonly used for nutrient requirement recommendations
In this section, we assume that a ruminant nutrition model is an integrated set of equations and transfer coefficients that describe nutrient requirements and feed utilization by cattle and sheep for use in formulating diets on farms. In this section, we summarize the nutrition models most often used in developing feeding standards. We summarize here the approaches used to predict requirements and nutrient supply in these models and how they have evolved over time based on the state of knowledge of biological processes and ability to predict them under field conditions.
USA National Research Council (NRC)
In the United States, National Research Council (NRC) committees are formed at regular intervals to evaluate the accumulated scientific knowledge and to propose more accurate estimates of requirements and feed values at a level that can be readily applied in practical ration formulation. Until 1970, total digestible nutrients (TDN) and crude protein (CP) were used to estimate available energy and protein in feeds, respectively, with reasonable success, given the knowledge about feed digestive losses, the narrow genetic base of cattle to which they were applied in North America, laboratory analytical capabilities available, and the ability of advisors and producers to apply them in the field, including limitations in quantifiable inputs such as feed and animal weights. The development of the California net energy (NE) system using the comparative slaughter technique (Lofgreen & Garrett, 1968) and the studies conducted at the USDA-ARS Beltsville Research Center on net energy for lactation using respiration chambers (Moe et al., 1972) provided enough information to implement net energy systems in the National Research Council nutrient requirement recommendations for Beef (NRC, 1970) and Dairy (NRC, 1971) cattle. These systems predict more accurately the requirements and performance on a given diet by basing maintenance requirements on metabolic body size (NEm), tissue (NEg), and milk (NEl) composition and differential feed values for different physiological functions (e.g. feed NEm, NEg, and NEl). Discounts for depression in ruminal digestibility with level of intake and feed cell wall received further refinements (Van Soest, 1994; Van Soest & Fox, 1992; Van Soest et al., 1984).
A major advancement in accounting for more of the variation in meeting protein requirements was the launch of ruminant nitrogen and metabolizable protein (MP) systems by Burroughs et al. (1974), Institut National de la Recherche Agronomique (INRA, 1989), Agricultural Research Council (ARC, 1980), and the National Research Council (NRC, 1985) to predict rumen microbial protein production. These systems are based on predicting microbial protein production (MCP) from one microbial pool through various means of estimating intake of fermentable organic matter. Two pools of feed protein (degraded and undegraded) are used to estimate variable ruminally degradable protein (RDP) of feeds to predict N available for microbial growth and ruminally undegradable protein (RUP) that escapes degradation in the rumen. The MP system was implemented in the 1989 and 2001 Dairy NRC (NRC, 1989; 2001) and the 1996 Beef NRC (NRC, 1996; 2000). Theses systems were based on static and deterministic calculations of carbohydrate and protein degradability and yield of microbial protein, with no provision for microbial maintenance and ruminal N recycling. Additionally, the NRC (1971) energy discounts were fixed at three times maintenance level of intake while those proposed by Van Soest et al. (1979; 1984) were variable according to digestion rate.
The next improvement in NRC systems came when the Beef (NRC, 2000) and Dairy (NRC, 2001) revisions moved from the use of tabular feed energy and protein (RUP and RDP) values to predicting them from feed analysis. The NRC (2000) developed a model with two levels of solution for different uses, depending on the questions to be answered, level of knowledge of the user, and information available to drive the model. Level 1 retained the use of tabular feed energy values but implemented the Burroughs et al., (1974) MP system. The second level of solution uses the Cornell Net Carbohydrate and Protein System (CNCPS) rumen model (Russell et al., 1992; Van Soest, 1994) to predict carbohydrate and protein fermentation and microbial growth and digestible energy derived from feeds, using feed analysis for feed carbohydrate and protein fractions and the integration of feed digestion and passage rates based on level of intake. The NRC (2001) uses summative equations (Weiss, 1993; 1999; Weiss et al., 1992) to predict feed digestible energy and microbial protein production was predicted as in the Beef NRC level 1 (13% of TDN), with the effect of level of intake on feed energy and protein fractions escaping ruminal digestion being accounted for. For the first time, both systems provide equations for predicting amino acid requirements and supply, and guidelines for meeting amino acid requirements.
Institut National de la Recherche Agronomique (INRA)
Feed biological values - In the INRA (1989) system, each feed has two NE values: lactation (UFL) and meat production (UFV), where one UFL or UFV is the NE content of 1 kg of barley for milk (1700 kcal NEl) or meat (1820 Mcal NEg), respectively. The NE values of feedstuffs are calculated from their GE, DE, ratio of ME to GE (metabolizability), and the efficiency of ME utilization for lactation, maintenance, or fattening. The feed GE is assumed to contain 18.8 MJ kg-1 DM (4.49 Mcal kg-1 DM, assuming 1 cal = 4.184 J). The ME to GE ratio was developed with sheep and dairy cattle data (N = 346), and is a function of crude fiber (CF), protein content of the diet (CP), and feeding level (FL). Partial efficiencies (k) are computed from metabolizability of the diet. The protein value of feeds and the animal requirements are both expressed in terms of true protein truly digested and absorbed in the small intestine (PDI). The PDI is a sum of the feed protein ruminally undegraded and truly digested in the small intestine (PDIA) and the microbial true protein that is truly digested in the small intestine (PDIM), as shown in Equation (1) . When a degradable N deficient diet is fed, PDI is called PDIN (Equation 2) and similarly, when a ruminal fermentable energy deficient diet is fed, PDI is called PDIE (Equation 3). Each feed has two PDIM values; the microbial true protein that could be synthesized from the nitrogen it supplies (PDIMN) and the amount of microbial protein that could be synthesized from the feed energy available in the rumen (PDIME). These are summed for two different applications: (a.) when protein supply is the sum of undegraded feed (PDIA) and the protein that could be synthesized by the degraded protein it supplies (PDIMN) (Equation 2) or (b.) when protein supply is the sum of undegraded feed (PDIA) and microbial protein that could be synthesized from its fermentable energy (PDIME) (Equation 3).

The PDI values are obtained from four feed characteristics: CP, CP degradability, fermentable organic matter (FOM), and true digestibility in the small intestine of undegraded dietary true protein (amino acids). The degradability values are from a standardized in sacco method. The FOM is computed from digestible organic matter (DOM), silage fermentable products (FP), ether extract (EE), and undegraded N (BNDN) as shown in Equation (4).
Microbial crude protein is estimated as 145 g kg-1 FOM for energy substrates and 0.9 × degraded CP for protein substrates. It is assumed to contain 80% amino acids that are 80% intestinally digestible. Recycled nitrogen is not included as a source of nitrogen for microbial growth.
Energy and nutrient requirements - The INRA (1989) system estimates maintenance requirements based on live body weight (LBW) of beef and dairy cows as 0.07 × LBW0.75 Mcal of NEl (0.084 × LBW0.75 Mcal of NEm, assuming km/kl = 1.2), which is increased by 10% for loose housed and by 20% for grazing and decreased 10% if dry. The MP (or PDI) required for maintenance is 3.25 × LW0.75 g d-1. Energy reserves are computed as 6 Mcal kg-1 body weight change with an 84% efficiency of mobilization. Allometric relationships between the empty body weight (EBW) and LBW, the weight of the chemical components and the weight of the fat-free body mass are used to predict energy and protein requirements for growth. Coefficients in the equations are parameters from the Gompertz equation (Taylor, 1968), which represents changes in live weight over time. Initial and final weights with growth curve coefficients are given for six classes of bulls, two classes of steers and two classes of heifers for finishing cattle, and two classes each for male and female cattle. The amount of lipids deposited daily is proportional to the daily live weight gain raised to the power 1.8, and daily protein gain is calculated for the gain in the fat-free body mass. Requirement for lactation is based on milk composition and for pregnancy is based on days pregnant.
Commonwealth Scientific and Industrial Research Organization (CSIRO)
Feed biological values - In the CSIRO (1990) system, empirical equations are used to predict forage ME values from dry matter digestibility (DMD), organic matter digestibility (OMD), or acid detergent fiber (ADF). Grains are given fixed values, based on metabolism trials with sheep. No adjustments are made in ME values for level of intake. Protein degradability of forages is predicted from CP and ADF contents with empirical equations, and RUP is CP minus degradable protein. An empirical equation is used to predict intestinal digestibility of RUP. Microbial crude protein yield is 170 g kg 1 DOM for the first growth of temperate legumes and grasses, 130 g kg-1 DOM for all other fresh and dried forages and mixed diets, and 95 g kg-1 DOM for silages. Microbial protein adjusted for 20% nucleic acids is assumed to have a 70% intestinal digestibility, giving a 56% MP value to microbial crude protein. Inefficient capture of N from ruminally degraded protein is assumed to be compensated for by recycled N. CSIRO (1990) concluded that although recycling N can offset intermittent inadequacies of ruminally degraded protein, it will not sustain the animal through a chronic inadequacy of N, which is consistent with Van Soest (1994) and NRC (2000; 2001).
Energy and nutrient requirements - The NEm (MJ d-1) is computed as 0.28 × LBW0.75 with adjustment factors for Bos taurus (1.4), Bos indicus (1.2), gender (1 for castrates and females and 1.15 for bulls), and age (e-0.03 × Age). Additional adjustments are made for ME intake for production, grazing, and cold stress. The efficiency of utilization of ME (i.e. conversion to NE) is computed with via energy metabolizability coefficients that vary by physiological stages. The MP requirements for maintenance (g d-1) consist of endogenous urinary protein (EUP = 37 × Log(LBW) 42.2), endogenous fecal protein (EFP = 15.2 × DMI), and dermal protein loss (DPL = 0.11 × LBW0.75). Energy reserves are assumed to vary with body condition score (BCS; scale of 1 to 8 for Dairy) and live weight change (MJ kg-1 weight change = 10.1 + 2.47 × BCS), which is used with an efficiency of 80% for maintenance and 84% for lactation. Requirements for growth are based on a size scaling approach, which uses a standard reference weight (SRW). This SRW is defined as the weight at which skeletal development is complete and the empty body contains 25% fat, which corresponds to a condition score of 3 on a 0 to 5 scale (Beef). Adjustments are made for rate of gain or loss of body weight. Requirement for lactation is based on milk composition and for pregnancy is based on days pregnant.
Agricultural and Food Research Council (AFRC)
Equations and coefficients used to develop the AFRC (1993) system were based on Agricultural Research Council (ARC, 1980) and subsequent technical reviews on energy (AFRC, 1990), protein (AFRC, 1992), mineral (AFRC, 1991), and voluntary intake (AFRC, 1991).
Feed biological values - The proportion of ME in the GE (qm, feed metabolizability) or the ME concentration in the dry matter (M/D) is computed from GE that is assumed to contain 18.8 MJ kg-1 DM (4.49 Mcal kg-1 DM). The feed qm is used in linear equations to compute efficiency coefficients for the physiological functions of maintenance, lactation, growth, conceptus, and energy reserves. The ME value is adjusted for level of intake (L). The MCP synthesized is computed as g MJ-1 of fermentable ME (FME), which is defined in Equation (5).

where FME is fermentable metabolizable energy, Mcal (or MJ) kg-1 DM, ME is metabolizable energy, Mcal (or MJ) kg-1 of DM, MEFat is ME from fat, and MEFermentation is ME from fermentation acids.
The MCP value is assumed to contain 75% amino acids, which have an intestinal digestibility of 85%, giving a 63.75% MP value to MCP, which is computed from an equation sensitive to the level of feeding that gives 8.8, 10, 10.9 and 11.5 g of MCP MJ-1 FME (36.8, 41.8, 45.6, and 48.1 g Mcal-1 of FME) for 1x, 2x, 3x and 4x, respectively; as shown in Equation (6).
where L is the level of intake.
The MCP is assumed to be limited by the supply of effective ruminally degraded protein (ERDP), which is the sum of 80% of the quickly and all of the slowly degraded protein (QDP and SDP, respectively). The QDP is defined as the cold water extracted N while the SDP is computed from an equation based on water-soluble N content, potentially degradable N, degradation rate, and rumen outflow rate. The outflow rate of the diet is a function of level of feeding. Recycled N is not included, and is assumed to compensate for losses of degraded protein above the QDP adjustment. The undegraded digestible protein (UDP) is assumed to have an intestinal digestibility of 90% after subtracting the ADIN protein.
Energy and nutrient requirements - The ME system for assessing the energy requirements of ruminants was initially presented by Blaxter (1962). The NEm requirement is based on energy for fasting metabolism and activity allowance as shown in Equation (7) .
where F is fasting metabolism requirement, MJ d-1; C1 is 1.15 for bulls or 1 for other cattle; LBW is live body weight, kg; and A is activity allowance, MJ d-1.
The MP required for maintenance (g d-1) is computed as 2.19 × LBW0.75. Growth requirements for energy are computed from a quadratic equation based on castrates of medium-sized breeds, with correction factors for mature body size and plane of nutrition. Input variables are body weight and weight change (kg d-1), correction factors for growth maturity (early, medium and late) and gender (bulls, castrates and heifers). Requirement for lactation is based on milk composition and for pregnancy is based on days pregnant. Depletion and repletion of energy reserves is computed as 19 MJ kg-1 live weight change, with mobilized energy utilized with an efficiency of 84%. Net energy values are computed from coefficients (k) applied to ME for the relevant metabolic process.
Cornell Net Carbohydrate and Protein System (CNCPS)
The CNCPS is a mechanistic, deterministic, and static mathematical model that was developed from basic principles of rumen function, microbial growth, feed digestion and passage and animal physiology with the objective of being capable of evaluating diet and animal performance in each unique production situation. It was first published in 1992 and 1993 in a series of four papers (Fox et al., 1992; O'Connor et al., 1993; Russell et al., 1992; Sniffen et al., 1992), and has been continually refined and improved over the last 10 years (Ainslie et al., 1993; Fox & Tylutki, 1998; Fox et al., 1995; 1999; 2002; Pitt et al., 1996; Tedeschi, 2001; Tedeschi et al., 2000a; 2000b; 2000c; 2001; 2002a; 2002b; 2002c; 2003; Tylutki et al., 1994). Recently, a paper was published with the objective of providing all of the equations currently in the CNCPS model and a summary of model evaluations and sensitivity analyses that have been conducted for cattle (Fox et al., 2004) and for sheep (Cannas et al., 2004). This model is probably the most widely known for practical applications (McNamara, 2004).
The CNCPS has evolved to contain a biologically based structure and hierarchy for evaluating all classes of cattle and sheep diets with the purpose of adjusting nutrient requirements and feed utilization over wide variations in cattle and sheep, feed, management, and environmental conditions. The approach taken and level of aggregation of variables is based on experiences of the authors in working with farmers and consultants in attempting to apply accumulated knowledge to diagnose nutrition related problems with performance and developing more accurate feeding programs. Separate submodels were developed by primary physiological function categories (feed intake and composition, rumen fermentation, intestinal digestion, metabolism, maintenance, growth, pregnancy, lactation and reserves) so that new information can be incorporated into the submodels affected.
The CNCPS uses information and codes that can be universally obtained, understood, and applied to describe cattle, and can be easily used in program formulas to calculate responses. Although not universally implemented, all of the critical carbohydrate and protein fractions can be routinely determined by feed testing laboratories. The user must have some nutritional knowledge to use it because of the risks associated with not knowing how to choose inputs. However, with experience it can be used to evaluate the interactions of animal type and production level, environment, feed composition, and management factors. Changes in the ration needed to meet animal and rumen fermentation requirements under widely varying conditions can also be identified.
Feed biological values - The absorbed energy and amino acids available to meet requirements depend on accurate determination of dry matter intake (DMI), ingredient content of carbohydrate (CHO) and protein fractions, microbial growth on the fiber CHO (FC) and nonfiber CHO (NFC) consumed, and the unique rates of digestion and passage of the individual feed CHO and protein fractions that are being fed. The CNCPS has two levels of solution to accommodate the needs of different types of users: (1) Level 1 is intended for conditions where feeds cannot be characterized well or the user is not knowledgeable enough to use the CNCPS rumen model with confidence and (2) Level 2 is intended for users who have adequate information on feed composition and DMI and an understanding of how to use the level 2 rumen model. Both levels use NRC (1996; 2000) equations to predict DE, ME, NEm and NEg while NEl is computed using equations from NRC (1971; 2001). Level 1 computes TDN and MP values with empirical equations based on those developed by Weiss et al. (1992), Weiss (1993; 1999) and NRC (2001).
Once the TDN is computed at a maintenance level of intake, it is adjusted for other levels of intake (Tedeschi, 2001, Ch. 2). The MP from microbial protein, which is assumed to be 64% true protein, is calculated as 13% of TDN, the same equation as is used in level 1 of the beef NRC (2000). The TDN discounted for level of DMI is used by NRC (2001) and CNCPS level 1, whereas NRC (2000) level 1 uses undiscounted TDN. Undegraded protein from feed is calculated from CP intake and undegraded CP (%RUP) and has an intestinal digestibility of 80%. In level 2 of the CNCPS, ruminally available TDN and MP are derived mechanistically from digestion (Kd) and passage (Kp) rates (Russell et al., 1992; Sniffen et al., 1992). The amount of ruminally degraded and escaped CHO and protein are computed using Equations (8) and (9), respectively.
where RD is amount degraded in the rumen, kg; RE is the amount escaped from the rumen, kg; I is intake, kg; kd is degradation rate, % h-1; and kp is passage rate, % h-1.
Feed not digested in the rumen passes undegraded to the intestines where it may or may not undergo further digestion. Each feed component (NDF, CP, soluble CP, NDFIP and ADIP, lignin, fat, ash; Fox et al., 2004; Tedeschi et al., 2002b) is assigned its own kd, which can be modified to accommodate variations in feed processing. The kp values depend on factors such as DMI, particle size, lignification and the ratio of forage to concentrate. Sugars usually have a high kd (> 60%) and are almost completely digested in the rumen, but many carbohydrates and proteins (e.g. B fraction components) have a low kd and are not completely digested by ruminal microorganisms. This system of calculating ruminal disappearance assumes that: (1) kd rate is a simple first order rate, (2) each feed component operates as a single pool, (3) ruminal microorganisms are always in excess, (4) there is no lag-time before the initiation of fermentation, and (5) kp depends only on intake and physically effective NDF. While one might argue that these assumptions are not always valid, this simplification has been a great advantage in describing feeds and evaluating the model.
Rumen microorganisms can be categorized according to the types of carbohydrate they ferment. In the CNCPS, they are categorized into those that ferment fiber and nonfiber carbohydrates. Generally, FC microorganisms ferment cellulose and hemicellulose and grow more slowly, and utilize ammonia as their primary N source for microbial protein synthesis. On the other hand, NFC microorganisms ferment starch, pectin and sugars, grow more rapidly and can utilize ammonia and amino acids as nitrogen sources. The FC and NFC microorganisms have different maintenance requirements (0.05 and 0.15 g of carbohydrate per g of microorganism per hour, respectively). In recent years, it has become apparent that most bacteria have another avenue for non-growth energy dissipation that is distinctly different from maintenance energy, and this dissipation has been called "energy spilling" (Russell & Wallace, 1997).
The impact of maintenance on yield is most apparent when energy is limiting, but bacteria are more apt to spill energy when it is in excess. The energy status of bacteria can be envisioned as a balance of anabolic and catabolic rates, and most bacteria grow twice as fast if they are supplied with preformed amino acids. The CNCPS does not have an energy spilling function per se, but it has a peptide stimulation algorithm that increases yield by as much as 18% if peptides and amino acids are available (Russell & Sniffen, 1984). Thus, the degradable protein requirement is for supporting optimal utilization of NFC and FC to meet respective microbial growth requirements. The rate of microbial growth of each category is directly proportional to the rate of carbohydrate digestion, so long as a suitable N (and branched-chain amino acids) source is available (Tedeschi et al., 2000a; 2000b). The extent of digestion in the rumen depends on digestion rates of FC and NFC feed fractions and how rapidly the feed passes out of the rumen. The extent of digestion thus depends on factors such as level of intake, particle size, rate of hydration, lignification, and characteristics of each carbohydrate and protein fraction.
One of the critical factors affecting microbial growth is ruminal pH. The CNCPS describes physical characteristics of feeds as related to their effectiveness in stimulating chewing, rumination and increased rumen motility based on their total cell wall content and particle size within classes of feeds known as physically effective NDF (peNDF) based on Mertens (1997). Factors other than particle size that influence the peNDF value are degree of lignification of the NDF, degree of hydration, and bulk density. Beauchemin (1991) published an excellent review of the factors influencing buffer production and ruminal pH in cattle. The relationship between CNCPS peNDF values, rumen pH and FC digestion has been documented (Pitt et al., 1996). Total microbial yield and FC growth rate rapidly declines below a pH of 6.2, which relates to a diet peNDF content of 20%. The CNCPS reduces microbial yield by 2.5% units for each % drop in diet peNDF below 20%. Thus, the diet peNDF must be accurately predicted in order to microbial amino acid production and cell wall digestion.
The small intestine is assumed to lack the enzymes to digest cellulose and hemicellulose, but the colon has fibrolytic bacteria. To account for hindgut fiber digestion, intestinal digestion of CHO B2 is assigned a digestibility of 20%, based on Sniffen et al. (1992). Intestinal CHO B1 digestibility depends on type of grain, degree and type of processing, and level of intake above maintenance (Knowlton et al., 1998; Sniffen et al., 1992). Guidelines for intestinal digestion of the CHO B1 for growing beef steers and lactating dairy cows consuming feed at two to three times maintenance level of intake are: whole corn, 30 to 50%; cracked corn, 50 to 70%; dry rolled corn, 70 to 80%; corn meal, 80 to 90%; whole high moisture corn, 80 to 90%; high moisture ground corn, 85 to 95%; steam flaked corn, 92 to 97%; dry rolled sorghum, 60 to 70%; dry ground sorghum, 70 to 80%; and steam flaked Sorghum, 90 to 95%. Guidelines for intestinal digestion of the CHO B1 fraction for high producing dairy cows (above 45 kg milk) are: whole corn, 30 to 40%; cracked corn, 40 to 60%; corn meal, 70 to 90%; and rolled high moisture corn, 75 to 85% (Knowlton et al., 1998). It is also recommend the use of 90% for intestinal digestion of the CHO B1 fraction in processed small grains (i.e. wheat, barley and oats). Protein B1, B2 and B3 are assumed to have an intestinal digestibility of 100, 100, and 80%, respectively.
The equations used to compute NE derived from feeds are empirical, but the validations indicate they have represented the complexity of energy and protein metabolism reasonably well in predicting animal responses in combination with the rumen model described above. Apparent TDN is the sum of total tract digestible nutrients. The DE values for each feed are based on the assumption that 1 kg of TDN is equal to 4.409 Mcal of DE. Because Kp increases as the intake increases, apparent TDN is adjusted for level of intake. The CNCPS uses the NRC (1971; 2000) equations to predict ME and NE. Variations in ME are in part due to variations in ruminal methane production. The NEl values are based on the respiration chamber data of Moe (1981). Evaluation of the predicted NEm and NEg values for growing cattle demonstrated little bias across a wide range of diet ME (NRC, 2000).
First limiting in the CNCPS is accurate determination of DMI. It is extremely important to have actual DMI values to input into the CNCPS; the predicted DMI is only used as a benchmark for diagnostic purposes or for use where accurate DMI is not available. The interactions of DMI, digestion and passage have several implications: (1) the growth rate of each microbial pool that digests respective available carbohydrate fractions, and absorbable microbial amino acids produced, will depend on the special characteristics and intake of the feeds being fed, which in turn determines the demand for the nitrogen source required by each pool, (2) the percentage of cell wall that escapes digestion will change, depending on digestion and passage rates, and (3) the site of digestion and, depending on the whole tract passage rate, the extent of digestion alter.
The CNCPS has several outputs that can be used to assess whether protein or energy is the first limiting nutrient for milk production or growth. Two of the N outputs (rumen N balance and peptide balance) show the N status of the ruminal bacteria, but the peptide balance is not a requirement per se. The peptide balance is the amount of peptides needed to maximize protein production from NFC bacteria. A negative peptide balance indicates that the yield of microbial protein from NFC bacteria could be increased by adding ruminally degraded true protein to the diet. If the total flow of microbial protein or escape protein exceeds the protein needs of the animal, production will not increase. The remaining two N outputs (MP balance and AA allowable milk or gain) reflect the needs and supply of protein and essential amino acids to the animal. Scrutiny of all four N balances is essential in diet evaluation.
Energy and nutrient requirements - Energy available for productive functions depends on the proportion of energy consumed that must be used for meeting maintenance (NEm) requirements, and therefore it is considered first in evaluating a diet and animal performance. Maintenance requirements in the CNCPS are determined by accounting for breed, physiological state, activity, urea excretion, heat or cold stress and environmental acclimatization effects (Fox et al., 1992; Fox & Tylutki, 1998). Additionally, in growing cattle the NEm of each breed is adjusted using a 1 to 9 BCS. Because previous plane of nutrition can affect organ size, NEm is decreased or increased 5% for each BCS below or above 5 (1 to 9 scale), respectively in growing cattle. In a recent evaluation of three comparative slaughter experiments with Nellore cattle fed high forage diets, Tedeschi et al. (2002c) reported the NEm of bulls and steers were similar, about 77.2 kcal kg-0.75 EBW. As in the AFRC, the NEm requirement is adjusted for activity and energy needed to maintain a normal body temperature for all classes of cattle. The current effective temperature index (CETI) uses current temperature and relative humidity to adjust predicted intake for temperature effects. At temperatures below 20oC and relative humidity above 50%, the CETI is reduced. Conversely, at temperatures above 20oC, the CETI is increased. Effects on NEm and intake are small within the range of CETI of 16 to 25 °C (Fox & Tylutki, 1998), but performance declines if the monthly CETI is greater than 25oC (Fox & Tylutki, 1998).
Growth requirements are based on empty body tissue composition of the gain expected, based on expected mature size for breeding herd replacements or expected weight at a particular final composition, considering body size, effect of dietary ingredients, and anabolic implants (Fox et al., 1992; 1999; Guiroy et al., 2002; Tedeschi et al., 2002c; Tylutki et al., 1994) as adapted by the NRC (2000; 2001). Shrunk body weight (SBW) is adjusted to a weight equivalent to that of a standard reference animal at the same stage of growth. In beef or dairy cows, mature weight is defined as the weight at which additional added body mass does not contain additional net protein gain, a condition assumed to occur by 4 years of age and at a BCS of 5 on a 1 to 9 scale for beef cows or at BCS 3 on a 1 to 5 scale for dairy cows. For growing cattle to be harvested for beef, mature weight is the expected weight at the target body composition. Thus, for beef and dairy herd replacement heifers, SRW is always 478 kg, but the SRW of growing and finishing steers, heifers, or bulls is 400, 435, 462, or 478 kg when the harvest target is 22, 25, 27, or 28% body fat. The net energy for gain (NEg) is based on empirical relationships described by the NRC (2000). Recent research indicates that the growth rate for dairy herd replacement heifers affects first lactation milk production (Fox et al., 1999; NRC, 2000; 2001; Van Amburgh et al., 1998). The amino acid requirements for maintenance depend on the prediction of sloughed protein and net tissue turnover losses, as predicted from metabolic fecal nitrogen, urinary nitrogen loss, and scurf protein.
The pregnancy requirements and weight gain from growth of the gravid uterus based on expected calf birth weight and day of gestation (Bell et al., 1995; NRC, 2000; 2001). Energy and protein required for lactation are calculated from actual milk production and components. Crude milk protein is adjusted to true milk protein (crude protein % × 0.93) to compute requirements. Metabolizable energy required for lactation is computed from milk energy with an efficiency of 64.4% (Moe, 1981). Metabolizable protein requirements are computed from milk yield and milk protein content and MP is converted to milk protein with an efficiency of 65% (NRC, 1985). Since actual milk production of beef cows usually is not measured, their lactation requirements are estimated from age of cow, time of lactation peak, expected peak milk yield based on breed and calf weaning weights, day of lactation, duration of lactation, milk fat content, milk solids not fat, and protein as described by NRC (2000).
Body reserves are used to meet requirements when nutrient intake is inadequate. The reserves model uses BCS rather than BW to compute energy reserves because most beef and dairy producers monitor BCS to manage energy reserves. Further, since there are significant exchanges in body water and fat throughout lactation (Andrew et al., 1994), body weight does not adequately account for changes in energy balance. After reaching maturity, body weight changes reflect use or deposition of energy reserves (Fox et al., 1999; NRC, 2000; 2001). Weight gain and loss after maturity has nearly the same composition as weight gain during growth (Fox et al., 1999; NRC, 2000; Otto et al., 1991). The CNCPS uses the reserves model developed for the NRC (2000) and adapted for dairy cattle (NRC, 2001) as described by Fox et al. (1999). The cycle of reserve depletion and replenishment during lactation and the dry period is reflected by predicted condition score change. Modifications and evaluations for dynamic application of the CNCPS model concepts for lactating dual-purpose cows (Reynoso-Campos et al., 2004) and growth (Tedeschi et al., 2004) have been published.
Metabolic and Dynamic Systems
There are several models that employ dynamic modeling at the metabolism level, such as enzyme-substrate relationships, to ultimately predict animal responses and performance to different substrates. Generally, these models have been developed in support of research rather than for application. As research tools, mechanistic, dynamic and deterministic models enable scientists to integrate existing information, identify research needs and evaluate alternative hypotheses. However, their complexity and lack of appropriate information at the farm level limits their usage by consultants and/or producers. Nonetheless, these models aggregate the basic scientific knowledge that is necessary to increase our ability to understand certain biological mechanisms and identify priorities for fundamental and applied research. Such models include MOLLY (Baldwin, 1995; Baldwin et al., 1987a; 1987b), Dijkstra et al. (1992), Danfær (1990), Sainz & Wolff (1990a; 1990b), Hanigan et al. (2004).
As an example of the differences in philosophy and approaches between research and application modeling, the models of Baldwin et al. (1987a; 1987b), Dijkstra et al. (1992), and Danfær (1990) are all derived from the analyses of France et al. (1982), and therefore share many common features, including:
Model equations are based on saturation kinetics (i.e. Michaelis-Menten), so that the overall system is more stable than if linear mass-action equations were used,
Inputs are based on detailed chemical and physical properties of the feeds, so that the models require information that often is lacking in field and even in many research situations; models differ as to the level of aggregation of feed components, and
Different microbial pools with specific substrate preferences allow for variable fermentation patterns under different diets, and for interactions among structural and non-structural carbohydrate fermentation.
Since the main objective was to evaluate available data and concepts for adequacy, feed descriptions (input data) are limited to those characteristics that can be measured in the laboratory. For example, detailed chemical and physical properties of the feeds are required inputs, but not digestion and passage rate constants because these are considered to be animal-dependent. This constraint limits the applicability of the models for practical use, but enables researchers to focus on the identification of research priorities.
Future developments in the modeling field must accompany improved understating of the underlying biology. In fact, modeling and research must go hand in hand. This fact, long understood by physical scientists, is only now being realized by biologists: "... based upon the past, mechanistic models of metabolic processes will continue to evolve as our knowledge of regulatory mechanisms improve and that modeling analyses will continue to be a valuable means of placing advances in our knowledge in context with overall aspects or ruminant digestion and metabolism and productive functions in growing and lactating animals" (Baldwin, 2000).
Comparison of mathematical models
Comparison of mathematical models for adequacy and appropriateness is not an easy task since models require different set of inputs and sometimes a common input has a different connotation among models.
On the requirement computations, Arnold & Bennett (1991a ou 1991b) evaluated the ability of four growth models (Loewer et al., 1983; Notter, 1977; Oltjen et al., 1986; Sanders & Cartwright, 1979) to predict weight gain, body composition, and feed intake. As expected, predicted intake was the most influential measurement upon the relative differences in simulating growth and composition among the models; that's why actual intake is necessary to ascertain good accuracy and evaluation of models. The definition of mature weight was different among models and higher prediction performance was obtained when the mature weight of the simulated animal was relatively adjusted to the specific definition of each model. The authors concluded each model would perform differently upon the same production scenario regardless of the similarity of inputs used. Additionally, models were not able to accurately estimate body com position or intake (Arnold & Bennett, 1991a ou 1991b). The authors concluded that more detailed and complex mechanistic models are needed to account for more of the variation.
Bannink & Visser (1997) reviewed the ability of three mechanistic rumen models (Baldwin et al., 1987b; Danfær, 1990; Dijkstra et al., 1992) to predict the dynamics of ruminal fermentation and microbial growth. The authors found large differences in the microbial functions of substrate fermentation, substrate incorporation, and microbial synthesis among these models. They also differ in extramicrobial ruminal functions, and microbial mechanisms had important consequences for simulated nutrient outputs from the rumen.
Cannas (2000) compared the feeding systems described above (AFRC, CSIRO, INRA, NRC, and CNCPS) in predicting the energy and protein requirements of dairy cows. The requirements for ME for maintenance under thermoneutral conditions were higher in the CSIRO and CNCPS systems than in the INRA and AFRC systems, while NRC had intermediate values. Milk production requirements were similar among all systems. Total energy requirements differed by about 8% between the highest (CSIRO) and the lowest (AFRC) estimate. The energy requirements of cold stressed cows were similar in the CNCPS and CSIRO systems, the only two that accounted for these environmental variables. The MP requirements for maintenance were much higher in the NRC and CNCPS systems than in the CSIRO, INRA and AFRC systems. The MP requirements for milk production were slightly higher in the INRA and CNCPS systems than in the others. The ranking of total MP requirements differed by about 25% between the highest (CNCPS) and lowest (AFRC) estimates. The energy and protein requirements for pregnancy were very different among systems, both in the approach used and in the predicted requirements. Areas with great differences surfaced in the assessment of requirements for growth of heifers and for body reserves. The approaches used in the partitioning of nutrients between growth and reserves for heifers and the prediction of the energy, fat and protein content of reserves differed between systems.
Fox et al. (2004) summarized the numerous evaluations that have been conducted to determine the accuracy of CNCPS submodels (e.g., growth, body reserves, and rumen). For a model to be useful on-farm, however the combination of model equations must accurately predict animal responses. When the CNCPS reserves model was used to adjust supply of energy to account for changes in BCS, the model accounted for 90% of the variation in the milk production of individual Holstein cows with a mean bias of 1.3%. The model accounted for 89% of the variation in ADG of individual steers with mean bias of 90 g d-1 (7.4% underprediction bias).
Several papers have been published on the application of the CNCPS in warm climates. The CNCPS accounted for 72% of the variation in live weight gain of Nellore bulls and steers with a 2% bias and explained 71% of the variation in milk production of Zebu crossbred cows with a 10% bias (Lanna et al., 1996). The 10% bias for the lactating cows is believed to be due to difficulties in establishing the maintenance requirements of the animals because of the wide variation in their percentage of Holstein and Zebu. Juarez-Lagunes et al. (1999) conducted two experiments using the CNCPS to characterize the carbohydrate and protein fractions and corresponding rates of digestion of 15 tropical pasture grasses and to evaluate their ability to support milk production by dual purpose cows. Lanna et al. (1996) and Juarez-Lagunes et al. (1999) concluded that the CNCPS was more accurate than the empirical, tabular NRC (1984; 1989) systems under tropical conditions when the feeds and cattle types could be characterized adequately to provide accurate inputs into the CNCPS.
Rueda-Maldonato et al. (2003) demonstrated the usefulness of using the CNCPS to predict performance of dual-purpose cows and Nellore steers in identifying the most profitable management system in the Western Amazon region of Brazil. Reynoso-Campos et al. (2004) demonstrated that a dynamic application of the CNCPS can facilitate more accurate monitoring and management of cyclic changes in energy and protein balances over the calving interval of dual-purpose cows, which can help producers to achieve productivity and profitability goals.
The CNCPS has been linked to a crop, soil, and manure nutrient management program (Cornell Cropware; Rasmussen et al., 2002) to evaluate its potential to improve environmental and economic sustainability of a 650 cow commercial dairy (Tylutki et al., 2004). A summary of a five-year study indicated that the precision nutrient management system developed resulted in a 26% increase in animal numbers, a 9% increase in milk/cow, a 45% increase in total milk, a 48% decrease in purchased feed, a 52% decrease in feed cost per kg of milk sold, and 17 and 28% decreases in total manure N and P, respectively. These improvements could be explained by better forage production, quality, and storage (38% increases in proportion of feeds grown on farm) and the ability of CNCPS to use these high forage diets efficiently.
In recent years, mineral requirements have received a great deal of consideration because accurate prediction of mineral requirements may minimize mineral excretion and environmental pollution. Tedeschi (2001, Ch. 1) compared the prediction of mineral requirements of ARC (1980), CSIRO (1990), AFRC (1991), and NRC (2000; 2001) systems with equations developed for typical cattle production in Brazil (Castro et al., 1993; Lana et al., 1992; Pires et al., 1993a; 1993b; Silva Sobrinho et al., 1987). It was concluded the net requirements for growth estimated by Lana et al. (1992) and Pires et al. (1993a) were very close to that recommended by both AFRC (1991) and NRC (2000; 2001) systems for Ca, but only Lana et al. (1992) estimates for P was closely related to AFRC (1991) and NRC (2000; 2001) recommendations. Although the ARC (1980), AFRC (1991), and NRC (2000) had similar net requirements, the absorption coefficients used by NRC (2000) and ARC (1980) are different, which lead to distinctly different dietary estimates. Also, the net requirement for maintenance is similar, but the absorption coefficient differs between NRC (2000), ARC (1980), and AFRC (1991). We conclude the lack of information for endogenous losses and absorption coefficients for major minerals in tropical conditions requires the use of values from experiments conducted in different conditions from those found in the tropics. Inconsistencies in these coefficients also were found between different nutrient requirement systems (AFRC, 1991; ARC, 1980; CSIRO, 1990; Fox et al., 2004; NRC, 2000; 2001).
Studies with pen-fed growing cattle consuming high-forage diets indicated that the NRC (2000) tabular system had an overprediction bias because intake effects were not considered and the carbohydrate and protein fractions were not adequately described (Tedeschi, 2001, Ch. 2). The mean square error were similar in all evaluations (tabular, and levels 1 and 2 of the CNCPS), but the CNCPS level 2 had the highest accuracy (lowest RMSPE) followed by level 1. Although it uses similar carbohydrate and protein fractions as CNCPS level 1, the CNCPS level 2 accounted for more of the variation in animal performance because variables such as digestion rates, effects of level of intake, microbial growth on cell wall and noncell wall carbohydrate fractions, rate of passage, rumen pH, and ruminal nitrogen deficiency, on feed ME and MP values were considered.
More recently, Offner & Sauvant (2004) performed a comparison of three models (Baldwin et al., 1987b; Lescoat & Sauvant, 1995; Russell et al., 1992) on their ability to predict various ruminal parameters and digestive characteristics with observed experimental data covering a wide range of feeding situations. Results underlined the fairly good capacity of the Lescoat & Sauvant (1995) model to predict starch digestion in the rumen and ruminal pH. The duodenal flow of microbial N was best predicted by the CNCPS model (Fox et al., 2004). Unfortunately, the models did not accurately predict fiber digestion in the rumen or volatile fatty acids concentrations. The authors recommended that future improvements in rumen modeling could be considered by pooling the advantages of each model.
Research Priorities
Priorities for research and routine feed analysis procedures that need to be implemented depend on the ratio of cost to benefit and the procedures available to measure sensitive variables. There is little value in developing more complex models for amino acid balancing until the first limiting factors can be accurately predicted. This was demonstrated when measured duodenal flows from 80 diets were not predicted as accurately with the dynamic, low level aggregation rumen model of Baldwin et al. (1987a) as with the CNCPS (Sauvant, 1991). The sensitivity analysis of Fox et al. (2004) indicated that the rumen model can be sensitive to all of the CHO and protein pools under certain conditions.
Similarly, due to the lack of better description of feed samples, laboratorial methods that accurately and precisely predict the nutritive value of feeds used in ruminant diets are needed. Robinson et al. (2004) three key components that determine the energy value of a ruminant feed are fat (high energy density), non-fiber carbohydrates (high digestibility), and digestibility of fibrous carbohydrates. Nonetheless, the prediction of digestibility of the latter one has proven to be troublesome. Robinson et al. (2004) evaluated the accuracy and precision of six unified prediction approaches for ME: two from NRC (2001), two from the University of California at Davis (UCD) and two from ADAS (Stratford, UK). The authors concluded that there are differences among the six predictive approaches in the number of laboratorial assays, and their costs, as well as that the NRC approach (three empirical equations that require categorical description of feeds; therefore, inappropriate for mixed feeds). No procedure was able to consistently discriminate the ME values of individual feeds within feedstuffs determined in vivo among these approaches.
Preliminary sensitivity analysis based on Monte Carlo simulations have indicated that the current fractionation scheme of protein does not increase the variability in the RUP or MCP measurements, but has an impact on which inputs become more critical (Cristina Lanzas, personal communication). The following concerns have been raised regarding the current feed protein fractionation structure in the CNCPS.
1. The assigned digestion rates for protein B fractions are based on the number of pools and rates identified by curve-peeling technique of data based on protein in vitro degradation when incubated with protease from Streptomyces griseus. The low rates for the B3 protein fraction (0.1 to 1.5 % h-1) are not supported by recent research data (Coblentz et al., 1999). If the B3 diges tion rate was assigned wrongly to the B3 pool as the result of this approach, then one should be concerned about the assigned B2 rates;
2. The NDF and ADF systems (Van Soest et al., 1991) were developed to measure available cell wall and may not be appropriate for fractionating protein especially for protein concentrates, which have a large protein B2 Mathematical models in ruminant nutrition pool, which is estimated by difference; thus it contains the accumulated analytical error. The protein B3 rate is based on the assumption that NDIN minus ADIN represents N bound to the fiber that is potentially di- gestible. This implies that it may be released from the fiber matrix at a degradation rate similar to the avail able NDF. Nonetheless, the amount of protein associ ated with the cell wall is relatively small (2% of the N) and remains fairly constant (Butler & Bailey, 1973), but the laboratory measurement of NDIN is 3 to 5 times larger and more variable;
3. The ADIN measure may not represent a totally unavail able pool. Lucas' tests (regression of digestible pro tein on protein content) have shown that for some feeds, ADIN does not behave as a completely indigest ible entity (slope different than unity). The ADIN and N indigestibility in forages have almost a 1 to 1 rela tionship. Nakamura et al. (1994) found poor relation ships between ADIN and N indigestibility for protein concentrates. The high levels of ADIN from distiller's grains have been associated with heat damage during processing (Van Soest, 1994); however, it may be pos- sible that prolamin proteins (such as zein) may be re- covered in the ADIN fraction; and
4. The lack of a reliable and feasible laboratory assay to estimate NPN in the soluble protein may affect the cal culation of MCP. It is known that the protein A frac tion is rapidly converted into ammonia and that pep tides from this protein fraction do not contribute to theruminal peptides pool, which is derived from the degraded protein. We have shown via simulation mod eling that a failure in accounting for these solubilized peptides is one of the major factors that contributes to the under prediction of MP allowable milk (low MCP prediction) indiets based on high quality alfalfa silage, which affects NFC microbial protein production (Aquino et al., 2003).
The ability to describe metabolic transactions, and their resultant affects on nutrient requirements, is critical to raise food-producing animals in efficient ways around the world. Complex models, ever grounded in validated research data, will continue to be enhanced. The only way to eventually define the true complexity of the organisms that we are dealing with is to have an ordered model approach which, in a planned iterative fashion, asks complex questions and increases our knowledge with the clear answers we receive (McNamara, 2004).
There are several limitations in modeling the dynamics of metabolism as discussed by McNamara (2004). The main one is the lack of detailed and accurate data. Similarly, the rapid dynamic changes in metabolic flux during lactation, especially in late pregnancy and early lactation pose another major limitation. It is likely that these limitations arise from the experimental focus and design. Another major restriction is the complexity of the system itself: "this might seem an incredibly obvious statement, but I think that proper experiments are often not done because too many scientists simply either do not appreciate the true complexity of the system, or they do but are unwilling or unable to actually study it" (McNamara, 2004).
The development and deployment of sustainable agriculture concepts require an insightful knowledge of the dynamics of agricultural systems at both the farm and regional levels. At the farm level, management decisions affect soil fertility, food production, animal care, and ultimately income whereas at the region level, the interactions between agro-ecological and socio-economic aspects are important in the sustainability of the environment where the farm resides through nutrient flows, water supply, productivity, and longevity of the operation (Bontkes & Van Keulen, 2003).
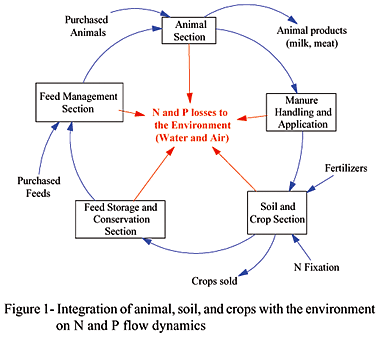
The efficient use of nutrients in agriculture to improve profitability while protecting water and air quality relies on our ability to understand and manage the complex interactions and impacts of decisions made in developing animal-soil-crop-environmental system (ASCES) on farms. Concerns about N and P concentrations underscore the necessity of simulating nutrient flows and their environmental impacts (Berntsen et al., 2003). Nonetheless, few simulation models (Kebreab et al., 2004; Thornley & Verberne, 1989) have been developed that are able to adequately explain the pattern of observed behavior of the integrated ASCES (such as DSSAT1 1 http://www.icasa.net; , SWAT2 2 http://www.brc.tamus.edu/swat; , CENTURY3 3 http://www.nrel.colostate.edu/projects/century ). A principal limitation of these models is they focus only on a specific subsystem (crop, water, and soil, respectively) and their lack of feedback relationships, that is, the manner in which the integrated system developed affects future outcomes.
Therefore, the development of a model to predict nutrient flows and fate on livestock farms, using systems dynamics modeling is necessary to understand the impact of the intrinsic nonlinear behavior of different subsystems on environment pollution as depicted in Figure 1.
This type of model can be used to predict how alternative farm-level nutrient management strategies will influence N and P utilization and losses as well as farm financial performance over time. The great concern in NH3 air emission is mainly caused by the uncertainty in the NH3 emission fractions from animal manure and the major concern in N2O emission is due to the uncertainty in the fractions relating total nitrification and denitrification to NO2 emissions (de Vries et al., 2003; Kroeze et al., 2003). Therefore, a dynamic model that simulates the flow and behavior of N compounds can assist in detecting the effects, extent, and prevention of N pollution into the environment.
FINAL REMARKS
Mathematical models integrate our scientific knowledge of feeds and feeding, intake, and digestion and passage rates upon feed energy values, escape of dietary protein, and microbial growth efficiency to estimate energy and nutrient supply and requirements and feed utilization in each unique farm production scenario. Therefore, they have an important role in assisting the improvement of feeding systems. These models can be used to further improve cattle and sheep production systems by accounting for more of the variation in predicting requirements and supply of nutrients while minimizing the environmental impacts through reduced nutrient excretion in an economically feasible fashion.
For the coming decades, producing meat and milk from cattle will become more efficient in the use of nutrients by using mathematical models to accurately predict requirements and feed utilization in each unique production setting. These mathematical models must allow inputs from each situation to be adjusted in a logical way until the cattle and feeds are accurately described. Then, when predicted and observed performance match, improved feeding programs can be developed for that unique situation where nutritional safety (excess supply) factors and nutrient excretion are minimized. The challenge will be to develop systems that are aggregated at a level that can reflect our understanding of the underlying biology; yet, be usable on farm considering information available, ability to monitor and quantify key input variables and animal responses, and knowledge and time available of the consultant using the models.
The CNCPS is a mechanistic, deterministic, and static mathematical model that was developed (and continues to be improved) from basic biological principles to assist producers, consultants, and researchers in evaluating diets and animal performance. Models such as the CNCPS enable nutritionists to identify sources of variation and can be used to formulate more economical and environmentally friendly rations. By more accurately formulating diets in each unique production situation, the need for expensive, and often environmentally detrimental, nutritional safety factors can be minimized
Animal models are used for a variety of purposes, including the simple description of observations, prediction of responses to management, and explanation of biological mechanisms. Depending upon the objectives, a number of different approaches may be used, including classical algebraic equations, predictive empirical relationships, and dynamic, mechanistic models. The latter offer the best opportunity to make full use of the growing body of knowledge regarding animal biology. Continuing development of these types of models and computer technology and software for their implementation holds great promise for improvements in the effectiveness with which fundamental knowledge of animal function can be applied to improve animal agriculture and reduce its impact on the environment.
REFERENCES
AFRC. Nutritive requirements of ruminant animals: energy (Report 5). Nutrition Abstracts and Reviews. Series B, v.60, p.729-804, 1990.
AFRC. A reappraisal of the calcium and phosphorus requirements of sheep and cattle (Report 6). Nutrition Abstracts and Reviews, v.61, p.573-612, 1991.
AFRC. Voluntary intake of cattle (Report 8). Nutrition Abstracts and Reviews, v.61, p.816-823, 1991.
AFRC. Nutritive requirements of ruminant animals: protein (Report 9). Nutrition Abstracts and Reviews, v.62, p.787-835, 1992.
AFRC. Energy and protein requirements of ruminants. Wallingford: CAB International, 1993. 159p.
AINSLIE, S.J.; FOX, D.G.; PERRY, T.C.; KETCHEN, D.J.; BARRY, M.C. Predicting amino acid adequacy of diets fed to Holstein steers. Journal of Animal Science, v.71, p.1312-1319, 1993.
ANDREW, S.M.; WALDO, D.R.; ERDMAN, R.A. Direct analysis of body composition of dairy cows at three physiological stages. Journal of Dairy Science, v.77, p.3022-3033, 1994.
AQUINO, D.L.; TEDESCHI, L.O.; LANZAS, C.; LEE, S.S.; RUSSELL, J.B. Evaluation of CNCPS predictions of milk production of dairy cows fed alfalfa silage. In: CORNELL NUTRITION CONFERENCE FOR FEED MANUFACTURERS, Syracuse, 2003. Proceedings. Syracuse, NY: New York State College of Agriculture & Life Sciences, Cornell University, 2003. p.137-150.
ARC. The nutrient requirements of ruminant livestock. London: The Gresham Press, 1980. 351p.
ARNOLD, R.N.; BENNETT, G.L. Evaluation of four simulation models of cattle growth and body composition: Part I - Comparison and characterization of the models. Agricultural Systems, v.35, p.401-432, 1991a.
ARNOLD, R.N.; BENNETT, G.L. Evaluation of four simulation models of cattle growth and body composition: Part II - Simulation and comparison with experimental growth data. Agricultural Systems, v.36, p.17-41, 1991b.
BALDWIN, R.L. Modeling ruminant digestion and metabolism. New York: Chapman & Hall, 1995. 578p.
BALDWIN, R.L. Introduction: History and Future of Modelling Nutrient Utilization in Farm Animals. In: MCNAMARA, J.P.; FRANCE, J.; BEEVER, D.E. (Ed.) Modelling nutrient utilization in farm animals. Wallingford: CABI Publishing, 2000. p.1-9.
BALDWIN, R.L.; FRANCE, J.; GILL, M. Metabolism of the lactating cow. I. Animal elements of a mechanistic model. Journal of Dairy Research, v.54, p.77-105, 1987a.
BALDWIN, R.L.; THORNLEY, J.H.M.; BEEVER, D.E. Metabolism of the lactating cow. II. Digestive elements of a mechanistic model. Journal of Dairy Research, v.54, p.107-131, 1987b.
BANNINK, A.; VISSER, H.D. Comparison of mechanistic rumen models on mathematical formulation of extramicrobial and microbial processes. Journal of Dairy Science, v.80, p.1296-1314, 1997.
BEAUCHEMIN, K.A. Ingestion and mastication of feed by dairy cattle. Veterinary Clinics of North America: Food Animal Practice, v.7, p.439-463, 1991.
BELL, A.W.; SLEPETIS, R.; ENRHARDT, R.A. Growth and accretion of energy and protein in the gravid uterus during late pregnancy in Holstein cows. Journal of Dairy Science, v.78, p.1954-1961, 1995.
BERNTSEN, J.; PETERSEN, B.M.; JACOBSEN, B.H.; OLESEN, J.E.; HUTCHINGS, N.J. Evaluating nitrogen taxation scenarios using the dynamic whole farm simulation model FASSET. Agricultural Systems, v.76, p.817-839, 2003.
BLAXTER, K.L. The utilization of the energy of food by ruminants. In: ENERGY METABOLISM OF FARM ANIMALS, 2., Wageningen, 1962. Proceedings. Wageningen: Pudoc, 1962. p.211.
BONTKES, T.S.; VAN KEULEN, H. Modelling the dynamics of agricultural development at farm and regional level. Agricultural Systems, v.76, p.379-396, 2003.
BURROUGHS, W.; TRENKLE, A.; VETTER, R.L. A system of protein evaluation for cattle and sheep involving metabolizable protein (amino acids) and urea fermentation potential of feedstuffs. Veterinary Medicine/Small Animal Clinician, v.69, p.713-722, 1974.
BUTLER, G.W.; BAILEY, R.W. Chemistry and biochemistry of herbage. London: Academic Press, 1973.
CANNAS, A. Sheep and cattle nutrient requirement systems, ruminal turnover, and adaptation of the Cornell Net Carbohydrate and Protein System to sheep. Ithaca: Cornell University, 2000. 350p. (Thesis - PhD).
CANNAS, A.; TEDESCHI, L.O.; FOX, D.G.; PELL, A.N.; VAN SOEST, P.J. A mechanistic model for predicting the nutrient requirements and feed biological values for sheep. Journal of Animal Science, v.82, p.149-169, 2004.
CASTRO, A.C.G.; COELHO DA SILVA, J.F.; VALADARES FILHO, S.C. Body content and nutritional requirements for macroelements for cattle. Revista da Sociedade Brasileira de Zootecnia, v.22, p.360-371, 1993.
COBLENTZ, W.K.; FRITZ, J.O.; FICK, W.H.; COCHRAN, R.C.; SHIRLEY, J.E.; TURNER, J.E. In situ disappearance of neutral detergent insoluble nitrogen from alfalfa and eastern gamagrass at three maturities. Journal of Animal Science, v.77, p.2803-2809, 1999.
CSIRO. Feeding standards for Australian livestock. Ruminants. Melbourne: 1990. 266p.
DANFÆR, A. A dynamic model of nutrient digestion and metabolism in lactating dairy cows. Foulum, Denmark: National Institute of Animal Science, 1990. (Thesis - PhD).
DE VRIES, W.; KROS, J.; OENEMA, O.; DE KLEIN, J. Uncertainties in the fate of nitrogen II: A quantitative assessment of the uncertainties in major nitrogen fluxes in the Netherlands. Nutrient Cycling in Agroecosystems, v.66, p.71-102, 2003.
DIJKSTRA, J.; NEAL, H.S.S.C.; BEEVER, D.E.; FRANCE, J. Simulation of nutrient digestion, absorption and outflow in the rumen: model description. Journal of Nutrition, v.122, p.2239-2256, 1992.
FOX, D.G.; TYLUTKI, T.P. Accounting for the effects of environment on the nutrient requirements of dairy cattle. Journal of Dairy Science, v.81, p.3085-3095, 1998.
FOX, D.G.; VAN AMBURGH, M.E.; TYLUTKI, T.P. Predicting requirements for growth, maturity, and body reserves in dairy cattle. Journal of Dairy Science, v.82, p.1968-1977, 1999.
FOX, D.G.; BARRY, M.C.; PITT, R.E.; ROSELER, D.K.; STONE, W.C. Application of the Cornell net carbohydrate and protein model for cattle consuming forage. Journal of Animal Science, v.73, p.267-277, 1995.
FOX, D.G.; SNIFFEN, C.J.; O'CONNOR, J.D.; RUSSELL, J.B.; VAN SOEST, P.J. A net carbohydrate and protein system for evaluating cattle diets: III. Cattle requirements and diet adequacy. Journal of Animal Science, v.70, p.3578-3596, 1992.
FOX, D.G.; TYLUTKI, T.P.; ALBRECHT, G.L.; CEROSALETTI, P.E.; TEDESCHI, L.O. Environmental protection and the Cornell University nutrient management planning system: Future perspectives. In: CORNELL NUTRITION CONFERENCE FOR FEED MANUFACTURERS, Syracuse, 2002. Proceedings. Syracuse, NY: New York State College of Agriculture & Life Sciences, Cornell University, 2002. p.79-98.
FOX, D.G.; TEDESCHI, L.O.; TYLUTKI, T.P.; RUSSELL, J.B.; VAN AMBURGH, M.E.; CHASE, L.E.; PELL, A.N.; OVERTON, T.R. The Cornell Net Carbohydrate and Protein System model for evaluating herd nutrition and nutrient excretion. Animal Feed Science and Technology, v.112, p.29-78, 2004.
FRANCE, J.; THORNLEY, J.H.M. Mathematical models in agriculture: A quantitative approach to problems in agriculture and related sciences. London: Butterworths, 1984. 335p.
FRANCE, J.; THORNLEY, J.H.M.; BEEVER, D.E. A mathematical model of the rumen. Journal of Agricultural Science, v.99, p.343-353, 1982.
GILL, M.; BEEVER, D.E.; FRANCE, J. Biochemical bases needed for the mathematical representation of whole animal metabolism. Nutrition Abstract Review, v.2, p.181-200, 1989.
GUIROY, P.J.; TEDESCHI, L.O.; FOX, D.G.; HUTCHESON, J.P. The effects of implant strategy on finished body weight of beef cattle. Journal of Animal Science, v.80, p.1791-1800, 2002.
HAEFNER, J.W. Modeling biological systems: Principles and applications. 1.ed. New York: Chapman & Hall, 1996. 473p.
HANIGAN, M.D.; CROMPTON, L.A.; REYNOLDS, C.K.; WRAY-CAHEN, D. An integrative model of amino acid metabolism in the liver of the lactating dairy cow. Journal of Theoretical Biology, v.228, p.271-289, 2004.
INRA. Ruminant nutrition. Recommended allowances and feed tables. Montrouge, France: Institut National de la Recherche Agronomique, John Libbey Eurotext, 1989. 389p.
JUAREZ LAGUNES, F.I.; FOX, D.G.; BLAKE, R.W.; PELL, A.N. Evaluation of tropical grasses for milk production by dual-purpose cows in tropical Mexico. Journal of Dairy Science, v.82, p.2136-2145, 1999.
KEBREAB, E.; MILLS, J.A.N.; CROMPTON, L.A.; BANNINK, A.; DIJKSTRA, J.; GERRITS, W.J.J.; FRANCE, J. An integrated mathematical model to evaluate nutrient partition in dairy cattle between the animal and its environment. Animal Feed Science and Technology, v.112, p.131-154, 2004.
KNOWLTON, K.F.; GLENN, B.P.; ERDMAN, R.A. Performance, ruminal fermentation, and site of starch digestion in early lactation cows fed corn grain harvested and processed differently. Journal of Dairy Science, v.81, p.1972-1984, 1998.
KROEZE, C.; AERTS, R.; VAN BREEMEN, N.; VAN DAM, D.; VAN DER HOEK, K.; HOFSCHREUDER, P.; HOOSBEEK, M.; DE KLEIN, J.; KROS, H.; VAN OENE, H.; OENEMA, O.; TIETEMA, A.; VAN DER VEEREN, R.; DE VRIES, W. Uncertainties in the fate of nitrogen I: An overview of sources of uncertainty illustrated with a Dutch case study. Nutrient Cycling in Agroecosystems, v.66, p.43-69, 2003.
LANA, R.P.; FONTES, C.A.A.; PERON, A.J.; QUEIRÓZ, A.C.; PAULINO, M.F.; SILVA, D.J. Body composition, growth and requirements of energy, protein and macrominerals (calcium, phosphorus, magnesium, sodium and potassium) in steers of five breed types. 3. Body content, weight gain and macromineral requirements. Revista da Sociedade Brasileira de Zootecnia, v.21, p.538-544, 1992.
LANNA, D.P.D.; FOX, D.G.; BOIN, C.; TRAXLER, M.J.; BARRY, M.C. Validation of the CNCPS estimates of nutrient requirements of growing and lactating Zebu germplasm in tropical conditions. In: ANNUAL MEETING OF THE AMERICAN SOCIETY OF ANIMAL SCIENCE, Rapid City, 1996. Proceedings. Rapid City: ASAS, 1996. v.74, Suppl. 1 p.287.
LESCOAT, P.; SAUVANT, D. Development of a mechanistic model for rumen digestion validated using the duodenal flux of amino acids. Reproduction, Nutrition, Development, v.35, p.45-70, 1995.
LOEWER, O.J.; SMITH, E.M.; TAUL, K.L.; TURNER, L.W.; GAY, N. A body composition model for predicting beef animal growth. Agricultural Systems, v.10, p.245-256, 1983. LOFGREEN, G.P.; GARRETT, W.N. A system for expressing net energy requirements and feed values for growing and finishing beef cattle. Journal of Animal Science, v.27, p.793-806, 1968.
MCNAMARA, J.P. Research, improvement and application of mechanistic, biochemical, dynamic models of metabolism in lactating dairy cattle. Animal Feed Science and Technology, v.112, p.155-176, 2004.
MERTENS, D.R. Creating a system for meeting the fiber requirements of dairy cows. Journal of Dairy Science, v.80, p.1463-1481, 1997.
MOE, P.W. Energy metabolism of dairy cattle. Journal of Dairy Science, v.64, p.1120-1139, 1981.
MOE, P.W.; FLATT, W.P.; TYRRELL, H.F. Net energy value of feeds for lactation. Journal of Dairy Science, v.55, p.945-958, 1972.
NAKAMURA, T.; KLOPFENSTEIN, T.J.; BRITTON, R.A. Evaluation of acid detergent insoluble nitrogen as an indicator of protein quality in nonforage proteins. Journal of Animal Science, v.72, p.1043-1048, 1994.
NOTTER, D.R. Simulated efficiency of beef production for a cow-calf-feedlot management system. Lincoln: University of Nebraska, 1977. (Thesis - PhD).
NRC. Nutrient requirements of beef cattle. 4.ed. Washington, DC: National Academy Press, 1970. 55p.
NRC. Nutrient requirements of dairy cattle. 4.ed. Washington, DC: National Academy Press, 1971. 54p.
NRC. Nutrient requirements of beef cattle. 6.ed. Washington, DC: National Academy Press, 1984.
NRC. Ruminant nitrogen usage. Washington, DC: National Academy Press, 1985. 138p.
NRC. Nutrient requirements of dairy cattle. 6.ed. Washington, DC: National Academy Press, 1989. 157p.
NRC. Nutrient requirements of beef cattle. 7.ed. Washington, DC: National Academy Press, 1996. 242p.
NRC. Nutrient requirements of beef cattle. updated 7.ed. Washington, DC: National Academy Press, 2000. 242p.
NRC. Nutrient requirements of dairy cattle. 7.ed. Washington, DC: National Academy Press, 2001. 381p.
O'CONNOR, J.D.; SNIFFEN, C.J.; FOX, D.G.; CHALUPA, W. A net carbohydrate and protein system for evaluating cattle diets: IV. Predicting amino acid adequacy. Journal of Animal Science, v.71, p.1298-1311, 1993.
OFFNER, A.; SAUVANT, D. Comparative evaluation of the Molly, CNCPS, and LES rumen models. Animal Feed Science and Technology, v.112, p.107-130, 2004.
OLTJEN, J.W.; BYWATER, A.C.; BALDWIN, R.L.; GARRETT, W.N. Development of a dynamic model of beef cattle growth and composition. Journal of Animal Science, v.62, p.86-97, 1986.
OTTO, K.L.; FERGUSON, J.D.; FOX, D.G.; SNIFFEN, C.J. Relationship between body condition score and composition of ninth to eleventh rib tissue in Holstein dairy cows. Journal of Dairy Science, v.74, p.852-859, 1991.
PIRES, C.C.; FONTES, C.A.A.; GALVÃO, J.G.; QUEIRÓZ, A.C.; COELHO DA SILVA, J.F.; PAULINO, M.F. Nutritional requirements of finishing beef cattle. III - Calcium and phosphorus requirements for weight gain. Revista da Sociedade Brasileira de Zootecnia, v.22, p.133-143, 1993a.
PIRES, C.C.; FONTES, C.A.A.; GALVÃO, J.G.; QUEIRÓZ, A.C.; PEREIRA, J.C.; PAULINO, M.F. Nutritional requirements of finishing beef cattle. IV - Requirements for magnesium, sodium and potassium. Revista da Sociedade Brasileira de Zootecnia, v.22, p.144-154, 1993b.
PITT, R.E.; VAN KESSEL, J.S.; FOX, D.G.; PELL, A.N.; BARRY, M.C.; VAN SOEST, P.J. Prediction of ruminal volatile fatty acids and pH within the net carbohydrate and protein system. Journal of Animal Science, v.74, p.226-244, 1996.
RASMUSSEN, C.N.; KETTERINGS, Q.M.; ALBRECHT, G.L. Cornell Cropware version 1.0, a CuNMPS Software Program. In: DEVELOPING AND APPLYING NEXT GENERATION TOOLS FOR FARM AND WATERSHED NUTRIENT MANAGEMENT TO PROTECT WATER QUALITY, Ithaca, 2002. Proceedings. Ithaca: Cornell Animal Science Department, 2002. p.13-29 (Mimeo 220 and Crop and Soil Science Research Series E-02-1).
REYNOSO-CAMPOS, O.; FOX, D.G.; BLAKE, R.W.; BARRY, M.C.; TEDESCHI, L.O.; NICHOLSON, C.F.; KAISER, H.M.; OLTENACU, P.A. Predicting nutritional requirements and lactation performance of dual-purpose cows using a dynamic model. Agricultural Systems, v.80, p.67-83, 2004.
ROBINSON, P.H.; GIVENS, D.I.; GETACHEW, G. Evaluation of NRC, UC Davis and ADAS approaches to estimate the metabolizable energy values of feeds at maintenance energy intake from equations utilizing chemical assays and in vitro determinations. Animal Feed Science and Technology, v.114, p.75-90, 2004.
RUEDA-MALDONATO, B.L.; BLAKE, R.W.; NICHOLSON, C.F.; FOX, D.G.; TEDESCHI, L.O.; PELL, A.N.; FERNANDES, E.C.M.; VALENTEM, J.C.; CARNEIRO, J.C. Production and economic potentials of cattle in pasture-based systems of the western Amazon region of Brazil. Journal of Animal Science, v.81, p.2923-2937, 2003.
RUSSELL, J.B.; SNIFFEN, C.J. Effect of carbon-4 and carbon-5 volatile fatty acids on growth of mixed rumen bacteria in vitro. Journal of Dairy Science, v.67, p.987-994, 1984.
RUSSELL, J.B.; WALLACE, R.J. Energy yielding and consuming reactions. In: STEWART, P.N.H.A.C.S. (Ed.) The rumen microbial ecosystem. London: Blackie Academic & Professional, 1997. p.246-282.
RUSSELL, J.B.; O'CONNOR, J.D.; FOX, D.G.; VAN SOEST, P.J.; SNIFFEN, C.J. A net carbohydrate and protein system for evaluating cattle diets: I. Ruminal fermentation. Journal of Animal Science, v.70, p.3551-3561, 1992.
SAINZ, R.D.; WOLFF, J.E. Development of a dynamic, mechanistic model of lamb metabolism and growth. Animal Production, v.51, p.535-549, 1990a.
SAINZ, R.D.; WOLFF, J.E. Evaluation of hypotheses regarding mechanisms of action of growth promotants and repartitioning agents using a simulation model of lamb metabolism and growth. Animal Production, v.51, p.551-558, 1990b.
SANDERS, J.O.; CARTWRIGHT, T.C. A general cattle production systems model. I: Structure of the model. Agricultural Systems, v.3, p.217-227, 1979.
SAUVANT, D. The use of modelling to predict animal responses to diet. In: RALSTON PURINA INTERNATIONAL SCIENTIFIC ADVISORY BOARD, Paris, 1991. Proceedings. Paris, 1991. p.34.
SILVA SOBRINHO, A.G.; GARCIA, J.A.; COELHO DA SILVA, J.F.; SILVA, D.J. Requerimentos de macrominerais (Ca, P, Mg, Na e K) para seis grupos genéticos de bovídeos. Revista da Sociedade Brasileira de Zootecnia, v.16, p.40-51, 1987.
SNIFFEN, C.J.; O'CONNOR, J.D.; VAN SOEST, P.J.; FOX, D.G.; RUSSELL, J.B. A net carbohydrate and protein system for evaluating cattle diets: II. Carbohydrate and protein availability. Journal of Animal Science, v.70, p.3562-3577, 1992.
TAYLOR, C.S. Time taken to mature in relation to mature weight for sexes, strains and species of domesticated mammals and birds. Animal Production, v.10, p.157-169, 1968.
TEDESCHI, L.O. Development and Evaluation of Models for the Cornell Net Carbohydrate and Protein System: 1. Feed Libraries, 2. Ruminal Nitrogen and Branched-Chain Volatile Fatty Acid Deficiencies, 3. Diet Optimization, 4. Energy Requirement for Maintenance and Growth. Ithaca, NY: Cornell University, 2001. 414p. Thesis (Ph.D. Dissertation).
TEDESCHI, L.O.; FOX, D.G.; RUSSELL, J.B. Accounting for ruminal deficiencies of nitrogen and branched-chain amino acids in the structure of the Cornell net carbohydrate and protein system. In: CORNELL NUTRITION CONFERENCE FOR FEED MANUFACTURERS, Rochester, 2000. Proceedings . Rochester: New York State College of Agriculture & Life Sciences, Cornell University, 2000a. p.224-238.
TEDESCHI, L.O.; FOX, D.G.; RUSSELL, J.B. Accounting for the effects of a ruminal nitrogen deficiency within the structure of the Cornell net carbohydrate and protein system. Journal of Animal Science, v.78, p.1648-1658, 2000b.
TEDESCHI, L.O.; FOX, D.G.; TYLUTKI, T.P. Potential environmental benefits of ionophores in ruminant diets. Journal of Environmental Quality, v.32, p.1591-1602, 2003.
TEDESCHI, L.O.; FOX, D.G.; GUIROY, P.J. A decision support system to improve individual cattle management. 1. A mechanistic, dynamic model for animal growth. Agricultural Systems, v.79, p.171-204, 2004.
TEDESCHI, L.O.; FOX, D.G.; CHASE, L.E.; WANG, S.J. Whole-herd optimization with the Cornell net carbohydrate and protein system. I. Predicting feed biological values for diet optimization with linear programming. Journal of Dairy Science, v.83, p.2139-2148, 2000c.
TEDESCHI, L.O.; PELL, A.N.; FOX, D.G.; LLAMES, C.R. The amino acid profiles of the whole plant and of four residues from temperate and tropical forages. Journal of Animal Science, v.79, p.525-532, 2001.
TEDESCHI, L.O.; BAKER, M.J.; KETCHEN, D.J.; FOX, D.G. Performance of growing and finishing cattle supplemented with a slow-release urea product and urea. Canadian Journal of Animal Science, v.82, p.567-573, 2002a.
TEDESCHI, L.O.; FOX, D.G.; PELL, A.N.; LANNA, D.P.D.; BOIN, C. Development and evaluation of a tropical feed library for the Cornell Net Carbohydrate and Protein System model. Scientia Agricola, v.59, p.1-18, 2002b.
TEDESCHI, L.O.; BOIN, C.; FOX, D.G.; LEME, P.R.; ALLEONI, G.F.; LANNA, D.P.D. Energy requirement for maintenance and growth of Nellore bulls and steers fed high-forage diets. Journal of Animal Science, v.80, p.1671-1682, 2002c.
THORNLEY, J.H.M.; VERBERNE, E.L.J. A model of nitrogen flows in grassland. Plant, Cell and Environment, v.12, p.863-886, 1989.
TYLUTKI, T.P.; FOX, D.G.; ANRIQUE, R.G. Predicting net energy and protein requirements for growth of implanted and nonimplanted heifers and steers and nonimplanted bulls varying in body size. Journal of Animal Science, v.72, p.1806-1813, 1994.
TYLUTKI, T.P.; FOX, D.G.; MCMAHON, M. Implementation of nutrient management planning on a dairy farm. The Professional Animal Scientist, v.20, p.58-65, 2004.
VAN AMBURGH, M.E.; GALTON, D.M.; BAUMAN, D.E.; EVERETT, R.W.; FOX, D.G.; CHASE, L.E.; ERB, H.N. Effects of three prepubertal body growth rates on performance of Holstein heifers during first lactation. Journal of Dairy Science, v.81, p.527-538, 1998.
VAN SOEST, P.J. Nutritional ecology of the ruminant. 2.ed. Ithaca: Comstock Publishing Associates, 1994. 476p.
VAN SOEST, P.J.; FOX, D.G. Discounts for net energy and protein. In: CORNELL NUTRITION CONFERENCE FOR FEED MANUFACTURES, Rochester, 1992. Proceedings. Rochester: New York State College of Agriculture & Life Sciences, Cornell University, 1992. p.40-68.
VAN SOEST, P.J.; FADEL, J.; SNIFFEN, C.J. Discount factors for energy and protein in ruminant feeds. In: CORNELL NUTRITION CONFERENCE FOR FEED MANUFACTURERS, Syracuse, 1979. Proceedings. Syracuse: New York State College of Agriculture & Life Sciences, Cornell University, 1979. p.63-75.
VAN SOEST, P.J.; ROBERTSON, J.B.; LEWIS, B.A. Methods for dietary fiber, neutral detergent fiber, and nonstarch polysaccharides in relation to animal nutrition. Journal of Dairy Science, v.74, p.3583-3597, 1991.
VAN SOEST, P.J.; FOX, D.G.; MERTENS, D.R.; SNIFFEN, C.J. Discount factors for energy and protein - fourth revision. In: CORNELL NUTRITION CONFERENCE FOR FEED MANUFACTURERS, Syracuse, 1984. Proceedings. Syracuse: New York State College of Agriculture & Life Sciences, Cornell University, 1984. p.121-136.
WEISS, W.P. Predicting energy values of feeds. Journal of Dairy Science, v.76, p.1802-1811, 1993.
WEISS, W.P. Energy prediction equations for ruminant feeds. In: CORNELL NUTRITION CONFERENCE FOR FEED MANUFACTURERS, Rochester, 1999. Proceedings. Rochester: New York State College of Agriculture & Life Sciences, Cornell University, 1999. p.176-185
WEISS, W.P.; CONRAD, H.R.; ST. PIERRE, N.R. A theoretically-based model for predicting total digestible nutrient values of forages and concentrates. Animal Feed Science and Technology, v.39, p.95-110, 1992.
Received May 06, 2004
Accepted December 01, 2004
- AFRC. Nutritive requirements of ruminant animals: energy (Report 5). Nutrition Abstracts and Reviews. Series B, v.60, p.729-804, 1990.
- AFRC. A reappraisal of the calcium and phosphorus requirements of sheep and cattle (Report 6). Nutrition Abstracts and Reviews, v.61, p.573-612, 1991.
- AFRC. Voluntary intake of cattle (Report 8). Nutrition Abstracts and Reviews, v.61, p.816-823, 1991.
- AFRC. Nutritive requirements of ruminant animals: protein (Report 9). Nutrition Abstracts and Reviews, v.62, p.787-835, 1992.
- AFRC. Energy and protein requirements of ruminants Wallingford: CAB International, 1993. 159p.
- AINSLIE, S.J.; FOX, D.G.; PERRY, T.C.; KETCHEN, D.J.; BARRY, M.C. Predicting amino acid adequacy of diets fed to Holstein steers. Journal of Animal Science, v.71, p.1312-1319, 1993.
- ANDREW, S.M.; WALDO, D.R.; ERDMAN, R.A. Direct analysis of body composition of dairy cows at three physiological stages. Journal of Dairy Science, v.77, p.3022-3033, 1994.
- AQUINO, D.L.; TEDESCHI, L.O.; LANZAS, C.; LEE, S.S.; RUSSELL, J.B. Evaluation of CNCPS predictions of milk production of dairy cows fed alfalfa silage. In: CORNELL NUTRITION CONFERENCE FOR FEED MANUFACTURERS, Syracuse, 2003. Proceedings Syracuse, NY: New York State College of Agriculture & Life Sciences, Cornell University, 2003. p.137-150.
- ARC. The nutrient requirements of ruminant livestock London: The Gresham Press, 1980. 351p.
- ARNOLD, R.N.; BENNETT, G.L. Evaluation of four simulation models of cattle growth and body composition: Part I - Comparison and characterization of the models. Agricultural Systems, v.35, p.401-432, 1991a.
- ARNOLD, R.N.; BENNETT, G.L. Evaluation of four simulation models of cattle growth and body composition: Part II - Simulation and comparison with experimental growth data. Agricultural Systems, v.36, p.17-41, 1991b.
- BALDWIN, R.L. Modeling ruminant digestion and metabolism New York: Chapman & Hall, 1995. 578p.
- BALDWIN, R.L. Introduction: History and Future of Modelling Nutrient Utilization in Farm Animals. In: MCNAMARA, J.P.; FRANCE, J.; BEEVER, D.E. (Ed.) Modelling nutrient utilization in farm animals Wallingford: CABI Publishing, 2000. p.1-9.
- BALDWIN, R.L.; FRANCE, J.; GILL, M. Metabolism of the lactating cow. I. Animal elements of a mechanistic model. Journal of Dairy Research, v.54, p.77-105, 1987a.
- BALDWIN, R.L.; THORNLEY, J.H.M.; BEEVER, D.E. Metabolism of the lactating cow. II. Digestive elements of a mechanistic model. Journal of Dairy Research, v.54, p.107-131, 1987b.
- BANNINK, A.; VISSER, H.D. Comparison of mechanistic rumen models on mathematical formulation of extramicrobial and microbial processes. Journal of Dairy Science, v.80, p.1296-1314, 1997.
- BEAUCHEMIN, K.A. Ingestion and mastication of feed by dairy cattle. Veterinary Clinics of North America: Food Animal Practice, v.7, p.439-463, 1991.
- BELL, A.W.; SLEPETIS, R.; ENRHARDT, R.A. Growth and accretion of energy and protein in the gravid uterus during late pregnancy in Holstein cows. Journal of Dairy Science, v.78, p.1954-1961, 1995.
- BERNTSEN, J.; PETERSEN, B.M.; JACOBSEN, B.H.; OLESEN, J.E.; HUTCHINGS, N.J. Evaluating nitrogen taxation scenarios using the dynamic whole farm simulation model FASSET. Agricultural Systems, v.76, p.817-839, 2003.
- BLAXTER, K.L. The utilization of the energy of food by ruminants. In: ENERGY METABOLISM OF FARM ANIMALS, 2., Wageningen, 1962. Proceedings Wageningen: Pudoc, 1962. p.211.
- BONTKES, T.S.; VAN KEULEN, H. Modelling the dynamics of agricultural development at farm and regional level. Agricultural Systems, v.76, p.379-396, 2003.
- BURROUGHS, W.; TRENKLE, A.; VETTER, R.L. A system of protein evaluation for cattle and sheep involving metabolizable protein (amino acids) and urea fermentation potential of feedstuffs. Veterinary Medicine/Small Animal Clinician, v.69, p.713-722, 1974.
- BUTLER, G.W.; BAILEY, R.W. Chemistry and biochemistry of herbage London: Academic Press, 1973.
- CANNAS, A. Sheep and cattle nutrient requirement systems, ruminal turnover, and adaptation of the Cornell Net Carbohydrate and Protein System to sheep. Ithaca: Cornell University, 2000. 350p. (Thesis - PhD).
- CANNAS, A.; TEDESCHI, L.O.; FOX, D.G.; PELL, A.N.; VAN SOEST, P.J. A mechanistic model for predicting the nutrient requirements and feed biological values for sheep. Journal of Animal Science, v.82, p.149-169, 2004.
- CASTRO, A.C.G.; COELHO DA SILVA, J.F.; VALADARES FILHO, S.C. Body content and nutritional requirements for macroelements for cattle. Revista da Sociedade Brasileira de Zootecnia, v.22, p.360-371, 1993.
- COBLENTZ, W.K.; FRITZ, J.O.; FICK, W.H.; COCHRAN, R.C.; SHIRLEY, J.E.; TURNER, J.E. In situ disappearance of neutral detergent insoluble nitrogen from alfalfa and eastern gamagrass at three maturities. Journal of Animal Science, v.77, p.2803-2809, 1999.
- CSIRO. Feeding standards for Australian livestock. Ruminants. Melbourne: 1990. 266p.
- DANFÆR, A. A dynamic model of nutrient digestion and metabolism in lactating dairy cows. Foulum, Denmark: National Institute of Animal Science, 1990. (Thesis - PhD).
- DE VRIES, W.; KROS, J.; OENEMA, O.; DE KLEIN, J. Uncertainties in the fate of nitrogen II: A quantitative assessment of the uncertainties in major nitrogen fluxes in the Netherlands. Nutrient Cycling in Agroecosystems, v.66, p.71-102, 2003.
- DIJKSTRA, J.; NEAL, H.S.S.C.; BEEVER, D.E.; FRANCE, J. Simulation of nutrient digestion, absorption and outflow in the rumen: model description. Journal of Nutrition, v.122, p.2239-2256, 1992.
- FOX, D.G.; TYLUTKI, T.P. Accounting for the effects of environment on the nutrient requirements of dairy cattle. Journal of Dairy Science, v.81, p.3085-3095, 1998.
- FOX, D.G.; VAN AMBURGH, M.E.; TYLUTKI, T.P. Predicting requirements for growth, maturity, and body reserves in dairy cattle. Journal of Dairy Science, v.82, p.1968-1977, 1999.
- FOX, D.G.; BARRY, M.C.; PITT, R.E.; ROSELER, D.K.; STONE, W.C. Application of the Cornell net carbohydrate and protein model for cattle consuming forage. Journal of Animal Science, v.73, p.267-277, 1995.
- FOX, D.G.; SNIFFEN, C.J.; O'CONNOR, J.D.; RUSSELL, J.B.; VAN SOEST, P.J. A net carbohydrate and protein system for evaluating cattle diets: III. Cattle requirements and diet adequacy. Journal of Animal Science, v.70, p.3578-3596, 1992.
- FOX, D.G.; TYLUTKI, T.P.; ALBRECHT, G.L.; CEROSALETTI, P.E.; TEDESCHI, L.O. Environmental protection and the Cornell University nutrient management planning system: Future perspectives. In: CORNELL NUTRITION CONFERENCE FOR FEED MANUFACTURERS, Syracuse, 2002. Proceedings Syracuse, NY: New York State College of Agriculture & Life Sciences, Cornell University, 2002. p.79-98.
- FOX, D.G.; TEDESCHI, L.O.; TYLUTKI, T.P.; RUSSELL, J.B.; VAN AMBURGH, M.E.; CHASE, L.E.; PELL, A.N.; OVERTON, T.R. The Cornell Net Carbohydrate and Protein System model for evaluating herd nutrition and nutrient excretion. Animal Feed Science and Technology, v.112, p.29-78, 2004.
- FRANCE, J.; THORNLEY, J.H.M. Mathematical models in agriculture: A quantitative approach to problems in agriculture and related sciences. London: Butterworths, 1984. 335p.
- FRANCE, J.; THORNLEY, J.H.M.; BEEVER, D.E. A mathematical model of the rumen. Journal of Agricultural Science, v.99, p.343-353, 1982.
- GILL, M.; BEEVER, D.E.; FRANCE, J. Biochemical bases needed for the mathematical representation of whole animal metabolism. Nutrition Abstract Review, v.2, p.181-200, 1989.
- GUIROY, P.J.; TEDESCHI, L.O.; FOX, D.G.; HUTCHESON, J.P. The effects of implant strategy on finished body weight of beef cattle. Journal of Animal Science, v.80, p.1791-1800, 2002.
- HAEFNER, J.W. Modeling biological systems: Principles and applications. 1.ed. New York: Chapman & Hall, 1996. 473p.
- HANIGAN, M.D.; CROMPTON, L.A.; REYNOLDS, C.K.; WRAY-CAHEN, D. An integrative model of amino acid metabolism in the liver of the lactating dairy cow. Journal of Theoretical Biology, v.228, p.271-289, 2004.
- INRA. Ruminant nutrition. Recommended allowances and feed tables. Montrouge, France: Institut National de la Recherche Agronomique, John Libbey Eurotext, 1989. 389p.
- JUAREZ LAGUNES, F.I.; FOX, D.G.; BLAKE, R.W.; PELL, A.N. Evaluation of tropical grasses for milk production by dual-purpose cows in tropical Mexico. Journal of Dairy Science, v.82, p.2136-2145, 1999.
- KEBREAB, E.; MILLS, J.A.N.; CROMPTON, L.A.; BANNINK, A.; DIJKSTRA, J.; GERRITS, W.J.J.; FRANCE, J. An integrated mathematical model to evaluate nutrient partition in dairy cattle between the animal and its environment. Animal Feed Science and Technology, v.112, p.131-154, 2004.
- KNOWLTON, K.F.; GLENN, B.P.; ERDMAN, R.A. Performance, ruminal fermentation, and site of starch digestion in early lactation cows fed corn grain harvested and processed differently. Journal of Dairy Science, v.81, p.1972-1984, 1998.
- KROEZE, C.; AERTS, R.; VAN BREEMEN, N.; VAN DAM, D.; VAN DER HOEK, K.; HOFSCHREUDER, P.; HOOSBEEK, M.; DE KLEIN, J.; KROS, H.; VAN OENE, H.; OENEMA, O.; TIETEMA, A.; VAN DER VEEREN, R.; DE VRIES, W. Uncertainties in the fate of nitrogen I: An overview of sources of uncertainty illustrated with a Dutch case study. Nutrient Cycling in Agroecosystems, v.66, p.43-69, 2003.
- LANA, R.P.; FONTES, C.A.A.; PERON, A.J.; QUEIRÓZ, A.C.; PAULINO, M.F.; SILVA, D.J. Body composition, growth and requirements of energy, protein and macrominerals (calcium, phosphorus, magnesium, sodium and potassium) in steers of five breed types. 3. Body content, weight gain and macromineral requirements. Revista da Sociedade Brasileira de Zootecnia, v.21, p.538-544, 1992.
- LANNA, D.P.D.; FOX, D.G.; BOIN, C.; TRAXLER, M.J.; BARRY, M.C. Validation of the CNCPS estimates of nutrient requirements of growing and lactating Zebu germplasm in tropical conditions. In: ANNUAL MEETING OF THE AMERICAN SOCIETY OF ANIMAL SCIENCE, Rapid City, 1996. Proceedings Rapid City: ASAS, 1996. v.74, Suppl. 1 p.287.
- LESCOAT, P.; SAUVANT, D. Development of a mechanistic model for rumen digestion validated using the duodenal flux of amino acids. Reproduction, Nutrition, Development, v.35, p.45-70, 1995.
- LOEWER, O.J.; SMITH, E.M.; TAUL, K.L.; TURNER, L.W.; GAY, N. A body composition model for predicting beef animal growth. Agricultural Systems, v.10, p.245-256, 1983.
- LOFGREEN, G.P.; GARRETT, W.N. A system for expressing net energy requirements and feed values for growing and finishing beef cattle. Journal of Animal Science, v.27, p.793-806, 1968.
- MCNAMARA, J.P. Research, improvement and application of mechanistic, biochemical, dynamic models of metabolism in lactating dairy cattle. Animal Feed Science and Technology, v.112, p.155-176, 2004.
- MERTENS, D.R. Creating a system for meeting the fiber requirements of dairy cows. Journal of Dairy Science, v.80, p.1463-1481, 1997.
- MOE, P.W. Energy metabolism of dairy cattle. Journal of Dairy Science, v.64, p.1120-1139, 1981.
- MOE, P.W.; FLATT, W.P.; TYRRELL, H.F. Net energy value of feeds for lactation. Journal of Dairy Science, v.55, p.945-958, 1972.
- NAKAMURA, T.; KLOPFENSTEIN, T.J.; BRITTON, R.A. Evaluation of acid detergent insoluble nitrogen as an indicator of protein quality in nonforage proteins. Journal of Animal Science, v.72, p.1043-1048, 1994.
- NOTTER, D.R. Simulated efficiency of beef production for a cow-calf-feedlot management system. Lincoln: University of Nebraska, 1977. (Thesis - PhD).
- NRC. Nutrient requirements of beef cattle 4.ed. Washington, DC: National Academy Press, 1970. 55p.
- NRC. Nutrient requirements of dairy cattle 4.ed. Washington, DC: National Academy Press, 1971. 54p.
- NRC. Nutrient requirements of beef cattle 6.ed. Washington, DC: National Academy Press, 1984.
- NRC. Ruminant nitrogen usage Washington, DC: National Academy Press, 1985. 138p.
- NRC. Nutrient requirements of dairy cattle 6.ed. Washington, DC: National Academy Press, 1989. 157p.
- NRC. Nutrient requirements of beef cattle 7.ed. Washington, DC: National Academy Press, 1996. 242p.
- NRC. Nutrient requirements of beef cattle updated 7.ed. Washington, DC: National Academy Press, 2000. 242p.
- NRC. Nutrient requirements of dairy cattle 7.ed. Washington, DC: National Academy Press, 2001. 381p.
- O'CONNOR, J.D.; SNIFFEN, C.J.; FOX, D.G.; CHALUPA, W. A net carbohydrate and protein system for evaluating cattle diets: IV. Predicting amino acid adequacy. Journal of Animal Science, v.71, p.1298-1311, 1993.
- OFFNER, A.; SAUVANT, D. Comparative evaluation of the Molly, CNCPS, and LES rumen models. Animal Feed Science and Technology, v.112, p.107-130, 2004.
- OLTJEN, J.W.; BYWATER, A.C.; BALDWIN, R.L.; GARRETT, W.N. Development of a dynamic model of beef cattle growth and composition. Journal of Animal Science, v.62, p.86-97, 1986.
- OTTO, K.L.; FERGUSON, J.D.; FOX, D.G.; SNIFFEN, C.J. Relationship between body condition score and composition of ninth to eleventh rib tissue in Holstein dairy cows. Journal of Dairy Science, v.74, p.852-859, 1991.
- PIRES, C.C.; FONTES, C.A.A.; GALVÃO, J.G.; QUEIRÓZ, A.C.; COELHO DA SILVA, J.F.; PAULINO, M.F. Nutritional requirements of finishing beef cattle. III - Calcium and phosphorus requirements for weight gain. Revista da Sociedade Brasileira de Zootecnia, v.22, p.133-143, 1993a.
- PIRES, C.C.; FONTES, C.A.A.; GALVÃO, J.G.; QUEIRÓZ, A.C.; PEREIRA, J.C.; PAULINO, M.F. Nutritional requirements of finishing beef cattle. IV - Requirements for magnesium, sodium and potassium. Revista da Sociedade Brasileira de Zootecnia, v.22, p.144-154, 1993b.
- PITT, R.E.; VAN KESSEL, J.S.; FOX, D.G.; PELL, A.N.; BARRY, M.C.; VAN SOEST, P.J. Prediction of ruminal volatile fatty acids and pH within the net carbohydrate and protein system. Journal of Animal Science, v.74, p.226-244, 1996.
- RASMUSSEN, C.N.; KETTERINGS, Q.M.; ALBRECHT, G.L. Cornell Cropware version 1.0, a CuNMPS Software Program. In: DEVELOPING AND APPLYING NEXT GENERATION TOOLS FOR FARM AND WATERSHED NUTRIENT MANAGEMENT TO PROTECT WATER QUALITY, Ithaca, 2002. Proceedings Ithaca: Cornell Animal Science Department, 2002. p.13-29 (Mimeo 220 and Crop and Soil Science Research Series E-02-1).
- REYNOSO-CAMPOS, O.; FOX, D.G.; BLAKE, R.W.; BARRY, M.C.; TEDESCHI, L.O.; NICHOLSON, C.F.; KAISER, H.M.; OLTENACU, P.A. Predicting nutritional requirements and lactation performance of dual-purpose cows using a dynamic model. Agricultural Systems, v.80, p.67-83, 2004.
- ROBINSON, P.H.; GIVENS, D.I.; GETACHEW, G. Evaluation of NRC, UC Davis and ADAS approaches to estimate the metabolizable energy values of feeds at maintenance energy intake from equations utilizing chemical assays and in vitro determinations. Animal Feed Science and Technology, v.114, p.75-90, 2004.
- RUEDA-MALDONATO, B.L.; BLAKE, R.W.; NICHOLSON, C.F.; FOX, D.G.; TEDESCHI, L.O.; PELL, A.N.; FERNANDES, E.C.M.; VALENTEM, J.C.; CARNEIRO, J.C. Production and economic potentials of cattle in pasture-based systems of the western Amazon region of Brazil. Journal of Animal Science, v.81, p.2923-2937, 2003.
- RUSSELL, J.B.; SNIFFEN, C.J. Effect of carbon-4 and carbon-5 volatile fatty acids on growth of mixed rumen bacteria in vitro Journal of Dairy Science, v.67, p.987-994, 1984.
- RUSSELL, J.B.; WALLACE, R.J. Energy yielding and consuming reactions. In: STEWART, P.N.H.A.C.S. (Ed.) The rumen microbial ecosystem London: Blackie Academic & Professional, 1997. p.246-282.
- RUSSELL, J.B.; O'CONNOR, J.D.; FOX, D.G.; VAN SOEST, P.J.; SNIFFEN, C.J. A net carbohydrate and protein system for evaluating cattle diets: I. Ruminal fermentation. Journal of Animal Science, v.70, p.3551-3561, 1992.
- SAINZ, R.D.; WOLFF, J.E. Development of a dynamic, mechanistic model of lamb metabolism and growth. Animal Production, v.51, p.535-549, 1990a.
- SAINZ, R.D.; WOLFF, J.E. Evaluation of hypotheses regarding mechanisms of action of growth promotants and repartitioning agents using a simulation model of lamb metabolism and growth. Animal Production, v.51, p.551-558, 1990b.
- SANDERS, J.O.; CARTWRIGHT, T.C. A general cattle production systems model. I: Structure of the model. Agricultural Systems, v.3, p.217-227, 1979.
- SAUVANT, D. The use of modelling to predict animal responses to diet. In: RALSTON PURINA INTERNATIONAL SCIENTIFIC ADVISORY BOARD, Paris, 1991. Proceedings Paris, 1991. p.34.
- SILVA SOBRINHO, A.G.; GARCIA, J.A.; COELHO DA SILVA, J.F.; SILVA, D.J. Requerimentos de macrominerais (Ca, P, Mg, Na e K) para seis grupos genéticos de bovídeos. Revista da Sociedade Brasileira de Zootecnia, v.16, p.40-51, 1987.
- SNIFFEN, C.J.; O'CONNOR, J.D.; VAN SOEST, P.J.; FOX, D.G.; RUSSELL, J.B. A net carbohydrate and protein system for evaluating cattle diets: II. Carbohydrate and protein availability. Journal of Animal Science, v.70, p.3562-3577, 1992.
- TAYLOR, C.S. Time taken to mature in relation to mature weight for sexes, strains and species of domesticated mammals and birds. Animal Production, v.10, p.157-169, 1968.
- TEDESCHI, L.O. Development and Evaluation of Models for the Cornell Net Carbohydrate and Protein System: 1. Feed Libraries, 2. Ruminal Nitrogen and Branched-Chain Volatile Fatty Acid Deficiencies, 3. Diet Optimization, 4. Energy Requirement for Maintenance and Growth. Ithaca, NY: Cornell University, 2001. 414p. Thesis (Ph.D. Dissertation).
- TEDESCHI, L.O.; FOX, D.G.; RUSSELL, J.B. Accounting for ruminal deficiencies of nitrogen and branched-chain amino acids in the structure of the Cornell net carbohydrate and protein system. In: CORNELL NUTRITION CONFERENCE FOR FEED MANUFACTURERS, Rochester, 2000. Proceedings . Rochester: New York State College of Agriculture & Life Sciences, Cornell University, 2000a. p.224-238.
- TEDESCHI, L.O.; FOX, D.G.; RUSSELL, J.B. Accounting for the effects of a ruminal nitrogen deficiency within the structure of the Cornell net carbohydrate and protein system. Journal of Animal Science, v.78, p.1648-1658, 2000b.
- TEDESCHI, L.O.; FOX, D.G.; TYLUTKI, T.P. Potential environmental benefits of ionophores in ruminant diets. Journal of Environmental Quality, v.32, p.1591-1602, 2003.
- TEDESCHI, L.O.; FOX, D.G.; GUIROY, P.J. A decision support system to improve individual cattle management. 1. A mechanistic, dynamic model for animal growth. Agricultural Systems, v.79, p.171-204, 2004.
- TEDESCHI, L.O.; FOX, D.G.; CHASE, L.E.; WANG, S.J. Whole-herd optimization with the Cornell net carbohydrate and protein system. I. Predicting feed biological values for diet optimization with linear programming. Journal of Dairy Science, v.83, p.2139-2148, 2000c.
- TEDESCHI, L.O.; PELL, A.N.; FOX, D.G.; LLAMES, C.R. The amino acid profiles of the whole plant and of four residues from temperate and tropical forages. Journal of Animal Science, v.79, p.525-532, 2001.
- TEDESCHI, L.O.; BAKER, M.J.; KETCHEN, D.J.; FOX, D.G. Performance of growing and finishing cattle supplemented with a slow-release urea product and urea. Canadian Journal of Animal Science, v.82, p.567-573, 2002a.
- TEDESCHI, L.O.; FOX, D.G.; PELL, A.N.; LANNA, D.P.D.; BOIN, C. Development and evaluation of a tropical feed library for the Cornell Net Carbohydrate and Protein System model. Scientia Agricola, v.59, p.1-18, 2002b.
- TEDESCHI, L.O.; BOIN, C.; FOX, D.G.; LEME, P.R.; ALLEONI, G.F.; LANNA, D.P.D. Energy requirement for maintenance and growth of Nellore bulls and steers fed high-forage diets. Journal of Animal Science, v.80, p.1671-1682, 2002c.
- THORNLEY, J.H.M.; VERBERNE, E.L.J. A model of nitrogen flows in grassland. Plant, Cell and Environment, v.12, p.863-886, 1989.
- TYLUTKI, T.P.; FOX, D.G.; ANRIQUE, R.G. Predicting net energy and protein requirements for growth of implanted and nonimplanted heifers and steers and nonimplanted bulls varying in body size. Journal of Animal Science, v.72, p.1806-1813, 1994.
- TYLUTKI, T.P.; FOX, D.G.; MCMAHON, M. Implementation of nutrient management planning on a dairy farm. The Professional Animal Scientist, v.20, p.58-65, 2004.
- VAN AMBURGH, M.E.; GALTON, D.M.; BAUMAN, D.E.; EVERETT, R.W.; FOX, D.G.; CHASE, L.E.; ERB, H.N. Effects of three prepubertal body growth rates on performance of Holstein heifers during first lactation. Journal of Dairy Science, v.81, p.527-538, 1998.
- VAN SOEST, P.J. Nutritional ecology of the ruminant 2.ed. Ithaca: Comstock Publishing Associates, 1994. 476p.
- VAN SOEST, P.J.; FOX, D.G. Discounts for net energy and protein. In: CORNELL NUTRITION CONFERENCE FOR FEED MANUFACTURES, Rochester, 1992. Proceedings Rochester: New York State College of Agriculture & Life Sciences, Cornell University, 1992. p.40-68.
- VAN SOEST, P.J.; FADEL, J.; SNIFFEN, C.J. Discount factors for energy and protein in ruminant feeds. In: CORNELL NUTRITION CONFERENCE FOR FEED MANUFACTURERS, Syracuse, 1979. Proceedings Syracuse: New York State College of Agriculture & Life Sciences, Cornell University, 1979. p.63-75.
- VAN SOEST, P.J.; ROBERTSON, J.B.; LEWIS, B.A. Methods for dietary fiber, neutral detergent fiber, and nonstarch polysaccharides in relation to animal nutrition. Journal of Dairy Science, v.74, p.3583-3597, 1991.
- VAN SOEST, P.J.; FOX, D.G.; MERTENS, D.R.; SNIFFEN, C.J. Discount factors for energy and protein - fourth revision. In: CORNELL NUTRITION CONFERENCE FOR FEED MANUFACTURERS, Syracuse, 1984. Proceedings Syracuse: New York State College of Agriculture & Life Sciences, Cornell University, 1984. p.121-136.
- WEISS, W.P. Predicting energy values of feeds. Journal of Dairy Science, v.76, p.1802-1811, 1993.
- WEISS, W.P. Energy prediction equations for ruminant feeds. In: CORNELL NUTRITION CONFERENCE FOR FEED MANUFACTURERS, Rochester, 1999. Proceedings Rochester: New York State College of Agriculture & Life Sciences, Cornell University, 1999. p.176-185
- WEISS, W.P.; CONRAD, H.R.; ST. PIERRE, N.R. A theoretically-based model for predicting total digestible nutrient values of forages and concentrates. Animal Feed Science and Technology, v.39, p.95-110, 1992.
Publication Dates
-
Publication in this collection
22 Feb 2005 -
Date of issue
Jan 2005
History
-
Received
06 May 2004 -
Accepted
01 Dec 2004