Abstracts
The citrus sudden death (CSD) disease affects dramatically citrus trees causing a progressive plant decline and death. The disease has been identified in the late 90's in the main citrus production area of Brazil and since then there are efforts to understand the etiology as well as the mechanisms its spreading. One relevant aspect of such studies is to investigate spatial patterns of the occurrence within a field. Methods for determining whether the spatial pattern is aggregated or not has been frequently used. However it is possible to further explore and describe the data by means of adopting an explicit model to discriminate and quantify effects by attaching parameters to covariates which represent aspects of interest to be investigated. One alternative involves autologistic models, which extend a usual logistic model in order to accommodate spatial effects. In order to implement such model it is necessary to take into account the reuse of data to built spatial covariates, which requires extensions in methodology and algorithms to assess the variance of the estimates. This work presents an application of the autologistic model to data collected at 11 time points from citrus fields affected by CSD. It is shown how the autologistic model is suitable to investigate diseases of this type, as well as a description of the model and the computational aspects necessary for model fitting.
spatial statistics; plant disease; binary response variable; pseudolikelihood; bootstrap
A morte súbita dos citros (MSC) é uma doença com efeitos dramáticos em árvores de citros causando declínio progressivo e morte. Ela foi identificada no final da década de 90 em uma das principais áreas de produção no Brasil e desde então esforços são empregados para entender a sua etiologia e os seus mecanismos de dispersão. Um aspecto relevante para estudos é a investigação do padrão espacial da incidência dentro de um campo. Métodos para determinar se o padrão espacial é agregado ou não têm sido freqüentemente utilizados. Entretanto é possível explorar e descrever os dados adotando um modelo explícito, com o qual é possível discriminar e quantificar os efeitos com parâmetros para covariáveis que representam aspectos de interesse investigados. Uma das alternativas é adoção de modelos autologísticos, que estendem o modelo de regressão logística para acomodar efeitos espaciais. Para implementar esse modelo é necessário que se reutilize os dados para extrair covariáveis espaciais, o que requer extensões na metodologia e algoritmos para avaliar a variância das estimativas. Este trabalho apresenta uma aplicação do modelo autologístico a dados coletados em 11 pontos no tempo em um campo de citros afetado pela MSC. É mostrado como o modelo autologístico é apropriado para investigar doenças desse tipo, bem como é feita uma descrição do modelo e dos aspectos computacionais necessários para a estimação dos parâmetros.
estatística espacial; doença de plantas; variável resposta binária; pseudoverossimilhança; bootstrap
STATISTICS
Autologistic model with an application to the citrus "sudden death" disease
Modelo autologístico com aplicação para a doença "morte súbita" dos citrus
Elias Teixeira KrainskiI; Paulo Justiniano Ribeiro JuniorI, * * Corresponding author < paulojus@ufpr.br> ; Renato Beozzo BassaneziII; Luziane FrancisconI
IUFPR - Lab. de Estatística e Geoinformação, C.P. 19081 - 81531-990 - Curitiba, PR - Brasil
IIFundecitrus - Depto. Científico, C.P. 391 - 14801-970 - Araraquara, SP - Brasil
ABSTRACT
The citrus sudden death (CSD) disease affects dramatically citrus trees causing a progressive plant decline and death. The disease has been identified in the late 90's in the main citrus production area of Brazil and since then there are efforts to understand the etiology as well as the mechanisms its spreading. One relevant aspect of such studies is to investigate spatial patterns of the occurrence within a field. Methods for determining whether the spatial pattern is aggregated or not has been frequently used. However it is possible to further explore and describe the data by means of adopting an explicit model to discriminate and quantify effects by attaching parameters to covariates which represent aspects of interest to be investigated. One alternative involves autologistic models, which extend a usual logistic model in order to accommodate spatial effects. In order to implement such model it is necessary to take into account the reuse of data to built spatial covariates, which requires extensions in methodology and algorithms to assess the variance of the estimates. This work presents an application of the autologistic model to data collected at 11 time points from citrus fields affected by CSD. It is shown how the autologistic model is suitable to investigate diseases of this type, as well as a description of the model and the computational aspects necessary for model fitting.
Key words: spatial statistics, plant disease, binary response variable, pseudolikelihood, bootstrap
RESUMO
A morte súbita dos citros (MSC) é uma doença com efeitos dramáticos em árvores de citros causando declínio progressivo e morte. Ela foi identificada no final da década de 90 em uma das principais áreas de produção no Brasil e desde então esforços são empregados para entender a sua etiologia e os seus mecanismos de dispersão. Um aspecto relevante para estudos é a investigação do padrão espacial da incidência dentro de um campo. Métodos para determinar se o padrão espacial é agregado ou não têm sido freqüentemente utilizados. Entretanto é possível explorar e descrever os dados adotando um modelo explícito, com o qual é possível discriminar e quantificar os efeitos com parâmetros para covariáveis que representam aspectos de interesse investigados. Uma das alternativas é adoção de modelos autologísticos, que estendem o modelo de regressão logística para acomodar efeitos espaciais. Para implementar esse modelo é necessário que se reutilize os dados para extrair covariáveis espaciais, o que requer extensões na metodologia e algoritmos para avaliar a variância das estimativas. Este trabalho apresenta uma aplicação do modelo autologístico a dados coletados em 11 pontos no tempo em um campo de citros afetado pela MSC. É mostrado como o modelo autologístico é apropriado para investigar doenças desse tipo, bem como é feita uma descrição do modelo e dos aspectos computacionais necessários para a estimação dos parâmetros.
Palavras-chave: estatística espacial, doença de plantas, variável resposta binária, pseudoverossimilhança, bootstrap
INTRODUCTION
Brazil is the major citrus region in the world and is responsible for about 28% of the worldwide orange juice production and for 80% of the concentrated juice. Citrus growers, industry and scientists are constantly aiming for higher productivity, control of the production process and capacity. Such targets are threatned by various diseases among which is the citrus sudden death (CSD), a new and destructive disease first observed in the late 90's in southwest Minas Gerais and northern São Paulo States, Brazil (Gimenes-Fernandes & Bassanezi, 2001). This disease causes the decline and death of sweet oranges (Citrus sinensis (L.) Osb.) and some mandarins (C. reticulata Blanco) grafted onto either Rangpur lime (C. limonia Osb.) or Volkamerian lemon (C. volkameriana V. Tem. & Pasq.), the most used rootstocks because under São Paulo conditions citrus grafted on these rootstocks can be grown without irrigation (Gimenes-Fernandes & Bassanezi, 2001; Román et al., 2004).
After the report of CSD, many efforts have been carried out to understand the etiology as well as the mechanisms of the spreading of this disease. Search for infectious agents in CSD-symptomatic trees including fungi, exogenous and endogenous bacteria and phytoplasmas, and viroids produced negative results (Bassanezi et al., 2003; Román et al., 2004). Only two virus, CTV and a new virus Tymoviridae, tentatively called Citrus sudden death associated virus (CSDaV), have been found in CSD-affected trees, and their association with the disease has been studied (Coletta Filho et al., 2005; Maccheroni et al., 2005). However, the extreme variability and complexity of CTV and the very low concentration of CSDaV make the CSD etiology very difficulty to be proven. Before CSD-causal agent identification, studies on spatial patterns of CSD-affected plants could be useful to make inferences about the nature of the causal agent.
Several methods, such as the analysis of ordinary runs (Madden et al., 1982), intraclass correlation (k) (Xu & Ridout, 2000), binomial index of dispersion (D) and binary form of Taylor's power law (Madden & Hughes, 1995) and spatial autocorrelation analysis (Gottwald et al., 1992), have been used to investigate the development of CSD epidemics in space, as well as the resulting spatial patterns (Bassanezi et al., 2003; Bassanezi et al., 2005; Lima et al., 2006). At the individual tree scale, ordinary run analysis of CSD-symptomatic trees indicated clustering of symptomatic trees mainly within rows.
At the middle scale of small groups of trees, the D and k indexes for various quadrat sizes suggested the aggregation of CSD-symptomatic trees for almost all plots within the quadrat sizes tested, and the index of aggregation increased with quadrat size. Estimated parameters of the binary form of Taylor's power law provided an overall measure of aggregation of CSD-symptomatic trees for all quadrat sizes and the intensity of aggregation was also a function of quadrat size and disease incidence.
The largest tested scale was the entire plot level. Spatial autocorrelation analysis of proximity patterns suggested that aggregation often existed among quadrats of various sizes up to three lag distances. These results were interpreted as indicating that the disease is caused by a biotic factor, and that the disease was transmitted within a local area of influence of approximately six trees in all directions, including adjacent trees (Bassanezi et al., 2003; Bassanezi et al., 2005). Based on the similarities of CSD symptoms and its spatial patterns with Citrus tristeza, caused by Citrus tristeza virus and transmitted by aphids, the current hypothesis is that CSD is caused by virus and vectored by flying vectors.
All above described spatial analyses only allow to characterize the pattern as aggregated, regular or random, and are useful in a preliminary step of analysis to accumulate evidences about the spatial pattern diagnostic of incidence. A characteristic aspect of such methods is the fact that the spatial configuration is treated as a lattice. Another possible approach for the analysis of a large number of plants would be to consider the plants with the disease as a point process in space and use the distance between infected trees to infer about the spatial pattern (Spósito et al., 2007) or using percolation methods to infer probabilities given the status of the neighbours (Santos et al., 1998). However, such methods are not designed to quantify the effects of spatial effects represented by covariates since they do not assume an explicit model relating such covariates with the presence of the disease, neither allow for other covariates of potential interest.
One alternative investigated here is the adoption of an autologistic model which relates the probability of a unit to become diseased given the status of neighbouring plants in space and/or time, taken as covariates and therefore having an associated coefficient parameter. The regular arrangement favors for the adoption of autoregressive type of models for the analysis, which allows for the detection of usual covariate effects as well as the assessment of the relevance of the spatial effects. The latter are particularly useful for the description and hypothesis tests on the patterns of the disease, which may suggest propagation mechanisms and control strategies.
For binary data such as presence/absence of the disease, the autologistic model describes the probability of a tree to become infected given the status of the neighbouring trees. The model parameters have a direct interpretation as odds of being infected, incorporating explicitly the dependence structure. In agricultural applications the model has being initially adopted the study the incident of Phytophthora for bell pepper (Gumpertz et al., 1997) with attempts to expand the model to describe spatial temporal patterns of pine beetles (Gumpertz et al., 1999; Zhu et al., 2005). Here we further explore the model considering the particular aspects of citrus groves and CSD. The model reports the analysis of data collected at 11 different time points in a field with presence of CSD.
MATERIAL AND METHODS
The logistic regression model is currently widely used for the analysis of binary outcomes such as presence or absence of a certain attribute of interest. For presence of plant disease it is particularly relevant to consider a possible spatial dependence given it is reasonable to assume that neighbouring trees are more likely to have similar status, which reflects an eventual aggregation in the spatial pattern of the disease. The autologistic model (Besag 1972) extends the usual logistic regression accounting for such spatial structure by modeling the conditional probability of a tree to be infected given the status of the neighbouring trees.
Autologistic model
The autologistic model describes the probability pij of a plant in the ith row and jth column having the disease, given the status of the neighbouring plants depending on the value of a covariate connected to the outcome, through the link function,
with yi-1, j and yi+1, j being the status in the adjacent rows which are combined to produce the row covariate; yi-1, j and yi, j+1 the status of plants in adjacent columns producing the column covariate; λ1 and λ2 are the respective parameters measuring the effect of such spatial covariates. The separation of row and column effects accommodates the fact that the spacing is typically different within and between rows, allowing to study directional effects.
A naïve method to obtain parameter estimates for λ = {λ1,λ2} is based on the maximization of the pseudo-likelihood (Besag 1975)
where f () is the density of the Bernoulli probability distribution. This estimation method provides consistent parameter point estimates, it however underestimates the associated standard errors and therefore inferences on model parameters can be misleading. Intuitively this is caused by the reuse of data, given the fact that an observation is used as a response variable as well as to build the covariates in the model.
One possible solution is to use resampling methods. However within the context of spatial patterns this is not straightforward given the need to preserve the spatial structure. This can be achieved by block resampling (Cressie, 1993) for instance using a Gibbs sampler (Gumpertz et al., 1997). The basic idea is to sample from the distribution of each observation yij conditioning on the current status of the neighbours, with probabilities given by the autologistic model of equation (λ). This is a sequential algorithm that opperates as follows: we start with observed values y(0) from which we obtain parameter estimates λ(0) by maximizing of the pseudo-likelihoodof equation (2). Next we generate B bootstrap samples (y(1),..., y(B)) obtaining estimates ( (1), ...,
(1), ...,  (B)) for each of them. The bootstrap samples are obtained through the following steps: i. starting from an arbitrary location (tree), update its status by sampling from the Bernoulli distribution f (
(B)) for each of them. The bootstrap samples are obtained through the following steps: i. starting from an arbitrary location (tree), update its status by sampling from the Bernoulli distribution f ( (0), y(t)) with the probability given by the fitted model parameters and current status of the plants, in a random sequence until the cycle is completed, i.e. the status of all the trees are updated generating a bootstrap sample with artificial data y(t); ii. when a cycle is completed, obtain parameter estimates by maximizing pseudolikelihood function given by equation (2); iii. repeat steps i and ii until the required number B of bootstrap samples is obtained.
(0), y(t)) with the probability given by the fitted model parameters and current status of the plants, in a random sequence until the cycle is completed, i.e. the status of all the trees are updated generating a bootstrap sample with artificial data y(t); ii. when a cycle is completed, obtain parameter estimates by maximizing pseudolikelihood function given by equation (2); iii. repeat steps i and ii until the required number B of bootstrap samples is obtained.
The simulation algorithm ensures that the chain of the parameter estimates converges to the correct distribution and therefore, the variance of the estimator is then given simply by the variance of the estimates (
(1), ..., (B)) . It is also advisable to disregard a certain number m of initial resamples, the so called burn-in period when the chain may not yet have converged, and also trimming the simulations taking one at each k steps to reduce the number of stored simulations. These procedures were implemented as part of the present work in a freely available and open source add-on package Rcitrus (Krainski & Ribeiro Júnior, 2007) from the R statistical environment for statistical analysis (R Development Core Team, 2007).
(B)) . It is also advisable to disregard a certain number m of initial resamples, the so called burn-in period when the chain may not yet have converged, and also trimming the simulations taking one at each k steps to reduce the number of stored simulations. These procedures were implemented as part of the present work in a freely available and open source add-on package Rcitrus (Krainski & Ribeiro Júnior, 2007) from the R statistical environment for statistical analysis (R Development Core Team, 2007).
Models
The data considered here were collected on a citrus grove with presence of CSD, in the municipality of Comendador Gomes (19º73' S, 49º06' W; altitude 705 m), Minas Gerais State, Brazil. The trees were arranged in 20 rows of 48 plants with spacing of 7.5 m between rows and 4 m within rows. Data were collected at 11 time points between 05/11/2001 and 07/10/2002. The incidence ranged from 14.9% at the first visit to 45.7% on the final date. The response variable used here is the presence/absence of CSD on each tree.
Three candidate models were considered for the analysis, the first (m1) considering as spatial covariates the neighbouring observations within and between rows as the response variable, measured at the same time and defined as follows:
Model m2, considers the same neighbourhood, however with data reflecting the status of the plants at the previous observation time:
Finally, model m3 combines the two previous models considering covariates built with contemporary and previous status of the neighbours:
The significance tests for the regression parameters are based on the usual approximation for generalized linear models assuming that  ~ N(0,1) . For m1, the significance test for the coefficients allows the detection of the relevance of the spatial effect as well as testing for effects of the status of close neighbours given by the within row covariate, and more distant neighbours given by the between rows covariate. Model m2 assess the predictive ability of the model through the lagged information built in the covariate allowing to inspect the conjecture the present status of the trees would allow to predict the probability of trees the become infected at the next observation time. The covariate effects assess patterns of the disease spread. Model m3 combines lagged and contemporary covariates in this order, attempting to check whether the latter further the model fit accounting for infection factors not captured by the lagged covariate.
~ N(0,1) . For m1, the significance test for the coefficients allows the detection of the relevance of the spatial effect as well as testing for effects of the status of close neighbours given by the within row covariate, and more distant neighbours given by the between rows covariate. Model m2 assess the predictive ability of the model through the lagged information built in the covariate allowing to inspect the conjecture the present status of the trees would allow to predict the probability of trees the become infected at the next observation time. The covariate effects assess patterns of the disease spread. Model m3 combines lagged and contemporary covariates in this order, attempting to check whether the latter further the model fit accounting for infection factors not captured by the lagged covariate.
The three models considered here suggest different mechanisms to explain the spread of the disease and therefore the model selection is itself a goal in the study. The Akaike Information Criteria (AIC) provides a measure used to assess and compare model fits and is given by the penalization of the log-likelihood by model complexity and is given by , where p is the number of parameters included in the model. Another measure widely used is the BIC (Bayesian Information Criteria), which increases the penalty function as the sample size increases. In both cases smaller values indicate a better fitted model. These measured values can be used to guide the model selection, however, being a criteria and therefore arbitrarily defined, they should not replace the interpretation and contextual information, specially when the differences between the models are small, specially in the particular case of these spatial models where the likelihood is just an approximation.
RESULTS AND DISCUSSION
Significant effects were found only for the covariate number of neighbours within row for models m1 e m2 and the spatial covariate was not significant for the first and second data collections (Table 1). Overall similar results were found for model m2.
Model m3 includes two spatial covariates: S1 is number of within row neighbours at present time and S2 at previous time. Estimated coefficients and p-values are also shown in Table 1. Some combinations of relevant results are as follows. Both spatial covariates are significant at the 5% significance level for times 3, 5 and 6; for times 2, 4, 7, 8 and 11, only S1 was significant; and only S2 for times 9 e 10. It is important to notice a potential (nearly) collinearity effect since the values of the two covariates can be similar, specially when the incidence is nearly the same between two consecutive observations in time.
Table 2 shows the Akaike Information Criteria (AIC), which is used to assess the fitted models. This criteria shows that model m1 is preferable for most of the observation periods (2,4,5,6,7,8 e 11), that m3 is better supported for time 3 and m2 for times 9 and 10. Similar results were obtained with the BIC criterium.
The major advantage of having an explicit model is the possibility of quantifying the probability of disease in a particular tree given the status of the neighboring plants. In the current study the spatial covariates counts the number of infected neighboring trees and therefore assume values 0, 1 or 2. The coefficient associated with the spatial covariate allows computing the increment in the odds of a plant having the disease as the number of infected neighbours increases. The three models considered the status within and between rows, however in an overall way, fitted models here indicate that only the knowledge of the status of the within rows neighbours is relevant. This shows evidence that the spatial pattern is present and that conditioning only on close neighbours is sufficient for the description.
The estimated coefficients for model m2 are -1.773 and 0.366. The value e0.366 is the increment in the odds of having the disease of a plant with k infected neighbours compared with another one with k-1 infected neighbours or, in other words, the increment of one infected neighbour increases the probability of the disease by a factor of 1.442. Consider now under this model we aim to compute the probability of a tree to become diseased at a particular time, given the data was collected at the previous time. For the third evaluation, the probability of a tree to become infected is 0.145, 0.197 and 0.261 for zero, one or two infected neighbours, respectively. For the subsequent times the coefficients are -1.557 and 0.482 and these probabilities are now 0.174, 0.254 and 0.356 showing an increase of the odds from one to another time interval. Similar results could be computed for other time points and models using the fitted coefficients.
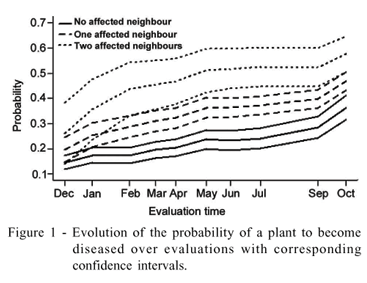
Figure 1 summarizes the computed probabilities from the second (2001-12-05) to the eleventh (2002-10-07) collection times. The lines with different patterns provide the profiles of the probabilities for plants with zero, one and two infected neighbours and the corresponding shaded lines are the confidence intervals. The consistent message is that the probability rises with the increase of the incidence, reflected by the intercept coefficient in association with the spatial pattern given the by the coefficients associated to the covariate. From the third observation, the confidence intervals do not overlap, indicating that the infective pressure is greater for two than one, and one than zero, infected neighbours.
CONCLUSIONS
Autologistic models provide a tool to further explore and describe spatial patterns of plant diseases beyond currently adopted methods, allowing a better understanding of the mechanisms of the spread of the disease, not only by detecting spatial patterns but also quantifying them through the associated coefficients of the effects of disease presence in different neighbourhood structures. An important feature of the autologistic model applied to individual trees is the objectivity when analysing original data, without the need of some sort of arbitrary discretization, as needed by methods based in quadrats.
The results found here for CDS points to the presence of spatial patterns in the disease for which evidence becomes clear as the incidence rises. In general, there is evidence of aggregation for levels of incidences higher than 20%. From the third data collection time onwards there was a noticeable increase of the probability of a plant to become diseased in the presence of infected neighbours as given for instance by the m2 model fit that shows evidence of infective pressure. Notice however that the detection can be influenced by the time interval between observations. In an overall view the within row effect is stronger, reflecting the spacing adopted in the field and supporting the conjecture of the spatial pattern, i.e. the closer the plants the higher the infective pressure.
The autologistic model has a potential do be widely adopted to investigate spatial patterns. It requires an extra computational burden compared with usual generalized linear models, which we have overcame with our own and freely available computational implementation. Further attempts to explore more flexible and general descriptions of the spatial patterns, ways to combine a sequence of time observations are steps to be followed in our investigation. The methodology also suggests a way to objectively combine data from different fields, allowing for an investigation of the effects of choices of spacing between trees, age, type of citrus, seasonal effects, tree combinations and other properties that can vary among different fields.
ACKNOWLEDGEMENTS
To Fundecitrus and CNPq (Proc. 50.0043/02-7) for financial support.
Received October 25, 2007
Accepted February 15, 2008
- BASSANEZI, R.B.; BERGAMIN FILHO, A.; AMORIM, L.; GIMENES-FERNANDES, N.; GOTTWALD, T.R.; BOVÉ, J.M. Spatial and temporal analyses of citrus sudden death as a tool to generate hypotheses concerning its etiology. Phytopathology, v.9, p.502-512, 2003.
- BASSANEZI, R.B.; BERGAMIN FILHO, A.; AMORIM, L.; GOTTWALD, T.R. Spatial and temporal analyses of citrus sudden death in Brazil. In: CONFERENCE OF THE INTERNATIONAL ORGANIZATION OF CITRUS VIROLOGISTS, Riverside, 2005. Proceedings Riverside: International Organization of Citrus Virologists, 2005. p.217-229.
- BESAG, J. Nearest-neighbour systems and the auto-logistic model for binary data. Journal of the Royal Statistics Society, Series B, v.34, p.75-83, 1972.
- BESAG, J. 'Statistical analysis of non-lattice data'. The Statistician, v.24, p.179-195, 1975.
- COLETTA FILHO, H.D.; TARGON, M.L.P.N.; TAKITA, M.A.; MÜLLER, G.W.; SANTOS, F.A.; DORTA, S.O.; DE SOUZA, A.A.; ASTÚA-MONGE, G.; FREITAS-ASTÚA, J.; MACHADO, M.A. Citrus tristeza virus variant associated with citrus sudden death and its specific detection by RT-PCR. In: CONFERENCE OF THE INTERNATIONAL ORGANIZATION OF CITRUS VIROLOGISTS, Riverside, 2005. Proceedings Riverside: International Organization of Citrus Virologists, 2005. p.499.
- CRESSIE, N. Statistics for spatial data New York: John Wiley, 1993. 928p.
- GIMENES-FERNANDES, N.; BASSANEZI, R.B. Doença de causa desconhecida afeta pomares cítricos no norte de São Paulo e sul do Triângulo Mineiro. Summa Phytopathologica, v.27, p.93, 2001.
- GOTTWALD, T.R.; REYNOLDS, K.M.; CAMPBELL, C.L.; TIMMER, L.W. Spatial and spatiotemporal autocorrelation analysis of citrus canker epidemics in citrus nurseries and groves in Argentina. Phytopathology, v.82, p.843-851, 1992.
- GUMPERTZ, M.L.; GRAHAM, J.M.; RISTAINO, J.B. Autologistic model of spatial pattern of phytophthora epidemic in bell pepper: effects of soil variables on disease presence. Journal of Agricultural, Biological and Environmental Statistics, v.2, p.131-156, 1997.
- GUMPERTZ, M.L.; WU, C.-T.; PYE, J.M. Logistic regression for southern pine beetle outbreaks with spatial and temporal autocorrelation. Forest Science, v.46, p.95-107, 1999.
- KRAINSKI, E.T.; RIBEIRO JÚNIOR, P.J. Rcitrus: functions for the analysis of citrus disease data. R package version 0.3-0 Curitiba:UFPR/LEG, 2007.
- LIMA, R.R.; DEMÉTRIO, C.G.B.; RIBEIRO JÚNIOR, P.J.; RIDOUT, M. Uma comparação de técnicas baseadas em quadrats para caracterização de padrões espaciais em doenças de plantas. Revista de Matemática e Estatística, v.24, p.7-26, 2006.
- MACCHERONI, W.; ALEGRIA, M.C.; GREGGIO, C.C.; PIAZZA, J.P.; KAMLA, R.F.; ZACHARIAS, P.R.A.; BAR-JOSEPH, M.; KITAJIMA, E.W.; ASSUMPÇÃO, L.C.; CAMAROTTE, G.; CARDOZO, J.; CASAGRANDE, L.C.; FERRARI, F.; FRANCO, S.F.; GIACHETTO, P.F.; GIRASOL; JORDÃO JÚNIOR, H.; SILVA, V.H.A.; SOUZA, L.C.A.; AGUILAR-VILDOSO, C.I.; ZANCA, A.S.; ARRUDA, P.; KITAJIMA, J.P.; REINACH, F.C.; FERRO, J.A.; SILVA, A.C.R. Identification and genomic characterization of a new virus (Tymoviridae Family) associated with citrus sudden death disease. Journal of Virology, v.79, p.3028-3037, 2005.
- MADDEN, L.V.; HUGHES, G. Plant disease incidence: distributions, heterogeneity, and temporal analysis. Annual Review of Phytopathology, v.33, p.529-564, 1995.
- MADDEN, L.V.; LOUIE, R.; ABT., J.J.; KNOKE, J.K. Evaluation of tests for randomness of infected plants. Phytopathology, v.72. p.195-198, 1982.
- R DEVELOPMENT CORE TEAM. R: a language and environment for statistical computing. Vienna, R Foundation for Statistical Computing, 2007.
- ROMÁN, M.P.; CAMBRA, M.; JUÁREZ, J.; MORENO, P.; DURAN-VILA, N.; TANAKA, F.A.O.; ALVES, E.; KITAJIMA, E.W.; YAMAMOTO, P.T.; BASSANEZI, R.B.; TEIXEIRA, D.C.; JESUS JÚNIOR, W.C.; AYRES, A.J.; GIMENES-FERNANDES, N.; RABENSTEIN, GIROTTO, L.F.; BOVÉ, J.M. Sudden death of citrus in Brazil: A graft-transmissible bud union disease. Plant Disease, v.88, p.453-467, 2004.
- SANTOS, C.B.; BARBIN, D.; CALIRI, A. Percolação e o fenômeno epidêmico: uma abordagem temporal e espacial da difusão de doenças. Scientia Agricola, v.55, p.418-427, 1998.
- SPÓSITO, M.B.; AMORIM, l.; RIBEIRO JÚNIOR, P.J.; BASSANEZI, R.B.; KRAISNKI, E.T. Spatial patterns of trees affected by black spots in citrus groves in Brazil. Plant Disease, v.91, p.36-40, 2007.
- XU, X.M.; RIDOUT, M.S. Effects of quadrat size and shape, initial epidemic conditions, and spore dispersal gradient on spatial statistics of plant disease epidemics. Phytopathology, v.90, p.738-750, 2000.
- ZHU, J.; HUANG, H.C.; WU, J. Modeling spatial-temporal binary data using Markov random fields. Journal of Agricultural, Biological and Environmental Statistics, v.10, p.212-225, 2005.
Publication Dates
-
Publication in this collection
16 Sept 2008 -
Date of issue
2008
History
-
Received
25 Oct 2007 -
Accepted
15 Feb 2008