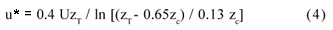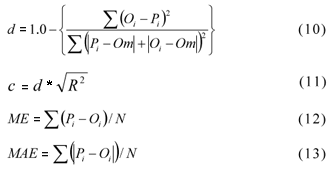Abstracts
Leaf wetness duration (LWD) is a key parameter in agrometeorology because it is related to plant disease occurrence. As LWD is seldomly measured in a standard weather station it must be estimated to run warning systems for schedule chemical disease control. The objective of the present study was to estimate LWD over turfgrass considering different models with data from a standard weather station, and to evaluate the correlation between estimated LWD over turfgrass and LWD measured in a 'Niagara Rosada' vineyard, cultivated in a hedgerow training system, in Jundiaí, São Paulo State, Brazil. The wetness sensors inside the vineyard were located at the top of the plants, deployed at an inclination angle of 45º and oriented southwest, with three replications. The methods used to estimate LWD were: number of hours with relative humidity above 90% (NHRH > 90%), dew point depression (DPD), classification and regression tree (CART) and Penman-Monteith (PM). The CART model had the best performance to estimate LWD over turfgrass, with a good precision (R² = 0.82) and a high accuracy (d = 0.94), resulting in a good confidence index (c = 0.85). The results from this model also presented a good correlation with measured LWD inside the vineyard, with a good precision (R² = 0.87) and a high accuracy (d = 0.96), resulting in a high confidence index (c = 0.93), showing that LWD in a 'Niagara Rosada' vineyard can be estimated with data from a standard weather station.
Vitis labrusca; LWD estimate; relative humidity; dew point temperature
A duração do período de molhamento (DPM) é uma variável agrometeorológica chave para a ocorrência de doenças de plantas. Como a DPM é raramente medida nas estações meteorológicas, ela deve ser estimada quando se pretende empregar sistemas de alerta de controle químico. Desse modo, o objetivo do presente estudo foi avaliar a estimativa da DPM sobre gramado por diferentes modelos a partir de dados meteorológicos obtidos em uma estação meteorológica padrão e verificar as relações entre a DPM estimada para o gramado e a medida em um vinhedo de 'Niagara Rosada', conduzido em espaldeira, em Jundiaí, SP, Brasil. Os sensores de molhamento no vinhedo foram instalados no topo das plantas com um ângulo de inclinação de 45º e com a face superior do sensor voltada para sudoeste, com três repetições. Os quatro modelos de estimativa da DPM foram: número de horas com umidade relativa do ar acima de 90% (NHUR > 90%), depressão do ponto de orvalho (DPO), árvore de classificação e regressão (CART) e o de Penman-Monteith (PM). O modelo CART estimou melhor a DPM no gramado, apresentando uma boa precisão (R² = 0,82) e uma ótima exatidão (d = 0,94), resultando num bom índice de confiabilidade (c = 0,85). Esta estimativa também apresentou uma boa correlação com a DPM medida no interior do vinhedo, com uma precisão razoável (R² = 0,87) e uma ótima exatidão (d = 0,96), resultando num ótimo índice de confiabilidade (c = 0,93), o que permite concluir que é possível estimar a DPM no vinhedo de 'Niagara Rosada' por meio de dados medidos ou estimados na estação meteorológica padrão.
Vitis labrusca; estimativa da DPM; umidade relativa; temperatura do ponto de orvalho
Estimating leaf wetness duration over turfgrass, and in a 'Niagara Rosada' vineyard, in a subtropical environment
Estimativa da duração do período de molhamento sobre o gramado e em vinhedo de 'Niagara Rosada' em condição subtropical
Jorge LuluI; Paulo Cesar SentelhasII, * * Corresponding author < pcsentel@esalq.usp.br> ; Mário José Pedro JúniorIII; José Ricardo Macedo PezzopaneIV; Gabriel Constantino BlainIII
IUSP/ESALQ - Programa de Pós-Graduação em Física do Ambiente Agrícola
IIUSP/ESALQ - Depto. de Ciências Exatas, Av. Pádua Dias, 11, C.P. 09 - 13418-900 - Piracicaba, SP - Brasil
IIISAA/APTA/IAC - Centro de Pesquisa e Desenvolvimento de Ecofisiologia e Biofísica, Av. Barão de Itapura, 1481, C.P. 28 - 13012-970 - Campinas, SP - Brasil
IVUFES/CEUNES - Centro Universitário do Norte do Espírito Santo, R. Humberto de Almeida Francklin, 257 - 29933-415 - São Mateus, ES - Brasil
ABSTRACT
Leaf wetness duration (LWD) is a key parameter in agrometeorology because it is related to plant disease occurrence. As LWD is seldomly measured in a standard weather station it must be estimated to run warning systems for schedule chemical disease control. The objective of the present study was to estimate LWD over turfgrass considering different models with data from a standard weather station, and to evaluate the correlation between estimated LWD over turfgrass and LWD measured in a 'Niagara Rosada' vineyard, cultivated in a hedgerow training system, in Jundiaí, São Paulo State, Brazil. The wetness sensors inside the vineyard were located at the top of the plants, deployed at an inclination angle of 45º and oriented southwest, with three replications. The methods used to estimate LWD were: number of hours with relative humidity above 90% (NHRH > 90%), dew point depression (DPD), classification and regression tree (CART) and Penman-Monteith (PM). The CART model had the best performance to estimate LWD over turfgrass, with a good precision (R2 = 0.82) and a high accuracy (d = 0.94), resulting in a good confidence index (c = 0.85). The results from this model also presented a good correlation with measured LWD inside the vineyard, with a good precision (R2 = 0.87) and a high accuracy (d = 0.96), resulting in a high confidence index (c = 0.93), showing that LWD in a 'Niagara Rosada' vineyard can be estimated with data from a standard weather station.
Key words:Vitis labrusca, LWD estimate, relative humidity, dew point temperature
RESUMO
A duração do período de molhamento (DPM) é uma variável agrometeorológica chave para a ocorrência de doenças de plantas. Como a DPM é raramente medida nas estações meteorológicas, ela deve ser estimada quando se pretende empregar sistemas de alerta de controle químico. Desse modo, o objetivo do presente estudo foi avaliar a estimativa da DPM sobre gramado por diferentes modelos a partir de dados meteorológicos obtidos em uma estação meteorológica padrão e verificar as relações entre a DPM estimada para o gramado e a medida em um vinhedo de 'Niagara Rosada', conduzido em espaldeira, em Jundiaí, SP, Brasil. Os sensores de molhamento no vinhedo foram instalados no topo das plantas com um ângulo de inclinação de 45º e com a face superior do sensor voltada para sudoeste, com três repetições. Os quatro modelos de estimativa da DPM foram: número de horas com umidade relativa do ar acima de 90% (NHUR > 90%), depressão do ponto de orvalho (DPO), árvore de classificação e regressão (CART) e o de Penman-Monteith (PM). O modelo CART estimou melhor a DPM no gramado, apresentando uma boa precisão (R2 = 0,82) e uma ótima exatidão (d = 0,94), resultando num bom índice de confiabilidade (c = 0,85). Esta estimativa também apresentou uma boa correlação com a DPM medida no interior do vinhedo, com uma precisão razoável (R2 = 0,87) e uma ótima exatidão (d = 0,96), resultando num ótimo índice de confiabilidade (c = 0,93), o que permite concluir que é possível estimar a DPM no vinhedo de 'Niagara Rosada' por meio de dados medidos ou estimados na estação meteorológica padrão.
Palavras-chave:Vitis labrusca, estimativa da DPM, umidade relativa, temperatura do ponto de orvalho
INTRODUCTION
Leaf wetness duration (LWD) is defined as the period of time when free water, caused by dew, rain or irrigation, remains deposited on plants tissues. LWD is a very important variable for epidemiology of plant diseases, since the majority of the pathogens, mainly fungus and bacteria, requires wetness on the plants tissues for infection, which include germination and penetration processes. Considering the importance of LWD for potential disease risk and for decision-making of when to spray, this is one of the most promising areas of the operational agrometeorology (Hoppmann & Wittich, 1997).
LWD is a variable of difficult measurement or estimation, because it is governed not only by the atmospheric conditions but also by the structure and composition of the vegetable community (Magarey et al., 2001; Sentelhas et al., 2005). So, LWD is seldom measured in conventional or automatic weather stations. Even when LWD measurements are available, they often fail to represent places that are distant from a meteorological station, due to the spatial variability of the wetness occurrence (Rao et al., 1998). Therefore, some models have been developed to estimate LWD using meteorological variables, such as air temperature, vapor pressure and wind speed (Francl & Panigrahi, 1997; Kim et al., 2002; Dalla Marta et al., 2005). Due to the shortage of LWD measurements, both in standard weather stations and in crop fields, the objective of the present study was to assess four different models to estimate LWD over turfgrass and in a 'Niagara Rosada' vineyard.
MATERIAL AND METHODS
The field trial was carried out in Jundiaí, São Paulo State, Brazil (23º12' S; 46º53' W; Altitude 715 m), from November 11, 2005 to March 5, 2006 (115 days). The LWD was measured in a 'Niagara Rosada' vineyard (2 × 1 m) cultivated in a hedgerow training system, using electronic wetness sensors (painted flat plate, printed circuit, model 237, Campbell Sci., Logan, UT) installed at the top of the plant, deployed with an angle of 45º to horizontal and facing southwest (Top-SW), with three replications, connected in a datalogger, programmed to read data every five seconds and to store averages or totals at every 20 min.
In the standard weather station (SWS), LWD was recorded in a reference position, at 30 cm height over turfgrass, at a 30º angle to horizontal and with the sensor surface facing south (Sentelhas et al., 2004). Also, air temperature (T), relative humidity (RH), wind speed at two meters (U), net radiation (Rn) and rainfall (P) were measured with the same frequency of the crop LWD.
Standard weather data were used to estimate LWD by four different models: number of hours with relative humidity above 90% - NHRH > 90% (Sentelhas, 2004), dew point depression - DPD (Gillespie et al., 1993), classification and regression tree - CART (Gleason et al., 1994) and Penman-Monteith - PM (Sentelhas, 2006), as follows:
NHRH > 90%: RH = 90% was considered as limit for the beginning of dew deposition (Sentelhas, 2004). The number of intervals of 20 min (during one day) with RH above 90% divided by three was considered as LWD (h).
DPD: the difference between T and the dew point temperature (To) was suggested as a LWD estimate method by Gillespie et al. (1993), being the time interval when DPD stays below two specific limits: 2.0ºC for the dew onset and 3.8ºC for the dew dry-off (Rao et al., 1998).
CART: the non-parametric procedure of classification for LWD estimate, suggested by Gleason et al. (1994), was adapted for data collected every 20 min and applied for the interval of 12h20 (day 1) to 12h00 (day 2). This model was developed to estimate LWD from DPD, U and RH data, using a binary classification tree with knots (categories) and branches to verify if an interval of 20 min presents wetness or not (Figure 1), through equations 1 and 2.


PM: as presented by Sentelhas et al. (2006), this model eliminates the need of the air temperature measurement at the crop height by assuming that the air temperature measured over turfgrass at the SWS, usually between 1.5 and 2.0 m height, represents the air temperature at the same height on the crop canopy (turfgrass, in this case). For this approach, a new resistance is added to the model, which was assumed as the aerodynamic resistance (ra, s m1), described for Monteith & Unsworth (1990):
where: zc is the sensor height (0.3 m), zT the air temperature measure height (~ 1.7 m) and u* the friction speed (m s1), given by the wind logarithmic profile (Pedro Júnior & Gillespie, 1982b):
where: UzT is the wind speed at zT (m s1).
According Sentelhas et al. (2006), to estimated LWD at 30 cm over turfgrass, the ra value is simplified to:
Using the presented relationships, the latent heat flow (LE) for an artificial leaf can be estimated for each interval of time (20 min, in this case) using the Penmam-Monteith equation (Monteith & Unsworth, 1990):
where: s is the slope of the saturation vapor pressure curve (h PaºC1), esTa the saturated vapor pressure for the air temperature measured at the SWS (h Pa), ea the actual air vapor pressure (h Pa), γ* the modified psychrometer constant (assumed to be 0.64 kPa K1 with moisture and heat transfer to both sides of sensor during dew, and 1.28 kPa K1 for evaporation from one side of a sensor after rain), and rb the boundary layer resistance for heat transfer (s m1), given by Campbell & Norman (1998):
where: d is the effective dimension of the mock leaf (flat plate wetness sensor), equal to 0.07 m, and Uzc = (0.651*UzT) the wind speed at the turfgrass high (m s1).
The maximum wetness holding capacity of the mock leaf was considered to be 0.8 mm for dew. When there is rainfall, it initiates or increases wetness and is added to the positive LE reservoir up to 0.6 mm.
Using the same procedure adopted by Pedro Júnior & Gillespie (1982a) and Sentelhas et al. (2006), wetness onset occurs when LE > 0 or rain begins, and wetness dry-off occurs when the condensation and/or rain accumulated by the model is consumed by an equivalent amount of evaporation. The time interval considered to obtain daily LWD was between 12h20 (day n) and 12h00 (day n +1).
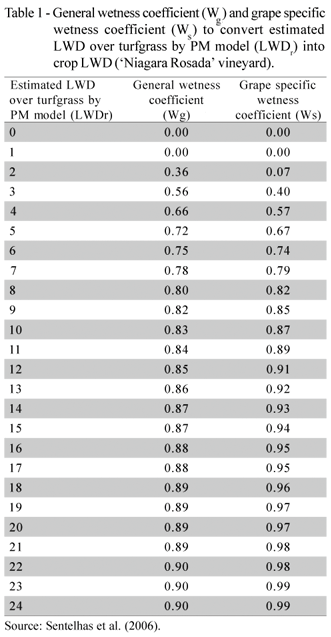
According Sentelhas et al. (2006), two wetness coefficients W (general and specific for grape) were used to convert estimated LWD over turfgrass by PM model into crop LWD ('Niagara Rosada' vineyard), as follows:
where: LWDc is the adjusted crop LWD ('Niagara Rosada' vineyard), LWDr the estimated LWD over turfgrass (at 30 cm height) by PM model, Wg the general wetness coefficient and Ws the grape specific wetness coefficient.
The general wetness coefficient (Wg) and grape specific wetness coefficient (Ws), to convert estimated LWD over turfgrass by PM model (LWDr) into crop LWD ('Niagara Rosada' vineyard), suggested by Sentelhas et al. (2006), are presented in Table 1.
The LWD data estimated by the four models and measured by electronic wetness sensors were compared by linear regression, analyzing the determination coefficient - R2, the agreement index - d (Willmott et al., 1985), the confidence index - c (Camargo & Sentelhas, 1997) and the errors (mean error - ME and mean absolute error - MAE):
where: Pi is the estimated LWD (h), Oi the measured LWD (h) and Om the average measured LWD (h).
The precision of the estimates is given by the determination coefficient (R2), which indicates the degree of dispersion in relation to the average (the random error). The accuracy is given by the agreement index " d" (Willmott et al., 1985), which ranges from zero, for no agreement, to 1, for the perfect agreement. As product of the two previous indexes, a new index was proposed by Camargo & Sentelhas (1997), called confidence index " c" , which gathers in only one index the precision and accuracy of estimates.
RESULTS AND DISCUSSION
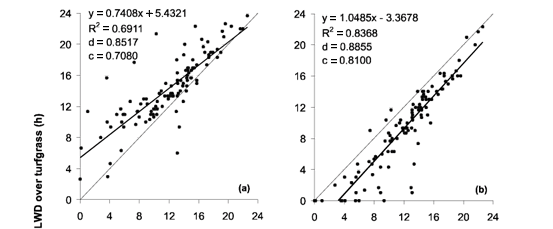
The best LWD estimate model over turfgrass was CART (Figure 2d), presenting a good precision (R2 = 0.8225) and high accuracy (d = 0.9363), resulting in a good confidence index (c = 0.8492). This performance was better than that found by Kim et al. (2004), using the CART model in 15 places of the United States, from May to September of 1998 and 1999 on the other hand, PM model (Figure 2a) obtained the worst performance, showing low accuracy (d = 0.8517) and precision (R2 = 0.6911), resulting in the lowest confidence index (c = 0.7080). The NHRH > 90% and DPD models (Figures 2b and 2c, respectively) had a slightly inferior performance compared to the CART model, however they also estimated LWD over turfgrass very well. The NHRH > 90% model presented a good precision (R2 = 0.8368) and a good accuracy (d = 0.8855), resulting in a good confidence index (c = 0.8100). The DPD model also presented a good precision (R2 = 0.8234) and a little better accuracy (d = 0.9111), resulting in a good confidence index, superior to the NHRH > 90% model (c = 0.8267).
Except for PM model (Figure 2a), all the other models underestimated the LWD over turfgrass (Figures 2b, 2c and 2d, respectively). On average, the PM model overestimated the LWD around 2.6 h. However, for higher LWD values, such overestimate was smaller. The NHRH > 90%, DPD and CART models underestimated the LWD around 2.9, 2.3 and 1.7 h, respectively.
Analyzing the errors (Table 2), NHRH > 90% model presented the highest values of mean error (ME = 2.8 h) and mean absolute error (MAE = 2.9 h), whereas CART model obtained the lowest errors (ME = -1.1 h and MAE = 1.7 h). Similar ME values for the CART model in standard condition over turfgrass were found by Kim et al. (2004) for five places of United States (temperate climate) and Kim et al. (2005) for four places of Costa Rica (tropical climate). From May to September of 1998 and 1999, the ME values obtained for Kim et al. (2004) were -1.6 h for Bondville, IL, -0.8 h for Monmouth, IL, -0.6 h for St. Charles, IL, -1.0 h for Sidney, NE, and -1.0 h for West Point, NE. Kim et al. (2005), from November to April (2000/01), obtained ME values of -0.4 h for Liberia and -1.2 h for Mojica. For the same period in 2002/03, the authors obtained ME values of -0.4 h for Ceiba, -1.6 h for Liberia, -0.9 h for Mojica, and -0.5 h for Santa Cruz. The PM and DPD models were those that presented intermediate errors: PM model with ME = 2.3 h and MAE = 2.6 h, and DPD model with ME = -2.0 h and MAE = 2.3 h. Sentelhas (2004) obtained ME = 0.8 h and MAE = 1.1 h, a little smaller in magnitude, for the PM model in standard condition over turfgrass.
The relationship between estimated LWD over turfgrass, except for the PM model, and measured LWD inside the 'Niagara Rosada' vineyard was good (Figure 3). The estimated LWD over turfgrass for the CART model obtained a good performance and the best correlation with measured LWD at the top of 'Niagara Rosada' grapevine (Figure 3d), presenting a reasonable precision (R2 = 0.8708) and a very high accuracy (d = 0.9609), resulting in a high confidence index (c = 0.9332). Sentelhas (2004), in Piracicaba, SP, Brazil, correlating estimated LWD over turfgrass with estimated LWD at the top of cotton crop canopy, during the growing season of 2001/02, also for the CART model, obtained a similar precision to the present study (R2 = 0.8796). The poorest correlation with LWD inside the 'Niagara Rosada' vineyard was obtained with estimated LWD by the PM model (Figure 3a), presenting a low precision (R2 = 0.6701) and a reasonable accuracy (d = 0.8243), resulting in a low confidence index (c = 0.6748). For the cotton, Sentelhas (2004), obtained a better precision between estimated LWD over turfgrass and estimated LWD at the top of the crop canopy by the PM model (R2 = 0.8491).
The estimated LWD for the NHRH > 90% and DPD models presented intermediate and good correlations with LWD inside the vineyard. For NHRH > 90% model the following statistical indexes obtained were: R2 = 0.9038; d = 0.9283; c = 0.8825, whereas for DPD model these indexes were: R2 = 0.8855; d = 0.9471; c = 0.8912. Figures 3b and 3c present these correlations. The results obtained with NHRH > 90% and DPD models were better than obtained by Sentelhas (2004) for the cotton crop, when comparing LWD estimated over turfgrass and at the top of the canopy.
Except for the PM model (Figure 3a), all the other models underestimated the LWD inside the vineyard through the estimated LWD over turfgrass (Figures 3b, 3c and 3d). The PM model overestimated the LWD inside the vineyard around 2.9 h. The NHRH > 90%, DPD and CART models underestimated the LWD around 2.4, 1.9 and 1.6 h, respectively, being almost systematic deviations for the PM, NHRH > 90% and DPD models, which can be corrected, or changing the limits or empirically.
Analyzing the errors (Table 3), the PM model presented a high mean error (ME = -2.7 h) and mean absolute error (MAE = 2.9 h). CART model obtained the lowest errors (ME = 0.7 h and MAE = 1.6 h), while NHRH > 90% and DPD models obtained intermediate errors (NHRH > 90% model with ME = 2.3 h and MAE = 2.4 h, and DPD model with ME = 1.6 h and MAE = 1.9 h). So, the CART model was the best LWD estimate method inside the vineyard through the LWD estimated over turfgrass, presenting the best confidence index " c" and the lowest ME and MAE.
A poor correlation was obtained between measured crop LWD inside the 'Niagara Rosada' vineyard (Top-SW) and estimated crop LWD obtained from LWD estimated over turfgrass by PM model multiplied by Wg (Figure 4a), presenting a low precision (R2 = 0.6698), reasonable accuracy (d = 0.8692) and a low confidence index (c = 0.7113) and overestimating the crop LWD around 2.3 h. Sentelhas et al. (2006) obtained a very higher precision (R2 = 0.9054) when comparing measured crop LWD and estimated LWD by multiplying estimated turfgrass LWD and Wg for four crop canopies: apple, cotton, grape and muskmelon. Analyzing the errors (Table 4), crop LWD estimate presented a high mean error (ME = 1.8 h) and mean absolute error (MAE = 2.3 h), higher than obtained by Sentelhas et al. (2006), who found ME = 0.3 and MAE = 1.3.
A better correlation, but also poor, was obtained between measured crop LWD inside the 'Niagara Rosada' vineyard (Top-SW) and estimated LWD over turfgrass by PM model multiplied by Ws (Figure 4b), presenting a low precision (R2 = 0.6699), reasonable accuracy (d = 0.8815) and low confidence index (c = 0.7215) and overestimating the crop LWD around 2.1 h. A very better precision (R2 = 0.8967) was obtained by Sentelhas et al. (2006) for the same comparison with independent LWD data at the top of the vineyard (Jundiaí, 2005/06), but with a smaller dataset (54 days). Analyzing the errors (Table 4), crop LWD estimates presented ME = 0.88 h and MAE = 2.1 h, higher than obtained by Sentelhas et al. (2006).
Correlations between estimated LWD over turfgrass for the four different models and measured LWD at the top of the 'Niagara Rosada' grapevine by simple linear regression (Figure 3) showed that the data dispersion was small, presenting good statistical indexes, except using the LWD estimated over turfgrass by the PM model. The test to estimate LWD inside the 'Niagara Rosada' vineyard from estimated LWD over turfgrass by PM model multiplied by general wetness coefficient (Wg) and grape specific wetness coefficient (Ws) did not result in a good performance, which can be related to the accuracy of the sensors of the SWS. As this model requires several inputs from weather variables, any problem with the accuracy of these sensors will be reflected on LWD values. In this contest net radiation and relative humidity measurements represent the main problems, as mentioned by Sentelhas and Gillespie (2008).
CONCLUSIONS
The NHRH > 90%, DPD and CART models had a good performance estimating LWD over turfgrass, mainly the CART model. These estimates also presented good correlations with measured LWD inside the 'Niagara Rosada' vineyard, showing that is possible to estimate the LWD inside the crop from estimated LWD over turfgrass. On the other hand, the PM physical model did not estimate the LWD satisfactorily, which can be related to the sensors accuracy in the standard weather station, especially for measuring net radiation and relative humidity.
ACKNOWLEDGEMENTS
To FAPESP for the scholarship to the first author and for supporting the present study. To IAC for the experimental area. To Prof. José Eduardo Macedo Pezzopane (UFES) for the wetness sensors used in the field experiment. To CNPq for the fellowships for the second and third authors.
Received March 13, 2007
Accepted May 30, 2008
- CAMARGO, A.P.; SENTELHAS, P.C. Avaliação do desempenho de diferentes métodos de estimativa da evapotranspiração potencial no Estado de São Paulo, Brasil. Revista Brasileira de Agrometeorologia, v.5, p.89-97, 1997.
- CAMPBELL, G.S.; NORMAN, J.M. Introduction to environmental biophysics. 2 ed. New York: Springer, 1998. 286p.
- DALLA MARTA, A.; MAGAREY, R.D.; ORLANDINI, S. Modelling leaf wetness duration and downy mildew simulation on grapevine in Italy. Agricultural and Forest Meteorology, v.132, p.84-95, 2005.
- FRANCL, L.J.; PANIGRAHI, S. Artificial neural network models of wheat leaf wetness. Agricultural and Forest Meteorology, v.88, p.57-65, 1997.
- GILLESPIE, T.J.; SRIVASTAVA, B.; PITBLADO, R.E. Using operational weather data to schedule fungicide sprays on tomatoes in southern Ontario, Canada. Journal of Applied Meteorology, v.32, p.567-573, 1993.
- GLEASON, M.L.; TAYLOR, S.E.; LOUGUIN, T.M.; KOEHLER, K.L. Development and validation of an empirical model to estimate the duration of dew periods. Plant Disease, v.78, p.1011-1016, 1994.
- HOPPMANN, D.; WITTICH, K.P. Epidemiology-related modelling of the leaf wetness duration as an alternative to measurements, taking Plasmopara viticola as an example. Zeitschrift für Pflanzenkrankheiten und Pflanzenschutz, v.104, p.533-544, 1997.
- KIM, K.S.; TAYLOR, S.E.; GLEASON, M.L. Development and validation of a leaf wetness duration model using a fuzzy logic system. Agricultural and Forest Meteorology, v.127, p.53-64, 2004.
- KIM, K.S.; TAYLOR, S.E.; GLEASON, M.L.; KOEHLER, K.J. Model to enhance site-specific estimation of leaf wetness duration. Plant Disease, v.86, p.179-185, 2002.
- KIM, K.S.; TAYLOR, S.E.; GLEASON, M.L.; VILLALOBOS, R.; ARAUZ, L.F. Estimation of leaf wetness duration using empirical models in northwestern Costa Rica. Agricultural and Forest Meteorology, v.129, p.53-67, 2005.
- MAGAREY, R.D.; SEEM, R.C.; RUSSO, J.M.; ZACK, J.W.; WAIGHT, K.T.; TRAVIS, J.W.; OUDEMANS, P.V. Site-specific weather information without on-site sensors. Plant Disease, v.85, p.1216-1226, 2001.
- MONTEITH, J.L.; UNSWORTH, M.H. Principles of environmental physics. 2 ed. New York: Edward Arnold, 1990. 291p.
- PEDRO JÚNIOR, M.J.; GILLESPIE, T.J. Estimating dew duration. I. Utilizing micrometeorological data. Agricultural Meteorology, v.25, p.283-296, 1982a.
- PEDRO JÚNIOR, M.J.; GILLESPIE, T.J. Estimating dew duration. II. Utilizing standard weather station data. Agricultural Meteorology, v.25, p.297-310, 1982b.
- RAO, P.S.; GILLESPIE, T.J.; SCHAAFSMA, A.W. Estimating wetness duration on maize ears from meteorological observations. Canadian Journal of Soil Science, v.78, p.149-154, 1998.
- SENTELHAS, P.C. Duração do período de molhamento foliar: aspectos operacionais da sua medida, variabilidade espacial em diferentes culturas e sua estimativa a partir do modelo de Penman-Monteith. Piracicaba: USP/ESALQ, 2004. 161p. (Livre-Docência).
- SENTELHAS, P.C.; GILLESPIE, T.J . Estimating hourly net radiation for leaf wetness duration modelling by Penman-Monteith equation. Theoretical and Applied Climatology, v.91, p.205-215, 2008.
- SENTELHAS, P.C.; GILLESPIE, T.J.; BATZER, J.C.; GLEASON, M.L.; MONTEIRO, J.E.B.A.; PEZZOPANE, J.R.M.; PEDRO JÚNIOR, M.J. Spatial variability of leaf wetness duration in different crop canopies. International Journal of Biometeorology, v.49, p.363-370, 2005.
- SENTELHAS, P.C.; GILLESPIE, T.J.; GLEASON, M.L.; MONTEIRO, J.E.B.A.; HELLAND, S.T. Operational exposure of leaf wetness sensors. Agricultural and Forest Meteorology, v.126, p.59-72, 2004.
- SENTELHAS, P.C.; GILLESPIE, T.J.; GLEASON, M.L.; MONTEIRO, J.E.B.A.; PEZZOPANE, J.R.M.; PEDRO JÚNIOR, M.J. Evaluation of a Penman-Monteith approach to provide " reference" and crop canopy leaf wetness duration estimates. Agricultural and Forest Meteorology, v.141, p.105-117, 2006.
- WILLMOTT, C.J.; ACKLESON, S.G.; DAVIS, R.E.; FEDDEMA, J.J.; KLINK, K.M.; LEGATES, D.R.; O'DONNELL, J.; ROWE, C.M. Statistics for the evaluation and comparison of models. Journal of Geophysical Research, v.90, p.8995-9005, 1985.
Publication Dates
-
Publication in this collection
21 Jan 2009 -
Date of issue
Dec 2008
History
-
Accepted
30 May 2008 -
Received
13 Mar 2007