ABSTRACT
Widely disseminated in both national and international scenarios, greenhouses are agribusiness solutions which are designed to allow for greater efficiency and control of the cultivation of plants. Bearing this in mind, the construction of greenhouses should take into consideration the incidence of wind, and other such aspects of comfort and safety, and ensure they are factored into the design of structural elements. In this study, we evaluated the effects of pressure coefficients established by the European standard EN 13031-1 (2001) and the Brazilian standard ABNT (1988), which are applicable to the structures of greenhouses with flat roofs, taking into account the following variables: roof slope, external and internal pressure coefficients and height-span ratio of the structure. Using the ANSYSTM computer program, zones of columns and roof were discretized by the Beam44 finite element to identify the maximum and minimum stress portions connected to the aerodynamic coefficients. With this analysis, we found that, in the smallest roof slope (a equal to 20°), the frame stress was quite similar for standards adopted. On the other hand, for the greatest inclination (a equal to 26°), the stress was consistently lower under the Brazilian standard. In view of this, we came to the conclusion that the differences between stresses when applying both standards were more significant at the higher degrees of height-span ratio and roof slope.
wind action; pitched roof; structural modeling
Introduction
Agricultural construction technology, especially for growing plants, faces great challenges when it comes to the design of protected environments capable of allowing greater production efficiency in smaller areas. According to Shamshiri and Ismail (2013)Shamshiri, S.; Ismail, W.I.W. 2013. A review of greenhouse climate control and automation systems in tropical regions. Journal of Agricultural Science and Applications 2: 175-182., these construction systems have the purpose of improving the quality and predictability of crops, entailing the control of a number of factors, such as humidity, temperature, solar radiation, internal carbon dioxide levels, and protection of crops from the action of rain, strong winds and pests (Straten et al., 2010Straten, G. van; Willigenburg, G. van; Henten, E. van; Ooteghem, R. van 2010. Optimal Control of Greenhouse Cultivation. CRC Press, Boca Raton, FL, USA.;Emekli et al., 2010Emekli, N.Y.; Kendirli, B.; Kurunc, A. 2010. Structural analysis and functional characteristics of greenhouses in the Mediterranean region of Turkey. African Journal of Biotechnology 9: 3131-3139.; Ali-Nezhad and Eskandari, 2012Ali-Nezhad, F.M.; Eskandari, H. 2012. Effect of architectural design of greenhouse on solar radiation interception and crops growth conditions. International Journal of Agriculture and Crop Sciences 4: 122 –127.). Thus, the optimal growth of a certain crop will be affected by the greenhouse’s architectural design. This being the case, a study on the structural design of greenhouses based on applicable normative instructions takes on great importance (Iribarne et al., 2007Iribarne, L.; Torres, J. A.; Peña, A. 2007. Using computer modeling techniques to design tunnel greenhouse structures. Computers in Industry 58: 403-415.; Ali-Nezhad and Eskandari, 2012Ali-Nezhad, F.M.; Eskandari, H. 2012. Effect of architectural design of greenhouse on solar radiation interception and crops growth conditions. International Journal of Agriculture and Crop Sciences 4: 122 –127.).
The extensive use of this agricultural construction technique has increased concern over its safety against structural damage. As pointed out by von Zabeltitz (2011)Zabeltitz, C. 2011. Integrated Greenhouse Systems for Mild Climates: Climate Conditions, Design, Construction, Maintenance, Climate Control. Springer, Berlin, Germany., such safety concerns are already under discussion in countries where the protected crop technique is largely used. In this sense, ABNT (2012)Brazilian Technical Standards Association [ABNT]. 2012. NBR 16032: Structures of Greenhouse and Nursery Farms – Requirements for Design, Construction, Maintenance and Restoration. = Estrutura de Estufa e Viveiro Agrícola – Requisitos de Projeto, Construção, Manutenção E Restauração. ABNT, Rio de Janeiro, RJ, Brazil (in Portuguese). was recently published to standardize procedures for greenhouse designs in Brazil. This standard is based on the wording of the standard of the European Committee for Standardization — CEN, EN-13031-1 (2001)European Standard [EN]. 2001. BS EN 13031-1 - Greenhouses: Design and Construction - Part 1: Commercial Production Greenhouses. European Standard, Bruxelles, Belgium., but takes geographical conditions in Brazil into account.
According to Buyuktas et al., (2011)Buyuktas, K.; Yilmaz, S.; Ertekin, C. 2011. The comparison of costs by computer aided and interactive greenhouse design application. African Journal of Agricultural Research 6: 3355-3362., the failure to make static calculations and consider existing environmental factors may lead to damage to greenhouses in adverse weather conditions. Because of the characteristics of the light construction of greenhouses, stress from extreme wind speeds can lead to damage to the greenhouse structure itself (Elsner et al., 2000Elsner, B. von; Briassoulis, D.; Waaijenberg, D.; Mistriotis, A.; Zabeltitz, C. von; Gratraud, J.; Russo, G.; Suay-Cortes, R. 2000. Review of structural and functional characteristics of greenhouses in European Union countries. Part I. Design requirements. Journal of Agricultural Engineering Research 75: 1-16.). The effects of wind are taking on increasing importance in the structural design of greenhouses given the need for larger facilities that allow for a more favorable internal climate for cultivation. Therefore, the main purpose of this study was to analyze, through computer modeling, the behavior of stress on the structures of pitched roof greenhouses resulting from the differences in wind pressure coefficients, as established by both the Brazilian standard (ABNT, 1988Brazilian Technical Standards Association [ABNT]. 1988. NBR 6123: Forces due to Wind on Edifications. = Forças devidas ao Vento em Edificações. ABNT, Rio de Janeiro, RJ, Brazil (in Portuguese).) and the European standard (EN 13031-1, 2001European Standard [EN]. 2001. BS EN 13031-1 - Greenhouses: Design and Construction - Part 1: Commercial Production Greenhouses. European Standard, Bruxelles, Belgium.).
Materials and Methods
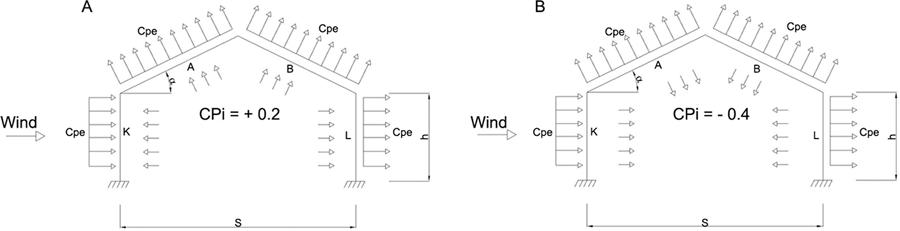
The structural behavior of a greenhouse frame subject to wind action was simulated by considering the ratio between column height (h) and structure span (s), as well as the roof slope (a), as set out in EN (2001)European Standard [EN]. 2001. BS EN 13031-1 - Greenhouses: Design and Construction - Part 1: Commercial Production Greenhouses. European Standard, Bruxelles, Belgium. and ABNT (1988)Brazilian Technical Standards Association [ABNT]. 1988. NBR 6123: Forces due to Wind on Edifications. = Forças devidas ao Vento em Edificações. ABNT, Rio de Janeiro, RJ, Brazil (in Portuguese).. The structure span (Figure 1) was set at 8 m, and under the extreme conditions of EN (2001)European Standard [EN]. 2001. BS EN 13031-1 - Greenhouses: Design and Construction - Part 1: Commercial Production Greenhouses. European Standard, Bruxelles, Belgium., with  ≤ 0.3 and
≤ 0.3 and  ≥ 0.6, the resulting heights of the columns amounted to 2.40 m and 4.80 m, respectively. By using these heights and varying the roof slope, we obtained the reference heights (from base to roof ridge) at the extreme levels of 3.86 m and 4.35 m, 6.26 m and 6.75 m, respectively. Thus, based on such conditions, the external and internal pressure coefficients were extracted with reference to both standards.
≥ 0.6, the resulting heights of the columns amounted to 2.40 m and 4.80 m, respectively. By using these heights and varying the roof slope, we obtained the reference heights (from base to roof ridge) at the extreme levels of 3.86 m and 4.35 m, 6.26 m and 6.75 m, respectively. Thus, based on such conditions, the external and internal pressure coefficients were extracted with reference to both standards.
– External (Cpe) and internal (Cpi) pressure coefficients applied to the wall and roof zones. A) internal pressure, B) internal suction. (K and L represents the column zones and A and B represents the roof zones). K and A represent the column and roof zones in upwind position and, L and B represent the column and roof zones in downwind position.
External and Internal Pressure Coefficients
The aerodynamic coefficients were obtained from the geometric characteristics of the preset models, with wind applied perpendicularly to the roof ridge, so that the wind pressure developed on the same plane of the frame (Figure 1). For the purposes of this research, we should emphasize that, for the wind direction parallel to the roof ridge, the pressure coefficient variations would be less significant. However, this condition should also be taken into account by agricultural greenhouse designs.
In accordance with EN 13031-1 (2001)European Standard [EN]. 2001. BS EN 13031-1 - Greenhouses: Design and Construction - Part 1: Commercial Production Greenhouses. European Standard, Bruxelles, Belgium., with wind applied perpendicularly to the roof ridge, and column heights of 2.40 m and 4.80 m, we obtained the external pressure coefficients shown in Table 1. To obtain such coefficients, we considered a variation of angle (α), setting limits as established by the European standard at 20° and 26°.
The ABNT (1988)Brazilian Technical Standards Association [ABNT]. 1988. NBR 6123: Forces due to Wind on Edifications. = Forças devidas ao Vento em Edificações. ABNT, Rio de Janeiro, RJ, Brazil (in Portuguese)., with wind applied perpendicularly to the roof ridge, and for heights of 2.40 m and 4.80 m, the external coefficients (Table 1) are associated with the ratios  ratios and the slopes previously established were considered for the standardization of results. According to
ratios and the slopes previously established were considered for the standardization of results. According to  ≤ 0.5 and 0.5 <
≤ 0.5 and 0.5 < < 1.5, respectively. The Brazilian standard also considers the ratio of length and construction width, which in this study ranged from two to four.
< 1.5, respectively. The Brazilian standard also considers the ratio of length and construction width, which in this study ranged from two to four.
The external coefficients for the roof planes, according to the Brazilian standard. are associated with angles ranging from 0° to 60°. However, for the purposes of comparison with the European standard, we applied external coefficients of 20° and 26° (Table 1).
With regard to the internal pressure coefficients under the said European standard, the internal pressure (Cpi equal to +0.2) and internal suction (Cpi equal to -0.4) situations should be considered. These amounts are connected to wind applied perpendicularly to the roof ridge and for single span greenhouses.
In the case of the Brazilian standard ABNT (1988)Brazilian Technical Standards Association [ABNT]. 1988. NBR 6123: Forces due to Wind on Edifications. = Forças devidas ao Vento em Edificações. ABNT, Rio de Janeiro, RJ, Brazil (in Portuguese)., the internal pressure coefficients are calculated considering the dominant openings, entailing the control of these coefficients by applying the upwind or downwind ratio of the dominant openings. Therefore, for comparison purposes, the amounts established by the European standard EN 13031-1 (2001)European Standard [EN]. 2001. BS EN 13031-1 - Greenhouses: Design and Construction - Part 1: Commercial Production Greenhouses. European Standard, Bruxelles, Belgium. were considered, i.e. +0.2 and -0.4.
As asserted by Mistriotis and Briassoulis (2002)Mistriotis, A.; Briassoulis, D. 2002. Numerical estimation of the internal and external aerodynamic coefficients of a tunnel greenhouse structure with openings. Computers and Eletronics in Agriculture 34: 191-205., few experiments have been conducted on internal pressure coefficients for greenhouses, especially in situations with different openings, windows and fans, which require different system settings. In addressing this issue, computational modeling can contribute an important alternative for ascertaining these coefficients.
Combining internal and external coefficients helps to ascertain the pressure coefficient (C) to be applied on each structure zone. Typically, wind speed characteristics (which depend on the conditions of each design, i.e. wind speed and the basic factors connected to topography, roughness and construction dimensions, together with probabilistic concepts) have been used to ascertain the load for each part of the agricultural greenhouse frame applying Equation 1.
F - C . q . L (1)
where: F - action of the wind perpendicularly applied along the axis of each frame element [N m−1]; C - Pressure coefficient, based on external and internal coefficients; q - wind dynamic pressure (q equal to 0.613.Vk) [N m−2], whereVk is the characteristic wind speed [m s−1];L - Distance between the frames [m].
By applying the F actions on the respective frame zones, for each discretized finite element, we obtained results linked to the pressure coefficient (C). Therefore, to accomplish the purposes of this research, considering that dynamic pressure and the distance between frames are characteristics of each design, unit amounts were adopted to account for the wind action. This way, the action accounted for the component of actionC (i.e., the pressure coefficient itself) and the results attained would qualitatively represent the effects of this coefficient on the stress; given that the stress portion will be shown without units.
Computational modeling
To analyze the influence of the pressure coefficients on the structure stress conditions, we applied the finite element method using the ANSYS program (ANSYSTM, version 10.0). At each geometrically modeled frame line, a mesh with three-dimensional BEAM44 elements was generated, having 3 elements per line (Figure 2A). The BEAM44 element was used to represent a tubular steel profile with a commercial square section equal to 60 mm × 60 mm and a thickness of 2 mm, applied to all of the frame zones. The use of profiles with greater or smaller stiffness which allow for suitable internal pressure on the structural elements should be considered as particularities of each design, and could be evaluated by means of a structural optimization analysis.
The total constraint of movements of the column bases was assumed. The action of component C was applied linearly along the length of each structural element (Figure 2B) and, in order to consider the structure’s self-weight, the gravitational acceleration (9.81 m s-2) was activated. For the purpose of steel characterization, we applied Young’s modulus equal to 21 × 1010 Pa, Poisson’s ratio of 0.30 and density equal to 7.86 × 103 kg m−3.
Results and Discussion
Distribution of stress portions
As a result of the modeling, we obtained extreme levels consisting of the maximum and minimum stress portions (direct stress and bending stress). Figures 3A and 3B were obtained from the wind and the structure’s self-weight amounts. For an objective analysis of the results obtained with ANSYSTM, for the finite elements generated in each frame zone (K, A, B and L), the extreme levels of the maximum and minimum stress portions were extracted. These results, shown in Figures 4A to D and Figures 5A to D, corresponding to the researched cases (Table 2), were obtained setting the roof slopes α (20° and 26°), the ratios Cpi coefficients (-0.4 and +0.2), as well as the external coefficients stipulated by the European and Brazilian standards. In the zone most influenced by the aerodynamic coefficients (zone K), with a roof slope set at 20º (Figures 4A andB, and Figures 5A and B) for each ratio Cpi value (suction or pressure), the values of extreme stresses were close in both standards. Therefore, with the imposition of α equal to 20°, the stress distribution in the column (zone K) will be similar to both European and Brazilian standards. (0.3 and 0.6) and
(0.3 and 0.6) and  (0.3 or 0.6) and each
(0.3 or 0.6) and each
– Distribution of stresses resulting from the aerodynamic coefficients and self-weight of the structure. A) Maximum stress portion, B) Minimum stress portion.
– Maximum stress portions influenced by the aerodynamic coefficient. A) a equal to 20° and
 equal to 0.3, B) a equal to 20° and
equal to 0.3, B) a equal to 20° and  equal to 0.6, C) a equal to 26° and
equal to 0.6, C) a equal to 26° and  equal to 0.3, D) a equal to 26° and
equal to 0.3, D) a equal to 26° and  equal to 0.6. K and A represent the column and roof zones in upwind position and, L and B represent the column and roof zones in downwind position.
equal to 0.6. K and A represent the column and roof zones in upwind position and, L and B represent the column and roof zones in downwind position.
– Minimum stress portions influenced by the aerodynamic coefficient. A) a equal to 20° and
 equal to 0.3, B) a equal to 20° and equal to 0.6, C) a equal to 26° and
equal to 0.3, B) a equal to 20° and equal to 0.6, C) a equal to 26° and  equal to 0.3, D) a equal to 26° and
equal to 0.3, D) a equal to 26° and  equal to 0.6. K and A represent the column and roof zones in upwind position and, L and B represent the column and roof zones in downwind position.
equal to 0.6. K and A represent the column and roof zones in upwind position and, L and B represent the column and roof zones in downwind position.
– Cases researched and their parameters. Internal pressure or Suction Coefficient (Cpi), Height-Span Ratio
 ) and Roof Slope (a ,°).
) and Roof Slope (a ,°).
On the other hand, with the imposition of α equal to 26º (Figures 4C and D, andFigures 5C and D), the stress portions in zone K were greater when calculated in accordance with the European standard. For Cpi equal to -0.4 and 0.2, respectively. In this same order of Cpi and with Cpi equal to -0.4 and 0.2, respectively. However, for aCpi amounts. In this situation (a equal to 26°), the use of the Brazilian standard allows for using less rigid profiles for the columns. equal to 0.3, the differences in maximum stresses were equal to 14 % and 11 % when we applied
equal to 0.3, the differences in maximum stresses were equal to 14 % and 11 % when we applied equal to 0.6, the maximum stress portions obtained as per the European standard were 5 % and 6 % greater than the values obtained in accordance with the Brazilian standard. The differences found for the minimum stresses, with the ratio
equal to 0.6, the maximum stress portions obtained as per the European standard were 5 % and 6 % greater than the values obtained in accordance with the Brazilian standard. The differences found for the minimum stresses, with the ratio  equal to 0.3, were 15 % and 13 % for
equal to 0.3, were 15 % and 13 % for  ratio equal to 0.6, the difference in minimum stresses was equal to 5 % for both
ratio equal to 0.6, the difference in minimum stresses was equal to 5 % for both
In the corresponding zone B of the roof (where the lowest maximum and minimum stress portions occur), the highest values were obtained when the European standard was applied, except for the situation calculated with Cpi equal to +0.2 (Figures 4A and 5A). In zone A, the calculations in accordance with the European standard also resulted in higher stress portions, except in the case where Cpi equal to +0.2 were adopted (Figures 4C and 5C). equal to 0.3, a equal to 20° and
equal to 0.3, a equal to 20° and  equal to 0.3, a equal to 26° and
equal to 0.3, a equal to 26° and
In the zones where the columns are positioned, in which K is more critical than L, for each of the Cpi equal to +0.2, by setting a equal to 26°, in zone A we found a reduction of 25 % in the maximum and minimal stress portions, compared to the amount of the simulation with a equal to 20°. For this same analysis, when applying the European standard, there was a 45 % reduction in the stress portions. ratios, the stress portions were more intense with higher roof slopes (a equal to 26°). With regard to the influence of the roof slope in the simulation in accordance with the Brazilian standard coefficients, with
ratios, the stress portions were more intense with higher roof slopes (a equal to 26°). With regard to the influence of the roof slope in the simulation in accordance with the Brazilian standard coefficients, with  equal to 0.3 and
equal to 0.3 and
By setting a equal to 26° and Cpi equal to +0.2, to evaluate the parameter Cpi equal to -0.4, the stress reduction for these standards was equal to 2 % and 7 %, respectively. , the amount of 0.6 led to a reduction in the stress portions to 10 % and 12 % in the simulation in accordance with the Brazilian and European standards, respectively. For the same
, the amount of 0.6 led to a reduction in the stress portions to 10 % and 12 % in the simulation in accordance with the Brazilian and European standards, respectively. For the same  (i.e., equal to 0.6) and
(i.e., equal to 0.6) and
The variation in minimum stress portions for the roof slope was similar to the variation in the maximum stress portions, but with a slightly higher variation in the ratio Cpi equal to -0.4 (this was the only combination that had an ineffective performance when changing the angle from 20° to 26°). The increases in the maximum stress portion for ABNT (1988)Brazilian Technical Standards Association [ABNT]. 1988. NBR 6123: Forces due to Wind on Edifications. = Forças devidas ao Vento em Edificações. ABNT, Rio de Janeiro, RJ, Brazil (in Portuguese). and EN (2001)European Standard [EN]. 2001. BS EN 13031-1 - Greenhouses: Design and Construction - Part 1: Commercial Production Greenhouses. European Standard, Bruxelles, Belgium. were 17 % and 53 %, respectively, whereas, for the minimum stress portions, they reached 19 % and 57 %, for each standard, respectively. equal to 0.3 and
equal to 0.3 and
When comparing the calculation results for single and multi-span greenhouses, in accordance with the EN 13031-1 (2001)European Standard [EN]. 2001. BS EN 13031-1 - Greenhouses: Design and Construction - Part 1: Commercial Production Greenhouses. European Standard, Bruxelles, Belgium. and Chinese standards, Tong et al., (2013)Tong, L.; Jin, J.; Zhou, F. 2013. Comparative study on calculation of wind loads on greenhouse structures between codes of China and Europe. Transactions of the Chinese Society of Agricultural Engineering 29: 174-181.reported that the European standard establishes greater pressure coefficients and wind profile than the Chinese standard. Therefore, the internal forces were higher when applying the European standard’s procedures. Thus, these authors concluded that the European standard is more comprehensive for dimensioning factors concerning wind.
Distribution of Solar Radiation
In addition to the construction’s position in relation to the hemisphere (latitude), the roof slope also affects the incidence of solar radiation; given that slightly sloping roofs are not suitable due to the losses of reflection and absorption (Garg and Prakash, 2000Garg, H.P.; Prakash, J. 2000. Solar Energy: Fundamentals and Applications. McGraw-Hill, New Delhi, India.). According to the latter authors and Critten (1993)Critten, D.L. 1993. A review of the light transmission into greenhouse crops. Acta Horticulturae 328: 9-31., radiation incident angles smaller than 30° are appropriate. Roofs with inclinations close to 30° are described as ideal for maximizing the solar radiation for the Mediterranean region (Soriano et al., 2009Soriano, T.; Hernández, J.; Montero, J. I.; Antón, A.; Castilla, N. 2009. Solar radiation transmission in Mediterranean plastic greenhouses. Acta Horticulturae 807: 73-78.).
In the case of the roof slopes evaluated in this study (20° and 26°), the amount of 26° was favorable for locations at higher latitudes. This is due to the higher roof slope, which reduces the sunlight incidence angle, and favors the distribution of solar radiation and the internal microclimate inside the greenhouse. In regions closer to the Equator, a roof slope equal to 20° could be further investigated in view of the smaller zenith angle. However, an angle of 26° favors solar irradiance over a period covering an entire year with the solstice occurring in the opposite hemisphere with a higher zenith angle.
The results of this analysis directly impact the dimensioning of the structural elements of greenhouses, as well as the aspect of comfort. Therefore, when an environment needs either a greater volume or a reduction in load on the roof’s structural elements, the angle value should be set at 26°.
Future perspectives
Research must be conducted experimentally with prototypes tested in a wind tunnel, to confront the differences in results of stress distribution obtained by computational modeling.
In addition to the aspects discussed in this study, structural optimization is relevant to obtaining consistency with the particular characteristics of each greenhouse (including aspects of strength and stability within secure limits), thus widening the sustainable use of this type of rural construction.
Conclusion
Differences between stresses estimated in greenhouse frames, using the coefficients established by Brazilian and European standards, were more significant for the greater amounts of height-span ratio and roof slope. The maximum and minimum stress portions took place in the column’s most critical zone (zone K) for both values of height-span ratio and for roof slope amounting to 20°, which resulted in similar values for both standards. However, with roof slope equal to 26°, these stress portions were lower when the Brazilian standard was applied. The main similarities connected to the results for the stress portions, were found in simulations with roof slope equal to 20°, height-span ratio equal to 0.3 and internal pressure coefficients equal to -0.4. Establishing the roof plane slope at the highest amount (equal to 26°) is a strategy that allows a larger volume for greenhouses with better thermal comfort conditions, while simultaneously reducing wind stresses on the roof zone.
Acknowledgement
The authors would like to acknowledge the support of the Coordination for the Improvement of Higher Level Personnel (CAPES) by means of scholarship grants for the Master’s degree program research.
References
- Ali-Nezhad, F.M.; Eskandari, H. 2012. Effect of architectural design of greenhouse on solar radiation interception and crops growth conditions. International Journal of Agriculture and Crop Sciences 4: 122 –127.
- Brazilian Technical Standards Association [ABNT]. 2012. NBR 16032: Structures of Greenhouse and Nursery Farms – Requirements for Design, Construction, Maintenance and Restoration. = Estrutura de Estufa e Viveiro Agrícola – Requisitos de Projeto, Construção, Manutenção E Restauração. ABNT, Rio de Janeiro, RJ, Brazil (in Portuguese).
- Brazilian Technical Standards Association [ABNT]. 1988. NBR 6123: Forces due to Wind on Edifications. = Forças devidas ao Vento em Edificações. ABNT, Rio de Janeiro, RJ, Brazil (in Portuguese).
- Buyuktas, K.; Yilmaz, S.; Ertekin, C. 2011. The comparison of costs by computer aided and interactive greenhouse design application. African Journal of Agricultural Research 6: 3355-3362.
- Critten, D.L. 1993. A review of the light transmission into greenhouse crops. Acta Horticulturae 328: 9-31.
- Elsner, B. von; Briassoulis, D.; Waaijenberg, D.; Mistriotis, A.; Zabeltitz, C. von; Gratraud, J.; Russo, G.; Suay-Cortes, R. 2000. Review of structural and functional characteristics of greenhouses in European Union countries. Part I. Design requirements. Journal of Agricultural Engineering Research 75: 1-16.
- Emekli, N.Y.; Kendirli, B.; Kurunc, A. 2010. Structural analysis and functional characteristics of greenhouses in the Mediterranean region of Turkey. African Journal of Biotechnology 9: 3131-3139.
- European Standard [EN]. 2001. BS EN 13031-1 - Greenhouses: Design and Construction - Part 1: Commercial Production Greenhouses. European Standard, Bruxelles, Belgium.
- Garg, H.P.; Prakash, J. 2000. Solar Energy: Fundamentals and Applications. McGraw-Hill, New Delhi, India.
- Iribarne, L.; Torres, J. A.; Peña, A. 2007. Using computer modeling techniques to design tunnel greenhouse structures. Computers in Industry 58: 403-415.
- Mistriotis, A.; Briassoulis, D. 2002. Numerical estimation of the internal and external aerodynamic coefficients of a tunnel greenhouse structure with openings. Computers and Eletronics in Agriculture 34: 191-205.
- Shamshiri, S.; Ismail, W.I.W. 2013. A review of greenhouse climate control and automation systems in tropical regions. Journal of Agricultural Science and Applications 2: 175-182.
- Soriano, T.; Hernández, J.; Montero, J. I.; Antón, A.; Castilla, N. 2009. Solar radiation transmission in Mediterranean plastic greenhouses. Acta Horticulturae 807: 73-78.
- Straten, G. van; Willigenburg, G. van; Henten, E. van; Ooteghem, R. van 2010. Optimal Control of Greenhouse Cultivation. CRC Press, Boca Raton, FL, USA.
- Tong, L.; Jin, J.; Zhou, F. 2013. Comparative study on calculation of wind loads on greenhouse structures between codes of China and Europe. Transactions of the Chinese Society of Agricultural Engineering 29: 174-181.
- Zabeltitz, C. 2011. Integrated Greenhouse Systems for Mild Climates: Climate Conditions, Design, Construction, Maintenance, Climate Control. Springer, Berlin, Germany.
Edited by
Publication Dates
-
Publication in this collection
Mar-Apr 2016
History
-
Received
20 Feb 2015 -
Accepted
17 Aug 2015