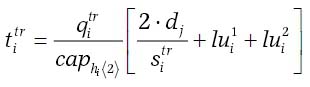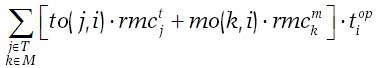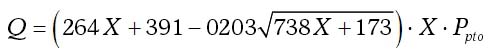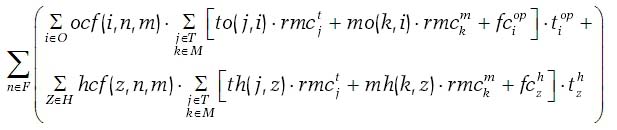ABSTRACT
Capacity planning in agricultural field operations needs to give consideration to the operational system design which involves the selection and dimensioning of production components, such as machinery and equipment. Capacity planning models currently onstream are generally based on average norm data and not on specific farm data which may vary from year to year. In this paper a model is presented for predicting the cost of in-field and transport operations for multiple-field and multiple-crop production systems. A case study from a real production system is presented in order to demonstrate the model’s functionalities and its sensitivity to parameters known to be somewhat imprecise. It was shown that the proposed model can provide operation cost predictions for complex cropping systems where labor and machinery are shared between the various operations which can be individually formulated for each individual crop. By so doing, the model can be used as a decision support system at the strategic level of management of agricultural production systems and specifically for the mid-term design process of systems in terms of labor/machinery and crop selection conforming to the criterion of profitability.
machinery management; decision support system; strategic management; binary programming
Introduction
Agricultural production adheres to intensification and extensification trends leading, on the one hand, to diversity of resource allocation and cropping practices and, on the other, to an increased geographic dispersion of fields dedicated to crop production. The diversity of management practices requires a tailored decision making process at both the strategic and the tactical management levels. Existing information and decision support systems provide a number of services to farmers. However, these services use closed specifications and do not provide the farmers with the ability to tailor their systems according to their practical needs (Sørensen et al., 2010Sørensen, C.G.; Pesonen, P.; Fountas, S.; Suomi, P.; Bochtis, D.D.; Pedersen, S.M. 2010. A user-centric approach for information modelling in arable farming. Computers and Electronics in Agriculture 73: 44-55.; Kaloxylos et al., 2014Kaloxylos, A.; Groumas, A.; Sarris, V.; Katsikas, L.; Magdalinos, P.; Antoniou, E.; Politopoulou, Z.; Wolfert, S.; Brewster, C.; Eigenmann, R.; Terol, C.M. 2014. A cloud-based farm management system: architecture and implementation. Computers and Electronics in Agriculture 100: 168-179.). In addition to the diversification of management, increasing geographic dispersion also leads to the engagement of farmers in supply chain activities, especially in the case of biomass production. However, such an engagement provides cost-effective solutions for supply chain activities which can increase farm business income and, additionally, reduce the ownership cost of machinery due to increased usage (Tatsiopoulos and Tolis, 2003Tatsiopoulos, I.P.; Tolis, A.J. 2003. Economic aspects of the cotton-stalk biomass logistics and comparison of supply chain methods. Biomass and Bioenergy 24: 199-214.).
Therefore, new tools for different planning levels should be made available to farmers that also include logistics management functionalities (Sørensen and Bochtis, 2010Sørensen, C.G.; Bochtis, D.D. 2010. Conceptual model of fleet management in agriculture. Biosystems Engineering 105: 41-50.), especially when considering logistics operations as an inseparable part of the production system, capacity planning is a central task in the farm management process as well as a prerequisite for operations scheduling (Orfanou et al., 2013Orfanou, A.; Busato, P.; Bochtis, D.D.; Edwards, G.; Pavlou, D.; Sørensen, C.G.; Berruto R. 2013. Scheduling for machinery fleets in biomass multiple-field operations. Computers and Electronics in Agriculture 94: 12-19.; Bochtis et al., 2013). Capacity planning considers the system design involving the selection of production components, such as the selection and dimensioning of machinery and equipment, taking into account the operational demands, resource availability, potential working methods, and the associated cost (Bochtis et al., 2014Bochtis, D.D.; Sørensen, C.G.; Busato, P. 2014. Advances in agricultural machinery management: a review. Biosystems Engineering 126: 69-81.). A number of studies focusing on machinery capacity planning have been conducted (e.g. Berruto and Maier, 2001Berruto, R.; Maier, D.E. 2001. Analyzing the receiving operation of different grain types in a single-pit country elevator. Transactions of the ASAE 44: 631-8.; Søgaard and Sørensen, 2004Søgaard, H.; Sørensen, C. 2004. A model for optimal selection of machinery sizes within the farm machinery system. Biosystems Engineering 89: 13-28.; Sahu and Raheman, 2008Sahu, R.; Raheman, H. 2008. A decision support system on matching and field performance prediction of tractor implement system. Computers and Electronics in Agriculture 60: 76-86.; Busato et al., 2013Busato, P.; Sørensen, C.G.; Pavlou, D.; Bochtis D.D.; Berruto, R.; Orfanou A. 2013. DSS tool for the implementation and operation of an umbilical system applying organic fertilizer. Biosystems Engineering 114: 9-20.; Busato and Berruto, 2014Busato, P.; Berruto, R. 2014. A web-based tool for biomass production systems. Biosystems Engineering 120: 102-116.; Busato, 2015Busato, P. 2015. A simulation model for a rice-harvesting chain. Biosystems Engineering 129: 149-159.). However, planning in general is based on average norm data and not on specific farm data that may vary from year to year. To address this concern, a model is presented in this paper on the cost prediction of in-field and transport operations for multiple-field and multiple-crop production systems. The proposed model refers to the strategic level of decision making in an agricultural production system pertaining to the design of the labor/machinery system in connection with the types of crops selected.
Materials and Methods
Model overview
The overall structure of the model is presented in Figure 1. The main software components of the system are an SQL data base, where series of data are pre-stored, the processing component that has built in the MATLAB programming language, and a graphical user interface where the scenario-specific inputs are provided to the system and also, the output of the system is presented. The pre-stored data include all the coefficients for machinery management (e.g. data bases of coefficient standards from the American Society of Agricultural and Biological Engineers (ASABE), crop-specific parameters (e.g. biomass types, expected yields, average dry matter, etc.), productive means (dosages of insecticides, herbicides, etc.), and the cost of various external services (e.g. irrigation cost). The pre-stored data base also includes ranges for realistic values of the scenario-specific parameters (e.g. in-field working speed for a particular machine) in order to prevent any mistaken value being inserted by the user and also to provide a suggestion for the parameters that might not be available for a particular scenario. The scenario-specific data as regards input data such as machinery dimensioning (e.g. operating width and power), crop allocation, field features (e.g. area), network distances (e.g. distances between fields and distances of each field to the delivery facility), operational data (e.g. working speeds), and monetary costs (e.g. fuel cost and labor wages). All the processing of data takes place in the MATLAB environment. This automated procedure allows for a comparison of operational time and total costs of many scenarios that differ in terms of parameter (e.g. working speed) without having to insert all data from scratch.
Model inputs
Fields and crop related data
Let F = {1, 2, 3…} and C = {1, 2, 3…} represent the set of fields which constitutes the cultivation area of the system (e.g. a farm) and the set of crops that is cultivated in the production system, respectively. The numerical input parameters for each individual field include the area of each field, ai, i ∈ F, the width of the field area (assuming a rectangular field shape), xi, i ∈ F, the distance from the delivery facility (depot or bioenergy production plant), di, i ∈ F, and the average speed for a transport operation between the field and the farm, sitr, i ∈ F. Finally, the classifying of soil workability, Wori = {1, 2, 3…}, i ∈F, is based on three classes that correspond to a dimensionless soil texture adjustment parameter: 1, fine; 2, medium, and 3, coarse texture soils (ASAE, 2009aAmerican Society of Agricultural Engineers [ASAE]. 2009a. ASAE D497.6 Agricultural machinery management data. p. 360-367. In: ASAE standards. ASAE, St. Joseph, MI, USA.). Soil workability is needed for the selection of coefficients from the database for estimating the variables related to in-field machinery performance.
A crop can be allocated to different fields and conversely, in a field a number of crops can be allocated. This fact results in a clustering of the production system area that is described by a F |×|C| matrix A in which element aij provides the area of the field i ∈ F allocated to crops j ∈ C (aij = 0 if crop j is not cultivated in field i ; individual field area: cf (i, j) : C × F ↦ {0,1} is defined where cf(i, j) = 1 if crop i is cultivated in field j, and cf(i, j) = 0 otherwise. Each production area of a field in which an individual crop is cultivated will be referred to as a “production unit” (the number of production units in the production system is equal to the number of non-zero elements of the previously defined matrix, or equivalent to the cardinality of the set: |{aij / i ∈ F, j ∈ C, aij, ≠ 0}|. ). Furthermore, a binary decision function
). Furthermore, a binary decision function  ; total area allocated to a crop
; total area allocated to a crop  ; total production area
; total production area
Resources related input
In a production system different types of labor could be involved, for example: family people, seasonal, specialized, etc., with a different hourly cost and productivity level. Let L = {1, 2, 3, …} represent the set of the different types of labor. A cost, c1l, i ∈ L is assigned to each labor type.
Let T = {1, 2, 3, …} represent the set of available tractors. Each tractor i ∈ T is characterized by the values of cost, c1t , power, p1t , and time used for other activities not related to the production system under consideration, u1t . The vehicle type (2-wheel drive or 4-wheel drive) is defined by the following binary parameters vti2WD ∈ {0,1} and vti4WD ∈ {0,1} (note that the following condition stands: vti4WD ∈ {0,1} \ {vti2WD} ).
Let M = MNMF ∪ MIMF ∪ MOMF represent the machinery set where MNNF = {1, 2, 3,…}, MIMF = {|MNMF|, |MNMF| + 1,...}, and MOMF = {|MIMF|, |MIMF| + 1,...} represents the sub-sets of the machinery dedicated to neutral material flow operations (there is neither material addition nor material removal to/from the field, e.g. tillage, mowing, etc.), to input material flow operations (where a quantity of a ‘‘commodity’’ is transported by the machine and is distributed in the field area, e.g., seed, fertilizer, etc.), and output material flow operations (where a quantity of a ‘‘commodity’’ is transported out of the field area, e.g., harvesting), respectively (according to the terminology found in Bochtis and Sørensen, 2009Bochtis, D.D.; Sørensen, C.G. 2009. The vehicle routing problem in field logistics part I. Biosystems Engineering 104: 447–457.). The set of the self-propelled machines is represented by MSP ⊆ M. A machine is identified by the values of purchasing cost cim,i ∈ M, working width wim ,i ∈ M, hourly use for other activities uim ,i ∈ M , hopper capacity capi,i ∈ MIMF ∪ MOMF, in the case of input and output material flow operations, and power pim, i ∈ MSP in the case of self-propelled machines. Furthermore, a labor type is allocated to each machine. This allocation generates the binary decision function lm(i, j):L x M ↦ {0,1} where lm(i, j) = 1 if labor type i is assigned to machinery j, and lm(i, j) = 0 otherwise.
Let P = {1, 2, 3…} represent the set of the productive means. Each productive mean is identified by the value of the cost cip, i ∈ P. For the allocation of a productive mean to each production unit the binary function pfc(i,j,k): P x F x C ↦ {0,1} is defined. Each element of the function domain is associated with the value 1 (in the case where the productive mean i is applied to the k crop cultivated in the field j) or 0 (otherwise).
Operation functions
Operational data with regard to information related to field and transport operations, the allocation of machinery to them, and the assignment of these operations to the different production units. In the operations data set, a set of operations is generated, O = {1, 2 , 3,...}. Each operation oi, i ∈ O is characterized by the vector: oi → <{m},{j},{k}, OFi >, that describes the selected “entities” related to the specific operation, where m ∈ T,j ∈ M,k ∈ C,OFi ⊆ {x ∈ F|cf(k,x) = 1}. The input numerical parameters are the operating speed siop,i ∈ O the working width wie,i ∈ O , the number of repetitions (passes) nirep,i ∈ O , the skipped area skiop,i ∈ O (an integer number providing the field-work tracks that are skipped between two sequential track traversals of the machine; zero value corresponds to complete area coverage), the number of the workers/operators committed to the operation Iiop,i ∈ O , and the labor coefficient Icoiop,i ∈ O . The working width that is entered in the operations data set is not necessarily the same as the one in the machinery data set. The former provides the effective working width wei<wthoi<1>,i ∈ O . The pre-stored database, however, provides as default the number of the theoretical working width for various items of equipment.
In the current presentation, for reasons of simplicity, it has been assumed that when an operation is assigned to a specific crop and specific field, the operation relates to all of the area of the field allocated to the cultivation of that crop. Consequently (since aij provides the area of the field i ∈ F that is allocated to crop j ∈ C) in each field the operations is carried out in the area: aj,oi<3>, i ∈ O,i ∈ OFi), the total area subjected to the operation in question is  ).
).
The decision functions involved in the operations include: to( i,j ): T x O ↦ {0,1}, depending on whether tractor i ∈ T is assigned to operation i ∈ O, mo( i,j ): M x O ↦ {0,1} , or if machine i ∈ M is assigned to operation i ∈ O, and ocf( i,j,K ): O x C x F ↦ {0,1} , depending on whether operation j ∈ C is assigned to crop j ∈ C cultivated in field k ∈ F.
Analogously, in the case of field operations, a set of transport operations, H = {1,2,3,...}, is generated, and each transport operation is symbolized as hi, i ∈ H. A transport operation is characterized by a vetor hi → <{m},{j},{c}, HFi> which describes the selected “entities” related to the transport operation, where m ∈ T,j ∈ M,k ∈ C,HFi ⊆ {x ∈ F| cf(k,x) = 1} . The numerical parameters inputted are the transport speed, sitr, i ∈ H, the total quantity, qitr, i ∈ H , the loading/unloading time in the field lui1, i ∈ H, the loading/unloading time in the farm (or plant), lui2, i ∈ H, the number of the workers/operators committed to the transport tasks, litr, i ∈ H , and the labor coefficient lcoitr, i ∈ H .
Analogously, as in the case of field operations the following decision functions are defined: th(i,j): T x O ↦ {0,1}, depending on whether tractor i ∈ T is assigned to transportation operation i ∈ H, mh(i,j): T x O ↦ {0,1} , or if machine i ∈ M is assigned to operation i ∈ H, hcf(i,j,k): O x C x F ↦ {0,1} , or if operation i ∈ H is assigned to crop j ∈ C cultivated in field k ∈ F.
External services and income functions
For this function different types of external services are selected. Let S={1, 2, 3,…} represent the set of potential external services to the production system. For each service type i ∈ S , a cost, cis is assigned. For the allocation of an external service to each production unit the function sfc(i,j,k): s x F x C ↦ {0,1} was defined. Each element of the function domain is associated with the value 1, in cases where the service i is applied to the k crop cultivated in the field j, or 0 otherwise, during the repeated assignment of services to production units as an input to the system. The total area of the production system where an external service i is applied is given by:  .
.
Income can be derived either from product sales or from subsidies for the specific product. For each type of crop a number of sub-products could be cultivated for profit; for example, the grain, the straw, crop residues, etc. Let sPi = {1, 2,…} represent the set of potential products from the cultivation of crop i ∈ C. For each one of the sub-products from each crop the values of the sale price and the subsidy (if any) per unit are inserted into the system, symbolized by cijc and cijc , i ∈ C, i ∈ sPi, respectively. For the allocation of a sale action and the corresponding subsidy for a sub-product of a production unit the following functions are introduced: in1cf(i,j): C x sPi x F ↦ {0,1} and in2cf(i,j): C x sPi x F ↦ {0,1} , respectively, where in1fc(i, j, k) = 1 if the sub-product j of crop i that is cultivated in field k is sold; otherwise 0.
Processes
Operational time
For an operation oi in the cropped area j ∈ OFi the operational time is the summation of the effective time and the turning time: titurn, where
is the time that is allocated to turnings and is a function of the number of turns that a machine has to execute for a given operating width and given field dimensions. The transport time for a transportation operation on hi for the material removal from the cropped area j ∈ HFi can be written as:
It should be noted that for the same crop in different areas allocated it is not necessary to assign the same operations (for example, different farm practices can be followed for the same crop cultivated in different fields). Nevertheless, in the current study, it is assumed that for a specific crop the set of operations are identical for all the fields where this crop has been established (analogously in the case of transport operations). Under this assumption OFi ≡ HFi ≡ {x ∈ F|cf(k,x) =1} .
Variable costs
The variable cost for the execution of an operation includes labor, fuel, and repair and maintenance costs. The labor cost for an operation is estimated based on the assignment of labor type to the machine which carried out the specific operation and the associated hourly cost. For an individual operation oi ∈ O can be written as:
Analogously, the labor cost in the case of a transport operation hi, i ∈ H can be written as:
For the calculation of accumulated repair and maintenance costs, the following equation given by the Agricultural Machinery Management Data ASAE Standard, (ASAE, 2009bAmerican Society of Agricultural Engineers [ASAE]. 2009b. ASAE EP496.3 Agricultural machinery management. p. 354-357. In: ASAE standards. ASAE, St. Joseph, MI, USA.) was used:
where, rmcit is the hourly repair and maintenance cost for typical field operating speeds of the tractor i ∈ T, (€), RF1it and RF2it are repair and maintenance factors (ASAE, 2009aAmerican Society of Agricultural Engineers [ASAE]. 2009a. ASAE D497.6 Agricultural machinery management data. p. 360-367. In: ASAE standards. ASAE, St. Joseph, MI, USA.), and ait is the accumulated use of tractor (h). Analogously the maintenance cost rmcim of a machine i ∈ M is estimated.
The repair and maintenance cost for a field operation oi ∈ O can be written as:
and for a transport operation hi, i ∈ H as:
The fuel cost (fciop, i ∈ O,fcitr, i ∈ H) for an operation oi ∈ O is given by: fciop. tiop, while the fuel cost for a transport operation hi, i ∈ H is given by: fcitr. titr . For fuel consumption estimation, the equation regarding the measure of specific volumetric fuel consumption given at Agricultural Machinery Management Data ASAE Standard (ASAE, 2009aAmerican Society of Agricultural Engineers [ASAE]. 2009a. ASAE D497.6 Agricultural machinery management data. p. 360-367. In: ASAE standards. ASAE, St. Joseph, MI, USA.) was used:
where, Q is the diesel fuel consumption at partial load for operation (l/h), X = P/Prated is the ratio of equivalent power-take-off (PTO) power, P, required by the operation to the rated PTO power, Prated, that is considered as 83 % of the gross fly wheel. The equivalent PTO power is calculated by: P = Pdb /(EmEt)+ Ppto , where Em is the mechanical efficiency of the transmission and power train, typically 0.86 for tractors with gear transmission (this number is used by the system), Et provided by the system’s data base (built upon ASAE (2009a)American Society of Agricultural Engineers [ASAE]. 2009a. ASAE D497.6 Agricultural machinery management data. p. 360-367. In: ASAE standards. ASAE, St. Joseph, MI, USA. clause 3, table provided), Ppto is the PTO power required by the implement (kW), and Pdb the drawbar power required for the implement. The former power requirement is given by Ppto = a + b.w + cf, where a, b, c are machine specific parameters (ASAE (2009a)American Society of Agricultural Engineers [ASAE]. 2009a. ASAE D497.6 Agricultural machinery management data. p. 360-367. In: ASAE standards. ASAE, St. Joseph, MI, USA. Table 2), w the working width, and F → t/h the material feed, while the latter is calculated using: Pdb = D.s/3.6, where the implement draft, D, is computed using a different approach for field and transport operation cases.
Field operations
For the estimation of the implement draft in the case of field operations the following equation (provided in ASABE D497, 2009) was adopted:
A, B, C (machine-specific parameters) are selected from a data base that has been constructed based on Table 1 in ASABE D497 (2009), and de is the tillage depth and is provided by the system data base that gives the suggested tillage depth for each type of operation. , where parameters
, where parameters
Transport operations
For the estimation of the draft requirements in the case of transport operations the following equation provided in ASABE EP496 (2009) was applied: D = Rsc + MR, where Rsc is the soil and crop resistance and MR the total motion resistance. In the transport operations, depending on the direction of travel, both the weight of the full loaded trailer and the weight of the empty trailer are considered. For the out of field transport the hard soil coefficient is considered. The total of implement motion resistance is estimated by: MR = ∑RM, as the summation of each individual wheel supporting the implement which can be assumed as RM = 0.55m where m is the dynamic wheel load and the 0.55 coefficient has been estimated assuming the surface to be concrete (ASABE 497 (2009), Clause 3.2.1.1).
Model outputs
Taking into account all the previously defined functions and processes, the various cost elements can be calculated by the following equation. The total operations cost is given by:
The total service cost is given by:
The total productive means cost is given by:
The total manpower cost is given by:
The total expenses are derived from the summation of the above elements. The margin is estimated by subtracting the total expenses cost from the total product sales and subsidies which are given by:
Results
Case study description
To demonstrate the model’s capability, a case study that refers to a real production system located in the Piedmont region in North Western Italy, is presented. The production system consists of seven (7) fields of which the operational features are presented in Figure 2. The total area of the production system is 91.50 ha (1 ha = 10,000 m2) in which 41 ha are allocated to wheat production and 50.5 ha to maize production. Figure 2 presents a topological configuration of the production system. Note that the field shapes represent a micrograph of the real shapes of the fields. In the specific production system, the storage facility where biomass is transported after harvesting and handling operations is at the farm (on-farm storage of the crop/biomass). The distances of the different fields from the farm have a high variation, a fact that provides a good perception of the influence of the cost for the transportation of resources and the movement of equipment from farm to field, and for the transportation of the crop/biomass form field to farm.
Once the fields and equipment are inserted, the user, in order to complete the field operations, should add the productive means costs. The productive means used by the farmer include: Potassium Chloride 2006; Ammonia Nitrate; Enesco; Logran; Aqua/Water; Urea; Potassium Chloride; Corn-seed hybrid; Mikado; and Ghibli. The current commercial price and the dosage of each individual input are provided from the pre-stored data base.
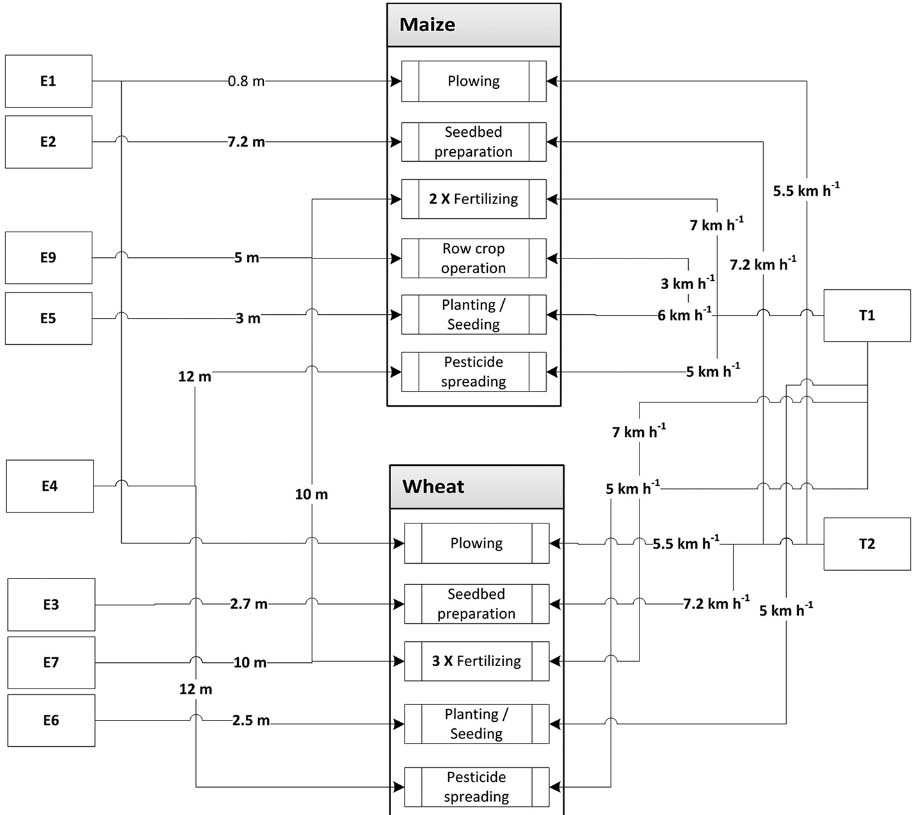
Once the tractors, equipment, and productive means are inserted, the user was able to proceed to enter the field operations and the logistic operation. Figure 3 presents the allocation of the various equipment and tractors to the selected field operations for both maize and wheat crops, as well as the operating width of equipment and the working speed of the tractors. For all of the transport operations (maize crop, wheat grain, and wheat straw) the tractor with the higher power (Tractor 4WD 70 kW) combined with transport trailer equipment was committed to the operation.
Table 2 lists the available tractors and equipment and their purchase price. Note that the user selects each individual machinery item from the graphical user interface and all the related parameters (lifetime, suggested accumulated use, repair and maintenance coefficients, etc.) are provided by the pre-stored data base.
Model implementation
The model allows for breaking down the operation in a way that captures the complexity inherent in a real farm situation. Its functionality allows for each individual field to be selected for specific operations (for the same crop), different rates of input resources (e.g. fertilizer), and also, related to logistic operations, the selection of different delivery locations and distances (farm or processing plant). The output provides results per crop or per single field. All of the results per crop are the weighted average from the data from a single field.
Table 3 presents in detail the average mechanical operation costs per single operation for maize production (cultivated in fields 5, 6, and 7). The three major costs are related to plowing, transport operation, and between-row fertilizing of the crop. Average expenditure for transporting the grain is as expensive as the plowing operation. This is due to the relatively long distances of the three maize fields from the delivery location (5, 10, and 13 km).
Table 4 presents the operation costs for wheat production, referring to fields 1 to 4. In the case of wheat, the logistic operations are on average less costly (34 € ha−1, including the transportation of both grain and straw) since the average distance from the fields is quite small compared to the fields where maize is cultivated.
Table 5 presents the summary of costs and revenues for both maize and wheat production. For maize the profit is 639 € ha−1, the output/input ratio is 1.44 (if we include EU contribution). It means that for each € spent it returned back to the producer 1.44 € in vendible product, including contribution. Operation cost accouts for approximately 13 % of the total cost. The results also provide an average production cost per t of grain which is 111 € t−1 in the specific case. This considerably high production cost stems from the high cost of renting of land (app. 350 € ha−1 according to the prevailing current values in the specific area) which implies 24 % of the production costs.
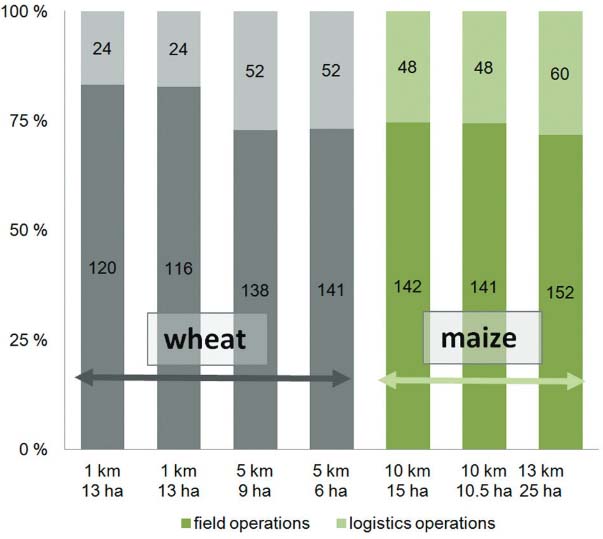
For wheat, the profit is approximately 532 € ha−1 and the output/input ratio about 1.50 (if we include EU contribution). Operational cost accounts for approximately 14 % of the total cost. From Figure 4 we can understand the importance of the cost of logistics and operations. Wheat crops must be collected in the form of two products, grain and straw with a resultant increase in transport costs. In fact, the logistics cost at 5 km (52 € ha−1) is comparable to the logistic cost of maize at 10 km (48 € ha−1). These costs have a significant impact on the total operations cost since they account for between 16 % and 28 % of the total mechanical operations cost, and they are often unknown and not very well evaluated. The slightly less operations cost for field 7 compared to field 6 is due to the longer shape of field 7 since they are located at the same distance from the farm (see Figure 2). Field 7 requires less turning per ha and this implies lower operation time and costs.
The increase of distance also implies an increase in the field operations cost, because the operations include transfer of equipment from field to farm as well, and this extra cost is a function of the field distance from the farm.
Finally, a sensitivity analysis was carried out to investigate the variability of critical output parameters, i.e. transport cost, operations cost, and profit, against the variability of the yield. As can be seen in Figure 5, operations cost is the least sensitive to yield variations, and transport cost varies almost analogously to variations in yield, while the profit presents high variations in yield changes. The increased sensitivity of profit is reasonable since the yield directly and linearly affects sales income.
− Transport cost, operations cost, and profit changes due to yield variations for wheat and maize production.
In order to investigate further the effect of sales income and specifically of the sale price on profit, which is inherently the most important output parameter from the farmer’s perspective, the change in profit with changes in the sales price has also been investigated in the basis production scenario. Specifically, if the sales price is reduced by 10 % from the one considered in the basis scenario, profit will be reduced by 19 % for wheat production (431.1 €) and by 20 % for maize production (508.5 €), and if the sales price increased by 10 % from the one considered in the basis scenario the profit will be increased by 19 % in the case of wheat production (633.1 €) and by 31 % in the case of maize production (833.5 €).
Discussion
A model for the cost prediction of in-field and transport operations for multiple-fields and multiple-crop production systems was presented and demonstrated in a real production system scenario. It was shown that the proposed model can deal with variability, in terms of input parameter values, in the production of a typical farm and provide cost predictions for complex cropping systems where labor and machinery are shared between the various operations that the farm manager plans for each individual crop. By so doing, the model can be used as a decision support system at the strategic level of agricultural production systems and specifically for the mid-term design process of the system in terms of labor/machinery and crop selection according to the criterion of profit.
This detailed analysis of cost allows for the consideration of the sensitivity of the model. Any change in parameters, e.g. working speed, field distance, field shape etc., can be seen in the results, both at farm level, crop level, or at a single field level. The incidence of logistics operation, often unknown, range from 16 % for fields nearby up to 28 % for fields more distanced from the farm. This is a very important consideration where an expansion of farm activities implies renting of new plots, and could lead to better rental agreement if the owner of the land knows the magnitude of the influence of the distance on revenues.
In Figure 4 it can be seen that for the same crop and the same field distance, a different operational cost is the result. This occurs due to the differentiation of the field shapes and areas. Although the inclusion of the field shape is rather simple in the model presented (through the consideration of only rectangular fields) there is still an effect on the results derived regarding the cost of the field operations (and consequently the total cost and profit). The inclusion of complex sub-models that take into account the shape of the field independent of its geometrical complexity, the operations plan, i.e. coverage pattern (Bochtis et al., 2013), and the in-field obstacles (e.g. Zhou et al., 2014Zhou, K.; Jensen, A.L.; Sørensen, C.G.; Busato, P.; Bochtis, D.D. 2014. Agricultural operations planning in fields with multiple obstacle areas. Computer and Electronics in Agriculture 109: 12-22.) will provide an in-depth re-presentation of the actual task times elements and consequently a more accurate estimation of the in-field operations cost contribution.
As regards the model itself, the mathematical description was oriented towards the building of a number of binary decision variables, including:
cf (i, j) : C × F ↦ {0,1} for the allocation of a crop to a field
lm(i, j) : L × M ↦ {0,1} for the allocation of a labor type to an operation
pfc(i, j,k) : P × F × C ↦ {0,1} for the allocation of a productive mean to a crop to a field
sfc(i, j,k) : S × F × C ↦ {0,1 }for the allocation of a service in a crop in a field
to(i, j,k) : T × O ↦ {0,1} for the allocation of a tractor to a field operation
mo(i, j) : M × O ↦ {0,1} for the allocation of an item of equipment to a field operation
the analogous previous two in the case of transport operations
ocf (i, j,k) :O × C × F ↦ {0,1} for the allocation of an operation to a crop.
This model development approach, in combination with the use of an engineering programming environment, provides the potential for the inclusion of numerous binary programming optimization models (e.g. which crops are allocated to which fields, which machinery is allocated to which operations, which production means are allocated to which crop, etc.) either according to single-criterion or multiple-criteria goals. Furthermore, the pre-stored data bases provided to the user in connection with the graphical user interface provide the potential for a web-based decision support tool. All of the above require further research in the direction of the work presented in this study.
References
- American Society of Agricultural Engineers [ASAE]. 2009a. ASAE D497.6 Agricultural machinery management data. p. 360-367. In: ASAE standards. ASAE, St. Joseph, MI, USA.
- American Society of Agricultural Engineers [ASAE]. 2009b. ASAE EP496.3 Agricultural machinery management. p. 354-357. In: ASAE standards. ASAE, St. Joseph, MI, USA.
- Berruto, R.; Maier, D.E. 2001. Analyzing the receiving operation of different grain types in a single-pit country elevator. Transactions of the ASAE 44: 631-8.
- Bochtis, D.D.; Sørensen, C.G. 2009. The vehicle routing problem in field logistics part I. Biosystems Engineering 104: 447–457.
- Bochtis, D.D.; Sørensen, C.G.; Busato, P. 2014. Advances in agricultural machinery management: a review. Biosystems Engineering 126: 69-81.
- Bochtis, D.D.; Dogoulis. P.; Busato, P.; Sørensen, C.G.; Berruto, R.; Gemtos, T. 2013a. A flow-shop problem formulation of biomass handling operations scheduling. Computers and Electronics in Agriculture 91: 49-56.
- Bochtis, D.D.; Sørensen, C.G.; Busato, P.; Berruto, R. 2013b. Benefits from optimal route planning based on B-patterns. Biosystems Engineering 115: 389-395.
- Busato, P. 2015. A simulation model for a rice-harvesting chain. Biosystems Engineering 129: 149-159.
- Busato, P.; Berruto, R. 2014. A web-based tool for biomass production systems. Biosystems Engineering 120: 102-116.
- Busato, P.; Sørensen, C.G.; Pavlou, D.; Bochtis D.D.; Berruto, R.; Orfanou A. 2013. DSS tool for the implementation and operation of an umbilical system applying organic fertilizer. Biosystems Engineering 114: 9-20.
- Kaloxylos, A.; Groumas, A.; Sarris, V.; Katsikas, L.; Magdalinos, P.; Antoniou, E.; Politopoulou, Z.; Wolfert, S.; Brewster, C.; Eigenmann, R.; Terol, C.M. 2014. A cloud-based farm management system: architecture and implementation. Computers and Electronics in Agriculture 100: 168-179.
- Orfanou, A.; Busato, P.; Bochtis, D.D.; Edwards, G.; Pavlou, D.; Sørensen, C.G.; Berruto R. 2013. Scheduling for machinery fleets in biomass multiple-field operations. Computers and Electronics in Agriculture 94: 12-19.
- Sahu, R.; Raheman, H. 2008. A decision support system on matching and field performance prediction of tractor implement system. Computers and Electronics in Agriculture 60: 76-86.
- Søgaard, H.; Sørensen, C. 2004. A model for optimal selection of machinery sizes within the farm machinery system. Biosystems Engineering 89: 13-28.
- Sørensen, C.G.; Bochtis, D.D. 2010. Conceptual model of fleet management in agriculture. Biosystems Engineering 105: 41-50.
- Sørensen, C.G.; Pesonen, P.; Fountas, S.; Suomi, P.; Bochtis, D.D.; Pedersen, S.M. 2010. A user-centric approach for information modelling in arable farming. Computers and Electronics in Agriculture 73: 44-55.
- Tatsiopoulos, I.P.; Tolis, A.J. 2003. Economic aspects of the cotton-stalk biomass logistics and comparison of supply chain methods. Biomass and Bioenergy 24: 199-214.
- Zhou, K.; Jensen, A.L.; Sørensen, C.G.; Busato, P.; Bochtis, D.D. 2014. Agricultural operations planning in fields with multiple obstacle areas. Computer and Electronics in Agriculture 109: 12-22.
Edited by
Publication Dates
-
Publication in this collection
Sep-Oct 2016
History
-
Received
29 July 2015 -
Accepted
13 Nov 2015