ABSTRACT:
Artificial neural networks (ANN) are computational models inspired by the neural systems of living beings capable of learning from examples and using them to solve problems such as non-linear prediction, and pattern recognition, in addition to several other applications. In this study, ANN were used to predict the value of the area under the disease progress curve (AUDPC) for the tomato late blight pathosystem. The AUDPC is widely used by epidemiologic studies of polycyclic diseases, especially those regarding quantitative resistance of genotypes. However, a series of six evaluations over time is necessary to obtain the final area value for this pathosystem. This study aimed to investigate the utilization of ANN to construct an AUDPC in the tomato late blight pathosystem, using a reduced number of severity evaluations. For this, four independent experiments were performed giving a total of 1836 plants infected with Phytophthora infestans pathogen. They were assessed every three days, comprised six opportunities and AUDPC calculations were performed by the conventional method. After the ANN were created it was possible to predict the AUDPC with correlations of 0.97 and 0.84 when compared to conventional methods, using 50 % and 67 % of the genotype evaluations, respectively. When using the ANN created in an experiment to predict the AUDPC of the other experiments the average correlation was 0.94, with two evaluations, 0.96, with three evaluations, between the predicted values of the ANN and they were observed in six evaluations. We present in this study a new paradigm for the use of AUDPC information in tomato experiments faced with P. infestans. This new proposed paradigm might be adapted to different pathosystems.
Keywords:
Phytophthora infestans; ANN; AUDPC; artificial intelligence; plant breeding
Introduction
Tomato late blight, caused by Phytophthora infestans (Mont.) de Bary, can cause complete loss if it is not properly controlled, and has been considered one of the most devastating tomato diseases worldwide (Irzhansky and Cohen, 2006Irzhansky, I.; Cohen, Y. 2006. Inheritance of resistance against Phytophthora infestans in Lycopersicon pimpinellifolium L3707. Euphytica 149: 309–316.). Nowicki et al. (2012)Nowicki, M.; Foolad, M.R.; Nowakowska, M.; Kozik, E.U. 2012. Potato and tomato late blight caused by Phytophthora infestans: an overview of pathology and resistance breeding. Plant Disease 96: 4–17. reported yield losses of up to 100 % caused by the pathogen. Genetic resistance is considered the most efficient method for controling plant pathogens, since it reduces production costs, facilitates disease management, and does not have the impacts produced by fungicides.
The area under the disease progress curve (AUDPC) is a valuable tool for measuring harvest losses due to pathogen attack (Ferrandino and Elmer, 1992Ferrandino, F.J.; Elmer, W.H. 1992. Reduction in tomato yield due to Septoria leaf spot. Plant Disease 76: 208–211.) and in epidemiological studies of polycyclic diseases, especially those regarding quantitative resistance studies (Jeger and Viljanen-Rollinson, 2001Jeger, M.; Viljanen-Rollinson, S. 2001. The use of the area under the disease-progress curve (AUDPC) to assess quantitative disease resistance in crop cultivars. Theoretical and Applied Genetics 102: 32–40.). The conventional estimator of AUDPC is the equation developed by Shaner and Finney (1977)Shaner, G.; Finney, R. 1977. The effect of nitrogen fertilization on the expression of slow-mildewing resistance in Knox wheat. Phytopathology 67: 1051–1056., which considers the information of multiple severity evaluations, and yields a single value.
Jeger and Viljanen-Rollinson (2001)Jeger, M.; Viljanen-Rollinson, S. 2001. The use of the area under the disease-progress curve (AUDPC) to assess quantitative disease resistance in crop cultivars. Theoretical and Applied Genetics 102: 32–40. proposed a method for calculating the AUDPC with only two evaluations for the wheat pathosystem – Puccinia striiformis f. sp. tritici, which was later validated by Mukherjee et al. (2010)Mukherjee, A.K.; Mohapatra, N.K.; Nayak, P. 2010. Estimation of area under the disease progress curves in a rice-blast pathosystem from two data points. European Journal of Plant Pathology 127: 33–39. for the rice pathosystem – Pyricularia grisea. Nonetheless, Jeger and Viljanen-Rollinson (2001)Jeger, M.; Viljanen-Rollinson, S. 2001. The use of the area under the disease-progress curve (AUDPC) to assess quantitative disease resistance in crop cultivars. Theoretical and Applied Genetics 102: 32–40. reinforce that the methodology has three assumptions that should be satisfied: first, the resistance must be expressed as the disease rate and not as the absence of symptoms; second, the disease evaluated has to be present in all plants during the same timeframe; and third, the disease progress has to be continuous. These assumptions make the application of this method to the tomato pathosystem difficult - Phytophthora infestans. Thus, the artificial neural network (ANN) methodology stands out because it is based on machine learning, regardless of the model, with wide application in agricultural sciences.
ANN are defined as non-algorithmic computations characterized by systems that, at a certain level, resemble the structure of the human brain (Braga et al., 2000Braga, A.D.P.; Carvalho, A.P.L.F.; Ludermir, T.B. 2000. Artificial Neural Networks: Theory and Applications = Redes Neurais Artificiais: Teoria e Aplicações. Livros Técnicos e Científicos, Rio de Janeiro, RJ, Brazil. (in Portuguese).). In practice, they constitute data modeling tools (Goyal, 2013Goyal, S. 2013. Artificial neural networks in vegetables: a comprehensive review. Scientific Journal of Crop Science 2: 75–94.). This methodology has been widely used in agriculture, and it can go beyond human capacity to evaluate large data banks and relate them to a specific desirable characteristic. ANN have been used in simulation studies to predict genetic values (Silva et al., 2014Silva, G.N.; Tomaz, R.S.; Castro, I.S.; Nascimento, M.; Bhering, L.L. 2014. Neural networks for predicting breeding values and genetic gains. Scientia Agricola 71: 494–498.; Peixoto et al., 2015Peixoto, L.A.; Bhering, L.L.; Cruz, C.D. 2015. Artificial neural networks reveal efficiency in genetic value prediction. Genetics and Molecular Research 14: 6796–6807.), and in association with genomic analysis (Gianola et al., 2011Gianola, D.; Okut, H.; Weigel, K.A.; Rosa, G.J. 2011. Predicting complex quantitative traits with Bayesian neural networks: a case study with Jersey cows and wheat. BMC Genetics 12: 87.; Ehret et al., 2015Ehret, A.; Hochstuhl, D.; Gianola, D.; Thaller, G. 2015. Application of neural networks with back-propagation to genome-enabled prediction of complex traits in Holstein-Friesian and German Fleckvieh cattle. Genetics Selection Evolution 47: 22.).
This study aimed to investigate the prediction capacity of ANN to obtain AUDPC values for tomato late blight using a lower number of evaluations to improve the process efficiency.
Materials and Methods
Plant material, inoculation, and assessment
Experiments were performed in Viçosa, MG-Brazil (20°45′14″ S and 42°52′53″ W, altitude of 648.74 m). According to Köppen's classification, the climate is Cwa, average relative humidity of 80 %, average yearly maximum and minimum temperatures of 26.4 and 14.8 °C, respectively, and average yearly rainfall of 1.221.4 mm. Late-blight resistance was assessed in 192 tomato (Solanum lycopersicum) accessions (Table 1) from the Germplasm Bank of the Universidade Federal de Viçosa (BGH-UFV) in the field.
Area under the disease-progress curve (AUDPC) averages for one hundred and ninety tomato accessions, assessed for late-blight caused by Phytophythora infestans in four independent experiments.
Accessions were evaluated in four experiments in a randomized block design with three replications and three plants per plot. Experiment 1 was performed from Jan to May 2009, consisting of 53 accessions; Experiment 2 from Apr to Aug 2009, consisting of 47 accessions; Experiment 3 from Feb to May 2010, consisting of 52 accessions; and Experiment 4, from Mar to July 2010, with 52 accessions (Table 1). The cultivars Santa Clara, Deborah, and Fanny were adopted as a susceptibility pattern in each experiment.
Plants were inoculated with a mix of sporangia originating from different P. infestans strains collected from different regions of Brazil, 45 days after planting, according to Abreu et al. (2008)Abreu, F.B.; Silva, D.J.H.; Cruz, C.D.; Mizubuti, E.S.G. 2008. Inheritance of resistance to Phytophthora infestans (Peronosporales, Pythiaceae) in a new source of resistance in tomato (Solanum sp. (formely Lycopersicon sp.) Solanales, Solanaceae). Genetics and Molecular Biology 31: 493–497.. Disease severity evaluations were made following the diagrammatic scale proposed by Corrêa et al. (2009)Corrêa, F.M.; Bueno Filho, J.S.S.; Carmo, M.G.F. 2009. Comparison of three diagrammatic keys for the quantification of late blight in tomato leaves. Plant Pathology 58: 1128–1133., and were started 3 days after inoculation at regular intervals of 3 days, totaling five evaluations (day 3, 6, 9, 12 and 15 after inoculation, DAI – evaluations 1 to 5) for experiment 1 and six evaluations (3, 6, 9, 12, 15 and 18 DAI – evaluations 1 to 6) for the other experiments. The percentage of damaged leaf area was measured by visual evaluation. The following evaluations were used for the area under the disease progress curve (AUDPC) calculation, according to the methodology proposed by Shaner and Finney (1977)Shaner, G.; Finney, R. 1977. The effect of nitrogen fertilization on the expression of slow-mildewing resistance in Knox wheat. Phytopathology 67: 1051–1056., using the following equation: yi and yi +1 correspond to the percentage of damaged leaf area observed in the evaluations i and (i+1); ti and ti + 1 are the time considered in days i and (i + 1); and n is the total number of evaluations. , where:
, where:
Phenotypic data analysis
Variance analysis was performed using the GENES computer application (Cruz, 2013Cruz, C.D. 2013. Genes: a software package for analysis in experimental statistics and quantitative genetics. Acta Scientiarum Agronomy 35: 271–276.), which considers the AUDPC estimates. Scott and Knott (p < 0.05) clustering was used for mean grouping and definition of genotype groups, where those that showed lower means were considered representative groups of the most resistant genotypes.
ANN construction and statistical analysis
We considered an ANN Multilayer Perceptron (MLP) having an input layer with one to three neurons for experiment 1; and one to four neurons for experiments 2, 3, and 4; a hidden layer with two to 16 neurons iteratively established; and a single neuron output layer. The ANN were generated using the MATLAB® software (MATLAB, 2010) through the integration module script of the GENES computer application (Cruz, 2013Cruz, C.D. 2013. Genes: a software package for analysis in experimental statistics and quantitative genetics. Acta Scientiarum Agronomy 35: 271–276.). Training algorithm trainlm and 1000 timings were used for ANN training. Logistic sigmoid activation and hyperbolic tangent functions were considered in the hidden neuron layer.
ANN input consisted of severity evaluations, measured as a percentage of damaged leaf area. As input values, all 14 possible evaluation combinations were considered for experiment 1 (Table 2), and 30 possible combinations for the other experiments (Table 2). For each evaluation combination, the ANN were deployed five times. Genotypes used during the training process were randomly taken in each experiment, as well as replications used for training. One thousand three hundred and twenty ANN architectures were assessed, considering the number of neurons, the hidden layer activation functions, and the number of evaluations in the input layer. Evaluations were made as a sample of a random variable X, transformed into a random variable Z, by the equation: Zi =(X1 + (Xi − Max) (X1 − X0)) / (Max − Min); where the Max corresponds to the maximum of Xi; Min, to the minimum of Xi; X0 and X1, to the minimum and maximum of Zi, respectively, established as being zero and one. ANN input and output pairs were randomly applied to the training process. Two criteria were used for ANN stop, a minimum mean squared error (MSE) of 10−10 or a maximum of 1000 training timings. = 30), vide
= 30), vide  , see
, see
Average correlation for training and validation using different severity evaluation combinations. Training and validation were performed with four and five plants, respectively, using the same accession.
The ANN values predicted during validation were back-transformed into the random variable X in order to recover actual values and for further comparisons. Correlation between estimated AUDPC and predicted ANN values was used to define the best evaluated combinations for estimating the AUDPC (Shaner and Finney, 1977Shaner, G.; Finney, R. 1977. The effect of nitrogen fertilization on the expression of slow-mildewing resistance in Knox wheat. Phytopathology 67: 1051–1056.).
Thereafter, the evaluations (or measurements) that provided the best AUDPC predictions in all experiments were used in 100 new analyses, generating new AUDPC values predicted by ANN. Then, Scott-Knott clustering was performed, at 5 % probability, for comparison of grouped results obtained from conventionally calculated. AUDPC.
Three scenarios (1, 2 and 3) were considered. The first scenario consisted of utilizing severity assessment of all genotypes, considering all evaluations and four plants per genotype during the training stage, the validation being performed on the five plants remaining. This scenario aimed to generate information that would allow inferring ANN capacity to train and predict the AUDPC with the data available. In the second scenario, all genotypes were considered during the training stage. Four plants per genotype were taken for training and the five remaining for the validation process, considering all evaluation combinations. Such procedures aimed to create information able to measure ANN capacity to establish an optimum evaluation number for AUDPC prediction. In the third scenario, the replicates of 70 % of the genotypes were taken at the training stage and the genotypes remaining for validation processing, also considering all evaluation combinations. This last scenario aimed to create information capable of establishing an optimum number of measurements and to evaluate network capability to extrapolate a learning curve for different genotypes.
Analyses were performed using the GENES software (Cruz, 2013Cruz, C.D. 2013. Genes: a software package for analysis in experimental statistics and quantitative genetics. Acta Scientiarum Agronomy 35: 271–276.) and R Core team. ANN was performed with MATLAB® (Matrix Laboratory, version 7.10) using a script presented in the integration module of the GENES computer application (Cruz, 2013Cruz, C.D. 2013. Genes: a software package for analysis in experimental statistics and quantitative genetics. Acta Scientiarum Agronomy 35: 271–276.).
Data extrapolation
The implemented ANN with the best results in their respective experiments were considered for AUDPC prediction in all experiments, i.e., for the experiments for which they were trained and for those they were not trained. Only ANN that used two to three inputs were considered.
Results and Discussion
Five evaluations were performed for phenotypic analysis in experiment 1, since, due to the fast progression of disease, severity reached the plateau between the fourth and fifth evaluation. For the other experiments, six evaluations were performed. Accessions were sorted into groups using Scott-Knott clustering, according to the AUDPC. The groups with comparatively lower AUDPC values versus groups which had a susceptibility pattern were considered a possible source of resistance. Therefore, groups “c” and “d” of Experiment 1, group “b” of Experiment 2, groups “c” and “d” of Experiment 3, and group “b” of Experiment 4 (Table 1) were considered potential sources of resistance to late blight because they showed lower severity than the susceptibility pattern groups.
Using ANN to analyze the data in scenario 1 to evaluate tomato - P. Infestans pathosystem, resulted in expectations being met and were very efficient. ANN construction in this scenario provided a correlation coefficient (r2) similar to that observed in the training (Figure 1A) and validation (Figure 1B) stages, showing ANN capacity to predict the AUDPC, regardless of the model. Average quadratic error reached acceptable levels at both stages (9.4183.10−7 and 3.067.10−5, respectively). The best ANN had two neurons in the hidden layer, using the logistic sigmoid activation function. Several authors (Goyal, 2013Goyal, S. 2013. Artificial neural networks in vegetables: a comprehensive review. Scientific Journal of Crop Science 2: 75–94.) have reported the efficiency of neural networks in studies in terms of classification, prediction, and mainly in model adjustment, which was the case in the present study.
Area under the disease-progress curve (AUDPC) estimates - transformed data - of the genotypes considered during training (A) and validation (B) for scenario 1. (×) corresponds to estimates calculated according to Shaner and Finney (1977)Shaner, G.; Finney, R. 1977. The effect of nitrogen fertilization on the expression of slow-mildewing resistance in Knox wheat. Phytopathology 67: 1051–1056. and () the artificial neural networks predicted values.
For scenario 2, which aimed at establishing a minimum optimum number of evaluations (measurements) to predict the AUDPC, it was demonstrated that ANN are an efficient and appropriate tool for identifying with the lower number of evaluations during training and validation using the same set of genotypes. Results of the average correlation coefficient (Table 2. Using the fourth and fifth evaluation provided an ( ) between AUDPC values and ANN predicted values during training and validation stages are presented in
) between AUDPC values and ANN predicted values during training and validation stages are presented in  ), during the network validation stage, greater than 84 % for Experiment 1, and greater than 93 % for the remaining experiments. In this case, three neurons were usually enough for the prediction process, regardless of the activation function. Considering the third, fourth and fifth evaluation, the (
), during the network validation stage, greater than 84 % for Experiment 1, and greater than 93 % for the remaining experiments. In this case, three neurons were usually enough for the prediction process, regardless of the activation function. Considering the third, fourth and fifth evaluation, the ( ) exceeded 96 %, using four neurons in the hidden layer, where the logistic sigmoid activation function showed the best results. Results of this scenario imply the realization of a full evaluation in a reduced number of plants per genotype followed by a reduced number of evaluations in the plants to be predicted by ANN.
) exceeded 96 %, using four neurons in the hidden layer, where the logistic sigmoid activation function showed the best results. Results of this scenario imply the realization of a full evaluation in a reduced number of plants per genotype followed by a reduced number of evaluations in the plants to be predicted by ANN.
ANN were effective in predicting the AUDPC using a lower number of evaluations to validate non trained genotypes in scenario 3, demonstrating their capacity to predict and extrapolate values. This implies using ANN to predict AUDPC without being necessarily trained for a given group of genotypes, since previous ANN training has been performed under the conditions of the current experiment, or that it does not have outstanding peculiarities when compared to the experiments for which ANN was trained. Considering only the fourth and fifth evaluation, the ANN was capable of predicting AUDPC with an (Table 3. The ANN constructed showed architecture similar to the previous cases. ) greater than 87 % in all experiments. AUDPC values predicted by ANN showed an (
) greater than 87 % in all experiments. AUDPC values predicted by ANN showed an ( ) greater than 93 % when using the third, fourth and fifth evaluations. Results are shown in
) greater than 93 % when using the third, fourth and fifth evaluations. Results are shown in
Average correlations for training and validation using different combinations of severity evaluations. Training was used in 70 % of the accessions and validation in the other 30 % for each experiment.
Grouping of the prediction averages performed by ANN were very similar, sometimes equal, to that formed through the conventional method (Table 4). Even though in both cases, AUDPC averages were very similar, sometimes genotype classification had changed, but this change was not an obstacle to the selection of sources of resistance.
Accession grouping according to Scott-Knott clustering, comparing area under the disease-progress curve (AUDPC) averages conventionally calculated, with six evaluations, and by artificial neural networks (ANN), with three evaluations (A) - 3rd, 4th and 5th - and two evaluations (B) - 4th and 5th.
Potential ANN candidates were selected in scenario 3 where the extrapolation capacity was confirmed. The ANN were considered using two evaluations - the fourth and fifth – and then three evaluations – the third, fourth and fifth. Results were promising and are shown in Table 5. The ( )results between AUDPC and ANN predicted values, of an ANN trained to one experiment predicting the others considering two and three evaluations, exceeded 91 and 95 %, respectively.
)results between AUDPC and ANN predicted values, of an ANN trained to one experiment predicting the others considering two and three evaluations, exceeded 91 and 95 %, respectively.
Average correlations between predicted values by artificial neural networks (ANN) and conventional calculation according to Shaner and Finney (1977)Shaner, G.; Finney, R. 1977. The effect of nitrogen fertilization on the expression of slow-mildewing resistance in Knox wheat. Phytopathology 67: 1051–1056.. The ANN used in each case predicted the area under the disease-progress curve of all plants from the other experiments.
Research concerning artificial intelligence has been showing remarkable advances since 1980's, reflecting the practical use of ANN (Ding et al., 2013Ding, S.; Li, H.; Su, C.; Yu, J.; Jin, F. 2013. Evolutionary artificial neural networks: a review. Artificial Intelligence Review 39: 251–260.). The capacity of learning from a set of examples and of accurately predicting desired responses has made possible an incremented ANN use in agricultural sciences as well as making valuable studies available for researchers in this field of study (Goyal, 2013Goyal, S. 2013. Artificial neural networks in vegetables: a comprehensive review. Scientific Journal of Crop Science 2: 75–94.). With respect to plant disease evaluations, the ANN have been used in image processing, as a means of evaluating disease severity, thus reducing the subjectivity of evaluation (Patil and Kumar, 2011Patil, J.K.; Kumar, R. 2011. Advances in image processing for detection of plant diseases. Journal of Advanced Bioinformatics Applications and Research 2: 135–141.; Tiger and Verma, 2013Tiger, B.; Verma, T. 2013. Identification and classification of normal and infected apples using neural network. International Journal of Science and Research 2: 160–160.).
Considering that disease evaluation represents a significant investment in time, space, human and economic resources, the use of an efficient methodology to evaluate disease progress that saves resources is highly desirable. The AUDPC measurement of quantitative resistance evaluation for polycyclic pathogens, resulting from calculations from periodic evaluations, is extremely common and necessary, such as in the present study. In this sense, ANN utilization represents an interesting alternative, since it has allowed for the selection of putative sources of resistance with a reduced number of evaluations. Also, according to Mukherjee et al. (2010)Mukherjee, A.K.; Mohapatra, N.K.; Nayak, P. 2010. Estimation of area under the disease progress curves in a rice-blast pathosystem from two data points. European Journal of Plant Pathology 127: 33–39., when evaluations are frequent during the outbreak they can inadvertently affect disease progress, given anthropic interference.
This new paradigm could save land, fertilizers, water, supplies for training and management of tomato fields, besides the human resources that are necessary for maintenance of the experiments. The application of this approach is highly practical for the evaluation of experiments regardless of the model, still considering that factors like unbalancing are not a great problem. Therefore, ANN could improve the efficiency of the screening process of sources of resistance.
ANN also ensures the researcher, considering the tomato × late-blight pathosystem, uses all conventional evaluations in only a few replicates of the experiment to train the ANN and later to estimate AUDPC for the other replicates of each genotype. This would imply a 0.97 correlation between estimated value, using three evaluations as input, at nine, twelve and fifteen dpi; and that would be obtained with six evaluations, or by performing the evaluations only at 12 and 15 days, and have a 0.87 correlation. At first, the practical use of this method could seem unviable regarding its practicability, since the researcher would have to efficiently separate the plants to be evaluated in all measurements from the plants to be evaluated more often; however, the use of ANN shows great potential for overcoming this.
ANN also proved to be efficient in AUDPC prediction of non-trained genotypes. AUDPC values predicted by the network are very close to those obtained using conventional calculation, and the classification of genotype groups also proved to be very similar or even identical in some cases (Table 4). Sometimes there was little change in the groups; however, it was observed that this was due to the insertion or exclusion of one or a few genotypes in a certain group, which alters the groups of the other genotypes. Nevertheless, this is not a problem to selecting sources of resistance, since the separation of genotypes with lower AUDPC continues to occur. Thus, the selection of sources of resistance using AUDPC predicted by ANN is promising, since even with the changes in genotype groups, ANN was efficient in distinguishing genotypes which showed lower severity averages. Apparently, the practical application of the strategy utilized in this scenario is difficult, because the researcher would have to evaluate 70 % of the plants during the measurement period (six measurements or evaluations), and only with the remaining is it possible to estimate AUDPC with a lower number of replicates. Notwithstanding, it is important to highlight the network capacity for extrapolating its learning for another group of accessions, and is, thus, effective in a broader approach.
ANN extrapolation that was generated from an experiment and test for the others proved to be very effective in reflecting the conventional calculation (Table 5), making it the use of neural networks for this purpose unquestionable. This demonstrates the importance of maintaining databases which have, for example, measurements of disease severity, AUDPC, among others, so that in the near future it would be possible to implement an evaluation program using ANN, and take advantage of all potentialities of this tool. We have demonstrated in this study that even when using a limited dataset, it was possible to estimate the AUDPC of experiments performed in different micro-sites and in different time frames. Thus, it was possible, for example, using severity data and the AUDPC of Experiment 1 (performed under atypical in Jan 2009), to infer about the AUDPC of accessions of Experiment 4 (installed after 10 months) with a correlation greater than 96 % using a reduced number of evaluations.
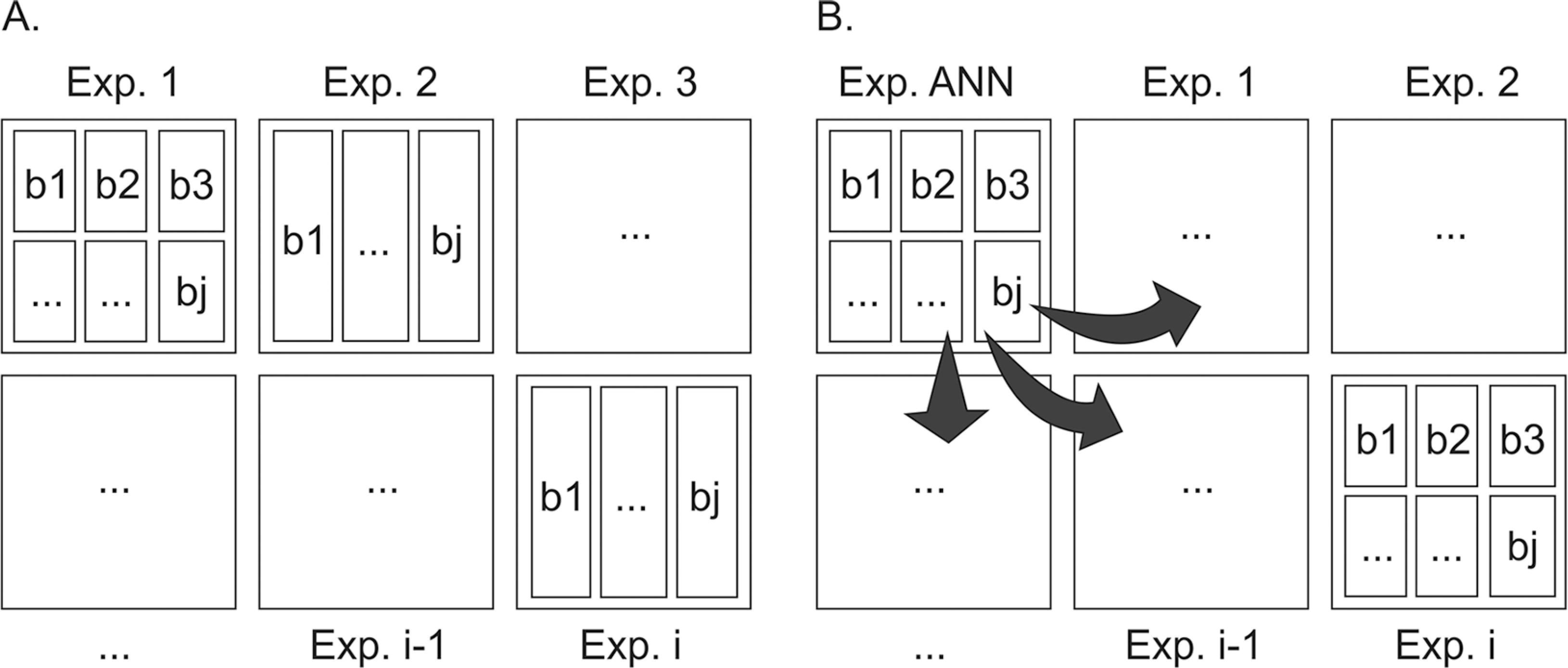
It is important to emphasize that the application of structured networks in the present study of AUDPC prediction in other experiments, should be recommended with reservation, since database availability for ANN training is limited. Also, as previously reported, the practical use of the strategies presented in scenario 1, 2 and 3, such as they were assessed, is also quite limited because it requires evaluations of samples from both plants and accessions to be applied. For this reason, the practical use of ANN in the routine work of a breeding program essentially necessitates a change in the current disease evaluation system paradigm (Figure 2A), even for tomato × P. infestans pathosystem. The new proposed paradigm (Figure 2B) presents a practical course of action which is based on planting representative accessions in a fraction of the experimental field (considering experimentation principles). These will serve as a basis for conventional evaluation and following ANN training along with historical data, are to be used in experiment prediction in the remaining experimental area, a contemporary of the ANN. In this, a reduced number of evaluations should be performed. Finally, we would like to emphasize that accumulating information in databases to be used in network training upgrading is necessary and should be routine practice in breeding programs.
Change in the paradigm of disease-progress evaluation in tomato. A) Current paradigm, in which i evaluations are performed in individual experiments, separated in space and time. B) New paradigm, where an experiment is undertaken for artificial neural networks (ANN) prediction/update, using representative genotypes of the other contemporary experiments separated in space; and using historical data with genotypes separated in time and exposed to different environmental conditions. The predicted ANN should be able to efficiently predict the contemporary experiments where only relevant measurements were performed.
In this way, with the aim of screening the resistant accessions we recommend the application of this new paradigm and the performing of only two to three evaluations at 12 and 15 or at 9, 12 and 15 days after inoculation, respectively, followed by prediction using ANN.
Moreover, ANN could be used for AUDPC prediction following the principles of other methods. Simko and Piepho (2012)Simko, I.; Piepho, H.P. 2012. The area under the disease progress stairs: calculation, advantage, and application. Phytopathology 102: 381–389. proposed a series of evaluations for the AUDPC calculation, where different weights are attributed to the first and last evaluations, which are often penalized in other evaluation systems. ANN could, for example, be trained with the first, the last, and a reduced series of intermediate evaluations, and still allow for the AUDPC to be obtained, and reduce either costs or time.
Acknowledgements
To CAPES - Coordination for the Improvement of Higher Level Personnel, FAPEMIG - Minas Gerais State Foundation for Research Support and CNPq - Brazilian National Council for Scientific and Technological Development, for financial support and scholarships granted.
References
- Abreu, F.B.; Silva, D.J.H.; Cruz, C.D.; Mizubuti, E.S.G. 2008. Inheritance of resistance to Phytophthora infestans (Peronosporales, Pythiaceae) in a new source of resistance in tomato (Solanum sp. (formely Lycopersicon sp.) Solanales, Solanaceae). Genetics and Molecular Biology 31: 493–497.
- Braga, A.D.P.; Carvalho, A.P.L.F.; Ludermir, T.B. 2000. Artificial Neural Networks: Theory and Applications = Redes Neurais Artificiais: Teoria e Aplicações. Livros Técnicos e Científicos, Rio de Janeiro, RJ, Brazil. (in Portuguese).
- Corrêa, F.M.; Bueno Filho, J.S.S.; Carmo, M.G.F. 2009. Comparison of three diagrammatic keys for the quantification of late blight in tomato leaves. Plant Pathology 58: 1128–1133.
- Cruz, C.D. 2013. Genes: a software package for analysis in experimental statistics and quantitative genetics. Acta Scientiarum Agronomy 35: 271–276.
- Ding, S.; Li, H.; Su, C.; Yu, J.; Jin, F. 2013. Evolutionary artificial neural networks: a review. Artificial Intelligence Review 39: 251–260.
- Ehret, A.; Hochstuhl, D.; Gianola, D.; Thaller, G. 2015. Application of neural networks with back-propagation to genome-enabled prediction of complex traits in Holstein-Friesian and German Fleckvieh cattle. Genetics Selection Evolution 47: 22.
- Ferrandino, F.J.; Elmer, W.H. 1992. Reduction in tomato yield due to Septoria leaf spot. Plant Disease 76: 208–211.
- Gianola, D.; Okut, H.; Weigel, K.A.; Rosa, G.J. 2011. Predicting complex quantitative traits with Bayesian neural networks: a case study with Jersey cows and wheat. BMC Genetics 12: 87.
- Goyal, S. 2013. Artificial neural networks in vegetables: a comprehensive review. Scientific Journal of Crop Science 2: 75–94.
- Irzhansky, I.; Cohen, Y. 2006. Inheritance of resistance against Phytophthora infestans in Lycopersicon pimpinellifolium L3707. Euphytica 149: 309–316.
- Jeger, M.; Viljanen-Rollinson, S. 2001. The use of the area under the disease-progress curve (AUDPC) to assess quantitative disease resistance in crop cultivars. Theoretical and Applied Genetics 102: 32–40.
- Mukherjee, A.K.; Mohapatra, N.K.; Nayak, P. 2010. Estimation of area under the disease progress curves in a rice-blast pathosystem from two data points. European Journal of Plant Pathology 127: 33–39.
- Nowicki, M.; Foolad, M.R.; Nowakowska, M.; Kozik, E.U. 2012. Potato and tomato late blight caused by Phytophthora infestans: an overview of pathology and resistance breeding. Plant Disease 96: 4–17.
- Peixoto, L.A.; Bhering, L.L.; Cruz, C.D. 2015. Artificial neural networks reveal efficiency in genetic value prediction. Genetics and Molecular Research 14: 6796–6807.
- Patil, J.K.; Kumar, R. 2011. Advances in image processing for detection of plant diseases. Journal of Advanced Bioinformatics Applications and Research 2: 135–141.
- Shaner, G.; Finney, R. 1977. The effect of nitrogen fertilization on the expression of slow-mildewing resistance in Knox wheat. Phytopathology 67: 1051–1056.
- Silva, G.N.; Tomaz, R.S.; Castro, I.S.; Nascimento, M.; Bhering, L.L. 2014. Neural networks for predicting breeding values and genetic gains. Scientia Agricola 71: 494–498.
- Simko, I.; Piepho, H.P. 2012. The area under the disease progress stairs: calculation, advantage, and application. Phytopathology 102: 381–389.
- Tiger, B.; Verma, T. 2013. Identification and classification of normal and infected apples using neural network. International Journal of Science and Research 2: 160–160.
Edited by
Publication Dates
-
Publication in this collection
Jan-Feb 2017
History
-
Received
31 July 2015 -
Accepted
19 Mar 2016