ABSTRACT
Even though data visualization is a common analytical tool in numerous disciplines, it has rarely been used in agricultural sciences, particularly in agronomy. In this paper, we discuss a study on employing data visualization to analyze a multiplicative model. This model is often used by agronomists, for example in the so-called yield component analysis. The multiplicative model in agronomy is normally analyzed by statistical or related methods. In practice, unfortunately, usefulness of these methods is limited since they help to answer only a few questions, not allowing for a complex view of the phenomena studied. We believe that data visualization could be used for such complex analysis and presentation of the multiplicative model. To that end, we conducted an expert survey. It showed that visualization methods could indeed be useful for analysis and presentation of the multiplicative model.
multiplicative model; complex trait; graphical methods
Introduction
Agronomists and plant breeders often conduct factorial experiments to study influence of yield components on crop yield. This influence is described by the multiplicative model (e.g. Sparnaaij and Bos, 1993Sparnaaij, L.D.; Bos, I. 1993. Component analysis of complex characters in plant breeding. I. Proposed method for quantifying the relative contribution of individual components to variation of the complex character. Euphytica 70: 225−235.; Piepho, 1995Piepho, H.P. 1995. A simple procedure for yield component analysis. Euphytica 84: 43−48.; Kozak and Mądry, 2006Kozak, M.; Mądry, W. 2006. Note on yield component analysis. Cereal Research Communications 34: 933−940.):
where Y is a complex trait (e.g. plant grain yield per unit area), while X1, X2, … , Xk are multiplicative components of the complex trait (e.g. of plants per unit area and mean plant yield). Methods of so-called yield component analysis are used to analyze the model (1). These methods should take into account an order in which yield components develop during ontogeny: they can develop in a particular sequence or at the same time. Different methods are used for these two scenarios: sequential yield component analysis (e.g. Eaton and Kyte, 1978Eaton, G.W.; Kyte, T.R. 1978. Yield component analysis in cranberry. Journal of the American Society for Horticultural Science 103: 578−583.; Eaton and MacPherson, 1978Eaton, G.W.; MacPherson, E.A. 1978. Morphological components of yield in cranberry. Horticultural Research 17: 73−82.) for the former and non-sequential yield component analysis (e.g. Piepho, 1995Piepho, H.P. 1995. A simple procedure for yield component analysis. Euphytica 84: 43−48.; Kozak, 2004Kozak, M. 2004. New concept of yield components analysis. Biometrical Letters 41: 59−69.) for the latter. In addition, a valid method for the yield component analysis will not ignore the multiplicative nature of the model (1). A proper analysis of the model (1) allows one to answer some questions about that model: Which components in the multiplicative model have the strongest influence on the complex trait? Is this influence positive or negative? Unfortunately, these methods usually provide only a small amount of information about model (1) and offer poor interpretation possibilities for agronomists and plant breeders (for more details see Fraser and Eaton, 1983Fraser, J.; Eaton, G.W. 1983. Applications of yield component analysis to crop research. Field Crop Abstracts 36: 787−796.; Sparnaaij and Bos, 1993Sparnaaij, L.D.; Bos, I. 1993. Component analysis of complex characters in plant breeding. I. Proposed method for quantifying the relative contribution of individual components to variation of the complex character. Euphytica 70: 225−235.; Kozak and Mądry, 2006Kozak, M.; Mądry, W. 2006. Note on yield component analysis. Cereal Research Communications 34: 933−940.; Kozak and Verma, 2009Kozak, M.; Verma, M.R. 2009. Multiplicative yield component analysis: what does it offer to cereal agronomists and breeders? Plant, Soil and Environment 55: 134−138.).
These drawbacks can be overcome by using data visualization to support analysis and interpretation of data following the model (1). Unfortunately, agronomy has missed its chance to use data visualization even though many scientific fields benefit from data visualization (Kozak, 2010aKozak, M. 2010a. Basic principles of graphing data. Scientia Agricola 67: 483−494.). This paper, thus, aims to study the usefulness of graphical methods in analyzing the multiplicative model (1) in agronomy and plant breeding research. We will study this by means of the expert study. It will be the first report of this type of research.
Materials and Methods
Visualization techniques
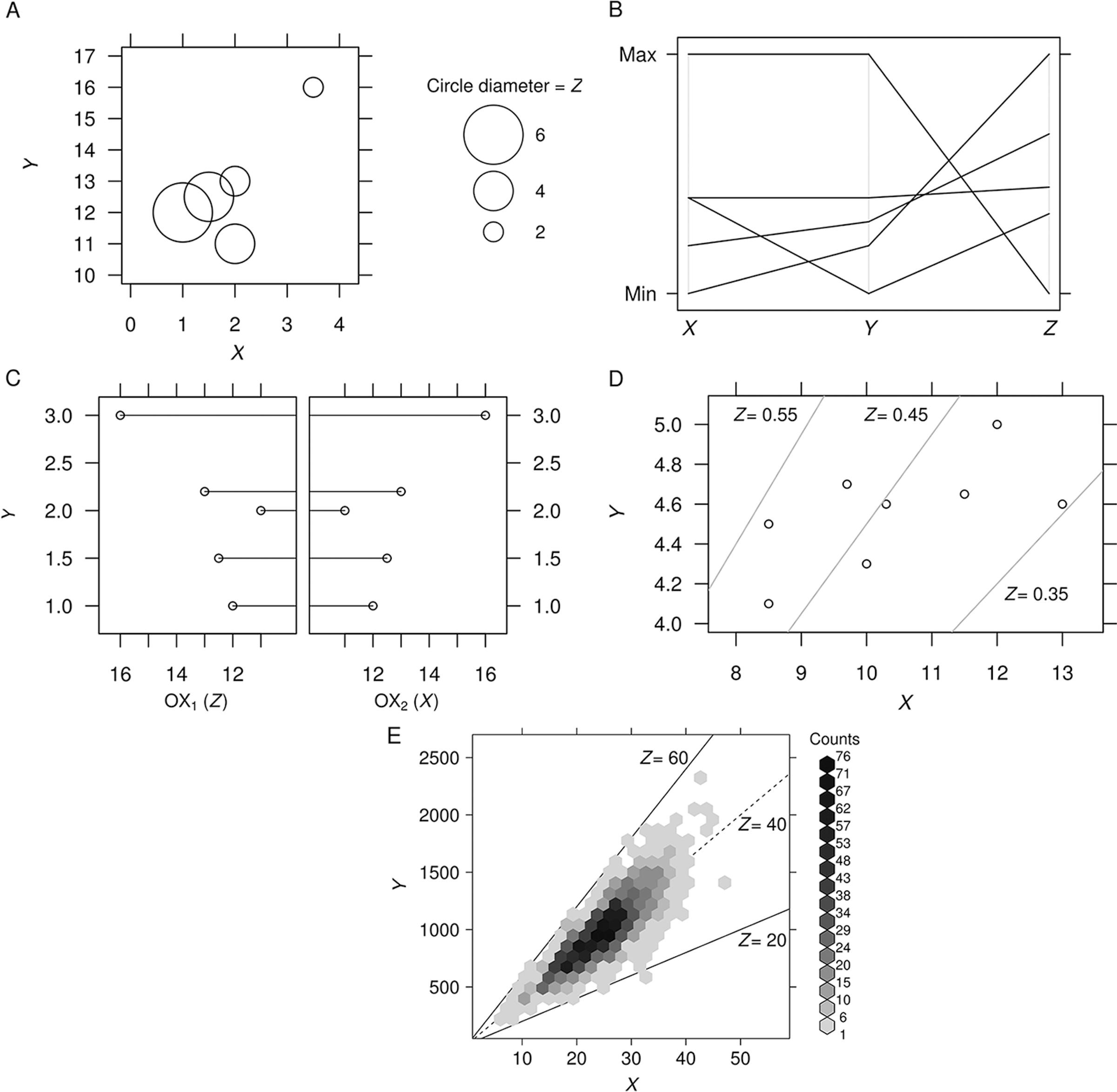
The visualization techniques used in the survey were as follows (Figure 1):
− Types of graphs studied in the expert survey. Starting from the left, the types are : (A) bubble plot, (B) parallel coordinate plot, (C) two-side plot, (D) MM-contour plot, and (E) HEX-MM-contour plot.
-
Bubble plot (e.g. Cleveland, 1994Cleveland, W.S. 1994. The Elements of Graphing Data. 2ed. Hobart Press, Summit, NJ, USA.; Jacoby, 1998Jacoby, W.G. 1998. Statistical Graphics for Visualizing Multivariate data. Sage, Thousand Oaks, CA, USA. (Sage University Papers Series, 7−120).; Harris 1999Harris, R.L. 1999. Information graphics: A Comprehensive Illustrated Reference. Management Graphics, Atlanta, GA, USA.). This graph is used for the 3D data. Two variables are presented on the axes of the plane while a third variable is coded by size (area or diameter) of a circle; other symbols are seldom used. We used the circle diameter, which is usually considered the best choice (e.g. Wilkinson, 2005Wilkinson, L. 2005. The Grammar of Graphics. 2.ed. Springer, New York, NY, USA.; Markus and Gu, 2010Markus, K.A.; Gu, W. 2010. Bubble plots as a model-free graphical tool for continuous variables. p. 65-94. In: Vinod, H.D., ed. Advances in social science research using R. Springer, New York, NY, USA. ; Madsen, 2011Madsen, B. 2011. Statistics for Non-Statisticians. Springer, Berlin, Germany.; Rougier et al., 2014Rougier, N.P.; Droettboom, M.; Bourne, P.E. 2014. Ten simple rules for better figures. PLoS Computational Biology 10: e1003833.). One can use the circle color to code information about possible groups in the data.
-
Parallel coordinate plot (e.g. Inselberg, 1985Inselberg, A. 1985. The plane with parallel coordinates. The Visual Computer 1: 69−91., 2002Inselberg, A. 2002. Visualization and data mining of high-dimensional data. Chemometrics and Intelligent Laboratory Systems 60: 147– 159.; Wegman, 1990Wegman, E.J. 1990. Hyperdimensional data analysis using parallel coordinates. Journal of the American Statistical Association 85: 664−675.). This graph is used for multidimensional data. Each variable is presented on its axis; all axes are parallel, and they can be either horizontal or vertical (we used the vertical one). The distances between the axes are identical. Having the same length, the axes start with a minimum and end with a maximum of the variable they represent. On axes, only two values are shown (minimum and maximum values). One can use color and type of line to code information about groups.
-
Two-side plot. This graph is used for 3D data. It is built based on a 2D scatter plot, but the x-axis is divided into two axes (each for one variable) while the y-axis remains unchanged. The lines in the graph area connect data points for the same observation unit. One can use color and type of points to code information about groups.
-
MM-Contour plot (Wnuk et al., 2013Wnuk, A.; Górny, A.G.; Bocianowski, J.; Kozak, M. 2013. Visualizing harvest index in crops. Communications in Biometry and Crop Science 8: 48−59.). This graph is used for 3D data. It is based on a contour plot in which two variables are presented on the axes. The third variable is represented by additional lines inside the plotting region; these lines are determined by the multiplicative model and can be treated as a third axis. One can use color and type of points to code information about groups.
-
HEX-MM-Contour plot, that is, the hexbinplot (Carr et al., 1987Carr, D.B.; Littlefield, R.; Nicholson, W.; Littlefield, J. 1987. Scatterplot matrix techniques for large N. Journal of the American Statistical Association 82: 424−436.) joined with the MM-Contour plot. This graph is used for large 3D data. The original hexbinplot is useful for large 2D data sets. It is based on a 2D scatterplot, but instead of plotting single observations, they are combined into bins. Frequency of the observations in the bins is represented by the bin color. The HEX-MM-Contour plot uses additional lines added to the plotting region (like those in the MM-Contour plot) to present 3D data. In this graph, it is not possible to code information about groups.
Note that we recreated the MM-Contour plot, HEX-MM-Contour plot, and two-side plot for analyzing and presenting the multiplicative model. Thus, these plots have never been presented or published before this study, so we can be certain that the experts had never seen them before. We also used the trellis version of all proposed graphs. The trellis display is for data that contain qualitative factors (genotypes in our study) (Cleveland, 1993Cleveland, W.S. 1993. Visualizing Data. Hobart Press, Summit, NJ, USA.; Becker et al., 1994Becker, R.A.; Cleveland, W.S.; Shyu, M.J.; Kaluzny, S.P. 1994. Trellis Displays: User’s Guide. AT&T Bell Laboratories, Berkeley Heights, NJ, USA. (Technical Report)., 1996bBecker, R.; Cleveland, W.S.; Shyu, M. 1996b. The visual design and control of trellis display. Journal of Computational and Graphical Statistics 5: 123−155.; Becker and Cleveland, 1996aBecker, R.A.; Cleveland, W.S. 1996a. S-PLUS Trellis Graphics User's Manual. MathSoft, Seattle, WA, USA.; Cleveland and Fuentes, 1997Cleveland, W.S.; Fuentes, M. 1997. Trellis Display: Modeling Data from Designed Experiments. AT&T Bell Laboratories, Berkeley Heights, NJ, USA. (Technical Report).). Figure 2 shows an example of how it works: the panels represent 2D scatter plots for each of the three genotypes, each panel having the same x- and y-scales.
Plant material
The graphs studied were used for data from two field experiments: (i) with winter wheat and (ii) with spring barley.
Winter wheat
The data were obtained from a filed experimental conducted in Poznań in 2006. The one-factor experiment was arranged in the randomized complete block design with 32 genotypes (factor levels) of winter wheat (breeding lines included) in three replications. The experiment was set up at the light, sandy-loam soils with low content of plant-available nitrogen; soil was classified as medium or low quality. Nitrogen fertilizer was applied at the dose 76 kg N ha−1 (divided in three sub-rates); other fertilizers were supplied at optimal rates. During the vegetation season, the fields were irrigated and standard chemical protection was applied. Field was divided into plots (size 1.7 m−2; about 300 plants m−2). Grain yield and biomass yield (only vegetative parts) were measured from about 20 randomly selected plants per plot. The harvest index (HI) was calculated according to the formula HI = grain yield / biomass yield. We considered a multiplicative model of grain yield (t ha−1) as a product of two non-sequential components: biomass yield (t ha−1) and harvest index. This model was visualized in a bubble plot, a parallel coordinate plot, a two-side plot, and an MM-Contour plot.
Spring barley
This field experiment with spring barley was conducted in Chylice, Poland, in three growing seasons (1999, 2001, 2002). A three-factor experiment arranged as a split-plot design was conducted in four replications. The following factors were studied: genotype (2 levels), sowing date (2 levels) and N fertilization (4 levels). Experiment was set up on phaeozem classified as good quality soil. In the main plots (sub-blocks), genotype and sowing date were distributed randomly in blocks, and N fertilization within sub-blocks. From these plots, various yield-contributing characters were calculated or measured. Full data contain 48 combinations and about twenty-two thousand observations. We analyzed a sequential multiplicative model of grain yield per spike (mg) as a product of number of grains per spike and average grain weight per spike (mg) (usually represented by thousand grain weight). Average grain weight per spike was calculated as ratio of grain yield per spike and number of grains per spike, which two variables were directly measured. In the expert study, this model was visualized by HEX-MM-Contour plot.
In the expert survey bubble plot, MM-Contour plot, parallel coordinate plot and two-side plot were developed for two research situations with raw data for 7 and 32 genotypes of winter wheat in three replications (respectively n = 21 and n = 96), and HEX-MM-Contour plot was made for 1 genotype of spring barley in 8 experimental combinations (n = 4086). These research situations differ in number of observations, number of factors and their levels in the experiment, as well as order of development of yield components during ontogeny.
Expert survey
We conducted an expert survey in Sept and Oct 2012 among ten experts from eight universities and research institutes in Poland. Five experts were agronomists working with factorial experiments, including studies on yield components' and the other five experts were statisticians (specialized in statistics for agricultural sciences). At the beginning of each interview, the experts were informed about the objective of the study, its outline, and expectations from the expert. The person conducting the survey (Agnieszka Wnuk) explained and described the graphs to the expert (on a color paper sheet). Later, the experts also received a color paper sheet with each graph, with a description of the experiment and the model (see the subsection Plant material). The experts were asked to read this material and answer the questionnaire (in unlimited time).
The survey questionnaire included eight questions. However, in this paper we focus on two key questions where the experts evaluated the usefulness of the graphs in two aspects of their use: possibility of (i) reading and (ii) interpreting data in the multiplicative model. These questions were as follows: “Please rate simplicity of reading data from this graph” and “Please rate simplicity of interpreting data in the multiplicative model from this graph”. The questions were closed and we used a five-point scale to describe whether the graph is: very easy, easy, medium, difficult, very difficult in these aspects. To be effective in reading data, the graph must allow for decent visual estimation of the values for most observations. It means that the graph does not have elements that can obscure observations, scales must help estimate the values of all variables, all groups need to be easily identified and distinguishable in the graph, etc. On the other hand, a graph is effective in interpreting data in the multiplicative model when it allows one to study data structures, i.e., relationships between the variables in the model, outlier values, variability of the variables, etc. Raw data are analyzed to study relationships between the variables in the model for each level of the grouping factor or factor combinations (Kozak and Verma, 2009Kozak, M.; Verma, M.R. 2009. Multiplicative yield component analysis: what does it offer to cereal agronomists and breeders? Plant, Soil and Environment 55: 134−138.). These graphs should allow one to determine which components have a greater influence on the complex trait (e.g. yield). Coding all three variables in the model must be effective and should allow for an easy analysis of the relationships between these variables.
For each scale point from the five-point scale values +2, +1, 0, –1, –2 were assigned. The total rating of graph for the group (independently) takes range form +10 to –10, where:
– total rating from +10 to +4 represents a graph that is very easy or easy in reading/interpreting data
– total rating from +3 to –3 represents the graph that is at medium difficulty in reading/interpreting data
– total rating from –4 to –10 represents a graph that is difficult or very difficult in reading/interpreting data
Mean absolute deviation (MAD) was used to estimate variability of the expert opinions (within each group) about usefulness of the graphs. A high MAD value represents a large variation in the opinion of the experts (in groups) on the reading or interpreting data from the graph, while a low value represents small variation (so, large agreement).
All graphs and calculations in this paper were performed in R (R Core Team, 2015R Core Team. 2015. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria.) with the help of the packages graphics (R Core Team, 2015R Core Team. 2015. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria.) and lattice (Sarkar, 2008Sarkar, D. 2008. Lattice Multivariate Data Visualization with R. 2008. Springer, New York, NY, USA.).
Results
Figure 3 shows the results of the expert survey. For raw data with seven genotypes of winter wheat in three replications, bubble plot, MM-Contour plot and two-side plot, according to both groups of experts, allowed for easy or very easy reading and interpreting data on the multiplicative model. However, for the two-side plot, an average mean absolute deviation (MAD = 0.96) was observed in the agronomist group for interpretation data in the multiplicative model (Figure 4). Three out of five experts claimed that this graph was very easy to use, but the two others claimed it was at medium difficulty. However, only one of these two experts reported doubts about possibilities of interpretation 2D relationship between variables on the divided axes (OX). There was also some variation connected with reading data (MAD = 0.72). For these both aspects, statisticians considered the two-side plot easy or very easy to use with small MAD (Figure 4). Both groups evaluated parallel coordinate plot as offering a medium difficulty for reading data (with average MAD within groups; Figure 4). However, the groups assessed its interpretation possibilities differently (Figure 3): for agronomists it was easy to use, while for statisticians it was of medium difficulty. In both cases, the opinions had average variability (Figure 4). For such data, as discussed above (with the small number of observations, 7 groups 3 replications each), they showed minor differences in usefulness between the graphs.
− Summary of the results of the expert survey: evaluations of usefulness of the graphs for reading data and interpretation of the multiplicative model by agronomists (lower row) and statisticians (upper row). Columns in the graph represent research situations and trellis version for raw data with 32 genotypes (in 3 replications). Graphs with the highest usefulness for both reading and interpretation would be placed in the upper right corner, and the smallest, in the left bottom corner of a panel.
− Mean absolute deviation (MAD) used to estimate variability of the experts’ opinions (within group) about usefulness of the graphs. MAD ranges here from 0 to 1.92, with the following possible values: 0, 0.32, 0.4, 0.48, 0.64, 0.72, 0.8, 0.88, 0.96, 1.04, 1.12, 1.2, 1.28, 1.36, 1.44, 1.52, 1.6, 1.68, 1.76, 1.92. The highest MAD (for both reading and interpretation) represent the upper right corner, and the smallest, left bottom of a panel.
The second column in Figure 3 shows the results of the expert survey for the data with 32 genotypes of winter wheat (in 3 replications). The larger number of observations (n = 96) and groups (32 genotypes) caused a substantial decrease of the usefulness for all graphs compared to the previous situation (Figure 3). According to the experts, this was mainly due to difficulties in recognizing the genotypes and overlapping of the points. Reading and interpreting the data in bubble and parallel coordinate plots were difficult or very difficult (both groups were very consistent in this assessment − note the small MADs in Figure 4). Genotypes were very difficult to recognize because of the large overlap and the color use to code information on 32 genotypes. Note that for parallel coordinate plot and bubble plot, it is also possible to use type of line or circle line to differentiate genotypes; however, for so many observations it would not be effective either (e.g. Cleveland and McGill, 1984bCleveland, W.S.; McGill, R. 1984b. The many faces of a scatterplot. Journal of the American Statistical Association 79: 807−822.; Mackinaly, 1986MacKinaly, J. 1986. Automating the design of graphical presentations of relational information. ACM Transactions on Graphics 5: 110−141.; Wilkinson, 2005Wilkinson, L. 2005. The Grammar of Graphics. 2.ed. Springer, New York, NY, USA.).
A relatively smaller decrease of usefulness than that observed for the two above-mentioned graphs was observed for the MM-Contour plot and two-side plot. Both groups of experts claimed that reading data and interpreting of the multiplicative model from two-side plot is of medium difficulty (Figure 3). However, for statisticians, an average MAD was observed while for agronomists, the answers were more scattered (Figure 4). Seven out of ten experts reported problems with overlap and ineffective recognition of some genotypes, and, therefore, difficulties with interpretation of the 2D relationship between the divided axes. The MM-Contour plot was evaluated as easy for reading data by agronomists, but with high MAD of 1.44 (Figure 4). This was because three agronomists considered this graph very easy to read, but the other two claimed it was difficult. However, these two experts did not offer any particular comments to justify such a low grade. The agronomists evaluated interpretation of the model as medium difficulty, with MAD = 1.28. In this case, three experts evaluated the graph as very easy or easy, one expert as of medium difficulty, and one as difficult to interpret data. Statisticians, however, claimed that the usefulness of the MM-Contour plot was of medium difficulty for both aspects. They were not consistent in their assessments, with MAD of 0.80 for reading and 1.12 for interpreting data (Figure 4). Both the MM-Contour plot and two-side plot are more useful for a large number of observations than the bubble plot or parallel coordinate plot. This is probably because these graphs use color and type of point to code information about groups, which makes the groups easier to recognize when overlap is large.
For data with 32 genotypes (in three replications), most of the studied graphs are difficult to use. The MM-Contour plot and two-side plot are more useful than the other graphs; nevertheless, the user may have problems to recognize genotypes. This can make data interpretation almost impossible in some cases (e.g. with bubble plot or parallel coordinate plot). We must remember that for raw data, it is crucial to analyze the relative strength of the components influence on the complex trait for each genotype. This is why we decided to use a trellis version of the graphs. Instead of coding information about groups in color, type of points, or both, they are now placed in separate panels (like in Figure 2). This makes reading and interpreting data for a single genotype easier.
The third column of Figure 3 shows that both agronomists and statisticians appreciated the quality of the trellis version of the studied graphs. The trellis display was effective especially for bubble and parallel coordinate plots. The experts evaluated reading and interpreting data from the bubble plot as easy or very easy. However, statisticians were not very consistent in their evaluations for interpretation, with MAD = 1.12 (Figure 4). This resulted from an extreme grade of one of the experts, in whose opinion the graph was very difficult to use. Since this expert did not have any specific complains, we do not know why he gave such a low grade. The remaining experts evaluated the trellis version of bubble plot as very easy or easy to interpret data. Both groups evaluated parallel coordinate plot in the trellis version as easy for reading data, but of medium difficulty for interpreting data (Figure 3). The within-group experts’ opinions on this graph were more varied for the trellis version than for the standard version (Figure 4). The trellis version of the two-side plot was evaluated as easy or very easy to use. MAD, however, was smaller (as compared to its standard version) but still on the average level for agronomists; statisticians were more consistent (Figure 4). The trellis version of MM-Contour plot was evaluated as easy or very easy to use for both aspects (Figure 3). Also, the within-group variability for this graph was much lower than for the standard version. It is rather clear, then, that when 32 genotypes were studied, the graphs in the trellis version were much more useful than their respective standard forms. This was because the groups were easier to distinguish when presented in separate panels than by different points or line types.
The HEX-MM-Contour plot was presented only in the trellis version because of the large number of observations and factor combinations of the data we used. The experts evaluated this graph for one genotype of spring barley, in eight experimental combinations (n = 4086). The results are not shown in the graphical version because this graph would include only two observations. Statisticians claimed that both reading and interpreting data in the multiplicative model had medium difficulty (mean grades were 3 and 2 with respective MADs of 0.72 and 0.48). Agronomists, on the other hand, evaluated this graph as easy or very easy in both these aspects: six for reading data (MAD = 0.96) and four for interpreting data in the model (MAD = 1.44). MAD for interpreting data was so large because three experts claimed that this graph was very easy to use, one of them that it was of medium difficulty, but one that it was very difficult to use. A similar situation was observed for reading data. The experts in both groups reported problems with proper interpretation of the strength and direction of the relationships between all variables.
Summary of the expert survey
Table 1 shows graphs that can be recommended for analysis and presentation of raw data in the multiplicative model. For data with seven genotypes of winter wheat (in 3 replications), the bubble plot, MM-Contour plot and two-side plot can be used. The parallel coordinate plot might be used as well, but clearly, its usefulness is smaller than that of the previous graphs. In the case of data with 32 genotypes of winter wheat (in 3 replications), one can use the MM-Contour plot and two-side plot (in their standard versions) (Table 1). The MM-Contour plot and two-side plot in standard versions require sufficient attention by the user; nevertheless, their trellis versions will be more useful. Reading and interpreting data will be easier, and groups will not have to be differentiated by color or type of point; but at the same time, such graphs require more space. Both bubble and parallel coordinate plots showed to be useful only in the trellis version. For data with a large number of observations and factors, HEX-MM-Contour plot (in trellis version) is of medium difficulty.
− Graphs that can be recommended for analysis and presentation of raw data in the multiplicative model. The table contains graphs that were evaluated by the experts as very easy, easy or of medium difficulty to use at least.
Discussion
Data visualization is a rapidly developing discipline of knowledge. Thanks to the development of computer techniques, graphs are better and better adapted to specific tasks of data analysis than a few years ago (e.g. Cleveland and McGill, 1984aCleveland, W.S.; McGill, R. 1984a. Graphical perception: theory, experimentation, and application to the development of graphical methods. Journal of the American Statistical Association 79: 531−554., 1985Cleveland, W.S.; McGill, R. 1985. Graphical perception and graphical methods for analyzing scientific data. Science, New Series 229: 828−833.; Cleveland 1993Cleveland, W.S. 1993. Visualizing Data. Hobart Press, Summit, NJ, USA.; Krzanowski, 1997Krzanowski, W.J. 1997. Recent trends and developments in computational multivariate analysis. Statistics and Computing 7: 87−99.; van Wijk, 2005Van Wijk, J.J. 2005. The value of visualization. p. 79-86. In: VIS 05. IEEE Visualization, Piscataway, NJ, USA.). The analysis and presentation of the multiplicative model in agronomy and plant breeding are examples of such specific tasks. As far as we know, graphical methods have rarely been used for this purpose. Usually, a scatterplot was used, but it focuses on presenting a 2D relationship between traits. Thus, how could it be effective? Not only does the model (1) include at least three variables, but also the variables are in a specific (non-linear) relationship. To support this task, then, we proposed several three- and multidimensional graphs and conducted the expert survey to verify whether they can be useful to analyze the model (1).
Expert studies are often used in various areas of science, wherever deep knowledge about a certain topic is required. For example, to evaluate such complex topic as the multiplicative model, one should have interdisciplinary knowledge of statistics, agronomy, and plant breeding. Expert studies are common, but they have rarely been used to evaluate usefulness of data visualization. Rare examples are studies conducted by Donaldson-Selby et al. (2007)Donaldson-Selby, G.; Hill, T.; Korrubel, J. 2007. Photorealistic visualisation of urban greening in a low-cost high-density housing settlement, Durban, South Africa. Urban Forestry & Urban Greening 6: 3−14., evaluating the credibility and potential usefulness of the photo-realistic visualization of urban greening; Sanyal et al. (2010)Sanyal, J.; Zhang, S.; Dyer, J.; Mercer, A.; Amburn, P.; Moorhead, R.J. 2010. Noodles: A tool for visualization of numerical weather model ensemble uncertainty: visualization and computer graphics. IEEE Transactions 16: 1421−1430., evaluating the usefulness of visualization for operational weather forecasting; or Opiyo and Horvath (2010)Opiyo, E.Z.; Horvath, I. 2010. Exploring the viability of holographic displays for product visualisation. Journal of Design Research 8: 169−188., evaluating the usefulness of the holographic displays for 3D product visualization. Our study showed that the proposed graphs could indeed be complementary to traditional yield component analysis. The graphs actually allow for an easy analysis and comprehensive interpretation data in the multiplicative model, helping to answer questions that methods of multiplicative model analysis might fail to answer. The study also showed that the experts were willing to use the proposed graphs in their work with the multiplicative model.
A number of observations and a method of coding information about groups are the key criteria of whether a graph will be useful to analyze the multiplicative model. For a small number of groups and observations (such as seven genotypes of winter wheat with three replications per genotype), all proposed graphs could be used. Still, the parallel coordinate plot will likely be slightly less effective than the others due to its atypical coordinate system. For such data, the way of coding information only slightly differentiates usefulness of the graphs. However, for a larger number of groups and observations (e.g., 32 genotypes of winter wheat with 3 replications per genotype), it would be difficult to use any of the proposed graphs. The reason is a large overlap of points and difficulties in recognizing groups. A combination of color and type of points (like used in MM-Contour plot and two-side plot) is usually more useful to code information about groups than color only (like in parallel coordinate plot and bubble plot). The use of color for this purpose is less effective because it strongly depends on a possibility of recognizing and distinguishing colors by the reader (a difficult task for color blind people) or equipment quality (monitor, printer, projector) (e.g. Few, 2006Few, S. 2006. Information Dashboard Design: The Effective Visual Communication of Data. O'Reilly, Sebastopol, CA, USA.; Zeileis et al., 2009Zeileis, A.; Hornik, K.; Murrell, P. 2009. Escaping RGBland: selecting colors for statistical graphics. Computational Statistics & Data Analysis 53: 3259−3270.; Wegman and Said, 2011Wegman, E.J.; Said, Y. 2011. Color theory and design. WIREs Computational Statistics 3: 104−117.). According to many researchers, using both color and type of points provides the highest distinguishability especially for a large number of observations and groups (e.g. Chambers et al., 1983Chambers, J.M.; Cleveland, W.S.; Kleiner, B.; Tukey, P.A. 1983. Graphical Methods for Data Analysis. Wadsworth, Pacific Grove, CA, USA.; Cleveland and McGill, 1984bCleveland, W.S.; McGill, R. 1984b. The many faces of a scatterplot. Journal of the American Statistical Association 79: 807−822.; Cleveland, 1994Cleveland, W.S. 1994. The Elements of Graphing Data. 2ed. Hobart Press, Summit, NJ, USA.).
Another important issue is a way of coding all three variables in a graph. It can affect quality of both reading and interpreting the data. According to Cleveland and McGill (1984a)Becker, R.A.; Cleveland, W.S. 1996a. S-PLUS Trellis Graphics User's Manual. MathSoft, Seattle, WA, USA., the position of the symbol along the axis is the most precise reading of observation values, more precise than for example by length or area of the symbol. For the two-side plot, which uses axes to present all variables in the model (1), experts reported problems only with reading data for a large number of observations (32 groups), but they still considered the graph useful. Experts also pointed out small problems with interpreting the relationship between variables represented on the divided axes. Although the direction of the relationship between these variables is easy to see, determining its strength is not. Although possible, it is not as intuitive as in the standard scatter plot (the modification of which two-side plot is). It usually takes time to get used to such untypical graphs. The parallel coordinate plot is also an untypical graph. Both agronomists and statisticians reported many additional problems with it. Although commonly used for multidimensional data sets (Ge et al., 2009Ge, Y.; Li, S.; Lakhan, V.C.; Lucieer, A. 2009. Exploring uncertainty in remotely sensed data with parallel coordinate plots. International Journal of Applied Earth Observation and Geoinformation 11: 413–422.; Kozak 2010bKozak, M. 2010b. Use of parallel coordinate plots in multi-response selection of interesting genotypes. Communications in Biometry and Crop Science 5: 83−95.; Kusano et al., 2011Kusano, M.; Redestig, H.; Hirai, T.; Oikawa, A.; Matsuda, F.; Fukushima, A.; Arita, M.; Watanabe, S.; Yano, M.; Hiwasa-Tanase, K.; Ezura, H.; Saito, K. 2011. Covering chemical diversity of genetically-modified tomatoes using metabolomics for objective substantial equivalence assessment. PLoS One 6: e16989.; Eastham et al., 2012Eastham, S.D.; Coates, D.J.; Parks, G.T. 2012. A novel method for rapid comparative quantitative analysis of nuclear fuel cycles. Annals of Nuclear Energy 42: 80−88.; Winderbaum et al., 2012Winderbaum, L.; Ciobanu, C.L.; Cook, N.J.; Paul, M.; Metcalfe, A.; Gilbert, S. 2012. Multivariate analysis of an LA-ICP-MS trace element dataset for pyrite. Mathematical Geosciences 44: 823–842.), it is relatively new. Its unusual coordinate system can be problematic for a new user (Wegman, 1990Wegman, E.J. 1990. Hyperdimensional data analysis using parallel coordinates. Journal of the American Statistical Association 85: 664−675.; Wegman and Carr, 1993Wegman, E.J.; Carr, D.B. 1993. Statistical graphics and visualization. Handbook of Statistics 9: 857−958.; Kozak, 2010bKozak, M. 2010b. Use of parallel coordinate plots in multi-response selection of interesting genotypes. Communications in Biometry and Crop Science 5: 83−95.). It has advantages, such as possibility of presenting more than three variables, which is not the case with most of the other graphs studied. However, this does not affect our conclusion that the parallel coordinate plot is not useful for the multiplicative model.
The remaining graphs (bubble plot, MM-Contour plot and HEX-MM-Contour plot) present two variables on the axes of the plane and a third variable by using a reference line or diameter of the circle. Coding information about a third variable is always problematic, because it is linked to reducing quality of reading or interpreting data on the graphs (e.g. Jacoby, 1998Jacoby, W.G. 1998. Statistical Graphics for Visualizing Multivariate data. Sage, Thousand Oaks, CA, USA. (Sage University Papers Series, 7−120).; Few, 2006Few, S. 2006. Information Dashboard Design: The Effective Visual Communication of Data. O'Reilly, Sebastopol, CA, USA.). The bubble plot is one of the most commonly used graphs for 3D data in many fields of science (e.g. Varma et al., 2008Varma, V.A.; Pekny, J.F.; Blau, G.E.; Reklaitis, G.V. 2008. A framework for addressing stochastic and combinatorial aspects of scheduling and resource allocation in pharmaceutical R&D pipelines. Computers and Chemical Engineering 32: 1000–1015.; Comas et al., 2012Comas, C.; Avilla, J.; Sarasúa, M.J.; Albajes, R.; Ribes-Dasi, C. 2012. Lack of anisotropic effects in the spatial distribution of Cydia pomonella pheromone trap catches in Catalonia, NE Spain. Crop Protection 34: 88−95.). For many users, its main advantage is simplicity, and it is indeed simple to use. Its construction makes data interpretation very intuitive: the larger circle size, the greater value of the third variable. However, some experts reported difficulties with evaluating the value of the third variable and comparing the sizes of bubbles. This happened even for a small number of observations and groups. In the MM-Contour plot and HEX-MM-Contour plot, the third variable is represented by lines, which can be used as an additional axis. According to the experts, reading data relative to these lines on the MM-Contour plot is only a little less accurate than reading in relation to the axes of the graph. This problem is more serious for the HEX-MM-Contour plot because it does not allow for typical reading of individual observations – they are combined into bins, which can be troublesome for new users. The experts also noticed that for both graphs interpreting the relationship between variables on the axes and the one represented by reference lines is slightly more difficult than that between the variables represented by the axes.
The expert survey showed that the trellis display considerably increased usefulness of the studied graphs under the large number of groups and observations (like for 32 genotypes), a phenomenon already reported (Cleveland, 1993Cleveland, W.S. 1993. Visualizing Data. Hobart Press, Summit, NJ, USA.; Becker et al., 1994Becker, R.A.; Cleveland, W.S.; Shyu, M.J.; Kaluzny, S.P. 1994. Trellis Displays: User’s Guide. AT&T Bell Laboratories, Berkeley Heights, NJ, USA. (Technical Report)., 1996bBecker, R.; Cleveland, W.S.; Shyu, M. 1996b. The visual design and control of trellis display. Journal of Computational and Graphical Statistics 5: 123−155.; Becker and Cleveland, 1996aBecker, R.A.; Cleveland, W.S. 1996a. S-PLUS Trellis Graphics User's Manual. MathSoft, Seattle, WA, USA.; Cleveland and Fuentes, 1997Cleveland, W.S.; Fuentes, M. 1997. Trellis Display: Modeling Data from Designed Experiments. AT&T Bell Laboratories, Berkeley Heights, NJ, USA. (Technical Report).). Showing group in separate panels and sharing the same scales allow one to avoid many problems with recognition of the groups and large overlap of points. It also enhances interpretation of relationships between variables and their comparison for all considered levels of the studied factor. The trellis display is not limited to standard graphs, but it could also be used for any new graph. Despite its obvious advantages, the trellis display is still rarely used, especially in plant sciences (rare examples of its use are Čobanović et al., 2007Čobanowić, K.; Nicolić-Đorić, E.; Matavdžić, B. 2007. Use of trellis graphics in the analysis of results from field experiments in agriculture. Metodološki Zvezki 4: 71−92.; Szabó et al., 2008Szabó, G.; Elek, Z.; Szabó, S. 2008. Study of heavy metals in the soil-plant system. Cereal Research Communications 36: 403−406.; Kozak et al., 2010Kozak, M.; Wnuk, A.; Gozdowski, D.; Wyszyński, Z. 2010. Visualizing bivariate relationships with hexagonally binned data. Colloquium Biometricum 40: 31−40.; Wnuk et al., 2013Wnuk, A.; Górny, A.G.; Bocianowski, J.; Kozak, M. 2013. Visualizing harvest index in crops. Communications in Biometry and Crop Science 8: 48−59.).
In addition to showing the usefulness of data visualization in agronomy, we showed that expert studies could be very useful to evaluate visualization of methods. The direct interview supported by the questionnaire enables one to ask the experts detailed questions and learn their impression about the studied graphs. In our case, including two groups of experts enabled us to consider various sides of the problem studied. Agronomists evaluated graphs primarily in terms of their use in practice (e.g., ease to use and clear representation of the biological phenomena). Statisticians focused on capabilities for data analysis and interpretation of the multiplicative model, with the focus on statistical accuracy. Obviously, we might have included a third group of experts, mainly those in visualization, which might offer some more information about the graphs. Unfortunately, the very small number of experts in visualization working for agronomy and plant breeding made it practically impossible. We hope that our study will trigger a change in thinking about data analysis in agronomy by showing that not only can data visualization be helpful, but it can also support complex data analyses by statistical methods.
References
- Becker, R.A.; Cleveland, W.S. 1996a. S-PLUS Trellis Graphics User's Manual. MathSoft, Seattle, WA, USA.
- Becker, R.A.; Cleveland, W.S.; Shyu, M.J.; Kaluzny, S.P. 1994. Trellis Displays: User’s Guide. AT&T Bell Laboratories, Berkeley Heights, NJ, USA. (Technical Report).
- Becker, R.; Cleveland, W.S.; Shyu, M. 1996b. The visual design and control of trellis display. Journal of Computational and Graphical Statistics 5: 123−155.
- Carr, D.B.; Littlefield, R.; Nicholson, W.; Littlefield, J. 1987. Scatterplot matrix techniques for large N. Journal of the American Statistical Association 82: 424−436.
- Chambers, J.M.; Cleveland, W.S.; Kleiner, B.; Tukey, P.A. 1983. Graphical Methods for Data Analysis. Wadsworth, Pacific Grove, CA, USA.
- Cleveland, W.S. 1993. Visualizing Data. Hobart Press, Summit, NJ, USA.
- Cleveland, W.S. 1994. The Elements of Graphing Data. 2ed. Hobart Press, Summit, NJ, USA.
- Cleveland, W.S.; Fuentes, M. 1997. Trellis Display: Modeling Data from Designed Experiments. AT&T Bell Laboratories, Berkeley Heights, NJ, USA. (Technical Report).
- Cleveland, W.S.; McGill, R. 1984a. Graphical perception: theory, experimentation, and application to the development of graphical methods. Journal of the American Statistical Association 79: 531−554.
- Cleveland, W.S.; McGill, R. 1984b. The many faces of a scatterplot. Journal of the American Statistical Association 79: 807−822.
- Cleveland, W.S.; McGill, R. 1985. Graphical perception and graphical methods for analyzing scientific data. Science, New Series 229: 828−833.
- Comas, C.; Avilla, J.; Sarasúa, M.J.; Albajes, R.; Ribes-Dasi, C. 2012. Lack of anisotropic effects in the spatial distribution of Cydia pomonella pheromone trap catches in Catalonia, NE Spain. Crop Protection 34: 88−95.
- Čobanowić, K.; Nicolić-Đorić, E.; Matavdžić, B. 2007. Use of trellis graphics in the analysis of results from field experiments in agriculture. Metodološki Zvezki 4: 71−92.
- Donaldson-Selby, G.; Hill, T.; Korrubel, J. 2007. Photorealistic visualisation of urban greening in a low-cost high-density housing settlement, Durban, South Africa. Urban Forestry & Urban Greening 6: 3−14.
- Eastham, S.D.; Coates, D.J.; Parks, G.T. 2012. A novel method for rapid comparative quantitative analysis of nuclear fuel cycles. Annals of Nuclear Energy 42: 80−88.
- Eaton, G.W.; Kyte, T.R. 1978. Yield component analysis in cranberry. Journal of the American Society for Horticultural Science 103: 578−583.
- Eaton, G.W.; MacPherson, E.A. 1978. Morphological components of yield in cranberry. Horticultural Research 17: 73−82.
- Few, S. 2006. Information Dashboard Design: The Effective Visual Communication of Data. O'Reilly, Sebastopol, CA, USA.
- Fraser, J.; Eaton, G.W. 1983. Applications of yield component analysis to crop research. Field Crop Abstracts 36: 787−796.
- Ge, Y.; Li, S.; Lakhan, V.C.; Lucieer, A. 2009. Exploring uncertainty in remotely sensed data with parallel coordinate plots. International Journal of Applied Earth Observation and Geoinformation 11: 413–422.
- Harris, R.L. 1999. Information graphics: A Comprehensive Illustrated Reference. Management Graphics, Atlanta, GA, USA.
- Inselberg, A. 1985. The plane with parallel coordinates. The Visual Computer 1: 69−91.
- Inselberg, A. 2002. Visualization and data mining of high-dimensional data. Chemometrics and Intelligent Laboratory Systems 60: 147– 159.
- Jacoby, W.G. 1998. Statistical Graphics for Visualizing Multivariate data. Sage, Thousand Oaks, CA, USA. (Sage University Papers Series, 7−120).
- Kozak, M. 2004. New concept of yield components analysis. Biometrical Letters 41: 59−69.
- Kozak, M. 2010a. Basic principles of graphing data. Scientia Agricola 67: 483−494.
- Kozak, M. 2010b. Use of parallel coordinate plots in multi-response selection of interesting genotypes. Communications in Biometry and Crop Science 5: 83−95.
- Kozak, M.; Mądry, W. 2006. Note on yield component analysis. Cereal Research Communications 34: 933−940.
- Kozak, M.; Verma, M.R. 2009. Multiplicative yield component analysis: what does it offer to cereal agronomists and breeders? Plant, Soil and Environment 55: 134−138.
- Kozak, M.; Wnuk, A.; Gozdowski, D.; Wyszyński, Z. 2010. Visualizing bivariate relationships with hexagonally binned data. Colloquium Biometricum 40: 31−40.
- Krzanowski, W.J. 1997. Recent trends and developments in computational multivariate analysis. Statistics and Computing 7: 87−99.
- Kusano, M.; Redestig, H.; Hirai, T.; Oikawa, A.; Matsuda, F.; Fukushima, A.; Arita, M.; Watanabe, S.; Yano, M.; Hiwasa-Tanase, K.; Ezura, H.; Saito, K. 2011. Covering chemical diversity of genetically-modified tomatoes using metabolomics for objective substantial equivalence assessment. PLoS One 6: e16989.
- MacKinaly, J. 1986. Automating the design of graphical presentations of relational information. ACM Transactions on Graphics 5: 110−141.
- Madsen, B. 2011. Statistics for Non-Statisticians. Springer, Berlin, Germany.
- Markus, K.A.; Gu, W. 2010. Bubble plots as a model-free graphical tool for continuous variables. p. 65-94. In: Vinod, H.D., ed. Advances in social science research using R. Springer, New York, NY, USA.
- Opiyo, E.Z.; Horvath, I. 2010. Exploring the viability of holographic displays for product visualisation. Journal of Design Research 8: 169−188.
- Piepho, H.P. 1995. A simple procedure for yield component analysis. Euphytica 84: 43−48.
- R Core Team. 2015. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria.
- Rougier, N.P.; Droettboom, M.; Bourne, P.E. 2014. Ten simple rules for better figures. PLoS Computational Biology 10: e1003833.
- Sanyal, J.; Zhang, S.; Dyer, J.; Mercer, A.; Amburn, P.; Moorhead, R.J. 2010. Noodles: A tool for visualization of numerical weather model ensemble uncertainty: visualization and computer graphics. IEEE Transactions 16: 1421−1430.
- Sarkar, D. 2008. Lattice Multivariate Data Visualization with R. 2008. Springer, New York, NY, USA.
- Sparnaaij, L.D.; Bos, I. 1993. Component analysis of complex characters in plant breeding. I. Proposed method for quantifying the relative contribution of individual components to variation of the complex character. Euphytica 70: 225−235.
- Szabó, G.; Elek, Z.; Szabó, S. 2008. Study of heavy metals in the soil-plant system. Cereal Research Communications 36: 403−406.
- Van Wijk, J.J. 2005. The value of visualization. p. 79-86. In: VIS 05. IEEE Visualization, Piscataway, NJ, USA.
- Varma, V.A.; Pekny, J.F.; Blau, G.E.; Reklaitis, G.V. 2008. A framework for addressing stochastic and combinatorial aspects of scheduling and resource allocation in pharmaceutical R&D pipelines. Computers and Chemical Engineering 32: 1000–1015.
- Wegman, E.J. 1990. Hyperdimensional data analysis using parallel coordinates. Journal of the American Statistical Association 85: 664−675.
- Wegman, E.J.; Carr, D.B. 1993. Statistical graphics and visualization. Handbook of Statistics 9: 857−958.
- Wegman, E.J.; Said, Y. 2011. Color theory and design. WIREs Computational Statistics 3: 104−117.
- Wilkinson, L. 2005. The Grammar of Graphics. 2.ed. Springer, New York, NY, USA.
- Winderbaum, L.; Ciobanu, C.L.; Cook, N.J.; Paul, M.; Metcalfe, A.; Gilbert, S. 2012. Multivariate analysis of an LA-ICP-MS trace element dataset for pyrite. Mathematical Geosciences 44: 823–842.
- Wnuk, A.; Górny, A.G.; Bocianowski, J.; Kozak, M. 2013. Visualizing harvest index in crops. Communications in Biometry and Crop Science 8: 48−59.
- Zeileis, A.; Hornik, K.; Murrell, P. 2009. Escaping RGBland: selecting colors for statistical graphics. Computational Statistics & Data Analysis 53: 3259−3270.
Edited by
Publication Dates
-
Publication in this collection
Mar-Apr 2017
History
-
Received
23 Nov 2015 -
Accepted
23 May 2016