Abstract
The motion of a particle constrained to move between two walls one of which is moveable is solved. We determine analytically the effective forces that act on the particle or on the moveable wall. The quantal version of the solution is briefly discussed.
Inverse Dynamics in the Classical Fermi Accelerator
M.S. Hussein1 1 Supported in part by CNPq (Brazil). e-mail: hussein@if.usp.br 2 Supported by the National Science Foundation , and M.P. Pato
Nuclear Theory and Elementary Particle Phenomenology Group,
Departamento de Física Nuclear, Instituto de Física,
Universidade de São Paulo. C.P. 66318, 05389-970, São Paulo, SP, Brazil
V. Kharchenko2 1 Supported in part by CNPq (Brazil). e-mail: hussein@if.usp.br 2 Supported by the National Science Foundation
Institute for Theoretical Atomic and Molecular Physics at the
Harvard-Smithsonian Center for Astrophysics
60 Garden Street
Cambridge, Massachusetts 02138 U.S.A.
Received June 22, 1997
The motion of a particle constrained to move between two walls one of which is moveable is solved. We determine analytically the effective forces that act on the particle or on the moveable wall. The quantal version of the solution is briefly discussed.
I. Introduction
Classical Mechanics text books discuss friction forces without paying much attention to the dvnamics behind their origin. It would be useful for didatical purposes, to develop simple models that allows one to "derive'' friction forces and thus enables one to discuss their properties.
In this paper we fully solve a simple one-dimentional problem for this purpose. The problem at hand is that of the motion of a particle of mass m constrained within a region bounded by two walls one with infinite mass and the other with arbitrary mass M > m.
When the wall with mass M is oscillating the system is called a Fermi Accelerator [1] and has been investigated in the past by Ulam [2]. Usually Ulam's model has been used for he investigation of the stochastic acceleration of the light particles in collisions with the moving heavy obJects [2-5]. In this paper we study a simpler problem of a free movable wall. The model can be schematized as in Fig. 1. In contrast to the Fermi accelerator, we study the inverse process, where the kinetic energy of the light particle is ransferred to the heavy particle - the movable wall. Upon hitting the fixed wall the particle loses momentum but not energy whereas collision with the movable wall allows for loss of momentum and energy. Our model is relevant to studies involvin the confinement of ultracold neutrons in bottles [6]. Further, it is analytically fully soluble. In Section II, for a given value z º m/M, we solve, fully the problem and obtain the value of the velocities of the particle, nn, and the movable wall, Vn, after their nth collision. In Section III, we discuss the effective force that acts on the light particle due to the collisions with the wall. In Section IV we give a brief discussion of the quantum mechanicaI solution recently obtained by Hussein and Kharchenko [7]. Finally, in Section V we present our concluding remarks.
II. Exact solution of the Inverse Fermi Accelerator
The conservation of momentum and energy after the n collision is given by the following recursive formula
The solution of the above equations can be written in a matrix form
where we have introduced the parameter
Recursion relation given by Eq.2 allows to evaluate the velocities of the light and heavy particles after n-th collisions, if their initial velocities are known:
Momentum and energy transfer between heavy and light sub-systems is stopped after some number of collisions. i. e. there is a critical n, nc, after which the particle always lags behind the now moving wall.
To obtain a closed expression for Vn and nn we first recognize that Eq.(2) can be thought of as an evolution equation for a two-dimensional velocity vector which we call
This vector is not conserved, neither its length nor its direction, and the velocity evolution matrix  describes these changes.
describes these changes.
It is possible however, to define a constant-length vector in the phase space form the energy conservation equation Eq.1b. vis [8]
Clearly
which is a constant. In this case the collisional evolution of the system is described by the phase Fn of the  n vector
n vector
Thus
n evolves in a circle and the matrix that relates the components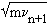 and
and 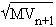 to
to 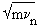 and
and 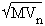 is an elementary rotation
is an elementary rotation
Call
Thus
which is the rotation matrix in two dimensions through angle a. Clearly, after n collisions the velocity evolution matrix is given by Bn
Thus
Or finally the velocity vector projections from the Eq.(5) satisfy the eliptic equations
and
where the initial phase angle F0 can be calculated via the initial velocities of the Eq.(4). The magnitude of the total phase Fn = na+ F0 is restricted: |Fn| £ 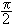 and it allows the evaluation of the maximum number of collisions Nmax, for a system with arbitrary initial conditions and mass ratio z = m/M. Indeed, according to Eq.(14)
and it allows the evaluation of the maximum number of collisions Nmax, for a system with arbitrary initial conditions and mass ratio z = m/M. Indeed, according to Eq.(14)
where the function Int[x] gives the greatest integer less than or equal to x. The evolution of velocities, Eq.(14), is more simple in the case of zero initial velocity of the moveable wall, V0 = 0. The initial phase F0 = O and
The total number of collisions n = n(0)c between particle and wall is restricted by the conditions Vn£ nn, or tg(nc(0)) £ 1/z1/2. The last inequality can be written as the restriction of the total angle of rotation in the phase space na:
For the adiabatic limit z = m/M << 1 the elementary phase angle a is very small (a 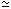 2z1/2), Fnc(0)
2z1/2), Fnc(0)
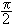 and critical value nc(0) can be estimated as
and critical value nc(0) can be estimated as
To verify the above findings, we have numerically solved Eq.(2), taking for initial conditions n(0) = n0 = 1, V(0) = 0, r(0) = 0, R(0) = R0 = 1 (see Fig. 1). The results are shown in Figs. 2 and 3 for z = 4 ×10-2 and 10-4, respectively. The value of nc in Figs. 2 is 5, close to
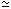 4. In Fig. 3, we have nc(0)
4. In Fig. 3, we have nc(0)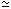 78. compared to
78. compared to 
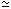 78.5. Further, Fig. 3 shows a rather smooth function of time. The agreement with the analytical results, Eq.(19), is excellent. This would allow the extraction of an effective friction force which we discuss in the following section.
78.5. Further, Fig. 3 shows a rather smooth function of time. The agreement with the analytical results, Eq.(19), is excellent. This would allow the extraction of an effective friction force which we discuss in the following section.
Figure 2. The velocities nn and Vn vs. t for z = 4 ×10-2, m = n0 = R0 = 1.
Figure 3. Same as Fig.2 for z = 10-4.
For a system with arbitrary initial velocities the critical (or total) number of collisons between particle and moveable wall nc is defined as a maximal value of n satisfying velocity conditions nn³ Vn, or tg Fn£  :
:
For the adiabatic limit z = m/M £ 1 the elementary phase angle a is very small (a 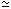 2z1/2 ), and one can derive the asymptotic formula
2z1/2 ), and one can derive the asymptotic formula
It is important to note, that the intial phase angle F0 can be positive or negative, depending on the relative orientation of the particle and the wall velocities. If the wall initially moves to the left, F0 < O and the number of collisions ns, needed to stop the wall or to change the wall velocity direction is
where the initial kinetic energies of the light particle and the moveable wall are denoted by k0 and K0 respectively. The situation during these ns, collisions can be described as an acceleration of the particle as the kinetic energy of the wall is transferred to it until the wall comes to a halt, followed by the inverse Fermi acceleration when the particle losses energy. The critical number of collisions for arbitrary initial velocities is
where n(-)c and n(+)c are critical number of collisions for the initial movable wall velocity towards and away from the stationary wall. Phase space diagrams for the different initial conditions are shown in the Fig. 4. From the Eqs. (22), (23) it is not difficult to extract the collisionless condition n(+) = (n(0)c -ns) £ 0, that is identical to the velocity relation V0³ n0. According to Eq. (22) the maximal number of the collisions nededed to stop the wall is ns
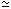 n(0)c and thus n(-)c = 2n(0)c
n(0)c and thus n(-)c = 2n(0)c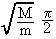 . This result shows a good agreement with our general estimate of the maximal number of collisions from Eq.(16): Nmax =
. This result shows a good agreement with our general estimate of the maximal number of collisions from Eq.(16): Nmax = 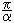
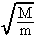 , which is given for the particular case of asymptotically small value of z. The method of finite rotation in phase space, developed in his Section, provides the exact evaluation of the velocity evolution matrix. Natural generalization of this method for the completely quantal Fermi accelerator system allows also to find the exact quantum solution, as has been shown in [7].
, which is given for the particular case of asymptotically small value of z. The method of finite rotation in phase space, developed in his Section, provides the exact evaluation of the velocity evolution matrix. Natural generalization of this method for the completely quantal Fermi accelerator system allows also to find the exact quantum solution, as has been shown in [7].
The phase space diagram for the positive (a) and negative (b) velocity projection of moveable wall.
III. The particle-wall effective force
In this section the particle wall effective force is studied for the strong adiabatic condition, when the parameter z << 1 and elementary rotational angle a 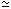 2z1/2 is very small. The critical number of collisions in this case is very large (see Eqs.(19),(23)) and for the description of the velocity evolution of both the particle and the wall we can use a quasi-continuous variable n related with the time
2z1/2 is very small. The critical number of collisions in this case is very large (see Eqs.(19),(23)) and for the description of the velocity evolution of both the particle and the wall we can use a quasi-continuous variable n related with the time
We write for the time variation of the kinetic energy of m the following rate equation
where Fef, represents the effective force felt by m due to its collisions with the moveable wall. Clearly, from conservation of total energy,
Since, from Eq. (17)
Or with Eq. (24)
thus
and
which gives
or
Now Rn(t) can be obtained from Eq.(32) by simple integration. A closed expression is obtained by setting az-1/2 ~ 2 which is an excellent approximation for  << 1. We thus find
<< 1. We thus find
Putting things together, we finally obtain for the effective force the following expression
or
and
The above functions peak at n0/ , z1/2n0/
, z1/2n0/ and R0/
and R0/ z1/2n0 respectively. Before we end this section, we give in the following the expression for the acceleration of the movable wall, d2R/dt2. From Eq.(34), we find
z1/2n0 respectively. Before we end this section, we give in the following the expression for the acceleration of the movable wall, d2R/dt2. From Eq.(34), we find
The numerically generated effective force is shown as functions of n0-n, V and t, in Figs. 5, 6 and 7, respectively, for z = 10-4. The agreement with our analytical formulae, Eqs. (35), (36) and (37) is excellent. We should mention, however, that Eqs. (35-38) are approximate formulae valid in the limit of a very large number of collisions and at times shorter than the time, tc, at which the velocities attain their terminal values. Clearly, at longer times the acceleration is identically zero. Before we end this section, we comment on the difference between the effective "friction" force, given by m and the acceleration force M
and the acceleration force M . Whereas the movable wall of mass M receives energy through energy - and momentum-conserving collisions with m, the particle suffers also momentum-nonconserving collisions with the fixed wall. In each of these collisions, say the nth one, a quantity of momentum, 2mnn, is lost to the fixed wall. This is basically the reason why Fef/m, Eq.(37), is qualitativelv different from
. Whereas the movable wall of mass M receives energy through energy - and momentum-conserving collisions with m, the particle suffers also momentum-nonconserving collisions with the fixed wall. In each of these collisions, say the nth one, a quantity of momentum, 2mnn, is lost to the fixed wall. This is basically the reason why Fef/m, Eq.(37), is qualitativelv different from  of Eq.(38).
of Eq.(38).
Figure 5. The friction force corresponding to the case of z = 10-4 (Fig.3).
Figure 6. Same as Fig.5 but vs. V.
Figure 7. Same as Fig.6 but vs. time.
IV. Semiquantal treatment of the inverse Fermi accelerator
In a recent work [7] two of us soived the problem of the inverse Fermi accelerator quantum mechanically for the light and heavy particles. The solution was obtained for different limits: the semi-quantal, the full Born-Oppenheimer and the exact solutions were presented. It is instructive to compare the classical results obtained in the present paper. with the semi-quantal solution. where the moving wall is treated classically while the particle quantum mechanically. The quantized motion of the particle is fully described by the normalized wave function
n = 1,2 ....
The eigenenergies, e1 are
The classical "Hamiltonian" that describes the motion of the wall is accordingly given by
It is clear that there are infinite number of Hamiltonians corresponding to the infinite number of eigenstates of m described by (39). From the equation of motion follows
On the other hand, the conservation of total energy gives
Thus
With Eq.(44), Eq.(42) becomes
Notice, that all reference to quantum mechanics in (45) is contained in the definition of the terminal velocity V¥, Eq. (44). We see from (38) and (45) an apparent equality between the classical and semiquantal treatments of the inverse Fermi accelerator. There is, however, an important difference between the two. As we have discussed in Section III, Eq.(38) is valid only at times shorter than the limiting time tc. On the other hand, when treated quantum mechanically, the particle will have continuous distribution of velocities. Accordingly the interaction between wall and the particle may be considered "continuous'' thus making Eq.(45) valid for all times.
V. Conclusions
In this paper the classical solution of the inverse Fermi accelerator is presented in details. The effective "friction" force that acts on the particle due to its collisions with the moveable wall in derived. A semiquantal solution of the problem is also presented. The classical and quantal accelerating forces that act on the movable wall were found to be identical at times shorter than the critical time at which classically the particle and wall attain their terminal velocities.
Aknowledgement
This work was partially supported by the National Science Foundation through a grant for the Institute for Theoretical Atomic and Molecular Physics at Harvard University and Smithsonian Astrophysical Observatory.
References
-
1.
- E. Fermi. Phys. Rev. 75, 1169 (1949). 2.
- S. Ulam, Proc. 4th Berkeley Symposium on Mathematics and Probability 3, 315 (Berkeley-Los Angeles, 1961). 3.
- A.J. Lichtenberg and A.M. Lieberman, Regular and Chaotic dynamics, Springer, Berlin, 1992. 4.
- G. M. Zaslavsky, Chaos in dynamic systems, Harwood Academic Publishers, New York, 1985. 5.
- J. V. Jose and K. Cordery, Phys. Rev. Lett., 56, 290 (1986). 6.
- W. Mampe, P. Ageron. C. Bates, J. M. Pendlebury and A. Steyerl, Phys. Rev. Lett. 63, 593 (1989). 7.
- M.S. Hussein and V. Kharchenko, Ann. Phys. (NY) (1995), in press. 8.
- R.H. Romer, Am. J. Phys. 35, 862 (1967).
- 1. E. Fermi. Phys. Rev. 75, 1169 (1949).
- 2. S. Ulam, Proc. 4th Berkeley Symposium on Mathematics and Probability 3, 315 (Berkeley-Los Angeles, 1961).
- 3. A.J. Lichtenberg and A.M. Lieberman, Regular and Chaotic dynamics, Springer, Berlin, 1992.
- 4. G. M. Zaslavsky, Chaos in dynamic systems, Harwood Academic Publishers, New York, 1985.
- 5. J. V. Jose and K. Cordery, Phys. Rev. Lett., 56, 290 (1986).
- 6. W. Mampe, P. Ageron. C. Bates, J. M. Pendlebury and A. Steyerl, Phys. Rev. Lett. 63, 593 (1989).
- 7. M.S. Hussein and V. Kharchenko, Ann. Phys. (NY) (1995), in press.
- 8. R.H. Romer, Am. J. Phys. 35, 862 (1967).
Publication Dates
-
Publication in this collection
14 June 1999 -
Date of issue
Dec 1997
History
-
Received
22 June 1997




















































