On the Thermodynamics of Ionized Gases

On the Thermodynamics of Ionized Gases

Christine Fernandes Xavier

Departamento de Estado Sólido e Ciência dos Materiais, UNICAMP

Caixa Postal 6165, Campinas, Brazil

G. M. Kremer

Departamento de Física, Universidade Ferderal do Paraná

Caixa Postal 19081, 81531-990, Curitiba, SP, Brazil

Dedicated to Roberto Luzzi on the occasion of his sixtieth birthday

Received March 20, 1997

The transport coefficients of a completely ionized gas are determined from an extended thermodynamic theory of mixtures of ideal gases in the presence of external electromagnetic fieds. The Onsager relations for the transport coefficients in the presence of external magnetic flux density are also discussed.

I. Introduction

The extended thermodynamic theory for a mixture of n ideal gases was first formulated by Kremer [1] as a field theory whose objective was the determination of 13 n fields of partial mass densities, partial velocities, partial pressure tensors and partial heat fluxes.

Recently Pennisi and Trovato [2] analised the same problem and incorporated the electric charge of the constituents and the influence of electromagnetic fields, but they have not obtained the dependence of the transport coefficients on the external magnetic flux density. It is well known in the literature of ionized gases that the transport coefficients do depend on the external magnetic flux density (see for example Balescu [3] or Rodbard, Bezerra Jr. and Kremer [4]).

The purpose of this work is to obtain - from a phenomenological extended thermodynamic theory of a fully ionized gas - the laws of Navier-Stokes, Fourier and Ohm and to find the dependence of the transport coefficients on the external magnetic flux density. In Section II we base on [1] and remind the principal features of extended thermodynamics of mixtures of n ideal gases, while in Section III we present the so-called one-fluid theory of an ionized gas whose objective is the determination of the five fields of density, velocity and temperature. The constitutive equations for the partial pressure deviators and partial heat fluxes are calculated in Section IV by the use of a method akin to the Maxwellian iteration method of kinetic theory of gases (see [5]). The laws of Navier-Stokes, Fourier and Ohm are obtained in Section V and the transport coefficients are calculated as functions of the external magnetic flux density. In Section VI we discuss the Onsager reciprocity relations in the presence of external axial fields. The representation and the inverse of second- and fourth-order tensors that depend on an axial field are given in the Appendix.

Cartesian notation for tensors with the usual summation convention is used. Parentheses denote symmetrization of all indices while angular parentheses indicate traceless symmetrization.

II. A reminder of extended thermodynamics of mixtures

We may say that objective of extended thermodynamics of ionized gases is the determination of 13n fields of

- partial mass densities, - partial velocities, - partial pressure tensors, and - partial heat flux vectors, (2.1)

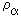
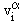
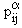
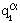
where a = 1,2,...,n denotes the constituents of a mixture of electrons, ions and neutral particles.

To achieve this objective, we need 13 n field equations that are based on the following balance equations for the moments (2.1):

In the above equations = and are higher-order moments while , and are production terms. The production term is constrained by the relation

which expresses the conservation of the total momentum density. Moreover, and are the electric charge and the mass of a particle of constituent a in the mixture, E_i is the external electric field and B_i the external magnetic flux density.

To close the system of equations (2.2)-(2.5) we assume , , , and as constitutive quantities that depend on the basic fields (2.1). Through the explotation of the principle of material frame-indifference and of the entropy principle we get the following linearized constitutive equations:¹

We have introduced above the velocity difference .

III. The one-fluid theory

It is usual in the literature (see for example [3]) to describe an ionized gas by the so-called one-fluid theory whose objective is the determination of five fields of mass density r, velocity v_i and temperature T. These fields are defined with respect to the partial fields as:

where n_a = r_a/m_a is the number density of constituent a and n = å_a = 1ⁿ n_a. Here we shall suppose that all constituents have the same temperature, which is the temperature of the mixture T.

To determine the five fields above we base on the following balance equations for the mass density r, momentum density rv_i and internal energy density re:

where E^* = E+(v×B). The above equations were obtained by summing over all constituents of the mixture the equations (2.2), (2.3) and the trace of equation (2.4). Moreover, we have introduced the electric current density I_i, the pressure tensor p_ij, the heat flux vetor q_i and the internal energy density through the relationships:

where u_i^a and r_ae_a are the diffusion velocity and the internal energy density of constituent a in the mixture, respectively, which are defined by

To get a system of field equations from (3.2)-(3.4) one has to consider e, p_ij, q_i and I_i as constitutive quantities that depend on the basic fields r, v_i, T. Since we are dealing with an ideal gas and interested only in a linear theory, e and are known functions of r and T. In the next section we shall show how to get the constitutive equations for p_áijñ, q_i and I_i from the system of field equations of extended thermodynamics.

IV. The Maxwellian iteration method

In most applications of plasma physics the ionized gas is in a state of complete ionization, i.e., it is considered as a binary mixture of ions (a = I) and eletrons (a = E). Here we shall restrict ourselves to this case.

First we note that there are only n-1 linearly independent diffusion velocities, since

For the binary mixture in study we have u_i ^I = -r _Eu_i ^E/r _I and the following relationship hold:

On the other hand, in a linearized theory equations (3.5)₂ and (3.6)₂ reduce to:

since .

To get the constitutive equations for p_áijñ^a and q_i^a we proceed as follows: we insert the constitutive equations (2.7)-(2.10) into the equations (2.3), (2.5), and into the traceless part of equation (2.4), consider only linear terms in the resulting equations. Hence

by performing some rearrangements. Equation (4.4) follows by subtraction of the ion equation from the electron equation. Now we use an iteration method akin to the Maxwellian iteration of kinetic gas theory (see [5]). For the first iteration step we insert the equilibrium values I_i⁽⁰⁾ = 0, p_{áij ñ}^a(0) = 0 and q_i^a(0) (a = E,I) into the left hand side of equations (4.4)-(4.6) and obtain the first iterated values I_i⁽¹⁾, p^a(1)_{áij ñ} and q_i^a(1) on the right hand side:

In the above equations we have introduced

where m_a (a = E,I) is the chemical potential of constituent a. For simplicity from now on we shall drop the index (1) that denotes the iterated value.

From the system of equations (4.9) we obtain:

by using equations (B.4) and (B.5) of ^{Appendix B}, where

The coefficients a₁^a through a₆^a are given in ^{Appendix A}.

Now by the use of equation (B.9) of ^{Appendix B}, it follows from the system of equations (4.8):

where

The coefficients b₁^a through b₅^a are also given in ^{Appendix A}.

V. The laws of Navier-Stokes, Fourier and Ohm

In a linearized theory the presure tensor and the heat flux vector of the mixture are given by equations (4.3). Hence by the use of equations (4.14) and (4.3)₁, one can get

which is the mathematical expression of the law of Navier-Stokes. The fourth-order tensor h_áijñáklñ is identified with the coefficient of shear viscosity and it is given by

On the other hand, the law of Fourier is obtained from equations (4.12) and (4.3)₂:

K_ij denotes the tensor of thermal conductivity and L_ij the tensor of a electrical thermal effect. They are given by

Finally the law of Ohm follows from equations (4.7) and (4.12):

In the above equation we identify S_ij as the electrical resistivity tensor and L^*_ij the tensor of a thermal electrical effect. The expressions for S_ij and L^*_ij read:

VI.The Onsager relations

In a linearized theory the entropy flux is given by (see equation (9.2)₃ of [1]):

or by the use of equation (5.3):

where according to (5.4)₂, D_ij is given by

On the other hand, one can obtain from equations (5.5) and (4.11) that

where the coefficient D_ij^* is given, in conformity with (5.7), by:

In a linear irreversible thermodynamics (see for example [6])

are identified as thermodynamic fluxes while I_i and as thermodynamic forces. Besides, the following symmetric relations are postulated for the coefficients in the presence of a magnetic flux density B:

which are known as the Onsager reciprocity relations.

The relationships (6.6) are satisfied since the coefficients are expressed in a form like the one given by equation (4.13). However, the relationship (6.7) is not satisfied in general as it can be seen from equations (6.3) and (6.5). In order to get such a relationship we base on [1] and assume that:

• the production term of the partial heat fluxes do not depend on the diffusion fluxes, so that H

  ^V

  _EE = H

  ^V

  _IE = 0;

• the production term of the partial momentum density do not depend on the partial heat fluxes, so that M

  ^q

  _EE = M

  ^q

  _EI = 0.

With the two above assumptions it is easy to show from equations (A.4), (A.5), (A.6), (A.8)₂ and (A.9) from ^{Appendix A} that a^a₄ = a₅^a = a₆^a = 0 for a = E,I, and from equation (4.13)₂ thet L_ij^E = L_ij^I = 0. Hence, it follows

Appendix A: Scalar Coefficients

The scalar coefficients of q_i^a are given by:

provided H^q_EI¹ 0, and where

The scalar coefficients of p^a_áijñ are:

where:

with

Appendix B: Representation and Inverse of Tensors

Let T_ij be an isotropic second-order tensor that is a function of the axial vector B. The representation of T_ij is given by:

where a, b and c are scalar coefficients that depend on B². The inverse of T_ij is obtained from the Cayley-Hamilton theorem, which can be written as:

with I₁, I₂ and I₃ denoting the scalar invariants

Hence for T_ij given by (B.1) we have

where

Let T_ijkl be and isotropic fourth-order tensor symmetric in the indices (i,j) and (k,l) that is a function of the axial vector B, and let S_ij be an arbitrary symmetrical tensor. According to the tables of Smith [7] the representation of the tensor T_ijkl S_kl, which is linear in S and depends on the skew-symmetric tensor W_ij = e_ijkB_k, is given by

where a₁ through a₈ depend on (W²)_rr. By taking the derivative of equation (B.6) with respect to S and returning to the axial vector B, we get the desidered representation for T_ijkl. Since we are interested only in the fourth-order tensor T_{áijñákl ñ}, which is symmetric and traceless in (i,j) and (k,l), by performing the symmetrization it reduces to:

where a through e are scalar coefficients tha depend on B².

The inverse of T_áijñáklñ is found by the use of the relationship

and it reads

Acknowledgement

One of the authors (G. M. K.) gratefully acknowledges the support of the Conselho Nacional de Desenvolvimento Cientí fico e Tecnológico of Brazil.

References

1.
• G. M. Kremer, Int. J. Engng. Sci. 25, 95 (1987).
2.
• S. Pennisi and M. Trovato, Continuum Mech. Thermodyn. 7, 489 (1995).
3.
• R. Balescu Transport Processes in Plasmas Vol.1 (Classical Transport), North-Holland, Amsterdam (1988).
4.
• M. G. Rodbard, A. G. Bezerra Jr. and G. M. Kremer, Phys. Plasmas 2, 642 (1995).
5.
• E. Ikenberry and C. Truesdell, J. Rational Mech. Anal. 5, 1 (1956).
6.
• S. R. de Groot and P. Mazur, Non-equilibrium Thermodynamics, North-Holland, Amsterdam (1962).
7.
• G. F. Smith, Int. J. Engng. Sci. 9, 899 (1971).

Appendix A

Appendix B

¹

We have restricted to a classical ideal gas where

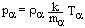and dropped out all constants of integrations.

Publication Dates

• Publication in this collection
  14 June 1999
• Date of issue
  Dec 1997

History

• Received
  20 Mar 1997