General aspects of the thermodynamical formalism

General aspects of the thermodynamical formalism

Evaldo M. F. Curado

Centro Brasileiro de Pesquisas Físicas,

Rua Xavier Sigaud 150, Rio de Janeiro, Brazil

Received 07 December, 1998

We present some recent developments concerning general aspects of the thermodynamical formalism. Through simple arguments, we exhibit some basic entropies that have most of the thermodynamic properties of the Shannon entropy. Their stabilities are also analysed, and several points concerning nonextensive thermodynamics are discussed.

I Introduction

The growing field of research concerning nonextensive thermodynamics has a hard task to do. In order to have nonextensivity it could be necessary to release the well-known Boltzmann-Gibbs-Shannon (BGS) entropy and, maybe, to substitute it by another entropic form. We are therefore obliged to relax some of the Khinchin axioms, because they lead only to the BGS entropy. Relaxing the fourth axiom, related to additivity, the possible entropy of a nonextensive system must obey only the first three Khinchin axioms, but these axioms are so weak that an enormous amount of entropic forms are allowed.

With the proposition by Tsallis [1] of a different entropic form that has been shown to satisfy the whole thermodynamic formalism [2] and to have very interesting properties [1, 2, 3], the study of alternative forms of entropy in the study of nonextensive physical problems has begun. These alternative forms have been used principally in problems where the standard statistical mechanics fails, as for example in some problems with long range interactions, long term memory or some kind of intrinsic fractality [4]. This relatively new field of research on nonextensive generalizations of standard Boltzmann-Gibbs statistical mechanics is very promising but has been centered on applications of Tsallis statistics and not many papers have been dedicated to the general aspects of the nonextensive statistical mechanics. To discuss these general aspects let us start with the Khinchin axioms [5], that provide some of the conceptual tools of information theory. These axioms are:

• The entropy is a function only of the probabilities. It is continuous and differentiable with respect to them;

• The entropy has a maximum at the equiprobability configuration;

• The addition of a null event does not change the value of the entropy, that is,

  S(

  p

  ₁,

  p

  ₂, ¼,

  p_W) =

  S(

  p

  ₁,

  p

  ₂, ¼,

  p_W,

  p_W+1 = 0);

• Let a system S (with an entropy

  S) be composed by two sub-systems, S

  ^A (with an entropy

  S^A) and S

  ^B (with an entropy

  S^B). Let {

  p_ij} be the probability distributions associated to the system S and {

  } ({

  }) the probability distributions associated to the sub-system A (B). The fourth axiom says that

where the sum over i (j) refers to the states of sub-system A (B). The term S^B({}|) means the conditional entropy of system B under the situation where the system A is at the state i. When the two sub-systems are independent, not correlated, we get directly the additivity property of the entropy S({p_ij}) = S^A({}) + S^B({}).

Khinchin has shown that only the Shannon entropic form satisfies these axioms. If the fourth axiom is a little bit relaxed and, instead, we assume only the less restrictive condition that the entropies are additive when the sub-systems are not correlated, then the Renyi entropy [6] also satisfies the axioms. In order to try to restrict the huge number of entropic forms allowed by relaxing the fourth axiom, we study some basic properties that any reasonable entropy must present and the limitations imposed by these properties.

We will show in this paper that there are some basic entropic forms that satisfy almost automatically the first three axioms and are the "basis'' for other more complex entropic forms. This can be reached by an analysis of the symmetry of permutation of the probabilities, S(p₁, ¼, p_i,¼, p_j, ¼, p_W) = S(p₁, ¼, p_j,¼, p_i, ¼, p_W) , that any entropic form must obey. The value of the entropy should not depend on the position of the probabilities, but only on their values. We also analyse the thermodynamical-like formalism behind them and their stability. We show some conditions that must be obeyed by more complex entropies in order to satisfy the first three axioms and the whole structure of thermodynamics. The stability of these entropies is analysed and some general properties of more complex entropies are discussed.

II Generality of the thermodynamical formalism

Recently, two very interesting papers have appeared, illustrating in a clear way, the generality of the thermodynamical formalism [7, 8]. Essentially their results allow us to say that a large amount of the systems which present some quantity ("entropy'') that tends to an extremum, minimum or maximum does not matter, subjected to some constraints, should have a formalism analogous to the well-known thermodynamical formalism. This statement could appear strong, but the demonstration is really simple, and the interested people should read these papers for further details. Here only one point of these results will be sketched, related to the connection between the first and second laws of thermodynamics. Let us assume a phase space with a finite number of states, W, for simplicity. We postulate, as usual, an entropic form depending only of the probabilities of these states, that is, S = S({p_i}) , continuous with respect to the probabilities, differentiable and concave. 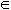Let us say, for analogy with standard thermodynamics, that we have, besides the constraint of the sum of probabilities , one constraint that we call U which depends on {p_i} and on a set of parameters {_i} ,

Suppose that we have other constraints, let us call them V_m, depending on the probabilities and on other (external) parameters ,

where the latin index i is related to the states and the greek index m is related to the constraints.

So, to find the extremum of the general entropy proposed, S({p_i}), with the constraint given by eqs.(1), (2) and , we have to extremize the function f:

where a, b and {l_m} are the Lagrange parameters which are considered fixed. After writing f with the solutions obtained by its extremization with respect to the probabilities, we have df = 0 , implying that

since . We have then, as consequence of the application of the Maximum Entropy Principle (MEP), the complete analogy of the first law of thermodynamics (obviously, the functions S, U, and {V_m} are now functions of the equilibrium probability distribution obtained by the extremization of f). Note that we have here a completely general entropic form S, satisfying only some basic requirements of concavity and analiticity ! Clearly, if we call T º (b^-1), the eq.(4) can be rewritten as dU = TdS - å_mTl_m dV_m. If we call dQ = TdS and dW = å_mTl_m dV_m the first law dU = dQ - dW is reobtained, for a general proposal of the entropic forms S({p_i}) ! We could then say that if some problem obeys the MEP, with some entropic form, then there exists an analogy of the first law of thermodynamic for this problem. It does not matter if the entropic form is different from Shannon's, this result depends only on the existence of a MEP for the system studied. In fact, the role played by the constraints given by eqs. (1) and (2) are, formally, absolutely equivalent. We have written them in a different form only to emphasize the analogy with thermodynamics, where one constraint, the energy, has a special role. We also could say, reversing the reasoning and on very general grounds, that the existence of some conservation law in some system involving some quantity that always tends to increase or decrease, implies the existence of a MEP for this system if it is possible to adopt this quantity as an entropic form. Also, as shown in [7, 8], the entire thermodynamical formalism is preserved and the Legendre transformations and the Euler relations are formally reobtained.

III Simplest entropies

The Shannon and Tsallis entropies have some very interesting features that other entropies do not have. Besides the thermodynamical formalism, that a large number of entropic forms satisfy, see [7, 8], these two entropies also have two differential points: simplicity and explicitness. By simplicity we mean that they have a simple form like

and satisfy all the basic Khinchin postulates - with the only exception of the fourth one for the Tsallis form. By explicitly we mean that, with these entropies, it is possible to obtain, explicitly, the probability distributions, the partition functions and all the relevant thermodynamical functions. This second point is extremely restrictive and only very few entropic forms satisfy this requirement. Clearly, this is not a physical limitation but rather an aesthetic one. The question about the existence of other entropic forms which have all the standard properties of entropies - with the exception of additivity - and which also allow us to obtain, explicitly, distribution probabilities, partition functions and all thermodynamic functions, is not obvious. We will try to find in this paper the simplest entropic forms that satisfy these points based mainly on the symmetry property of permutation of probabilities in the entropic forms.

To show the existence of simple forms of entropy, let us assume, as usual, that the entropic forms we are searching are functions only of the probabilities. Furthermore, the simplest way to write an entropic form respecting the symmetry of permutation of the probabilities is to write it as eq.(5), where all the functions s(p_i) are the same function (continuous, differentiable, definite concavity), independent of the index i. We note that, with this form, in order to satisfy the Khinchin axiom of null event we need only to define functions s(p) such that s(0) = 0. Also, to satisfy the desired condition that S(0,¼,1, ¼, 0) = 0, it is sufficient to add a global constant to the entropy S if our previous proposal of S does not fulfill this requirement. The axiom of having a maximum at equiprobability is not so obviously satisfied and we will return to it later, in section (IV). Hereafter, for simplicity, we will use adimensional entropic forms, i.e., we fix the constant k = 1. With respect to the constraints, we assume only the one given by eq.(1) (also for simplicity), which depends on parameters ({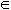_i}) that could be, for example, eigenvalues of the Hamiltonian (or any other operator). We will from now on call all the generalized functions by the name of their similar functions in thermodynamic (energy, free energy etc.). We believe that this will aid to easier understand the connections and analogies that the generalized formalism will present and will not lead to any misleading comprehension. Also, all the results obtained below are only formal, we have not studied in detail the "thermodynamical'' consequences of the new entropic forms introduced.

With respect to the constraints we have two situations:

a) usual constraints, given by the mean values of operators; and

b) arbitrary constraints, given by arbitrary forms of eq.(1).

III.1 Mean Value Constraints

Let us first start with the former case. For simplicity we will assume only one constraint (the extension to more constraints is straightforward). We have:

The extremization of the function

leads us to

where s¢(p_i) means ds(p_i)/dp_i. Assuming also that the function s¢(p_i) is invertible, we get for the probability distribution,

where g º (s¢)^-1 is the inverse function of s¢. We are here at the crucial point. To get the probability distribution and partition function explicitly we have to separate the Lagrange parameter a from the other ones (in our case we have only one more, b). In order to separate a from b we have two possibilities for the function g, which should satisfy one of the two following forms:

III.1.1 Product form

Let us analyse the product form given by eq. (12). The function that satisfies this condition is the exponential, so we have:

As g º (s¢)^-1 then (s¢)^-1 = exp . Furthermore s¢(p_i) µ log(p_i) implying

As and as the functions s(p_i) are adapted (using the constants of integration) to satisfy the first three Khinchin axioms, we get, without any additional hypotheses, only assuming that we want simple entropic forms, the Shannon entropy The validity of the whole structure of thermodynamics for this entropic form is obviously well-known by everybody.

III.1.2 Sum form

The eq. (11) could be satisfied by a linear function, i.e.,

As g º (s¢)^-1 , we have that (s¢)^-1(x) µ x, implying s¢(p_i) µ p_i. This result leads us to

Again, as S({p_i}) = 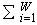s(p_i), we get,

This entropic form is known as "enstrophy'' and is related to the vorticity in turbulence problems. In these systems the enstrophy tends to be minimized instead of maximized. Also, this entropic form seems to be related to the Tsallis entropy with q = 2, but the constraints used by his theory (the so-called q-expectation values) are not mean values like here. Therefore, this entropy, with mean values, can not be reduced to a particular case of Tsallis q-statistical mechanics. What can we say about the existence of a thermodynamical formalism for this type of entropy? Could we succeed here to develop, explicitly, with the enstrophy, all the structure of the Legendre transformations present in the Shannon and Tsallis entropy? To answer this let us first minimize the enstrophy, eq. (13) with the constraints given by eqs. (7) and (8). This lead us to the following equation for the probability distribution (linear in the parameters 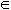_i):

The sum rule leads us to the expression for a:

The enstrophy and the "energy'' equation (8) can then be written as:

allowing us to immediately recognize that the following expressions are nicely satisfied:

where

Partition Function

Clearly we could define a partition function such that f(b) º f(Z) with Z = Z(b) . The definition of the partition function for the Shannon and Tsallis entropy is straightforward, but here this definition is not so immediate. The better way is to note that in both the Shannon and Tsallis entropy, when all the probabilities are equal (p_i = , "i), the expression obtained by the entropy (S = logW for Shannon and for Tsallis form) is exactly similar to the function f(Z) in equations like eq. (18), i.e., f(Z) = log Z for the Shannon and for the Tsallis entropy. Also, this functional form is the same as the one that appears in the relation between the free energy and the partition function in both cases (see [2] for details). To get the same relations here we note that, for the enstrophy, when all the probabilities are equal we have S = . So, along the lines exposed above, we impose that the eq.(21) be equal to , giving us the explicit expression for the partition function of the enstrophy:

Free Energy

We can also define a "free energy'' in a complete analogous way to standard thermodynamics. The free energy F = U - TS , where we have defined T = (b)^-1 , can be written as:

It is obvious that the expressions F = U - TS = -T are correct, exemplifying the connection and analogy with the thermodynamical formalism. The whole structure of Legendre transformation is preserved, and it would be very interesting to see this type of formalism applied to problems of turbulence, a kind of thermodynamics of turbulence, obtained from the minimization of the enstrophy.

Forbidden gap in the probability distribution

Substituting the eq. (15) in eq.(14) we get the following expression for p_i :

First we can see immediately that when T ® ¥ all p_i's go to the same value, . Also, considering that the probability distribution can not be negative nor greater than 1, these constraints lead to restrictions in the temperature range (we assume, as in Tsallis statistics, that p_i º 0 whenever the expression in the right hand side is £ 0). Here, because of the convexity of the enstrophy, the situation is inverse with respect to the usual statistical mechanics. The lowest allowable positive temperature does not privilege the lowest level and the highest negative temperature does not favor the highest level as standard statistical mechanics does. The actual situation is more subtle. Further, there exists a gap of forbidden temperatures which includes the zero temperature. The necessity of a gap (or cut-off) in turbulence problems has received support recently [9] (see also [10]), where the authors empirically assumed a cut-off in order to eliminate negative values of the probability distribution, with remarkable experimental agreement. Here, in this formalism, the cut-off is a natural exigency and is completely similar to the cut-off existing in the Tsallis statistics for example [1].

III.2 Arbitrary Constraints

We change in this case the equation of the constraint. We use equations (6) and (7) and replace eq.(8) by:

where s(p_i) is the same function of the probability present in the entropic form.

The extremization of the function,

gives us,

where s¢(p) = . Assuming that s¢ is invertible and calling g this function, i.e.,

we get:

To separate the Lagrange parameter a from b we have only two possibilities for the function g; this function should have one of the two following forms:

III.2.1 Product form

The solution for eq.(26) is :

implying that

This leads us to

By renaming + 1 = q, summing up over all W states and adequately choosing the constants of integration, we end up with the Tsallis entropy

The validity of the whole thermodynamic formalism for this entropic form was shown in [2]. Also, many very interesting properties and applications of this entropy have been shown in many papers in the literature, see [1, 2, 3, 4, 12]. This entropic form has also been applied to many problems that present probability distributions decaying algebraically, with excellent fitting in many situations. This entropy was derived here without any ad hoc hypotheses, only by searching for the simplest forms that satisfy the symmetry of permutation of the probabilities and allow the probabilities and partition functions to be obtained explicitly.

III.2.2 Sum form

A solution for eq. (27) is:

As g º (s¢)^-1 , we have that (s¢)^-1(x) µ log(x), implying: s¢(p_i) µ exp(-bp_i), where b is a constant. This result leads us to

Therefore, the entropy function s(p) is proportional to the exponential of the probability plus a constant. Again, as and by carefully choosing the constant needed to satisfy the first three Khinchin axioms, we get,

We could also add a constant = exp(-b) - 1 to get the property S(0, 0, ¼, 1, ¼, 0) = 0 but this is not so relevant here. This entropic form is unknown, at least to me, but it has very nice properties (let us call it the exponential entropy). Following the procedure of section(III) and adopting the constraint of the energy as

we get:

for the probability distribution,

exhibiting a logarithmic decay of the parameters

_i .

For the partition function we obtain:

for the exponential entropy:

for the energy:

and for the free energy:

where

The following relations are valid:

where we have called T = (b)^-1, and b is the Lagrange parameter. Clearly, all the thermodynamical relations, Legendre transformations, Euler relations etc, are also valid here. It is also possible to explicitly obtain all the relevant thermodynamical functions.

So, with the four simplest entropies presented here, and depending on the constraints, we cover practically all important types of possible behaviour of the probability distribution as a function of the parameters {

_i} - namely, the exponential case (Shannon entropy), the power law distribution (Tsallis entropy), the linear distribution (enstrophy) and a logarithmic distribution (exponential entropy). In some sense the Shannon entropy is the inverse to the exponential entropy (the probability distribution associated with Shannon's entropy - which is logarithmic in the probabilities - is exponential in the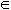 _i's and the probability distribution related to the exponential entropy - which is exponential in the probabilities - is logarithmic in the {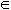_i}). Also the partition function is inverse in both cases, a sum of exponentials in the Shannon case and a sum of logarithms in the exponential case. The function f(Z) is also, in some sense inverse. f(Z) is a logarithm of Z using the Shannon entropy and is an exponential of Z using the exponential entropy. Apparently, these considerations do not have any practical consequence and are only amusing similarities - or anti-similarities. The table (1) summarizes these entropies, the constraints used and the type of separations - sum or product.

Table 1:
Simplest entropic forms

IV Stability

One important question with respect to these entropic forms is related to their stability. The stability of the Shannon entropy in the equilibrium state is one of the most important pillars of statistical mechanics. The Tsallis entropy has also shown similar properties of stability and we could ask about the stability of other entropic forms. The answer is rather more general then one could expect from the analysis of the two other entropic forms presented in this paper. In fact, we will analyse the stability of the general entropic form given by eq.(5), where the functions s(p_i) are concave or convex, under the presence only of the constraint 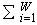p_i = 1 . The stability of this general entropic form under this constraint could be made by analysing the coefficients of the powers of l that appear from the determinant of the matrix M given by

where . If the coefficients of l have the same sign we have a maximum; otherwise, if the coefficients are alternately positive and negative there is a minimum [11]. For entropic forms like eq.(5) we have that S_ij = 0 whenever i ¹ j. Also, calculating this determinant for the equiprobability configuration, we can see that all S_ii have the same value, say a. The determinant of this matrix for a system with W states can then be written in a general form as:

showing that, for this type of entropic form, the equiprobability is an extremum of the entropy regardless of its specific function. The only requirement is that the functions s(p) be concave or convex. This convexity condition fixes the value of a: concave functions s(p) give a < 0 - corresponding to a situation of maximum - and convex functions give a > 0 - corresponding to a situation of minimum. So, if we choose the function s(p) to be a concave function, the entropic form S = 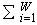s(p_i) will have a maximum at equiprobability! A relevant question here is if this is a global maximum or only a local one. We can proove that this is a global maximum by noting that the property of (any) concave function g(x)

where the {x_i} are points, applied to the concave functions s(p) leads us to

implying that

and by then showing that any configuration {p_i} must satisfy the inequality

So, if we write the entropic form S as in eq.(5) and assume that the function s(p) is concave, then this entropic form has a global maximum for equiprobability. The Khinchin axiom of the maximum of the entropy for equiprobability is obtained here as a consequence of the symmetry of permutation of the probabilities. Another question of lower importance remains: is this the only maximum or there are other local (not global) maxima? A strong negative argument to this question can be given, again, by the symmetry of permutation of probabilities in the entropic forms. Let us suppose, for example, that there are other maxima, besides that of equiprobability, and let us consider the situation where the number of other maxima is the minimum. This lower number of (hypothetic) maxima will occur when only one probability is different from all the others, that are all equal among themselves. Due to the symmetry of permutation of the probabilities we can see that there are W more maxima besides the maximum associated with the equiprobability. But as the form of the entropy does not depend on the number of states of the system, we can easily see that an entropic form like eq.(5) that admits other maxima than the maximum of equiprobability, will have to admit an infinite number of them (when W ® ¥), which is unacceptable, even if these maxima are not global maxima. Note that other configurations of {p_i} different from those discussed above actually have even more maxima than W, because the number of permutations is greater. So, there is only one (global) maximum (or minimum if the function s(p) is convex) - namely that obtained for equiprobability.

V Complex Entropic Forms

The previous results can be extended if we have, instead of an entropic form as above, entropic forms like S¢ = F(S) where S can be written as S = 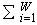s(p_i). If the function F is monotonically increasing (or decreasing), then the extremization of S¢ with some constraints, gives a probability distribution with the same behaviour as the extremization of S does. This is so because, for example, for mean value constraints we have:

But as and (because we have assumed that the function F was monotonically increasing or decreasing), we get

implying that we have only a renormalisation of the parameters a and b. For example the Renyi entropy can be seen as a monotonic function of the Tsallis entropy (or the enstrophy for q = 2). So, the extremization of this entropy with the same constraints leads to a power law probability distribution as the Tsallis entropy would provide. The parameters of the probability distribution are changed but the behaviour of the distribution is the same. In particular, the new parameters are not anymore the Lagrange parameters, but are related to them.

With respect to the stability conditions, we can immediately see that an increasing function F(S) has the same maxima that S has. Then, S¢ = F(S) also has only one maximum at equiprobability, just as S has. Therefore, for this large class of entropic forms, including all entropic forms of the type F(S), where F is a monotonic increasing function, the Khinchin axiom for the maximum of the entropy at equiprobability is obtained as a consequence. The only basic initial assumption is that the entropic forms are symmetric with respect to the permutation of the probabilities, continuous, differentiable and monotonous functions of the basic entropies. The axiom of Khinchin related to the invariance of the entropy if a null event is added is trivially satisfied here by adopting a function s(p) such that s(0) = 0. To satisfy the condition that the entropy S will be zero if we have one event with probability one, it is enough to add a global constant to the previous definition of the entropy. So, these two axioms are, in some sense, trivially satisfied here.

A different approach in the direction of more complex nonextensive thermodynamics could be tried using for example, instead of arbitrary constraints as done in section (III.2), a normalized constraint of the type (see [13]):

where in fact the new probability distribution

is being used. This procedure is equivalent to assume a new entropy S_P, given by

(where we have inverted the relation given by eq. (34)), and to adopt constraints of type mean value. To get this new entropy, we have, first, to consider the inverted equation (34),

which, after summing up, gives us a relation between

s(p_i) and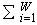 s^-1(P_i). This relation can be written in general form as:

where f is some function (related to s). Then, the new entropy could be written as:

If the function f is monotonous and the function s^-1 has a definite concavity, then the previous comments are valid. In general, this new entropic form does not lead to an explicit evaluation of the probability distribution (even if the previous entropy does), because it does not satisfy the requirements type sum or product. But, again, even if this explicit evaluation does not happen, this entropic form can easily satisfy the three Khinchin axioms and, if the function f is monotonous and s^-1 has a definite concavity, also the stability at equiprobability is guaranteed.

Other symmetric entropic forms

There is another general entropic form that trivially satisfies the symmetry of permutation of probabilities. This form could be written as:

with s(0) = 1. But taking the logarithm on both sides, we come back to an entropic form like eq.(5). Therefore the new entropies that appear using eq.(35) are essentially exponentials of the entropies already obtained. These strange entropies are, for example,

that correspond, respectively, to the exponentials of the Tsallis (and enstrophy too), exponential and Shannon entropies. These forms are then reduced to the previous one, and because the exponential is a monotonous function, all the comments made in the beginning of the section (5) are valid here.

VI Conclusion

We have shown some new results concerning general aspects of the thermodynamical formalism and exhibited some general properties of entropic forms based, essentially, on the symmetry of permutation of probabilities that an entropic form must satisfy. This symmetry indicates the simplest way to write general entropies, and the requirements of simplicity and explicitly allow us to derive some basic entropic forms that satisfy the whole thermodynamical formalism and where all ``thermodynamical" functions, probability distributions and partition functions can be explicitly calculated. Two of these entropies are already well known, one of them being the Boltzmann-Gibbs-Shannon entropy and the other one being the Tsallis entropy. Two more basic entropies were derived, one of them being essentially the enstrophy. Each one presents different types of decay of the probability distribution with respect to the parameters ( "energy levels'', for example). The stability of these basic forms was studied and the existence of a maximum at equiprobability was proved to be of general validity for these forms. This stability should also be valid for monotonic functions of these basic forms. In fact, the Khinchin axioms are satisfied here in an almost trivial way (the axiom of null event is really trivially satisfied). So, we have analysed, on theoretical grounds, the way an entropic form could be written, established some, in this sense, "basic'' entropies and the conditions (monotonicity) that more complex entropic forms should obey. The entropic forms that satisfy these requirements automatically satisfy the three remaining Khinchin axioms, are stable and satisfy the whole structure of transformations and relations of thermodynamics. It will be very interesting to complete some proofs indicated here and, in future works, to establish clearly the real important properties an entropic form should have to be successfully applied in nonextensive thermodynamics. The connection with real problems will be given, always, by the way probability distributions will decay with the parameters associated with the existing constraints (energy for example).

We acknowledge R. S. Mendes, A. R. Plastino, L. Borland, D. Prato and C. Tsallis for very fruitful discussions and interesting comments. We also acknowledge the financial support by CNPq and Pronex.

References

[1]
• C. Tsallis, J. Stat. Phys. 52, 479 (1988).
[2]
• E. M. F. Curado and C. Tsallis, J. Phys. A 24, L69 (1991); 24, 3178(E) (1991); 25 1019 (1992).
[3]
• A. M. Mariz, Phys. Lett. A 165, 409 (1992); A. R. Plastino and A. Plastino, Phys. Lett. A 177, 177 (1993); M. O. Caceres, ibid. 218, 471 (1995); C. Tsallis, Phys. Lett. A 206, 389 (1995); A. K. Rajagopal, Phys. Rev. Lett. 76, 3469 (1996); A. K. Rajagopal, R. S. Mendes and E. K. Lenzi, Phys. Rev. Lett. 80, 218 (1998); M.L. Lyra and C. Tsallis, Phys. Rev. Lett. 80, 53 (1998); L. Borland, Physica A 245, 67 (1998).
[4]
• A. R. Plastino and A. Plastino, Phys. Lett. A 174, 384 (1993); A. R. Plastino and A. Plastino, Phys. Lett. A 193, 251 (1994); D. H. Zanette and P. A. Alemany, Phys. Rev. Lett. 75, 366 (1995); C. Tsallis, S. V. F. Levy, A. M. C. Souza and R. Maynard, Phys. Rev. Lett. 75, 3589 (1995); A. R. Plastino and A. Plastino, Physica A 222, 347 (1995); D. A. Stariolo and C. Tsallis, Ann. Rev. Comp. Phys. II, Ed. D. Stauffer (World Scientific, Singapore, 1995); T. J. P. Penna, Phys. Rev. E 51, R1 (1995); V. H. Hamity and D. E. Barraco, Phys. Rev. Lett. 76, 4664 (1996); A. Lavagno, G. Kaniadakis, M. Rego-Monteiro, P. Quarati and C. Tsallis, Astrophys. Lett. and Commun. 35, 449 (1998).
[5]
• A. I. Khinchin, Mathematical Foundations of Information Theory, Dover, New York, 1957.
[6]
• A. Renyi, Wahrscheinlichkeitsrechmung, Deutscher Verlag der Wissenschaften, Berlin, 1966; see also A. Wehrl, Rev. Mod. Phys. 50, 221 (1978).
[7]
• A. Plastino and A. R. Plastino, Phys. Lett. A 226, 257 (1997).
[8]
• R.S. Mendes, Physica A 242, 299 (1997).
[9]
• X. -P. Huang and C. F. Driscoll, Phys. Rev. Lett. 72, 2187 (1994).
[10]
• B. M. Boghosian, Phys. Rev. E 53, 4754 (1996); C. Anteneodo and C. Tsallis, Journal of Molecular Liquids 71, 255 (1997).
[11]
• H. Hancock, Theory of Maxima and Minima, Dover, New York, 1960.
[12]
• C. Tsallis, Chaos, Solitons and Fractals 6, 539 (1995); Physica A 221, 277 (1995).
[13]
• C. Tsallis, R. S. Mendes and A. R. Plastino, Physica A 261, 534 (1998).

Publication Dates

• Publication in this collection
  17 Sept 1999
• Date of issue
  Mar 1999

History

• Received
  07 Dec 1998