Interband magneto-absorption in narrow-gap semiconductor quantum wells

Interband Magneto-Absorption in Narrow-Gap Semiconductor Quantum Wells

V. López-Richard^(a), G. E. Marques^(a), and C. Trallero-Giner^(b)

^aDepartamento de Física, Universidade Federal de São Carlos,

13565-905 São Carlos S.P., Brazil

^bDepartamento de Física Teórica,

Universidad de La Habana-10400, C. Habana, Cuba

Received February 6, 1999

A theoretical study of optical properties in narrow gap semiconductor quantum wells has been developed using an 8x8 Kane Hamiltonian. The interband transition selection rules have been obtained and a detailed description of the interband absorption using Voight and Faraday scattering configurations has been given. Interesting effects produced by the intraband admixture, such as spin-flip transitions, will be discussed. The complementation of measurements using different scattering configurations will be analyzed.

I Introduction

A good knowledge of the full electronic structure is an essential feature in order to get the best understanding of the optical and transport properties of a semiconductor heterostructure. Due to the great development reached by growth centers which use epitaxial techniques, the smoothness of interfaces is in the scale of one monolayer and this progress has permitted the experimental observation of a number of ultra fine aspects present in these properties. The application of external electric and\or magnetic fields and internal strains occurring due to the mismatch of lattice parameters at the interfaces, have the effect of breaking some hidden degeneracies and they may help to study as well as to explore these properties as possible optoelectronic devices.

The spatial confinement of carriers, the strong valence band mixing and conduction-valence band coupling lead to the observed complex subband dispersions with very interesting effects on the optical properties in the heterostructures, such as: large excitonic effects and oscillator strengths, special selection rules for optical transitions between levels, etc.

Magnetooptical techniques have reached their most advanced sophistication when applied to semiconductors with crystalline zinc-blende structure. It has already been pointed that band theories developed for diamond-type semiconductors are not directly applicable to zinc-blende-type systems, since the lack of inversion symmetry in the latter type induces a k-linear term in the Hamiltonian which is responsible for the coupling of ladders with different spin orientations.

Here we will be interested in study the magnetooptical properties in zinc-blende type CdTe-CgHgTe quantum wells as a function of the applied magnetic field. The main interest in structures based on HgCdTe solid solutions resides in their potential applications as infrared optical modulators, lasers, detectors and emitters [4]. In these narrow-gap structures the large nonparabolicity, the very strong interband mixing, the small effective mass of carriers and the possibility to reach the zero-gap semiconductor structures provide a rich variety of novel optical and electronic properties [5][6].

In order to be able to explore properly these properties one needs a good Hamiltonian model in which the intersubband couplings are considered and that is able to bring magnetic and internal strain fields within the same framework. Hence we will deal with a full 8x8 Hamiltonian, firstly proposed by Kane [7] and Luttinger [8] and later extended by Weiler [9]. The eigenstates obtained by such an approach consist in a combination of G point Bloch functions whose weights will define the character of the corresponding state at given conditions. This treatment shows the realistic picture of the energy dispersions of all carriers.

In this work we have selected a suitable basis set to expand the eigenstates of the quantum well Hamiltonian which contains its natural symmetry [10] and parity. It helps not only the reduction of the size of the Hamiltonians handled as well as the time spent with the numerical calculations and the unambiguous identification of admixed states which facilitates enormously the interpretation of the theoretical results.

The case of interband absorption for different polarizations of the incident light as well as for different scattering configurations will be discussed. There are many features related to band admixture that will be analyzed. The band coupling increases, in principle, the number of allowed transitions though some of them will appear to be very weak to be experimentally detected. Some effects like spin-flip transitions attract special interest and will be discussed. The anisotropic behavior of the absorption coefficient make complementary the results obtained using different configurations.

II Basic Hamiltonian Model

The functions | jñ , which are the periodic Bloch function at k = 0 will be numbered from j = 1,...,8 are order c⁺, hh⁺, lh⁺, so⁺, c^-, hh^-, lh^-, so^-, to represent the carrier type and the signs labeling the z-component of the total angular momentum J = L+S, respectively as

For this set of Bloch functions, the full k.p Hamiltonian can be written, in the Hermitian form, as:

where the operators in each matrix element is defined in terms of the creation ( annihilation ) operator as

In these expressions F, P, g₁, g₂, g₃ are the parameters associated to the effective masses and , q, N_w are the Luttinger and Weiler[9] parameters associated to the gyromagnetic factor[10] of all carriers in the full k.p model. Also, s = measures the energy in terms of the free electron cyclotron energy w_c, = defines the cyclotron radius, Edefines the band offset energy for conduction(valence) band at the interface of the heterostructure and E_g(D₀) is the band gap(spin-orbit energy) of the material in the quantum well structure.

The system treated in this work consists of a single quantum well with a magnetic field pointing along the(001) growth direction ( axis). In order to obtain a complete set of Landau levels for k.p Hamiltonian in the quantum well, the following set of basis functions will be used to expand the eigenstates {|(a)ñ}[1][2],

where repeated indexes represent sum over quantum numbers, |k_yñ = e^iky^y represents the free planewave component,| N ^j ñ is the quantum oscillator functions and the corresponding Landau level. Also, the envelope function component is a combination of all classical quantum well wavefunctions for the pure (parabolic) carrier type-j in subband-i. In this way, the chosen basis set contains the natural symmetry properties for the quantum well structure. The Landau level index N and the subband index m of the renormalized ''carrier'' are included in the index a. Finally, the notation used for labeling the subbands (e^-(+), hh^-(+), lh^-(+), so^-(+)) coincides with the dominant spinor component for the carrier character at B₀ = 0 or, equivalently, at k_|| = 0.

The quantum well magneto solutions split into two blocks formed by envelope functions with even symmetry {|A_j(a)ñ} and odd symmetry {|B_j(a)ñ} on the coordinate z. The spinor egeinstate is formed with mixture of symmetries which defines two Hilbert subspaces denoted with indexes I and II. This spinor egeinstate for each subspace has the general form:

These states no longer can be classified in symmetric or antisymmetric states, as in the parabolic model, but there is rather fixed arrangement of the spatial symmetry in each envelope function component, in order to characterize each eigenstate in the Hilbert subspace. Furthermore, the Landau levels corresponding to states of the same Hilbert subspace will never show level crossings for a given B₀.

III Optical Transitions

The matrix element for the electron-radiation interaction Hamiltonian is given by

where k_irepresents the photon wavevector, is the polarization of light, h is the refractive index, V is the volume of the crystal and is the momentum operator. The last term in the expression above, defines a polarization matrix P_j¢_{, j} = á j^¢| ( ·P ) | j ñ , for the incident light with circular polarization or in the Faraday configuration where = (

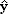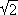i ) /and for linear polarizations or in the Voight configuration where = _i, i = x, y, z for the Cartesian coordinates. In this way, the corresponding selection rules for each optical transition in all configurations can be easily obtained.

For the Faraday configuration with s polarizations, the mixed symmetry Hilbert subspace is preserved or, saying differently, there will be only transitions between initial and final Landau levels belonging to the same subspace I or II. These transitions satisfy the selections rules shown in Table I.

Table I:
Selection rules for magnetooptical transitions in QW under Faraday configuration

For the Voight configuration where k ^ B|| || (denoted in the following as v^z) we find a different situation. Here only the components lh and so of the Landau levels for the valence band will be coupled with the Landau levels of electrons in the conduction band. Thus, the allowed transitions will be possible if they involve one initial state in one of the Hilbert subspace and the final state in the other subspace. Therefore there will be an admixture of the states or interchange of subspaces produced by the optical excitation, with the selection rules being represented in the Table II.

Table II:
Selection rules for magnetooptical transitions in QW under Voight configuration

In all cases the numbering of the Landau levels starts from N = 0 for each carrier type.

IV Magnetoabsorption coefficient

The magnetoabsorption coefficient is calculated as

The functions

are the oscillator strengths for the transitions. For the Faraday and Voigth configurations, s(v^z), they will be denoted as G(^z)(N_c, m_c; N_v, m_v), where N_c(v) indicates the Landau level of the corresponding conduction (valence) subband m_c(v). Notice that a sum is running over indexes j and j^¢ and the Landau levels selection rules are already implicit. The subband Landau levels will be denoted as subband label (N_c(v), m_c(v)).

For simplicity, only the strongest resonance peak, in the range of energy of our study will be denoted alphabetically and indicating the conduction Landau level N involved in transition. As an example we show in Table III some peaks for the one Faraday configuration.

Notice that the transitions A⁺(N) and C⁺(N) involve ''spin-flip'' from the initial to the final states whereas B⁺(N) and D⁺(N) preserve the spin component.

V Results and Discussion

All calculations shown here were made for a quantum well of L_z = 100 Å with the solid solution, Hg_0.8Cd_0.2Te/CdTe at T = 24K. We have also used all material parameters listed by Weiler [9] for concentrations ranging from x = 18% to x = 35% of Cd in the solid solution. At x = 2% of Cd, which is just above the semimetal-semiconductor transition, the band gap of the quantum well is E_g = 79.0 meV at T = 24K.

In Fig. 1 we show the calculated oscillator strength, as a function of the magnetic field, for a number of optical transitions with s⁺ polarization. As the magnetic field increases, one can observe a very clear interchange of oscillator strengths (intensities) between transitions A⁺(3), from the subspace I, and B⁺(3), from the subspace II . Close to B₀ = 13 Tesla both transitions have nearly the same strength and, for higher fields, B⁺(3) oscillator strength is the dominant one and the transition A⁺(3) almost disappears above B₀ = 15Tesla. An explanation for this fact is the following. The conduction Landau level involved in both transitions is e^-(3,1) and the valence levels involved are hh⁺(0,2) for A⁺(3) and hh^-(3,3) for B⁺(3) respectively. These two valence levels anticross near B₀ = 13 Tesla thus yielding an interchange of character of the corresponding transitions.

Figure 1.
Calculated transition strengths as a function of the magnetic field for transitions A⁺(N), B⁺(N), D⁺(N), and F⁺(N) for Landau levels from N = 3 to N = 5.

For sake of comparison, Fig. 2 shows the calculated magnetoabsorption spectrum for the s⁺ Faraday configuration as a function of the energy. In order to reveal the observed anisotropy in the oscillator strength we are showing the evolution of all three spectra as the field increases. The energy broadening has been fixed to 1 meV for all the levels thus, the relative height of a peak is a direct measure of the corresponding oscillator strength. The thin solid line is the total spectrum resulting from the sum A⁺(3) (dotted line) and B⁺(3) (thick solid line) contributions and, the information in each spectrum is complementary. On can observe that shape and position (resonance) of peaks change drastically with increasing magnetic field. Its is very clear that some transitions may appear while others will disappear. Our interest was focused in those transitions and energy where an interchange of character will be observed. The strongest transition in each case is expected to be the one that preserves the Landau level index and the subband symmetry. Above 14 Tesla the exchange already occurred. Notice also that the ''spin-flip'' like transitions A⁺(N) and C⁺(6) almost disappeared due to the overlapping of the stronger peaks B⁺(3),D⁺(8) . The existence of such anisotropy in the magnetooptical spectrum is a direct consequence of the peculiar symmetry properties inherent into this system.

Figure 2.
Theoretical absorption spectra for different magnetic fields using s⁺ polarization. The solid thin lines represent the total absorption. The solid dark lines are the contributions from transitions B⁺(N) and the dashed lines are the contributions from spin-flip like transitions A⁺(N).

• [1]G. E. Marques and V. A. Chitta, J. Phys. C 20, L727 (1987).
• [2]V. A. Chitta and G. E. Marques, Semicond. Sci. Technol. 3, 564 (1988).
• [3]H. -R. Trebin, U. Rössler, Y. Ranvaud, Phys. Rev. B 20, 686 (1979).
• [4]J. R. Meyer, C. A. Hoffman, and F. J. Bartoli, in Narrow-gap II-VI compounds for optoelectronic and electromagnetic applications, edited by P. Capper (Chapman & Hall, London, 1997).
• [5]M. Schultz, U. Merket, A. Sonntag, U. Rössler, R. Winkler, T. Colin, P. Helgesen, T. Skauli and S. Lovold; Phys. Rev. B 37, 14.772(1998).
• [6]R. Cingolani and K. Ploog, Adv. Phys. 40, 535 (1991).
• [7]E. O. Kane, Semiconductor and Semimetals, Willardson, R.K. e Beer, A.C., eds. (Academic Press, New York, 1966), vol. 1, p.75.
• [8]J. M. Luttinger, W. Kohn, Phys. Rev. 97, 869 (1955).
• [9]M. H. Weiler, in Magnetooptical Properties of Hg_1-xCd_xTe Alloys, edited by R. K. Willardson and A. C. Beer, Semiconductors and Semimetals, Vol 16, p.119, (Academic, New York, 1981.
• [10]H. A. Carmona, N. Studart, and G.E. Marques, Superlattices and Microstructures 12, 337 (1992).

Publication Dates

• Publication in this collection
  23 Feb 2001
• Date of issue
  Dec 1999

History

• Received
  06 Feb 1999