Abstract
Recent progress in the study and understanding of the properties of interfaces between reactants in irreversible reaction systems, gained from Monte Carlo simulations, is reviewed and discussed. The displacement of unstable phases by stable ones causes the formation of interfaces. This mechanism is particularly relevant close to first-order irreversible phase transitions, where phase coexistence is observed. Different variants of the monomer-momomer and the monomer-dimer models exhibit such transitions, and they are therefore suitable for the study of interfacial properties. More specifically, due to stimulating experimental findings, the monomer-dimer model, which mimics the catalytic oxidation of carbon monoxide, has been the subject of extensive studies, which are discussed in detail.
Dynamics of reactant interfaces in irreversible reaction systems
Ezequiel V. Albano
Instituto de Investigaciones Fisicoquímicas Teóricas y Aplicadas, (INIFTA),
CONICET, UNLP, CIC (Bs. As.). Sucursal 4, Casilla de Correo 16, (1900) La Plata. Argentina
FAX : 0054-221-4254642, E-mail: ealbano@inifta.unlp.edu.ar
Received 15 November 1999
Recent progress in the study and understanding of the properties of interfaces between reactants in irreversible reaction systems, gained from Monte Carlo simulations, is reviewed and discussed. The displacement of unstable phases by stable ones causes the formation of interfaces. This mechanism is particularly relevant close to first-order irreversible phase transitions, where phase coexistence is observed. Different variants of the monomer-momomer and the monomer-dimer models exhibit such transitions, and they are therefore suitable for the study of interfacial properties. More specifically, due to stimulating experimental findings, the monomer-dimer model, which mimics the catalytic oxidation of carbon monoxide, has been the subject of extensive studies, which are discussed in detail.
I Introduction
The study of far-from-equilibrium systems has become one of the most challenging fields of multidisciplinary research [1, 2]. While nonequilibrium phenomena are ubiquitous in nature and play a crucial role in many areas of science and technology, they are far from being understood at a fundamental level, as their equilibrium counterparts are. This is partly due to their richness and complexity. Examples of far-from-equilibrium systems beyond those in physics and physical chemistry include markets [3], weather [4], collective behaviour of living organisms [5], earthquakes, and fault dynamics [6]; etc.
Within a physical chemistry context, the study of nonequilibrium surface chemical reactions has attracted growing attention, motivated by both technical applications and scientific interest. Examples of the former are: the large-scale fabrication of chemicals via heterogeneously catalyzed reactions; the treatment of automotive exhaust, reducing environmental pollution; coating, corrosion and passivation of surfaces; synthesis and refinement of hydrocarbons. Furthermore, scientific interest in the study of these processes is due to the emergence of a rich and complex variety of physical chemistry phenomena including, e.g., chaos, bistability, critical phenomena and irreversible phase transitions, propagation and interference of chemical waves of adsorbed reactants, and chemical oscillations.
Recent development of experimental techniques such as scanning tunneling microscopy (STM), low energy electron diffraction (LEED), high resolution electron energy loss spectroscopy (HREELS), ultraviolet photoelectric spectroscopy (UPS), and photoelectron emission microscopy (PEEM) [7, 8], among others, allows scientists to gather detailed physical and chemical information about surfaces, adsorbates and reaction products. Perhaps the most dramatic example of this progress is the recent STM-based measurement of reaction-rate parameters at a microscopic level for the catalytic oxidation of CO [9]. Remarkably, these parameters agree very well with those previously obtained by means of macroscopic measurements.
Also, surface reaction systems are certainly a challenging scientific field for the development and application of analytical methods and theories, including recent advances in the area of nonlinear dynamics [10]. Complementing these very well established experimental and analytical approaches, computer simulations have recently become a powerful tool for the study of a great variety of processes occurring in nature in general [11, 12, 13], as well as surface chemical reactions in particular [14].
On the other hand, the study of growing interfaces under nonequilibrium conditions is one of the most active areas in physics and physical chemistry [15]. In particular, the structure of an interface and the dynamics of roughening are issues of considerable interest. For heterogeneously-catalyzed reactions, an interface may exist between two reactant species. The characteristics of the interface may depend on the specific reaction system. In some cases it may undergo large fluctuations during the reaction, and its perimeter may look quite rough (fractal like); occasionally the interface is essentially flat. Under these circumstances Monte Carlo simulation has become a powerful tool for the study of reaction interfaces.
It should be mentioned that the propagation of concentration fronts, involving the interface between reactants in far-from-equilibrium heterogeneous reactions, has recently been very well documented in various experimental systems (see [16, 17, 18, 19] and references therein). The observed spatio-temporal patterns also include trigger waves, rotating spirals and turbulence.
Within this context, the aim of this work is to offer a critical overview of recent progress, mainly due to Monte Carlo simulations, in understanding the dynamics of reactant interfaces in irreversible reaction systems. We will restrict ourselves to cases in which the catalyst is in contact with a reservoir which supplies the reacting species, and the rate of reaction at the surfaces is very high, since the formation of reactant interfaces in diffusion-limited reactions has been already reviewed [14].
II Brief Phenomenological and Theoretical Background
For a growing interface, there is a clear distinction between the growth direction and that perpendicular to it. So it may not be surprising that scaling is different along these two directions. Therefore, an interface lacks of self-similarity but, instead, can be regarded as a self-affine object [20].
Based on general scaling arguments it can be shown that the stochastic evolution of a driven interface along a strip of width L is characterized by long-wavelength fluctuations (w(L, t)) which have the following time- and finite-size-behavior [15] :
where F(x) µ xb for x < < 1 and F(x) ® 1 for x >> 1, with z = a/b, and where a and b are the roughness and growth exponents, respectively. Thus, for an infinite system (L ® ¥), one has w(t) µ tb, as t ® ¥. Note that w is also known as the interface width.
It is reasonable to expect that scaling behaviour should still be given correctly after coarse-graining and passing to the continuous limit. In fact, the dynamics of an interface between two phases, one of which is growing into the other, is believed to be correctly described by a simple nonlinear Langevin equation proposed by Kardar, Parisi and Zhang (KPZ) [15, 21] :
where h( , t) is the height of the interface at location
, t) is the height of the interface at location  and time t. The first term of the right hand side of Eq. (2) describes the relaxation of the interface by a surface tension D, while the second term is the lowest-order nonlinear term that can appear in the interface-growth equation, and accounts for the dependence of the grow rate on the local slope of the interface. In most theoretical studies the stochastic term h(
and time t. The first term of the right hand side of Eq. (2) describes the relaxation of the interface by a surface tension D, while the second term is the lowest-order nonlinear term that can appear in the interface-growth equation, and accounts for the dependence of the grow rate on the local slope of the interface. In most theoretical studies the stochastic term h( , t) is assumed to be Gaussian and d-function correlated.
, t) is assumed to be Gaussian and d-function correlated.
For a surface-reaction lattice-gas model, an interface may exist between two reactant species. So, for a stochastic reactive interface propagation one may expect the exponents to assume KPZ values for a one-dimensional interface, namely b = 1/3, a = 1/2 and z = 3/2. However, under actual reaction conditions the characteristics of the interface may depend on the specific reaction system.
III Interface Propagation in the Monomer-Dimer Reaction System
The lattice-gas version of the reaction 2A + B2® 2AB, which mimics the oxidation of carbon monoxide (i.e., A is CO, B2 is O2 and AB is CO2), was proposed by Ziff et al. [22]. It is assumed that the reaction proceeds according to Langmuir-Hinshelwood mechanism:
where S is an empty site on the surface, while (a) and (g) refer to the adsorbed and gas phase, respectively.
The monomer-dimer (MD) model uses a square lattice to represent the catalytic surface. The Monte Carlo algorithm for the simulation of the MD model is as follows : i) A or B2 molecules are selected randomly with relative probabilities YA and YB, respectively. These probabilities are the relative impingement rates of both species, which are proportional to their partial pressures. Due to the normalization, YA + YB = 1, the model has a single parameter, i.e., YA. If the selected species is A, a surface site is selected at random, and if that site is vacant, A is adsorbed on it [Eq.(3)]. Otherwise, if that site is occupied, the trial ends and a new molecule is selected. If the selected species is (B2), a pair of nearest neighbor sites is selected at random and the molecule is adsorbed on them only if they are both vacant [Eq.(4)]. ii) After each adsorption event, the nearest neighbors of the added molecule are examined in order to account for the reaction given by Eq.(5). If more than one [B(a), A(a)] pair is identified, one is selected at random and removed from the surface (for more details on the MD and the simulation technique see, e.g., [2, 10, 14, 22, 23] ).
The model is intrinsically irreversible and it is also assumed that both dissociation of the dimer and reaction between a pair of adjacent species of different type are instantaneous. The MD model basically retains the adsorption-desorption selectivity rules of the Langmuir-Hinshelwood mechanism. It has no energy parameters, and the only independent parameter is YA. Obviously, these crude assumptions imply that, for example, diffusion of adsorbed species is neglected, desorption of the reactans is not considered, and lateral interactions are ignored. Efforts to overcome these shortcomings have led to numerous variants of the MD model, see, e.g., [14].
Interest in the MD model also arises due to its rich and complex irreversible critical behavior. In fact, in two dimensions and for the asymptotic regime (t ® ¥), the system reaches a stationary state whose nature depends solely on the parameter YA. For YA£ Y1A@ 0.3907 (YA³ Y2A@ 0.5250) the surface becomes irreversibly poisoned by B (A) species, while for Y1A < YA < Y2A a steady state with sustained production of AB is observed. Fig. 1 shows plots of the rate of AB production (RAB) and the surface coverages of A (qA) and B (qB) versus YA. Just at Y1A and Y2A the MD model exhibits irreversible phase transitions (IPT's) between the reactive regime and poisoned states, which are of second and first order, respectively. The second-order IPT belongs to the universality class of directed percolation and is very well understood [24, 25]. Furthermore, as is shown in Fig. 1, when YA increases toward Y2A the catalytic activity increases, but when Y2A is reached large A clusters suddenly emerge and cover every lattice site. The transition occurs abruptly, with discontinuity of the coverages and activity, implying that this is a first-order IPT. However, just at YA = Y2A, the two adsorbed phases (a B-rich phase, and a solid A-phase) coexist [22]. Based upon this observation Ziff et al. determined Y2A = 0.525 ± 0.001 [22]. This figure was later improved using the constant-coverage ensemble [26] which prevents the occurrence undesired effects due to long-lived metastable states and gives Y2A = 0.52560 ± 0.00001 [26].
Plots of the rate of AB production (RAB) and the surface coverage with A (qA) and B (qB) species versus YA, for the MD model.
In order to investigate the properties of the interface between the A-poisoned state and the reactive regime, Brosilow et al. [27] simulated the MD model on the square lattice in a rectangular geometry of L × M sites. The left-most column of M sites was initially occupied by B-atoms, the right-most L/2 columns were initially occupied by A-species, and the remaining sites were initially vacant. In order to prevent A-poisoning, whenever a B-species was removed (through reaction) from the left-most column of the lattice, it was immediately replaced by another B-species. Running simulations for (YA³ Y2A), the imposed geometry causes the appearance of an interface between the reactive state and an A-poisoned state. The width of the reactive phase (x) is found to scale with YA as x = k(YA - Y2A)-n, with n @ 0.40 and k @ 0.74.
Another scenario for the propagation of a reaction front requires the displacement of an unstable phase by a stable one, and the formation of an interface where most reaction events take place. This condition holds, e.g., close to first-order IPTs, as is shown schematically in Fig. 2, where an explanation of the underlaying mechanism is also given. An interface formed during the coexistence between a reactive state with no large A-clusters and an A-rich phase characterized by a large A-cluster, can clearly be observed in the snapshot configuration shown in Fig. 3.
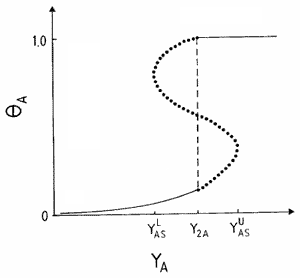
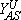 and
and 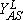 are the upper and lower spinodal points, respectively. Between Y2A and
are the upper and lower spinodal points, respectively. Between Y2A and 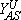 the reactive state is unstable and is displaced by the A-rich phase. On the contrary, between
the reactive state is unstable and is displaced by the A-rich phase. On the contrary, between 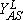 and Y2A the reactive state displaces the A-rich phase.
and Y2A the reactive state displaces the A-rich phase.Typical snapshot configuration showing the interface between an A-rich phase (large cluster shown in black) and the reactive phase. Results obtained for the monomer-dimer model using the constant-coverage ensemble with a lattice of side L = 512.
Monte Carlo simulations due to Moller et al. [28] demonstrated that a monomer-dimer model, which is intended to describe the catalytic oxidation of carbon monoxide and includes reactant-assisted surface reconstruction, can support the propagation of trigger waves even if surface diffusion is not explicitly considered. However, after this early work, most simulations have been performed within the framework of the MD model as proposed by Ziff et al. [22].
In fact, Evans and Ray [29] have studied the displacement of the reaction interface for YA below the A-poisoning transition Y2A. Within this regime one expects that the reactive state will displace the A-poisoned one (see e.g. Fig. 2), resulting in a propagation velocity (Vp) normal to the interface. Studying this case, Evans et al. [29] proposed that Vp must vanish as (YA® Y2A), where both states become equistable, so one has
with g > 0. The limit of high diffusivity of the reactants can be well described by mean-field reaction-diffusion equations, which give g = 1 [29]. It is interesting to notice that if diffusion is restricted or even suppressed, simulations give values of g very close to unity, suggesting that the exponent is independent of the surface diffusivity of the reactants [29]. In this case the propagation of the reaction interface has also been described in terms of the KPZ framework (see Eq. (2)) and scaling arguments [29]. From Monte Carlo simulations at the first-order IPT it is reported that b  0.3, i.e., a figure close to the KPZ value (b = 1/3). However, it is expected that the operation of a weak stabilizing effect may play an important role in the reaction system. This effect can be described by introducing correction terms of higher-order in Eq. (2) [29].
0.3, i.e., a figure close to the KPZ value (b = 1/3). However, it is expected that the operation of a weak stabilizing effect may play an important role in the reaction system. This effect can be described by introducing correction terms of higher-order in Eq. (2) [29].
Very recently, Chávez et al. [30] studied the dynamics of front propagation in the catalytic oxidation of CO on Pt(100) by means of a cellular automaton simulation. It is found that the dynamic scaling exponents of the interface are well described by Eq. (1) with a = 1/2 and b = 1/3. It is also reported that in the absence of surface diffusion the interface dynamics can successfully be described using the KPZ equation (2).
Goodman et al. [31] studied the propagation of concentration waves in the MD surface reaction model. They found that the model supports trigger waves within the bistable regime of the process, i.e., close to the first-order irreversible phase transition, as already discussed in Fig. 2. Within that regime one has coexistence of a stable state with a metastable one. At the boundary between the two, the stable state will displace the metastable one and the boundary will move, so this process leads to the propagation of concentration fronts (trigger waves). Goodman et al. [31] found that the velocity of the A-front depends on the diffusion rate D of A-species (diffusion of B is neglected), and the sticking probability of A-molecules (YA). The velocity of the front vanishes when approaching the poisoning transition at Y2A(D) (note that the critical point now depends on D), according to Eq. (6), with g  1, in agreement with the results of Evans et al. [29].
1, in agreement with the results of Evans et al. [29].
As suggested by the experimental work of Haas et al. [18], the propagation of reaction fronts on narrow channels has also been simulated [32], using the ZGB model on the square lattice with rectangular geometries of sides L × M (L << M). Thus L is the width of the channel and M its length. Free boundary conditions were taken along the channel while the opposite ends are assumed to be in contact with A and B-sources, respectively. If A or B-species are removed from the ends of the channels (i.e., the "sources"), due to the reaction process, they are immediately replaced. The propagation of the B concentration profile was studied starting with a sample fully covered by A, except for the first and second columns, which are covered by B (the B-source), and left empty, respectively. The propagation of the A profile was followed using a similar procedure. Under these conditions one always has two competing interfaces along the channel. Fig. 4 shows a set of snapshot configurations, taken at different times, obtained using channels of size L = 20 and M = 100, corresponding to the propagation of the reactive phase (left side of the snapshots) into an otherwise fully A-poisoned phase (right side of the snapshots).
Typical snapshot configurations obtained during the displacement of the A-poisoned phase (right-hand side of the figures) by the reactive phase (left-hand side of the figures). Results obtained with channels of size L = 20 and M = 100 and taking YA = 0 : 515. The snapshots are plotted for different times (measured in Monte Carlo Steps (MCS)), from top to bottom: t = 25 MCS, t = 100 MCS, t = 400 MCS and t = 900 MCS, respectively.
In order to develop a more quantitative description of the propagation, a number of definitions are needed. The concentration profiles of the reactants, qA(x) and qB(x), are measured along the length of the channel x in the M-direction and averaged over each column of lattice sites of length L. Fig. 5 shows a set of concentration profiles obtained for the same times as the snapshots shown in Fig. 4. After determining smooth and well averaged profiles one can get insight into the propagation by measuring the moments of the profiles, which in subsequent steps can be used to determine the propagation velocity and the width of the profiles. In fact, the moments of nth order of the profiles can be evaluated according to [33]
Concentration profiles obtained during the displacement of the A-poisoned phase by the reactive phase. Lattice size L = 20, M = 100, PA = 0.515. a) B-profiles, b) A-profiles. The profiles are plotted for different times : t = 25,
Using Eq. (7) the fluctuation in the position of the profile, i.e., its mean-square width, is given by
and the velocity of propagation can be obtained from the first moment:
where distances are measured in lattice units (LU) and time in MCts.
Monte Carlo simulation results show that the front propagation velocity depends on YA and the channel width L, as is shown, for example, in Fig. 6. This figure also shows that the displacement of A- and B-poisoned channels by the reactive regime stops at certain (L-dependent) critical values, YAc2(L) and YAc1(L), respectively. By means of an extrapolation to the thermodynamic limit it is possible to identify these critical values with the critical points of the MD model, namely YAc1(L ® ¥) = Y1A and YAc2(L ® ¥) = Y2A , respectively. It is also found that close to YAc2, when the propagation of the B-profile ceases, the speed of the A-profile undergoes a sharp change. This behavior can be correlated with the first-order irreversible phase transition between the stationary reactive regime and the A-poisoned state observed in the MD model at Y2A (see Fig. 1). So far, the main conclusions that can be extracted from Fig. (6) can be summarized as follows: a) there are two critical pressures, YAc1(L) and YAc2(L), which depend on the width of the channel, at which propagation of one profile or the other stops; b) within these critical values, propagating A and B profiles coexist; c) B-profiles propagate faster than A-profiles. All these observations appear in qualitative agreement with the experimental results reported in Fig. 2(a) of the paper of Haas et al. [18]. However, the underlying physics is different: in the simulations the displacement of a poisoned phase by the invading reactive phase takes place within a range of pressures where the later is unstable, while the former is stable. In contrast, the experiment may show the propagation of coexisting phases within a bistable regime [18]. As discussed above, the simulations also show a jump in the velocity of the A-front close to YAc2(L). In the experiments, A fronts are not studied above YAc2, so the occurrence of the jump in actual conditions cannot be ruled out. The occurrence of such jump a may be a nice prediction of the (simple) MD model which, in principle, seems to be supported by the fact that the jump can effectively be correlated with the first-order poisoning transition; first-order transition-like behavior has already been observed experimentally [34].
Plots of the propagation velocities of B- and A-profiles vs YA obtained for channels of width a) L = 3 and b) L = 10. The lines shown the critical pressures at which propagation stops.
It is well known that lattice-gas modeling of surface reactions, in contrast to traditional mean-field treatments, provides a realistic description of the fluctuations and correlations resulting from the adsorption and reaction processes. In a deterministic process described by a set of reaction-diffusion equations, the interface between coexisting phases may have a fixed width [31]. This width should be of the order of the size of the region near the propagating front. In contrast, in the lattice-gas description one has shot noise in the pressure of the incoming reactants, and statistical fluctuations, as extra sources of broadening, which leads to wandering of the front [31]. Fig. 7 shows the dependence of the reaction interface width (see Eq. (8)) as a function of time, obtained for channels of fixed width and at various pressures, when the A-poisoned phase is displaced by the reactive phase. Two different regimes can clearly be observed. For low A-pressures, well inside the reactive state, the fluctuations diverge and the poisoned state will ultimately be completely displaced. For high enough A-pressures, well inside the A-poisoned state, the fluctuations saturate, i.e., the reactive state can not displace the stable poisoned state, and the interface remains bounded. The crossover between these two regimes is observed just at the critical pressure YAc2(L), where a log-log plot of wL2vs t gives a straight line. Based on general dynamic scaling arguments similar to those used to describe interface fluctuations in thin-film growth (see Eq. (1)), it can be expected that the stochastic evolution of a driven interface along a strip of width L may be characterized by long-wavelength fluctuations (wL2(t, DYA)) which have the following time- and pressure-dependence [32] :
Log-log plots of w2 versus t measured at different pressures and for channels of different width. Data obtained during the displacement of a A-poisoned phase by a reactive phase. a) L = 5, from top to bottom the pressures are: 0.4819, 0.4845, 0.4852, 0.4859 and 0.4872; b) L = 30, from top to bottom the pressures are: 0.5192, 0.5202, 0.5211, 0.5215 and 0.5238; and c) L = 5, from top to bottom the pressures are: 0.4852, 0.4872, 0.4898, 0.5000 and 0.5349.
where DYA = YA - YAc2(L), with F(x) = constant for x ® 0 (i.e.,DYA® 0) and F(x) ® x-b* for x ® ¥ (i.e., DYA > 0 and t ® ¥). Thus, just at the critical pressure the fluctuations are given by w2L(t) µ tb* as t ® ¥; while away from criticality, the fluctuations may diverge according to w2L(DYA) µ DYA-d, with d = -hb*. Notice that b = b* /2, where b has been defined in Eq. (1). It is found that for narrow channels b* depends on L, but increasing the channel width one has b*® 1 for L ® ¥, that is b ® 1/2, pointing out that the noise should dominate the nonlinear and surface tension terms in the KPZ equation. It is also found that d is sensitively dependent on the channel width L, with d ® 3/2 for L ® ¥ [32].
If the time and pressure dependences of w2L(t, DYA) are well described by Eq. (10), one may expect a data collapse in the log-log plots of w2t-b* versus t (DYA)h. The excellent quality of the collapse (see Fig. (8) for L = 5 and L = 20) strongly suggests the validity of the scaling hypothesis involved in the derivation of Eq. (10). Furthermore, all these results demonstrate that the standard dynamic formalism developed for the description of a rough interface [15] is suitable for the rationalization of the interface behaviour in far-from-equilibrium reactive systems.
Scaling plots of w2t-b versus t(DPA)a obtained for channels of different widths and at different pressures. a) L = 5 and b) L = 20.
A different variant of the monomer-dimer model, namely the reaction AB + C ® 1/2 A2 + CB, was proposed by Yaldram and Khan (YK) [35]. This irreversible reaction model mimics the reaction between NO and CO over a single-crystal catalyst, i.e., AB is NO, C is CO, A2 is N2, and CB is CO2. According to the Langmuir-Hinshelwood mechanism, the reaction steps are :
where S again represents an empty site on the surface, and (a) and (g) refer to the adsorbed and gas phase, respectively.
Simulations due to Yaldran et al. [35] showed that, in contrast to the MD model already discussed, the YK model has no reactive state on the square lattice. A proof of this finding was later given by Brosilow and Ziff [36]. However, increasing the coordination number of the lattice, it was found that the YK model on the hexagonal lattice has a finite reaction window, capable of sustaining a reactive stationary state [35]. On the other hand, Meng et al. [37] have shown that adding a new reaction channel, in order to decrease the possibility of poisoning one may enhance the reactivity of the system and consequently modify the nature of the poisoning transition. In fact, for simulations on the square lattice, the addition of the side-reaction channel
causes the opening of a reaction window with a continuous IPT close to Y1C 0.262 and a first order IPT close to Y2C
0.262 and a first order IPT close to Y2C 0.501. This behavior is reminiscent to the MD model discussed above.
0.501. This behavior is reminiscent to the MD model discussed above.
Very recently Tamaro et al. [38] studied the reactive removal of unstable mixed CO + NO adlayers using a lattice gas model. Due to the presence of pre-adsorbed species, the steps given by equations (11) and (12) are not considered. Furthermore, in order to account for the diffusion of the reactants, the hopping of all species (except for O-atoms, whose mobility is negligible) is considered. An interesting contribution of this work, which may also be generalized to other systems involving mixed species, is the development of an elaborate treatment for the chemical diffusion of mixed adlayers reflecting the interference of the adsorbed species on the surface due to co-adsorption. Simulations are started with the surface fully covered by an (AB + C)-adlayer, which constitutes an unstable state, in the sense that vacating a single site may produce the dissociation of AB and its reaction with C, and the subsequent creation of more vacancies, triggering an autocatalytic reaction. Subsequently, a very small number of adspecies is desorbed and the reactive removal of the mixed adlayer is followed. Due to the high mobility of most adsorbed species, initially an exponential increase in the number of highly dispersed vacancies is observed. This is followed by a transition to a reaction interface propagation regime of adlayer removal. In this stage a chemical wave develops that propagates into the (AB + C)-covered (unstable) part of the surface.
IV Brief Oveview of Interface Propagation Studies in the Monomer-Monomer Reaction System
The monomer-monomer (MM) model assumes the following Langmuir-Hinshelwood reaction scheme :
where S is an empty site on the surface, while (a) and (g) refer, as above, to the adsorbed and gas phases, respectively. The Monte Carlo algorithm is similar to that for MD model, but since now both species are monomers, adsorption attempts on empty sites are always successful. The impingement rate of A and B-species is YA and YB, respectively. So, taking YA + YB = 1, the MM process has a single parameter, namely YA (for more details see [29, 39]).
The phase diagram of the MM model is quite simple: for YA < Y1A = 1/2 (YA > Y1A) the catalyst becomes poisoned by A (B)-species, respectively. So, one has a first-order IPT where Y1A = 1/2 is a trivial critical point given by the stoichiometry of the reaction. In contrast to the MD model, now the reaction window has zero-width. It becomes clear that the dimer deposition mechanism, which requires two adjacent sites for adsorption, causes the occurrence of a finite-width reaction window in the MD model.
The properties of the interface between an A-rich and a B-rich patch in the monomer-monomer (MM) model, as described by equations (16-18), has been studied by Kang and Weinberg [33]. The MM model is simulated on the square lattice. Initially, the left half of the lattice is completely filled with particles of species A and the right half is completely filled with particles of species B. Two columns of sites between the A and B domains are left vacant in order to allow adsorption. Monte Carlo simulations are performed applying periodic boundary conditions in the vertical direction and using sufficiently wide lattices so that the reactive zone does not reach the horizontal edges. A and B-species are selected with equal probability, i.e., just at the critical point of the MM model. In is found that fluctuations in the particle density resulting from the formation of clusters in the reactive zone play a significant role in the interfacial roughening. Overhangs, holes, fingers and clusters are observed. A more quantitative understanding can be obtained by measuring the roughness of the interfacial region between reacting species. Kang et al. [33] use two different measures. In the first one the roughness is obtained considering the distribution of sites forming the external perimeter of each of the A and B domains. This measure wh, known as the diffusion hull, was introduced to study the diffusion frontier of an interface [40] and it can be obtained using equation (8). For the second measure, the roughness wA considers the external perimeter of the A domain. The interface possition xA for each row of sites is defined as the minimum value of x among all the external perimeter sites in that row. Then wA can also be obtained using equation (8) replacing x by xA and taking averages over all the rows of the lattice. A similar definition of wB holds for the interface of B domains, and since both domains are equivalent an average between wA and wB is taken, giveng wr, i.e., the average roughness of the surface of the domains. The quantity xA - xB for each row of sites is a measure of the width of the reactive zone for that row, so the average width of the reactive zone wm can be evaluated. It is found that the interface roughness scales as w ~ tb, where the exponent b is equal to 1/2 for wh, wr and wm. Although all measures scale with the same exponents one always has wm > wh > wr.
These results can be compared with previous studies of Gouyet et al. [40] for a pure diffusive (nonreactive) system. In this case wm also scales with b = 1/2, but wh scales with b » 0.286, implying that, in the long time limit, the diffusion hull is smooth on the length scale of wm. In contrast, for the reaction system the roughness of the external perimeter grows as fast as the width of the reactive zone (b = 1/2 for both measures), so the fingers of the A and B domains have the same length scale as the width of the reactive zone. The difference between the diffusion system and the reaction system arises from particle-particle correlations introduced by the reaction mechanism, i.e., it is more likely to find an AA or a BB nearest-neighbor pair in the reaction system than in the diffusion system [33]. Introducing nearest-neighbor repulsive interactions in the reaction system, the interface becomes smoother and large clusters are found to be absent within the zone of vacant sites [33].
The interface properties of another variant of the MM model, proposed earlier by Ziff et al. [41], has also been studied by Kang et al. [42, 43]. In this MM model reaction also occurs between nearest neighbor AB pairs, but adsorption takes place immediately at any site vacated by the reacting particles, with equal probabilities for A and B. As the reaction proceeds, the originally flat interface between A and B domains becomes rough. Clusters of one species will be formed in the domain of the other species. It is found that the interface width wr scales with b = 1/2 as in the purely diffusive system [40], however the roughness of the external perimeter wh scales with b » 0.455, i.e., a larger value than that expected for a pure diffusive system. So, within error bars the exponents of the roughness are the same for both variants of the MM model, suggesting that the behavior of the interface should be independent of whether the reaction rate is infinitely higher than the adsorption rate or vice versa. Simulation results also shown that the fractal dimension of the external perimeter of the reaction front is equal to that of external perimeter of the diffusion front, given by Df» 1.33 ± 0.01 [42], which is different than the fractal dimension of the hull, Dh = 7/4 [40].
V Conclusions
Recent progress in the understanding of interface propagation in surface reaction models has been reviewed and discussed. Particular attention is addressed to the monomer-dimer and monomer-monomer models. However, all of the concepts and ideas developed here are expected to hold in more general models exhibiting discontinuous transitions into absorbing states. In fact, the existence of coexisting phases close to first-order transitions provides the natural mechanism for the displacement of phases, with the consequent formation of interfaces.
All the results reviewed here support the idea that standard dynamic scaling formalism developed for the description of rough interfaces (Eq. (1)), and the stochastic Langevin equation due to Kardar, Parisi and Zhang (Eq. (2)), are suitable for the rationalization of interfacial behavior in far-from-equilibrium reactive systems such as the MD and the MM models.
However, much work remains to be done in order to clarify the role of high surface mobility of the reactants in the behavior of reaction interfaces. Furthermore, the interplay between interface propagation and nucleation phenomena is a topic which merits further study. As recently proposed [44], more elaborate models for the MD reaction are capable of reproducing the propagation of chemical waves, rotating spirals, and turbulence. The characterization of the interfaces in such processes is of great interest, and will certainly contribute to the understanding of the dynamics of front propagation in reaction systems.
Acknowledgments
This work is supported financially by CONICET, UNLP, CIC (As. As.), ANPCyT (Argentina) and the Volkswagen Foundation (Germany).
References
[1] See, e.g., a set of very interesting articles recently published in Science 284, 79 (1999).
[2] J. Marro and R. Dickman. Nonequilibrium Phase Transitions in Lattice Models (Cambridge University Press, Cambridge, 1999).
[3] D. Chowdhury and D. Stauffer, Eur. Phys. J. B, 8, 477 (1999); T. Lux and M. Marchesi, Nature 397, 498 (1999).
[4] D. T. Shindell et al., Nature 399, 452 (1999).
[5] E. V. Albano, Phys. Rev. Lett. 77, 2129 (1996).
[6] D. D. Oglesky, R. J. Archuleta and S. B. Nielsen, Science 280, 1055 (1998).
[7] K. Christmann, Introduction to Surface Physical Chemistry (Steinkopff Verlag, Darmstadt, 1991), pp. 1-274.
[8] J. H. Block, M. Ehsasi and V. Gorodetskii, Prog. Surf. Sci., 42, 143 (1993).
[9] J. Wintterlin, S. Volkening, T. V. W. Janssens, T. Zambelli, and G. Ertl, Science, 278, 1931 (1997).
[10] V. P. Z. Zhdanov and B. Kasemo, Surf. Sci. Report, 20 (3), 111 (1994).
[11] K. Binder, in The Monte Carlo Method in Condensed Matter Physics, edited by K. Binder (Springer-Verlag, Berlin, 1992), pp. 1-22.
[12] Applications of the Monte Carlo method in Statistical Physics, 2nd ed. K. Binder, ed. (Springer-Verlag, Berlin 1984), pp. 1-341.
[13] K. Binder and D. Heermann, Monte Carlo simulations in Statistical Physics, Springer Series in Solid State Sciences, v. 80. (Springer Verlag, Berlin, 1992), pp 1-129.
[14] E. V. Albano, H. Chem. Rev. 3, 389 (1996).
[15] A. L. Barabási and H. E. Stanley, Fractal Concepts in Surface Growth (Cambridge University Press, Cambridge, 1995), pp. 1-366.
[16] R. Imbhil, Prog. Surf. Sci. 44, 185 (1993).
[17] R. Imbhil and G. Ertl, Chem. Rev. 95, 697 (1995).
[18] G. Haas, M. Bar, I. G. Kevrekides, P. B. Rasmussen, H. H. Petermund, and G. Ertl, Phys. Rev. Lett. 75, 3560 (1995).
[19] S. Jabubith, H. H. Rotermund, W. Engel, A. von Oertzen and G. Ertl, Phys. Rev. Lett. 65, 3013 (1990).
[20] Fractal and disordered systems, A. Bunde and S. Havlin edited by (Springer-Verlag, Berlin, 1991).
[21] M. Kardar, G. Parisi, and Y. C. Zhang, Rev. Lett. 56, 889 (1986).
[22] R. M. Ziff, E. Gulari, and Y. Barshad, Phys. Rev. Lett. 56, 2553 (1986).
[23] J. W. Evans, Langmuir 7, 2514 (1991).
[24] G. Grinstein, Z.-W. Lai, and D. A. Browne, Phys. Rev. A 40, 4820 (1989).
[25] I. Jensen, H. C. Fogedby, and R. Dickman, Phys. Rev. A 41, 3411 (1990).
[26] R. M. Ziff and B. J. Brosilow, Phys. Rev. A 46, 4630 (1992).
[27] B. J. Brosilow, E. Gulari, and R. M. Ziff, J. Chem. Phys. 99, 1 (1993).
[28] P. Moller, K. Wetzl, M. Eiswirth, and G. Ertl, J. Chem. Phys. 85, 5328 (1986).
[29] J. W. Evans and T. R. Ray, Phys. Rev. E 50, 4302 (1994).
[30] F. Chávez, L. Vicente, A. Perera and M. Moreau, J. Chem. Phys. 110, 8118 (1999).
[31] R. H. Goodman, D. S. Graff, L. M. Sander, P. Leroux-Hugon, and E. Clément, Phys. Rev. E 52, 5904 (1995).
[32] E. V. Albano, Phys. Rev. E 55, 7144 (1997).
[33] H. C. Kang and W. H. Weinberg, Phys. Rev. E 47, 1604 (1993).
[34] M. Ehsasi et al., J. Chem. Phys. 91, 4949 (1989).
[35] K. Yaldram and M. A. Khan, J. Catal. 131, 369 (1991) and 136, 279 (1992).
[36] B. J. Brosilow and R. M. Ziff, J. Catal. 136, 275 (1992).
[37] B. Meng, W. H. Weinberg and J. W. Evans, Phys. Rev. E. 48, 3577 (1993).
[38] M. Tammaro and J. W. Evans, J. Chem. Phys. 108, 7795 (1998).
[39] P. Meakin and D. J. Scalapino, J. Chem. Phys. 87, 731 (1987).
[40] J. F. Gouyet, M. Rosso, and B. Sapoval, "Fractal surfaces and interfaces", in Fractal and Disordered Systems, edited by A. Bunde and S. Havlin, (Springer-Verlag, Berlin, 1991), p. 229.
[41] K. Fichthorn, E. Gulari and R. Ziff, Phys. Rev. Lett. 63, 1527 (1989).
[42] H. C. Kang and W. H. Weinberg, Phys. Rev. E. 48, 3464 (1993).
[43] H. C. Kang and W. H. Weinberg, J. Chem. Phys. 100, 1630 (1994).
[44] R. J. Gelten et al., J. Chem. Phys. 108, 5921 (1998).
- [1] See, e.g., a set of very interesting articles recently published in Science 284, 79 (1999).
- [2] J. Marro and R. Dickman. Nonequilibrium Phase Transitions in Lattice Models (Cambridge University Press, Cambridge, 1999).
- [3] D. Chowdhury and D. Stauffer, Eur. Phys. J. B, 8, 477 (1999);
- T. Lux and M. Marchesi, Nature 397, 498 (1999).
- [4] D. T. Shindell et al., Nature 399, 452 (1999).
- [5] E. V. Albano, Phys. Rev. Lett. 77, 2129 (1996).
- [6] D. D. Oglesky, R. J. Archuleta and S. B. Nielsen, Science 280, 1055 (1998).
- [7] K. Christmann, Introduction to Surface Physical Chemistry (Steinkopff Verlag, Darmstadt, 1991), pp. 1-274.
- [8] J. H. Block, M. Ehsasi and V. Gorodetskii, Prog. Surf. Sci., 42, 143 (1993).
- [9] J. Wintterlin, S. Volkening, T. V. W. Janssens, T. Zambelli, and G. Ertl, Science, 278, 1931 (1997).
- [10] V. P. Z. Zhdanov and B. Kasemo, Surf. Sci. Report, 20 (3), 111 (1994).
- [11] K. Binder, in The Monte Carlo Method in Condensed Matter Physics, edited by K. Binder (Springer-Verlag, Berlin, 1992), pp. 1-22.
- [12] Applications of the Monte Carlo method in Statistical Physics, 2nd ed. K. Binder, ed. (Springer-Verlag, Berlin 1984), pp. 1-341.
- [13] K. Binder and D. Heermann, Monte Carlo simulations in Statistical Physics, Springer Series in Solid State Sciences, v. 80. (Springer Verlag, Berlin, 1992), pp 1-129.
- [14] E. V. Albano, H. Chem. Rev. 3, 389 (1996).
- [15] A. L. Barabási and H. E. Stanley, Fractal Concepts in Surface Growth (Cambridge University Press, Cambridge, 1995), pp. 1-366.
- [16] R. Imbhil, Prog. Surf. Sci. 44, 185 (1993).
- [17] R. Imbhil and G. Ertl, Chem. Rev. 95, 697 (1995).
- [18] G. Haas, M. Bar, I. G. Kevrekides, P. B. Rasmussen, H. H. Petermund, and G. Ertl, Phys. Rev. Lett. 75, 3560 (1995).
- [19] S. Jabubith, H. H. Rotermund, W. Engel, A. von Oertzen and G. Ertl, Phys. Rev. Lett. 65, 3013 (1990).
- [20] Fractal and disordered systems, A. Bunde and S. Havlin edited by (Springer-Verlag, Berlin, 1991).
- [21] M. Kardar, G. Parisi, and Y. C. Zhang, Rev. Lett. 56, 889 (1986).
- [22] R. M. Ziff, E. Gulari, and Y. Barshad, Phys. Rev. Lett. 56, 2553 (1986).
- [23] J. W. Evans, Langmuir 7, 2514 (1991).
- [24] G. Grinstein, Z.-W. Lai, and D. A. Browne, Phys. Rev. A 40, 4820 (1989).
- [25] I. Jensen, H. C. Fogedby, and R. Dickman, Phys. Rev. A 41, 3411 (1990).
- [26] R. M. Ziff and B. J. Brosilow, Phys. Rev. A 46, 4630 (1992).
- [27] B. J. Brosilow, E. Gulari, and R. M. Ziff, J. Chem. Phys. 99, 1 (1993).
- [28] P. Moller, K. Wetzl, M. Eiswirth, and G. Ertl, J. Chem. Phys. 85, 5328 (1986).
- [29] J. W. Evans and T. R. Ray, Phys. Rev. E 50, 4302 (1994).
- [30] F. Chávez, L. Vicente, A. Perera and M. Moreau, J. Chem. Phys. 110, 8118 (1999).
- [31] R. H. Goodman, D. S. Graff, L. M. Sander, P. Leroux-Hugon, and E. Clément, Phys. Rev. E 52, 5904 (1995).
- [32] E. V. Albano, Phys. Rev. E 55, 7144 (1997).
- [33] H. C. Kang and W. H. Weinberg, Phys. Rev. E 47, 1604 (1993).
- [34] M. Ehsasi et al., J. Chem. Phys. 91, 4949 (1989).
- [35] K. Yaldram and M. A. Khan, J. Catal. 131, 369 (1991) and 136, 279 (1992).
- [36] B. J. Brosilow and R. M. Ziff, J. Catal. 136, 275 (1992).
- [37] B. Meng, W. H. Weinberg and J. W. Evans, Phys. Rev. E. 48, 3577 (1993).
- [38] M. Tammaro and J. W. Evans, J. Chem. Phys. 108, 7795 (1998).
- [39] P. Meakin and D. J. Scalapino, J. Chem. Phys. 87, 731 (1987).
- [40] J. F. Gouyet, M. Rosso, and B. Sapoval, "Fractal surfaces and interfaces", in Fractal and Disordered Systems, edited by A. Bunde and S. Havlin, (Springer-Verlag, Berlin, 1991), p. 229.
- [41] K. Fichthorn, E. Gulari and R. Ziff, Phys. Rev. Lett. 63, 1527 (1989).
- [42] H. C. Kang and W. H. Weinberg, Phys. Rev. E. 48, 3464 (1993).
- [43] H. C. Kang and W. H. Weinberg, J. Chem. Phys. 100, 1630 (1994).
- [44] R. J. Gelten et al., J. Chem. Phys. 108, 5921 (1998).
Publication Dates
-
Publication in this collection
17 Oct 2001 -
Date of issue
Mar 2000
History
-
Received
15 Nov 1999





























