Abstract
There are many theoretical arguments indicating that there should be new Physics around the TeV scale which can be discovered in the next decade. We briefly review some of the possible scenarios which give rise to a plethora of new signals at collider experiments.
Is there new Physics around the corner?
O. J. P. Éboli
Instituto de Física Teórica,
Universidade Estadual Paulista
Rua Pamplona 145, São Paulo, SP 01405-900, Brazil
E-mail: boli@ift.unesp.br
Received 7 January, 2000
There are many theoretical arguments indicating that there should be new Physics around the TeV scale which can be discovered in the next decade. We briefly review some of the possible scenarios which give rise to a plethora of new signals at collider experiments.
I New Physics Scenarios
In the last few years it has been established that the interactions of the gauge bosons with the fermions are well described by the Standard Model (SM) [1]. However, we have not observed the SU(2)LÄ U(1)Y symmetry breaking mechanism yet. At present, the best available limit on the SM Higgs mass arises from searches at the CERN LEP collider. The ALEPH Collaboration analysis of the 1999 data with integrated luminosities of 29 pb-1 at  = 191.6 GeV and 69.5 pb-1 at
= 191.6 GeV and 69.5 pb-1 at  = 195.6 GeV [2] yields MH > 98.8 GeV at 95% CL.
= 195.6 GeV [2] yields MH > 98.8 GeV at 95% CL.
The precision measurements performed at the Z peak exhibit an agreement at the per mile level with the SM theoretical predictions [1]. Such a precision allows us to obtain information on the Higgs boson via loop effects despite its contribution being only logarithmic upon the Higgs mass. Performing a global fit to the available data within the framework of the SM allow us to constraints the Higgs mass [3]; see Fig. 1. At the 95% CL the SM Higgs mass is bounded from above MH < 230 GeV. Therefore, we should be able to start probing the symmetry breaking mechanism in the next few years at the Tevatron or the LHC if the SM describes correctly this mechanism.
However this might be not the whole story! The analysis of the stability of the SM vacuum implies that the quartic Higgs coupling is bounded from below, which corresponds to a lower limit on the Higgs mass [4]. Requiring that the SM vacuum is stable up to the GUT scale (1016 GeV), we must have MH > 130 GeV. Moreover, the running quartic Higgs coupling is given by
which exhibits a pole, termed Landau pole, at a finite scale L. This pole signals the appearance of new physics. Again, assuming the SM to be valid up to the GUT scale leads to MH < 180 GeV [5].
From the above discussion, the SM with one Higgs doublet might describe the whole particle physics up to the GUT scale provided 130 < MH < 180 GeV. However, even if the Higgs is discovered in this mass range it is unlikely that the SM is the whole truth since it is unnatural to have a light scalar in a model with a very heavy scale (GUT one) because there is no mechanism to protect the Higgs mass to be of the order of the heavy scale due to radiative corrections. One solution to the naturalness problem is to introduce supersymmetry (SUSY) at the TeV scale. In this case, there should be plenty of new particles waiting to be found in the next few years.
Another distinct possibility is that the symmetry breaking mechanism does not exhibit a Higgs boson. This happens in models with dynamical symmetry breaking. Here, theoretical arguments also point that the new physics scale is low enough to be tested in the next generation of colliders. In fact, the scattering WW ® WW violates unitarity for energies larger than 4pv  3 TeV if there is no Higgs boson [6]. This indicates that we should have new states at this energy scale or that the theory becomes strongly interacting. Again there will be plenty of excitement when we start to probe the TeV scale if this is the correct scenario!
3 TeV if there is no Higgs boson [6]. This indicates that we should have new states at this energy scale or that the theory becomes strongly interacting. Again there will be plenty of excitement when we start to probe the TeV scale if this is the correct scenario!
Recently there has been a great interest in the possibility that the scale of quantum gravity is of the order of the electroweak scale [7] instead of the Planck scale Mpl 1019 GeV. The known constructions of a consistent quantum gravity theory require the existence of extra dimensions [8], which should have been compactified. A simple argument based on the Gauss' law in arbitrary dimensions shows that the Planck scale is related to the radius of compactification (R) of the n extra dimensions and the quantum gravity scale by
1019 GeV. The known constructions of a consistent quantum gravity theory require the existence of extra dimensions [8], which should have been compactified. A simple argument based on the Gauss' law in arbitrary dimensions shows that the Planck scale is related to the radius of compactification (R) of the n extra dimensions and the quantum gravity scale by
where MS is the (4 + n)-dimensional fundamental Planck scale or the string scale. Thus the largeness of the 4-dimensional Planck scale Mpl (or smallness of the Newton's constant) can be attributed to the existence of large extra dimensions of volume Rn. If one identifies MS ~ 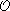 (1 TeV), this scenario resolves the original gauge hierarchy problem between the weak scale and the fundamental Planck scale, and lead to rich low energy phenomenology. The n = 1 case corresponds to R
(1 TeV), this scenario resolves the original gauge hierarchy problem between the weak scale and the fundamental Planck scale, and lead to rich low energy phenomenology. The n = 1 case corresponds to R  108 km, which is ruled out by observation on planetary motion. In the case of two extra dimensions, the gravitational force is modified on the 0.1 mm scale; a region not subject to direct experimental searches yet. However, astrophysics constraints from supernova has set a limit MS > 30 TeV for n = 2 [9], and thus disfavored as a solution to the gauge hierarchy problem as well as for a direct collider search.
108 km, which is ruled out by observation on planetary motion. In the case of two extra dimensions, the gravitational force is modified on the 0.1 mm scale; a region not subject to direct experimental searches yet. However, astrophysics constraints from supernova has set a limit MS > 30 TeV for n = 2 [9], and thus disfavored as a solution to the gauge hierarchy problem as well as for a direct collider search.
Generally speaking, when the extra dimensions get compactified, the fields propagating there give rise to towers of Kaluza-Klein states [10], separated in mass by 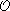 (1/R). In order to evade strong constraints from electroweak precision measurements the SM fields are assumed to live on a 4-dimensional hypersurface, and only gravity propagates in the extra dimensions. This assumption is based on new ideas about the D-branes [11]. If gravity becomes strong at the TeV scale, Kaluza-Klein (KK) gravitons should play a rôle in high-energy particle collisions, either being radiated or as a virtual exchange state. There has been much work in the recent literature to explore the collider consequences for the KK gravitons [12, 13].
(1/R). In order to evade strong constraints from electroweak precision measurements the SM fields are assumed to live on a 4-dimensional hypersurface, and only gravity propagates in the extra dimensions. This assumption is based on new ideas about the D-branes [11]. If gravity becomes strong at the TeV scale, Kaluza-Klein (KK) gravitons should play a rôle in high-energy particle collisions, either being radiated or as a virtual exchange state. There has been much work in the recent literature to explore the collider consequences for the KK gravitons [12, 13].
The above new physics scenarios are just a representative set of the large number of possible extensions of the SM. In the following we describe some of their phenomenological implications and the respective signals at colliders. Our main point is that these models give rise to such a large number of new topologies that their study will cover almost all new physics possibilities, even the ones not considered here, guaranteeing that the experiments will not miss any new physics sign in the TeV scale!
II Higgs Searches
Nowadays LEP II is the machine with the largest capability to study the production of Higgs bosons provided MH is not too large. At LEP energies the main Higgs production mechanism is [14]
whose total cross section we present in Fig. 2. This process allow us to probe Higgs masses up to 
 - 95 GeV [14].
- 95 GeV [14].
SM Higgs production cross section at LEP as a function of MH for different center-of-mass energies [14].
The SM Higgs signal depends on its possible decays which are display in Fig. 3. Taking into account the Z and Higgs decay channels, the SM Higgs production topologies are the ones shown in Table 1. An important feature of these Higgs topologies is the presence of jets tagged as b-jets since a light Higgs has a large branching ratio into b pairs. The main SM backgrounds for the Higgs search are the W+W - and ZZ productions whose cross sections are roughly 20 and 1 pb respectively. An efficient way to reduce the background is to require the presence of b-tagged jets in the event. In fact, b-tagging reduces the signal by a factor 0.60 while the W+W - background is reduced by a factor 0.01 and 10% of the ZZ background survives.
pairs. The main SM backgrounds for the Higgs search are the W+W - and ZZ productions whose cross sections are roughly 20 and 1 pb respectively. An efficient way to reduce the background is to require the presence of b-tagged jets in the event. In fact, b-tagging reduces the signal by a factor 0.60 while the W+W - background is reduced by a factor 0.01 and 10% of the ZZ background survives.
Final state topologies and expected frequencies for a SM Higgs boson at LEP II. Here, l stands for e± and m±.
In the LEP II experimental searches, a neural network is used to analyze the data, where many variables are considered like visible energy, missing transverse momentum, invariant mass of jet pairs, displaced vertices, etc. We summarize in Table 2 the 95% CL lower limits on the SM Higgs mass obtained by the negative results at 189 GeV of the four LEP collaborations, as well as the values expected assuming that just the background has been observed [15]. We also present in this table the combined limit of the four collaborations. Notice that the limits derived from data are usually smaller than the expected ones. This is due to a slight overall excess of events which is not accumulated in a single bin. This excess can originate from statistical fluctuations or simply a systematic underestimate of the backgrounds.
Lower bound on the SM Higgs mass derived by the four LEP Collaborations using the data taken at 189 GeV. For comparison we present the expected limits assuming that only the background was observed. The last line was obtained combining the four experiments.
In its last year of operation LEP will be able to extend the above limits on the SM Higgs. For instance, running at 198 GeV with an integrated luminosity of 200 pb-1 per experiment, its is possible to discover SM Higgs bosons with masses up to 105 GeV or to rule out SM Higgs bosons with masses up to 107 GeV. The next machine that will be able to improve these limits is the RUN II of the Tevatron whose performance is summarized in Fig. 4. As we can see from this figure, the Tevatron can exclude Higgs masses up to 120 GeV for an integrated luminosity of 2 fb-1. In order to probe the whole range of allowed Higgs masses we have to wait until the CERN Large Hadron Collider starts operating.
Combined CDF and DØ integrated luminosity needed to discover/rule out a SM Higgs as a function of its mass.
III Anomalous Higgs Interactions
A very interesting possibility is that the new physics manifests itself modifying the SM Higgs production and decays. Let us assume that there is a Higgs boson and that the new physics is rather heavy compared to the electroweak scale. In this case we can parametrize the deviations from the SM using effective lagrangians with a linear representation of the SU(2)LÄ U(1)Y symmetry. A set of possible effective operators is
which modify the couplings of the Higgs to gauge bosons. The operators
F,1 and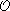 BW contribute at tree level to the vector-boson two-point functions, and consequently are severely constrained by low-energy data [16]. The present 95% CL limits on these operators for 90 GeV £ MH£ 800 GeV and mtop = 175 GeV, read
BW contribute at tree level to the vector-boson two-point functions, and consequently are severely constrained by low-energy data [16]. The present 95% CL limits on these operators for 90 GeV £ MH£ 800 GeV and mtop = 175 GeV, read
A surprising fact is that these residual interactions can modify considerably the Higgs physics even when we take into account these bounds! For instance, we show in Fig. 5 the allowed Higgs mass region by the low energy precision data including the effect of the operators 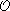 F,1 and
F,1 and  BW [17]. Notice the dramatic change with comparison with Fig. 1!
BW [17]. Notice the dramatic change with comparison with Fig. 1!
The effect of the additional Higgs interactions on the properties of an intermediate mass Higgs can be more easily seen in processes that are suppressed in the SM, such as the Higgs decay into two photons. In the SM, this decay occurs only at one-loop level, and it can be enhanced (or suppressed) by the anomalous interactions [18]. Moreover, these effective interactions also lead to new topologies for Higgs search at LEP [19]
Recently the L3 analyzed these signals [20], obtaining the 95% CL limits on L as a function of the Higgs mass for fWW = fBB = 1; see in Table 3.
IV Supersymmetric Models
Weak scale supersymmetric models received a lot of attention not only due to its intrinsic beauty but also for providing a solution for the naturalness (hierarchy) problem. We should not forget that these models are perturbative and consequently we can make reliable predictions, contrary to what happens in strongly interacting models like technicolor. In my point out of view, SUSY models are a excellent framework for preparing the analyses of experiments since they possess a large parameter space in its more general form which, in turn, gives rise to many distinct predictions and topologies.
In supersymmetric models the spectrum is more than two times bigger than the SM one since we have to introduce one supersymmetric partner for each SM particle and also enlarge the Higgs sector. Moreover, since the supersymmetric partners are not degenerated in mass with the SM particles we must also add a supersymmetry breaking sector, and consequently new free parameters. Altogether the number of SUSY parameters is larger than 100 being this the source of its rich phenomenology.
Here, I will just give a broad view of some popular SUSY scenarios. Initially we divide the SUSY models into two classes according they exhibit or not a discrete symmetry called R-parity. R-parity is related to the particle spin (S), lepton number (L), and baryon number (B) through R = (-1)(3B + L + 2S), being all the SM particles R-even while their superpartners are R-odd. Neither gauge invariance nor supersymmetry require its conservation.
Let us start by the models with R-Parity conservation. In this case the lightest supersymmetric particle (LSP) is stable and SUSY particles are only produced in pairs. One popular model is the so called Constrained Minimal Supersymmetric Standard Model (CMSSM) which uses supergravity to reduce the number of free parameters to 5 at the GUT scale. In the CMSSM it is assumed that SUSY breaking is communicated to our sector by gravitational interactions [21], resulting that the free parameters are a common SU(2) gaugino mass (M2), a common scalar mass (m0), the ratio of the VEV of the two Higgs doublets in the model (tanb), the Higgs mixing parameter m and the common trilinear coupling A0. In the CMSSM, the LSP is neutral and weak interacting, therefore, it is not observed in detectors. The decays of the SUSY particles lead to the production of LSP's due the R-parity conservation. Therefore, one of the main properties of CMSSM topologies is the presence of substantial missing energy. For example, the production of the SUSY partners of W± (charginos  ±) can lead to the following topology in e+e- colliders
±) can lead to the following topology in e+e- colliders
where only the decay product of the W*'s are observed.
Other models exhibiting R-parity conservation are the so called the Gauge Mediated SUSY Breaking models (GMSB), where the breaking of supersymmetry is mediated by gauge interaction between our sector and the hidden sector. In this case the characteristic energy scale can be much smaller than the Planck mass. This implies that the gravitino starts playing an important rôle in the phenomenology of these models since it is the LSP. In this case the gravitinos are not observed, also leading to missing energy signatures. However, these models also possess the additional property that the next to lightest SUSY particle (NLSP) decays into its SM partner and a gravitino  . If the NLSP is the SUSY partner of taus, the events will present a large number of taus due to
. If the NLSP is the SUSY partner of taus, the events will present a large number of taus due to  ® t +
® t +  . On the other hand, if the NLSP is the SUSY partner of the neutral gauge bosons
. On the other hand, if the NLSP is the SUSY partner of the neutral gauge bosons  0, there will be photon rich samples due to
0, there will be photon rich samples due to  0® g+
0® g+  . Clearly the GMSB models have a phenomenology very distinct of the CMSSM. For instance GMSB models can lead to events presenting two photons and missing transverse energy in hadronic colliders via
. Clearly the GMSB models have a phenomenology very distinct of the CMSSM. For instance GMSB models can lead to events presenting two photons and missing transverse energy in hadronic colliders via
We can classify the models without R-parity according to the mechanism of R-parity breaking, which can be explicit or spontaneous. The explicit break of R-parity takes place by adding the following terms to the superpotential
which contain the quark and lepton superfields Q, U, D and L. In this scenario there are 48 extra free parameters! The SUSY phenomenology is modified substantially since SUSY particles can decay into SM ones and the LSP is no longer stable. Moreover, SUSY particles can also be produced as resonances, leading to new clear signatures. Typical bounds on the l's are of the order of 1% except when these new interaction can lead to a fast proton decay. For instance, l¢11kl¢¢11k < 10-22 in this case [22].
In this scenario, there can be events presenting many jets and/or leptons, with or without missing energy, due to complex cascade decays and to the fact that the LSP is unstable. For instance, the OPAL collaboration defines nine topologies in their searches for charginos [23], see Table 4. Notice that there are many new channels with respect to the CMSSM search that leads to a pair of W's and missing energy. Since there are so many new and distinct topologies in models with R-parity violation it is possible that we find a sign of new physics, even if it is not supersymmetric, when looking desperately for SUSY!
Topologies studied by the OPAL collaboration in their search for charginos assuming that R-parity is explicitly broken.
V Low Scale Quantum Gravity
The phenomenology of models with low scale quantum gravity differ from the SM one since they exhibit towers of Kaluza-Klein gravitons. Despite the graviton interaction with SM particles being suppressed by powers of the Planck mass, they can give rise to visible effect since we have to sum up the contribution of the whole graviton tower, which trades the Planck mass by the quantum gravity scale MS; see for instance [7]. Virtual graviton exchanges modifies the SM cross sections according to
where E is a characteristic energy scale of the process sSM, sI and sG are associated, respectively, to the SM, interference graviton-SM, and pure graviton contributions. An interesting feature of the virtual graviton exchange is that it is insensitive on the number of extra dimensions. The signature of graviton exchange is the modification of the energy dependence of the cross section, as well as changes in angular distributions. Notice that the graviton contribution increases so rapidly with energy that it eventually leads to unitarity violation. At this point, either there is the appearance of new states to enforce unitarity or the model becomes strongly interacting.
Since graviton-matter interactions are not enhanced, gravitons escape detection leading to missing energy signatures. In graviton emission we must also sum over all graviton masses
which leads to an enhancement of the cross section
Notice that graviton emission depends strongly on the number of extra dimensions and that it eventually gives rise to unitarity violation.
The presently available data from LEP and Tevatron constrain the quantum gravity scale to be larger than  1 TeV [24]. For instance, let us study the limits that can be obtained from the process e+e-® gg [26]. The LEP Collaborations use this reaction to set bounds on contact interactions whose contribution is written as
1 TeV [24]. For instance, let us study the limits that can be obtained from the process e+e-® gg [26]. The LEP Collaborations use this reaction to set bounds on contact interactions whose contribution is written as
where z is the cosine of the polar scattering angle. The leading graviton exchange contribution can also be cast into this form with, for n ¹ 2,
Employing the 95% C.L. limits on L+ (GeV) obtained by the LEP Collaborations [26] we obtained the limits showed in Table 5.
VI Final Remarks
There are strong theoretical arguments that the next decade will be very exciting for particle physics since for the first time we will probe the symmetry breaking sector of the electroweak interactions. There are many viable new physics scenarios, however the experiments will be looking for so many signals of new physics that we can be almost sure that new physics will be observed.
Acknowledgments
This work was supported by Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq), by Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP), and by Programa de Apoio a Núcleos de Excelência (PRONEX).
References
[1] OPAL Collaboration, L3 Collaboration, DELPHI Collaboration ALEPH Collaboration, LEP Electroweak Working Group, and SLD Heavy Flavour and Electroweak Groups, preprint CERN-EP/99-15.
[2] ALEPH Collaboration, Contribution to the 19th International Symposium on Lepton and Photon Interactions at High-Energies, Stanford (1999), hep-ex/9908016.
[3] M. Swartz, results presented at the 1999 Lepton-Photon Symposium, Stanford, August 9-14, 1999.
[4] M. Sher, Phys. Rep. 179, 273 (1989); G. Isidori, Phys. Lett. B 337, 141 (1994); J. Espinosa and M. Quiros, Phys. Lett. B 353, 257 (1995).
[5] J. Casas, J. Espinosa, M. Quiros, and A. Riotto, Nucl. Phys. B 436, 3 (1995); L. Maiani, G. Parisi, and R. Petronzio, Nucl. Phys. B 136, 115 (1978).
[6] B.W. Lee, C. Quigg, and H.B. Thacker, Phys. Rev. D 16, 1519 (1977).
[7] N. Arkani-Hamed, S. Dimopoulos, and G. Dvali, Phys. Lett. B 429, 263 (1998); I. Antoniadis, N. Arkani-Hamed, S. Dimopoulos, and G. Dvali, Phys. Lett. B 436, 257 (1998); I. Antoniadis and C. Bachas, Phys. Lett. B 450, 83 (1999).
[8] See, for instance, M.B. Green, J.H. Schwarz, and E. Witten, Superstring Theory, Cambridge Press (1987).
[9] S. Cullen and M. Perelstein, hep-ph/9903422; V. Barger, T. Han, C. Kao, and R. Zhang, hep-ph/9905474.
[10] See, e. g., Modern Kaluza-Klein Theories, eds. T. Appelquist, A. Chodos, and P. Freund, Addison-Wesley Pub. (1987).
[11] I. Antoniadis, Phys. Lett. B 246, 377 (1990); J. Lykken, Phys. Rev. D 54, 3693 (1996); K. Dienes, E. Dudas, and T. Ghergetta, Phys. Lett. B 436, 55 (1998). G. Shiu and S.-H. Tye, Phys. Rev. D 58, 106007 (1998); Z. Kakushadze and S.-H. Tye, Nucl. Phys. B 548, 180 (1999); L.E. Ibanez, C. Munoz, and S. Rigolin, hep-ph/9812397.
[12] N. Arkani-Hamed, S. Dimopoulos, and G. Dvali, Phys. Rev. D 59, 086004 (1999).
[13] A.K. Gupta, N.K. Mondal, and S. Raychaudhuri, hep-ph/9904234; P. Mathews, S. Raychaudhuri, and K. Sridhar, Phys. Lett. B 455, 115 (1999) and hep-ph/9904232; T. Rizzo, Phys. Rev. D 59, 115010 (1999), hep-ph/9902273, hep-ph/9903475 and hep-ph/9904380; S.Y. Choi et al., Phys. Rev. D 60, 013007 (1999); K. Agashe and N.G. Deshpande, Phys. Lett. B 456, 60 (1999); K. Cheung and W.-Y. Keung, hep-ph/9903294; D. Atwood, S. Bar-Shalom, and A. Soni, hep-ph/9903538; C. Balazs et al., hep-ph/9904220; K. Cheung, hep-ph/9904510; K.Y. Lee, H.S. Song, and J. Song, hep-ph/9904355; Hooman Davoudiasl, hep-ph/9904425; G. Shiu, R. Shrock, and S.-H. Tye, hep-ph/9904262; T. Han, J. Lykken, and Ren-Jie Zhang, Phys. Rev. D 59, 105006 (1999); O. Éboli et al., hep-ph/9908358.
[14] See for instance, M. Carenna and P. Zerwas (editors), CERN yellow report, CERN-96-01 (hep-ph/9602250).
[15] ALEPH, DELPHI, L3, and OPAL Collaborations, preprint ALEPH 99-081 CONF 99-052, submitted to the International Europhysics Conference on High Energy Physics, Tampere, Finland, 1999.
[16] A. De Rújula, M.B. Gavela, P. Hernández, and E. Massó, Nucl. Phys. B 384, 3 (1992) 3; K. Hagiwara, S. Ishihara, R. Szalapski, and D. Zeppenfeld, Phys. Rev. D 48, 2182 (1993).
[17] L. Hall and C. Kolda, Phys. Lett. B 459, 213 (1999).
[18] F. de Campos, M.C. Gonzalez-Garcia, and S.F. Novaes, Phys. Rev. Lett. 79, 5210 (1997); M.C. Gonzalez-Garcia, S.M. Lietti, and S.F. Novaes, Phys. Rev. D 57, 7045 (1998); F. de Campos, M.C. Gonzalez-Garcia, S.M. Lietti, S.F. Novaes, and R. Rosenfeld, Phys. Lett. B 435, 407 (1998); M.C. Gonzalez-Garcia, S.M. Lietti, and S.F. Novaes, Phys. Rev. D 59, 075008 (1999); M.C. Gonzalez-Garcia, Int. J. Mod. Phys. A 14, 3121 (1999).
[19] O. Éboli, M.C. Gonzalez-Garcia, S.M. Lietti, and S.F. Novaes, Phys. Lett. B 434, 340 (1998).
[20] L3 Collaboration, L3 Reference 2365, March 5, 1999.
[21] For details, see for instance, M. Drees and S. P. Martin, hep-ph/9504324 and references therein.
[22] V. Barger, G.F. Guidice, T. Han Phys. Rev. D 40, 2987 (1989).
[23] OPAL Collaboration, G. Abbiendi et al.,. Eur. Phys. J. C 11, 619 (1999).
[24] See for instance, T. Rizzo, hep-ph/0001247.
[25] Kingman Cheung, Phys. Rev. D 61, 015005 (2000).
[26] ALEPH Collaboration, Phys. Lett. B 429, 201 (1998); and contribution to the 1999 winter conference ALEPH 99-022; L3 Coll., Phys. Lett. B 413, 159 (1997); and submission to ICHEP'98, L3 Internal Note 2269; DELPHI Collaboration, Phys. Lett. B 433, 429 (1998); OPAL Coll., Phys. Lett. B 438, 379 (1998); and OPAL Physics Note PN381.
- [3] M. Swartz, results presented at the 1999 Lepton-Photon Symposium, Stanford, August 9-14, 1999.
- [4] M. Sher, Phys. Rep. 179, 273 (1989);
- G. Isidori, Phys. Lett. B 337, 141 (1994);
- J. Espinosa and M. Quiros, Phys. Lett. B 353, 257 (1995).
- [5] J. Casas, J. Espinosa, M. Quiros, and A. Riotto, Nucl. Phys. B 436, 3 (1995);
- L. Maiani, G. Parisi, and R. Petronzio, Nucl. Phys. B 136, 115 (1978).
- [6] B.W. Lee, C. Quigg, and H.B. Thacker, Phys. Rev. D 16, 1519 (1977).
- [7] N. Arkani-Hamed, S. Dimopoulos, and G. Dvali, Phys. Lett. B 429, 263 (1998);
- I. Antoniadis, N. Arkani-Hamed, S. Dimopoulos, and G. Dvali, Phys. Lett. B 436, 257 (1998);
- I. Antoniadis and C. Bachas, Phys. Lett. B 450, 83 (1999).
- [8] See, for instance, M.B. Green, J.H. Schwarz, and E. Witten, Superstring Theory, Cambridge Press (1987).
- [10] See, e. g., Modern Kaluza-Klein Theories, eds. T. Appelquist, A. Chodos, and P. Freund, Addison-Wesley Pub. (1987).
- [11] I. Antoniadis, Phys. Lett. B 246, 377 (1990);
- J. Lykken, Phys. Rev. D 54, 3693 (1996);
- K. Dienes, E. Dudas, and T. Ghergetta, Phys. Lett. B 436, 55 (1998).
- G. Shiu and S.-H. Tye, Phys. Rev. D 58, 106007 (1998);
- Z. Kakushadze and S.-H. Tye, Nucl. Phys. B 548, 180 (1999);
- [12] N. Arkani-Hamed, S. Dimopoulos, and G. Dvali, Phys. Rev. D 59, 086004 (1999).
- [13] A.K. Gupta, N.K. Mondal, and S. Raychaudhuri, hep-ph/9904234; P. Mathews, S. Raychaudhuri, and K. Sridhar, Phys. Lett. B 455, 115 (1999) and hep-ph/9904232;
- T. Rizzo, Phys. Rev. D 59, 115010 (1999), hep-ph/9902273, hep-ph/9903475 and hep-ph/9904380;
- S.Y. Choi et al., Phys. Rev. D 60, 013007 (1999);
- K. Agashe and N.G. Deshpande, Phys. Lett. B 456, 60 (1999);
- K. Cheung and W.-Y. Keung, hep-ph/9903294; D. Atwood, S. Bar-Shalom, and A. Soni, hep-ph/9903538; C. Balazs et al., hep-ph/9904220; K. Cheung, hep-ph/9904510; K.Y. Lee, H.S. Song, and J. Song, hep-ph/9904355; Hooman Davoudiasl, hep-ph/9904425; G. Shiu, R. Shrock, and S.-H. Tye, hep-ph/9904262; T. Han, J. Lykken, and Ren-Jie Zhang, Phys. Rev. D 59, 105006 (1999);
- [16] A. De Rújula, M.B. Gavela, P. Hernández, and E. Massó, Nucl. Phys. B 384, 3 (1992) 3;
- K. Hagiwara, S. Ishihara, R. Szalapski, and D. Zeppenfeld, Phys. Rev. D 48, 2182 (1993).
- [17] L. Hall and C. Kolda, Phys. Lett. B 459, 213 (1999).
- [18] F. de Campos, M.C. Gonzalez-Garcia, and S.F. Novaes, Phys. Rev. Lett. 79, 5210 (1997);
- M.C. Gonzalez-Garcia, S.M. Lietti, and S.F. Novaes, Phys. Rev. D 57, 7045 (1998);
- F. de Campos, M.C. Gonzalez-Garcia, S.M. Lietti, S.F. Novaes, and R. Rosenfeld, Phys. Lett. B 435, 407 (1998);
- M.C. Gonzalez-Garcia, S.M. Lietti, and S.F. Novaes, Phys. Rev. D 59, 075008 (1999);
- M.C. Gonzalez-Garcia, Int. J. Mod. Phys. A 14, 3121 (1999).
- [19] O. Éboli, M.C. Gonzalez-Garcia, S.M. Lietti, and S.F. Novaes, Phys. Lett. B 434, 340 (1998).
- [22] V. Barger, G.F. Guidice, T. Han Phys. Rev. D 40, 2987 (1989).
- [23] OPAL Collaboration, G. Abbiendi et al.,. Eur. Phys. J. C 11, 619 (1999).
- [25] Kingman Cheung, Phys. Rev. D 61, 015005 (2000).
- [26] ALEPH Collaboration, Phys. Lett. B 429, 201 (1998);
- and contribution to the 1999 winter conference ALEPH 99-022; L3 Coll., Phys. Lett. B 413, 159 (1997);
- and submission to ICHEP'98, L3 Internal Note 2269; DELPHI Collaboration, Phys. Lett. B 433, 429 (1998);
- OPAL Coll., Phys. Lett. B 438, 379 (1998);
Publication Dates
-
Publication in this collection
07 Jan 2002 -
Date of issue
June 2000
History
-
Received
07 Jan 2000
























