Abstract
In this paper we obtain the Lie symmetries and the Noether symmetries for several physical systems, all of them involving a charged particle in the presence of some electromagnetic field. We also obtain first integrals for these systems and discuss briefly their Lie algebra. In some examples we discuss their integrability.
Symmetries and invariants for some cases involving charged particles and general electromagnetic fields: a brief review
O. M. Ritter
Departametno de Física
Universidade Federal de Santa Catarina
88040-900, Florianópolis, SC, Brazil
Received 11 October, 1999
In this paper we obtain the Lie symmetries and the Noether symmetries for several physical systems, all of them involving a charged particle in the presence of some electromagnetic field. We also obtain first integrals for these systems and discuss briefly their Lie algebra. In some examples we discuss their integrability.
I Introduction
The idea of symmetry is extremely important in physics, both classic and modern. It can be said that the abstract formulation of this idea, that is the group concept, is one of the great unifying ideas of mathematics. Sophus Lie applied the group concept to differential equations trying to integrate them. His success permitted to unify and extend the existent integration techniques. In the last two or three decades the application of Lie's method growed quickly. Actually, with the growing importance of non-linear differential equations, Lie's procedure constitues, perhaps, the only existent method to attack such problems in a systematic way, in the attempt of its integration. Besides this, chaotic behavior has became very important in physics and applied mathematics. So it's important to determine conditions for the absence of this chaotic behavior looking for parameter values for which the system can be completely (or, at least, partially) integrated. It's well known that the concept of integrability, in it's various formulations, is related to the existence of first integrals. So the search for first integrals is one of the possible ways to decide by the integrability of a system.
The symmetry method (see Olver [1986])1, introduced by Lie, is one of the methods used to accomplish this goal (Bueno et al [1986])2. Lie's method consists in finding the continuous symmetry transformations that leave a system of differential equations invariant. These symmetry transformations constitues a Lie group. Once you have obtained the symmetry group, there are some ways to find first integrals.
Another method used in obtaining first integrals is Noether's Theorem (Sarlet and Cantrijn [1981])3.
In this paper we analize a number of situatons in which a charged particle interacts with an electromagnetic field. We find the Lie and Noether symmetries and first integrals associated with these problems. For some of them we discuss their integrability.
Some of the results obtained are new and some are already known, although they have been obtained from an original point of view most of the time. In this sense the paper is a kind of review for this type of systems.
In next section we put the general problem of a particle in an electromagnetic field and outline the method of Lie and the Noether theorem. In third section we analize a number of diferent cases. And, finally, in last section we make some comments in conclusion.
II Symmetries for the general problem of a charged particle in a general electromagnetic field
A. a) Lie symmetries
In this work we will use point transformations only. In a certain sense this is a strong limitation but, for our purposes in this paper the above supposition will be sufficient.
The symmetry vector fields can be obtained from the invariance of the system of second-order differential equations
under the infinitesimal transformations
where i = 1, ..., n to permit a greater generality.
The symmetry evolutionary vector field has the form
The Lie conditions for the invariance of the system (1) are
where
is the second prolongation of the vector field (3), and
where k = 1, 2, ...m, hi(0) = hi, e xi =  .
.
The m-th prolongation of U is the vector field
The motion of a charged particle in the presence of a general electromagnetic field can be described by Lorentz equations:
where Fi(t, xj) = eEi(t, xj), with e being the electric charge and Ei the electric field, b = e/c, with c being the speed of light, and Bk(t, xj) being the magnetic field. As usual, the eijk are the permutation symbols. We have taken the mass equal to one. By now, we can also neglect the term coming from the radiation reaction due to acceleration of the electric charge. Applying the Lie conditions for invariance (4) to equation (8) and using the equations of motion (8) we obtain
When we try to solve the above equation we arrive to the following system of linear partial differential equations:
A general solution of the equations (10a) can be obtained independently of the functional form of Fi and Bk; it can be written as
where fi(t) e h(t) are functions of time and will be determined by equations (10b, c, d). They will depend on the functional form of Fi(t, xj) and Bk(t, xi). In three-dimensional space, equations (10b, c, d) give rise to 30 equations. The solution of these equations will, as well, depend on the form of Fi and Bk.
Once we have solved equations (10) and obtained the Lie symmetries vector fields for the problem we can use some known methods to achieve first integrals. In this work we will make use of two of these methods. The first one makes use of the following theorem ( I.C. Moreira et al. [1985])4:
"If I is a first integral for a given system of differential equations, then the quantity I¢ = U(1)I is a first integral for any symmetry vector field associated with this system".
The other method for finding invariants that we will use was introduced by Prince [1979]5 and can be resumed in a few simple steps:
i) Find the invariants for the first prolongation of the vector field pr(1)U;
ii) obtain a system of first order differential equations invariant under pr(2)U;
iii) integrate these equations obtaining integration constants in terms of invariants;
iv) invert these funtions obtaining the invariants in terms of the xi's and t.
II.b Noether symmetries
In this work we will apply the Noether Theorem to the general case of a charged particle in the presence of an electromagnetic field. As in the case of the Lie method, we will restrict ourselves to point transformations.
We will assume a Lagrangian system described by the Lagrangian  (x, xi, t) and consider an infinitesimal point transformation in the (t, xi) space, defined by (2a-b). These infinitesimal transformation are said to leave the action integral invariant up to gauge terms, if a function f(t, xi) exists, such that for each differentiable curve t®xi(t), we have
(x, xi, t) and consider an infinitesimal point transformation in the (t, xi) space, defined by (2a-b). These infinitesimal transformation are said to leave the action integral invariant up to gauge terms, if a function f(t, xi) exists, such that for each differentiable curve t®xi(t), we have
This will be the case if and only if
where prU(1) is the first prolongation of the vector field U.
So an infinitesimal symmetry like (2a-b) will be a Noether symmetry for a given Lagrangian system and a function f, if it satisfies equation (13). If this is so, to each Noether symmetry (2a-b) there corresponds a first integral I(t, xi, xi) given by
Let us now apply Noether's theorem for the case of a charged particle in a general electromagnetic field. The lagrangian for such a system can be written as
where Ai(t, xj) is the vector potential, V is the electrical potential, and the mass was taken equal to one, as before. Applying the first part of Noether's Theorem, equation (13) to the above lagrangian, we obtain
Equation (16) gives rise to a system of linear partial differential equations in the functions x and hi:
If we know Ai and V, we can solve equations (17) and find the functions x,hi and f, thus obtaining Noether's symmetries for the system.
III Symmetries for some particular cases of charged particle in an electromagnetic field
In this section we present a certain number of cases of physical interest, all of them concerning the problem of a charged particle in the presence of some electromagnetic field.
A. I. Basic particular cases
1. (i) Simple harmonic oscillator
Anderson and Davison [1974]6 first, and Wulfman and Wybourne [1976]7 have discussed extensively this case. Prince and Eliezer [1980]8 generalized this problem to the time-dependent n-dimensional oscillator.
The one-dimensional differential equation for the harmonic oscillator can be written, with an adequate choice of units as
Comparing this equation with (8) we see that Fi(t, xj) = -xi and Bk(t, xj) = 0. Solving equations (10) for this case, we find the following Lie symmetry vector fields
These vectors constitues the base of an eight-parameter Lie group, with an associated Lie algebra of dimension eight. This is a semi-simple algebra as can be seen by constructing the metric tensor
and by showing that the determinant
according to the Cartan criterion. As the metric is undefined, we can conclude that the Lie algebra is that of a non-compact Lie Group. The three vectors U1, U3, U5 form an associated compact Lie algebra with a negative defined metric gij = -2dij (i, j = 1, 3, 5). These three vectors generate a compact subgroup: SO(3). The full global eight parameter group is SL(3, R).
The first integrals for this system are easily obtained by any of the methods outlined above, or using Noether's theorem.
2. (ii) Kepler's problem
The classic Kepler problem (see Prince and Eliezer[1981])9, with potential energy V = -k/r , has fundamental importance in classical mechanics. Associated with this problem there are three first integrals: energy, angular momentum and the Runge-Lenz vector. The equation of motion and corresponding Lagrangian for the problem are
where m is constant and r = (x2 + y2 + z2) . Let's consider the motion restrict to the (x, y)-plane. This is guarantee by the constancy of the angular momentum L.
. Let's consider the motion restrict to the (x, y)-plane. This is guarantee by the constancy of the angular momentum L.
Comparing equation (20) with (8) we verify that Fi(t, xj) = mxi/r3 and Bk = 0, with i = 1,2.
If we now compare the lagrangian (20) with the general one (15), we obtain that Ai = 0, and eV = -m/r. Solving general equations (10a-d) we obtain the Lie point symmetries for the problem. Solving general equations (17a-d) we get the Noether symmetries for the system.
In the Noether case we obtain two independent vector fields of symmetry
In the Lie case we get the two vector fields (21) and an extra vector field given by
corresponding to a scale symmetry admitted by the equation of motion.
The Noetherian vector fields form a two-parameter abelian subgroup of the three-parameter Lie group. The only non-vanishing structure constants are
The metric tensor of the algebra is given by
This is a non-semi-simple algebra and is a semi-direct sum of the of the solvable subalgebra {U1,U3} and the simple subalgebra {U2}.
If we use equation (14) of the Noether theorem, we can obtain the first integrals associated with each of the two symmetry vector fields
To obtain the x and y components of the Runge-Lenz vector we use the Lie symmetry vector field given by (22) and the method developed by Prince [1979] and briefly discussed at the end of section 2a:
3. (iii) Constant magnetic field
Let's consider now the classic case of a charged particle in an uniform magnetic field. This problem has been studied under several points of view ( Sivardière [1988]10, Moreira [1983]11). The motion is a combination of a circular one with that of a free particle. A very simple and interesting approach given to this problem makes use of a vector constant of motion named Landau vector which is used also in the quantum case. The conservation of the Landau vector is associated with the conservation of the motion of the center of mass of the system. The Landau vector is related to the center of the orbit. It has dimension of linear momentum and is composed of two terms: the first is the kinetic linear momentum and the second comes from the interaction between the charged particle and magnetic field. Obviously the Landau vector is not the only constant of motion associated to this problem.
Let's compute the Lie symmetries for this problem starting from the general equation (8) and making Fi(t, xj) = 0, B k(t, xj) = B0 = const., when k = 3 and Bk = 0 when k = 1, 2. With this choice the magnetic fiel is along the z-axes. The equations of motion for the system are
Solving equations (10a-d) we obtain a twelve-parameter group from which we get the following Lie symmetry vector fields
The first integrals for this system are easily obtained by any of the methods described above. If we use the Prince [1979] method and take, for instance, the vector field U1 we arrive after a little algebra to the components of the Landau vector
In vectorial form
We can use this same procedure to obtain a number of first integrals, some of which we list in correspondence with the vector field used in its construction
Using the method with the rotation vector field U4 we arrive also to the following first integral
where I9 is the z-component of the canonical angular momentum in the direction of the magnetic field. It must be remembered that the canonical angular momentum is not conserved, only its z-component. As in the case of the Landau vector, the conservation of Lz is associated to an aditional degenerecency of the problem. With the same initial velocity but with different initial positions, the charged particle describes a different orbit with the same energy.
If we now apply the Noether theorem to this problem w'll get an eight-parameter Lie group. The vector fields forming this group constitues a subgroup of the previous one (26) obtained directly from the equations of motion. The symmetry vector fields obtained via Noether theorem are among those found in (26): U1, U2, U4, U5, U6, U9, U10, U11. Using the second part of Noether theorem we reobtain almost all of the first integrals (27a-d, 28, 29).
B.II. Generalisations
Let's now discuss some more general cases. W'll begin by considering systems with no magnetic field.
a) Vanishing magnetic field:  = 0.
= 0.
(i) The anisotropic Kepler problem
The so called anisotropic Kepler (see for instance Gutzwiller [1989]12) problem has been studied in the last years as an interesting example of a two-dimensional system with chaotic behavior. This potential has been studied in the context of the physics of semiconductors. It can appear also in certain models with three different masses interacting in a plane.
The anisotropic Kepler potential, in the two-dimensional case, has the form
with m ¹ 1. In obtaining the Lie group of symmetries for the system we get two vector fields
together with the comutation relation between them [U1, U2] = U1.
As we can see, the kind of anisotropy introduced in the Kepler potential has destroyed the rotation symmetry, but preserved the group of scalings. The angular momentum is no longer a conserved quantity as it was in the usual Kepler problem, when m = 1.
We can 't find a second conserved quantity, besides the energy, by any method we use. If this was so, we could guarantee the integrability of the system in the sense of Liouville (see Arnold, [1976]13). The non-integrability of this potential was established by Yoshida [1987]14.
(ii) The Kepler problem with a linear force
A possible generalisation of the above cases could be given by an equation of motion joining two cases: the Kepler problem with the harmonic oscillator. The equations of motion for this case are
Comparing this equation with the general equation (8) we see that Fi =  - w2xi , B = 0. Solving equations (10) we obtain the vector fields
- w2xi , B = 0. Solving equations (10) we obtain the vector fields
which form a four-parameter Lie group. The three last vector fields form the group of rotations SO(3). From this we have the conservation of angular momentum. From the first vector field we find the conservation of energy. These are the conserved quantities for this system.
(iii) The Hidrogen atom in an electric field
Another interesting physical situation comes from the classic theory of the excitation of a hidrogen atom under a monocromatic linearly polarized electric field . Consider the hamiltonian
where E0 and w are, respectively, the electric field and its frequency. The z-coordinate points in the direction of the external field. The only symmetry admitted by the equation of motion is the axial symmetry, relative to z-axis, and the only conserved quantity for the system is the component of the angular momentum in the z-direction.
The one-dimensional aproximation in a model studied by Casati [1987]15, has the hamiltonian
The corresponding equation of motion does have no Lie symmetries.
b) Non-vanishing magnetic field:  ¹ 0.
¹ 0.
(i) Charge submitted to a Coulombian potential and to an external magnetic field
This is a physically important problem. It's the classical analogue of the case of a hidrogen atom under a magnetic field. An atom submitted to a strong, static uniform magnetic field can present chaotic behavior, both in classical as in quantum cases. This case can be described if we take in the general equation (8) Fi(t,  ) =
) =  , where r = (dijxixj)
, where r = (dijxixj) , B1 = B2 = 0, B3 = B. Solving equations (10) we can get the Lie symmetries. Let's analyze some particular cases.
, B1 = B2 = 0, B3 = B. Solving equations (10) we can get the Lie symmetries. Let's analyze some particular cases.
1.)B = B0(const.);  = 0. This is the classical problem of a non-relativistic hidrogen atom under the action of an external constant, uniform, magnetic field. For this case we get
= 0. This is the classical problem of a non-relativistic hidrogen atom under the action of an external constant, uniform, magnetic field. For this case we get
These vector fields also represent Noether symmetries and so we have the conservation of energy and of the z-component of the angular momentum. This doesn't guarantee the integrability of the system. Several studies led to the non-integrability of the system (Hasegawa, Robnik and Wunner, [1989]16; Delande [1986]17).
2.) B = 0; a = 0 ® a = const. This is the usual Kepler problem. We have already discussed the two-dimensional case. The extension to three-dimensional case is obvious. For this case we obtain the vector fields
3.)B = B0 = const., a = a(t) . Solving equations (10) for this system we arrive to a particular case with a non-trivial symmetry structure: if a = C0exp{kt}, where C0 and k are constants, we have
4.)B = B(t), a = a(t). In this case we disregard the electric fields arising from the variation of the magnetic field. We can think of slowly varying magnetic fields. If B(t) and a(t) are arbitrary functions, we find only one vector field : U = -y¶x + x¶y.
An interesting particular case appear when solving equations (10):
where the Ci's are arbitrary constants. In this case we find the following group of vector fields
(ii) Harmonic oscillator in the presence of a magnetic field - In what follows we will be looking for the symmetries for some cases of oscillators in the presence of magnetic fields. We will show the existence of an "inverse Zeeman efect" for situations where the magnetic field, when assuming certain values, reinstall the symmetries of an anisotropic oscillator.
(1.) General case - Let's consider the general case (in which all the frequencies are different and there's no relation between then and the magnetic field) of an anisotropic oscillator in the presence of a constant magnetic field. The equations of motion take the form
where  is a frequency tensor. The eigenvalues
is a frequency tensor. The eigenvalues  ,
,  ,
,  of the matrix
of the matrix  are the proper frequencies of the oscillator. It will be isotropic whenever
are the proper frequencies of the oscillator. It will be isotropic whenever  =
=  =
=  . On the other side
. On the other side
represents the external field. If we compare equation (39) with the general equation (8), we verify that Fi(t, xj) = - xj and b = e/c . We choose a coordinate system in which wij2 is diagonal and the external magnetic field points in the z-direction. We will be considering the three-dimensional case. The extension to the n-dimensional case is straightforward.
xj and b = e/c . We choose a coordinate system in which wij2 is diagonal and the external magnetic field points in the z-direction. We will be considering the three-dimensional case. The extension to the n-dimensional case is straightforward.
Solving equations (10) we obtain the following group of vector fields
where w = eB/c and
gi = {(1/ 2)(  +
+  + w2) ± (1/2) [(
+ w2) ± (1/2) [( +
+  + w2) - 4
+ w2) - 4
 ]
]  }
} , with i = 1, 2. One stands for the + signal and two for the - signal. The vector fields above form a Lie algebra with dimension nine, associated to a nine-parameter Lie group.
, with i = 1, 2. One stands for the + signal and two for the - signal. The vector fields above form a Lie algebra with dimension nine, associated to a nine-parameter Lie group.
(2.) Isotropic oscillator with external magnetic field - Let's consider now the case of an isotropic, three-dimensional oscillator in the presence of an external, constant magnetic field directed along the z-direction. We must note that if we want to find the symmetries of an isotropic or an anisotropic oscillator all we have to do is to make the magnetic field equal to zero in the general equations (10). These cases are well known (Prince and Eliezer, [1980]). The n-dimensional oscillator with frequencies depending on time is well studied (Prince and Eliezer, [1980]) and could be easily obtained from equations (10) taking w = w(t) and B = 0.
The problem of an isotropic oscillator with magnetic field is a particular case of the general one discussed above. All we have to do is to solve the system of equations (10) with w1 = w2 = w3 = w0. Doing this we arrive to the following group of vector fields:
where w = eB/ c, and gi =  , with i = 1, 2. We have taken the signal + when i = 1 and - when i = 2. So we have a twelve-parameter Lie group.
, with i = 1, 2. We have taken the signal + when i = 1 and - when i = 2. So we have a twelve-parameter Lie group.
From the point of view of the algebra of the group, the system is equivalent to an oscillator with only two equal frequencies. This can be seen from the fact that the magnetic field is perpendicular to the plane (x, y) and so must affect equally both frequencies x and y. This implies that the system acts as if it has two equal frequencies in the (x, y) plane and a different frequency in the z-direction.
(3.) Semi-isotropic oscillator with an external magnetic field: an inverse "Zeeman effect"
Let's return to the general case (1.) especified by equations (39). If we solve equations (10) for that case without the imposition that the frequencies and the magnetic field can assume any value, then naturally appears a very interesting solution
with the following group of vector fields
where w = eB/ c as before and gi = w3 ±  with i = 1, 2, the signal being + when i = 1 and - when i = 2.
with i = 1, 2, the signal being + when i = 1 and - when i = 2.
Analizing the above vector fields and the associated algebra, we can see that this is the same symmetry group as that of the isotropic oscillator. So if we have a semi-isotropic oscillator with two equal frequencies w1 = w2 < w3, then we can reobtain the symmetries of the isotropic oscillator applying to the system an external magnetic field
in the z-direction. This is a kind of inverse Zeeman efect. In the quantum analog of this system we verify that the application of an external magnetic field like (45) implies the return of the degenerescence of the system.
If we consider the time-dependent case, where both the frequencies and the magnetic field are varying with time, then we find that the same condition for isotropisation still holds:
where W is a number with frequency dimension. In fact, if we choose, as before, a coordinate system where wij2 is diagonal and the magnetic field in the z-direction, we obtain the condition (43a-b) again. Obviously we are considering slow varying magnetic field, so that, in a first aproximation, we can discard the corrections in the equations of motion of the system to make them compatibles with Maxwell equations.
(iii) The charge - monopole problem - Let's consider the equation of motion for this problem
where a = eg/e. This equation describes the motion of an electric charge e in the field of a magnetic monopole g, fixed at the origin. Poincaré [1896]18 has shown that the trajectory of the charge is over a cone with the apex at the origin. The direction of the symmetry axis of the cone is given by the generalised angular momentum:
It should be remembered that this problem doesn't admit a conventional Lagrangian description. This description, necessary to the quantisation of the system, can be done through generalisations of several kinds. Jackiw [1980]19 applied the Noether theorem to a Lagrangian with a singular potential to get the dynamical symmetry group [SO(3) × SO(2, 1)]. He was able to get the quantisation of the system.
To obtain the Lie symmetries (Moreira et al. [1985a]20) for this problem we must return to the general equation (8). Comparing (46) with (8) we verify that Fi = 0, b = a and  =
=  /r3. Solving equations (10) we obtain the following group of vector fields
/r3. Solving equations (10) we obtain the following group of vector fields
This is a group containing two subgroups: SO(3) and SO(2,1).
Conserved quantities - W'll begin by using the Prince method [1979] to find first integrals. Let's take, for instance, the vector field U4 and the corresponding first prolongation pr(1)U4 = x¶y - y¶x -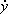 ¶
¶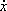 +
+ 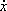 ¶
¶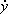 . The invariant functions generated by U4(1) can be obtained solving the system
. The invariant functions generated by U4(1) can be obtained solving the system
Some of the invariants we obtain are
u
1 =
x
2 +
y
2 ;
v
1 =
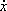
2 +
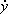
2;
v
2 =
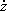
2. So the system of equations
is invariant under U4(2). Comparing these equations we arrive at
which, when integrated, give the kinetic energy as a first integral:
To obtain some other first integrals we will use the method described in section 2 (I.C. Moreira et al. [1985]). To do so we must use the first prolongation of the vector fields (48a-b) and apply them to I1. Repeating systematically such procedure we arrive to
By applying these two methods, we can arrive, in a similar manner, to the conservation of the generalized angular momentum
We must observe that I1 is conserved for any kind of force perpendicular to  and I2 and I3 are conserved for any force perpendicular to
and I2 and I3 are conserved for any force perpendicular to  and
and  .
.
The first integrals (49) permit us to determine the trajectory of the charge in the field of the monopole and to find the temporal dependence of the separation distance between the particles.
The orbital part of  :
:  =
=  ×
×  has constant magnitude and precess around
has constant magnitude and precess around  . If we take the instant of closest aproximation as being t = 0, I3 will be the square of that distance: I3 =
. If we take the instant of closest aproximation as being t = 0, I3 will be the square of that distance: I3 =  .
.
The rotation rate of the vector position can be easily obtained using spherical coordinates. From the constancy of L2 it follows the validity of a relation similar to Kepler's second law for the charge on the cone: its vector position describe equal areas in equal times. Besides this, as the force is normal to the surface, the motion of the charge will be a geode sic on the cone (the conservation of I1 and L guarantee this).
Symmetries of Sokolov's Lagrangian
Sokolov [1976]21 builds a lagrangian formalism, rotationaly invariant, trying to avoid the difficulties arising from the Dirac theory of magnetic monopole, namely, the singularity of the potential and the need to apply the Dirac's condition in order to obtain the quantisation of the system. He wrote a lagrangian in a four-dimensional space where the coordinates are the three Euler angles and the separation distance r between the charges. In these coordinates the lagrangian has the form
Applying the Noether condition (13) to the above lagrangian we arrive to the Noether vector fields
The vector fields above form, in spherical coordinates, the same group structure already obtained with the Lie symmetries. The seventh vector field U7 appears due to the introduction of the g coordinate. The second part of Noether's theorem allow us to obtain the first integrals associated with these vector fields:
where these first integrals correspond to the ones in equations (65a-d) in spherical coordinates.
As a final remark we mention that if we repeat the above calculations considering that the magnetic charge of the monopole can change in time, the only vector fields we obtain are those corresponding to rotation: Uij = xi¶j - xj¶i, with i, j = 1, 2, 3 (i ¹ j).
(iv) Electric charge in the field of a magnetic monopole with electric charge - Schwinger [1969]22 has used the idea of dyon, that is, a magnetic monopole with electric charge. Let's consider then the case of a charged particle in the field of a dyon. The equations of motion are
where b = ke and a = eg/c as before. Comparing this equation with (8) we verify that Fi = - , b = e/c, Bk = gxk/ r3. Solving equations (10) we obtain the vector fields
, b = e/c, Bk = gxk/ r3. Solving equations (10) we obtain the vector fields
This is a four-parameter group containing, as a subgroup, the group of rotations SO(3). The symmetry group for this case is a sub group of that obtained for the monopole, as should be.
The same kind of analisis made by Sokolov for the monopole problem can be repeated for this case. We can introduce an aditional variable, using as coordinates the separation r between the charges and the Euler angles a,b and g. In this case, a and b correspond to the spherical coordinates q and f, and g is the aditional angular variable. In these coordinates the lagrangian for this system has the form
where pg = -eg/c , is the canonical momentum corresponding to g. Applying the Noether theorem to this lagrangian we obtain both the vector fields:
and the corresponding first integrals:
where pb = r2  and pa = r2
and pa = r2  sin2b - (eg/c) cosb. So we have obtained the conservation of energy and of the generalized angular momentum vector
sin2b - (eg/c) cosb. So we have obtained the conservation of energy and of the generalized angular momentum vector  =
=  -( eg/c)
-( eg/c)  .
.
(v) Electric charge interacting with magnetic dipole.
This is an important physical problem. It has been discussed as a chaotic scattering problem by Jung and Scholz [1988]23. Almeida et al. [1991]24 had shown the non-integrability of this system. The equation of motion for this case reads
where l = eA0/c , and  = A0
= A0 3 is the magnetic momentum taked along the z-axis and
3 is the magnetic momentum taked along the z-axis and  = R-5[3(
= R-5[3(  ·
·  )
)  - R2
- R2 ] . Comparing equation (53) with (8) and solving (10) we obtain
] . Comparing equation (53) with (8) and solving (10) we obtain
The algebra of the group stands from [U1,U2] = 0 ; [U1,U3] = U1 ; [U2,U3] = 0, corresponding to a1Åa2 .
(c) Time-dependent generalizations
Leach and Gorringe [1990]25 analysed the Lie symmetries for the equation
where  =
=  ×
×  . In this section, analysing a particular case of this equation, we will discuss a method for generating integrable systems with a given symmetry structure. W'll try to find, in each particular case, a specific transformation that transform the original system into another one with a known solution. We can take the inverse point of view, that is, that of looking for all differential equations which are equivalent to a given one with known solution (Duarte [1991]26). If we use an invertible point transformation the structure of the Lie symmetries is preserved.
. In this section, analysing a particular case of this equation, we will discuss a method for generating integrable systems with a given symmetry structure. W'll try to find, in each particular case, a specific transformation that transform the original system into another one with a known solution. We can take the inverse point of view, that is, that of looking for all differential equations which are equivalent to a given one with known solution (Duarte [1991]26). If we use an invertible point transformation the structure of the Lie symmetries is preserved.
W'll find the general expression (Moreira and Ritter [1991]27) for the system of differential equations equivalent to the equation
This equation is a particular case of equation (54) but it has a sufficient degree of generality for our purpose here. It contains, as particular cases, the equation of the Kepler problem and that of the charge-monopole problem. The Lie algebra associated with equation (54) is a1ÅSO(3), with a1 representing the symmetry under time translation and SO(3) the rotational invariance. The vector fields associated with (55) are
If we make the invertible point transformation
equation (55) will be transformed to the equation
where  =
=  ×
×  and
and
We will find firstly the most general equation (55) with a scale symmetry. If we impose this symmetry
and use the Lie conditions for the equation (55), we find
Equation (61) has the symmetry vector fields U1,U2,U3,U4 and the additional symmetry vector field
The Lie algebra associated with these vector fields is a2 Å S O(3).
The time-dependent equation, with the same Lie symmetry structure but with transformed symmetry vector fields, obtained from (61) and (57), is
If we search for a particular case of equation (55) with the additional symmetry
the Lie conditions lead to the equation
The Lie algebra associated with the symmetry vector fields U1, ..., U6 is, in this case, sl(2, R) Å SO(3). The transformed equation is
where the fi are given by (59).
Time-dependent case of the Kepler problem - This case was analysed by Katzin and Levine [1983]28 and will be recovered here using the method outlined above. Let m = -3, C1 = 0 in (55). Solving (59), with f1 = 0, we get
Making f4 = W-1(t) equation (55) is reduced to the equation
under the point transformation
Equation (68) is the equation analysed by Katzin and Levine [1983]. The symmetry vector fields for the Kepler problem are U1,U2,U3 and U4 in (56), and
The symmetry vector fields for (68), obtained by Katzin and Levine, can be determined directly from (56), (69) and (70). By using the transformation(69) the conserved Laplace-Runge-Lenz vector can be generalized for equation (68). It takes the form
Other possible generalizations - We can apply the above results to other interesting cases. For instance, the equation describing the charge- monopole problem is a particular case of (55): choosing C2 = 0, n = -3 we are lead to
Solving (59) for this case and choosing f3 = 1, f = W-1(t) we obtain
which describes a charge-monopole interaction plus a time-dependent linear force. We can make a further generalization by including the force C2R-4R. Equation (72) then becomes
with the same Lie symmetry group as the charge-monopole equation: sl(2, R) Å SO(3) (Moreira et al [1985]).
Another possible generalization is the problem of the interaction between an electric charge and a magnetic dipole discussed above. The Lie algebra for this problem is a1 Å a2. Applying the point transformation (57) to equation (53) that describes this problem we arrive to
where we have used f = W-1(t). This equation has the same Lie structure as that of the charge-magnetic dipole equation.
IV Conclusions
We have applyed the Lie and Noether methods to a number of systems, all of them involving charged particles in presence of electromagnetic fields. Even using only point symmetry transformations we can conclude that these methods are very effective. Nowadays the knowledge of invariants is a powerful tool in the investigation of non-linear dynamical systems in view of the connection between them and the integrability of such systems. We have analysed some of these systems in the context of electromagnetic phenomena. Obviously, these methods can be used in other fields of theoretical physics and constitue, themselves, an active research field. The theory of the continuous Lie groups has a much broader scope them it can be thought reading this paper. The applications of the Lie groups include such areas as, for instance, algebric topology, differential geometry, bifurcation theory, special functions, numerical analysis, control theory, classical and quantum physics, dynamical systems, etc...
[24] M.A. Almeida, I.C. Moreira, and H. Yoshida, (1991) - Preprint IF/UFRJ 31/91.
- [1] P.J. Olver, Applications of Lie Groups to Differential Equations, Springer-Verlag, New York, (1986).
- [2] L.P. Bueno, I.C. Moreira, O.M. Ritter, F.C. Santos, Rev. Bras. Fís. 16, 559 (1986).
- [3] W. Sarlet, and F. Cantrijn, Siam Review, 23, 467 (1981).
- [4] I.C. Moreira, O.M. Ritter, F.C. Santos, Rev. Bras. Fís. 15, 174 (1985a).
- [5] G.E. Prince, (1979), Department of Applied Mathematics, Research Report La Trobe University, Melbourne.
- [6] R.L. Anderson, and S.M. Davison, J. Math. Analysis Applic. 48, 301 (1974).
- [7] C.E. Wulfman, and B.G. Wybourne, J. Phys. A: Math. Gen. 9, 507 (1976).
- [8] G.E. Prince, and C.J. Eliezer, J. Phys. A: Math. Gen. 13, 815. (1980).
- [9] G.E. Prince, and C.J. Eliezer, J. Phys. A: Math. Gen. 14, 587 (1981).
- [10] J. Sivardière, Eur. J. Phys. 9, 61 (1988).
- [11] I.C. Moreira, Supl. Ciên. Cult. 35, 334 (1983).
- [12] M.C. Gutzwiller, Physica 38D, 160 (1989).
- [13] V.I. Arnold, (1976) Méthodes Mathématiques de la Mécanique Classique Mir, Moscow.
- [14] H. Yoshida, Physica 29D, 128 (1987).
- [15] G. Casati, B.V. Chirikov, D.L. Shepelyanoky, I. Guarnieri, Phys. Rep. 154, 77 (1987).
- [16] H. Hasegawa, M. Robnik, and G. Wunner, Prog. Theor. Phys. Suppl. 98, 198 (1989).
- [17] D. Delande, and J.C. Gay, Phys. Rev. Lett. 57, 2006 (1986).
- [18] H. Poincaré, Compt. Rendus 123, 530 (1896).
- [19] R. Jackiw, Ann. of Phys. 129, 183 (1980).
- [20] I.C. Moreira, O.M. Ritter, F.C. Santos, J. Phys. A: Math. Gen. 18, L427 (1985a).
- [21] V.V. Sokolov, Sov. J. Nucl. Phys. 23, 330 (1976).
- [22] J. Schwinger, Science 165, 757 (1969).
- [23] C. Jung, and H.J. Scholz, J. Phys. A: Math. Gen. 21, 2301 (1988).
- [25] P.G.L. Leach, and V.M. Gorringe, J. Phys. A: Math. Gen. 23, 2765 (1990).
- [26] L.G. Duarte, (1991) - Master thesis - IF/UFRJ.
- [27] I.C. Moreira, O.M. Ritter, J. Phys. A: Math. Gen. 24, 3181 (1991).
- [28] G.H. Katzin, and J. Levine, J. Math. Phys. 24, 1761 (1983).
Publication Dates
-
Publication in this collection
07 Jan 2002 -
Date of issue
June 2000
History
-
Received
11 Oct 1999




































































































