The two-dimensional quantum Heisenberg antiferromagnet with Ising-like anisotropy

The two-dimensional quantum Heisenberg antiferromagnet with Ising-like anisotropy

Alessandro Cuccoli, Valerio Tognetti, Tommaso Roscilde, Paola Verrucchi,

Dipartimento di Fisica dell'Università di Firenze

and Istituto Nazionale di Fisica della Materia (INFM),

Largo E. Fermi 2, I-50125 Firenze, Italy

and Ruggero Vaia

Istituto di Elettronica Quantistica del Consiglio Nazionale delle Ricerche,

via Panciatichi 56/30, I-50127 Firenze, Italy,

and Istituto Nazionale di Fisica della Materia (INFM)

Received on 5 August, 2000

We study the two dimensional quantum Heisenberg antiferromagnet on the square lattice with easy-axis exchange anisotropy by the semiclassical method called pure-quantum self-consistent harmonic approximation. In particular, we focus on the problem of the existence of a nite-temperature transition in such a model, and study the corresponding critical temperature as the spin value and the anisotropy vary. We find that an Ising-like transition characterizes the model even when the anisotropy is of the order of 10

^-2

J

(

J

being the intra-layer exchange integral). The good agreement found between our theoretical results and the experimental data for the compounds Rb

₂

MnF

₄

, K

₂

MnF

₄

, and K

₂

NiF

₄

shows that the insertion of the easy-axis exchange anisotropy, with quantum effects properly taken into account, provides a quantitative description and explanation of the real system's critical behaviour.

The easy-axis quantum Heisenberg antiferromagnet on the square lattice (EA-QHAF) is defined by the following Hamiltonian:

where i = (i₁, i₂) runs over the sites of a square lattice, d connects each site to its four nearest neighbours, J > 0 is the antiferromagnetic exchange integral and the anisotropy parameter m takes values m Î [0,1) for easy-axis models. The spin operators (a = x, y, z) are such that | |² = S(S + 1) and obey [, ] = ie_abgd_ij.

The anisotropy parameter m measures the strength of the easy-axis character of the model: For m = 0 the Ising-limit (equivalent to the Ising model if S = 1/2) is recovered; in the opposite limit, Eq. (1) with m = 1 describes the fully isotropic QHAF. At a classical level the EA-HAF is known to share its critical behaviour with the Ising model [1], with a finite-temperature second-order phase transition corresponding to the onset of Nèel antiferromagnetic order. The critical temperature is a decreasing function of m, and vanishes logarithmically in the isotropic limit [2].

When quantum effects are considered, one expects the critical behaviour of the model to remain the same, as the universality class of the system cannot be changed by short-ranged quantum fluctuations [3]; however, these may be responsible for an evident lowering of the critical temperature, as quantum disorder opposes the onset of Neèl order. In principle, this effect could be strong enough to push the critical temperature down to T_c = 0, thus destroying the transition itself; the parameter region where such a scenario could possibly occur is that of low critical temperatures (m 1) and strong quantum effects (S = 1/2) [4].

To address the problem of the existence of a finite temperature transition in the EA-QHAF, one needs to analyse the m-dependence of the critical temperature for different spins; results relative to precise spin and anisotropy values, typical output of quantum numerical simulations, are hence insufficient, albeit useful. The main goal of this paper is in fact to determine the critical temperature of the EA-QHAF as a function of both m and S, and compare our theoretical results with the available experimental data.

There exist several real compounds whose magnetic behaviour [5] is well described by the Hamiltonian Eq. (1); most of them, despite being characterized by a very weak easy-axis anisotropy (m 1), show a finite-temperature phase-transition. Whether the transition is due to the anisotropy-driven onset of two-dimensional Neèl order or to some other effect (such as the inter-layer exchange interaction), is not easily detectable experimentally, but strong indications in favour of the first possibility derive from the analysis of several thermodynamic quantities. This work confirms such a picture, as the critical temperatures relative to the compounds Rb₂MnF₄ [6] (S = 5/2, m = 0.994), K₂MnF₄ [7] (S = 5/2, m = 0.995) and K₂NiF₄ [8] (S = 1, m = 0.996) agree nicely with the theoretical results for the two-dimensional EA-QHAF.

In order to study the thermodynamic and critical behaviour of the model described by Eq. (1), we use the pure-quantum self-consistent harmonic approximation (PQSCHA) [9]: this approximation allows one to take into account exactly the full classical, and the linear quantum contributions to the thermodynamics of the system, thus approximating (one-loop level) the non-linear pure-quantum contribution only. As the latter plays a secondary role in determining the critical properties of models with a not-too-strong quantum character, the PQSCHA is an ideal tool to study the thermodynamic and critical behaviour of many quantum systems, as shown by its many successful applications [10], in particular to low-dimensional magnetic systems [11, 12].

The method, based on the path-integral formulation of quantum statistical mechanics, allows one to write statistical averages of quantum operators in the form of classical-like expressions: These may then be evaluated by classical (possibly numerical) techniques, like the transfer-matrix method in one dimension, or classical Monte Carlo simulation in two dimensions. In greater detail, the PQSCHA expression for the statistical average of a of quantum operator , for a magnetic system N spins, reads

where b = T^-1, _eff = ò d^Ns e -b_^eff, s = (s^x, s^y, s^z) is a classical unit vector, and ò d^Ns = P_{i = 1}^N òds_i.

Quantum effects come into play via the spin and temperature dependence of

_eff and O_eff: this dependence relates the original quantum system to an infinite class of classical easy-axis models, each defined by different parameters. This means that the PQSCHA reduces the study of quantum statistical averages to the evaluation of classical-like effective averages defined by Eq. (2), for to effective models which are different for different temperatures and spin values.

The specific PQSCHA expression for the effective Hamiltonian of the EA-QHAF is found to be

where, = S + 1/2, and t = T/J

² is the reduced temperature used hereafter.

The renormalization parameters are

where the coefficients

are self-consistently determined by solving Eqs. (4) and (5), with

and

k being the wave vector in the first Brillouin zone.

The temperature and spin dependent uniform term

does not enter the expressions for the statistical averages, but contributes to the free energy and to the related thermodynamic quantities.

If one defines the effective exchange integral and effective anisotropy,

Eq. (3) can be written in the form

showing that the thermodynamic behaviour of the EA-QHAF is that of a classical EA-HAF with exchange integral J_eff(t, S) and anisotropy parameter m_eff(t, S). As J_eff < J and m_eff > m we see that quantum fluctuations induce a softening of both the energy scale and the anisotropy, thus inducing a higher degree of disorder in the system.

In Fig. 1 we show j_eff = J_eff/J as a function of t, for different spin and anisotropy values: Quantum effects are markedly stronger for lower spins, while the m-dependence of the energy scale renormalization is seen to be extremely weak.

Figure 1.
Renormalized exchange integral j_eff = J_eff/J vs. t for S = 1/2, 1, and 5/2; different values of the anisotropy parameter m = 0.9, 0.5, and 0 are also shown by the dashed, full and dotted curves, respectively.

In Fig. 2, the ratio (m_eff - m)/m is plotted against m for different spin and temperature values: the quantum renormalization is here seen to more strongly affect the most anisotropic models, due to the fact that, when forced to align along the easy axis, each spin reacts with larger quantum fluctuations perpendicular to the axis itself.

Figure 2.
Ratio (m_eff-m)/m vs. m for S = 1/2, 1, and 5/2; different temperature values t = 0.001 and 0.1 are shown by the full and dashed curves, respectively.

From Eq. (7) we see that the symmetry properties of the original quantum Hamiltonian are preserved by the renormalization procedure leading to the effective Hamiltonian: this means that the critical behaviour of the EA-QHAF can be directly related to that of its effective classical counterpart. In particular, if

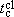(m) is the reduced critical temperature of a classical EA-HAF with anisotropy parameter m, then, for the quantum system, it is

For fixed S and m, the t dependence of j_eff and m_eff make Eq. (8) rather complicated. Its solution, however, can be obtained iteratively, once 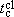(m) is available as an analytical function of m. To obtain such a function we used the classical Monte Carlo data reported in Refs. [13] and [14]: these data are well distributed over the interval 0 £ m < 1 and an accurate interpolating function t may hence be determined. In particular we have used

with a = 0.917, b = 0.068, c = 0.097, and d = 0.0636. The logarithmic dependence upon (1 - m²) is required in order to properly describe the logarithmic drop of 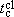for m ® 1; 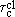has been set an even function of m to ensure the ferro- and antiferromagnetic models to be equivalent, as required for the static behaviour of classical magnetic systems.

Figure 3. Critical temperature t_c(S, m) of the EA-QHAF vs. -ln(1 - m) for S = 1/2, 1, 5/2, and ¥ (classical model). Large symbols indicate the experimentally determined critical temperatures for Rb₂MnF₄ (triangle), K₂MnF₄ (square), and K₂NiF₄ (circle). Small symbols are classical Monte Carlo data from Refs. [13] and [14], upwards and downwards triangles, respectively. 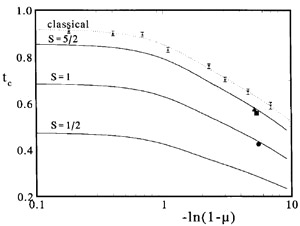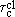The dotted curve is the interpolating function (m) (see text).

In Fig. 3 the resulting solution of Eq. (8) is plotted against -ln(1 - m) to expand the m 1 region, where data for real compounds are available; the agreement between our curves and the experimentally determined critical temperatures is very good for both S = 1 and S = 5/2, given also the fact that no best-fit procedure is involved in the comparison. On the other hand, the exactly known [15] critical temperature of the Ising model t_c(1/2,0) = 0.567, not represented in Figure, is not well reproduced in view of the large values of the renormalization coefficients Eq. (5), and we expect our results to be only qualitatively significant in the extreme S = 1/2 quantum case. This respect, we cannot give a definite answer to the problem, recently addressed in Ref. [4], of the existence of a finite m-interval, near the isotropic limit m = 1, where t_c(1/2, m)=0, i.e. where the EA-QHAF shows no finite-temperature transition.

In conclusion, we have studied the EA-QHAF in terms of the effective Hamiltonian determined by the PQSCHA method; by analyzing the critical temperature dependence on the anisotropy parameter m, the Ising-like phase-transition characterizing the model has been found to occur at finite temperature "m < 1 and "S ³ 1; a qualitative indication in favour of the validity of this result for S = 1/2 has also been obtained.

[4] N. S. Branco and J. Ricardo de Sousa, preprint, cond-mat/0006345 (June 2000).

• [1] M. Bander and D. L. Mills, Phys. Rev. B 38, 12015 (1988).
• [2] L. P. Kadanoff et al., Rev. Mod. Phys. 39, 395 (1967).
• [3] J. A. Hertz, Phys. Rev. B 14, 1165 (1976).
• [5] J. Kanamori, in Magnetism vol.1, ed. G.T.Rado e H.Suhl, Academic Press, New York (1963).
• [6] R. A. Cowley, G. Shirane, R. J. Birgeneau, H. J. Guggenheim, Phys. Rev. B 15, 4292 (1977).
• [7] R. J. Birgeneau, H. J. Guggenheim, G. Shirane, Phys. Rev. B 8, 304 (1973).
• [8] H. W. de Wijn, L. R. Walker, R. E. Walstedt, Phys. Rev. B 8, 285 (1973).
• [9] A. Cuccoli, V. Tognetti, P. Verrucchi and R. Vaia, Phys. Rev. A 45, 8418 (1992).
• [10] A. Cuccoli, R. Giachetti, V. Tognetti, R. Vaia, and P. Verrucchi, J. Phys., Condens. Matter 7, 7891 (1995).
• [11] A. Cuccoli, V. Tognetti, R. Vaia, and P. Verrucchi Phys. Rev. B 46, 11601 (1992).
• [12] A. Cuccoli, V. Tognetti, R. Vaia, and P. Verrucchi Phys. Rev. Lett. 77, 3439 (1996), Phys. Rev. B 56, 14456 (1997).
• [13] P. A. Serena, N. García and A. Levanyuk, Phys. Rev. B 47, 5027 (1993).
• [14] M. E. Gouvêa el al., Phys. Rev. B 59, 6229 (1999).
• [15] L. Onsager, Phys. Rev. 65, 117 (1944).

Publication Dates

• Publication in this collection
  09 Jan 2002
• Date of issue
  Dec 2000

History

• Received
  05 Aug 2000