Abstract
This paper reports results for rotational excitation of H2O and H2S molecules by electron impact. It is also a databasis including tables of previously published rotationally resolved cross sections for CH4, SiH4, GeH4, SnH4, PbH4, NH3, PH3, AsH3, SbH3, CF4, CCl4, SiCl4 SiBr4, and SiI4. Our scattering amplitudes were calculated using the Schwinger multichannel method with norm-conserving pseudopotentials and the rotational resolved cross sections were obtained with the help of the adiabatic nuclei rotation approximation. Our results are in good agreement with other theoretical data and experimental results when available.
Applications of the Schwinger Multichannel Method with Pseudopotentials to electron scattering from polyatomic molecules II. rotational excitation cross sections
Márcio T. do N. Varella,
Instituto de Física Gleb Wataghin,
Universidade Estadual de Campinas, UNICAMP,
13083-970, Campinas, SP, Brazil
Márcio H. F. Bettega,
Departamento de Física, Universidade Federal do Paraná,
Universidade Federal do Paraná
Caixa Postal 19044, 81531-990, Curitiba, PR, Brazil
Alexandra P. P. Natalense, Luiz G. Ferreira, and Marco A. P. Lima
Instituto de Física Gleb Wataghin,
Universidade Estadual de Campinas, UNICAMP,
13083-970, Campinas, SP, Brazil
Received on 14 March, 2000
This paper reports results for rotational excitation of H2O and H2S molecules by electron impact. It is also a databasis including tables of previously published rotationally resolved cross sections for CH4, SiH4, GeH4, SnH4, PbH4, NH3, PH3, AsH3, SbH3, CF4, CCl4, SiCl4 SiBr4, and SiI4. Our scattering amplitudes were calculated using the Schwinger multichannel method with norm-conserving pseudopotentials and the rotational resolved cross sections were obtained with the help of the adiabatic nuclei rotation approximation. Our results are in good agreement with other theoretical data and experimental results when available. All tables are available in the electronic version of the paper only [on the world wide web at http://www.sbf.if.usp.br/bjp/Vol31/Num1/].
I Introduction
It has been pointed out by different authors [1, 2] that rotational excitation of molecular gases is a relevant energy-loss mechanism in slow electron discharges. Although the average energy transfer per collision is only a fraction of one meV, the order of magnitude of rotational excitation cross sections can be 10-16 cm2 or even larger. As a result, pure rotational energy transfer can be quite effective in discharge environments or in the ionosphere of Earth [2].
The Schwinger Multichannel Method implemented with Pseudopotentials (SMCPP) [3] has been applied, along with the adiabatic-nuclei-rotation (ANR) approximation [4], to calculate rotational excitation cross sections for some polyatomic targets, such as XH4 (X: C, Si, Ge, Sn, Pb) [5], XH3 (X: N, P, As, Sb), CF4, CCl4, SiCl4, SiBr4 and SiI4 [6]. In this paper, we show differential, integral and momentum transfer rotational excitation cross sections of H2O and H2S molecules. We also present tables not reported in previous publications [5, 6, 7] and rotationally resolved momentum transfer cross sections for CX4 (X: F,Cl) and SiY4 (Y: Cl, Br, I) not published in Ref. [8]. This paper is complementary to Ref. [9], where elastic scattering of slow electrons by H2X molecules (X: O, S, Se, Te) was discussed and also to the companion paper [9], where we present elastic results for a wide range of molecules. However, we also intend to present here a complete databasis of our rotational excitation results, which can easily be compared to future experiments and other calculations.
Some of the molecules treated here are plasma processing gases [10, 11] and others are also of biological and environmental interest [11]. Despite their industrial and environmental importance, studies on electron interactions with these molecules are very scarce. To our knowledge, this is the first collection of rotational excitation cross sections by electron impact for some of the molecules cited above.
This paper is outlined as follows. In section II, we present a brief review of the theory and describe the main approximations used in our calculations. In Section III, we present our results and discussion. This section is divided in four subsections. In subsection III.a, we will report our new results for rotational excitation of water and sulfidric acid. In subsections III.b to III.d, we will show results for rotational excitaion of CH4, SiH4, GeH4, SnH4 and PbH4 (III.b); NH3, PH3, AsH3 and SbH3 (III.c); CF4, CCl4, SiCl4, SiBr4 and SiI4 (III.d).
II Theory
The implementation of pseudopotentials in the Schwinger multichannel method allows calculations of low-energy electron scattering by molecules containing atoms with many electrons with reduced computational effort [3]. The basic idea is to replace the core electrons and the nucleus of each atom in the molecule by the corresponding soft norm-conserving pseudopotential and to describe the valence electrons in a quantum chemistry framework (Hartree-Fock approximation in the present implementation). The cross sections for electron scattering by molecules with different atoms but with the same number of valence electrons can then be calculated with about the same computational effort. In the companion paper [9], we compare the actual number of electrons and the number of valence electrons for each one of the molecules studied here. For some of these molecules an all-electron cross section calculation would be impractical.
The Schwinger multichannel method has been described previously and we only review here some key features for completeness. In this method, the working expression for the scattering amplitude is
where
and
In the above equations |S
iñ is the product of a target state and a plane wave, V is the interaction potential between the incident electron and the target, |cmñ is a (N+1)-electron Slater determinant used in the expansion of the trial scattering wave function,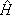 is the total energy of the collision minus the full Hamiltonian of the system, P is a projection operator onto the open channel space defined by target eigenfunctions, and
is the total energy of the collision minus the full Hamiltonian of the system, P is a projection operator onto the open channel space defined by target eigenfunctions, and 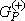 is the free-particle Green's function projected on the P-space.
is the free-particle Green's function projected on the P-space.
The form of the operator P and the set of (N+1)-electron Slater determinants define the main approximations in our scattering calculations. In this work, we do not consider real electronic excitations of the target by electron impact. The only open channel is then the elastic channel and the projection operator P is then defined by the target ground state. In the static-exchange calculations the Slater determinants |cmñ are constructed as:
where |F0ñ is the target ground electronic state, |fiñ are one-particle scattering functions and  is the antissymetrization operator. In our calculations, we use the molecular virtual orbitals to represent the functions |fiñ.
is the antissymetrization operator. In our calculations, we use the molecular virtual orbitals to represent the functions |fiñ.
The polarization of the target due to the electric field of the incident electron is taken into account in our method by including virtual electronic excited states of the target in the construction of the Slater determinants |cmñ:
In equation 5 the index j runs over the electronic states of the molecular target, beginning with the ground state up to some chosen excited state.
We use the norm-conserving pseudopotentials of Bachelet Hamann and Schlüter [12] to describe the nuclear potential and the core electrons of each atom. These pseudopotentials were implemented in the SMC method as described in Ref. [3]. The cartesian Gaussian functions used to describe the molecular and scattering orbitals were especially designed to be used in our pseudopotential calculations [13].
Our cross sections were obtained in the fixed-nuclei static-exchange approximation. We do not include the description of polarization effects, since they are known to be of little importance for the impact energy range we study here (5-30 eV). (We present static-exchange and polarized rotationally resolved DCS for water molecule at 2.14 and 6.0 eV.)
The adiabatic-nuclei-rotation (ANR) approximation expression for the G® G¢ rotational excitation scattering amplitude is given by [4]
In the above expression, f lab is the elastic scattering amplitude written in the laboratory-fixed frame (LF)11 The transformation of scattering amplitudes from molecular frame to laboratory frame can be easily performed [5, 14]. The transformation of scattering amplitudes from molecular frame to laboratory frame can be easily performed [5, 14]. .  in and
in and  out are, respectively, incoming and outgoing wave-vectors; W º (a, b, g) are the Euler angles defining the frame transformation [5, 14]; YG(W) are rotational eigenfunctions of the target; and G denotes a complete set of rotational quantum numbers. Among the molecules considered here, one finds spherical, symmetric and asymmetric-tops. In each of these three cases, one should observe the appropriate rotational quantum numbers, eigenfunctions and the correct degeneracies of rotational levels. The rotational eigenfunctions for both spherical and symmetric-tops are written as
out are, respectively, incoming and outgoing wave-vectors; W º (a, b, g) are the Euler angles defining the frame transformation [5, 14]; YG(W) are rotational eigenfunctions of the target; and G denotes a complete set of rotational quantum numbers. Among the molecules considered here, one finds spherical, symmetric and asymmetric-tops. In each of these three cases, one should observe the appropriate rotational quantum numbers, eigenfunctions and the correct degeneracies of rotational levels. The rotational eigenfunctions for both spherical and symmetric-tops are written as
where  are the well-known Wigner rotation matrices [14]; J is the total molecular angular momentum; and K and M are, respectively, its projection onto the quantization axis of molecular and laboratory frames. Rotational levels of spherical-tops present (2J + 1)2-fold degeneracies, related to K and M quantum numbers [5]. For such systems, the rotational excitation cross sections are given by
are the well-known Wigner rotation matrices [14]; J is the total molecular angular momentum; and K and M are, respectively, its projection onto the quantization axis of molecular and laboratory frames. Rotational levels of spherical-tops present (2J + 1)2-fold degeneracies, related to K and M quantum numbers [5]. For such systems, the rotational excitation cross sections are given by
where kJ¢ and kJ are outgoing and incoming wave vector moduli, respectvely. Symmetric-top rotational levels, on the other hand, are (2J + 1)-fold degenerated [7]. The cross sections, reminding that degeneracies are associated only with M quantum number, are written as
For asymmetric-tops, K is no longer a good quantum number, and the rotational eigenfunctions,  , are given by symmetry-adapted linear combinations of symmetric-top eigenfunctions [15]:
, are given by symmetry-adapted linear combinations of symmetric-top eigenfunctions [15]:
where
In the expressions above, t is a pseudo quantum number introduced to distinguish the asymmetric-top eigenfunctions [15]; and
Both symmetric and asymmetric-tops present permanent dipole moments. To take dipole-related long-range interactions into account, we apply a Born closure procedure to the dipole-allowed rotational excitation cross sections (J = 0 K = 0 ® J¢ = 1 K¢ = 0 for symmetric-tops and J = 0 t = 0 ® J¢ = 1 t¢ = 0 for asymmetric-tops.) We also take advantadge of the rotational energy transfer to avoid divergence of differential cross sections at forward scattering direction. The Born-closure procedure is carefully discussed elsewhere [7, 8].
III Results and Discussion
Due to the narrow spacing between neighbouring rotational levels of polyatomic molecules, experimental data concerning rotationally resolved cross sections are very scarce. Among the molecules addressed in this work, we could find rotationally resolved diferential cross sections for H2O [2] and CH4 [16]. Theoretical work is also sketchy. There are reported rotational excitation cross sections only for CH4 [5, 17, 18], SiH4 [5, 18], NH3 [7, 19, 20], H2O [21, 22, 23, 24] and H2S [19, 25]. We present our results below.
H2O and H2S
In Figs. 1 and 2 we show rotationally resolved differential cross sections (DCS) for water at 2.14 and 6.0 eV. In each figure, the rotationally elastic (00 ® 00) and dipole-allowed (00 ® 10) transitions are considered.
For both energies, we present two sets of calculations obtained at static-exchange (SE) and static-exchange plus polarization (SEP) levels of approximation. For comparison purposes, we also show theoretical SEP results of Jain and Thompson [21], Gianturco [22], Greer and Thompson [23] (6.0 eV only) and Gianturco et al. [24] (00 ® 10 rotational excitation only). Experimental data of Jung et al. [2] is also shown. Our DCS for the rotationally elastic excitation at 2.14 eV present a maximum between 50o and 90o not noticed either in the experimental data [2] or in the other calculations [21, 22], although our SEP result agrees very well with measurement at 15o and 30o. At 6.0 eV, our calculations show a better agreement in shape with other results, but one still observes discrepancy around 60o. It is to be pointed out that our elastic (rotationally unresolved) DCS showed disagreement with experimental data and previous calculations at incident energies below 8.0 eV, around 60o [8]. It is not surprising, therefore, that rotationally resolved cross sections present a similar behavior. All calculations and experimental DCS agree better for the 00 ® 10 excitation, which is mainly determined by dipole moment interactions. It is interesting to observe that our results at 2.14 eV are in better agreement with experimental data, lying below the other calculations. This was also to be expected, since our Born-corrected rotationally summed integral cross section (ICS) showed better agreement with measurements at lower energies [8].
Rotationally resolved differential cross sections for e--H2O scattering at 30 eV for J = 0 ® J¢ = 0, 1, 2, 3 excitations (summed over t¢). Solid lines: present results (SE approximation); stars: Gianturco et al. [24].
In Fig. 3, we compare our SE rotationally resolved DCS for H2O with calculations of Gianturco et al. [24] for J = 0 ® J¢ = 0, 1, 2, 3 excitations, where cross sections with same J¢ were summed over t¢. One notices good agreement in magnitude and very good agreement in shape for all rotational transitions, reflecting the observed good agreement of elastic (rotationally unresolved) DCS [8] at 30 eV.
In order to ilustrate the convergence of present SE calculations for water, we present in Fig. 4, and also in Tables I and II, rotationally summed DCS (RSDCS) at 10, 15 20, and 30 eV. For each energy, we show RSDCS summed from J = 0 up to J¢ = 0, 1, 2, 3, 4 and 7. (For a given J¢, we sum over t¢.) We also show elastic (rotationally unresolved) experimental DCS of Johnstone and Newell [26]. It is clear that convergence is achieved for J¢ = 4, because the dot-dashed lines, corresponding to RSDCS up to J¢ = 4, are often hidden by the solid thick line (RSDCS up to J¢ = 7). One can also observe significant contributions of rotationally inelastic excitations to RSDCS around 120o, where the rotationally elastic DCS present minima, and near the forward scattering direction (due to the dipole-allowed transition).

Rotationally summed differential cross sections for e--H2O scattering at 10, 15, 20 and 30 eV, from J = 0 up to different J¢. (For a given J¢, cross sections were summed over t¢.) Thin solid lines: J¢ = 0; dotted lines: J¢ = 1; short-dashed lines: J¢ = 2; long-dashed lines: J¢ = 4; thick solid lines: J¢ = 7 [8]; bullets: elastic (rotationally unresolved) experimental DCS of Johnstone and Newell [26].
In Fig. 5 we show SE rotationally resolved integral cross section (RSICS) for water, along with calculations of Gianturco et al. [24]. J = 0 ® J¢ = 0, 1, 2, 3 excitations are considered, and we again sum over t¢ for each J¢. In general, there is very good agreement both in shape and magnitude, although some discrepancy is found for the dipole-allowed excitation (at all energies) and also at 6.0 eV for 0 ® 0, 2 transitions. This behavior was to be expected, considering the observed behavior of elastic (rotationally unresolved) cross sections [8] (see also discussion of Figs. 1 and 2.)
Next, we show SE rotationally resolved DCS for H2S. We adress 00 ® 00 (Fig. 6) and 00 ® 10 (Fig. 7) excitations at 5, 7.5, 10, and 15 eV. Calculations of Gianturco [19] (00 ® 10 only) and of Jain and Thompson [25] are also presented for comparison purposes. One finds, in general, good agreement both in shape and magnitude. Some disagreement is found at 10 and 15 eV for the 00 ® 10 excitation, though. It is to be observed that our rotationally summed integral cross section (ICS) for H2S agrees well with experimental data [8].
Rotationally resolved ICS for 00 ® 00 and 00 ®10 excitations are shown in Fig. 8 (SE approximation), along with results of Jain and Thompson [25]. One notices very good agreement for the dipole-allowed excitation, although some discrepancy is found for the rotationally elastic ICS. Our results present a very broad maximum around 10 eV, while calculation of Ref. [25] show a narrower maximum 8 eV.
Rotationally resolved integral cross sections for e--H2O scattering. (All results are summed over t¢.) Upper part: Thick solid line: 0 ® 0 excitation (present SE result); bullets with thin solid line: 0 ® 0 excitation (Gianturco et al.[24]); thick long-dashed line: 0 ® 1 excitation (present SE result); squares with thin long-dashed line: 0 ® 1 excitation (Gianturco et al.[24]). Lower part: Thick solid line: 0 ® 2 excitation (present SE result); diamonds with thin solid line: 0 ® 2 excitation (Gianturco et al.[24]); thick long-dashed line: 0 ® 3 excitation (present SE result); triangles with thin long-dashed line: 0 ® 3 excitation (Gianturco et al.[24]).
Convergence of present SE calculations for sulfidric acid is illustrated in Fig. 9. We show rotationally summed DCS (RSDCS) at 10, 15, 20, and 30 eV. For each energy, we show RSDCS summed from J = 0 up to J¢ = 0, 1, 2, 3, 4 and 7. (For a given J¢, we sum over t¢.) (See also Tables III and IV.) We also show elastic (rotationally unresolved) experimental DCS of Gulley et al. [27]. It is clear that convergence is achieved for J¢ = 4, because the dot-dashed lines, corresponding to RSDCS up to J¢ = 4, are often hidden by the solid thick line (RSDCS up to J¢ = 7). One can also observe significant contributions of rotationally inelastic excitations to RSDCS above 60o, where the rotationally elastic DCS present minima, and near the forward scattering direction (due to the dipole-allowed transition).

Rotationally elastic (00 ® 00) differential cross sections for e--H2S at 5.0, 7.5, 10.0 and 15.0 eV. Solid lines: present results (SE approximation); stars: Jain and Thompson [25].
Rotationally resolved differential cross sections for e--H2S for the dipole-allowed (00 ® 10) excitation at 5.0, 7.5, 10.0 and 15.0 eV. Solid lines: present results (SE approximation); triangles: Gianturco [19]; stars: Jain and Thompson [25].
Rotationally resolved integral cross sections for e--H2S scattering. Upper part: 00 ® 00 excitation. Lower part: 00 ® 10 excitation. Solid lines: present SE result; stars: Jain and Thompson [25].
Rotationally summed differential cross sections for e--H2S scattering at 10, 15, 20 and 30 eV, from J = 0 up to different J¢. (For a given J¢, cross sections were summed over t¢.) Thin solid lines: J¢ = 0; dotted lines: J¢ = 1; short-dashed lines: J¢ = 2; long-dashed lines: J¢ = 4; thick solid lines: J¢ = 7 [8]; bullets: elastic (rotationally unresolved) experimental DCS of Gulley et al. [27].
Integral cross section (ICS) for water (upper part) and sulfidric acid (lower part). Solid lines: rotationally summed ICS (J¢ = 0 up to J¢ = 7); long-dashed lines: ICS for 00 ® 00 excitation; dotted lines: ICS for 00 ® 10 excitation; dot-dashed lines: rotationally summed inelastic ICS (J¢ = 1 up to J¢ = 7).
Finally, in Fig. 10 we show ICS for both H2O and H2S. For each molecule, we present ICS for 00 ® 00 and 00 ® 10 rotational excitations; inelastic rotationally summed (IRS) integral cross section, from J¢ = 1 up to J¢ = 7; and also rotationally summed ICS (RSICS), from J¢ = 0 up to J¢ = 7. (Integral and momentum transfer rotationally resolved cross sections are also shown in Tables V and VI, respectively.) For water molecule, it is clear that the dipole-allowed transition provides the most significant contribution to IRS integral cross section, being even greater than the rotationally elastic excitation, for incident energies below 10 eV. The less polar H2S molecule presents smaller ICS for the dipole-allowed rotational excitation, and, as a result, its IRS integral cross section is considerably smaller than the rotationally elastic ICS. It is interesting to observe that IRS integral cross section for water is almost as high as the elastic (rotationally summed) ICS, for E < 7.5 eV. As a result, one should expect rotational excitations to be an important energy-loss mechanism in slow-electron discharge environments containing water vapor.

XH4 (X = C, Si, Ge, Pb, Sn)
Tables VII to XI present our previously published [5] differential cross sections for rotational excitation of the XH4 (X = C, Si, Ge, Pb, Sn) molecules at selected energies. Our results were found to be in good agreement with previous calculations for CH4 [17, 18] and SiH4 [18]. Our results for methane also showed good agreement with experimental data [16]. Ref. [5] also shows tables with our integral cross sections and with our momentum transfer cross sections.
XH3 (X = N, P, As, Sb)
Tables XII to XIV present our differential cross sections from Ref. [7] at 10 eV, 20 eV, and 30 eV respectively. There are other theoretical elastic (rotationally unresolved) results in the literature for NH3, PH3, and AsH3 [19, 20, 28] and experimental data for NH3 and PH3 [29], all in good agreement with our rotationally summed cross sections. Our rotationally resolved cross sections for NH3 were found to be in good agreement with previous calculations [19, 20] (see Ref. [7]). Tables with our integral cross sections and with our momentum transfer cross sections are shown in Ref. [7].
CF4, CCl4, SiCl4, SiBr4, and SiI4
Our rotational momentum transfer cross sections are shown in Table XV. Tables with rotational integral cross sections are shown in Ref. [6]. Due to the large peripheral atoms, these molecules were found to have large rotationally inelastic cross sections (being comparable in magnitude with respective rotationally elastic cross sections). A detailed discussion is found in Ref. [6].
Tables
All tables are available only in the electronic version of the paper on the world wide web at http://www.sbf.if.usp.br/bjp/Vol31/Num1/.
Acknowledgments
A. P. P. N. acknowledges support from Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP). M. H. F. B., L. G. F. and M. A. P. L. acknowledge partial support from Brazilian agency Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq). M. T. N. V. acknoledges both FAPESP and CNPq. Our calculations were performed at CENAPAD-SP, at CENAPAD-NE and at CCE-UFPR.
References
[1] N. F. Lane, Rev. Mod. Phys. 52, 29 (1980).
[2] K. Jung, Th. Antoni, R Müller, K. H. Kochem and H. Erhardt, J. Phys. B 15, 3535 (1982).
[3] M. H. F. Bettega, L. G. Ferreira, and M. A. P. Lima, Phys. Rev. A 47, 1111 (1993).
[4] D. M. Chase, Phys. Rev. A 104, 838 (1956); A. Temkin and K. V. Vasavada, Phys. Rev. 160, 190 (1967); F. A. Gianturco and A. Jain, Phys. Rep. 143, 347 (1986).
[5] M. T. do N. Varella, M. H. F. Bettega, and M. A. P. Lima, Z. Phys. D 39, 59 (1997).
[6] M. T. do N. Varella, A. P. P. Natalense, M. H. F. Bettega, and M. A. P. Lima, Phys. Rev. A, accepted for publication (1999).
[7] M. T. do N. Varella, M. H. F. Bettega, A. J. R. da Silva, and M. A. P. Lima, J. Chem. Phys. 110, 2452 (1999).
[8] M. T. do N. Varella, M. H. F. Bettega, M. A. P. Lima, and L. G. Ferreira, J. Chem. Phys., accepted for publication (1999).
[9] A. P. P. Natalense, M. T. do N. Varella, M. H. F. Bettega, L. G. Ferreira and M. A. P. Lima, submitted for publication in Braz. J. Phys. (1999).
[10] M. Hayashi "Swarm Studies and Inelastic Electron-Molecule Collisions", edited by L. C. Pitchford, B. V. McKoy, A. Chutjian, and S. Trajmar, New York, p. 167 (1987).
[11] See, for example, L. G. Christophorou, J. K. Olthoff, and M. V. V. S. Rao, J. Phys. Chem. Ref. Data, 25, 1341 (1996); L. G. Christophorou, J. K. Olthoff, and M. V. V. S. Rao, J. Phys. Chem. Ref. Data, 26, 1 (1997); L. G. Christophorou, J. K. Olthoff, and Y. Wang, J. Phys. Chem. Ref. Data, 26, 1205 (1997).
[12] G. B. Bachelet, D. R. Hamann, and M. Schlüter, Phys. Rev. B 26, 4199 (1982).
[13] M. H. F. Bettega, A. P. P. Natalense, M. A. P. Lima, and L. G. Ferreira, Int. J. Quantum Chem., 60, 821 (1996).
[14] M. E. Rose, "Elementary Theory of Angular Momentum", Wiley, New York, (1957).
[15] C. Van Winter, Physica XX, 274 (1954); A. Jain and D. G. Thompson, Comput. Phys. Commun. 30, 301 (1983).
[16] R. Müller, K. Jung, K-H. Kochem, W. Sohn, and H. Ehrhardt, J. Phys. B: At Mol Phys 18, 3971 (1985).
[17] A. Jain, and D. G. Thompson, J. Phys. B 16, 3077 (1983); N. Abusalbi, R. A. Eades, T. Nam, D. Thirumalai, D. A. Dixon, D. G. Truhlar, and M. Dupuis, J. Chem. Phys. 78, 1213 (1983); F. A. Gianturco, Phys. Scri. T 23, 141 (1988); L. M. Brescansin, M. A. P. Lima, and V. McKoy Phys. Rev. A 40, 5577 (1989); F. A. Gianturco, J. A. Rodriguez-Ruiz, and N. Sanna Phys. Rev. A 52, 1257 (1995).
[18] A. Jain, Z. Phys. D 21, 153 (1991)
[19] F. A. Gianturco, J. Phys. B 24, 4627 (1991).
[20] A. Jain and D. G. Thompson, Phys. Rev. A, 16, 2593 (1983).
[21] A. Jain and D. G. Thompson, J. Phys. B 16, 3077 (1983).
[22] F. A. Gianturco, J. Phys. B 24, 3837 (1991).
[23] R. Greer and D. Thompson, J. Phys. B 27, 3533 (1994).
[24] F. A. Gianturco, S. Meloni, P. Paioletti, R. R. Lucchese ans N. Sanna, J. Chem. Phys. 108, 4002 1998.
[25] A. Jain and D. G. Thompson 17, 443 (1983).
[26] W. M. Johnstone and W. R. Newell, J. Phys. B 24, 3633 (1991).
[27] R. J. Gulley, M. J. Brunger and S. J. Buckman, J. Phys. 26, 2813 (1992).
[28] H. P. Pritchard, M. A. P. Lima, and V. McKoy Phys. Rev. A 39, 2392 (1989); T. N. Rescigno, B. H. Lengsfield, C. W. McCurdy, and S. D. Parker, Phys. Rev. A 45, 7800 (1992); C. Winstead, Q. Sun, V. McKoy, J. L. da S. Lino, and M. A. P. Lima, Z. Phys. D 24, 141 (1992); J. M. Yuan, and Z. J. Zhang, Z. Phys. D 28, 207 (1993).
[29] T. W. Shyn (private communication); D. T. Alle, R. J. Gulley, S. J. Buckman, and M. J. Brunger, J. Phys. B 25, 1533 (1992); M. Ben Arfa, and M. Tronc, J. Chim. Phys. Phys.-Chim. Biol. 85, 879 (1988).
- [1] N. F. Lane, Rev. Mod. Phys. 52, 29 (1980).
- [2] K. Jung, Th. Antoni, R Müller, K. H. Kochem and H. Erhardt, J. Phys. B 15, 3535 (1982).
- [3] M. H. F. Bettega, L. G. Ferreira, and M. A. P. Lima, Phys. Rev. A 47, 1111 (1993).
- [4] D. M. Chase, Phys. Rev. A 104, 838 (1956);
- A. Temkin and K. V. Vasavada, Phys. Rev. 160, 190 (1967);
- F. A. Gianturco and A. Jain, Phys. Rep. 143, 347 (1986).
- [5] M. T. do N. Varella, M. H. F. Bettega, and M. A. P. Lima, Z. Phys. D 39, 59 (1997).
- [6] M. T. do N. Varella, A. P. P. Natalense, M. H. F. Bettega, and M. A. P. Lima, Phys. Rev. A, accepted for publication (1999).
- [7] M. T. do N. Varella, M. H. F. Bettega, A. J. R. da Silva, and M. A. P. Lima, J. Chem. Phys. 110, 2452 (1999).
- [8] M. T. do N. Varella, M. H. F. Bettega, M. A. P. Lima, and L. G. Ferreira, J. Chem. Phys., accepted for publication (1999).
- [9] A. P. P. Natalense, M. T. do N. Varella, M. H. F. Bettega, L. G. Ferreira and M. A. P. Lima, submitted for publication in Braz. J. Phys. (1999).
- [10] M. Hayashi "Swarm Studies and Inelastic Electron-Molecule Collisions", edited by L. C. Pitchford, B. V. McKoy, A. Chutjian, and S. Trajmar, New York, p. 167 (1987).
- [11] See, for example, L. G. Christophorou, J. K. Olthoff, and M. V. V. S. Rao, J. Phys. Chem. Ref. Data, 25, 1341 (1996);
- L. G. Christophorou, J. K. Olthoff, and M. V. V. S. Rao, J. Phys. Chem. Ref. Data, 26, 1 (1997);
- L. G. Christophorou, J. K. Olthoff, and Y. Wang, J. Phys. Chem. Ref. Data, 26, 1205 (1997).
- [12] G. B. Bachelet, D. R. Hamann, and M. Schlüter, Phys. Rev. B 26, 4199 (1982).
- [13] M. H. F. Bettega, A. P. P. Natalense, M. A. P. Lima, and L. G. Ferreira, Int. J. Quantum Chem., 60, 821 (1996).
- [14] M. E. Rose, "Elementary Theory of Angular Momentum", Wiley, New York, (1957).
- [15] C. Van Winter, Physica XX, 274 (1954);
- A. Jain and D. G. Thompson, Comput. Phys. Commun. 30, 301 (1983).
- [16] R. Müller, K. Jung, K-H. Kochem, W. Sohn, and H. Ehrhardt, J. Phys. B: At Mol Phys 18, 3971 (1985).
- [17] A. Jain, and D. G. Thompson, J. Phys. B 16, 3077 (1983);
- N. Abusalbi, R. A. Eades, T. Nam, D. Thirumalai, D. A. Dixon, D. G. Truhlar, and M. Dupuis, J. Chem. Phys. 78, 1213 (1983);
- F. A. Gianturco, Phys. Scri. T 23, 141 (1988);
- L. M. Brescansin, M. A. P. Lima, and V. McKoy Phys. Rev. A 40, 5577 (1989);
- F. A. Gianturco, J. A. Rodriguez-Ruiz, and N. Sanna Phys. Rev. A 52, 1257 (1995).
- [18] A. Jain, Z. Phys. D 21, 153 (1991)
- [19] F. A. Gianturco, J. Phys. B 24, 4627 (1991).
- [20] A. Jain and D. G. Thompson, Phys. Rev. A, 16, 2593 (1983).
- [21] A. Jain and D. G. Thompson, J. Phys. B 16, 3077 (1983).
- [22] F. A. Gianturco, J. Phys. B 24, 3837 (1991).
- [23] R. Greer and D. Thompson, J. Phys. B 27, 3533 (1994).
- [24] F. A. Gianturco, S. Meloni, P. Paioletti, R. R. Lucchese ans N. Sanna, J. Chem. Phys. 108, 4002 1998.
- [25] A. Jain and D. G. Thompson 17, 443 (1983).
- [26] W. M. Johnstone and W. R. Newell, J. Phys. B 24, 3633 (1991).
- [27] R. J. Gulley, M. J. Brunger and S. J. Buckman, J. Phys. 26, 2813 (1992).
- [28] H. P. Pritchard, M. A. P. Lima, and V. McKoy Phys. Rev. A 39, 2392 (1989);
- T. N. Rescigno, B. H. Lengsfield, C. W. McCurdy, and S. D. Parker, Phys. Rev. A 45, 7800 (1992);
- C. Winstead, Q. Sun, V. McKoy, J. L. da S. Lino, and M. A. P. Lima, Z. Phys. D 24, 141 (1992);
- J. M. Yuan, and Z. J. Zhang, Z. Phys. D 28, 207 (1993).
- [29] T. W. Shyn (private communication);
- D. T. Alle, R. J. Gulley, S. J. Buckman, and M. J. Brunger, J. Phys. B 25, 1533 (1992);
- M. Ben Arfa, and M. Tronc, J. Chim. Phys. Phys.-Chim. Biol. 85, 879 (1988).
Publication Dates
-
Publication in this collection
20 Feb 2002 -
Date of issue
Mar 2001
History
-
Received
14 Mar 2000












 are expansion coeficients. The rotational excitation cross sections are given by
are expansion coeficients. The rotational excitation cross sections are given by 














