Abstract
The influence of an external constant uniform magnetic field on the Casimir energy associated with a Dirac field under antiperiodic boundary condition is computed using Schwinger's method. The obtained result shows that the magnetic field enhances the fermionic Casimir energy, in oposition to the bosonic Casimir energy which is inhibited by the magnetic field.
The influence of an external magnetic field on the fermionic Casimir effect
M.V. Cougo-Pinto* * e-mail: marcus@if.ufrj.br e-mail: farina@if.ufrj.br e-mail: tort@if.ufrj.br , C. Farina * e-mail: marcus@if.ufrj.br e-mail: farina@if.ufrj.br e-mail: tort@if.ufrj.br , A.C. Tort * e-mail: marcus@if.ufrj.br e-mail: farina@if.ufrj.br e-mail: tort@if.ufrj.br
Instituto de Física, Universidade Federal do Rio de Janeiro
CP 68528, Rio de Janeiro, RJ 21945-970, Brazil
Received on 3 July, 2000. Revised version received on 8 September, 2000
The influence of an external constant uniform magnetic field on the Casimir energy associated with a Dirac field under antiperiodic boundary condition is computed using Schwinger's method. The obtained result shows that the magnetic field enhances the fermionic Casimir energy, in oposition to the bosonic Casimir energy which is inhibited by the magnetic field.
H. B. G. Casimir showed in 1948 [1] that the presence of two closely spaced parallel metallic plates with no charge on them would shift the vacuum energy of the electromagnetic field by an amount
g(a) given by:
where
2 is the area of each plate, a is the separation between them and the relation a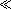
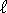 is assumed in order to implement the condition of small separation. As a consequence of this shift there is an attractive force on the plates which was measured by Sparnaay in 1958 [2] and more recently with high accuracy by Lamoreaux [3] and by Mohideen and Roy [4, 5]. This shift in energy is known as the Casimir energy and belongs together with its consequences and related phenomena to the realm of the so called Casimir effect [6, ?, 8]. Generally, the Casimir effect can be defined as the effect of non-trivial space topology on the vacuum fluctuations of any relativistic quantum field (cf., e.g., [6, 7]). The source of the non-triviality of the space topology is provided by several kinds of boundary conditions, background fields and constraints. Under this general definition the effect discovered by Casimir and given by the energy (1) can be viewed as a consequence of passing from the trivial topology of
is assumed in order to implement the condition of small separation. As a consequence of this shift there is an attractive force on the plates which was measured by Sparnaay in 1958 [2] and more recently with high accuracy by Lamoreaux [3] and by Mohideen and Roy [4, 5]. This shift in energy is known as the Casimir energy and belongs together with its consequences and related phenomena to the realm of the so called Casimir effect [6, ?, 8]. Generally, the Casimir effect can be defined as the effect of non-trivial space topology on the vacuum fluctuations of any relativistic quantum field (cf., e.g., [6, 7]). The source of the non-triviality of the space topology is provided by several kinds of boundary conditions, background fields and constraints. Under this general definition the effect discovered by Casimir and given by the energy (1) can be viewed as a consequence of passing from the trivial topology of 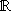 3 to the topology of
3 to the topology of 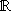 2 × [0, a], due to the boundary conditions imposed on the electromagnetic field by the metallic plates with separation a. The fermionic Casimir effect is of particular importance due to the fundamental role played by the electron in QED and the quarks in QCD. In the case of quarks we have a boundary condition of confinement given by nature, which makes the Casimir energy a natural ingredient in the hadron structure.
2 × [0, a], due to the boundary conditions imposed on the electromagnetic field by the metallic plates with separation a. The fermionic Casimir effect is of particular importance due to the fundamental role played by the electron in QED and the quarks in QCD. In the case of quarks we have a boundary condition of confinement given by nature, which makes the Casimir energy a natural ingredient in the hadron structure.
The fermionic Casimir energy was first computed by Johnson [9] in the context of the MIT-bag model [10] for a massless Dirac quantum field confined between parallel planes with separation a. A more realistic description of quarks and gluons inside a hadron requires the confining boundary conditions to be imposed on a spherical surface. The Casimir effect in spherical geometry for massive fields is a much more complicated problem and has only recently been completely solved for massive fermionic [11] and scalar [12] fields. In the case of confining planes the fermionic Casimir energy  (a) obtained by Johnson [9] is given by:
(a) obtained by Johnson [9] is given by:
where x = 7/4. As in the original Casimir effect this energy comes from a shift from the usual space
3 to the space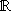 2 × [0, a]. If instead of compactifying one dimension
2 × [0, a]. If instead of compactifying one dimension 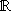 into [0, a] we compactify it into a circle S1 [13, 14] of radius a/2p we obtain for the Casimir energy associated with the massless Dirac field the expression (2), where now x is equal to 7 × 4 or -8 × 4, according to a choice of twisted or untwisted spin connection, which corresponds to antiperiodic or periodic boundary conditions with period a, respectively. We should notice the similarity of those three results, for the Casimir energy of the Dirac massless field under MIT, periodic and antiperiodic boundary conditions. They show that all these boundary conditions give rise to the same dependence on a and differ only on the multiplicative numerical factor x. We may take advantage of this fact by choosing the simplest boundary condition in a first investigation of a Casimir effect. In the case of a fermionic field the compactification into [0, a] provided by the MIT boundary condition [10] gives rise to the most complicated calculations, especially in the massive case [15]. The periodic and antiperiodic conditions are much simpler in the massless and massive case. Let us also notice that, as shown by Ford [14], in the case of the Dirac field the antiperiodic boundary condition avoids the causality problems which occurs for periodic boundary condition.
into [0, a] we compactify it into a circle S1 [13, 14] of radius a/2p we obtain for the Casimir energy associated with the massless Dirac field the expression (2), where now x is equal to 7 × 4 or -8 × 4, according to a choice of twisted or untwisted spin connection, which corresponds to antiperiodic or periodic boundary conditions with period a, respectively. We should notice the similarity of those three results, for the Casimir energy of the Dirac massless field under MIT, periodic and antiperiodic boundary conditions. They show that all these boundary conditions give rise to the same dependence on a and differ only on the multiplicative numerical factor x. We may take advantage of this fact by choosing the simplest boundary condition in a first investigation of a Casimir effect. In the case of a fermionic field the compactification into [0, a] provided by the MIT boundary condition [10] gives rise to the most complicated calculations, especially in the massive case [15]. The periodic and antiperiodic conditions are much simpler in the massless and massive case. Let us also notice that, as shown by Ford [14], in the case of the Dirac field the antiperiodic boundary condition avoids the causality problems which occurs for periodic boundary condition.
The results that we shall present here stems from the idea that vacuum fluctuations of a charged quantum field are affected not only by boundary conditions but also by external fields. Therefore, in the case of charged quantum fields it is natural and important to ask what kind of interplay occurs between the Casimir effect and the vacuum polarization effects, when boundary conditions and external field are both present. This question can be examined from two physically very distinct points of view. From one point of view we ask what is the influence of boundary conditions on the polarization effects of an external field and from the other we ask what is the influence of an external field on the Casimir energy of a charged field. We should expect on physical grounds the existence of such influences and it is necessary to calculate their features and magnitudes to clarify their role on and to obtain a deeper understanding of the Casimir and vaccum polarization effects. For a Dirac field the first point of view is conveniently treated by calculating an Euler-Heisenberg effective Lagrangian [16] with boundary conditions [17]. We present here the second point of view, in which we look for the precise influence of an external field on the Casimir energy of a Dirac field. The obtained results complement the ones obtained for the bosonic Casimir effect in external magnetic field [18]. We compute the influence of an external magnetic field on the Casimir energy of a charged Dirac field under antiperiodic boundary conditions and find that the energy is enhanced by the magnetic field. This result appears in opposition to the behaviour of a charged scalar field under Dirichlet boundary conditions, which has its Casimir energy inhibited by the external magnetic field. It is tempting to advance an explanation of this opposite behavior in terms of the spinorial character of the fields. After all the permanent magnetic dipoles of spin-half quantum field fluctuations should tend to paramagnetic alignment with the applied external field while the induced diamagnetic dipoles of the scalar quantum field tend to antialignment. However, it has been verified [19] that the magnetic properties of quantum vacuum depend not only on the spinorial character of the quantum field but also on the kind of boundary conditions to which it is submitted. Therefore, further investigations are necessary in order to formulate a sound physical explanation of the character of the change in the Casimir energy due to applied external magnetic fields.
We will take as external field a constant uniform magnetic field and as boundary condition on the Dirac field the antiperiodicity along the direction of the external magnetic field. The choice of a pure magnetic field excludes the possibility of pair creation at any field strength. The simplicity of antiperiodic boundary condition was remarked above and the other choices are obvious simplifying assumptions. These assumptions lead us to a convenient formalism to study the physical influence of an external field on the Casimir effect.
The influence of external field on vaccum fluctuations of quantum fields have been considered by Ambjørn and Wolfram [20] and by Elizalde and Romeo [21] for the case of quantum scalar field in (1 + 1)-dimensional space-time. Ambjørn and Wolfram have considered the case of a charged scalar field in the presence of an external electric field while Elizalde and Romeo consider the case of a neutral scalar field in a static external field with the aim of addressing the problem of the gravitational influence on the Casimir effect. Let us also note that in the Scharnhorst effect [22] we have the interaction of an electromagnetic external field with the electromagnetic vacuum fluctuations affected by boundary conditions. However, in this case the boundary conditions are imposed on the quantum electromagnetic field and not on the Dirac field. The effect is then a two-loop effect, since the coupling between the external field and the quantum electromagnetic vacuum field requires the intermediation of a fermion loop. Here the boundary condition is on the Dirac field, the quantum electromagnetic field need not to be considered and the external electromagnetic field is not subjected to boundary conditions. In this way the effects that we describe appear at the one loop level, although higher orders corrections can be obtained with more loops.
Let us proceed to the calculation of the influence of the external magnetic field on the Casimir energy of the Dirac field. We consider a Dirac field of mass m and charge e under antiperiodic boundary condition along the 
 axis. We implement the condition on planes perpendicular to
axis. We implement the condition on planes perpendicular to 
 and separated by a distance a. We consider those planes as large squares of side
and separated by a distance a. We consider those planes as large squares of side 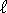 and the limit
and the limit 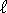 ® ¥ can be taken at the end of the calculations. The constant uniform magnetic field B is taken along the
® ¥ can be taken at the end of the calculations. The constant uniform magnetic field B is taken along the 
 axis with positive direction chosen to make positive the product eB, where B is the component of B on the
axis with positive direction chosen to make positive the product eB, where B is the component of B on the 
 axis. In order to calculate the Casimir energy of the Dirac field in the presence of the magnetic field we use a method proposed by Schwinger [23] and based on his proper-time representation for the effective action [24]. The method has been applied to several situations (cf. [18] for further references) and here also it will lead us quickly to the Casimir energy. We start with the proper-time representation for the effective action
axis. In order to calculate the Casimir energy of the Dirac field in the presence of the magnetic field we use a method proposed by Schwinger [23] and based on his proper-time representation for the effective action [24]. The method has been applied to several situations (cf. [18] for further references) and here also it will lead us quickly to the Casimir energy. We start with the proper-time representation for the effective action  (1) [24]:
(1) [24]:
where so is a cutoff in the proper-time s, Tr is the total trace including summation in coordinates and spinor indices and H is the proper-time Hamiltonian given by: H = (p - eA)2 - (e/2)smnFmn + m2, where p has components pm = -i¶m, A is the electromagnetic potential and F is the electromagnetic field, which is being contracted with the combination of gamma matrices smn = i[gm, gn]/2. The antiperiodic boundary condition gives for the component of p which is along the 
 axis the eingenvalues ±pn/a (n Î 2
axis the eingenvalues ±pn/a (n Î 2 -1), where by
-1), where by  we denote the set of positive integers. The other two space components of p are constrained into the Landau levels generated by the magnetic field while the time component p0 has as eigenvalues any real number w. Therefore, we obtain for the trace in (3) the expression:
we denote the set of positive integers. The other two space components of p are constrained into the Landau levels generated by the magnetic field while the time component p0 has as eigenvalues any real number w. Therefore, we obtain for the trace in (3) the expression:
where the first sum takes care of the four components of the Dirac spinor, the second sum is over the eigenvalues obtained from the antiperiodic boundary condition, the third sum is over the Landau levels with their degeneracy factor eB
2/2p, and the integral range of t and w are the measurement time T and the continuum of real numbers, respectively. Proceeding with Schwinger's method we use Poisson's summation formula [25] to invert the exponent in the second sum which appears in (4). We also write the sum over the Landau levels n¢ which appears in (4) in terms of the Langevin function L(x) = cothx - x-1 and substitute the trace obtained by these modifications into (3) to obtain:
where
(1)(B) is an expression which does not depend on a and
is the cutoff dependent expression which will give us the Casimir energy that we are looking for. The quantity
(1)(B) given in (5) is actually the (unrenormalized) Euler-Heisenberg Lagrangian [16]. In (5), it represents a density of energy uniform throughout space that gives no contribution to the Casimir energy, which by definition is set to zero at infinite separation of the plates. A term proportional to the area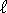 2, which is usual in vacuum energy calculations, does not appear here, due to the alternating character of the series in (6). After the elimination of the cutoff in (6) we continue with Schwinger's method [23] by using Cauchy theorem in the complex s plane to make a p/2 clockwise rotation of the integration path in (6). Let us notice that in (3) and (6) it is implicit that the integration path is slightly below the real axis, because s must have a negative imaginary part in order to render the trace contributions in (3), (4) and (6) well defined. Consequently, the poles of the Langevin function in (6), which are on the real axis, are not swept by the p/2 clockwise rotation of the integration path. We are led by the rotation to an expression in which the part of the Casimir energy which exists in the absence of the external magnetic field can be expressed in terms of the modified Bessel function K2 (formula 3.471,9 in [26]). In this way we obtain from (6) the expression:
2, which is usual in vacuum energy calculations, does not appear here, due to the alternating character of the series in (6). After the elimination of the cutoff in (6) we continue with Schwinger's method [23] by using Cauchy theorem in the complex s plane to make a p/2 clockwise rotation of the integration path in (6). Let us notice that in (3) and (6) it is implicit that the integration path is slightly below the real axis, because s must have a negative imaginary part in order to render the trace contributions in (3), (4) and (6) well defined. Consequently, the poles of the Langevin function in (6), which are on the real axis, are not swept by the p/2 clockwise rotation of the integration path. We are led by the rotation to an expression in which the part of the Casimir energy which exists in the absence of the external magnetic field can be expressed in terms of the modified Bessel function K2 (formula 3.471,9 in [26]). In this way we obtain from (6) the expression:
which gives the exact expression for the Casimir energy of the Dirac field in the presence of the external magnetic field B. When there is no external magnetic field the Casimir energy is given by the first term on the r.h.s. of equation (7). This term reduces to (2) with x = 7 × 4 in the limit of zero mass, as it should be expected. The second term on the r.h.s. of equation (7) measures the influence of the external magnetic field in the Casimir energy. The contribution of the magnetic field is governed by a quadrature, which is strictly positive, decreases monotonically as n increases and goes to zero in the limit n ® ¥. Consequently, we have by Leibnitz criterion a convergent alternating series in (7) and we may conclude that the external magnetic field increases the fermionic Casimir energy. This is the main result of this work, which elucidates part of the interplay between two of the most fundamental phenomena in relativistic quantum field theory, namely: the Casimir effect and the vacuum polarization properties due to an external field. The obtained enhancement of the fermionic Casimir energy by an external magnetic field may be compared with the opposite behaviour of the bosonic Casimir energy of an scalar field, which is inhibited by the external magnetic field. To see this we turn from spinorial QED to scalar QED keeping the same boundary conditions and external fields that we have been using. We obtain by calculations similar to the ones performed in [18] the following bosonic Casimir energy in the external magnetic field:
where the function  (x) = cosec(x) - x-1 was introduced in [18] and plays in scalar QED the same role played by the Langevin function in spinorial QED. The inhibition of the bosonic Casimir energy by the external field can then be seen in (8) by just noting that
(x) = cosec(x) - x-1 was introduced in [18] and plays in scalar QED the same role played by the Langevin function in spinorial QED. The inhibition of the bosonic Casimir energy by the external field can then be seen in (8) by just noting that  is strictly negative. Actually, this bosonic Casimir energy is completely suppressed in the limit B ® ¥.
is strictly negative. Actually, this bosonic Casimir energy is completely suppressed in the limit B ® ¥.
For strong magnetic fields regime changes in the charged vacuum may be easier to occur [27]. In this case the integral in equation (7) is dominated by the exponential function, whose maximum is exp(-amn) and occurs at s = 2am/n. Therefore, we are justified in substituting the Langevin function by 1 - x-1 in the strong magnetic field regime, which in the cases am 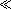 1 and am
1 and am  1 is described, respectively, by |B|
1 is described, respectively, by |B|  |fo|/a2 and |B|
|fo|/a2 and |B|  (|fo|/a2)(a/
(|fo|/a2)(a/ c), where fo is the fundamental flux 1/e and
c), where fo is the fundamental flux 1/e and  c is the Compton wavelength 1/m. In the strong field regime also the second term in (7) can be expressed in terms of a modified Bessel function (formula 3.471,9 in [26]), and the Casimir energy can be written as:
c is the Compton wavelength 1/m. In the strong field regime also the second term in (7) can be expressed in terms of a modified Bessel function (formula 3.471,9 in [26]), and the Casimir energy can be written as:
By using in this expression the leading term in the ascending expansion and then in the assymptotic expansion of the Bessel function (see formulas 8.446 and 8.451,6 in [26]) we obtain the following expressions for small and large mass limits, respectively:
We have obtained in (7) the general expression of the fermionic Casimir energy under the effect of an external magnetic field. The result shows that the external field increases the Casimir energy and reveals the interplay between two fundamental agents which are known to affect the Dirac vacuum fluctuations, namely: external fields and boundary conditions. We have derived expressions for the energy in the regime of strong magnetic field and in this regime we have also obtained the small and large mass limits. The approach we have followed here has a natural extension to more complicated gauge groups and consequently may be useful also in the investigation of the QCD vacuum.
The authors are indebted to Jan Rafelski and Ioav Waga for many enlightening conversations on the subject of this work. M. V. C.-P. and C. F. would like to acknowledge CNPq (The National Research Council of Brazil) for partial financial support.
References
[1] H. B. G. Casimir, Proc. Kon. Nederl. Akad. Wetensch. 51, 793 (1948).
[2] M. J. Sparnaay, Physica 24, 751 (1958).
[3] S. K. Lamoreaux, Phys. Lett. 78, 5 (1997).
[4] U. Mohideen U and A. Roy, Phys. Rev. Lett. 81, 4549 (1998).
[5] A. Roy and U. Mohideen, Phys. Rev. Lett., 82, 4380 (1999).
[6] V. M. Mostepanenko and N. N. Trunov, The Casimir Effect and its Applications (Clarendon, Oxford, 1997). V. M. Mostepanenko and N. N. Trunov, Sov. Phys. Usp. 31, 965 (1988).
[7] E. Elizalde, S. D. Odintsov, A. Romeo A, A. A. Bytsenko and S. Zerbini, Zeta Regularization Techniques with Applications (World Scientific, Singapore, 1994).
[8] G. Plunien, B. Muller and W. Greiner, Phys. Rep. 134, 89 (1986).
[9] K. Johnson, Acta Phys. Polonica B6, 865 (1975).
[10] A. Chodos, R. L. Jaffe, K. Johnson, C. B. Thorn and V. F. Weisskopf, Phys. Rev. D9, 3471 (1974). A. Chodos, R. L. Jaffe, K. Johnson and C. B. Thorn, Phys. Rev., D10 2559 (1974). T. DeGrand, R. L. Jaffe, K. Johnson and J. Kiskis, Phys. Rev. D12, 2060 (1975). J. F. Donoghue, E. Golowich and B. R. Holstein, Phys. Rev. D12, 2875 (1975).
[11] E. Elizalde, M. Bordag and K. Kirsten, J. Phys. A 31, 1743 (1998).
[12] M. Bordag, E. Elizalde, K. Kirsten and S. Leseduarte, Phys. Rev. D 56, 4896 (1997).
[13] B. S. DeWitt, C. F. Hart and C. J. Isham, it Physica 96A, 197 (1979).
[14] L. H. Ford, Phys. Rev. D21, 933 (1980).
[15] S. G. Mamaev and N. N. Trunov, Sov. Phys. J. 23, 551 (1980).
[16] W. Heisenberg, Z. Phys. 90, 209 (1935). H. Euler and B. Kockel, 1935 Naturwissensch. 23, 246 (1935). W. Heisenberg and H. Euler, Z. Phys. 98, 714 (1936). V. S. Weisskopf, K. Dan. Vidensk. Selsk. Mat. Fys. Medd.14, 3 (1936). reprinted in J. Schwinger, Quantum Electrodynamics (Dover, New York,1958). and translated into English in A. I. Miller, Early Quantum Electrodynamics: a source book (University Press, Cambridge, 1994).
[17] M. V. Cougo-Pinto, C. Farina, A. C. Tort and J. Rafelski, it Phys. Lett. B 434, 388 (1998).
[18] M. V. Cougo-Pinto, C. Farina, M. R. Negrão and A. C. Tort, J. Physics A, 4457 (1999).
[19] M. V. Cougo-Pinto, C. Farina, M. R. Negrão and A. C. Tort, Phys. Lett. B 483 (2000) 144.
[20] J. Ambjørn and S. Wolfram, Ann. Phys. NY 147, 33 (1983).
[21] E. Elizalde and A. Romeo, J. Phys. A 30, 5393 (1997).
[22] K. Scharnhorst, Phys. Lett. B236, 354 (1990). G. Barton, Phys. Lett. B 237, 559 (1990). G. Barton and K. Sharnhorst, J. Phys. A26, 2037 (1993). M. V. Cougo-Pinto, C. Farina, F. C. Santos and A. C. Tort, Phys. Lett. B446, 170 (1999); J. Physics A 32, 4463 (1999).
[23] J. Schwinger, Lett. Math. Phys. 24, 59 (1992).
[24] J. Schwinger, Phys. Rev. 82, 664 (1951).
[25] E. T. Whittaker and G. N. Watson, A Course of Modern Analysis (University Press, Cambridge, 1945).
[26] I. S. Gradshteijn and I. M. Ryzhik, Tables of Integrals, Series, and Products (Academic, New York, 1965).
[27] W. Greiner, B. Müller and J. Rafelski, Quantum electrodynamics of Strong Fields (Springer-Verlag, Berlin, 1985).
- [1] H. B. G. Casimir, Proc. Kon. Nederl. Akad. Wetensch. 51, 793 (1948).
- [2] M. J. Sparnaay, Physica 24, 751 (1958).
- [3] S. K. Lamoreaux, Phys. Lett. 78, 5 (1997).
- [4] U. Mohideen U and A. Roy, Phys. Rev. Lett. 81, 4549 (1998).
- [5] A. Roy and U. Mohideen, Phys. Rev. Lett., 82, 4380 (1999).
- [6] V. M. Mostepanenko and N. N. Trunov, The Casimir Effect and its Applications (Clarendon, Oxford, 1997).
- V. M. Mostepanenko and N. N. Trunov, Sov. Phys. Usp. 31, 965 (1988).
- [7] E. Elizalde, S. D. Odintsov, A. Romeo A, A. A. Bytsenko and S. Zerbini, Zeta Regularization Techniques with Applications (World Scientific, Singapore, 1994).
- [8] G. Plunien, B. Muller and W. Greiner, Phys. Rep. 134, 89 (1986).
- [9] K. Johnson, Acta Phys. Polonica B6, 865 (1975).
- [10] A. Chodos, R. L. Jaffe, K. Johnson, C. B. Thorn and V. F. Weisskopf, Phys. Rev. D9, 3471 (1974).
- A. Chodos, R. L. Jaffe, K. Johnson and C. B. Thorn, Phys. Rev., D10 2559 (1974).
- T. DeGrand, R. L. Jaffe, K. Johnson and J. Kiskis, Phys. Rev. D12, 2060 (1975).
- J. F. Donoghue, E. Golowich and B. R. Holstein, Phys. Rev. D12, 2875 (1975).
- [11] E. Elizalde, M. Bordag and K. Kirsten, J. Phys. A 31, 1743 (1998).
- [12] M. Bordag, E. Elizalde, K. Kirsten and S. Leseduarte, Phys. Rev. D 56, 4896 (1997).
- [13] B. S. DeWitt, C. F. Hart and C. J. Isham, it Physica 96A, 197 (1979).
- [14] L. H. Ford, Phys. Rev. D21, 933 (1980).
- [15] S. G. Mamaev and N. N. Trunov, Sov. Phys. J. 23, 551 (1980).
- [16] W. Heisenberg, Z. Phys. 90, 209 (1935).
- H. Euler and B. Kockel, 1935 Naturwissensch. 23, 246 (1935).
- W. Heisenberg and H. Euler, Z. Phys. 98, 714 (1936).
- V. S. Weisskopf, K. Dan. Vidensk. Selsk. Mat. Fys. Medd.14, 3 (1936). reprinted in J. Schwinger, Quantum Electrodynamics (Dover, New York,1958).
- and translated into English in A. I. Miller, Early Quantum Electrodynamics: a source book (University Press, Cambridge, 1994).
- [17] M. V. Cougo-Pinto, C. Farina, A. C. Tort and J. Rafelski, it Phys. Lett. B 434, 388 (1998).
- [18] M. V. Cougo-Pinto, C. Farina, M. R. Negrão and A. C. Tort, J. Physics A, 4457 (1999).
- [19] M. V. Cougo-Pinto, C. Farina, M. R. Negrão and A. C. Tort, Phys. Lett. B 483 (2000) 144.
- [20] J. Ambjørn and S. Wolfram, Ann. Phys. NY 147, 33 (1983).
- [21] E. Elizalde and A. Romeo, J. Phys. A 30, 5393 (1997).
- [22] K. Scharnhorst, Phys. Lett. B236, 354 (1990).
- G. Barton, Phys. Lett. B 237, 559 (1990).
- G. Barton and K. Sharnhorst, J. Phys. A26, 2037 (1993).
- M. V. Cougo-Pinto, C. Farina, F. C. Santos and A. C. Tort, Phys. Lett. B446, 170 (1999);
- J. Physics A 32, 4463 (1999).
- [23] J. Schwinger, Lett. Math. Phys. 24, 59 (1992).
- [24] J. Schwinger, Phys. Rev. 82, 664 (1951).
- [25] E. T. Whittaker and G. N. Watson, A Course of Modern Analysis (University Press, Cambridge, 1945).
- [26] I. S. Gradshteijn and I. M. Ryzhik, Tables of Integrals, Series, and Products (Academic, New York, 1965).
- [27] W. Greiner, B. Müller and J. Rafelski, Quantum electrodynamics of Strong Fields (Springer-Verlag, Berlin, 1985).
Publication Dates
-
Publication in this collection
18 Feb 2002 -
Date of issue
Mar 2001
History
-
Received
03 July 2000 -
Reviewed
08 Sept 2000













