The spacetime of a Dirac magnetic monopole

Abstract

We construct a spacetime whose only source of curvature is a Dirac magnetic monopole, and whose geometry inherits the structure of lines of singularities of the monopole electromagnetic potentials. The spacetime has the topology S³ × R, is stationary and asymptotically at but not asymptotically Minkowskian, with its at null infinity having the topology of S³. These mild pathologies, as acausality and string structure, allow the spacetime configuration to have a gravitational magnetic mass, which results proportional to the charge mu of the monopole. This suggests that the Dirac monopole may be the source of magnetic mass in gravitational configurations, which has no Newtonian analogue. Alsomu has the role of a NUT parameter in the metric of the spacetime, suggesting that the charge of the monopole can provide a physical realization of the NUT parameter.

The Spacetime of a Dirac Magnetic Monopole

Marcelo Costa de Lima¹ and Ivano Damião Soares²

¹Departamento de Física, Universidade Federal do Pará,

Belém, CEP 66075-900, PA, Brazil

² Laboratório de Cosmologia e Física Experimental de Altas Energias,

Centro Brasileiro de Pesquisas Físicas,

Rua Dr. Xavier Sigaud 150, Urca, Rio de Janeiro, CEP 22290-180, RJ, Brazil

Received on 9 November, 2001

We construct a spacetime whose only source of curvature is a Dirac magnetic monopole, and whose geometry inherits the structure of lines of singularities of the monopole electromagnetic potentials. The spacetime has the topology S³ × R, is stationary and asymptotically at but not asymptotically Minkowskian, with its at null infinity having the topology of S³. These mild pathologies, as acausality and string structure, allow the spacetime configuration to have a gravitational magnetic mass, which results proportional to the charge m of the monopole. This suggests that the Dirac monopole may be the source of magnetic mass in gravitational configurations, which has no Newtonian analogue. Also m has the role of a NUT parameter in the metric of the spacetime, suggesting that the charge of the monopole can provide a physical realization of the NUT parameter.

I Introduction

Magnetic monopoles are field configurations that arise naturally in gauge field theories, even at the classical level. The idea of a magnetic monopole was put forward originally by Dirac in a classical paper [1], and more recently remade by Wu and Yang [2] in its generalization for non-Abelian gauge theories. Two fundamental concepts are introduced in Dirac's original paper: (i) electromagnetism is a gauge-invariant manifestation of the non-integrability of the phase of the wave function; (ii) nodal lines of the wave function (spacelike lines along which the wave function vanishes) are singularity lines of the electromagnetic potential and the end points of nodal lines are points of singularity of the electromagnetic field. At this singularity there is a magnetic monopole, such that the total magnetic flux through a closed surface about this singularity is different from zero. In other words, although the pair of Maxwell equations dF = 0 imply that the total magnetic flux through any closed surface at a given instant of time must be zero, this is no longer true if a magnetic monopole is present inside the closed surface. Equation dF = 0 must be violated in some point of the surface. Furthermore, it must be violated in some point of any closed surface enclosing the monopole so that it is violated along a line of points - which we denote by string - extending from the monopole to infinity or to another pole of same strength and opposite sign. At this point, some questions may be posed to us. If the magnetic monopole generates gravitation, does the gravitational field inherits this structure of lines of singularities? And if it does, what are the physical consequences? An answer to these questions, and which is in part a motivation for this paper, is connected to the possibility of the physical realization of a magnetic gravitational mass generated by the charge of the Dirac monopole.

As a field theory, General Relativity also presents field configurations which may be associated with magnetic mass monopoles and strings. Weird configurations of this type are known in General Relativity since the discovery [3] and analysis [4] of the two parameter NUT vacuum solution. The remarkable feature of this solution emerges from a new parameter - the NUT parameter - and, as we will discuss, there are strong suggestions that this parameter is associated with the existence of magnetic gravitational charges and wire structures in the spacetime. The NUT solution was generalized by Brill to include electromagnetic fields as sources of curvature [5] but the physical origin of the NUT parameter remained obscure. We note that, in the NUT solution, the vanishing of the NUT parameter yields the Schwarzschild solution while its vanishing in the NUT-Brill solution results in the known Reissner-Nordström spacetime.

Although the physical origin of the NUT parameter is obscure, there has been suggestion in the literature that the two parameter NUT metric can be considered as a gravitational dyon. In fact, Hansen [6] showed that, for stationary and asymptotically flat solutions of vacuum Einstein's equations, two functions can be introduced - the mass potential F_M and the angular momentum potential F_J defined on the manifold of orbits of the timelike Killing vector - that characterize uniquely the local structure of these spacetimes. Expanding these potentials in multipole moments, it can be shown that, for the NUT solution, the monopole moment associated with F_M is the mass, while the monopole moment associated to F_J is the NUT parameter [7]. The NUT parameter a is then interpreted as a monopole source of angular momentum, and dual to the mass in the sense that there is a duality transformation [6, 8] in the plane (F_M, F_J) such that, by this transformation we may take the Schwarzschild solution (m,a = 0) into the pure NUT solution (m = 0, a). Later, Ramaswamy and Sen [9] were able to introduce a definition of dual (or magnetic) mass for stationary spacetimes and established the precise conditions for a spacetime to admit dual mass. They showed that for stationary spacetimes which have the null boundary at infinity with the topology of S³ (namely, a S¹ bundle over S²), precise expressions can be constructed at this boundary which characterize mass and dual mass, based on the Weyl curvature of the spacetime. However the spacetime must obviously be acausal. This is exactly the case of the NUT spacetime, where the dual mass is proportional to the NUT parameter. We note that spacetimes with asymptotic topology R × S² have dual mass vanishing identically, what excludes Reissner-Nordström as a candidate. The mass and the dual mass are associated with the electric and magnetic part of the Weyl tensor, respectively, and therefore the dual mass is denoted magnetic, in the sense of the duality of electromagnetism (a duality which is also present connected with the decomposition of the Weyl curvature in its electric and magnetic parts).

In order to understand the nature of the NUT parameter and its association with the dual or magnetic mass, we here construct a spacetime with topology S³ × R having a magnetic monopole as the only source of curvature. As it turns out, the magnetic charge of the monopole behaves in the solution as a NUT parameter, thus providing a physical source for the NUT parameter or dual mass. However pathologies in the solution will be present because geometrical structures of the spacetime must absorb the singularities of the monopole field, although these pathologies are in a sense necessary to a precise characterization of dual (magnetic) mass. We organize the paper as follows. In Section II we construct and analyse a spacetime manifold with topology S³ × R (a basic condition for the existence of dual mass) and electromagnetic fields on this manifold, solutions of Einstein-Maxwell equations. This construction is made in detail, using Hamilton quaternions and differential forms, which constitute a natural frame for this analysis. In Sections III and IV we examine relevant geometrical properties of the spacetime whose curvature is generated by the magnetic monopole. The curvature tensor and the electric and magnetic parts of the Weyl tensor are examined, as well as the asymptotic structure of the spacetime; the magnetic component of the Weyl curvature is fundamental in characterizing the dual gravitational mass, as discussed already. We also examine how the structure of wire singularities both in the electromagnetic fields and in the geometry of the spacetime are intrinsically merged, and use is made of the violation of the Poincaré Lemma in topologically non-trivial spacetime domains in order to characterize the nature of these singularities. We also introduce Misner's type coordinates to properly connect the electromagnetic potential to the geometry 1-forms, and relate gauge transformations of the potentials to transformations in temporal coordinates defined on S¹. In Section V conclusions are made, with some discussions on the pathologies of the solution as acausality, and possible interest of these objects for quantum gravity.

II The Spacetime with Topology S³ ×R Generated by the Dirac Monopole

The methods used in part of this Section are partially borrowed from Ref.[10] and are presented here for completeness. Calculations are not given in detail but they can be checked without difficulty.

Let E₄ be the four dimensional Euclidean space with Cartesian coordinates (a⁰, a¹, a², a³). We define the hypersurface S³ of E₄ as the set of points which satisfy

For every

a = (

a

⁰,

a

¹,

a

²,

a

³) and

b = (

b

⁰,

b

¹,

b

²,

b

³) Î

S

³ we define the multiplication law

This is the multiplication law of Hamilton quaternions [11]. Under (2)

S

³ becomes a group, acting on itself by left multiplication; namely, for a given

v Î

S

³, a left motion of

S

³ into itself is expressed as

and we have that

a¢ Î

S

³ for all

a Î

S

³.

S

³ is said simply transitive since for each

a Î

S

³ there exists only one left motion

v from

a to a given

a¢, namely,

v =

a

^-1

a¢.

S³ acting on itself by left multiplication (3) is a Lie group with the three independent left-invariant vectors fields

They are obtained by an arbitrary left motion

a of the three independent unit vectors (0, 1, 0, 0), (0, 0, 1, 0) and (0, 0, 0, 1) which define the tangent space of

S

³ at the identity (1, 0, 0, 0). We remark that a left-invariant vector field c(

a) on the Lie group

S

³ is defined by

vc(

a) = c(

va), for all

v,

a Î

S

³.

We have an analogous picture for right motions of S³ on itself, namely

with the corresponding right-invariant vector fields on

S

³,

Bases (4) and (6), expressed as e_(i)(a) = and d_(i)(a) = , constitute two distinct representations of the algebra of the Lie Group S³,

where

=

. They are related by an anti-isomorphism induced by the inverse map of

S

³ on itself, and obviously satisfy

Introducing on S³ the Euler angles (t, q, f) by the transformations

with

t Î [0, 2p], q Î [0, p] and f Î [0, 2p], the left-invariant vector fields

e

_(i) are expressed

with corresponding dual left-invariant 1-forms

satisfying

dw

ⁱ =

w

^j Ù w

^k. For future reference we give the right-invariant vector fields in this coordinate system,

Taking on the one dimensional manifold R the coordinate r (0 £ r < ¥), with vector field e₍₃₎ = and 1-form w³ = dr, the group S³ × R can be characterized by the left-invariant vector fields (e₍₀₎, e₍₁₎, e₍₂₎, e₍₃₎), which satisfy (7) and

and which are a basis for the left-invariant vector fields on

S

³ ×

R; correspondingly the invariant dual 1-forms (w

⁰, w

¹, w

², w

³) are a basis for the left-invariant 1-forms on

S

³ ×

R. The manifold

S

³ ×

R is the simply transitive covering group of the algebra (7) and (14).

The geometry is obtained by introducing on S³ × R the left-invariant metric g = g_abw^aw^b, where g_ab = diag(4A²(r), -B²(r), -B²(r), -1) such that the sections r=const. have the topology of S³; it assumes the form

In terms of the Lorentzian Cartan frame defined by

we have

g = h

_ABQ

^AQ

^B, with h

_AB =

diag(1, -1, -1, -1) ,

A,

B = 0, 1, 2, 3. By construction, this geometry has the right-invariant vector fields (13) as Killing vectors which act transitively on the surfaces

r =

const. Expressing the Maxwell tensor in this frame as

F =

F

_ABQ

^A Ù Q

^B, Maxwell's equations in this geometry are given by

where * denotes the dual operation. For a pure radial magnetic field in the frame (15), we obtain the solution

other components zero, where the constant m is the charge of the magnetic monopole, being proportional to the magnetic flux as shown unambiguously in Section III. The associated Maxwell energy-momentum tensor results in

(18)and, for this field configuration, Einstein-Maxwell equations yield the solution

A(

r) = m/2 and

B(

r)

² =

r

² + m

²/4 or, by a proper rescale of the time variable,

This solution is stationary, with Killing vectors (13) plus ¶/¶t. We mention that the orbits of the timelike Killing field ¶/¶t, which are defined on S³, are closed timelike geodesics, characterizing the acausal nature of the spacetime. The time coordinate t in (19) has period 2pm.

Also the spacetime is asymptotically flat for r ® ¥. However it is not asymptotically Minkowskian, since r®¥ has the topology of S³, by construction, and is therefore acausal. These characteristics allow the spacetime to be endowed with a dual (magnetic) gravitational mass, a point to be discussed in Section IV. Furthermore, in (19), m has the role of the NUT parameter, suggesting the charge of the monopole as a physical realization for the NUT parameter. In the local Cartan frame (15), the non-null components of the curvature tensor are given by

showing clearly that the magnetic monopole is the only source of curvature of the spacetime and consequently responsible for all the weird properties of the spacetime. If m = 0, the spacetime is flat. Note that the curvature tensor is regular everywhere and only the metric fails to be regular along the strings of the electromagnetic potentials A's associated with the magnetic field (17), as shown in the next Section. In this sense we say that the spacetime exhibits only mild singularities.

The electric and magnetic parts of the Weyl curvature tensor[12] with respect to the Killing vector field ¶/¶t are given, in the frame (15), respectively by

where

The fact that ~ () and ~ (), as r ® ¥, is crucial for the characterization of the spacetime as having zero electric gravitational mass (the usual Newtonian mass as defined asymptotically) and a non-zero magnetic gravitational mass, connected to the magnetic part of the Weyl curvature tensor and proportional to the charge m of the monopole.

III The Magnetic Monopole String Structure in the Gravitational Field. Integrability Conditions

Let us now examine how the spacetime inherits the string structure of the magnetic monopole. From (15) and (17) the monopole Maxwell tensor F can be expressed as the 2-form

Since

dF = 0, we may assume from Poincaré's Lemma [13] that there exists a potential 1-form A such that

F =

dA, namely, that the 2-form

F is exact. However the Poincaré's Lemma holds for topologically non complicated domains, that is not the case for the domain of definition of (22). To see this, let us integrate

dF = 0 in the 3-dim section of the spacetime

r =

const. that by construction is a

S

³. Taking into account that

S

³ is a Hopf fiber bundle[14], with base space

S

² coordinated by (q, f) and Hopf fibers homeomorphic to

S

¹ generated by the Killing field ¶/ ¶

t, this volume integral can be reduced to

which is different of zero for m ¹ 0. Since the manifolds

S

³ and

S

² have no boundary, this implies that in some point of

S

³ and of the section

S

² the equations

dF = 0 and

F =

dA are violated. To characterize topologically the domain of definition of

F, let us consider the manifold

S

³ which has no boundary. Now if we extract one point of

S

³ we obtain a boundary which is

S

². To see this, let us intersect

S

³ by a plane which, for simplicity, we take

a

² = 0. In the case of this particular section, the boundary is the unit sphere

S

². We can gradually diminish the radius of

S

² taking sections of type

a

² =

=

const. with increasing

such that the radius becomes very small, namely, (

a

⁰)

² + (

a

¹)

² + (

a

³)

² = 1 - (

)

² =

. This corresponds to the limiting situation of

extracting a point from

S

³, obtaining a boundary which is

S

² with radius

<< 1. Now

S

² is also a manifold without boundary, and therefore the second equality in (23) implies that

F=

dA is violated at some point of

S

². Therefore the topology of the domain of regularity of

F is

S

² with one point V removed, with corresponding

S

³ with one point removed. And Eq.(23) should actually be expressed

the non-null result of (23) coming from the contribution of the boundaries ¶(

S

³ - V) and ¶(

S

² - V). By continuously varying

r, we have in the spacetime a line of points where this violation occurs, defining what is denoted by a string structure. Indeed, associated to the field F given in (22) we may have the 1-form potentials

which are singular respectively at q = p and q = 0. In q = p/2 where both are well defined, they are related by the gauge transformation

Regularity and single-valuedness conditions on the wave function of a charged particle in interaction with this monopole magnetic field implies that the phase factor

S =

e(2mf) in the overlap region must be a multiple

n of 2p, which is Dirac's quantization, namely, 2m

e =

n (in units such that

=

c = 1). Here n is a characteristic of the particular string, corresponding to the quantized magnetic flux through

S

²(cf. [1]-[2]). We note that the boundary in

S

² - V appearing in the second integral of (24) is not homotopic equivalent for distinct

n's.

Going now to the gravitational field of the spacetime, defined from (15), let us consider the 1-form Q⁰ = (dt + mcosqdf). Its exterior derivative yields dQ⁰ = (-msinqdq Ù df). A discussion based on Poincaré's Lemma, analogous to the one leading to (24), shows us that the domain of definition of Q⁰ presents a line of singularities where the identity d²Q⁰ = 0 is violated (this being equivalent to the violation of the identity for the Riemann tensor = 0). What is the relation between these lines of singularities in the geometry and those of the electromagnetic potentials A? The answer is direct. The lines of singularities of the electromagnetic potentials A (cf. (25)) are inherited by the spacetime and coincide exactly with the lines of singularities which lead to the violation of d²Q⁰ = 0.

To see this, let us introduce coordinates which allow us to connect the 1-forms of the geometry with the electromagnetic potentials (25). We consider first the coordinate t in (19). From (15) we can express

up to a rescale of the time variable in Q

⁰ analogous as done in (19). In the metric (19), we have

g(

dt,

dt) = 1 - m

²(

cotgq/

B)

². Therefore this temporal coordinate makes the metric singular both in q = 0 and q = p. However we can define two new distinct temporal coordinates in such a way that the geometry is singular in a single value of the angle q, either q = 0 or q = p, of

S

³. This can be done by analyzing the topology induced by

S

³ on the space of the Euler angles (

t, q, f) introduced in (10), giving us a picture of

S

³ as the union of two solid tori with their surfaces identified.

Consider Eqs.(10) defining points in S³ and the cube of Fig.1 in the Cartesian space (t, q, f). Let us now make in (10) the transformations

with b = 2np. These transformations do not alter the points of S³, and therefore the planes t₀ and f₀ of the cube of Fig.1 must be identified respectively with the planes t₀ + b and f₀ + b. In this way, for each q = q₀ = const. we have a torus T² obtained by the identifications shown in Fig.2.

Now we show that the planes q = 0 and q = p are reduced, by identifications, to one-dimensional tori T¹, that is, circles S¹. Let us examine the case q = 0: from (10) we have that (a⁰ = cos (t + f)/2, a¹ = sin (t + f)/2, a² = 0, a³ = 0). These points of S³ remain invariant by the transformations

for any arbitrary constant d. Thus all points of the plane q = 0 related by (29) must be identified. In other words, all points of the straight lines

t + f =

,

an arbitrary constant, must be identified; each of the straight lines

t + f =

is reduced to a point that can be characterized by the constant

. This constant may then be used as a coordinate for the circle

S

¹ obtained by the identifications (28)-(29), and denoted by

t

_N,

Analogously, for q = p we have from (10) that (a⁰ = 0, a¹ = 0, a² = sin (t - f)/2, a³ = cos (t - f)/2). Now the points of S³ remain invariant by the transformation

with d an arbitrary constant. The points of q = p related by (31) must be identified. These points now belong to the straight lines

t - f = t

₀, t

₀ an arbitrary constant, each of which is reduced to a point characterized by t

₀ and this constant can be used as a coordinate for the circle

S

¹ obtained by the identifications (28)-(31), and denoted by

t

_S,

We can now use these coordinates t_N and t_S, together with (q, f), to characterize S³ as the union of two solid tori identified by its boundary, given by the torus T² corresponding to q = q₀ (0 < q₀ < p), as illustrated in Fig.3. We fix q₀ = p/2 such that each solid torus corresponds to a hemisphere of S³.

Note that by a rescale of t as done in (19), we have actually

These two new time variables have period 2pm, and are related by

A trivial calculation gives, for the Cartan metric 1-form Q⁰ (cf. (15))

Thus, as mentioned before, in the time coordinate t_N, the metric is regular at q = 0 and has a line of singularities along q = p, coinciding with the string of the electromagnetic potential A_N. Analogously, for t_S, the metric is regular at q = p and has a line of singularities along q = 0, coinciding with the string of the electromagnetic potential A_S. These time coordinates display clearly how the metric inherits the string structure of the magnetic monopole potentials. Note that the gauge transformations (27) which relate A_N and A_S also connect and . In general the gauge transformations of the electromagnetic potentials A's are absorbed by transformations in the temporal coordinates t_N and t_S defined on the S¹ manifolds at the center of the two solid tori of Figure 3. In this instance, Dirac's quantization of the charge of the monopole define the winding number n of the periodic coordinates t_N and t_S defined on S¹, where n is associated to the quantized magnetic flux through a two sphere enclosing the monopole. In a equivalent way, from the point of view of fiber bundle structure of S³, the winding number n characterizes the periodicity of the integral curves of the vector field ¶/¶t defined on the fibers homeomorphic to S¹. Coordinates (33) were originally introduced by Misner[4] in his analysis of the topology of the NUT geometry.

IV The S³ Null Infinity and the Gravitational Magnetic Mass

Let us discuss concisely the idea of dual (or magnetic) mass as defined by Ramaswamy and Sen[9]. They showed that for stationary spacetimes which have a null boundary at infinity with topology S³ (namely, having the structure of a principal S¹ fiber bundle over S²) precise expressions can be constructed at this boundary characterizing mass and dual mass, based on the Weyl curvature of the spacetime. This condition is essential since a null infinity with topology S² × R (with R being the null generators), e.g., in asymptotically Minkowskian spacetimes, the dual mass vanishes identically.

The introduction of a structure of null infinity with the S³ topology in the spacetime of (19) can be implemented as follows. To start, let us note that the spacetime has topology S³ × R, with the timelike Killing vector field ¶/¶t generating the S¹ Hopf fibers of S³. This implies that there exists closed timelike curves (in fact, closed timelike geodesics) and no global spacelike surfaces in the spacetime. Although the notion of spatial infinity cannot be introduced, the notion of null infinity exists. Let us define new coordinates x^a = (u, q, f, x) by u = t - r, x = r ^{- 1}, with u having also the period of 2 pm. In this new coordinate system, the geometry (19) takes the form

The Penrose conformal compactification of the spacetime at infinity can be implemented by introducing a conformal transformation on the geometry, with conformal factor W = x and to extend the coordinate chart to include x = 0, namely points at infinity r ® ¥ for all u, q, f. The spacetime manifold is now endowed with a three-sphere boundary at r ® ¥ infinity,that is, at W = 0. The geometrical structure of the null infinity 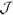is given by the vector field n^a = g^abÑ_bW | _{W = 0} = (¶/¶u)^a (which is the timelike Killing translation ¶/ ¶t on 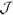) and the degenerate metric = W²g, evaluated at x = 0, dx = 0. Namely, the asymptotically flat null infinity 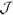is a null three-sphere coordinatized by x^a = (u, q, f), a = 0, 1, 2, with the degenerate metric _ab = diag(0, -1, -sin²q), and vector field n^a = (1, 0, 0) = ()^a.

Let us consider a BMS infinitesimal supertranslation generated by n^a on 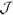; associated with this supertranslation the total energy-momentum p^a can be defined in a given gauge by p^a = K^abl_b, with l_b a covector on 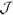such that n^al_a = -1 and K^ab is associated with the asymptotic electric part of the Weyl curvature tensor. From p^a the electric mass (the usual Newtonian mass)

is defined, at the instant represented by the cross section

S

² of

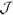
. To define the dual mass, the natural candidate to be considered is

^*

p

^a =

^*

K

^ab

l

_b, where

^*

K

^ab is the asymptotic magnetic part of the Weyl curvature tensor, resulting analogously

In the case of stationary spacetime (more specifically, in the absence of gravitational waves) both the electric gravitational mass (38) and the dual (or magnetic) gravitational mass (39) are well defined, gauge invariant and independent of the choice of

l

_a, and also independent of the choice of the cross section. The duality aspect is connected to the duality between the electric and magnetic parts of the Weyl curvature[12], analogous to the duality in electromagnetism, leading us to denote the above defined quantity (39) equivalently as dual mass or magnetic gravitational mass.

For our spacetime (19), the mass and the dual mass are calculated through the quantities defined on ,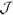

respectively. In the limit, only the following terms survive,

where

E

₃₃ and

H

₃₃ are the electric and magnetic components of the Weyl curvature of the spacetime given in (20)-(21). Note that the geometry

calculated at W = 0 in the coordinate system

x

^a = (

u, q, f,

x) is

|

_W=0 = -2

dudx - 2m

cos q

df

dx - (

dq

² +

sin

²q

df

²). It results

yielding from (38) and (39) the gravitational electric mass

M

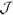
=0 and the dual(or magnetic)-gravitational mass

In this way, the charge of the Dirac magnetic monopole is the source for the magnetic gravitational mass of the spacetime. The fact that the spacetime inherits the structure of singularities of the monopole field is fundamental to turn it into a candidate with the mild pathologies (as acausality and asymptotically flat null infinity with the topology of S³) necessary for the definition of magnetic gravitational mass, with the charge of the monopole providing a possible physical realization of the NUT parameter.

V Conclusions an Final Comments

In this paper we basically construct a spacetime whose only source of curvature is a Dirac magnetic monopole, and whose geometry inherits the structure of singularities of the monopole electromagnetic potentials. The spacetime has topology S³ × R, is stationary and asymptotically flat but not asymptotically Minkowskian, by construction. The curvature tensor is regular everywhere and only the metric fails to be regular along the strings of the monopole electromagnetic potentials. The metric depends on one parameter m, the charge of the monopole; m has the role of the NUT parameter suggesting that the charge of the monopole constitutes a possible physical realization of the NUT parameter. The timelike lines are defined on S³ implying the existence of closed timelike geodesics and no global spacelike surfaces in the spacetime. Although the notion of spatial infinity cannot be introduced, the notion of null infinity exists, with the topology of S³. This structure plus the mild pathologies (as strings and acausality) turn the spacetime into a candidate for a gravitational configuration having magnetic gravitational mass, associated with the non-null magnetic part of the Weyl curvature present due to the monopole. In the framework introduced by Ramaswamy and Sen[9], where the spacetime is stationary (no gravitational waves are present), a precise definition of magnetic gravitational mass can be established dual to the definition of electric gravitational mass (the usual Newtonian mass as defined asymptotically), both definitions based on BMS supertranslations defined on the null infinity with topology S³ (a S¹ Hopf fiber bundle over S²). It turns out that the spacetime of the Dirac magnetic monopole is a configuration with zero electric gravitational mass, and magnetic gravitational mass proportional to the charge of the monopole.

Ashtekar and Sen[15] extended the framework of [15] to cases in which gravitational waves may be present (more specifically, in which the Bondi news function does not vanish). They showed that, while the electric gravitational mass can be radiated away in form of gravitational waves (with balance equations given by Bondi-Sachs analysis[16]) the magnetic gravitational mass cannot be radiated away. In this aspect, the magnetic gravitational mass of our model (which is proportional to the magnetic charge of the monopole) is in perfect accordance with Abelian Maxwell theory where both electric and magnetic charges are absolutely conserved, and opposed to non-Abelian Yang-Mills theories where both charges may be radiated away. We remark once again that in our model the electric gravitational mass is zero.

A possible extension of our paper to be examined would be to uncover the possible spacetime structures having magnetic monopole configurations in non-Abelian gauge theories[17] as the only source of curvature and how they could possibly be the source of electric and magnetic gravitational masses of these spacetime configurations.

We must comment that the spacetime structure discussed may not be of interest as a model for gravitational configurations of macroscopic objects, because of its pathologies as causality violation. However the interest in these configurations may come from quantum gravity where dual mass vacuum solutions are stationary points of the gravitational action functional and may play an important role in Euclidean quantum gravity.

Finally we mention that a tentative for establishing the equation of motion of point particles with magnetic gravitational mass were proposed in [18], based on the Jacobi equation for geodesic deviation where, by the same process of duality analogy, the electric part of the Weyl tensor is substituted by the its magnetic part.

Acknowledgments

One of us (IDS) would like to thank Dr. Eugenio Ramos B. de Mello for some useful comments on the paper, and also thank CNPq of Brazil for partial financial support.

References

[11] This multiplication law turns the vector space E₄ into an algebra, the algebra of Hamilton quaternions, which is an algebra with identity. Associativity and distributivity are also assumed.

• [1] P.A.M. Dirac, Proc. Roy. Soc. London, A 133, 60 (1931).
• [2] T.T. Wu and C.N. Yang, Phys. Rev. D12, 3845 (1975.
• [3] E. Newman, L. Tamburino and T. Unti, J. Math. Phys. 4, 915 (1963).
• [4] C.W. Misner, J. Math. Phys. 4, 924 (1963).
• [5] D.R. Brill, Phys. Rev. 133, 73 (1964).
• [6] R. Hansen, J. Math. Phys. 15, 46 (1974).
• [7] P. Kundu, J. Math. Phys. 22, 1236 (1981).
• [8] R. Geroch, J. Math. Phys. 12, 918 (1971).
• [9] S. Ramaswamy and A. Sen, J. Math. Phys. 22, 2612 (1981).
• [10] I. Oszvath and E.L. Schüking, Ann. Phys. 55, 166 (1969).
• [12] M. Novello and J.M. Salim, Fundamentals of Cosmic Physics vol.8, 201-342 (1983).
• [13] H. Flanders,Differential Forms, Academic Press (New York, 1963).
• [14] N. Steenrod, The Topology of Fibre Bundles, Princeton University Press (Princeton, 1951).
• [15] A. Ashtekar and A. Sen, J. Math. Phys. 23, 2168 (1982).
• [16] H. Bondi, M.G.J. Van der Burg and A.W.K. Metzner, Proc. R. Soc. (London) A269, 21 (1962);
• [17] T.T. Wu and C.N. Yang, in Properties of Matter Under Unusual Conditions, eds. H. Mark and S. Fernbach (Interscience, New York, 1969);
• [18] M. Novello, I. Damião Soares, J.M. Salim and C.A.P. Galvão, Journal of Physics A9, 547 (1976).

Publication Dates

• Publication in this collection
  26 Nov 2002
• Date of issue
  Mar 2002

History

• Received
  09 Nov 2001