The regime of electromagnetically induced transparency in optically dense media: from atoms to excitons

Abstract

The phenomenon of electromagnetically induced transparency (EIT) was discovered by Adriano Gozzini and coworkers in 1976 in Pisa. Novel schemes to investigate and exploit EIT in the optical domain have attracted much interest both in atomic and solid state systems. We discuss some of our recent theoretical results, in particular: i) a well developed EIT regime based on free exciton levels in undoped bulk crystalline Cu2O; ii) light dragging effects in moving media under EIT; iii) the coherent control of Cherenkov radiation in the EIT regime.

a07v322a

The Regime of Electromagnetically Induced Transparency in Optically Dense Media: from Atoms to Excitons

M. Artoni^a, F. Bassani^b, I. Carusotto^c, and G.C. La Rocca^d,b

^aINFM and LENS, Largo E. Fermi 2, I-50125, Florence, Italy

^bINFM, Scuola Normale Superiore, Piazza dei Cavalieri, I-56126 Pisa, Italy

^cLaboratoire Kastler-Brossel, Ecole Normale Superieure, 75231 Paris Cedex 05, France

^dDipartimento di Fisica "E.R. Caianiello'', Università di Salerno, I-84081 Baronissi (Sa), Italy

Received on 23 April, 2001

The phenomenon of electromagnetically induced transparency (EIT) was discovered by Adriano Gozzini and coworkers in 1976 in Pisa. Novel schemes to investigate and exploit EIT in the optical domain have attracted much interest both in atomic and solid state systems. We discuss some of our recent theoretical results, in particular: i) a well developed EIT regime based on free exciton levels in undoped bulk crystalline Cu₂O; ii) light dragging e ects in moving media under EIT; iii) the coherent control of Cherenkov radiation in the EIT regime.

I Introduction

In the context of optical pumping experiments on Na, Adriano Gozzini and coworkers observed for the first time in 1976 in Pisa a peculiar phenomenon: whenever the separation among two Zeeman sublevels of the two hyperfine components of the 3S ground state would equal the frequency difference between two laser modes nearly resonant with the D₁ line, no absorption would be induced, and therefore no fluorescence from the 3P level would be observed, as if Na would be "transparent" to the resonant light. This phenomenon, originally referred to as the Na "black line", was immediately explained by Ennio Arimondo et al. in terms of quantum coherence and interference whereby the ground state doublet is pumped into a coherent superposition state where the population is trapped due to destructive interference between the two distinct paths of absorption to the third excited level. After these seminal works [1], such a mechanism of coherent population trapping underlying electromagnetically induced transparency (EIT) has received increasing attention [2] because of the many applications, such as for instance subrecoil laser cooling [3], lasing without inversion [4], adiabatic transfer [5]. More recently, both in ultracold atomic clouds as well as in solids, EIT has been shown to open novel regimes of the electrodynamics of continuous media. We here present some of our recent theoretical results: in particular, a well developed EIT regime based on free exciton levels in undoped bulk crystalline Cu₂O [6]; light dragging effects in moving media under EIT [7]; and, in more detail, the coherent control of Cherenkov radiation in the EIT regime.

II EIT for intrinsic bulk exciton lines

The investigation of fundamental coherent optical effects in semiconductors is an important field of research where quantum interference plays a role: we are here concerned with electromagnetically induced transparency (EIT), so far demonstrated mostly for dilute atomic vapors. Condensed matter exhibits quite a variety of three-level systems where EIT could also be realized. Yet dephasings, which can easily break the coherence of the population trapping state, make it difficult to observe a large EIT effect in solids. For microwaves, EIT has been observed in ruby [8] using a strong external magnetic field, while in the infrared EIT has been observed in intersubband transitions in a quantum well [9]. For optical frequencies, EIT in solids has only been observed in an inhomogeneously broadened hole-burning Pr3+-doped Y2SiO5 crystal [10]. We predict a remarkable enhancement of electromagnetically induced transparency in an undoped bulk semiconductor exhibiting sharp free-exciton lines that correspond to intrinsic delocalized electronic states. We specifically consider the "yellow exciton" series in Cu₂O for which all the relevant spectroscopic parameters are available [11,12].

In Cu₂O both conduction and valence band extrema occur at the G point (O_h symmetry) and have, respectively, and symmetry, each twofold degenerate spin included. The four states of the 1S exciton manifold split into an upper quadrupole allowed threefold degenerate level and a lower forbidden nondegenerate level. The twelve states of the 2P exciton manifold are classified according to their symmetries as follows: , among which only the threefold degenerate states are dipole active and give rise to the second class 2P "yellow exciton" line [13]. In the following, we assume that the optically active 2P states are sufficiently separated from all others so that we can restrict ourselves only to the 1S and 2P exciton states. The longitudinal-transverse splitting of the second class 2P exciton is negligible. The inclusion of the complete 2P exciton manifold [14] would not change significantly the main results here discussed.

We are interested in the optical responce experienced by a weak probe beam of frequency w_p tuned around the 2P "yellow" exciton line of resonant frequency w_2P, while a strong coupling beam of frequency w_c and Rabi frequency W_c is nearly resonant with the 1S to 2P exciton transition of resonant frequency w_2P-1S = w_2P-w_1S. All relevant parameters in the effective hamiltonian describing this L three exciton level configuration can be determined from the usual envelope function picture of Wannier-Mott exciton states. The dipole forbidden 1S exciton state has a small linewidth (g_1S 0.1 meV) compared to that of the second class allowed 2P exciton state (g_2P 1 meV) and a well developed EIT can be established in the presence of the coupling beam. A transparency window about the 2P exciton line appears, while for very high pump intensities, or at least for W_c larger than about 2 g_2P, the Autler-Townes regime is eventually reached [2,12,6]. The optical susceptibility experienced by a probe polarized along x in the presence of a pump polarized along y is given by

with A 0.02 is a numerical constant proportional to the 2P exciton oscillator strength[6] whereas d_p = w_2P-w_p and d_c = w_2P-1S-w_c are the two relevant detunings.

Fig.1 shows the imaginary part of the susceptibility for pump intensities characterizing both EIT and Autler-Townes regimes for a probe tuned to the 2P exciton line. The actual transmission through a slab, including the effect of the complex background dielectric constant, is shown instead in Fig.2 anticipating a nearly 50% transmission due to EIT. Apart from the background absorption, the 1S exciton linewidth g_1S is the material parameter that mostly limits the possibility of achieving even larger EIT effects in this system. Finally, Fig.3 shows the transmission for parameters appropriate to the experiments by Fröhlich and coworkers [12] where a very tiny EIT effect could indeed be recognized: this figure reproduces well the differential transmission measured in [12] for a nearly resonant pump.

The observation of a fully developed EIT regime for intrinsic exciton lines in semiconductors would open the way to many opportunities involving either device applications of EIT or fundamental issues such as, e.g., the role of polaritonic effects and of ponderomotive forces in the EIT context.

III Fresnel light drag under EIT

The phase velocity of light depends on whether light is propagating in a moving or in a stationary medium. This effect, which gives rise to the familiar Fresnel light-drag [15], has been observed for the first time in Fizeau's flowing water experiment [16] and had a profound influence on the change of our perception of the nature of space and time at the turn of the century. Several other observations of light-drags have followed in which different dragging media and different interferometric measurement techniques have been employed. There still remains, however, a formidable challenge to perform high-precision measurements of light-drags as they have not yet reached the level of accuracy of other tests of special relativity [17].

In order to perform a high-precision measurement of the Fresnel-Fizeau effect one needs rather high sensitivity to velocity induced phase shifts which means large sample speeds. At the same time, in order to preserve high contrast of the interference fringe pattern, vibrations transmitted from the sample movement to the interfereometer itself have to be minimized. To this extent we here anticipate that precision can be improved through EIT when this is devised to occur in a slab of cuprous oxide (Cu₂O) used as a dragging medium. Improvements consist in quite large positive and negative light-drags that enable one to achieve high interferometric sensitivities even for low drag velocities. Large drags are associated with the steep dispersion occurring within a transparency window centered at the 2P exciton resonance and arising from the quantum interference in a specific pump-probe L configuration which involves the ground, the 1S and the 2P exciton levels, as shown above.

Not only can one increase precision, but in a sample rendered anisotropic by a suitable choice of the pump polarization one can also make the phase shift corresponding to the light-drag to vanish. This means that in a typical interferometric experiment no fringe shift would be observed for light propagating through the moving medium with respect to light propagating through the medium at rest. This somewhat surprising conclusion holds for all velocities of experimental interest while tuning of the light-drag to zero may turn out to be quite favorable for investigating the electromagnetic and mechanical balance of the momentum associated with light in EIT media.

We then examine Cu₂O under EIT as dragging medium and look at the Fresnel drag experienced by a weak probe beam of frequency w tuned about the 2P "yellow" exciton line of resonant frequency w_2P, while a strong beam of Rabi frequency W_c is resonant with the 1S to 2P exciton transition. For a pump Rabi frequency W_c» EIT takes place whereby a narrow transparency window with a rather steep dispersion appears around the 2P exciton line.

The effective dielectric tensor seen by the probe in the presence of the pump is in general anisotropic, depending on the pump polarization and on the detailed structure of the exciton levels involved. For the sake of simplicity, we here assume that the states are well separated from all other 2P states and the pump polarization is along the cubic axis ¢ (See Fig.4). The resulting dielectric tensor is uniaxial with the optical c-axis along ¢, i.e., Î_x¢x¢ = Î_||, Î_y¢y¢ = Î_z¢z¢ = Î_^ and Î_{j¢ ¹ k¢} = 0 and for a resonant pump beam one has

while Î_|| is obtained by setting W_c®0 in the above equation.

In a typical configuration [18,17] a slab of thickness L moves in one arm of an interferometer with constant velocity v = bc with respect to an observer in the laboratory frame S as sketched in Fig.4. The quantity of experimental relevance is the velocity dependent phase-shift Df experienced by the probe upon single-pass transmission. We do not account here for small tilt angles between the surface normal and the cavity axis employed in practice [17] to avoid multiple reflections. We give the phase-shift for a probe single-pass at normal incidence as it is sufficient here to illustrate the effect of frequency and angular dispersion associated with EIT on the light-drag.

The shift Df is a relativistic invariant and can be conveniently evaluated in the slab rest frame S ¢. Under EIT the dispersion equation for a probe polarized in the x¢y¢ plane is that of an extraordinary ray [19] whose complex refractive index is given by

with n^¢ and n^¢¢ respectively its real and imaginary parts. In the laboratory frame the single-pass phase shift, including contributions to first order in b, can be written as [7]

where Df₀ corresponds to the shift induced by a stationary slab and a_d represents the effective phase shift coefficient in terms of the probe laboratory frame frequency w. The usual definition [20] of the drag coefficient for the phase velocity of light can be related to the measurable quantity a_d [14]. Owing to EIT the absorptive part n^¢¢ only appears as a higher-order correction to Df and can therefore be neglected.

The magnitude and sign of the coefficient a_d can be controlled through the cleavage angle a and the coupling beam Rabi frequency W_c. In the following, we discuss numerical results for a resonant pump.

Fig.5 shows the variation of a_d as a function of W_c for a resonant probe. Notice that a_d vanishes at W_c 0.18 meV but can be as large as 17, that is over one order of magnitude larger than the a_d's of dragging glasses [17] typically used for high-precision measurements of the Fresnel-drag. This novel and important feature is due to the anisotropy and to the strong dispersion both characteristic of the EIT regime. Fig.6 shows instead the variation of a_d as a function of the probe detuning for fixed pump intensities. Because of EIT, transmission is quite large in the range |d_p| < 0.5 g_2P; for a slab thickness L = 25 mm this varies between 10 ¸ 30 % despite the 2P exciton resonance[6]. Apart from the background absorption, the 1S exciton linewidth g_1S is the material parameter that mostly limits the possibility of controlling the magnitude of a_d through EIT.

IV Cherenkov radiation in the EIT regime

The recent observation of ultraslow group velocities in coherently driven media [21,22,23] has opened the way towards new regimes of light propagation [24] and non-linear optics at very weak intensities [25]. Here, we investigate the effect of ultraslow group velocities on the Cherenkov radiation emitted by a charged particle uniformly moving with a velocity larger than the phase velocity of light. In the case of isotropic and non-dispersive media, the surface on which the intensity peaks coincides with the well known wave cone orthogonal to the wavevector of the emitted light and the aperture of which is determined by the usual Cherenkov coherence condition. In the case of highly dispersive media, as we show here, the intensity is instead peaked on the surface of a group cone [26] neither orthogonal to the phase nor to the group velocity of the emitted light and much narrower than the wave cone. First, we develop a general theory for Cherenkov emission in arbitrary dispersive and non-isotropic media from which we obtain analytical expressions for the electric field intensity profile and, in particular, for the group cone aperture. Then, as an example, we investigate the optical properties of an ultracold atomic cloud of ²³Na atoms in the EIT regime which appears to be amenable to the observation of such a singular behaviour.

Consider a charged point-like particle moving with constant velocity w = w = cb through a non-absorptive and homogeneous medium characterized by an anisotropic and dispersive hermitian dielectric tensor (w) = Î_i,j(w). The effects of a weak absorption will be considered afterward for the case of interest. Using Maxwell equations in Fourier space, we write the ( k,w) component of the radiated electromagnetic field E( k,w) in terms of the corresponding Fourier components of the current density J( k,w) = 2pq d(w- k· w) w as

where = d_i,j- is the projection operator onto the subspace orthogonal to k and k² = å_i k_i k_i is the square modulus of k.

The poles of (1) determine the propagating modes of the electromagnetic field through the well-known Fresnel equation [20]

For each wavevector k, the different modes are characterized by the frequency w_a and the polarization unit vector e^(a) normalized as áe^(a) | e^(a)ñ = å_ie^(a)*_ie^(a)_i = 1. We will not account here for longitudinal modes, assuming w²¹ 0 and det[(w)] ¹ 0 for all values of w. For each mode, the group velocity can be shown to be

This expression for v_g corresponds to the ratio of the Poynting vector S and the energy density u [20]. We shall also restrict our attention to the simple case of a medium with rotational symmetry around the direction of the charge velocity; in this case, the revolution symmetry of the dispersion surface w_a( k) = w guarantees the parallelism of the components of the group velocity and the wavevector perpendicular to the axis.

The electric field at a position x = ( x_^,z) = (x_^

_^,z) can be obtained from the inverse Fourier transform of (1). At sufficiently large distances from the charge trajectory, only the poles of (1) effectively contribute to the Fourier transform. In fact, the electric field at these distances is given by the resonant excitation of propagating modes, while the non-resonant contribution from all other modes decays out in space with a faster power law. In the electric dipole emission, a similar distinction is done between the near zone (kr << 1) and the radiation zone (kr >> 1). Within such an approximation we can write for the i^th component,

Here, = w/w is the direction of the charge velocity w and m_a = is a weight factor. In obtaining the expression (4) the angular integration in k_^ has been already performed in the large k_^ x_^ limit so that, for each position x_^, only the field components with k_^parallel to x_^ have a stationary phase and therefore give a nonvanishing contribution to the integral.

Depending on the velocity of the charged particle, for each direction

_^and frequency w, at most two distinct poles at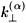 (a = 1,2) contribute to the integral, which correspond to propagating modes with wavevector k^(a) = (

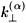_^,w/w) and polarization e^(a). As shown in Fig.7, at a given frequency w Cherenkov light is emitted into the mode a only if the k_z = w/cb plane has a non-vanishing intersection with the dispersion surface w_a( k) = w of the mode. In the case of a medium with rotational symmetry, this condition is satisfied if the particle velocity exceeds the phase velocity of mode a for k parallel to w, i.e.

and the intersection is the k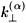_^ = circle. Here (w) are the eigenvalues of the dielectric constant in the plane perpendicular to the axis. For an isotropic medium, the condition (5) reduces to the usual Cherenkov condition b²Î(w) > 1 [27].

The theory developed up to now has considered the case of a non-absorptive medium for which the poles 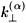are real; the effect of a weak absorption consists in the introduction of a small and positive imaginary part Im[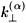] in the argument of the exponential in (4) without modifying the pole structure of the integral. The resulting damping factor e accounts for absorption of the emitted radiation during propagation.

We now consider a medium with a narrow transparency window centered at ; for a single polarization state a = 1, the absorption factor in the neighborhood of can be approximated by Im with h= ¶²Im[]/¶w². Inserting this expression into (4), we finally obtain an explicit expression for the electric field intensity profile

where e⁽¹⁾ is the polarization vector of the mode at frequency and A = . The radial velocity v_r is defined according to

where and are respectively the perpendicular and parallel components of the group velocity with respect to the direction = w/w of the charge velocity. As it can be observed in Fig.8, sufficiently far from the charge, i.e. at points x_^ >> x = h, the electric field intensity (6) is peaked on the group cone described by

whose aperture q is equal to

In general, q is different from the aperture f of the wave cone orthogonal to the wavevectors of the emitted radiation, which is instead given by tanf = / w . A simple physical interpretation of the group cone can be put forward in terms of group velocity [26] considering that, for each direction around the charge velocity, the burst of Cherenkov light is emitted into a group of modes centered at k⁽¹⁾ while the peak of the pulse moves in space with a velocity equal to the group velocity experiencing an almost negligible absorption. The cone defined by this geometrical construction (Fig.9) can be proven in all cases to be equivalent to the group cone defined by (8) and to coincide, for the case of an isotropic medium, with the group cone introduced by Frank [26]. Notice that this cone turns out to be in general neither orthogonal to the group velocity nor to the wavevector. In the case of isotropic and non-dispersive media, in which v_g = v_ph = , n being the refractive index, the group and the wave cones coincide and have an aperture f defined by the usual Cherenkov condition bn sinf = 1.

The weak dispersion of common dielectrics makes the difference between the group and the wave cones very small and has prevented upto now its experimental observation [26]. When the group velocity is much smaller than the phase velocity the group cone is expected to be well separated from the wave cone (fig.9) and to have an extremely narrow shape q << 1. Following the recent observations of ultraslow light in coherently driven hot [21,22] and cold [23] atomic gases, such media appear as promising candidates for the experimental characterization of the role of group velocity in Cherenkov radiation.

We consider a cloud of ultracold atoms in a three-level L-type configuration under EIT regime. In usual EIT experiments the effect of Doppler broadening in hot gases is overcome by choosing a dressing field co-propagating with the probe field [2]; unfortunately, the conical geometry of Cherenkov emission does not allow for such a choice, so that one is here forced to use an ultracold sample in which Doppler broadening is absent. We take, as a specific example, the case of ²³Na atoms (Fig.10) magnetically trapped in the M_F = -1 sublevel of the F_g = 1 ground state. Let w_g be the frequency of such a state. The other hyperfine component of the S_1/2 ground state is a metastable state with F_m = 2 approximately 1.8 GHz blue-detuned with respect to the ground state. A weak coherent field polarized along the trap magnetic field drives the optical transition from the metastable state to the F_e = 2 hyperfine component of the P_1/2 excited state. Its Rabi frequency W is smaller than the excited state linewidth g_e 2p·10 MHz while its frequency is taken to be exactly on resonance with the transition between the M_F = 0 Zeeman components w_dr = w_e[M_F = 0]-w_m[M_F = 0]. Assuming the charge velocity to be parallel to the trap magnetic field, the rotational symmetry of the system around the axis implies [28] the following decomposition of the dielectric tensor (w) = Î_z(w) |ñ á |+Î₊(w) | +ñ á₊ |+Î-(w) | -ñ á -|. For each frequency w and direction , the two propagating modes defined by (2) are generally non-degenerate except at high symmetry points and have elliptical polarizations; from the point of view of the spatial symmetry of the optical constants, the polarized atomic cloud is in fact not only uniaxial, but also optically active. Since the linewidth g_m of the metastable m state is orders of magnitude smaller [23] than that of the excited e state g_e, electromagnetically induced transparency (EIT) occurs on the ₊ polarization in a narrow frequency window of linewidth G = W²/g_e << g_e around w₊ = w_e[M_F = 0]-w_g [2] where absorption is quenched and dispersion enhanced so as to give slow light propagation. In the same frequency window w w₊, the transitions from the ground state to the M_F = -2,-1 sublevels of the excited state are sufficiently off-resonance (Dw_z,- = w_e[M_F = -1,-2]-w_e[M_F = 0] >> g_e) so as to give a positive and relatively frequency-flat background contribution to the - and components of the dielectric tensor

The oscillator strengths f_±,z are proportional to the atomic density times the square of the dipole moment of the optical transition and differ from each other depending on the relevant Clebsch-Gordan coefficients. The detunings Dw_z,- follow from the Zeeman splitting of the atomic levels, which implies that the background refraction can be experimentally controlled by tuning the magnetic field; with ²³Na atoms, a splitting Dw- of about 2p·40 MHz occurs in a reasonable magnetic field of the order of 80 G. Given the different magnetic moments of metastable and excited states, the weak dressing field can not effectively dress the optical transitions other than the resonant one between the M_F = 0 sublevels. Thanks to their large detuning with respect to w₊, all transitions involving the other hyperfine components of the excited state can be neglected.

The threshold velocity (5) for Cherenkov emission at w₊ is determined by the background refractive index (11). If the velocity is larger than the threshold value, light is radiated into a mode with non-vanishing ; in presence of EIT, such a radiation will propagate with ultraslow group velocity without being absorbed. The magnitude of the group velocity (3) is mainly determined by the dispersive properties of EIT while its direction depends on the background refractive index only. Group velocities as low as 17 m/sec have been reported in an ultracold sodium gas [23] and this means that the group cone would have an extremely narrow shape, practically a cylindrical one (q << 1). From the parameters of [23], the characteristic length turns out of the order of 10 mm and the background susceptibility is of the order of 10^-2, i.e. much larger than that usually found in gas Cherenkov counters [27].

The theory we have developed is based on the assumption of a homogeneous medium. This approximation is reasonable provided the overall size of the atomic cloud is much larger than the wavelength of the Cherenkov light whose detection should be performed within the cloud itself so to avoid reflection effects at the edges of the cloud. For the case of EIT media, a picture of the group cone can be taken exploiting the very large cross section for resonant two-photon absorption processes [30]: the absorption coefficient experienced by a laser field on resonance with another optical transition starting from the M_F = 0 sublevel of the metastable m state is in fact proportional to the local intensity of the Cherenkov radiation at w₊ which forms the narrow group cone [25]. Since the interaction of the charge with the atoms of the cloud results not only on Cherenkov emission but also on other heating and ionization processes [20], it is necessary to reduce the importance of such short-range processes by making the charge travel in a region of space free from atoms. For the case of an atomic cloud, this can be achieved e.g. by using the repulsive potential of a blue-detuned laser so as to create a sort of "tunnel" through the cloud; a small cylindrical hole with a radius of the order of the wavelength does reduce the yield of the Cherenkov radiation, but does not affect the qualitative features of the Cherenkov pulse propagating in the surrounding medium [29]. Unfortunately, the intensity of the Cherenkov radiation emitted by a single electron is rather low. For the ²³Na parameters and statistically independent electrons, a photon is emitted in the mode under consideration each 10⁷ electrons. This problem may be overcome by looking at the electric field generated by a very large number of electrons at a time: since the radial velocity v_r is much smaller than the charge velocity w, the profile of the group cone would not be smeared out even if the spatial extension of the bunch of electrons is much longer than the wavelength of the emitted light.

Unlike in isotropic and non-dispersive media, the group cone is here much narrower than the wave cone defined by the usual Cherenkov coherence condition and is neither orthogonal to the phase nor the group velocity. This conceptual distinction becomes of great physical relevance in media exhibiting slow light propagation. For the realistic case of a coherently driven ultracold ²³Na gas, the geometrical and dispersive properties of the dielectric tensor are shown to be favourable to the experimental characterization of the role of the group velocity in the process of Cherenkov emission.

References

[1]G. Alzetta, A. Gozzini, L. Moi, G. Orriols, Nuovo Cimento B36, (1976) 5; E. Arimondo, G. Orriols, Lett. Nuovo Cimento 17, (1976) 333.

[2]S. Harris, Physics Today 50, (1997) 36; E. Arimondo, Progress in Optics XXXV, Ed. E. Wolf (Elsevier Science, Amsterdam 1996) 257; and references therein.

[3]A. Aspect, E. Arimondo, R. Kaiser, N. Vansteenkiste, C. Cohen-Tannoudji, Phys. Rev. Lett. 61, 826 (1988).

[4]A.S. Zibrov, M.D. Lukin, D.E. Nikonov, L. Hollberg, M.O. Scully, V.L. Velichansky, H.G. Robinson, Phys. Rev. Lett. 75, 1499 (1995).

[5]K. Bergmann, H. Theuer, B.W. Shore, Rev. Mod. Phys. 70, 1003 (1998).

[6]M. Artoni, G.C. La Rocca and F. Bassani, EuroPhys. Lett.s 49, (2000) 445.

[7]M. Artoni, I. Carusotto, G.C. La Rocca, F. Bassani, Phys. Rev. Lett, 86, 2549 (2001).

[8]Y. Zhao, C. Wu, B. S. Ham, M. K. Kim, and E. Awad, Phys. Rev. Lett. 79, (1997) 641.

[9]G.B. Serapiglia, E. Parpalakis, C. Sirtori, K.L. Vodopyanov, C.G. Phillips, Phys. Rev. Lett. 84, (2000) 1019.

[10]B. S. Ham, M. S. Shahriar, and R.P. Hemmer, Opt. Lett.s 22, (1997) 1138; K. Ichimura, K. Yamamoto, and N. Gemma, Phys Rev. A 58, (1998) 4116.

[11]S. Nikitine, J.B. Grun, M. Sieskind, J. Phys. Chem. Solids 17, (1961) 292; Landolt-Börnstein, series III, 17 (Semiconductors), (Springer, Berlin, 1984).

[12]D. Fröhlich, A. Nothe, and K. Reimann, Phys. Rev. Lett. 55, (1985) 1335; D. Fröhlich, Ch. Neumann, B. Uebbing and R. Wille, phys. stat. sol. (b) 159, (1990) 297.

[13]F. Bassani and G. Pastori Parravicini, Electronic States and Optical Transitions in Solids (Pergamon Press, Oxford 1975); P. Yu and M. Cardona, Fundamentals of Semiconductors (Springer, Berlin 1996).

[14]M. Artoni et al., to be published.

[15]A. Fresnel, Ann. Chim. Phys. 9, 57 (1818).

[16]H. Fizeau, C. R. Acad. Sci. B 33, 349 (1851).

[17]G.A. Sanders et al., J. Opt. Soc. Am. B, 5, 674, (1988).

[18]W. Macek et al., J. Appl. Phys. 35, 2556 (1964).

[19]M. Born and E. Wolf, Principles of Optics, (Pergamon Press, Oxford 1993)

[20]L.D. Landau and E.M. Lifschitz, Electrodynamics of continuous media, (Nauka, Moscow 1982)

[21]M. M. Kash et al., Phys. Rev. Lett. 82, 5229 (1999)

[22]D. Budker , D. F. Kimball, S. M. Rochester, and V. V. Yashchuk, Phys. Rev. Lett. 83, 1767 (1999)

[23]L. V. Hau, S. E. Harris, Z. Dutton, and C. H. Behroozi, Nature 397, 594 (1999)

[24]D. F. Phillips et al., Phys. Rev. Lett. 86, 783 (2001); C. Liu, Z. Dutton, C. H. Behroozi, and L. V. Hau, Nature, 409, 490, (2001).

[25]G. S. Agarwal and W. Harshawardhan, Phys. Rev. Lett. 77, 1039 (1996); S. E. Harris and L. V. Hau, ibid. 82, 4611 (1999); H. Schmidt and A. Imamoglu, Opt. Lett. 21, 1936 (1996).

[26]I. M. Frank, Nucl. Instr. Meth. A 248, 7 (1986) and references therein

[27]J. V. Jelley, Cherenkov radiation and its applications, Pergamon Press, London (1958).

[28]J. F. Cornwell, Group theory in physics, Academic Press, London, 1994

[29]V. L. Ginsburg and I. M. Frank, Dokl. Akad. Nauk SSSR 56, 699 (1947); L. S. Bogdankevich and B. M. Bolotovskii, Zh. Exsp. Teor. Fiz. 32, 1421 (1957)

[30]S. E. Harris and Y. Yamamoto, Phys. Rev. Lett. 81, 3611 (1998);

Publication Dates

• Publication in this collection
  26 Nov 2002
• Date of issue
  June 2002

History

• Received
  23 Apr 2001