Cooper pairing and superconductivity in a spin fluctuation model for high-Tc cuprate superconductors

a08v32n3

Cooper Pairing and Superconductivity in a Spin Fluctuation Model for High-T_c Cuprate Superconductors

Eduardo C. Marino and Marcello B. Silva Neto

Instituto de Física, Universidade Federal do Rio de Janeiro,

Caixa Postal 68528, Rio de Janeiro - RJ, 21945-970, Brazil

Received on 28 February, 2002

We study the formation of Cooper pairs in high-T_c cuprate superconductors within a spin uctuation model for doped quantum Heisenberg antiferromagnets. The charge of the dopants (chargons) is associated to quantum skyrmion excitations of the Cu⁺⁺ antiferromagnetic spin background. We then compute the quantum skyrmion e effective interaction potential as a function of doping and temperature in order to study charge pairing. It becomes clear that Cooper pair formation is determined by the competition between the spin uctuations of the Cu⁺⁺ magnetic ions and the spins of the O^-- doped holes (spinons). The superconducting transition occurs when the effective potential allows for skyrmion bound states. Our theoretical predictions for the superconducting phase diagram of La_2-x Sr_xCuO₄ andYBa₂ Cu₃O_6+xare in good agreement with experiment.

I Introduction

Strongly correlated electron systems have been the object of intense studies, both theoretical and experimental, after numerous indications that the high temperature superconductivity, discovered in cuprate perovskites [1], arises from the doping of a Mott-Hubbard antiferromagnetic insulator. The strong correlating system deviates significantly from the usual Fermi liquid and a number of anomalies are observed in the so called underdoped regime. Among the most interesting ones are: Néel and metal-insulator transitions, linear dependence of the resistivity with temperature [2], the reduction of the density of states previous to superconductivity (pseudogap) [3], different responses for the optical probes of the spin and charge degrees of freedom (spin-charge separation) [4], etc., which have inspired a large amount of theoretical and experimental work for about fifteen years. In spite of that, even the nature of the ground state and of its elementary excitations have not yet been fully determined and many different pictures are available, ranging from a resonating liquid of spin singlets (Anderson's RVB) [4] until the recent proposed staggered flux phase (SF-phase) of Wen and Lee [5].

One of the most fundamental points yet to be understood is the mechanism of charge pairing. It is by now well established that antiferromagnetic spin correlations play an important role in the dynamics of the system, even after the destruction of the Néel state. Indeed, different spin-fluctuation models have been successfully used to explain the observed spectral weight in ARPES data of high-T_c materials [6], as well as other anomalies [7]. Moreover, the idea of spin-fluctuation induced charge pairing and superconductivity has been used recurrently [8].

In this work we propose a theory for high-T_c cuprates that takes into account the spin fluctuations of the Cu⁺⁺ magnetic ions and of the O^-- doped holes as independent degrees of freedom. The charge of the dopants (chargons) is associated to skyrmion quantum spin excitations of the Cu⁺⁺ background, which in the Néel phase are finite energy defects closely related to their classic counterparts whereas in the quantum disordered phase are nontrivial zero energy purely quantum mechanical excitations. The spin of the doped holes (spinons), on the other hand, is represented by chargeless, massless Dirac fermion fields [9]. We calculate the effective interaction potential between these quantum skyrmion topological excitations in order to study charge pairing. It becomes clear that Cooper pairing is controlled by the competition between the spin fluctuations of Cu⁺⁺ magnetic ions and those of the O^-- doped holes. Our predictions for the T_c line are in good agreement with experiment for both La_2-xSr_xCuO₄ and YBa₂Cu₃O_6+x.

II The model

It is generally accepted that the relevant electronic degrees of freedom in the perovskites are confined to two dimensions and reside in Copper-Oxide planes [10], like the one shown in Fig. 1. Our starting point will then be the generalized spin-fermion model described by the square lattice Hamiltonian

which arises from the strong coupling limit of the three band Hubbard Model (3BHM) [11]. In the above expression,

_i represent the localized spins of Copper ions, which interact through the superexchange J,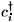 _,a, a = 1..N = 2, is the hole creation operator, t_p is the hopping term for holes, J_K is a Kondo like coupling between the spins of Cu⁺⁺ ions and the spins of O^-- holes, and we have retained the usually ignored onsite Coulomb repulsion between O^-- holes, U_p ¹ 0 with n_i,a = 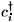,ac_i,a. Since realistic estimates from the 3BHM suggest that U_p/t_p ~ 10 [12], being rather large, and thus we can perform a t_p/U_p expansion. Second order perturbation theory in t_p/U_p will give rise to a superexchange J_p = 2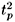/U_p between oxygen spins and we end up with a t-J model for the holes.

The mean field (large N) solutions of the t-J model are well known and it has been established that a p-flux phase has minimum energy, at least at the saddle-point level (N® ¥) [9]. We can write the electron in terms of a charged spinless boson m_i (chargon) and a chargeless spin-1/2 fermion f_i,a (spinon),

in such a way that the above object has exactly the same quantum numbers as the electron. We decouple the four particle interactions by introducing the d-wave auxiliary fields

which acquire a nonzero expectation value for

T <

T

^*, where

T

^* is the so called pseudogap temperature.

In terms of the new degrees of freedom, m_i and f_i,a, we see that the Hilbert space is twice as large as in the original t – J Hamiltonian. Furthermore, the resulting Hamiltonian has an extra Z₂ (Ising) symmetry [13] since now each piece is invariant under a change of sign in both the chargon and spinon fields

We shall then impose a constraint in order to account for the above discussed facts. We can write

where

N ³ 0 is an even number. With this constraint the only possible states in the Hilbert space are: a)

N = 0, no chargons and no spinons (a hole); b)

N = 2, one chargon and one spinon (one electron), or two chargons and no spinons (one Cooper pair), or no chargons and two spinons (a spin singlet); c)

N > 2, N chargons and no spinons (

N/2 Cooper pairs), or two spinons and

N-2 chargons (one spin singlet and (

N-2)/2 Cooper pairs). It is clear how the extra

Z

₂ symmetry forbids states with a single chargon and no spinon, and vice versa, since all physical states must be

Z

₂ invariant.

If we then neglect charge fluctuations, á m_i ñ |m_i|² = const., and if we recall that the order parameter D_ij has d-wave symmetry, thus vanishing linearly along the four Dirac points (±p/2,±p/2), we find that the lowest lying excitations of the p-flux phase are massless, chargeless, spin carrying Dirac Fermi fields [9] whose dynamics is described by the Lagrangian

where 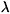= 1,2 label the only two inequivalent Fermi points at (p/2,±p/2) (see Fig. 2), ¶_m = (¶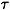,), g_m = (g₀,) = (is_z,s_x,s_y), v_F = 2ac is the dopant Fermi velocity (with a being the lattice spacing and c the constant amplitude of |c_ij|) and

o)dd and (

e)ven lattice sites.

The long wavelength fluctuations of the localized Cu⁺⁺ spins, on the other hand, are described by the CP^N-1 Lagrangian [14,15]

where =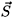

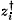
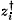_ij z_j, with ,z_i, i = 1..N = 2, being Schwinger boson fields such that 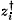z_i = 1, 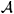_m = – i

_i¶_mz_i, 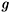₀ is a bare coupling constant, and we are using units where c = 1. It is now convenient to perform the local canonical transformation y® Uy, where

is a

SU(2) matrix, and

q is arbitrary. Now the Kondo coupling term in (1) reduces to a chemical potential term, since

U

^†

·

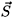
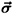
U = s

_z. Also, since

U

^†¶

_m

U = i

qs

_z

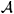
m+ negligible nondiagonal terms, we end up with the effective theory

where

where b = 1/

k_BT and we have set, for now,

v

_F = 1.

III Chargons as quantum skyrmions

In previous works [16], we have proposed a model for doping quantum Heisenberg antiferromagnets, that successfully described the magnetization curves and the AF part of the phase diagrams of both LSCO and YBCO. One of the important consequences of that model was the observation that each hole added to the CuO₂ planes creates a skyrmion topological defect on the Cu⁺⁺ spin background, in agreement with earlier proposals [17]. The dopant charge, in particular, was found to be attached to the skyrmion charge and consequently its dynamics becomes totally determined by the quantum skyrmion correlation functions. Despite the fact that the model proposed in [16] is restricted to the antiferromagnetic part of the phase diagram, we shall nevertheless pursue the picture in which skyrmions are in general the charge carriers of the doped holes. This will allow us to treat the bosonic variable m_i introduced above as a quantum skyrmion operator. In particular, we shall exploit this idea in the quantum disordered phase, d ³ d_AF, where the skyrmions are purely quantum mechanical and have zero energy (d is the in-plane doping parameter).

The full treatment of the quantum skyrmions of the theory described by (11) has been carried out in [18]. In the renormalized classical regime,

₀ <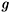 _c (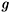_c = 8p/L), we have

where r_s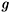 = 1/₀-1/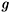_c and q is the spinon coupling. Conversely, for the theory studied in [16] the corresponding correlator was found to be

where the expressions for r

_s(d) and a(d) have been carefully determined in [16]. In particular,

with

n = 1 for YBCO and

n = 4 for LSCO, the factor of four being a consequence of the existence of four branches in the Fermi surface for this compound, as discussed in [16]. In the above expression a

_EM is the electromagnetic fine structure constant and we see that the contribution from the electromagnetic coupling is negligible. In this sense, we shall assume a

_EM = 0 in all the subsequent calculations.

The r_s(d) function is given by r_s(d) = r_s(0)[1 - Ad²], for YBCO and r_s(d) = r_s(0)[1 - Bd- Cd²]^1/2, for LSCO, and again the different behavior being ascribed to the form of the Fermi surface in each case [16]. The constants A,B and C have been evaluated from first principles in [16]. In order to obtain the d-dependence of the spin stiffness r_s and of the spinon coupling q in our model (11), we now match the two correlation functions in (12) and (13) (ordered phase), obtaining r_s = r_s(d) and

The sublattice magnetization in the ordered phase is given by M(d) = , and consequently d_AF can be obtained from r(d_AF) = 0, both in good agreement with experiment, see [16]. For d > d_AF, on the other hand, where r_s = 0, we shall assume that the expression for q(d) still holds. This is quite reasonable since q was introduced by a local canonical transformation, and at least locally there still is short range AF order.

IV Cooper pair formation

Let us now investigate the conditions for Cooper pairing. We shall first introduce in the partition function (10) the skyrmion current, 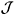m = ^mab¶_a

_b, through the identity

Integrating over 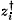,z_i and _a,y_a, we obtain, at leading order, the effective Lagrangian

where P

^mn(

x-

y,

-

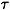
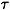
^¢) has Fourier transform given by P

^mn(

p,iÎ

_m) = P

(

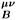
p,

iÎ

_m)+P

(

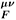
p,

iÎ

_m), which are respectively the contributions to the finite temperature vacuum polarization coming from the complex scalar fields

z_i (Schwinger bosons) and fermions y

_a,

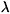
(spinons), see

Fig. 3.

In order to obtain the effective current-current interaction between skyrmions, we use an exponential representation for the d-function in (16) and integrate over

_m and the corresponding Lagrange multiplier field. The result is

where S^mn(p) = P^mn(p)/ p², x = (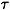,x) and p = (iÎ_m,p). The real time effective interaction energy between static skyrmions (Î_m = 0) is then

where r(

x) =

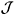
₀(

x) is the dopant charge density and S

⁰⁰(

x-

y;0) has Fourier transform given by S

⁰⁰(

p) = P

_B(

p)+P

_F(

p) with

and

In the above expressions, m is the inverse correlation length of the quantum disordered phase of the CP^N-1 model, where

and r_s = 0. At order N, it is given exactly by [15]

For two charges at positions x₁ and x₂, we have r(x) = d⁽²⁾(x–x₁)+d⁽²⁾(x–x₂). After discarding self-interactions, we obtain (r = x₁– x₂)

where we have also introduced the centrifugal barrier potential between the two charges that form the Cooper pair,

with

l specifying the relative orbital angular momentum of the pair and

M

^* the effective mass of the charges.

IV.1 Determination of d_SC

It is well known that in high-T_c cuprates, Cooper pairs form at relatively short distances. In this limit, large |p|, we have, at T = 0

The above expression clearly shows a competition between the spin fluctuations of the Cu⁺⁺ spins (first term) and of the O^-- doped spins (second term). For small enough doping, q² < 1/2, the potential is always repulsive and there is no charge pairing. For q² > 1/2, on the other hand, the potential has a minimum and charge (skyrmion) pairing occurs. We conclude that the critical doping for the onset of superconductivity is determined by the condition q²(d_SC) = 1/2. We observe that without the Cu⁺⁺ background, the interaction potential (26) would always have bound states for any q ¹ 0, at zero temperature, and d_SC = 0. This is what happens in the mean field phase diagram of Kotliar and Liu [19]. We see that the effect of the Cu⁺⁺ background is to shift the value of d_SC to its correct position in the phase diagram.

From expression (15) we see that d_SC is only determined by the geometry of the Fermi surface of the compound. Using that q²(d_SC) = 1/2 we get d = 0.318 and d = 0.079, which have a fairly good agreement with experiment. In particular, we see that d = 4d, a result that is verified by experiments, if we take in account the relation between d and the stoichiometric doping parameter x, namely d = x for LSCO and d = x-0.20 for YBCO. Another prediction of our model is that compounds with similar Fermi surfaces should have the same superconducting critical doping d_SC.

IV.2 Disorder

We can improve even further our agreement with experimental data for d_SC by considering disorder in the bonds of the Cu⁺⁺ antiferromagnetic lattice. In fact, disorder may be modelled in the ordered Néel phase of a doped antiferromagnet by considering a continuous random distribution of spin stiffnesses [20]. The effect of introducing a Gaussian×|r- r_s|^n-1 distribution, with exponentially suppressed magnetic dilution, in the original model [16], is a correction for a(d), namely a(d) ® a¢(d) = a(d) + n [20], and consequently we end up with

Choosing n = for both compounds, we get d_SC = , or equivalently x = 0.425 and x = 0.056, in good agreement with experiment.

IV.3 The superconducting transition line T_SC

The computations at finite temperature are a bit more involved. Since the integrals over the Feynman parameters in (20) and (21) can not be solved exactly, we shall make use of some temperature expansions. For P_B we shall expand in k_BT / m, since it is clear that m(T) > k_BT,"T. P_B will then be simply given by its zero temperature limit, where m = D. For P_F, on the other hand, such a low T expansion is not necessarily valid even for |p| k_BT. We will then have to split the integral over the Feynman parameter x in (21) into three parts. For 0 £ x £ x_c and 1-x_c £ x £ 1, x_c = (k_BT/|p|)², we use a high T expansion, while for x_c £ x £ 1-x_c we use the low T expression. We obtain

Inserting this in (24), we get V(r), and from the threshold conditions for the formation of bound states, namely V^¢(r₀) = 0 and V^¢¢(r₀) = 0, we obtain the relation

where a =

v_F/r₀, m = D, and r₀ is the minimum of the potential (it also measures the size of the Cooper pair).

V Comparison with experiment

In order to make contact with experimental data we need the doping dependence of D. For YBCO, we use D(d) = D₀[(d/d_AF)²-1], in agreement with the results of [16], with D₀ = 8.0 meV. For LSCO, we shall use an expression that fits the experimental data of [21], namely D(d) = D₀[(d/d_AF)²-1]^1/2, with D₀ = 0.87 meV. For the T = 0 AF quantum critical point d_AF, we know from experiments that d_AF = 0.22 for YBCO and d_AF = 0.02 for LSCO. Inserting in (29) the values of d_SC at T = 0, obtained previously, we get a relation that fixes M^* with respect to r₀. In Figs. 4 and 5 we plot the curve (29) for LSCO and YBCO, respectively, with r₀ = 38 &Aring, v_F = 0.1 eV Å for LSCO and v_F = 1.15 eV Å for YBCO, and l = 2 (d-vave pairing).

In Fig. 4 (LSCO), the dashed part is in the region where T > T^* and we should move to a new saddle-point. In Fig. 5 (YBCO) we have shifted the curve (dashed part) to the right in the regions x = [0.52,0.7] and x = [0.8,1] in order to comply with the effects of the out-of-plane O-Cu-O chains, which produce the observed 60 K and 90 K plateaus, where the extra holes do not enter in the CuO₂ planes. Furthermore, for YBCO, T^* is higher than T_max (x = 1) and therefore imposes no restrictions to our results.

VI Final remarks

We would like to remark that our theory (11) also gives a simple interpretation for the pseudogap phenomena. Indeed, for T_SC < T < T^* spinons are paired into d-wave singlets but chargons (skyrmions) repel each other and there is no superconducting state. Only for T < T_SC we do have Cooper pair formation and superconductivity.

Acknowledgements

The authors would like to acknowledge E. Miranda for useful comments. This work has been supported in part by FAPERJ and PRONEX - 66.2002/1998-9. E. C. M. was partially supported by CNPq and M. B. S. N. by FAPERJ.

References

[1] J. G. Bednorz and K. A. Muller, Z. Phys. B 64, 189 (1986).

[2] B. Batlogg, H. Takagi, H. L. Kao, and J. Kwo, in Electronic Properties of High-Tc Superconductors. The Normal State and The Superconducting State, Kuzmany et al., eds., (Springer-Verlag, Berlin/Vienna/New York) 1992.

[3] T. M. Rice, in Physics and Chemistry of Oxide Superconductors, Y. Iye and H. Yasuoka, eds., (Springer-Verlag, Berlin/New York) 1992.

[4] P. W. Anderson, in The Theory of Superconductivity in the High-Tc Cuprate Superconductors, Princeton University Press (1997).

[5] X-G. Wen and P. A. Lee, Phys. Rev. Lett. 76, 503 (1996).

[6] W. Ranter and X-G. Wen, Phys. Rev. Lett. 83, 3871 (2001); M. Franz and Z. Tesanovic, Phys. Rev. B 63, 064516 (2001).

[7] A. V. Chubukov and J. Schmalian, Phys. Rev. B 57, R11085 (1998); J. Schmalian, D. Pines and B. P. Stojkovi, Phys. Rev. Lett. 80, 3839 (1998).

[8] T. Moriya, K. Ueda, and Y. Takahashi, J. Proc. Soc. Jpn. 49, 2905 (1990); P. Monthoux, A. Balatsky, and D. Pines, Phys. Rev. Lett. 67, 3448 (1991); T. S. Nunner, J. Schmalian, and K. H. Bennemann, Phys. Rev. B 59, 8859 (1999).

[9] J. B. Marston and I. Affleck, Phys. Rev. B 39, 11538 (1989); X-G. Wen and P. A. Lee, Phys. Rev. Lett. 76, 503 (1996).

[10] Y. Iye, in Physical Properties of High Temperature Superconductors III, D. M. Ginsberg, eds., (World Scientific, Singapore), p. 285, 1989.

[11] V. J. Emery, Phys. Rev. Lett. 58, 2794 (1987).

[12] A. P. Kampf, Phys. Rep. 249, 219 (1994).

[13] T. Senthil and M. P. A. Fisher, Phys. Rev. B 62, 7850 (2000).

[14] A. V. Chubukov, S. Sachdev, and J. Ye, Phys. Rev. B 49, 11919 (1994).

[15] O. Starykh, Phys. Rev. B 50, 16428 (1994).

[16] E. C. Marino, Phys. Lett. A 263, 446 (1999); E. C. Marino and M. B. Silva Neto, Phys. Rev. B 64, 092511 (2001).

[17] P. B. Wiegmann, Phys. Rev. Lett. 60, 821 (1988); B. I. Schraiman and E. Siggia, Phys. Rev. Lett. 61, 467 (1990); R. J. Gooding, Phys. Rev. Lett. 66, 2266 (1991).

[18] E. C. Marino, Phys. Rev. B 61, 1588 (2000).

[19] G. Kotliar and J. Liu, Phys. Rev. B 38, 5142 (1988).

[20] E. C. Marino, Phys. Rev. B 65, 054418 (2002).

[21] B. Keimer et al., Phys. Rev. B 46, 14034 (1992).

[22] P. Burlet, et al., Dynamics of Magnetic Fluctuations in High-Tc Superconductors, NATO, ASI Series, Plenum, NY (1991).

Publication Dates

• Publication in this collection
  04 Dec 2002
• Date of issue
  Sept 2002

History

• Received
  28 Feb 2002