Abstract
This is a short review of the derivation of the spectrum of the Dirac operator in QCD4 in a finite volume V by means of the replica trick. The derivation is nonperturbative in the QCD coupling and it is in agreement with lattice results as well as chiral random matrix theory (ChRMT). Our results hold in the energy scale where chiral symmetry is broken and the Pion wavelength is much bigger than the size of the system (<IMG SRC="/img/fbpe/bjp/v32n4/a11img02.gif">pi >>> V ¼).
The Spectrum of  in QCD via Replicas
in QCD via Replicas
D. Dalmazi
UNESP, Campus de Guaratinguetá, DFQ
Av. Dr. Ariberto Pereira da Cunha, 333
CEP 12500-000, Guaratinguetá, SP, Brazil
Received on 15 January, 2002
This is a short review of the derivation of the spectrum of the Dirac operator in QCD4 in a finite volume V by means of the replica trick. The derivation is nonperturbative in the QCD coupling and it is in agreement with lattice results as well as chiral random matrix theory (ChRMT). Our results hold in the energy scale where chiral symmetry is broken and the Pion wavelength is much bigger than the size of the system (
p >>> V 1/4).
I Introduction and motivation
In this section we will recall some basic properties of the spectrum of the Dirac operator in QCD4 and explain why is it interesting to study such operator, for a review paper see [1]. First, let us start from the partition function of QCD4 in Euclidean space which corresponds to integrate over the gluons and Nf flavors of quarks.
where SYM represents the Yang-Mills action for the gluons and
The formulas in this section and in the next one hold for arbitrary integer Nf and Nc . In Euclidean space all gamma matrices can be chosen Hermitean and therefore the Dirac operator is anti-Hermitean and its eigenvalues are pure imaginary numbers which show up in pairs 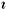
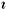 k due to g5
k due to g5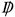 =
= 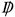 g5 . That is,
g5 . That is,
The pairing across the origin
k = 0 guarantees the definite-positiveness of the partition function which will allow us to use the Vaffa-Witten theorem [2] to derive the chiral symmetry breaking pattern. Positiveness of the partition function can be easily seen as follows,
In D = 3 we do not have such a pairing of eigenvalues since there is no g5, consequently the partition function for QCD3 does not have a definite sign in general [3,4]. For even Nf one can choose half of the masses as parity reflected (negative sign) to the other half such that we still have a definite sign for the partition function.
¿From the above we already see that the origin of the spectrum plays a special role. Such zero eigenvalues are closely related to chiral symmetry which is the main motivation to study the spectrum of the Dirac operator. More precisely, one can find a direct relation between spontaneous chiral symmetry breaking and the density of zero eigenvalues. Before we get there we first recall how spontaneous symmetry breaking can occur in the simpler example of the 2D Ising model in a external magnetic field since the situation is very similar to QCD.
The partition function of the Ising model is given by a sum over all spin configurations on each site of the lattice, i.e.,
Where J > 0 and H are constants and we have only two possibilities for the spin on each site si = ±1. Without magnetic field H = 0 we have a Z2 symmetry si® si since the nearest neighbor interaction is quadratic. Turning on the magnetic field we break explicitly the Z2 symmetry however we expect that in the limit H® 0 we recover it. It turns out that this is not the case and at low temperatures, even without magnetic field, all the spins line up and the up/down Z2 symmetry is broken in the vacuum although the Hamiltonian is Z2 symmetric in the limit H® 0 . We can measure the amount of spontaneous symmetry breaking by computing the magnetization :
It is assumed that we first take the thermodynamic limit N® ¥ then H® 0. Whenever m ¹ 0 the Z2 symmetry is spontaneously broken. In QCD4 the role of the magnetic field is played by the mass of the quarks m whose term breaks the chiral symmetry explicitly. The role of the magnetization is played by the chiral condensate <  f y f > :
f y f > :
Once again we take V ® ¥ before m ® 0 . If <  f y f > ¹ 0 the chiral symmetry is broken spontaneously. Next we derive a direct relation between the chiral condensate and the spectral density of the Dirac operator in QCD4. As a first step we derive the partition function w.r.t. the quark mass,
f y f > ¹ 0 the chiral symmetry is broken spontaneously. Next we derive a direct relation between the chiral condensate and the spectral density of the Dirac operator in QCD4. As a first step we derive the partition function w.r.t. the quark mass,
Now using the following representation of Dirac delta function,
delta function,
and the definition of the average macroscopic spectral density r(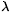 ) :
) :
It is a simple exercise to prove the following direct relation between spontaneous chiral symmetry breaking and the spectrum of the Dirac operator [5] :
From (6 ) we see that in order to have spontaneous chiral symmetry breaking we must have a non-vanishing average spectral density at the origin of the spectrum. Henceforth we will be interested in calculating the spectral density of the Dirac operator close to the origin of the spectrum in order to compare with similar results obtained in lattice [7] QCD and through ChRMT [1]].
II Partial quenching
As a first step it is convenient to write the average spectral density as a discontinuity equation as in (4), i.e.,
Notice that the probe mass z in the last equation is different from the original quark masses m. The mass z is called valence quark mass. In order to obtain the spectral density we just have to calculate S(z) defined below
Now the question is: How do we obtain S(z) ? By using the mathematical identity:
there are at least three different ways to proceed by introducing extra vallence quarks as we explain in the next three subsections.
II.1 Supersymmetric Method
Introducing two extra vallence quarks of opposite statistics in the partition function:
we can obtain S(z) using (8),
Each method has its own advantages and problems and they all depend on a convenient choice of parametrization of the manifold of the relevant degrees of freedom. The supersymmetric method becomes cumbersome for higher point spectral densities and requires an extension of the chiral symmetry breaking pattern to the supersymmetric case but it furnishes [6] nonperturbative results (in the valence quark mass z ) which are in full agreement with lattice [7] simulations and the ChRMT (see [1]). To learn more about this method see the book [8].
II.2 Bosonic replicas
In this case we introduce an arbitrary number of extra bosonic quarks with the same mass z, called replicas [9,10] , as follows:
And obtain S(z) by means of the replica limit n ® 0 :
II.3 Fermionic replicas
This case is similar to the last one, but instead of bosonic replicas we now add an arbitrary number of fermionic quark replicas,
and take again the replica limit,
Both replica methods can only be used, in general, perturbatively in the vallence quark mass z. It turns out that bosonic replicas do not work [11]. Mathematically, the reason for the failure is the lack of a replica symmetry breaking saddle point to expand around. From now on we will concentrate on the use of fermionic replicas. From (9) we see that all we need is the extended partition function Zn+Nf(z,m) . We need to know the partition function at low energies where chiral symmetry is broken. This is the subject of the next section.
III Low-energy QCD
When a continuum symmetry G is broken down to a subgroup H spontaneously, then Goldstone theorem establishes that massless bosons would appear in the spectrum and the number of such bosons is the same number of generators of the algebra of the coset G/H . On the other hand, it is believed that chiral symmetry is broken spontaneously in QCD at low-energy. Since at low-energy (large distances) we expect the lightest particles to play a major role, it is natural from the above to expect that the Goldstone bosons are the relevant degrees of freedom in low-energy QCD. In practice however we should take into account that chiral symmetry is only an approximate symmetry of QCD because the quarks are massive so the low-energy theory should also depend on the quark masses and in a way that it reproduces the covariance properties of the QCD partition function under changes of the mass matrix. Assuming also Lorentz covariance and the existence of the theta vacuum one can arrive at the chiral effective Lagrangian below ( see [12,13]) at leading order in a derivative expansion,
Where 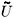 Î G/H , the quantity F is the pion decay constant and
Î G/H , the quantity F is the pion decay constant and  is the infinite volume limit of the chiral condensate. The quark mass matrix M is in principle, without replicas, a Nf× Nf matrix. The coset G/H depends on the fermion representation and on the number of colours, For instance, for fermions in the fundamental representation and Nc ³ 3 , i.e., for the Dyson index b = 2 , the QCD action in the chiral limit m ® 0 is invariant under independent global rotations of left and right-handed fermions which leads to a UL(Nf) × UR(Nf) , however when all the angles of the rotation are equal we have a U(1) transformation which is known to be broken by the chiral anomaly, thus reducing the quantum axial symmetry to SUL(Nf) × SUR(Nf) . If the chiral condensate is nonvanishing the chiral symmetry is broken down to the subgroup of rotations which are equal to left and right-handed fermions, i.e., vector SU(Nf) since those cannot be broken spontaneously according to the Vafa-Witten theorem. Therefore we end up with the coset (SUL(Nf) × SUR(Nf))/SU(Nf) which is equivalent to G/H = SU(Nf). The other cases b = 1,4 can be similarly derived (see [13] for a clear derivation ).
is the infinite volume limit of the chiral condensate. The quark mass matrix M is in principle, without replicas, a Nf× Nf matrix. The coset G/H depends on the fermion representation and on the number of colours, For instance, for fermions in the fundamental representation and Nc ³ 3 , i.e., for the Dyson index b = 2 , the QCD action in the chiral limit m ® 0 is invariant under independent global rotations of left and right-handed fermions which leads to a UL(Nf) × UR(Nf) , however when all the angles of the rotation are equal we have a U(1) transformation which is known to be broken by the chiral anomaly, thus reducing the quantum axial symmetry to SUL(Nf) × SUR(Nf) . If the chiral condensate is nonvanishing the chiral symmetry is broken down to the subgroup of rotations which are equal to left and right-handed fermions, i.e., vector SU(Nf) since those cannot be broken spontaneously according to the Vafa-Witten theorem. Therefore we end up with the coset (SUL(Nf) × SUR(Nf))/SU(Nf) which is equivalent to G/H = SU(Nf). The other cases b = 1,4 can be similarly derived (see [13] for a clear derivation ).
The effective Lagrangian
chiral is a good approximation when distances are large enough (low-energy), i.e., V1/4 >> 1/LQCD and the quark masses are small. The regime where we are interested in corresponds to further assume that the typical pion wavelength is much bigger than the size of the system, i.e., 1/mp =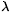 p >> V1/4 In this specific domain the pion wave function is like a constant inside the box and the zero momentum mode U0 dominates, such that we can neglect the kinetic term in
p >> V1/4 In this specific domain the pion wave function is like a constant inside the box and the zero momentum mode U0 dominates, such that we can neglect the kinetic term in 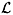 chiral . We can write
chiral . We can write 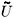 =
= 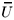 U0 and the integral over the nonzero modes
U0 and the integral over the nonzero modes 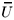 will become, in the infinite volume limit, an overall factor to the integral over the constant mode U0 henceforth called simply U. For b = 2 we should have an integral over SU(Nf), however in the sector of fixed topological charge n (number of instantons minus the number of anti-instantons) we can enlarge it to an integral over U(Nf) as follows. First, one can obtain the partition function in the sector of fixed topological charge
will become, in the infinite volume limit, an overall factor to the integral over the constant mode U0 henceforth called simply U. For b = 2 we should have an integral over SU(Nf), however in the sector of fixed topological charge n (number of instantons minus the number of anti-instantons) we can enlarge it to an integral over U(Nf) as follows. First, one can obtain the partition function in the sector of fixed topological charge 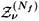 from the partition function with fixed theta angle through a Fourier transform:
from the partition function with fixed theta angle through a Fourier transform:
Notice that we have combined dqdU (SU(Nf)) ® dU(U(Nf)) and  = mV
= mV .
.
IV Spectral density via replicas
Now that we know the partition function for an arbitrary quark mass matrix we can return to our fermionic replicas formula:
and instead of the original quark mass matrix we have extra n masses z:
As a further simplification we restrict ourselves to the quenched (Nf= 0) case where the quark mass matrix only contains the replicas masses:
With the corresponding partition function:
It is very fortunate that there is an exact formula for  (z), at least for integer number of replicas n , we have up to an overall constant [14] :
(z), at least for integer number of replicas n , we have up to an overall constant [14] :
With In(z) being a modified Bessel function of first kind. For example, for n = 1 and n = 2 replicas we have
Although formula (13) is exact it is only true for integer number of replicas, but in order to take the replica limit n® 0 we need to know the partition function  for arbitrary complex number of replicas. That is, we need to continue the partition function to non-integer number of replicas which is the most difficult technical problem in replica calculations. We still do not know how to do it for arbitrary finite mass z but one can either do perturbations for z ® 0 (Taylor expansions) or take z ® ¥ (saddle point calculations ). It turns out that, in general, the first approximation can not be analytically continued to arbitrary number of replicas due to the presence of the so called t'Hooft - De Wit poles. On the other hand the saddle point approximation is much more suitable. For large z the integral (12) is localized around the saddle points which are solutions of the saddle point equations d(U +U) = 0 which imply U2 = 1 . Those equations have infinite solutions which can divided in n+1 classes labelled by an integer p = 0,1,¼, n. Each class of solution is represented by its diagonal element Up = diag(1,1,¼, 1,1,¼, 1) where the label p counts the number of entries 1 in the diagonal and consequently n p entries +1. For a given value of p we have
for arbitrary complex number of replicas. That is, we need to continue the partition function to non-integer number of replicas which is the most difficult technical problem in replica calculations. We still do not know how to do it for arbitrary finite mass z but one can either do perturbations for z ® 0 (Taylor expansions) or take z ® ¥ (saddle point calculations ). It turns out that, in general, the first approximation can not be analytically continued to arbitrary number of replicas due to the presence of the so called t'Hooft - De Wit poles. On the other hand the saddle point approximation is much more suitable. For large z the integral (12) is localized around the saddle points which are solutions of the saddle point equations d(U +U) = 0 which imply U2 = 1 . Those equations have infinite solutions which can divided in n+1 classes labelled by an integer p = 0,1,¼, n. Each class of solution is represented by its diagonal element Up = diag(1,1,¼, 1,1,¼, 1) where the label p counts the number of entries 1 in the diagonal and consequently n p entries +1. For a given value of p we have
Therefore it is clear that for z ® + ¥ the solution p = 0 (replica symmetric) dominates and all other solutions are exponentially suppressed. However, there comes an important subtlety. Namely, we are actually interested in the spectral density which will be calculated from a discontinuity equation at z = i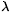 +
+  , thus large masses means in fact z ® +
, thus large masses means in fact z ® + 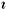 ¥ +
¥ +  and in this case all solutions are almost equally important. If, for instance,
and in this case all solutions are almost equally important. If, for instance,  > 0 (assumed here) the solutions with smaller p give the largest contributions but since the difference between them is infinitesimally small all saddle point classes should in principle be taken into account. Thus, we should sum over all of them,
> 0 (assumed here) the solutions with smaller p give the largest contributions but since the difference between them is infinitesimally small all saddle point classes should in principle be taken into account. Thus, we should sum over all of them,
where we have used the decomposition
and factored out the volume of redundant solutions in each of the n + 1 classes. The unitary matrix Vp is n × n and block-diagonal. It is convenient to write Vp in terms of matrices H and h which are Hermitean (n p) × (n p) and p × p respectively, such that the expansion around the diagonal saddle points means H,h ® 0 , i.e.,
The integral over dVp now reduces to integrals over Hermitean matrices which can be easily evaluated and continued to non-integer number of replicas. Typically, for instance for p = 0, we have for z ® ¥,
The result on the r.h.s. of (16) is an analytic function of the number of replicas and so will be the integral over dVp in (15). Still we have to continue the sum and the volume factor in (15) to arbitrary number of replicas. Fortunately, the same volume factor appears in [17], plugging back their continuation in our results it amounts to take into account only p = 0 and p = 1 saddle points while the other saddle points drop out in the replica limit. Consequently,
Besides the real contribution of the p = 0 saddle point calculated in [15,16] the chiral condensate S(z) gets an imaginary part comming from the nontrivial p = 1 saddle point [11] :
From the discontinuity equation we finally obtain the microscopic spectral density of the Dirac operator in the quenched case (Nf ® 0 ):
Our results hold for arbitrary topological charge n and the oscillating terms all came from the nontrivial saddle point p = 1. Using asymptotic expressions for Bessel functions we found full agreement with the corresponding ChRMT analytical result:
until the order 1/
4 where we stopped our calculation. It is remarkable that for half-integer values of n the large mass expansion terminates and the replica result becomes exact .V Conclusions and perspectives
We have been able to calculate the microscopic spectral density rS(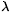 ) of the QCD Dirac operator close to the origin of the spectrum by means of fermionic replicas of quarks. Our results are perturbative and hold for large arguments
) of the QCD Dirac operator close to the origin of the spectrum by means of fermionic replicas of quarks. Our results are perturbative and hold for large arguments 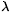 ® ¥ . In this region they overlap previous results obtained via ChRMT , lattice simulations and the supersymmetric method. Contributions of all saddle points is crucial for the correct result. We have assumed the continuation to arbitrary number of replicas of the work [17] which has not yet been proven to be unique. For instance, as commented in [18], we could add to our partition function, defined for integer number of replicas, an arbitrary extra factor which vanishes for integer number of replicas but gives a nontrivial contribution in the replica limit like, e.g.,
® ¥ . In this region they overlap previous results obtained via ChRMT , lattice simulations and the supersymmetric method. Contributions of all saddle points is crucial for the correct result. We have assumed the continuation to arbitrary number of replicas of the work [17] which has not yet been proven to be unique. For instance, as commented in [18], we could add to our partition function, defined for integer number of replicas, an arbitrary extra factor which vanishes for integer number of replicas but gives a nontrivial contribution in the replica limit like, e.g.,
since the extra term is arbitrary so it is the replica result. Clearly we might try to find relations between the partition function for different number of flavors and topological charges to avoid the addition of such arbitrary terms however we still do not have a proof of uniqueness of our replica result.
The opposite limit z ® 0 can not be continued in n in general, though we found for the special case n = 0 that r(z) = z/2 + ¼ . This is a very nontrivial result [11] which is also in agreement with other non-replica calculations (see [1,6]).
Concerning future calculations we should mention that we have assumed Nc ³ 3 and fermions in the fundamental representation (b = 2 ) but there are other cases Nc = 2 (b = 1) and adjoint fermions ( b = 4) which might be explored as well in D = 4 and D = 3. Besides, inclusion of chemical potential m ¹ 0 is phenomenologically and mathematically interesting (see[1,19]). The use of Virasoro constraints around nontrivial (replica nonsymmetric) saddle points is also of interest if we want to understand local correlators as fixed by the Virasoro constraints [20].
Acknowledgments
This work is a result of a collaboration with J.J.M. Verbaarschot during my sabbatical leave (sponsored by FAPESP) at the Physics Department of SUNY at Stony Brook. The author is partially supported by CNPq.
References
[1] J.J.M. Verbaarschot and T. Wettig (hep-ph/0003017) "Random Matrix Theory and Chiral Symmetry in QCD".
[2] C. Vafa and E. Witten, Nucl. Phys. B234, 173 (1984).
[3] J.J.M. Verbaarschot and I. Zahed, Phys. Rev. Lett. 73 (1994) 2288.
[4] G. Akemann, D. Dalmazi, P.H. Dammgaard, and J.J.M. Verbaarschot, Nucl. Phys. B 601, 77 (2001).
[5] T. Banks and A. Casher, Nucl.Phys. B169, 103 (1980).
[6] P.H. Damgaard, J.C. Osborn, D. Toublan, and J.J.M. Verbaarschot, Nucl. Phys. B547, 305 (1999).
[7] M.E. Berbenni-Bitsch, M. Göckeler, H. Hehl, S. Meyer, P.E.L. Rakow, A. Schäfer, and T. Wettig, Phys. Lett. B466, 293 (1999); hep-lat/9908043.
[8] K.B. Efetov, Adv. Phys. 32, 53 (1983); Supersymmetry in disorder and chaos (Cambridge University Press, Cambridge, 1997).
[9] S.F. Edwards and P.W. Anderson, J. Phys. F5, 865 (1975).
[10] J.J.M. Verbaarschot and M.R. Zirnbauer, J. Phys. A 17, 1093 (1985).
[11] D. Dalmazi and J.J.M. Verbaarschot, Nucl. Phys. B 592, 419 (2001).
[12] J. Gasser and H. Leutwyler, Annals of Phys. 158, 142 (1984).
[13] H. Leutwyler and A. Smilga, Phys. Rev. D46, 5607 (1992).
[14] R. Brower, P. Rossi and C.-I. Tan, Nucl. Phys. B190, [FS3] 699 (1981). A.D. Jackson, M.K. Sener, and J.J.M. Verbaarschot, Phys. Lett. B387, 355 (1996).
[15] P.H. Damgaard, K. Splittorff, Nucl. Phys. B572, 478 (2000).
[16] P.H. Damgaard, K. Splittorff, Phys. Lett. B476, 465 (2000).
[17] A. Kamenev and M. Mézard, J. Phys. A32, 4373 (1999); Phys. Rev. B60, 3944 (1999).
[18] M.R. Zirnbauer, cond-mat/9903338.
[19] S.M. Nishigaki and A. Kamenev , cond-mat/0109126.
[20] D.Dalmazi and J.J.M. Verbaarschot, Phys. Rev. D 64, 540021 (2001).
- [1] J.J.M. Verbaarschot and T. Wettig (hep-ph/0003017) "Random Matrix Theory and Chiral Symmetry in QCD".
- [2] C. Vafa and E. Witten, Nucl. Phys. B234, 173 (1984).
- [3] J.J.M. Verbaarschot and I. Zahed, Phys. Rev. Lett. 73 (1994) 2288.
- [4] G. Akemann, D. Dalmazi, P.H. Dammgaard, and J.J.M. Verbaarschot, Nucl. Phys. B 601, 77 (2001).
- [5] T. Banks and A. Casher, Nucl.Phys. B169, 103 (1980).
- [6] P.H. Damgaard, J.C. Osborn, D. Toublan, and J.J.M. Verbaarschot, Nucl. Phys. B547, 305 (1999).
- [7] M.E. Berbenni-Bitsch, M. Göckeler, H. Hehl, S. Meyer, P.E.L. Rakow, A. Schäfer, and T. Wettig, Phys. Lett. B466, 293 (1999); hep-lat/9908043.
- [8] K.B. Efetov, Adv. Phys. 32, 53 (1983);
- Supersymmetry in disorder and chaos (Cambridge University Press, Cambridge, 1997).
- [9] S.F. Edwards and P.W. Anderson, J. Phys. F5, 865 (1975).
- [10] J.J.M. Verbaarschot and M.R. Zirnbauer, J. Phys. A 17, 1093 (1985).
- [11] D. Dalmazi and J.J.M. Verbaarschot, Nucl. Phys. B 592, 419 (2001).
- [12] J. Gasser and H. Leutwyler, Annals of Phys. 158, 142 (1984).
- [13] H. Leutwyler and A. Smilga, Phys. Rev. D46, 5607 (1992).
- [14] R. Brower, P. Rossi and C.-I. Tan, Nucl. Phys. B190, [FS3] 699 (1981).
- A.D. Jackson, M.K. Sener, and J.J.M. Verbaarschot, Phys. Lett. B387, 355 (1996).
- [15] P.H. Damgaard, K. Splittorff, Nucl. Phys. B572, 478 (2000).
- [16] P.H. Damgaard, K. Splittorff, Phys. Lett. B476, 465 (2000).
- [17] A. Kamenev and M. Mézard, J. Phys. A32, 4373 (1999); Phys. Rev. B60, 3944 (1999).
- [18] M.R. Zirnbauer, cond-mat/9903338.
- [19] S.M. Nishigaki and A. Kamenev , cond-mat/0109126.
- [20] D.Dalmazi and J.J.M. Verbaarschot, Phys. Rev. D 64, 540021 (2001).
Publication Dates
-
Publication in this collection
12 Mar 2003 -
Date of issue
Dec 2002
History
-
Received
15 Jan 2002







































