Abstract
The compressible magnetohydrodynamic Kelvin-Helmholtz instability occurs in two varieties, one that can be called incompressible as it exists in the limit of vanishing compressibility (primary instability), while the other exists only when compressibility is included in the model (secondary instability). In previous work we developed techniques to investigate the stability of a surface of discontinuity between two different uniform ows. Our treatment includes arbitrary jumps of the velocity and magnetic fields as well as of density and temperature, with no restriction on the wave vector of the modes. Then it allows stability analyses of complex configurations not previously studied in detail. Here we apply our methods to investigate the stability of various typical situations occurring at different regions of the front side, and the near anks of the magnetopause. The physical conditions of the vector and scalar fields that characterize the equilibrium interface at the positions considered are obtained both from experimental data and from results of simulation codes of the magnetosheath available in the literature. We give particular attention to the compressible modes in configurations in which the incompressible modes are stabilized by the magnetic shear. For configurations of the front of the magnetopause, which have small relative velocities, we find that the incompressible MHD model gives reliable estimates of their stability, and compressibility effects do not introduce significant changes. However, at the anks of the magnetopause the occurrence of the secondary instability and the shift of the boundary of the primary instability play an important role. Consequently, configurations that are stable if compressibility is neglected turn out to be unstable when it is considered and the stability properties are quite sensitive on the values of the parameters. Then compressibility should be taken into account when assessing the stability properties of these configurations, since the estimates based on incompressible MHD may be misleading. A careful analysis is required in each case, since no simple rule of thumb can be given.
Compressible Kelvin-Helmholtz Instability at the Terrestrial Magnetopause
Alejandro G. González* * Researcher of the Consejo Nacional de Investigaciones Científicas y Tecnológicas
Instituto de Física Arroyo Seco, Universidad Nacional del Centro de la
Provincia de Buenos Aires, Pinto 399, 7000 Tandil, Buenos Aires, Argentina
Julio Gratton* * Researcher of the Consejo Nacional de Investigaciones Científicas y Tecnológicas , Fausto T. Gratton* * Researcher of the Consejo Nacional de Investigaciones Científicas y Tecnológicas ,
INFIP Instituto de Física del Plasma, Facultad de Ciencias Exactas y Naturales,
Universidad de Buenos Aires, Pabellón I, Ciudad Universitaria, 1428, Buenos Aires, Argentina
and Charles J. Farrugia
Space Science Center, University of New Hampshire at Durham, NH, USA.
Received on 30 June, 2002
The compressible magnetohydrodynamic Kelvin-Helmholtz instability occurs in two varieties, one that can be called incompressible as it exists in the limit of vanishing compressibility (primary instability), while the other exists only when compressibility is included in the model (secondary instability). In previous work we developed techniques to investigate the stability of a surface of discontinuity between two different uniform ows. Our treatment includes arbitrary jumps of the velocity and magnetic fields as well as of density and temperature, with no restriction on the wave vector of the modes. Then it allows stability analyses of complex configurations not previously studied in detail. Here we apply our methods to investigate the stability of various typical situations occurring at different regions of the front side, and the near anks of the magnetopause. The physical conditions of the vector and scalar fields that characterize the equilibrium interface at the positions considered are obtained both from experimental data and from results of simulation codes of the magnetosheath available in the literature. We give particular attention to the compressible modes in configurations in which the incompressible modes are stabilized by the magnetic shear. For configurations of the front of the magnetopause, which have small relative velocities, we find that the incompressible MHD model gives reliable estimates of their stability, and compressibility effects do not introduce significant changes. However, at the anks of the magnetopause the occurrence of the secondary instability and the shift of the boundary of the primary instability play an important role. Consequently, configurations that are stable if compressibility is neglected turn out to be unstable when it is considered and the stability properties are quite sensitive on the values of the parameters. Then compressibility should be taken into account when assessing the stability properties of these configurations, since the estimates based on incompressible MHD may be misleading. A careful analysis is required in each case, since no simple rule of thumb can be given.
I Introduction
The Kelvin-Helmholtz Instability (KHI) can occur in laboratory and astrophysical plasmas when two (or more) regions are in relative motion. Other properties of the plasma (like magnetic field, density and temperature) may also change across the transition layer. These changes modify the stability and other properties of the modes, thus complicating analysis. The KHI may occur at the terrestrial magnetopause, the boundary that separates the interplanetary magnetic field (IMF) present in the magnetosheath, and the geomagnetic field inside the magnetosphere. The relative motion is generated by the solar wind flowing through the magnetosheath. The flow velocity and the magnetic field are assumed parallel to the transition layer, and the magnetic field may change its direction (magnetic shear) and its magnitude across the transition. The low frequency magnetohydrodynamic (MHD) modes shall be our main concern here since their instability may produce large-scale turbulence. The KHI is considered a major source of anomalous transport of momentum from the solar wind into the magnetosphere, and a cause of viscous drag at the magnetopause. This is so particularly during periods of northward IMF, when the reconnection of magnetic lines is less likely to occur. We shall not consider other unstable modes that can also arise close to, and inside the magnetopause, in frequency ranges higher than those treated by MHD. These modes lead to microscopic turbulence that affects the transport properties of the plasma at smaller wavelengths. We shall also neglect dissipative effects so that our treatment shall be based on ideal MHD. The KHI at the magnetopause has been examined since the 1950's, and a large literature has grown on this subject. We quote here some recent reviews [?],[?] ,[?] among several others.
The theory of the KHI for arbitrary geometry is exceedingly complicated, but fortunately in many circumstances, the wavelength of the perturbation is very small as compared to the curvature radii of the transition layer. Then the problem can be treated in a plane slab geometry, in which the unperturbed quantities (density r, pressure p, magnetic field B and mass flow velocity u) depend only on the y coordinate (perpendicular to the transition layer). A differential equation for the linear MHD perturbations of stratified plasmas [?], and its generalization to include the effect of gravity [?], can be used as a starting point to investigate these problems.
If the wavelength of the perturbation is large as compared to the thickness of the transition layer, we can ignore the structure of the transition and assume it is a mathematical surface (at y = 0) separating two infinite, uniform plasma regions. The problem can then be treated by means of standard normal mode analysis. The equations of ideal MHD and the parameters of the configuration do not involve either a frequency or a length scale. Therefore the theory only predicts the (complex) phase velocity v of the perturbation (v = 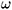 /kt), as a function of the parameters of the plasma, of the mass velocities of the uniform regions and of the wavenumber ktº (kx,0,kz) of the perturbation of the interface. Then an algebraic dispersion relation is obtained, whose roots yield v.
/kt), as a function of the parameters of the plasma, of the mass velocities of the uniform regions and of the wavenumber ktº (kx,0,kz) of the perturbation of the interface. Then an algebraic dispersion relation is obtained, whose roots yield v.
Within the incompressible MHD approximation (IMHD) it is possible to derive a simple formula for the phase velocity. Because of this, the IMHD result is often employed in space physics to interpret the observed data and to examine the stability of the configuration. Sometimes the tacit assumption is made that the compressibility effects thus neglected should (if any) improve stability. This assumption is based on well known theorems (see for example [?]) derived from a variational principle, according to which compressibility leads to a positive contribution to the energy of the plasma and so tends to stabilize it. However, these results cannot be applied here, since due to the presence of mass flow the plasma can sustain perturbations with a negative energy density that can lead to instability. This is a consequence of the transformation properties of the energy density W of a perturbation of wavenumber kt and frequency 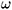 under Galilean transformations. Let the primes denote the quantities calculated in the reference frame of the plasma that moves with a velocity u º (ux,0,uz) with respect to the observer, and the quantities without primes refer to the observer frame. Then we have W¢/
under Galilean transformations. Let the primes denote the quantities calculated in the reference frame of the plasma that moves with a velocity u º (ux,0,uz) with respect to the observer, and the quantities without primes refer to the observer frame. Then we have W¢/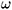 ¢ = W/
¢ = W/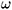 . Notice that the Doppler-shifted frequency in the plasma frame
. Notice that the Doppler-shifted frequency in the plasma frame 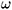 ¢ =
¢ = 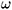 -u·kt can be negative if uk = u·kt/kt is sufficiently large (the phase velocity in the plasma frame is then v¢ = v-uk). Since W¢ is always positive, the energy density of the perturbation as measured in the laboratory frame is then negative. A negative energy density perturbation may lead to instability if it couples to a positive energy density perturbation, since both can grow without an external source of energy.
-u·kt can be negative if uk = u·kt/kt is sufficiently large (the phase velocity in the plasma frame is then v¢ = v-uk). Since W¢ is always positive, the energy density of the perturbation as measured in the laboratory frame is then negative. A negative energy density perturbation may lead to instability if it couples to a positive energy density perturbation, since both can grow without an external source of energy.
In IMHD, the instability arises from perturbations of the interface that are exponentially damped in both plasma regions (like surface gravity waves in water). The penetration depth of these perturbations is equal to their wavelength 2p/kt. The instability occurs when uk exceeds a critical value ui (see below), such that their energy density (in the laboratory frame) is positive in one region and negative in the other. These perturbations grow because energy is transferred across the interface from the negative energy density region to the other, and remains localized as it can not be transported away across the magnetic field. This instability will be called primary KHI. Notice that the Alfvén wave only transports energy along the field lines, and does not participate in the KHI if the transition region has a vanishing thickness.
The essential difference between IMHD and compressible MHD (CMHD) is that in the latter there are perturbations (the fast and slow magnetosonic waves) that propagate in the bulk of the plasma and transport energy across the magnetic field (see for example [?]) Consequently, the effect of compressibility on the Kelvin-Helmholtz instability is complex, leading to the stabilization of certain perturbations, the destabilization of others, and the occurrence of modes that have no analogue in IMHD and that may lead to new instabilities. Let us briefly discuss the basic physics involved.
Consider first the primary KHI. Due to compressibility, if uk is sufficiently large the perturbation may be able to propagate in both regions as fast magnetosonic waves. When this happens, the perturbation is stable, and it is seen by the observer as a pair of fast magnetosonic waves radiated away from the interface. One of these waves has a negative, and the other a positive energy density [?], [?]. In this way, perturbations that are unstable according to IMHD are stabilized by compressibility. However, in addition to this large-uk stabilization, there is another effect of compressibility on the primary KHI, namely that the critical value uc for the onset of the instability is lowered (uc £ ui). This is a destabilizing effect, since perturbations that are stable according to IMHD become unstable when compressibility is taken into account. As we shall show later, this effect is important in the magnetopause. The penetration depth of the unstable modes is also affected by compressibility, and is no longer given by 2p/kt.
Yet, there are further effects of compressibility. Due to the existence of the slow magnetosonic waves new kinds of perturbations of the interface are possible, that have no counterpart in IMHD. Some of these perturbations are stable evanescent oscillations, and other are slow magnetosonic waves in both regions (radiation of a pair of slow magnetosonic waves). However, some of these new perturbations may be unstable. These new instabilities (called secondary KHI) are found in intervals of uk that correspond to stable perturbations according to IMHD. They lie totally, or partially, below the critical value uc for the onset of the primary KHI. The occurrence of the secondary KHI is an additional destabilizing effect of compressibility. The growth rate of the secondary modes is usually small. However, we shall see that these modes cannot be ignored, since in some configurations of the magnetopause they are the only unstable modes present.
A substantial contribution to the understanding of the compressibility effects on the Kelvin-Helmholtz instability was given by Miura and Pritchett [?]. However, these effects have not yet been fully explored for general configurations with density and temperature discontinuities as well as magnetic field shear, such as those occurring in the magnetopause. For an extensive revision of the literature and of the main results on this subject, see refs. [?],[?] . Recently, we have developed techniques [?], [?], [?] to analyze the stability of an interface separating two uniform flows, with arbitrary jumps in the velocity, magnetic field, density and temperature, and with no restrictions on the wave vector of the perturbation.
The content of this paper is as follows. In Section II we outline the basic theory. In Section III we explain the techniques for analyzing the dispersion relation and the characteristics of the unstable modes. Section IV discusses the secondary KHI. A useful graphical technique that simplifies the complexity of the stability analysis is given in Section V. The physical parameters used in the applications to the magnetopause stability are introduced in Section VI. The results for two examples, (i) a model of the front side magnetopause, and (ii) an event observed at the near equatorial flank of the magnetopause are given in Section VII. We determine the stability of these configurations, and study the unstable modes that may occur in them. The final remarks are in Section VIII. We conclude that the effects of compressibility may introduce important changes with respect to the predictions of IMHD.
II Theory
We consider two semiinfinite, uniform plasma regions in relative motion. The geometry of the problem is shown in Fig. 1. Region 1 (y > 0), moves with a constant velocity  , and region 2 (y < 0) moves with a constant velocity
, and region 2 (y < 0) moves with a constant velocity  . The velocities
. The velocities  and
and  and the magnetic fields B1 and B2 are parallel to the interface (suffixes i = 1,2 denote quantities pertaining to region 1 and 2, respectively). At the interface, p, r, and B can have arbitrary discontinuities, subject to the equilibrium condition
and the magnetic fields B1 and B2 are parallel to the interface (suffixes i = 1,2 denote quantities pertaining to region 1 and 2, respectively). At the interface, p, r, and B can have arbitrary discontinuities, subject to the equilibrium condition
We shall assume ideal CMHD and consider the linear adiabatic perturbations of this configuration. Since the growth rate of the instability does not depend on  and
and  separately, but only on their difference 2u =
separately, but only on their difference 2u =  -
- , we use a reference frame moving with the average velocity u¢ = (
, we use a reference frame moving with the average velocity u¢ = ( +
+ )/2. In this frame u1 = u = uex, u2 = -u, and a is the angle between u and the wavenumber ktº (kx,0,kz) of a perturbation whose frequency is
)/2. In this frame u1 = u = uex, u2 = -u, and a is the angle between u and the wavenumber ktº (kx,0,kz) of a perturbation whose frequency is 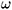 ; the phase velocity is then v =
; the phase velocity is then v = 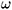 /kt. Once the phase velocity of the perturbation is found, we can obtain its value in the observer frame by means of the Galilean transformation v¢ = v-
/kt. Once the phase velocity of the perturbation is found, we can obtain its value in the observer frame by means of the Galilean transformation v¢ = v- .
.
The (Doppler-shifted) frequencies in the plasma frames are
1 =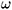 -ukkt in region 1 and
-ukkt in region 1 and 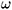 2 =
2 = 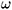 +ukkt in region 2, and the corresponding phase velocities are
+ukkt in region 2, and the corresponding phase velocities are
We shall denote by yi the angles between Bi and kt, and by ji the angles between Bi and u. The angle between kt and u is a, so that uk = ucosa. We employ the following notation:
In each one of the uniform regions, the general form of the perturbation is
In this formula, zi denotes the y-component of the displacement, and Ci and Di are constants. The penetration depth of the perturbation in region i is proportional to 1/Re(Gi).
When Re(Gi) = 0, it can be recognized that eq. (6) is the dispersion relation for the fast and slow magnetosonic waves in a semiinfinite uniform moving plasma; their wave vector is (kx,kt Im (Gi),kz). When Re (Gi) ¹ 0, eq. (6) is the dispersion relation for evanescent perturbations, and of course in this case the amplitudes of the exponentially growing perturbations (D1 and C2) in eq. ( 7) must vanish since the plasma extends to (+ or -) infinity.
The boundary conditions at y = 0 (continuity of z and of the normal stress) couple the perturbations of regions 1 and 2. The coupling leads to a matrix equation that relates the amplitudes Ci, Di:
Here
The matrix equation (8) may be used to investigate many problems involving localized modes as well as the reflection and transmission of magnetosonic waves. Since unstable modes and stable surface oscillations have Re(G1,2) ¹ 0, we must have C1 = D2 = 0 and then the corresponding dispersion relation is
The propagating modes have Re(G1,2) = 0, so that there is no restriction on the Ci, Di. In this case, the conditions T = 0 and S = 0 determine the poles and the zeros of the reflection coefficient. Notice that the sign of the y-component of the group velocity of magnetosonic waves may be different from the sign of Re(G1,2). Then one must examine the group velocities in each region, to ascertain which of these conditions yields the dispersion relation for radiation of a pair of waves, or for the total transmission of waves (and their time-reversed processes).
III Classification of the modes
To investigate the roots of the dispersion relation (10) it is useful to introduce a polynomial P associated to it. It is obtained by taking the numerator of the product TS, thus eliminating the square roots:
Clearly, the roots of P = 0 encompass the solutions of T = 0 ( 'true' roots) as well as those of S = 0 ('spurious' roots), and we must discard the latter when we look for localized modes. Accordingly, we call 'true branch' (T) the set of solutions of T = 0, and 'spurious branch' (S) the solutions of S = 0. The T branch and the S branch consist of several pieces (that we call 'segments'), each of which is a continuous manifold in the parameter space of the problem. They are arranged in such a way that any given T segment is bounded by one or more S segments (and vice-versa). Let us consider a root v (real or complex) of P that belongs to a certain segment Tj. If the parameters change, v moves along Tj until eventually it arrives to the boundary between Tj and a segment Sl of S. As it crosses this boundary, v ceases to belong to the true branch and becomes spurious. It is important to notice that the T-S boundaries occur only for v real, at the points where G1,2 = 0,¥. This is fortunate, since it simplifies considerably the analysis of the topology of the T and S branches.
A convenient way to visualize the real roots of the dispersion relation (10) and so unravel the topology of the T and S branches is to use a graphical method introduced by Chandrasekhar [?]. This method takes advantage of the fact that the problem of finding the roots v of P = 0 is equivalent to solve for v1 and v2 the coupled equations
From any given solution (v1,v2) of the system (12), one can obtain a root v = (v1+v2)/2 of P = 0. The real solutions of this system can be easily found graphically in a (v1,v2) diagram, as the intersections of the line L given by (12b) with the curves that are obtained solving the bicubic (in v1 and v2) equation (12a) for v2.
In Fig. 2 we show a typical Chandrasekhar diagram, corresponding to the plasma configuration (d) investigated in Section VII (notice that the scale of v2 is different from that of v1 for convenience in drawing). It suffices to consider a single quadrant, since the curves v2 = v2(v1) are symmetrical under reflections on both axes. In Fig. 2, the lines v2 = v1 and v2 = -v1 represent the v- and uk- axes (except from a scale factor  ).
).
The perturbation in the region i (i = 1,2) is a slow magnetosonic wave if bi £ | vi| £ mi, and a fast magnetosonic wave if qi £ | vi| . It is evanescent if 0 £ |vi| £ bi or mi £ | vi| £ qi (we shall call the latter the 'slow' and 'fast' evanescent perturbations, not to be confused with the slow and fast magnetosonic waves). A real root belongs to the T branch if Sign(
 ) ¹ Sign (
) ¹ Sign (
 ) (i. e., if | v1| < a1 and | v2| > a2, or | v1| > a1 and |v2| < a2); otherwise, it belongs to the S branch.
) (i. e., if | v1| < a1 and | v2| > a2, or | v1| > a1 and |v2| < a2); otherwise, it belongs to the S branch.
Both the T and S branches must be considered for the y-propagating modes (radiated or totally transmitted magnetosonic waves). It can be shown that all the roots of this type in the second and fourth quadrants of the (v1,v2) diagram correspond to radiation and those in the first and third quadrant to total transmission. According to these criteria we can classify the branch segments shown in Fig. 2. The true evanescent segments are represented by solid curves (labeled T1,  , T2), the spurious evanescent segments by gray dotted curves (labeled S1, S2, S3,
, T2), the spurious evanescent segments by gray dotted curves (labeled S1, S2, S3,  ), and the radiation segments by gray solid lines (labeled R1,
), and the radiation segments by gray solid lines (labeled R1,  , R2, R3,
, R2, R3,  ).
).
For any given uk there are five pairs of roots of P(v) = 0. Two pairs are always real, and are uninteresting for us since they are always spurious, or correspond to totally transmitted modes (they do not appear in Fig. 2 since they lie in the first and third quadrants). One root of a third pair lies on the curve formed by the segments labeled with the suffix 3 in Fig. 2 (S3, R3,  ,
,  ), or on its continuation in the first quadrant. The other root of this pair is found on a symmetrical curve lying in the third and fourth quadrants. This pair of roots is also uninteresting, since they are always either spurious or propagating modes. The remaining two pairs of roots, labeled A, A¢ and B, B¢, are important to us since they can be unstable. For the value of uk represented in Fig. 2 all these roots are real and represent stable surface oscillations, since the points lie on the segments
), or on its continuation in the first quadrant. The other root of this pair is found on a symmetrical curve lying in the third and fourth quadrants. This pair of roots is also uninteresting, since they are always either spurious or propagating modes. The remaining two pairs of roots, labeled A, A¢ and B, B¢, are important to us since they can be unstable. For the value of uk represented in Fig. 2 all these roots are real and represent stable surface oscillations, since the points lie on the segments  and T2, respectively.
and T2, respectively.
If we consider a larger value of uk, the line L must be displaced upwards, parallel to itself. Then the points B, B¢ move on the segment T2 until they coalesce for uk = ud2 when L is tangent to T2. For uk > ud2 the roots vB, vB¢ are complex conjugate, but they still belong to the T branch (since roots can pass to the other branch only for v real). Then uk = ud2 corresponds to marginal stability, and one of the roots vB, vB¢ is unstable for uk > ud2 (the other is damped). This instability persists until uk = ud6, when L is tangent to the segment R2. Then ud6 corresponds also to marginal stability, and for uk > ud6, vB, vB¢ are stable radiation modes. On the other hand, if one considers values of uk larger than that represented in Fig. 2, the points A, A¢ move along  and eventually pass into the segments R1,
and eventually pass into the segments R1,  , and then vA, vA¢ correspond to radiation modes.
, and then vA, vA¢ correspond to radiation modes.
Let us now consider smaller values of uk. As uk is reduced, L moves downwards. The points B, B¢ move on T2 until they pass into S2. It can be shown that for uk > 0, no new instability arises from the roots vB, vB¢. On the other hand, the points A, A¢ move along  until they coalesce for uk = ud3. When this happens, the double root vA = vA¢ is marginally stable. For ud1 < uk < ud3 we have instability, and vA, vA¢, are complex conjugate. Marginal stability is again achieved at uk = ud1. For uk < ud1 the points A, A¢ move along T1 until they pass into S1. No other instability related to vA, vA¢ occurs for uk > 0. Using diagrams like Fig. 2 it is possible to investigate the stability of any configuration of interest. However, this method is unpractical, since we need a new diagram for each orientation of kt, and in addition, we cannot determine the growth rate of the unstable modes.
until they coalesce for uk = ud3. When this happens, the double root vA = vA¢ is marginally stable. For ud1 < uk < ud3 we have instability, and vA, vA¢, are complex conjugate. Marginal stability is again achieved at uk = ud1. For uk < ud1 the points A, A¢ move along T1 until they pass into S1. No other instability related to vA, vA¢ occurs for uk > 0. Using diagrams like Fig. 2 it is possible to investigate the stability of any configuration of interest. However, this method is unpractical, since we need a new diagram for each orientation of kt, and in addition, we cannot determine the growth rate of the unstable modes.
In the case shown in Fig. 2 there are two unstable intervals (for uk > 0). The first (in order of increasing uk) involves vA, vA¢ and occurs for ud1 < uk < ud3. The second occurs for ud2 < uk < ud6, and involves vB, vB¢. This result is due to the special choice of parameters of Fig. 2. In general, there can be up to six positive values of uk corresponding to significant (i.e., belonging to the T branch) double roots of P(v) = 0, that we label ud1,...,ud6. Correspondingly, there can be up to three unstable intervals, namely
As the parameters are varied, it may happen that the pair (ud3, ud5), or the pair (ud4, ud5), coalesces and becomes complex. In the first case, the secondary interval A merges with the primary interval. In the second case, the secondary interval B merges with the primary interval (as in Fig. 2). In addition the secondary intervals (13a, b) may also overlap partially or totally. The secondary intervals can be extremely narrow for some values of the parameters, in particular they vanish when the perturbations are flutes in either region 1 or 2. For negative uk, a completely symmetrical result is obtained, in which the signs of ud1,...,ud6 are changed, the inequalities (13a-c) are reversed, and the roles of the root pairs (A, A¢) and (B, B¢) are exchanged. There are no simple formulae for ud1,...,ud6.
To find the double roots vd1,...,vd6 of P(v) and the corresponding uk values ud1,...,ud6 we must solve numerically for (u,v) the system
and discard the roots belonging to the S branch. The unstable intervals can then be mapped in the parameter space of the configuration (see Section V).
IV The secondary Kelvin-Helmholtz instability
With the help of diagrams like Fig. 2 it is easy to understand the role of the compressibility on the KHI. As Si increases, bi and mi approach ai, and qi increases without bound, so that in the incompressible limit (S1,S2® ¥) the secondary unstable intervals disappear, and we are left only with the primary unstable interval, that now extends to infinity. The secondary KHI is then a consequence of compressibility, as well as the large uk stabilization of the primary KHI at ud6. It is enlightening to see in more detail the origin of the secondary KHI. Notice that P(v1,v2) can be written in the form
In (15),
and P1, P2, P3, are polynomials whose coefficients are functions of a1, a2, A1, A2, r1 and r2. Then, in the limit S1,S2® ¥, if we assume that v1,2 remain finite, eq. (12a) reduces to Pinc = 0, whose solutions are:
These solutions yield, respectively, the roots
The roots (17a) and (17b) are stable, and correspond to Alfvén waves propagating in regions 1 and 2, respectively. The roots (17c) have been discussed by Axford [?],[?], Chandrasekhar [?] and Southwood [?]. They yield the incompressible (primary) Kelvin-Helmholtz instability for
Finally, the roots (17d) are spurious.
Some of the roots (17a-d) can coincide for special values of uk. For example, when
the roots va1, va2+, vK± ( or + according to the sign of  r1-
r1- r2) and vS- coincide and their value is
r2) and vS- coincide and their value is
This degeneracy corresponds to the point D1 (v1 = -a1, v2 = -a2), where the lines (16a d) cross. It can be verified that ui ³ uD, and that the equality holds only for  r1
r1  r2 = 0. Let us now assume that S1,S2 are large, but finite. Then the term
r2 = 0. Let us now assume that S1,S2 are large, but finite. Then the term  P1(v1,v2)+
P1(v1,v2)+ P2(v1,v2) in (15) can be treated as a small perturbation that couples the degenerate roots va1- , va2+, vK+ (or vK-), vS-. It can be shown that part of the degeneracy is removed, and some roots acquire an imaginary part. The unstable modes so arising (secondary KHI) have no analogue among the purely incompressible modes. It is interesting to observe that this instability appears around uk» uD, that is, in a range of uk that is stable according to IMHD, since it lies below ui.
P2(v1,v2) in (15) can be treated as a small perturbation that couples the degenerate roots va1- , va2+, vK+ (or vK-), vS-. It can be shown that part of the degeneracy is removed, and some roots acquire an imaginary part. The unstable modes so arising (secondary KHI) have no analogue among the purely incompressible modes. It is interesting to observe that this instability appears around uk» uD, that is, in a range of uk that is stable according to IMHD, since it lies below ui.
In addition to D1, there are three other points where degeneracy of the roots (17a-d) occurs, namely D2 (u = -uD, v = -vD), D3 (u = vD, v = uD) and D4 (u = -vD, v = -uD). The removal of the degeneracy at D2 due to compressibility leads to overstable modes like at D1. On the other hand, the removal of the degeneracies at D3 and D4 does not lead to instabilities.
V Stability diagrams
The problem of finding the localized eigenmodes is straightforward, if tedious, since we must calculate numerically the roots of the polynomial P (of degree ten), that depends on seven independent parameters. Six of them characterize the plasma configuration; they can be taken as the ratios rb = B2/B1, rs = S2/S1 and rd = r2/r1, the magnitude u of the relative velocity, and the angles j1 from B1 to u, and q from B1 to B2 (magnetic shear angle). The remaining is the angle y1 from B1 to kt, and identifies the perturbation we are considering.
Notice, however, that P (and its roots) depends on u only through the combination
Accordingly, we shall represent the results of the analysis by means of diagrams in which we plot the growth rate Im(v) of the unstable modes as functions of y1 and uk, keeping fixed the remaining parameters (rb, rs, rd, q) that determine P. An example is the stability diagram shown in Fig. 3, in which we have drawn a contour plot of Im(v) for the parameters of a case investigated in Section VI (case (d), rb = 1.5, rs = 2.67, rd = 0.117, q = -80º). In Fig. 3 we have also drawn the curve u = ui(y1) that gives the marginal stability condition (18) according to the incompressible model. All the points of the stability diagram above ui(y1) correspond to instability according to IMHD. Notice that the contour plot does not refer to a unique plasma configuration, since we have not yet specified u and j1. Then it can be used for all the configurations having the same values of rb, rs, rd and q. This is a distinct advantage since with a single graph we can study the effects of changing the magnitude of the relative velocity and its orientation with respect to the magnetic field.
In Fig. 3, we can see the main effects of compressibility: the large-uk stabilization and the small-uk destabilization of the primary instability, and the presence of the secondary instability in uk intervals that are stable according to IMHD. It should also be mentioned that for uk appreciably larger than ui(y1) (i.e., not very close to it) the growth rates calculated with CMHD are always smaller than those calculated with IMHD (17c).
To investigate a particular configuration by means of the stability diagram we must draw the curve C given by eq. (21), that depends on the two remaining parameters (u, j1) that characterize it. Following C we find the value of Im(v) for this configuration, for any perturbation characterized by the angle y1. Since the problem is invariant under the transformation (v® v, uk® uk), it suffices to calculate the contour plot for uk ³ 0; of course, we must then draw the curve C¢ given by uk = -ucosa in addition to C.
In the example shown in Fig. 3 we see that the configuration described by C and C¢ (u = 1.7A1, j1 = -89.9º) is stable according to IMHD, but is unstable if compressibility is taken into account. The unstable modes occur in the (approximate) range 40º£ y1£ 50º and they belong to the secondary KHI. Their maximum growth rate is small (Im(v) » 0.04A1), but significant. It can be observed that other configurations with the same values of rb, rs, rd and q can be more unstable. The extreme of Im(v) in Fig. 3 is » 2.115A1; it occurs for y1 » 25° and uk » 5A1, a value that requires a very large u.
The meaning of the large-uk stabilization can be clarified by means of an example. Let us consider in Fig. 3 a hypothetical configuration with u = 10A1 and j1 = -89.9°. The new curves Cn and  are similar to C and C¢, only scaled by the factor 10/1.7. Part of Cn (for 45°£ y1£ 113°) lies in the upper part of the stability diagram (uk > ud6) corresponding to stable perturbations: these are the large-uk modes stabilized by compressibility. However, this configuration is unstable, since Cn and
are similar to C and C¢, only scaled by the factor 10/1.7. Part of Cn (for 45°£ y1£ 113°) lies in the upper part of the stability diagram (uk > ud6) corresponding to stable perturbations: these are the large-uk modes stabilized by compressibility. However, this configuration is unstable, since Cn and  pass through the unstable part of the diagram (actually, its most unstable modes have Im(v) very close to the extreme value for the diagram). Clearly, configurations having very large u are always unstable, although large-uk stabilization may occur for some modes.
pass through the unstable part of the diagram (actually, its most unstable modes have Im(v) very close to the extreme value for the diagram). Clearly, configurations having very large u are always unstable, although large-uk stabilization may occur for some modes.
A few comments must be made concerning stability diagrams like Fig. 3. To draw them we calculate the roots of the dispersion relation at discrete points of a grid in the (y1,uk) plane. Sometimes, at the same point (y1,uk) there are two unstable roots (this happens when the secondary intervals A and B overlap, or when any one of them overlaps parts of the primary interval). In these instances we show only the larger Im(v). The secondary intervals are very narrow in some (y1,uk) regions, and may not show up, due to the coarseness of our grid (for the same cause some contours appear wavy in Fig. 3). Nothwithstanding these drawbacks, stability diagrams are extremely useful tools, since they provide an economical and fast way for finding the most interesting domains in parameter space. It is then possible to perform more precise and detailed calculations in these regions only, with confidence that we shall not miss anything relevant.
VI Parameters of magnetopause configurations
Before discussing the application of the theory to the magnetopause, it is convenient to review how the parameters used in our formulae can be obtained from the theoretical models or from spacecraft data. We assume that the outside region (as seen from the Earth) is region 1. In the applications, the parameters of the configuration (the flow velocities  and
and  and the angles yB1,
and the angles yB1, and yB1,
and yB1, from B1 to
from B1 to  and
and  , respectively) are given in a reference frame at rest with respect of the Earth. In our theory we use a reference frame moving with the average velocity u¢ = (
, respectively) are given in a reference frame at rest with respect of the Earth. In our theory we use a reference frame moving with the average velocity u¢ = ( +
+ )/2, then u1 = u, u2 = -u, with u = (
)/2, then u1 = u, u2 = -u, with u = ( -
- )/2. In what follows, all velocities are given in km/s. We employ the following formulae:
)/2. In what follows, all velocities are given in km/s. We employ the following formulae:
The angle d from u to u¢ is given by
In eqs. (23) and (24) the factor Sign(sinqu) is needed to obtain the correct determination of j1 and d. Finally, the phase velocity of the perturbation in the Earth's frame is given by
To consider the remaining parameters we must discuss separately the theoretical and spacecraft data.
Data derived from theoretical models
The conditions for the excitation of the Kelvin-Helmholtz instability on the dayside magnetopause were recently investigated in two papers. One, by Miura [?], reports numerical MHD simulations on the development of the instability, starting from hyperbolic tangent profiles of the unperturbed field quantities. One of the main results is that the magnetopause appears to be more KH unstable for northward IMF conditions than for southward pointing magnetic fields. However, the choice of parameters for the simulations is more adequate for the analysis of near flank configurations rather than dayside proper. The second paper [?] is based on a linear incompressible theory, and specifically addresses the distribution of the KH activity over the magnetopause surface. Charts of KHI growth rates, relying on input parameters provided by a MHD code that simulates the physical conditions of the frontside magnetosheath, are given. One of the main results is that under northward IMF conditions, the KH activity is restricted to some well defined regions of the magnetopause. Even when the IMF is due north, the activity decreases as the latitude increases from the magnetopause equator. In an third paper [?] the latitude dependence of the KHI is examined with a linear incompressible theory based on hyperbolic tangent profiles, using our incompressible theory for a tangential velocity discontinuity.
The data used here are given in Tables 1 and 2. Those of Table 1 (also used in [?]) proceed from ref. [?] and were calculated with the magnetosheath model of ref. [?], which is also described in [?]. The IMF is assumed to point exactly north. The positions are at equator, middle latitude, and high latitude, along a meridian about 3 hours east of noon. The main difference among these positions is the increase of the local magnetic shear angle.
We have in this case  = 0, then u = u¢ =
= 0, then u = u¢ =  /2, j1 = yB1,
/2, j1 = yB1, and v¢ = v-u¢cos(y1-j1). The model provides yB1,
and v¢ = v-u¢cos(y1-j1). The model provides yB1, , the shear angle q, the ratio rb = B2/B1, as well as the following quantities:
, the shear angle q, the ratio rb = B2/B1, as well as the following quantities:
In (??), u¥ and r¥ are the velocity and the density of the solar wind, far from the interaction region.
Because the magnetosheath model does not provide magnetospheric values for temperature and density, Table 2 complements the set of parameters needed in the theory. We assume u¥ = 500 km/s and use typical values of the density ratio and of the temperatures in both regions, often observed in spacecraft crossings of the magnetopause (expressed as rd = r2/r1, rs = S2/S1 and fs = S1/u¥). Clearly rd, rs and fs must satisfy the equilibrium condition (1). In terms of the f 's and r's this implies 2fd (1rd
(1rd ) = g
) = g (
( 1). So we first assign rd and fs, and then use this relation to calculate rs. Since
1). So we first assign rd and fs, and then use this relation to calculate rs. Since  must be positive, we need
must be positive, we need  > g
> g (
( 1)/2fd. When rb > 1 (as in case (a) below) this condtion sets a lower bound on fs.
1)/2fd. When rb > 1 (as in case (a) below) this condtion sets a lower bound on fs.
Using the data of Tables 1 and 2 we then find
and from these quantities we calculate the remaining parameters of our theory.
Spacecraft data
At the flanks of the magnetopause, the magnetosheath flow is supersonic and the effects of compressibility on the KHI are expected to be important. We shall examine a configuration at the near equatorial magnetopause at dusk, observed by Interball/tail during the event of January 11, 1997. This was at the tail of a coronal mass ejection passing Earth, during which the dynamic pressure of a high density solar wind strongly compressed the magnetosphere. As a consequence, Interball/tail was for some time in the magnetosheath, and reentered the magnetosphere, after the dynamic pressure returned to lower values. During the crossing of the magnetopause, from magnetosheath to low latitude boundary layer, the spacecraft measured the physical parameters necessary for a stability analysis. A detailed study of the event is given in ref. [?], together with a discussion of the Kelvin-Helmholtz instability, based on an incompressible model. We intend to revisit that configuration with our compressible theory. The interface that we shall consider is that between the magnetosheath and the low latitude boundary layer.
In the first line of Table 3 we give the parameters of the event (we use the definitions MA,1º A1/ , MS,1º S1/
, MS,1º S1/ ). The second line contains the parameters of a hypothetical configuration with a slightly larger value of MA,1, to ascertain the effect of this change.
). The second line contains the parameters of a hypothetical configuration with a slightly larger value of MA,1, to ascertain the effect of this change.
We must recognize that owing to measurement uncertainties, the spacecraft data do not comply with the equilibrium condition (1) at the interface. To emend this flaw, we replaced the measured rs (that is the less reliable datum) by the value derived using the remaining data in the equilibrium condition, expressed as 2 ,1 (1 rd
,1 (1 rd ) = g
) = g ,1(
,1( -1).
-1).
The expressions of u, u¢, j1, d and v¢ are given by eqs. (22)-(25), and the remaining quantities we need are:
We now investigate the stability of these configurations of the magnetopause.
VII Stability of some magnetopause configurations
Configurations near the front of the magnetopause
In the low latitude case (a) there is no magnetic shear, so that the flute modes are unstable, both in the incompressible limit and if compressibility is taken into account. In Fig. 4 we compare the growth rate obtained with the compressible model with that predicted by IMHD (eq. 17c). It can be noticed that there is no significant difference. An increase of the relative velocity by a factor of 3-4 does not change this conclusion.
The intermediate and high latitude cases are stable when compressibility is taken into account, a result that coincides with the predictions of IMHD. In Fig. 5 we show the stability diagram for the high latitude parameters. We can see the lowering of the critical value uc, due to compressibility (already mentioned in Section I). This effect is of no consequence for the configuration (c) owing to the low relative velocity, but it may be relevant for configurations with a large relative velocity (say, u » 1.5A1).
A configuration in the near flank of the magnetopause
The stability diagram corresponding to these parameters is shown in Fig. 3. It can be appreciated that this configuration is stable according to the IMHD model, but is unstable when compressibility is taken into account. Moreover, this instability corresponds to the secondary modes, which have no counterpart in IMHD. The growth rate of the instability is small, but significant, as can be seen in Fig. 6.
When the line C of the configuration passes close to the marginal stability line for the primary modes, as happened in this case, the stability properties of the configuration are very sensitive to slight changes of the parameters. This can be appreciated in Fig. 7, in which we show the growth rate of the instability, for a slightly different orientation of the relative velocity u with respect to the magnetic field (j1 = 75.5° instead of 89.9°). It can be noticed that this change produces a fourfold increase of the growth rate of the secondary instability (and a shift towards larger y1). The primary instability is also present now, although its growth rate is much smaller than that of the secondary modes. This is due to the small-uk destabilization phenomenon, since the modified configuration is still stable according to IMHD.
If we change the relative velocity, keeping the remaining parameters fixed (as if the solar wind had been slightly faster at that event), the line C of Fig. 3 shifts upwards, and the primary instability becomes dominant for a 30% (or larger) increase of u.
In Fig. 8 we show the stability diagram for case (e), where MA,1 differs from case (d) by 14%. The effect of this change is to increase the growth rate of the secondary instability with respect to the results of Fig. 6. This modified configuration is stable according to IMHD.
VIII Conclusions
Compressibility affects the Kelvin-Helmholtz instability by changing the unstable domains of the modes already present in the incompressible model as well as their growth rate. Modes with large uk (the projection of the relative velocity on the wave vector of the perturbation) are stabilized. At the same time the lower boundary of the unstable uk interval shifts downwards, thus destabilizing perturbations that are stable according to IMHD, for uk < ui (the critical value for marginal incompressible instability). On the other hand, the growth rate of the unstable modes above ui is reduced by compressibility. In addition, compressibility introduces new unstable modes (the secondary modes) that do not exist in IMHD, and that occur for uk below ui. For these reasons, compressibility may play an important role in determining the stability of configurations with a relative velocity of the order of ui.
For configurations of the front of the magnetopause, which have small relative velocities, the IMHD model gives reliable estimates of their stability, and compressibility effects do not introduce significant changes. However, compressibility must be taken into account when assessing the stability properties of configurations at the flanks of the magnetopause. As shown in Section VII, in these cases the occurrence of the secondary instability and the shift of the boundary of the primary instability play an important role. Then, configurations that are stable if compressibility is neglected turn out to be unstable when it is considered. In these situations, the stability properties are quite sensitive on the values of the parameters. The estimates based on IMHD may be misleading, and a careful analysis is required in each case, since no simple rule of thumb can be given. In these respects the stability diagrams introduced in Section V may prove useful, since a single graph allows to visualize the effect of changing the magnitude and orientation of the relative velocity.
Acknowledgments
We acknowledge grants from CONICET (PIP 4521/96 and PIP 4535/96), the University of Buenos Aires (Projects X151 and TX32) and NASA (grant NAG5-2834).
- [1] M. G. Kivelson and S. H. Chen. The magnetopause: Surface waves and instabilities and their possible dynamic consequences. AGU Monograph 90, Physics of Magnetopause, edited by P. Song, B. U. O. Sonnerup and M. F. Thomsen. Geophys. Mon. Ser. 90, AGU, Washington, DC, 257 (1995).
- [2] A. Miura. Kelvin-Helmholtz instability at the magnetopause: computer simulations. AGU Monograph 90, Physics of Magnetopause, edited by P. Song, B. U. O. Sonnerup, and M. F. Thomsen. Geophys. Mon. Ser. 90, AGU, Washington, DC, 285 (1995).
- [3] C. J. Farrugia, F. T. Gratton, and R. B. Torbert. Viscous-type processes in the solar wind-magnetosphere interaction. Special volume Challenge to Long-Standing Unsolved Space Physics Problems in the 20th Century. Space Science Review, 95 (1/2), 443 (2001).
- [4] S. Duhau and J. Gratton. Kelvin-Helmholtz instability of anisotropic plasma in a magnetic field. J. Plasma Phys. 13, 451 (1975).
- [5] F. Gratton, J. Gratton, and A. G. González. Convective instability of internal modes in accelerated compressible plasmas. Plasma Phys. Controlled Fusion 30, 435 (1988).
- [6] W. A. Newcomb. Compressibility effects on instability growth rates. Phys. Fluids 26, 3246 (1983).
- [7] M. G. Kivelson and D. J. Southwood. Coupling of global magnetospheric MHD eigenmodes to field line resonances. J. Geophys. Res. 91, 4345 (1986).
- [8] M. G. Kivelson and Z.-Y. Pu. The Kelvin-Helmholtz instability on the magnetopause. Planet. Space. Sci. 32, 1335 (1984).
- [9] A. G. González and J. Gratton. The Kelvin-Helmholtz instability in compressible plasmas, in Proc. VIII Latin-American Workshop on Plasma Physics. Vol. 1 (Review papers) p. 23. Tandil, Argentina (1998).
- [10] A. Miura and P. L. Pritchett P. Nonlocal stability analysis of the MHD Kelvin-Helmholtz instability in a compressible plasma. J. Geophys. Res. 87, 7431 (1982).
- [11] C. J. Farrugia, F. T. Gratton, L. Bender, J. M. Quinn, R. B. Torbert, N. V. Erkaev and H. K. Biernat. Recent work on the Kelvin-Helmholtz instability at the dayside magnetopause and boundary layer. Polar Cap Boundary Phenomena, edited by J. Moen et al., Kluwer Academic Publishers, Netherlands, 1 (1998).
- [12] A. G. González and J. Gratton. The Kelvin-Helmholtz instability in a compressible plasma: the role of the orientation of the magnetic field with respect to the flow. J. Plasma Phys. 51, 43 (1994).
- [13] A. G. González and J. Gratton. The role of a density jump in the Kelvin-Helmholtz instability of a compressible plasma. J. Plasma Phys. 52, 233 (1994).
- [14] A. G. González, J. Gratton and M. González. The Kelvin-Helmholtz instability in compressible plasmas with magnetic field shear. Proc. IX LAWPP, AIP Conf. Proc. 563, 47 (2001).
- [15] S. Chandrasekhar. Hydrodynamic and Hydromagnetic Stability Oxford Univ. Press (1961).
- [16] W. I. Axford. Quart. J. Mech. Appl. Math. 13, 314 (1960).
- [17] W. I. Axford. Can. J. Phys. 40, 654 (1962).
- [18] D. J. Southwood. The hydrodynamic stability of the magnetospheric boundary. Planet. Space Sci. 16, 587 (1968).
- [19] A. Miura. Dependence of the magnetopause Kelvin-Helmholtz instability on the orientation of the magnetosheath magnetic field. Geophys. Res. Lett. 22, 2993 (1995).
- [20] C. J. Farrugia, F. T. Gratton, L. Bender, H. K. Biernat, N. V. Erkaev, J. M. Quinn, R. B. Torbert and V. Dennisenko. Charts of joint Kelvin-Helmholtz and Rayleigh-Taylor instabilities at the dayside magnetopause for strongly northward interplanetary magnetic field. J. Geophys. Res. 103, 6703 (1998).
- [21] J. E. Contín, F. T. Gratton and C. J. Farrugia. A study of Kelvin-Helmholtz modes for hyperbolic tangent field profiles applied to the dayside magnetopause. Fluidos 2001, edited by J. C. Ferreri. ISBN 927-20148-0-9 (2001).
- [22] J. E. Contín. Ph. D. Thesis, Inestabilidades de láminas de corriente con flujos de plasma y aplicaciones a la magnetopausa diurna. Facultad de Ciencias Exactas y Naturales, Universidad de Buenos Aires (1999).
- [23] N. V. Erkaev. Results of the investigation of MHD flow around the magnetosphere. Geomagn. Aeron. 28, 455 (1988).
- [24] C. J. Farrugia, F. T. Gratton, J. Contin, C. C. Cocheci, R. L. Arnoldy, K. W. Ogilvie, R. P. Lepping, G. N. Zastenker, M. N. Nozdrachev, A. Fedorov, J.-A. Sauvaud, J. T. Steinberg, and G. Rostoker. Coordinated Wind, Interball/tail, and ground observations of Kelvin-Helmholtz waves at the near-tail, equatorial magnetopause at dusk: January 11, 1997. J. Geophys. Res. A4, 105, 7639 (2000).
Publication Dates
-
Publication in this collection
11 Feb 2003 -
Date of issue
Dec 2002
History
-
Received
30 June 2002






































