Hydrophobic models of protein folding and the thermodynamics of chain-boundary interactions

Hydrophobic models of protein folding and the thermodynamics of chain-boundary interactions

Ayse Erzan^I,II; Erkan Tüzel^III

^IDepartment of Physics, Faculty of Sciences and Letters Istanbul Technical University, Maslak 80626, Istanbul, Turkey

^IIFeza Gürsey Institute, P. O. Box 6, Cengelköy 81220, Istanbul, Turkey

^IIISchool of Physics and Astronomy, University of Minnesota, 116 Church St. SE, Minneapolis, MN 55455, USA

ABSTRACT

We review some results concerning the energetic and dynamical consequences of taking a generic hydrophobic model of a random polypeptide chain, where the effective hydrophobic interactions are represented by Hookean springs. Then we present a set of calculations on a microscopic model of hydrophobic interactions, investigating the behaviour of a hydrophobic chain in the vicinity of a hydrophobic boundary. We conclude with some speculations as to the thermodynamics of pre-biotic functions proteins may have discharged very early on in the evolutionary past.

I Introduction

The approach of a statistical physicist to biological problems is different from that of a biologist, in the same way that the approach of a physicist to any natural phenomenon is different from that of an engineer. The difference seems to lie in regarding any given instance of a particular phenomenon not as the product of an ingenious design, but only as a member of a very large ensemble of possible realizations of a generic rule, all governed by the same laws of physics. To a statistical physicist, a biological molecule is not, first and foremost, a high precision tool custom-made to perform a highly specialized task; it is rather a member of a very large set of possible outcomes of random processes, which, under nonequilibrium conditions, have conspired to produce a certian, albeit very improbable result. Moreover, as has already been thoroughly underlined by Eigen [1] and Maynard-Smith [2], biological entities typically correspond to sharply peaked probability distributions (''quasispecies") about some point in biological phase space, rather than unique solutions to some optimization problem. This distribution is of course reflected in the genetic code, and also must translate itself to the proteins that make up the organism.

Another source of deviations from perfect order is thermal noise. We would like to stress that the protein in its native state must essentially correspond to a self-organized system, i.e., the ''native state'' should be concieved of as the attractor of a dynamics [3]. This typically corresponds not to a unique conformation but to a set of conformations to which the trajectory of the phase point representing the molecule is confined after asymptotically long times (which may already be achieved in microseconds).

In this paper we will first review a simple model involving discrete torsional degrees of freedom [3]. The hydrophobic interactions driving the folding of the polypeptide chain [4, 5] are modeled by Hookean springs connecting pairs of hydrophobic residues. [6-12] This system, with harmonic interactions, under dissipative dynamics driven by random noise, leads to a distribution of energy states obeying a modified one-dimensional Ornstein-Uhlenbeck [13, 14] process, quite independently of the nature of the sequence of hydrophobic and polar residues, or the dimensionality of the space. It can be shown to obey the so called Wigner distribution [15-19]

over a very large range of energies e relative to some E_min. This distribution resembles that found for the vibrational energy density of real proteins [6].

The second consequence of this simple model of Hookean springs is that that under Metropolis Monte Carlo dynamics with random initial conditions, the model exhibits power law relaxation for the initial stages of decay, and at the later stages the relaxation obeys a stretched exponential ~ exp(-t^a), with the exponent a 1/4 [20]. This Kohlrausch-Williams-Watts type relaxation behaviour is observed experimentally for real proteins, and predicted theoretically [4,21-24]. At zero temperature the probability distribution function of the energy steps encountered along a relaxation path in phase space also obeys a stretched exponential form, with another exponent a 0.39. In [20] we show that a = a/ (a + 1), which yields a value for a in very good agreement with our simulation results.

In the second part of this review, we would like to discuss work done with P nar Önder [25], on the statistics of a hydrophobic chain near a hydrophobic boundary. The hydrophobic interaction arises from the competition between the energy and the entropy terms in the free energy. It turns out that so-called hydrophobic molecules can, in fact, lower the total internal energy when intermixed with the water molecules, but only in a low entropy state of water with a high degree of short range order. For low enough temperatures, this state is, in fact, the equilibrium state as it lowers the free energy. However, for somewhat higher temperatures, the entropy term in the free energy wins out, and the hydrophobic (non-polar) molecules seperate out from the water molecules, which are now in a completely disordered state. At still higher temperatures, even this segregation disappears.

The decorated lattice model proposed by Widom and co-workers [26-31] provides a microscopic basis for the statistical physics of the so called hydrophobic interaction, which is an effective, entropy driven phenomenon. We adapted the Widom model to investigate the behaviour of hydrophobic chains in the neighborhood of hydrophobic boundaries. The motivation was to eventually understand the role of hydrophobic surfaces in the process of protein folding, i.e., to see if they could provide a chaperoning effect. We have been able to treat certain aspects of the problem analytically, by restricting ourselves to two dimensions, and treating the wall-chain interaction in a one-dimensional approximation. Nevertheless the full solution still involves a certain amount of numerical manipulation. It is gratifying to find that within a given temperature interval, the hydrophobic chain prefers to adsorb on a hydrophobic boundary, and outside this interval it is more or less in a randomly coiled state. Moreover, within this interval, the chain is adsorbed in a more stretched or collapsed configuration, for lower and higher temperatures, respectively, and remains somewhat collapsed at temperatures high enough for it to have just desorbed from the wall. The interplay between the entropy of the water molecules and the entropy of the chain is what gives rise to this nonmonotonic behaviour.

In the last part we will briefly discuss the thermodynamics of the folding of hydrophobic or randomly polar and hydrophobic polypeptide chains near a hydrophobic wall and speculate as to the evolutionary possibilities to which this may have given rise, for the selection of those chains with narrowly defined native states [32].

The paper is organized as follows. In section II, we discuss the energetics and the glassy relaxation behaviour of the simple Hookean model, in section III, we present our results on the hydrophobic chain near a hydrophobic boundary, and in section IV, provide a brief summary of a scenario for protein-RNA co-evolution, with prospects for further research.

II A Gaussian model for protein folding

The Gaussian model of a polypeptide chain we considered [3, 20] consisted of a chain of N residues (treated as point vertices), chemical bonds of fixed length along the backbone, and N - 3 dihedral angles (see Fig. 1). We assumed that we are in a temperature range where the hydrophobic interactions are appreciably strong. The hydrophobic interactions between the non-polar residues will then act in such a way as to segregate them from the polar residues and the ambient water molecules. We mimick the effective hydrophobic interactions by placing Hookean springs between all pairs of non-polar residues.

In this study we were motivated by the model proposed by Halilo glu, Bahar, and Erman [9] where all interactions between the different residues are governed by confining square-law potentials [9-12,33]. In our model, however, the covalent bonds between residues are treated as fixed rods of equal length, the chemical angles are also taken to fixed. The residues located at the vertices may be polar P or hydrophobic H. All the hydrophobic vertices are to be connected to each other with springs of equal stiffness. This results in their being driven to the relatively less exposed center of the molecule in the low lying energy states, whereas the polar residues are closer to the surface. It is important to note that we treat all H - H pairs on an equal footing, i.e., there is no ''teleological" information that is fed into the system by connecting only those H - H pairs which are close to each other in the native configuration for a particular sequence.

It is known that real proteins are distinguished by H, P sequences that lead to unique ground states while a randomly chosen H, P sequence will typically give rise to a highly degenerate ground state. In the absence of detailed knowledge regarding the rules singling out the realistic H, P sequences we considered a generic H, P sequence obtained by choosing fifty percent of the residues to be hydrophobic and distributing them randomly along the chain. We have checked that our results were quite robust with respect to changing the sequence of hydrophobic or hydrophilic residues, or even taking all of them to be hydrophobic. (In the last section of this paper we will indulge in some speculation as to how those sequences with unique ground states may have been selected for.)

In this model, the energy of the molecule is given by

If we define Q_i = 1 for the ith vertex being occupied by a hydrophobic residue, and Q_i = 0 otherwise, we may write c_i,j = Q_iQ_j, and the interaction matrix then becomes

We take the bond angles q_i, i = 1 , N - 1, to have the alternating values of (-1)ⁱq, with q = 68^°. The dihedral angles f_i can take on the values of 0 and ±2p/3 . The state (conformation) of the system is uniquely specified once the numbers {f_i} are given.

In this study, we did not take into account steric effects explicitly. The constraints placed on the conformations due to the rigid chemical bond lengths and by restricting the chemical and dihedral angles to discrete values, prevent the molecule from trivially collapsing to a point. This has a similar effect to placing the chain on a tetrahedral lattice; however, since the chemical angles are slightly different from p/3, this is not exactly true, and the configurations are off lattice when compared to a tetrahedral structure. Since the chain has a certain rigidity and persistence, the volume of the folded structures to grows with N, the number of residues.

A. Dissipative dynamics of the Hookean chain

The position vectors r_i of each of the vertices in the chain can be expressed in terms of a sum over the directors R_i of unit length representing the chemical bonds, which may be obtained from R₁ by successive rotations M_k(q_k) and T_k(f_k) through the bond and the dihedral angles [34], viz.,

where we may choose R₁ to lie along any of the Cartesian directions in our laboratory frame without loss of generality. We obtain the torques that act at each of the vertices i by substituting this in equation (2) and taking the partial derivative with respect to f_i, viz.,

The system is assumed to evolve within a viscous environment, subject to random kicks from the surrounding molecules. As a numerical realization of this dissipative system, we explore the phase space under a dynamics based on relaxing pairs of rotational degrees of freedom, namely the dihedral angles, sampled with a probability which is a function of the conjugate torques,

We may write the Langevin equation for the positions of the vertices as

where z_r is a friction coefficient and x_r(i, t) is a Gaussian distributed noise term, delta correlated in i and in time. Equivalently, in terms of the state vector f = (f₁, , f_N), we have the Langevin equation

where the torque

_i is a function of all the angles {f}, z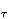 is the appropriate friction coefficient and x 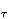is again a Gaussian random force delta correlated in space and time. Viewed in this way the dynamics is similar to a pinned interface or a charge density wave system [35-39] in 1 + 1 dimensions.

The dynamical rules we employ for the sequential updating of the system loosely correspond to a discrete version of the dissipative system envisaged in Eq.(8) above. In order to mimick the conservation of angular momentum, we choose pairs of vertices at a time, turning the f_i in opposite directions [3]. (This does not strictly conserve angular momentum, due to the fact that the axes of rotation are not necessarily parallel; however since the motion is highly dissipative, we do not think this is a big problem.) The choice of vertices for each updating operation is done according to the distribution of torques over the vertices of the chain.

The most natural probability distribution we can form out of the torques, without introducing any special scale into the problem, is P(i) = |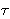_i|^h/S_j |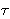_j|^h. Note that h is a parameter of our dynamics; we discuss below how changing h affects our results.

1. At each step, for that given configuration of the chain, we form two such independent distributions, one for {

_i > 0} and another for {_i < 0}.

2. We choose a pair of vertices ( one with positive, the other with a negative torque on them), according to the above distribution.

3. We then update the dihedral angles at the selected vertices, by incrementing them according to f_i (t + 1) = f_i (t) + sign(_i) × (2p/3).

After applying the search strategy based on changing the torques according to a distribution, we found that updating the maximal torques (h > 0) drives the system to a state with relatively high energies, whereas a random search (h = 0) or preferentially choosing the minimal torques (h < 0) gives rise to more successful strategies for reaching low lying energy states. Thus it can be said that h here plays the role of a coarse- or fine-graining parameter in the exploration of the energy landscape. It should be noted that incrementing preferentially those vertices with high torques on them corresponds, in the language of the Langevin equation (8) to relatively small friction coefficients z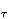; when h = 0, one simply has thermal noise, and no force term.

B. Distribution of energy states

The distribution of the energies of the discrete configurational states explored by the chain of N = 48 residues shown in Fig. 1, as it evolves under the above dynamics, is shown in Figs. 2, 3, for both positive and negative h. After the first 5000 steps were discarded, the statistics were taken over 5000 steps of the trajectory. We checked that the statistics were stationary at this point so that we may safely assume that we have reached the attractor for this dynamics.

The shape of the distribution essentially does not change with h for h < 0, while for positive h the peak shifts to successively higher values of the energy, and the distribution is distorted towards a Gaussian, indicating that the states explored are less correlated. These figures compare very favorably with the energy histograms obtained by Socci and Onuchic [40] for a Monte Carlo simulation on a lattice model of a proteinlike heteropolymer, the density of vibrational states found by ben-Avraham [6] and the ultraviolet absorption spectra reported by Mach et al. [41]. It should be observed that the distributions which we obtain are also extremely similar to the specific heat capacity C_P as a function of temperature as found by Chan for different proteins. [42] It is interesting to note that it is also very similar to the distribution of Euclidean distances to the global energy minimum in the phase space of large atomic clusters [43].

We were able to fit the simulation results very successfully with a distribution of the Wigner form (Figs. 2,3)

for h = -6 to h = 3. Here E₀ corresponds to the offset due to the lowest energy state attained for the different h, and it can be seen that it shifts the distribution to higher values of the energy for higher values of h. The distributions become Gaussian for h = 6 and h = 8. (See Ref.[3], Table Ia,b for the values of the fitting parameters)

It should be mentioned that the same energy distributions may be fit equally well (or better near the point E₀ and in the far tail) by the ''inverse Gaussian'' [44], where the probability density is given by,

This has the same functional form as the distribution of first passage times over a distance d for an Ornstein Uhlenbeck process [13, 14] with diffusion coefficient D and initial drift velocity v, in the regime of small times, if one makes the further identifications A = d²/(2D) and B = d/v. The parameters and estimated errors for the fits to the parameters A and B are given in Table II of Ref. [3]. Both the ''diffusion constant'' (mobility) and the ''drift velocity'' of the phase point along its trajectory in phase space depend on h, being maximum for h = 0 and decreasing for positive values of h. For h < 0 they are essentially independent of h.

C. Universality of the energy historgrams and the Ornstein-Uhlenbeck process

An Ornstein-Uhlenbeck (OU) process describes the diffusive motion of a particle subject to a drift velocity proportional to the distance from the origin [13, 14]. Such a process for a single particle in one dimension would be described by the Langevin equation,

with a Hookean force F(x) = -gx and a delta correlated random force x(t), á(x(t))²ñ = s². In the absence of the stochastic term which gives rise to diffusive motion, the velocity is simply proportional to the distance from the origin (or the point of equilibrium). For an initial displacement x(0) = d, the solution for the distribution of first passage times through the origin is given by

where r = g/z and y = exp(-rt).

We would now like to show that both the Wigner distribution (9) and the inverse Gaussian distribution (10) arise as limiting forms in an OU process. Clearly, without the stochastic term, the solution for (11) is simply x = dexp(-rt) = dy. We see that (12) goes over, in the limit of large times, i.e. y 1, to

On the other hand, for very small times, (12) becomes, to leading order,

where we have defined rd = v.

Since x = dy is the ''distance remaining to the origin,'' the distribution function (13) may just as well be considered as a function of x. For late times, we get f_W(x) µ x exp(-rx²/s²) which is in the form of the Wigner surmise (1). On the other hand, for very small times, x ~ d(1 - rt) = d - vt. The distance from the initial point, º (d - x)/v, becomes simply proportional to the time elapsed and we get the ''inverse Gaussian''(10) form,

where = (d/s)² and m = 1/r. It should be noted that (13 and 14) are numerically very similar.

Now let us observe that the energy E given in Eq.(2) obeys a one dimensional OU proces (11) under the dynamics given by (7). Since there is no explicit time dependence of E, we have

Substituting from (7) we get,

From (2) we find

We see that the second term is like an average of the product of differences (r_i - r_k) · (r_j - r_k) over (i, j) pairs (i ¹ j), and for a reasonably isotropic configuration, it vanishes. To the same approximation, we may assume that the second term in Eq.(17) is itself equal to a Gaussian stochastic noise, i.e., set x_E(t) = K å_ij c_ij (r_i - r_j) · x_i(t). This yields the required result, namely,

If under the given dynamics, the E distribution obeys one of the limiting forms (13) or (14), then the first passage time distribution for the attainment of the lowest energy state must obey, in turn, Eq. (12). This is the reason why the distributions of first passage times for rather general global optimization problems with quadratic cost functions [44] is the same as the form of the distribution of energy states which we find from our simulations.

That the same form is found experimentally for the spectral fluctuations of rather diverse confined systems of sufficient complexity [17, 16, 43, 45] seems to indicate that quadratic cost functions seem to be a sort of attractor, under coarse graining, for a large space of many-body interactions. The seemingly universal behaviour which ben-Avraham finds for the density of vibrational states [6] and the ultraviolet absorption spectra reported by Mach et al. [41] for various proteins, also display very similar curves. Thus there seems to be a striking universality [8] not only between different protein-like structures, but also between different ranges of length and energy scales. It is actually surprising that the density of vibrational states should have a behaviour similar to energy histograms obtained under our dynamics, since the former involve inertial degrees of freedom, while the latter arise from dissipative dynamics

It is also intriguing to compare the results for h > 0 (Fig. (2)) with the numerically obtained nth neighbor spacing distributions of the eigenvalues for Gaussian orthagonal matrices, as reported by Porter [18], where the identical shift of the peak and tendency to a symmetric Gaussian distribution is found. This we interpret as reinforcing our observation that larger h dynamics results in a more coarse-grained sampling of the energy landscape. A very similar sequence of distributions is obtained by Wales [43] for the energies of large atomic clusters, with successively further right-shifted peaks corresponding to distributions about higher metastable states.

D. Relaxation Behaviour

In order to investigate how the present model relaxes to equilibrium at a given temperature T, we have employed Metropolis Monte Carlo dynamics [20]. This consists of

a) choosing a pair (i, i¢) of dihedral angles randomly on the chain, and updating the (f_i, f_i¢) in a way that preserves angular momentum, incrementing them in opposite directions by Df = ±2p/3,

b) accepting the move with unit probability if DE < 0 and with probability p = exp(-bDE)) for DE > 0, where b is an effective inverse temperature, b = (k_BT)^–1 with k_B being the Bolzmann constant.

c) repeating the second step once before discarding the pair altogether and going to the first step.

We monitor the relaxation of the total energy as a function of ''time'' measured in the number of MC steps, (i.e., the number of pairs (i, i¢) sampled) until a steady state is reached, typically in about 10,000 steps for chains of N = 100. The results averaged over 20 randomly chosen initial configurations at zero temperature (b = ¥) are shown in Fig. 4. Defining º (E - E₀)/E_I, where E₀ is the (time- averaged) equilibrium energy and E_I, the initial value, we find that it obeys a power law, (t) ~ t^–s with s = 0.49±0.01 for the initial stages of the decay, while later stages can be fitted by a stretched exponential (t) ~ with a = 0.234±0.003.

We also performed simulations for different values of b, for chains of N = 48, averaging over 100 runs with random initial configurations. For b ® ¥, b = 0.5 and b = 0.3, the above relaxation behaviour continues to hold and the exponents do not seem to depend on b, with a 1/4 and s 1/2 as given in Table I.

Clearly one may write E(t), averaged over many independent runs, as áE(t)ñ = áE(0) - DE_i Q(t - t_i)ñ where Q is the Heavyside step function and t_i = , with 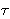_k being the waiting time at the kth step, not to be confused with the symbol for the torques in subsection IIA. Taking the time derivative one gets,

At zero temperature, the expectation value of can be calculated by carrying out an integration over the distibution of waiting times {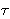_k}, and the distribution of energy steps encountered along the relaxation path. The expectation value, áñ is then,

It is important to note that the distribution of waiting times

_k is dependent only on the configuration of the chain at the k' th step and independent of the previous waiting times. Since the dynamics is just changing a pair of dihedral angles in opposite directions, for each conformation {f_i} one may define an associated chain of N(N - 1)/2 sites, with each site corresponding to a pair of angles (i, i¢) on the original chain. On the associated chain, a site will be assigned the value 1 if the corresponding pair of angles has at least one ''allowed'' move, and the value 0 if both moves are ''blocked'' under the Metropolis dynamics at zero temperature. Now the probabilities of encountering allowed or blocked moves as one takes successive Monte Carlo steps are simply given by the density of 1' s or 0' s on the associated chain at the kth relaxation step. Let us label these probabilities p_k and q_k = 1 - p_k. Then, in the k'th conformation, the probability of making a transition after precisely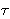 _k blocked moves simply obeys the first passage time distribution [13],

If we assume that the 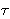are distributed identically at each step of the relaxation process (and therefore independently of the DE), then we can evaluate the averages in (21) immediately, and we end up with a simple linear decay for E(t). By contrast, to see how the relaxation times depend on the state of the system, we may argue that the larger the energy loss in a relaxation event, the longer it will take for the phase point to make a transition out of this state. Since m_k is roughly the expectation for 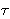_k, we assume that m_k ~ 1/DE_k. With the assumption that the energy steps encountered along a relaxation path are independently distributed, i.e., P(DE₁¼DE_M) = P(DE_s) for a process of M steps, one finds,

where I_j,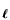(t) is

This is obtained by taking the integral representation for the delta-function in Eq.(21), and then performing the integrals over the

_k with the probability distribution (22), and finally performing the remaining integral using the residue theorem. Meanwhile we find that the probability distribution of the energy differences encountered along a relaxation path, P(DE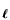), also is a stretched exponential P(DE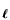) = P_o exp(-(DE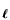)^a), with a = 0.39 ±0.02 (see Fig. 5). The angular brackets then take the form

which we approximate by DE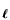 exp(-(DE_k)^a). The integration in equation (24) is then straightforward, leading, upon substitution in (23), to

where a_j = j (1 - a) (aj)^-a (1 + a)^–1 and

Substituting the above value of a we get a = 0.28 ±0.01 which is the result we obtained from the fits to the MC simulations within our error bounds.

The distribution of DE along a trajectory of the h-dynamics [3] is quantitatively different from the distribution of DE encountered along a Metropolis Monte Carlo path, and depends on h. This arises from the highly complex nature of the energy landscape, and the extremely important correlations that arise between the energy steps encountered depending upon how the phase space is being sampled. In particular, we have found out that in the limit of extremely large h, where no cooperativity remains, the distribution of DE along a trajectory of the dynamics is Poissonian, which would have led to a = 1/2 instead of 1/4.

The relaxation to the native states for several real proteins was investigated by Erman [23, 24], who also finds a stretched exponential relaxation with a = 1/4. Experiments on real proteins and polymers [4, 21, 22] yield 0.2 < a < 0.4. Our results seem to be closer to 1/4 and smaller than the values most commonly found for pinned charge density waves [39], or spin-glasses [46], namely 1/3. It should also be noted that glassy behaviour is obtained here in the absence of quenched randomness, or of frustration arising from steric hindrances, which we do not take into account.

Comparing the theoretical and experimental relaxation behaviour near the native state with the behaviour we observe at relatively high energies for random heteropolymers, we conclude that the relaxation behaviour, and therefore the dynamics and the structure of the energy landscape are universal over a very large range of energies, and are relatively independent of the specific sequence or the details of the dynamics.

III Hydrophobic chain near a hydrophobic boundary

In this section we will go back to the effective, entropy mediated hydrophobic interaction which is the driving force behind protein folding considered in the previous section as well as many other biological processes [4, 5, 47-50]. We will review some work which builds upon the model introduced by Widom and co-workers [26-30] to understand the microscopic mechanism leading to the effective attractive interaction between non-polar molecules placed in water, at least within a certain temperature interval. Then we will use this model to study the behaviour of a hydrophobic chain near a hydrophobic boundary, in two dimensions [25]. In trying to understand the behaviour of a hydrophobic chain in water, one must take into account both the hydrophobic interactions mediated by the orientational entropy of the water molecules, and the configurational entropy of the chain, while respecting its connectivity.

Although the behaviour of chains (or membranes) in the vicinity of spatial boundaries have been considered before [51-53], these studies have concentrated on temperature independent interactions.

With the inclusion, to various degrees of accuracy, of the entropy of the chain, we are able to take into account the competition between the entropy of the water molecules which can be constrained by the presence of hydrophobic molecules in their neighborhood, and the entropy of the chain. We find that although at low and high temperatures, the chain prefers to be in a random configuration, detached from the wall, there is an intermediate temperature range where it is adsorbed on to the wall, at least for the relative values of the hydrogen bond, dipole-induced dipole and solvation energies which we have assumed.

The motivation behind studying this particular system is to shed light upon the chaperoning role which might be played by a hydrophobic surface in facilitating the folding process.

A. Decorated lattice model of hydrophobic interactions

A decorated lattice model that mimics the solvent mediated hydrophobic interaction was suggested by Widom and his collaborators [26-30]. In this model, q-state Potts spins, {s_i}, are situated at lattice sites. These represent the polar solvent molecules. They can have any of the q different polarization directions. Hydrophobic molecules (HM), which are non-polar, can only be accommodated at interstitial sites, more precisely on the bonds connecting neighboring pairs (see Fig. 6). Lattice-gas variables, {s_ij}, s_ij = (0,1), located on the bonds (ij), indicate whether an interstitial site is empty or occupied by a HM.

The interaction energy between a pair of solvent molecules is given by (u - w) - u. The occupation of the instertitial site is not allowed unless the neighboring pair of Potts spins are in the ''special state" 1. The allowed states and their energies are summarized in Table II.

We have slightly modified this model, by introducing an energy of solvation and relaxing the prohibition against the occupation of the interstitial site in the disordered state. In this way we may actually write down a Hamiltonian for the water-and-hydrophobic solute system as,

The interaction energies are ordered so that

where v may be thought of as the solvation energy of the HM in the disordered state of the water molecules (see Table II).

The ordering of the various interaction energies may be seen to follow from elementary considerations. The interaction between water molecules and HM is always attractive, because of the dipole-induced dipole interaction. On the other hand water molecules can form short lived tetrahedral structures [54, 55] stabilized by hydrogen bonds [56], i.e., a type of short ranged order. Because these structures have an open cage like space between them [57], a HM can be accommodated there without breaking any hydrogen bonds. Thus, this ''ordered'' configuration is the minimum energy configuration of water molecules in the presence of a HM. In this model, the unique ordered state of the tetrahedrally bonded pentameric configurations of the water molecules [57], which is able to accommodate the HM without breaking any hydrogen bonds, is identified with the configuration where all the s_i are in the state 1.

If there are no HMs between the ordered water molecules, there still is an attractive interaction due to the hydrogen bonds and the dipole-dipole interactions, but the absolute value of the interaction energy is smaller, by precisely the amount contributed by the induced dipole interactions. At higher temperatures, water molecules will tend to be oriented randomly. This state, with no HM intermixed with the water molecules, we chose as the reference, i.e., the zero level of the energy. When water molecules are randomly oriented, they can still have hydrogen bonds between them, though fewer in comparison to the ordered state. However, unlike the ordered state, there will be less open space between them. To be able to accommodate a HM in a disordered region of water molecules, further hydrogen bonds have to be broken. Thus, the insertion of a HM within this disordered phase of water molecules is energetically unfavorable.

The Hamiltonian Eq.(30) may be rewritten in terms of two-state variables t_i, defined by

with t_i = {1,0}, if we allow a temperature dependent ''external field." In the partition function the multiplicity of the s_i ¹ 1 states can be taken care of by inserting a factor of (q - 1) for each Potts spin not in the ordered state, or a term -b(1 - t_i) ln(q - 1) into the Hamiltonian, to get,

Larger values of q are more realistic since q is the number of different orientations in which the solvent molecule can find itself. Apart from steric hindrances, we expect the orientation to be able to vary continuously, corresponding to some appropriate q ® ¥ limit [29]. Larger q values will clearly give rise to stronger entropy-mediated interactions between the solute molecules.

B. Effective hydrophobic pair interaction in the Mean Field Approximation

We would like to make use of this effective Hamiltonian to compute the self-interaction of a hydrophobic chain. To do this efficiently, we need an effective temperature dependent pair potential between the elements of the chain. In one dimension, one could perform a trace over the mediating solvent molecule between two HM, to obtain an effective interaction. However, in two or higher dimensions, correlations between solvent molecules may be built up over many different paths. Therefore we decided to compute the effective interactions between the solute molecules (without any effect felt from the presence of a wall) in the Mean Field Approximation. This is the subject of this section.

In the MFA, the Hamiltonian (31)on a cubic lattice in d dimensions, can be written as

where the sum runs over the bonds pointing to the nearest neighbor sites. The field átñ is the mean value of the random variables t_j associated with the neighboring water molecules, and it will be determined self-consistently. We have inserted m for later convenience in computing expectation values, and will otherwise set it to unity. We obtain the effective pair interactions between the solute (HM) molecules by performing the t sum in the partition function.

The partition function Z is defined as

i = 1,¼,2d, and átñ must be found from

which we solved numerically for each given temperature T, for d = 2.

We may define all the possible effective p-body interactions that may be built from these lattice gas variables, by writing the effective Hamiltonian

where (ij) denotes nn and nnn pairs and (ijk) triplets. Note that the nearest neighbor (nn) and next nearest neighbor (nnn) pairs are indistinguishable from each other in this ''tree" approximation, since the bonds issuing from the single central site may be freely interchanged with one another. The interaction constants may be determined by setting

By considering terms with all the s_i set to zero, only one different from zero, or a pair of them different from zero, etc., one is able to determine all the coupling constants k_p.

For the the two-body interactions k₂, which we will call M(b) from now on to simplify the notation, we find,

Substituting the numerical values for átñ in Eq.(37) one finally obtains the effective solute-solute interaction energy in two dimensions, which we plot, in Fig. 7, against the inverse temperature for different choices of q. The interaction between HMs is attractive for any finite temperature, as k₂ enters Eq.(35) with a negative sign.

To the lowest approximation [30] we will neglect the plaquette and triplet couplings k₄ and k₃ as being of higher order in the fluctuations. The linear term we will also neglect, because it is like a chemical potential, and this will be taken into account in the wall-particle effective interaction which we will now calculate in a one-dimensional approximation in the next subsection. The constant term of course cancels in all the expectation values, and may therefore be dropped from the start.

C. Effect of the boundary

In order to be able to estimate in closed form the effective interaction of a HM with the hydrophobic boundary, we will consider a one dimensional system, and compute the effective interaction between a hydrophobic insertion and the hydrophobic boundary from the free energy difference resulting from this insertion. We will then use this as an approximation to the true interaction between the solute and the hydrophobic wall, in the unique normal direction to the wall (a linear boundary) in two dimensions.

The Hamiltonian in Eq.(31) becomes, in one dimension,

For N being the length of the one-dimensional lattice of water molecules, the free energy cost F(N, T, r) of adding only one HM at an interstitial a distance r from the wall at temperature T is given by

where b^-1 = k_BT as usual, Z₀(N, T) is the partition function of the one dimensional system with s_i = 0 for all i, that is, no HM molecules, and Z(N, T, r) is the partition function computed in the presence of one HM a distance r from the wall. The effective interaction between the wall and a single HM is thus given by the free energy cost of bringing HM from bulk to distance r from the wall,

where r_b means a displacement from the wall beyond which the effect of the wall is no longer perceptible, namely a bulk site. In the thermodynamic limit

To compute the partition functions in (39), we used the transfer matrix method. From Eq.(38), the transfer matrices in one dimension are obtained as

Thus, the transfer matrix is conditional on the presence (or absence) of an interstitial HM at each bond connecting two water molecules, and we find,

for the two possible resulting transfer matrices. To get the transfer matrices in a more symmetric form, we have rewritten the third term in the Hamiltonian (Eq.(38)) as -b^–1 (2 - t_i - t_i+1) ln(q – 1). ¿From Eq. (40), we get, with one HM inserted at a distance r from the wall,

Notice that the left-most vector is fixed to be unity, signalling the presence of the hydrophobic wall. In the thermodynamic limit N ® ¥, this reduces to,

where we have defined

with

being the eigenvalues of (0), and a_kl the elements of its kth eigenvector.

We will use F^(I)(1, r), which we have calculated exactly in one dimension (Fig. 8), to give us an estimate of the interaction between the HM and the hydrophobic boundary in two dimensions.

Hydrophobic chain with intra-chain and chain-boundary interactions

We are interested in the behavior of a hydrophobic polymer chain in the presence of a hydrophobic wall. This means we have to respect the connectivity of the chain in performing the trace over the lattice gas variables corresponding to the HM. In other words, the phase space consists of allowed chain configurations.

To be able to treat the model at least in a semi-analytical way, we have considered two simplified sets of chain configurations, which we will outline below.

1. Modular chain or SOS model

We define a set of elementary modules, from which a large number of chain conformations can be built, such that only nearest neighbor modules come within the interaction range of each other. The subset of configurations that can be generated by random combinations of the modules that are shown in Fig. (9a) can clearly be seen as graphs (taking the boundary as the axis) without overhangs, as in a restricted solid-on-solid (SOS) model [58] in (1+1) dimensions, where successive steps are constrained to differ by at most one unit of height. Making use of the linearity of the chain and the restriction to nearest neighbor interactions between the modules, we used the transfer matrix along the chain to solve the partition function for our model Hamiltonian.

We labeled the modules in Fig. (9a) as 1, 2, 3 from left to right. A chain configuration is uniquely specified by associating a variable, u_i = {1,2,3}, i = 1,¼,N_m, with each module along the chain, and by specifying the distance of the first module from the wall. Note that the number of residues along the chain is given by 2N_m in this case. The interaction energy of each residue with hydrophobic wall is computed using F^(I)(1, r). We took M(b) defined in Eq.(37), to be the interaction energy between nearest and next nearest neighbor residues (see Fig.(9b)). Note that the nearest neighbor interaction (wavy line) connects residues belonging to modules twice removed from each other. Yet, since this occurs only in the (i, i + 1) = (2, 3) or (3, 2) combination, independently of the identity of the i - 1st module, it can still be accomodated within a nearest-neighbor Hamiltonian.

We model the effective Hamiltonian of a polymer with N_m modules as,

The vectors |u_iñ correspond to the three states of the variable u_i, i.e., (1,0,0), (0,1,0) etc., so that the coefficient of the pair interaction M(b) is conveniently written in terms of

The second term is the free energy cost of adding HMs to the solvent matrix, h₁(r_i, r_i–1) = -F^(I)(1, r_i–1) - F^(I)(1, r_i). The distance of the second residue on the ith module from the wall, r_i, is found from r_i = r + r_i, where r is the distance of the first module from the wall, and

Note that the displacement of the first residue on the ith module is the same as that of the second residue on the i–1st module, and therefore the expression for h₁ follows.

The partition function of the polymer is,

Explicitly,

Here, |r_i, u_iñ are × dimensional vectors, with being the size of the system in the direction orthoganal to the wall. The transfer matrix is given by a direct product

with

where k, = 1, 2, 3, (2 SETA 3) indicates an interchange of the indices 2 and 3 in the previous equation, and

where g, h = 1,¼ and z = 1, 2, 3. We note that only the diagonal, upper diagonal and lower diagonal elements of the matrices R^(z) are different from zero. However we have not been able to find a way to analytically diagonalize the matrices , or, for that matter R; they are not simply cyclic, but the matrix elements depend directly on the row (or column) index through the functions F^(I)(1, r_i). (See Eq.(13)). Therefore we have had to perform the matrix multiplications numerically.

We calculated the center of mass distance of the hydrophobic polymer from the hydrophobic boundary,

where the sum over the set W shall henceforth mean a trace over r₁, u₁, r_i, u_i, r_Nm, u_Nm. Defining a 3 × vector, |fñ such that

one may slightly rewrite Eq.(59) as,

and this is shown in Fig.(10) as a function of temperature. At intermediate temperatures the polymer chains are attracted to the wall so strongly that ár_cmñ 1.5 . The chains are predominantly in a zig-zag configuration confined very close to the wall, with half of them actually adsorbed on the wall, and the maximum number of nn and nnn interactions.

As b ® 0 (high temperatures) the intrachain interaction M also goes to zero, the entropy of the chain becomes the determining factor, and the chain floats free. At low temperatures, as the entropy term in the free energy becomes negligible, the equilibrium state is determined by energetic considerations, and the polymers desorb and take on random configurations, constraining a large number of water molecules in their neighborhood.

The average end to end distance of the polymer chain, projected on to the boundary, is given by

Defining |yñ by,

we get,

The temperature dependence is reported in Fig. (11). In the limit b ® 0, clearly áLñ = N_m(1 + ), which is what one sees in Fig.(11), with N_m = 30. It is interesting to note the non-monotonic behaviour of áLñ within the region of interest, namely the temperature interval for which the center of mass lies very close to the wall. This non-monotonicity arises from the competition between the entropy mediated effective self-interaction of the chain (leading to smaller L) and the interaction with the wall (completely shielding one side from the water by stretching out to adsorb on to the wall). This behaviour is also observed in the models we have considered in the subsequent sections.

Although the SOS model is exactly solvable in principle, it is unable to take into account configurations of the chain which fold on themselves, and we therefore have also considered a model where such conformations are allowed.

2. The n -fold model

In this section we take a different subset of chain configurations over which to perform exact summations. These configurations are shown in Fig.(12). If the length of the polymer is N_l then the energy of a chain with an integer number of folds N_l/n, is given by

where r is the distance from the wall and n_n = 3(n - 1)(N_l/n - 1) is the total number of nearest neighbor and next nearest neighbor pairs in this configuration. The partition function

is nontrivial to sum, again because of the complicated way in which the functions F^(I)(1, r + i - 1) depend on their arguments, viz. Eqs.(46,47), and the nonlinear dependence of n_n on n.

The center of mass displacement from the wall can be obtained in principle from

where the prime indicates that the summation is only over exact divisors of N_l. The mean value of the vertical distance between the first and last monomer is áLñ = áN_l/nñ, which can be calculated from,

To obtain these quantities, the partition function and the expectation values were summed numerically, inserting, for each different value of b, the numerical value of F^(I)(1, r + i - 1) and of M. For the numerical sums, of course a finite set of values had to be chosen for r. The results we find are qulitatively and quantitatively very close to our earlier results for the SOS-like model. [25]

In the low temperature limit, increasing the number of HM-water nn pairs lowers the energy and this is favorable since the entropy term in the free energy is suppressed, and the chain takes on relatively open, random configurations. At intermediate temperatures where the hydrophobic interactions are the most effective, the chain prefers to neighbor the hydrophobic wall at as many nn sites as possible, and therefore is adsorbed on the wall in the unfolded state. As the temperature is raised somewhat more, effective self interactions of the chain become more important, and the chain is in a more folded state, although still adhering close to the wall. At high temperatures it is advantageous to minimize the number of nearest neighbor sites at which the chain is in contact with water molecules, since the entropy of the water molecules is rather large, especially for large q. On the other hand, the entropy of the chain also favors open configurations, which win out in the high temperature limit. We found, with N_l = 50, áLñ is close to = 18.8, at both extremes, with the power being that of the self avoiding walk in two dimensions.

E. Monte Carlo simulations

Monte Carlo computations for 3×10⁵ random self avoiding walk configurations of length N = 20 were reported in Ref. [25]. Here we will report the results from 3×10⁴ configurations , generated via a genetic algorithm [60]. If a random walk passes through any lattice point which it has already visited, the configuration is discarded, and a new one generated. Each successfully generated configuration was decorated with the interaction potentials F^(I)(1, r) and M(b) from Eqs.(40,37), to finally compute the expectation values for the center of mass displacement from the wall and the longitudinal component of the end to end distance, in the canonical ensemble. The results we find (Figs. 13,14) are surprisingly close to those shown in Figs. (10,11), to the n-fold model results and to the MC results in [25].

IV Thermodynamics of early protein function

It has long been appreciated [34] that proteins are unique among possible amino acid chains in being able to fold into a unique ''native state'' and reversibly unfold to a random coil. Synthetically produced amino acid chains have degenerate ground states. Moreover, small to medium sized proteins typically fold and unfold at one go, without any intermediary states between the folded and the unfolded ones. This can be quantified by various measures of so called ''two-state cooperativity''[42, 61]. It is a challenge to understand the mechanism by which such amino-acid sequences were selected in the course of evolution or how biological evolution as we know it came to being in the first place. It would seem to be self-evident that the highly specific functions discharged by proteins in vivo would not have come into play unless two-state cooperativity had already been selected via some pre-biotic mechanisms. In Ref. [32], we have argued for a basic thermodynamic function which could have been fulfilled by proteins, namely that of a refrigerant in an adsorption refrigeration process.

Eigen identifies two essential properties of a biological system, or ''principles of organisation," as hypercycles and compartition, namely the containment and segregation of biological material [62]. The translation of RNA code means picking out a specific sequence of amino acids from a random jumble and transforming them into an ordered chain. As a result, the information carried by RNA is translated into specific intra-chain interactions as well as interactions with the ambient water, subject to given boundary conditions. Once the peptide chain is formed and wiggles free from the RNA molecule, it can behave as an active Brownian particle [63] responding to variations in temperature or other external stimuli in specific ways which enable it, in turn, to act upon them.

A common assumption regarding compartition is that porous rock could have played host to prebiotic processes. [2, 64] Recent evidence has been providedby Martin and Russel [65] that life could have originated in iron monosulfide precipitates on the ocean floor, whose pores, lined with certain lipids, may have provided the first simple cell-like structures.

We have already shown that due to hydrophobic interactions[25] those peptide chains that are near hydrophobic surfaces may adsorb on such surfaces at least within given temperature intervals. It may be conjectured that rock surfaces, with some lipids present, are favorable sites for adsorption, and act as guides for the peptide chains, helping them to fold. Upon folding, as a result of the reduction in entropy, heat will be given off, mostly to the surface of the rock. For special sequences, with specific intra-chain interactions, this folded state will be stable. If, now, the surface on which the proteins have adsorbed is heated, say by the emission of a hydrothermal vent [65], the chain will detach itself from the rock surface. If it is carried along by convective currents away from the heated wall, and in particular towards a cooler pocket, where, say it encounters a region of with a high pH, which lowers the denaturation temperature, this is where it will unfold, absorbing heat from its surroundings.

This, in fact describes an adsorption-refrigeration cycle driven by low quality heat [66-71]. The efficiency of such a refrigeration cycle operated by proteins undergoing a folding-denaturation transition would depend strongly on two parameters: the entropy gap between the folded and unfolded states of the amino-acid chain, and the rate of the folding-unfolding transition. One may now hypothesize that the accidental establishment of such a refrigeration cycle provided an evolutionary advantage to those RNA molecules that coded proteins that were efficient coolants, since, in an overheated environment, lower temperatures could enhance the replication rates of RNA. This completes the hypercycle.

If this scenario is correct, the fates of RNA chains would from then on be bound with the synthesis- and eventual evolution- of polypeptides. Those RNA sequences would be selected for, that were able to synthesize proteins that folded into lower entropy states, and did this in a very short time. Present day biological proteins have unique ground states leading to large entropy gaps. Small single domain proteins fold into their secondary structures within milliseconds [72], or even faster [73].

What we would like to emphasize here is the point of view that simple chemical and physical processes which set the stage for biological evolution, must already have provided a great deal of variety and complexity upon which the fortuitous emergence of self-replicating entities posessing a hereditary code could elaborate.

Acknowledgements

AE gratefully acknowledges partial support from the Turkish Academy of Sciences.

References

[1] M. Eigen, Naturwissenschaften, 10, 58 (1971).

[2] J. M. Smith and E. Szathmáry, Origins of Life (Oxford University Press, Oxford, 1999).

[3] E. Tüzel, A. Erzan, J. Stat. Phys.100, 405 (2000).

[4] H. Frauenfelder, S. G. Sligar, P. G. Wolynes, Science, 254, 1598 (1991).

[5] P.G. Wolynes, J.N. Onuchic, and D.Thirumalai, Science 276, 1619 (1995)

[6] D. ben-Avraham, Phys. Rev. B 47, 14559 (1993).

[7] K.A. Dill, S. Bromberg, K. Yue, K.M. Feibig, D.P. Yee, P.D. Thomas, and H.S. Chan, Protein Science 4, 561 (1995).

[8] M.M. Tirion, Phys. Rev. Lett. 77, 1905 (1996).

[9] T. Haliloglu, I. Bahar, and B. Erman, Phys. Rev. Lett. 79, 3090 (1997).

[10] B. Erman and K. Dill, J.Chem. Phys. 112, 1050 (2000).

[11] B. Erman, Comp. Theor. Polym, Sci. 9 295 (1999).

[12] B. Ewen, D. Richter, in Elastomeric Polymer Networks, edited by J. E. Mark and B. Erman, (Prentice Hall, 1992) p. 220.

[13] W. Feller, An Introduction to Probability Theory and its Applications Vol. II (Wiley, New York, 1957), p. 332ff.

[14] H. Risken, The Fokker-Planck Equation (Springer, Berlin, 1984).

[15] E. Wigner, Proc. Cambridge Phil Soc. 47, 790 (1951); Ann. Math. 62, 548 (1955).

[16] T. Brody, J, Flores, J.B. French, P.A. Mello, A. Pandey, and S.S.S. Wong, Rev. Mod. Phys. 53, 385 (1981).

[17] C.E. Porter, Statistical Theories of Spectra: Fluctuations (Academic Press, New York, 1965).

[18] C.E. Porter, J. Math. Phys. 4, 1039 (1963).

[19] M.L. Mehta, Random Matrices and the Statistical Theory of Energy Levels (Academic Press, New York 1967).

[20] E. Tüzel, A. Erzan, Phys. Rev. E 61, 1040 (2000).

[21] J.L. Green, J. Fan, and C.A. Angell, J. Phys. Chem. 98, 13780 (1994).

[22] J. Colmenero, A. Arbe, and A. Algeria, Phys. Rev. Lett. 71, 2603 (1993).

[23] B. Erman, I. Bahar, Macromol. Symp. 133, 33 (1998).

[24] I. Bahar, B. Erman, F. Kremer, and E.W. Fischer, Macromolecules, 25, 816 (1992).

[25] P. Önder, A. Erzan, Eur. Phys. J. E 9, 467 (2002).

[26] A.B. Kolomeisky, B. Widom, Faraday Discuss. 112, 81-89 (1999).

[27] B. Widom, Pol. J. Chem. 75, 507 (2001).

[28] G.T. Barkema and B. Widom, J. Chem. Phys. 113, 2349 (2000).

[29] G.M. Schütz, I. Ispolatov, G.T. Barkema, and B. Widom, Physica A 291, 24 (2001).

[30] D. Bedeaux, G.J.M. Koper, S. Ispolatov, and B. Widom, Physica A 291, 39 (2001).

[31] B. Widom, P. Bhimalapuram, and K. Koga, ''The Hydrophobic Effect," (review article), to appear in Phys. Chem and Chem. Phys. (2003).

[32] E. Tüzel, A. Erzan, ''A Thermodynamic Model for Prebiotic Protein Function," cond-mat/0107315, and submitted for publication in Phys. Rev. E.

[33] A. Yu. Grosberg, J. Stat. Phys. 38, 149 (1985).

[34] P.J. Flory, Statistical Mechanics of Chain Molecules, (Interscience, N.Y., 1969).

[35] T. Halpin Healy and Y.C. Zhang, Physics Reports, 254, 215 (1995).

[36] J. Krug, P. Meakin, and T. Halpin-Healy, Phys. Rev. A 45, 638 (1992).

[37] A. Erzan, E. Veermans, R. Heijungs, and L. Pietronero, Phys. Rev. B 41, 11522 (1990).

[38] E. Veermans, A. Erzan, R. Heijungs, and L. Pietronero, Physica A 166, 447 (1990).

[39] G. Parisi and L. Pietronero, Physica A 179, 16 (1991).

[40] N. D. Socci, J.N. Onuchic, J. Chem. Phys. 103, 4732 (1995).

[41] H. Mach, D.B. Volkin, C.J. Burke, and C.R. Middaugh, ''Ultraviolet Absorption Spectroscopy,'' in B.A. Shirley ed., Methods in Molecular Biology, edited by B.A. Shirley, Vol. 40: Protein Stability and Folding (Humana Press, Totowa, New Jersey, 1995) p. 91.

[42] H.S. Chan, Proteins: Structure, Fucntion and Genetics, 40, 543 (2000).

[43] M.A. Miller, J.P.K. Doye, and D. Wales, Phys. Rev. E 60 , 3701 (1999).

[44] C.N. Chen, C.I. Chou, C.R. Hwang, J. Kang, T.K. Lee, and S.P. Li, Phys. Rev. E 60, 2388 (1999).

[45] D. Bohigas, M. J. Giannoni, and C. Schmidt, Phys. Rev. Lett. 52, 1 (1984).

[46] M. Mezard, G. Parisi, and M. A. Virasoro, Spin Glass Theory and Beyond (World Scientific, Singapore, 1987).

[47] A. Ben-Naim, Hydrophobic Interactions (Plenum, New York and London, 1980).

[48] A. Ben-Naim, J. Chem. Phys. 90(12), 7412 (1989).

[49] A. Sali, E. Shakhnovich, J. Mol. Biol. 235, 1614 (1994).

[50] K.A. Dill et al., Protein Science, 4, 561-602 (1995).

[51] R.R. Netz, D. Andelman, Oxide Surfaces (Marcel Dekker Inc., New York, 2000)

[52] A. Stella, T. Jr. Phys., 18, 224 (1994).

[53] E. Eisenriegler, Polymers near surfaces (World Scientific, Singapore, 1993).

[54] G. Némethy, H.A. Scheraga, J. Chem. Phys., 36, 3382 (1961)

[55] R.A. Horne ed., Water and Aqueus Solutions Structure, Thermodynamics, and Transport Processes (John Wiley & Sons, London, 1972)

[56] C. Kittel, Introduction to Solid State Physics (John Wiley & Sons,Inc., 1986)

[57] M. Canpolat, F.W. Starr, A. Scala, M.R. Sadr-Lahijany, O. Mishima, S. Havlin, and H.E. Stanley, Chem. Phys. Lett. 294, 9 (1998); H.E. Stanley, S.V. Buldyrev, M. Canpolat, O. Mishima, and M.R. Sadr-Lahijany, Physica A 257, 213 (1998) and Phys. Chem. Chem. Phys. 2, 1551 (2000).

[58] G.H. Gilmer and P. Bannema, J. Appl. Phys. 43, 1347 (1972); H. van Beijeren, Phys. Rev. Lett. 38, 993 (1977); for a review see D.B. Abraham, in Phase Transitions and Critical Phenomena, Vol. 10, edited by C. Domb and J. Lebowitz, (Academic Press, New York, 1986).

[59] J.D. Bryngelson, E.M. Billings, Physics of Biological Systems (Springer, Berlin, 1997)

[60] Y. Sengün, Diploma Thesis, ITU (2003).

[61] H. Kaya and H.S. Chan, Phys. Rev. Lett. 85, 4823 (2000).

[62] M. Eigen, Steps towards Life, a Perspective on Evolution (Oxford University Press, Oxford, 1992); also see M. Eigen and P. Schuster, The Hypercycle (Springer, Berlin, 1979) p.109.

[63] F. Schweitzer, ''Active Brownian Particles with Internal Energy Depot" in Traffic and Granular Flow '99: Social, Traffic and Granular Dynamics, edited by D. Helbing, H.J. Herrmann, M. Schreckenberg. D.E. Wolf, (Springer, Berlin, 2000) p. 161; U. Erdmann (a), W. Ebeling, L. Schimansky-Geier, and F. Schweitzer, Eur. Phys. J. B 15, 105 (2000).

[64] S.A. Kauffmann, The Origins of Order: Self-Organization and Selection in Evolution (Oxford University Press, Oxford, 1999).

[65] W. Martin, M.J. Russell, Phil Trans. Royal Soc. B (Biol. Sci.) (London), 358, 59 (2003).

[66] Y.A. Çengel and M.A. Boles, Thermodynamics: an Engineering Approach (McGraw Hill, N.Y., 1996; in Turkish translation by Literatür Yay nevi, Istanbul, 1996) p. 549.

[67] J.S. Hsieh, Solar Energy Engineering (Prentice Hall, Englewood Cliffs, New Jersey, 1986) p.303.

[68] Y. Teng, R.Z. Wang, and J.Y. Wu, App. Therm. Eng. 17, 327 (1997).

[69] F. Meunier, F. Poyelle, and M.D. LeVan, App. Therm. Eng. 17, 43 (1997).

[70] M. Pons, App. Therm. Eng. 17, 615 (1997).

[71] H.T. Chua, K.C. Ng, A. Malek, and N.M. Ono, J. Appl. Phys. 89, 5151 (2001).

[72] A. Fersht, Structure and mechanism in protein science: a guide to enzyme catalysis and protein folding (W. H. Freeman, New York, 1998).

[73] U. Mayor, M. C. Johnson, V. Daggett, and A. R. Fersht, Proc. Natl. Acad. Sci. USA, 97, 13518 (2000).

Received on 9 May, 2003

Publication Dates

• Publication in this collection
  14 Nov 2003
• Date of issue
  Sept 2003

History

• Received
  09 May 2003
• Accepted
  09 May 2003