The bose metal: a commentary

The bose metal - a commentary

S. Doniach; D. Das

Departments of Applied Physics and Physics, Stanford University, Stanford CA, USA

ABSTRACT

We review the concept of the Bose metal state which arises in 2D superconductors in the quantum limit where vortex loops can grow spontaneously in (2+1) dimensions and, as zero point motions become larger, eventually lead to an insulating state. A nonlocal Coulomb charging term in a Josephson array type model leads to an effective transverse gauge field which can suppress the condensate of vortices in the superinsulating state leading to an intermediate Bose liquid which is not superfluid at T=0, the Bose metal state. We comment on recent work on this state and on other non-superfluid Bose liquids.

1 Formulation

We start from a 2D Josephson junction array model which can be expressed in terms of the Hamiltonian:

where denotes the nearest neighbor vector to site i, and dn_i = (n_i – n₀) with n_i the number density operator which is conjugate to the phase f_i of the superconducting order paramter and n₀ the average density of Cooper pairs. The dn_i satisfy the commutation relations

In the case V₁ = 0, the physics of this model is equivalent to that of a (2+1) dimensional XY model and exhibits a second order phase transition at T = 0 from the superconducting state to the insulating state at a critical value of V₀/J (Doniach 1981)¹.

In 1999, Das and Doniach (in a paper which we will refer to as DD1)² proposed that, as the nearest neighbor repulsion parameter V₁ is increased, a strong coupling phase transition occurs to a phase diagram in which a new Bose metal phase appears at T = 0 in between the superconductng state and the insulating state.

Here we review the properties of this Bose metal state and discuss its relation to various investigations more recently carried out by other authors.

2 Strong coupling transition

In the insulating phase of the junction array model the long range phase coherence of the superconducting order parameter is destroyed by quantum zero point fluctuations and instead the Cooper pair density dn_i acquires a non-zero ground state expectation value. In a path integral picture, these quantum fluctuation effects may be represented in terms of the infinite world lines for the Cooper pair bosons which occur in the superfluid state becoming finite loops (hence localized) in the insulator state.

In a dual picture, the effects of quantum zero point motion on the superfluid state may be expressed in terms of the growth of vortex loops in (2+1) dimensions. The critical point is reached when the entropic contributions of the vortex loops to the ground state path integral overcome the energetic costs, and a ''spaghetti'' transition occurs in which the insulating state is filled with vortex loops of infinite extension.

The physics in the dual picture may be expressed in terms a set of vortices at positions

_i of charge q_i = ±q and mass m_v interacting via a transverse gauge field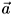 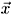with Hamiltonian:

As we shall see below, the action for the gauge field depends on the strength of the near neighbor repulsion V₁. For V₁/V₀ sufficiently large (i.e. under strong coupling conditions) it will turn out that the condensate of infinite vortex loops in the insulating state will be depleted at values of V₀ above those where the Cooper pair world lines form finite loops leading to loss of superconducting coherence of the superfluid state. Then a new state is reached in which neither the Cooper pair world lines are infinite (ie superfluid phase coherence) nor are the vortex loops infinite (as they would be in the ''superinsulator state''^2b where they form a condensate of vortices). The resulting quantum fluid state will turn out to have finite resistance at T = 0 due to uncondensed free vortices, so represents the Bose metal state.

The physics of this ''vortex superfluid'' depletion depends in an essential way on the strength of interaction with the transverse gauge field as will be further discussed below. So presumably this would not manifest itself in a perturbative approach to simple boson models such as as that discussed by Phillips and Dalidovich (2002)³ where the transverse gauge field effects are not considered.

3 Coupling to the transverse gauge field

The appearance of time delayed plasma oscillations of the model as expressed through the transverse gauge field 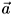in equn.(3), arises from the non-local character of the Coulomb charging term in (1). This was shown in DD1 to have two effects: it gives rise to a finite vortex mass which is proportional to the non-local coupling constant V₁, thus tending to inhibit the zero point motion of the vortices, and it induces a time delay in the propagation of plasmon waves, ie phase modes of the system. The net result of this is that the propagator for the transverse gauge field in (3) satisfies

where

_P is the plasmon velocity. In the limit V₁® 0, m_v ® 0 and (3) reduces to the usual vortex formulation of the Bose superfluid in (2+1)D where the vortices are coupled through the long range Coulomb potential.

The effects of these time delayed interactions on the super-insulator state of the liquid of vortex loops was originally studied by Feigelman et al⁴ in a 1993 paper. In this paper the vortices are represented as a gas of bosons. In applying their results to our model, we treat the vortex loops as a two component plasma of vortices and antivortices. Feigelman et al show that as the strength of the coupling of the gauge field to the vortices is increased, the density of the superfluid condensate, n_s is decreased. In our case this corresponds to a reduction of the superinsulator density. The physics of how this occurs may be understood by thinking in terms of the dephasing due to random Aharonov-Bohm (AB) phases exp(i ò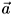·d) experienced by a vortex as a result of the slowly varying transverse gauge field acting on it.

As we discuss in our (2001) paper (Das and Doniach (2001)⁵ - referred to as DD2), when the gauge field fluctuations become very large, the AB phases may become of order p. In this case the vortices may be thought of as locally transmuting from bosons to fermions thus strongly reducing the density of the superinsulator condensate. As the vortex - gauge field coupling (which goes as the vortex mass and is proportional to V₁/J) is further increased, a phase transition occurs to a state in which the vortex loops are no longer infinite and the system starts to acquire a finite resistivity at T = 0. The properties of this Bose metal state are discussed in detail in DD1. It appears to be a new form of quantum liquid distinct from a superfluid in which, in the absence of disorder, the phase fluctuations at T = 0 have zero gap and the anomalous dispersion relation w_k µ k³.

Recently, the self consistent calculation of the transverse gauge field ­ induced reduction of the superinsulator density due to Feigelman et al (1993)⁴ has been examined in more detail by Jack and Lee (2002)⁶ who use a renormalization group argument in which both the gauge field propagator and the boson propagator are treated on an equal basis. The highest frequency contributions to the one-loop insertions are integrated out giving an effective field theory for the remaining fields with renormalized superfluid fraction and compressibility. The process is repeated till only the smallest frequency components of the propagators remain. The authors study the resulting phase diagram and argue that if n_s vanishes while the compressibility, k, of the bose liquid remains finite, then the system will be unstable through a second order transition to the formation of a homogeneous non-superfluid which they then refer to as a metallic state. Their result is in contrast to the arguments made in the Feigelman et al paper where they use a self-consistent approach to estimate the effects of the coupling of the vortices to the transverse gauge field on the gauge field propagator. (Note, however that Jack and Lee consider a model in which the bare interactions between vortices are short ranged, not coulombic as for the case studied by Feigelman et al, and which we considered in DD1.) This self-consistent approximation lead Feigelman et al, to conclude that the transition may be first order or, as discussed in DD1, Kosterliz-Thouless like. Based on the on experimental results of Mason and Kapitulnik⁷ as will be further discussed below, the transition appears to be second order. Thus the results of Jack and Lee provide arguments which help rationalize the experimental findings.

The contrasting case in which k diverges at finite n_s signals a tendency to phase separation. This may be a signal of a first order transition region in the phase diagram. For our model (equn (3)) (equivalently, the model studied by Feigelman et al) we start from a model with long range Coulomb repulsion between vortices of the same sign. Hence phase separation would be too costly in energy and the system would instead be expected to have a modulated density, which would result in some kind of supersolid phase. So the tendency to phase separation found in the Jack-Lee calculations may also signal a first order transition to this phase.

In their paper, Jack and Lee consider both the propagating gauge field model discussed above, and a model in which the gauge field fluctuations are overdamped. They find that the presence of gauge field damping increases the superinsulator density reduction effects, thereby enhancing the tendency of the system to form a metallic state. This is in line with the idea that the effects of Caldeira Leggett type dissipation may be expressed in terms of a transverse gauge field as discussed in DD2. Thus damping of vortex motion may in general be expected to have tendency to reduce the vortex condensate and thus promote the formation of the Bose metal state⁷.

4 Scaling behavior at the SC « BM and BM « INS boundaries

The experimental manifestations of the Bose metal (BM) appear most strongly in the scaling behavior of the resitivity as the two phase boundaries to the BM state are approached from within the state. Here we summarize the results discussed in DD1 and DD2 for completeness.

The SC « BM boundary.

As the superconducting state undergoes a transition to the BM state, we expect the resistivity to reflect that of a set of vortex loops moving in the quasi-random fluctuations of the gauge field. Thus the resistivity of the charged Cooper pair bosons, r_c is given in terms of the conductivity, s_v of the dual vortex variables via⁸

since it is the flux transport resulting from the motion of the unbound vortices which gives rise to a voltage across the sample. s_v is given by the Drude formula s_v = n_vft_tr/m_v, where n_vf is the density of free vortices (more precisely, of those vortex loops which are longer than the mean free path, so that different parts of the loop are uncorrelated) and t_tr is the transport time. We measure the transport time in terms of the normal core size of the vortices, where x₀ is the Ginzburg-Landau coherence length. Then

where R_Q = h/ = 6.45KW.

n_vf diverges as

as the superconducting boundary us approached, where R_c is the critical resistance at the SC« BM phase boundary, and n is the correlation length exponent.

Thus in general we can write

For a pure system, the boundary has the character of a (2+1)D XY model so that n 2/3. In disordered systems such as thin films, we expect n to deviate from this value. As discussed in DD1, this scaling behavior fits quite well with the data of Jaeger et al (1986)⁹ on the R_n dependence of R_ for disordered gallium films.

In finite applied magnetic fields, we can apply the same formula in terms of the density of free vortices injected by the field: x₊ scales as x₊ ~ (H – H_c0) where H_c0 is the critical field for the SC«BM transition. Hence for the magnetic field scaling we have

The BM « INS boundary.

As the magnetic field is further increased, the quantum zero point motion of the vortices grows till eventually they condense into a superinsulator state. As discussed above, there is theoretical evidence that this too will be a second order phase transition. At the present time there is no systematic theory of the scaling at this boundary, so we repeat the heuristic discussion from DD2 where we argue that this boundary should be characterized by two parameter scaling.

Since the voltage measured is a result of free vortex motion, we argue that resistance scales as R ~ V²/W² where V represents the voltage induced by the vortex motion: V = (h/2e)2pn_fLv with v the vortex velocity and L the distance over which they move. Then L scales as L ~ x ~ W^–1/z where W is the frequency scale for the diverging correlation length. Since mv² ~ W, v scales as v ~ As the boundary is approached we assume that the fraction of vortices which participate in the dissipative process scales as n_f ~ |d|^a where d ~ (H – H_c) measures the distance to the boundary of the superinsulator phase and a is an exponent to be determined. Putting these together we find R ~ d^2a/W^1+2/z.

At temperature T, the divergence of x is cut off by T so that W ~ T and the scaling fuction must vary with d/T^1/nz leading to

where f is the scaling function. At low T, the resistance saturates at finite values independent of T so f(x) ® x^–n(z+2) in this limit. Finally, since the resistance is non-critical as H is tuned through H_C, we find that 2a = n(z+2) so that the scaling formula ends up as

The data of Mason and Kapitulnik (1999)⁷ for MoGe films fits this two parameter scaling formula quite remarkably well with z = 1, n = 4/3 leading to a = 2 (see figure in DD2). Thus the argument for a Bose metal state is strongly substantiated by the observed scaling with field and temperature.

The exciton Bose liquid

Recently Paramekanti et al (2002)¹⁰ have described a novel model in which a non-superfluid Bose liquid is stable at T = 0 under appropriate conditions. In this model, instead of a Josephson junction coupling between quantum rotors, a ''ring-exchange'' plaquette operator couples sites of a square 2D lattice. In the quantum rotor representation the starting Hamiltonian is

where r is a site index and

f _r and n_r are conjugate variables:

The f_r are taken to be 2p periodic so that the eigenvalues of the number operators n_r are integers with mean boson density , which is generally taken to have the value = for the half-filling case.

If we think in terms of rotor raising and lowering operators:

then the interaction term takes the form

which has the effect of tunneling a boson to the right on a given row while simultanoeusly moving one to the left on the same plaquette one row up. Thus this Hamiltonian has the remarkable property of conserving boson number on each row and each column of the square lattice. Thinking of b^† as creating a particle and b as creating a hole in the uniform background boson denity, then _int leads to the propagation of particle hole pairs, or ''exciton'' ­ like objects from one side of the plaquette to the other. For this reason the authors term the quantum liquid phase of this model as the ''exciton Bose liquid'', or EBL.

These properties lead to an unusual set of collective phason modes for the model. On expanding the Lagrangian of the model

to quadratic order, the action becomes

where

which vanishes on both the k_x and k_y axes. Thus the model has a continuum of zero gap modes and therefore might be expected to exhibit conducting properties at T = 0.

Going beyond quadratic order, one sees that vortex configurations in which f_r winds by 2p around a plaquette are finite in energy rather than logarithmic as in the usual boson super fluid models. (However double vortex configurations in which the phase winds by 4p may be deformed into zero vorticity configurations). Thus one may expect ground states in which, as the kinetic energy term with strength U is increased the vorticity will increase, so that eventually a quantum insulator state will be reached.

We will not go into further details here, but note that the authors show that, in the quantum liquid state of the model, the real part of the optical conductivity takes the form

where D is a scaling dimension.

The quantum liquid also appears to be unstable to transformations into both superconducting (boson condensate) and insulating states (vortex condensate) depending on details of the parameters. Thus there are very interesting resemblances between the states of this non-superconducting Bose liquid model and the Bose metal model of DD. It would be worth while pursuing this resemblance to see whether addition of usual Josephson coupling terms to the ring exchange coupling of the EBL model could link the two different models, each of which exhibits a stable non-superconducting Bose liquid state at T = 0.

Acknowledgment

We thank Nadya Mason and Aharon Kapitulnik for many discussions, and the US department of Energy for support via the Complex Materials program at SSRL/SLAC. D. Das also acknowledges partial support from the Stanford Institute of Theoretical Physics.

Received on 23 May, 2003

• [1] S. Doniach, Phys. Rev. B24, 5063 (1981).
• [2] D. Das and S. Doniach, Phys. Rev. B 60, 1261 (1999).
• [3] A. Kraemer and S. Doniach. Phys. Rev. Lett. 81, 3523 (1998).
• [4] P. Phillips and D. Dalidovich, Phys. Rev. B65, 081101(R) (2002).
• [5] M. V. Feigelman, V. B. Geshkenbein, L. B. Ioffe, and A. I Larkin, Phys. Rev. B48, 16641 (1993).
• [6] D. Das and S. Doniach, Phys. Rev. B64, 134511 (2001).
• [7] R. L. Jack and D. K. K. Lee, Phys. Rev. B66, 104526 (2002).
• [8] N. Mason and A. Kapitulnik, Phys. Rev. B64, 134511 (2001).
• [9] D. Das and S. Doniach, Phys. Rev. B 57, 14440 (1998).
• [10] H. F. Jaeger, D. B. Haviland, A. M. Goldman, and B. G. Orr, Phys. Rev. B34, 4920 (1986).
• [11] A. Paramekanti, L. Balents and M. P. A. Fisher, Phys. Rev. B66, 054526 (2002).

Publication Dates

• Publication in this collection
  25 Nov 2005
• Date of issue
  Dec 2003

History

• Received
  23 May 2003