Ensemble formalism for nonequilibrium systems and an associated irreversible statical thermodynamics

Ensemble formalism for nonequilibrium systems and an associated irreversible statical thermodynamics

Áurea R. Vasconcellos; J. Galvão Ramos; Roberto Luzzi

Instituto de Física 'Gleb Wataghin', Universidade Estadual de Campinas, Unicamp, 13083-970, Campinas, SP, Brazil

ABSTRACT

It is reviewed what can be considered as the present research trends in what regards to the construction of an ensemble formalism - Gibbs' style - for the case of far-from-equilibrium systems. The main questions involved are presented accompanied with brief discussions. The construction of a nonequilibrium statistical operator is described and its applications commented, and, particularly, it is presented the derivation of an Irreversible Thermodynamics based on the statistical foundations that the nonequilibrium ensemble formalism provides.

I. INTRODUCTION

It is generally considered that the aim of Statistical Mechanics of many-body systems away from equilibrium is to determine their thermodynamic properties, and the evolution in time of their macroscopic observables, in terms of the dynamical laws which govern the motion of their constitutive elements. This implies, first, in the construction of an irreversible thermodynamics and a thermo-hydrodynamics (the latter meaning the particle and energy motion in fluids, rheological properties, etc., with the transport coefficients depending on the macroscopic thermodynamic state of the system). Second, we need to face the all-important derivation of a generalized nonlinear quantum kinetic theory and a response function theory, which are of fundamental relevance to connect theory with observation and experiment, basic for the corroboration of any theory [1], that is, the synthesis leg in the scientific method born in the seventeenth century.

Oliver Penrose [2] has noted that Statistical Mechanics is notorious for conceptual problems to which is difficult to give a convincing answer, mainly:

What is the physical significance of a Gibbs' ensemble?;

How can we justify the standard ensembles used in equilibrium theory?;

What are the right ensembles for nonequilibrium problems?;

How can we reconcile the reversibility of microscopic mechanics with the irreversibility of macroscopic behavior?

Moreover, related to the case of many-body systems out of equilibrium, the late Ryogo Kubo, in the opening address in the Oji Seminar [3], told us that statistical mechanics of nonlinear nonequilibrium phenomena is just in its infancy and further progress can only be hoped by closed cooperation with experiment. Some progress has been achieved since then, and we try in this review to describe, in a simple manner, some attempts in the direction to provide a path for one particular initial programme to face the questions posited above.

Statistical Mechanics is a grandiose theoretical construction whose founding fathers include the great names of James C. Maxwell, Ludwig Boltzmann and J. Willard Gibbs [4]. We may recall that it is fundamental for the study of condensed matter, which could be said to be statistical mechanics by antonomasia. Therefore statistical mechanics can be considered the science mother of the present day advanced technology, which is the base of our sophisticated contemporary civilization. Its application to the case of systems in equilibrium proceeded rapidly and with exceptional success: equilibrium statistical mechanics gave - starting from the microscopic level - foundations to Thermostatics, its original objective, and the possibility to build a Response Function Theory. Applications to nonequilibrium systems began, mainly, with the case of local equilibrium in the linear regime following the pioneering work of Lars Onsager (see, for example, [5]).

For systems arbitrarily deviated from equilibrium and governed by nonlinear kinetic laws, the derivation of an ensemble-like formalism proceeded at a slower pace than in the case of equilibrium, and somewhat cautiously. A long list of distinguished scientists contributed to such development, and among them we can mention Nicolai Bogoliubov, John Kirkwood, Sergei Krylov, Melvin Green, Robert Zwanzig, Hazimi Mori, Ilya Prigogine, Dimitri Zubarev. It must be added the name of Edwin Jaynes, who systematized, or better to say codified, the matter on the basis of a variational principle in the context of what is referred to as Predictive Statistical Mechanics [6-13], which is based on a framework provided by Information Theory.

It can be noticed that the subject involves a number of questions to which it is necessary to give an answer, namely

1. The question of the choice of the basic variables

2. The question of irreversibility

3. The question of the initial value condition

4. The question of historicity

5. The question of providing the statistical operator

6. The question of building a non-equilibrium grand-canonical ensemble

7. The question of the truncation procedure

8. The question of the equations of evolution (nonlinear quantum kinetic theory)

9. The question of a response function theory

10. The question of validation (experiment and theory)

11. The question of the approach to equilibrium

12. The question of a non-equilibrium statistical thermodynamics

13. The question of a thermo-statistical approach to complex systems

14. The question of a nonlinear higher-order thermo-hydrodynamics

15. The question of statistical mechanics for complex structured systems

which are addressed in [13,14].

In the study of the macroscopic state of nonequilibrium systems we face greater difficulties than those present in the theory of equilibrium systems. This is mainly due to the fact that a more detailed analysis is necessary to determine the temporal dependence of measurable properties, and to calculate transport coefficients which are time-dependent (that is, depending on the evolution in time of the nonequilibrium macrostate of the system where dissipative processes are unfolding), and which are also space dependent. That dependence is nonlocal in space and non-instantaneous in time, as it encompasses space and time correlations. Robert Zwanzig [15] has summarized the basic goals of nonequilibrium statistical mechanics as consisting of: (i) To derive transport equations and to grasp their structure; (ii) To understand how the approach to equilibrium occurs in natural isolated systems; (iii) To study the properties of steady states; and (iv) To calculate the instantaneous values and the temporal evolution of the physical quantities which specify the macroscopic state of the system. Also according to Zwanzig, for the purpose to face these items, there exist several approaches which can be classified as: (a) Intuitive techniques; (b) Techniques based on the generalization of the theory of gases; (c) Techniques based on the theory of stochastic processes; (d) Expansions from an initial equilibrium ensemble; (e) Generalization of Gibbs' ensemble formalism.

The last item (e) is connected with Penrose's questions noticed above concerning if there are, and what are, right ensembles for nonequilibrium problems. In the absence of a Gibbs-style ensemble approach, for a long time different kinetic theories were used, with variable success, to deal with the great variety of nonequilibrium phenomena occurring in physical systems in nature. We describe here a proposition for the construction of a Nonequilibrium Statistical Ensemble Formalism, or NESEF, for short, which appears to provide grounds for a general prescription to choose appropriate ensembles for nonequilibrium systems. The formalism has an accompanying nonlinear quantum transport theory of a large scope (which encompasses as particular limiting cases Boltzmann's and Mori's approaches), a response function theory for arbitrarily-away-from-equilibrium systems, a statistical thermodynamics (the so-called Informational Statistical Thermodynamics), and an accompanying Thermo-Hydrodynamics.

NESEF appears as a very powerful, concise, based on sound principles, and elegant formalism of a broad scope to deal with systems arbitrarily away from equilibrium. Zwanzig stated that the formalism "has by far the most appealing structure, and may yet become the most effective method for dealing with nonlinear transport processes" [15]. Later developments have confirmed Zwanzig's prediction. The present structure of the formalism consists in a vast extension and generalization of earlier pioneering approaches, among which we can pinpoint the works of Kirkwood [16], Green [17], Mori-Oppenheim-Ross [18], Mori [19], and Zwanzig [20]. NESEF has been approached from different points of view: some are based on heuristic arguments [18, 21-24], others on projection operator techniques [25-27] (the former following Kirkwood and Green and the latter following Zwanzig and Mori). The formalism has been particularly systematized and largely improved by the Russian School of statistical physics, which can be considered to have been initiated by the renowned Nicolai Nicolaievich Bogoliubov [28], and we may also name Nicolai Sergeivich Krylov [29], and more recently mainly through the relevant contributions by Dimitrii Zubarev [24,30], Sergei Peletminskii [22,23], and others.

These different approaches to NESEF can be brought together under a unique variational principle. This has been originally done by Zubarev and Kalashnikov [31], and later on reconsidered in Ref. [32] (see also Refs. [33] and [34]). It consists on the maximization, in the context of Information Theory, of Gibbs statistical entropy (to be called fine-grained informational-statistical entropy), subjected to certain constraints, and including non-locality in space, retro-effects, and irreversibility on the macroscopic level. This is the foundation of the nonequilibrium statistical ensemble formalism that we describe in general terms in following sections. The topic has surfaced in the section "Questions and Answers" of the Am. J. Phys. [6, 35]. The question by Baierlein [35], "A central organizing principle for statistical and thermal physics?", was followed by Semura's answer [6] that "the best central organizing principle for statistical and thermal physics is that of maximum [informational] entropy [...]. The principle states that the probability should be chosen to maximize the average missing information of the system, subjected to the constraints imposed by the [available] information. This assignment is consistent with the least biased estimation of probabilities."

The formalism may be considered as covered under the umbrella provided by the scheme of Jaynes' Predictive Statistical Mechanics [7]. This is a powerful approach based on the Bayesian method in probability theory, together with the principle of maximization of informational entropy (MaxEnt), and the resulting statistical ensemble formalism is referred-to as MaxEnt-NESEF. Jaynes' scheme implies in a predictive statistics that is built only on the access to the relevant information that there exists of the system [6-12]. As pointed out by Jaynes [8]. "How shall we best think about Nature and most efficiently predict her behavior, given only our incomplete knowledge [of the microscopic details of the system]? [...]. We need to see it, not as an example of the N-body equations of motion, but as an example of the logic of scientific inference, which by-passes all details by going directly from our macroscopic information to the best macroscopic predictions that can be made from that information" (emphasis is ours) [...]. "Predictive Statistical Mechanics is not a physical theory, but a method of reasoning that accomplishes this by finding, not the particular that the equations of motion say in any particular case, but the general things that they say in 'almost all' cases consisting with our information; for those are the reproducible things".

Again following Jaynes' reasoning, the construction of a statistical approach is based on "a rather basic principle [...]: If any macrophenomenon is found to be reproducible, then it follows that all microscopic details that were not under the experimenters' control must be irrelevant for understanding and predicting it". Further, "the difficulty of prediction from microstates lies [..] in our own lack of the information needed to apply them. We never know the microstates; only a few aspects of the macrostate. Nevertheless, the aforementioned principle of [macroscopic] reproducibility convinces us that this should be enough; the relevant information is there, if only we can see how to recognize it and use it" [emphasis is ours].

As noticed, Predictive Statistical Mechanics is founded on the Bayesian approach in probability theory. According to Jaynes, the question of what are theoretically valid, and pragmatically useful, ways of applying probability theory in science has been approached by Sir Harold Jeffreys [36,37], in the sense that he stated the general philosophy of what scientific inference is and proceeded to carry both the mathematical theory and its implementations. Together with Jaynes and others, the Nobelist Philip W. Anderson [38] maintains that what seems to be the most appropriate probability theory for the sciences is the Bayesian approach. The Bayesian interpretation is that probability is the degree of belief which is consistent to hold in considering a proposition as being true, once other conditioning propositions are taken as true [39]. Or, also according to Anderson: "What Bayesian does is to focus one's attention on the question one wants to ask of the data. It says in effect, how do these data affect my previous knowledge of the situation? It is sometimes called maximum likelihood thinking, but the essence of it is to clearly identify the possible answers, assign reasonable a priori probabilities to them and then ask which answers have been done more likely by the data" [emphasis is ours].

The question that arises is, as stated by Jaynes, "how shall we use probability theory to help us do plausible reasoning in situations where, because of incomplete information we cannot use deductive reasoning?" In other words, the main question is how to obtain the probability assignment compatible with the available information, while avoiding unwarranted assumptions. This is answered by Jaynes who formulated the criterion that: the least biased probability assignment {p_j}, for a set of mutually exclusive events {x_j}, is the one that maximizes the quantity S_I, sometimes referred to as the informational entropy, given by

conditioned by the constraints imposed by the available information. This is based on Shannon's ideas in the mathematical theory of communications [40], who first demonstrated that, for an exhaustive set of mutually exclusive propositions, there exists a unique function measuring the uncertainty of the probability assignment. This is the already mentioned principle of maximization of the informational-statistical entropy, MaxEnt for short. It provides the variational principle which results in a unifying theoretical framework for NESEF, thus introducing, as we have noticed, MaxEnt-NESEF as a nonequilibrium statistical ensemble formalism. It should be stressed that the maximization of S_I implies in making maximum the uncertainty in the information available (in Shannon-Brillouin's sense [40,41]), to have in fact the least biased probability assignment.

We proceed next to describe the construction of NESEF and of an irreversible thermodynamics founded on its premises. This is done, as indicated above, in the context of the variational principle MaxEnt, but an alternative derivation along traditional (heuristic) ways is also possible and described in Ref. [14].

II. A NONEQUILIBRIUM STATISTICAL ENSEMBLE FORMALISM

In the construction of nonequilibrium statistical ensembles, that is, a Nonequilibrium Statistical Ensemble Formalism (NESEF), basically consisting into the derivation of a nonequilibrium statistical operator (probability distribution in the classical case), first it needs be noticed that for systems away from equilibrium several important points need be carefully taken into account in each case under consideration [cf. the list of questions above], particularly:

(1) The choice of the basic variables (a wholly different choice than in equilibrium when it suffices to take a subset of those which are constants of motion), which is to be based on an analysis of what sort of macroscopic measurements and processes are actually possible, and, moreover one is to focus attention not only on what can be observed but also on the character and expectative concerning the equations of evolution for these variables (e.g. Refs. [15,42]). We also notice that even though at the initial stage we would need to introduce all the observables of the system, as time elapses more and more contracted descriptions can be used as enters into play Bogoliubov's principle of correlation weakening and the accompanying hierarchy of relaxation times [42].

It can be noticed that to consider all the observables of the system is consisting with introducing the reduced one-particle,

₁, and two-particle,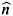 ₂, dynamical operators [13, 14, 42, 43] in classical mechanics given by

with r_j and p_j being the coordinate and linear momentum of the j-th particle in phase space and r and p the continuous values of position and momentum, which are called field variables (for the quantum case see [13]). For simplicity we are considering a system of N particles of mass m; the case of systems with several kinds of particles are straightforwardly included in the treatment: it suffices to introduce a second index to indicate them, i.e r_sj, p_sj, etc. [see Subsection IV.B below].

But it is pertinent to look for what can be termed as a generalized grand-canonical ensemble, what can be done [13] by introducing in place of

₁, and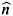 ₂ independent linear combination of them. For simplicity consider only 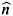₁, and the new variables are the densities of kinetic energy and of particles

and their fluxes of all order, namely,

where r = 1 for the vectorial flux or current, r > 2 for the other higher-order fluxes; r also indicates the tensorial rank, and

stands for the tensorial product of r-times the vector p/m, rendering a tensor of rank r. The contributions associated to 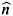₂ are of the form [13]

where p and p' are indexes h or n; r, r'= 0 (the densities),1,2,..., and [...] as above stands for tensorial product. The question of truncation of description, that is to take a reduced number of the above variables (associated to Bogoliubov's principle of correlation weakening and hierarchy of relaxation times) and the question of the approach to equilibrium is discussed elsewhere [13, 14] (In equilibrium, because there survive only the variables of Eqs. (8) only for r, r' = 0, there follows a nonextensive description, becoming approximately extensive in the thermodynamic limit [14]).

(2) It needs be introduced historicity, that is, the idea that it must be incorporated all the past dynamics of the system (or historicity effects), all along the time interval going from a starting description of the macrostate of the sample in the given experiment, say at t_o, up to the time t when a measurement is performed. This is a quite important point in the case of dissipative systems as emphasized among others by John Kirkwood and Hazime Mori. It implies in that the history of the system is not merely the series of events in which the system has been involved, but it is the series of transformations along time by which the system progressively comes into being at time t (when a measurement is performed), through the evolution governed by the laws of mechanics [16, 18].

(3) The question of irreversibility (or Eddington's arrow of time) on what Rudolf Peierls stated that: "In any theoretical treatment of transport problems, it is important to realize at what point the irreversibility has been incorporated. If it has not been incorporated, the treatment is wrong. A description of the situation that preserves the reversibility in time is bound to give the answer zero or infinity for any conductivity. If we do not see clearly where the irreversibility is introduced, we do not clearly understand what we are doing" [44].

The question is then to find the proper nonequilibrium statistical operator that MaxEnt-NESEF should provide. The way out of the difficulties pointed out above is contained in the idea set forward by John Kirkwood in the decade of the forties [16]. He pointed out that the state of the system at time t is strongly dependent on all the previous evolution of the nonequilibrium processes that have been developing in it. Kirkwood introduces this fact, in the context of the transport theory he proposes, in the form of a so-called time-smoothing procedure, which is generalized in MaxEnt-NESEF as shown below.

After the choice of the basic dynamical variables has been performed, and let us call them generically as {

_j(x)}, where x indicates the set of all variables on which the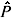 _j may depend [cf. Eqs. (2) and (3), and Eqs. (4) to (6) and (8)], introducing in MaxEnt-NESEF [13, 14, 31-34] the idea that it must be incorporated all the past history of the system (or historicity effects), all along the time interval going from the initial condition of preparation of the sample in the given experiment at, say, time t_o up to time t when a measurement is performed (i.e., when we observe the macroscopic state of the system), we proceed to maximize Gibbs' entropy (sometimes called fine-grained entropy)

with the normalization and constraints given at any time t' in the interval t_o < t' < t, namely

with

_j(x,t') being the nonequilibrium thermodynamic (macroscopic) variables for the description of the accompanying irreversible thermodynamics described in next section.

Resorting to Lagrange's procedure we find that

where

and the j_j are the corresponding Lagrange multipliers determined in terms of the basic macrovariables by Eq. (11), and operators 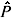_j are given in Heisenberg representation.

Further an additional basic step needs now be considered, namely a generalization of Kirkwood's time-smoothing procedure. This is done introducing an extra assumption on the form of the Lagrange multipliers j_j, in such a way, we stress, that (i) irreversible behavior in the evolution of the macroscopic state of the system is satisfied; (ii) the instantaneous state of the system is given by Eq. (11); (iii) it is introduced the set of quantities {F_j(x,t)} as intensive variables thermodynamically conjugated to basic macrovariables {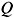_j(x,t) } , what allows a posteriori to generate satisfactory Thermodynamic and Thermo-Hydrodynamic theories. This is accomplished introducing the definition

where w(t,t') is an auxiliary weight function, which, to satisfy the four points just listed immediately above, must have well defined properties which are discussed elsewhere [32], and it is verified that

The function w(t,t') introduces the time-smoothing procedure, and, because of the properties it must have to accomplish its purposes, it is acceptable any kernel that the mathematical theory of convergence of trigonometrical series and transform integrals provides. Kirkwood, Green, Mori and others have chosen what in mathematical parlance is Fejèr (or Cesàro-1) kernel, while Zubarev introduced the one consisting in Abel's kernel for w in Eq. (15) - which apparently appears to be the best choice, either mathematically but mainly physically - that is, taking w(t,t') = eexp{e(t' - t)} , where e is a positive infinitesimal that goes to zero after the calculation of averages has been performed, and with t_o going to minus infinite. Once this choice is introduced in Eq. (12), in Zubarev's approach the nonequilibrium statistical operator, designated by r_e(t) , after integration by parts in time, can be written in the form

where

with being the unit operator, and it is introduced the auxiliary operator 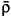(t,0) = exp{-(t,0) } , referred-to as an instantaneous quase equilibrium statistical operator, moreover

The operator (t,0) is designated as the informational-entropy operator, whose relevance and properties are discussed in [45].

In the framework of the nonequilibrium grand-canonical ensemble, namely, when the basic variables are those of Eqs. (4) to (8), we do have that

where

where Ä stands for fully contracted product of tensors, we recall that r and r' equal to 0 stands for the densities, and the F's are the nonequilibrium thermodynamic variables associated to the corresponding observable [13, 46].

Several important points can be stressed in connection with the nonequilibrium statistical operator of Eq. (16). First, the initial condition at time t_o ® -¥, is

what implies in a kind of initial Stosszahlanzatz, in the sense that the initial state is defined by the instantaneous generalized canonical-like distribution 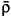, thus ignoring correlations among the basic variables prior to time t_o. Second, r_e(t) can be separated into two parts [13, 24, 30-33], see also [18], namely,

where 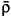(t,0) is the instantaneous distribution of Eq. (19). The first one, 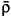, defines an instantaneous, at time t, distribution, which describes a "frozen" equilibrium providing at such given time the macroscopic state of the system, and for that reason is sometimes dubbed as the quasi-equilibrium statistical operator. This distribution describes the macrostate of the system in a time interval, around t, much smaller than the relaxation times of the basic variables (implying in a "frozen" equilibrium or quasi-equilibrium in such interval). But, of course, for larger time intervals the effect of the dissipational processes comes into action. The dynamics that has led the system to that state at time t from the initial condition of preparation at time t_o [cf. Eq. (21)], as well as its continuing dissipative evolution from that state at time t to eventually a final full equilibrium, is contained in the fundamental contribution 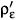(t). Furthermore, there exists a time-dependent projection operator 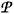(t) with the property that [32,33]

This projection procedure, a generalization of those of Zwanzig (apparently the first to introduce projection techniques in statistical physics [20]), Mori [19], Zubarev and Kalashnikov [27], and Robertson [28], has interesting characteristics. We recall that the formalism involves the macroscopic description of the system in terms of the set of macrovariables {

_j(x,t) } , which are the average over the nonequilibrium ensemble of the set of dynamical quantities {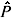_j(x)} . The latter are called the "relevant" variables, and we denote the subspace they define as the informational subspace of the space of states of the system. The remaining quantities in the dynamical description of the system, namely, those absent from the informational space associated to the constraints in MaxEnt, are called "irrelevant" variables. The role of the projection operation is to introduce what can be referred to as a coarse-graining procedure, in the sense that it projects the logarithm of the "fine-grained" statistical operator r_e(t) onto the subspace of the "relevant" (informational) variables, this projected part being the logarithm of the auxiliary (or quasi-equilibrium, or "instantaneous frozen", or "coarse-grained") distribution 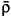(t,0) , and, consequently, the procedure eliminates the "irrelevant" variables, quite in the spirit of the Bayesian-based approach and MaxEnt. The "irrelevant" variables are "hidden" in the contribution 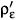(t) to the full distribution r_e(t) of Eq. (22), since it depends on the last term in the exponential of Eq. (16), where the differentiation in time drives ln 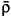outside the subspace of "relevant" (informational) variables. We stress that the projection operation is time dependent, such dependence corresponding to the fact that the projection 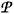(t) is determined by the macroscopic state of the system at the time the projection is performed. Further considerations of this projection procedure will appear in the kinetic and thermodynamics theories based on this informational approach. Moreover, geometrical-topological implications are derived and discussed in detail by Balian et al. [47].

Two further comments are of relevance. First, for a given dynamical quantity Â, its average value in MaxEnt-NESOM, that is, the expected value to be compared with the experimental measure, is given by

the last equality following after the separation given by Eq. (21) is introduced. This is the said generalization of Kirkwood time-smoothing averaging [16], and we can see that the average value is composed of two contributions: one is the average with the quasi-equilibrium distribution (meaning the contribution of the state at the time t), plus the contribution arising out of the dynamical behavior of the system (the one that accounts for the past history and future dissipational evolution). Moreover, this operation introduces in the formalism the so-called Bogoliubov's method of quasi-averages [42,48]. Bogoliubov's procedure involves a symmetry-breaking process, which is introduced in order to remove degeneracies connected with one or several groups of transformations in the description of the system. According to Eq. (24) the regular average with r_e(t) is followed by the limit of cancelling the ad hoc symmetry-breaking introduced by the presence of the weight function w in Eq. (14) (which is Abel's kernel in Zubarev approach, cf. Eq. (16), and follows for e going to +0), which imposes a breaking of the time-reversal symmetry in the dynamical description of the system. This is mirrored in the Liouville equation for r_e(t) : Zubarev's nonequilibrium statistical operator does satisfy Liouville equation, but it must be reckoned the fact that the group of its solutions is composed of two subsets, the one corresponding to the retarded solutions and the one corresponding to the advanced solutions. The presence of the weight function w (Abel's kernel in Zubarev's approach) in the time-smoothing or quasi-average procedure that has been introduced selects the subset of retarded solutions from the total group of solutions of Liouville equation. We call the attention (as Zubarev had; see Appendix in the book of reference [24]) that this has a certain analogy with Gell-Mann and Goldberger [49] procedure in scattering theory, where these authors promote a symmetry-breaking in Bogoliubov's sense in Schroedinger equation, in order to represent the way in which the quantum mechanical state has been prepared during times -¥ < t' < t, adopting for the wave function a weighted time-smoothing as the one used in Zubarev's approach to NESEF. More precisely, r_e(t) satisfies a Liouville equation of a form that automatically, via Bogoliubov's procedure, selects the retarded solutions, namely

where

_e is the modified Liouville operator

with being the regular Liouville operator and 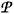(t) the projection operator of Eq. (23). Equation (25) is of the form proposed by Ilya Prigogine [50], with _e being composed of even and odd parts under time-reversal. Therefore, the time-smoothing procedure introduces a kind of Prigogine's dynamical condition for dissipativity [50,51].

Using Eq. (23) we can rewrite Eq. (25) in the form

viz., a regular Liouville equation but with an infinitesimal source, which introduces Bogoliubov's symmetry breaking of time reversal, and is responsible for disregarding the advanced solutions. Equation (27) is then said to have Boltzmann-Bogoliubov-Prigogine symmetry. Following Zubarev [24], Eq. (27) is interpreted as the logarithm of the statistical operator evolving freely under Liouville operator , from an initial condition at time t_o, and with the system undergoing random transitions, under the influence of the interaction with the surroundings. This is described by a Poisson distribution (w in the form of Abel's kernel), and the result at time t is obtained by averaging over all t' in the interval (t_o,t) [cf. Eq. (12)]. This is the time-smoothing procedure in Kirkwood's sense [cf. Eq. (24)], and therefore, it is introduced information related to the past history in the thermo-hydrodynamic macrostate of the system along its evolution from the initial t_o.

Two points need be considered here. One is that the initial t_o is usually taken in the remote past (t_o ® -¥), and the other that the integration in time in the interval (t_o,t) is weighted by the kernel w(t,t') (Abel's kernel in Zubarev's approach, Fejér's kernel in Kirkwood, Green , Mori approaches; and others are possible). As a consequence the procedure introduces a kind of evanescent history as the system macrostate evolves toward the future from the initial condition at time t_o (® -¥). Therefore, the contribution 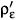(t) to the full statistical operator, that is, the one describing the dissipative evolution of the state of the system, to be clearly evidenced in the resulting kinetic theory, clearly indicates that it has been introduced a fading memory process. This may be considered as the statistical-mechanical equivalent of the one proposed in phenomenological continuum-mechanical-based Rational Thermodynamics [52,53]. In Zubarev's approach this fading process occurs in an adiabatic-like form towards the remote past: as time evolves memory decays exponentially with lifetime e^-1.

We may interpret this considering that as time evolves correlations established in the past fad away, and only the most recent ones strongly influence the evolution of the nonequilibrium system; here again is in action Bogoliubov's principle of correlations weakening. This establishes irreversible behavior in the system introducing in a peculiar way a kind of Eddington's time-arrow: Colloquially speaking, we may say that because of its fading memory, the system can only evolve irreversibly towards the future and cannot "remember" how to retrieve the mechanical trajectories that would return it to the past situations (what is attained when neglecting the advance solutions of Liouville equation). In a sense we may say that Boltzmann original ideas are here at work in quite general conditions [54,55], and in its evolution towards the future, once any external perturbating source is switched off, the system tends to a final state of equilibrium irrespective of the nonequilibrium initial condition of preparation.

Alvarez-Romero and Garcia-Colin [34] has presented an interesting alternative approach to the derivation of Zubarev's form of MaxEnt-NESEF, which however differs from ours in the interpretation of the time-smoothing procedure, which they take as implying the connection of an adiabatic perturbation for t' > t_o (we think that these authors mean adiabatic switch on of the interactions in H' responsible for the dissipative processes), instead of implying in a fading-memory interpretation. We need notice that both are interpretations which we feel are equally satisfactory and may be equivalent, but we side with the point of view of irreversible behavior following from - in Boltzmann-Bogoliubov-Prigogine's sense - adiabatic decorrelation of processes in the past. This is the fading-memory phenomenon, introduced in Zubarev's approach as a result of the postulated Poissonian random processes (on the basis that no real system can be wholly isolated), as already discussed. This interpretation aside, we agree with the authors in Ref. [34], in that the method provides adequate convergence properties (ensured by Abel's kernel in Zubarev' approach) for the equations of evolution of the system. These properly describe the irreversible processes unfolding in the media, with an evolution from a specific initial condition of preparation of the system and, after remotion of all external constraints - except thermal and particle reservoirs - tending to the final grand-canonical equilibrium distribution.

Moreover, the convergence imposed by Abel's kernel in Zubarev's approach appears as the most appropriate, not only for the practical mathematical advantages in the calculation it provides, but mostly important, by the attached physical meaning associated to the proposed adiabatic decoupling of correlations which surface in the transport equations in the accompanying MaxEnt-NESEF kinetic theory [56]. In fact, on the one hand this kinetic theory produces, when restrictions are applied on the general theory, the expected collision operators (as those derived in other kinetic theories) introducing, after the time integration in the interval (t_o,t) has been done, the expected terms of energy renormalization and energy conservation in the collision events. Furthermore, as pointed out by Zubarev [24], Abel's kernel ensures the convergence of the integrals in the calculation of the transport coefficients, which in some cases show divergences when, instead, Fejèr kernel is used (as in Green, Mori, etc. approaches). The procedure also appears as having certain analogies with the so-called repeated randomness assumptions [57,58] as discussed by del Rio and Garcia-Colin [59].

We need now to consider the construction of a MaxEnt-NESEF-based Nonlinear Kinetic Theory, that is, the transport (evolution) equations for the basic set of macrovariables that describe the irreversible evolution of the macrostate of the system. They are, in principle, straightforwardly derived, consisting in Heisenberg equations of motion for the corresponding basic dynamical variables (mechanical observables) or Hamilton equations in the classical case, averaged over the nonequilibrium ensemble, namely

Using the separation of the Hamiltonian as given by = _o + ', where _o is the kinetic energy and ' contains the interaction and the separation of the statistical operator as given by Eq. (21), it follows that Eq. (28) can be written in the form [56,60]

where on the right-hand side are present the contributions

As shown elsewhere [32, 56, 60] this Eq. (29) can be considered as a far-reaching generalization of Mori's equations [19,61]. It also contains a large generalization of Boltzmann's transport theory, with the original Boltzmann equation for the one-particle distribution retrieved under stringent asymptotic limiting conditions; details and discussions are given in Refs. [32] and [62].

In this Eq. (29), in most cases of interest the contribution J⁽¹⁾ is null because of symmetry properties of the interactions in ', and the term J⁽⁰⁾ provides a conserving part consisting in the divergence of the flux of quantity 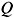_j(x,t) [63,64]. The last term, i.e. the one of Eq. (32), is the collision integral responsible for relaxation processes, which, evidently, cancels if ' or 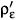is null, what clearly indicates that dissipative phenomena are described by these contributions to the Hamiltonian, and to the statistical operator in Eq. (21), respectively. Hence, as already anticipated, dissipation is not present in the instantaneous quasi-equilibrium operator 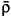(t,0) of Eq. (19), but in the nonequilibrium operator containing the history and time-smoothing characteristic of 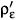(t) of Eqs. (16) and (22). We notice that if ' is null, so is 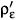(t), when _o coincides with the whole Hamiltonian corresponding to a full equilibrium condition.

The collision integral of Eq. (32) requires an, in general, quite difficult, and practically unmanageable, mathematical handling. But for practical use, it can be reformulated in the form of an infinite series of partial collision integrals in the form

where quantities W⁽ⁿ⁾ for n = 2,3,.... can be interpreted as describing two-particle, three-particle, etc., collisional processes. These partial collision integrals, and then the transport equation (29), are highly nonlinear, with complete details given in Refs. [56,60].

An interesting limiting case is the Markovian approximation to Eq. (29), consisting into retaining in the collision integral of Eq. (33) the interaction

' strictly up to second order (limit of weak interactions) [13,60,65] to obtain for a density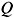 _j(x,t) the equation [13,22,63,64]

where

once 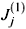is taken as null, and subindex nought indicates mechanical evolution under _o alone (interaction representation).

Finally, an additional step is the construction of the all important MaxEnt-NESEF response function theory for systems arbitrarily away from equilibrium, to connect theory with observation and measurement in the experimental procedure: see for example [66-81] and Chapter 6 in the book of Ref. [13]. We simply notice that as in the traditional response function theory around equilibrium [82, 83], the response of the system away from equilibrium to an external probe is expressed in terms of correlation functions but defined over the nonequilibrium ensemble. Moreover, also in analogy with the case of systems in equilibrium it is possible to construct a double time nonequilibrium thermodynamic Green function formalism [84-87].

In this way, through the realization of the basic steps we have described, a nonequilibrium statistical ensemble formalism - the MaxEnt-NESEF - can be built. We consider in continuation the use of NESEF for the construction of a Nonequilibrium Statistical Thermodynamics [46,88].

III. INFORMATIONAL-STATISTICAL THERMODYNAMICS

Several formulations of nonequilibrium thermodynamics at the phenomenological level are presently available. The first theory set forth to extend the concepts of equilibrium thermodynamics (or thermostatics) goes back to the early thirties, with the work of de Donder [89] and Onsager [90], giving rise to what is referred to as Classical (sometimes called Linear) Irreversible Thermodynamics [5,91,92], described in the already classical textbook by de Groot and Mazur [93]. Extension of Classical Irreversible Thermodynamics to encompass nonlinear conditions not so near to equilibrium, in what is termed Generalized Non-Equilibrium Thermodynamics is due to the Brussels' School [94]. The inclusion of nonlinear effects in Generalized Nonequilibrium Thermodynamics allows to incorporate in the theory a particular situation in the field of nonlinear complex systems [95-97], namely, the case of dissipative evolution in open irreversible systems, with the possible emergence of ordered patterns on a macroscopic scale, the so-called Prigogine's dissipative structures [98, 99]. Classical Irreversible Thermodynamics is a well established theory but within its own domain of validity, which has severe limitations. To remove such conceptual and practical limitations of this theory and, in particular, to encompass arbitrarily far-from-equilibrium situations, phenomenological Classical Irreversible Thermodynamics is being superseded by new attempts.

It is worth recalling that it is considered that the several approaches to Thermodynamics can be classified within the framework of at least four levels of description [100-102], namely:

(i) The so-called engineering approach or CK Thermodynamics (for Clausius and Kelvin), based on the two laws of Thermodynamics and the rules of operation of Carnot cycles;

(ii) The mathematical approach, as the one based on differential geometry instead of Carnot cycles, sometimes referred to as the CB Thermodynamics (for Caratheodory and Born);

(iii) The axiomatic point of view replacing Carnot cycles and differential geometry by a set of basic axioms, which try to encompass the previous ones and extend them; let us call it the TC Thermodynamics (for Tisza and Callen), or Axiomatic Thermodynamics;

(iv) The statistical-mechanical point of view, based of course on the substrate provided by the microscopic mechanics (at the molecular, or atomic, or particle, or quasiparticle, level) plus theory of probability, which can be referred to as Gibbsian Thermodynamics or Statistical Thermodynamics.

This field has not as yet achieved a definitive closed level of description and, therefore, it is natural for it to be the subject of intense discussion and controversy. Each school of thought has its virtues and defects, and it is not an easy task to readily classify within the above scheme the variety of existing theories: among several approaches we can mention and we apologize for those omitted, Rational Thermodynamics, as proposed by Truesdell [52]; what we call Orthodox Irreversible Thermodynamics, as proposed by B. Chan Eu [103]; Extended Irreversible Thermodynamics, originated and developed by several authors and largely systematized and improved by J. Casas Vázquez, D. Jou, and G. Lebon of the so-called Catalan School of Thermodynamics [104,405]; a Generalized Kinetic approach developed by L. S. García Colín and the so-called Mexican School of Thermodynamics [106]; the Wave approach to Thermodynamics due to I. Gyarmati [107]; the approach so-called Generics by M. Grmela [108]; the Holotropic approach by N. Bernardes [109]; Informational Statistical Thermodynamics (or Information-theoretic Thermodynamics) with mechanical statistical foundations, initiated by A. Hobson [110] and whose systematization and extension is described here.

We may say that Rational Thermodynamics and Generics belong to level (ii); Orthodox Irreversible Thermodynamics to level (i); Extended Irreversible Thermodynamics to level (iii); Holotropic Thermodynamics also to level (iii); Informational Statistical Thermodynamics, evidently, to level (iv).

The latter one, to be referred to as IST for short, is partially described next. This frontier area of Physics is presently under robust development, but, it ought to be stressed, not completely settled in a closed form. As noticed, several schools of thought are, in a sense, in competition and, consequently, the developments in the field are accompanied with intense and lively controversy (for a particular aspect of the question - the role of irreversibility and entropy - see Letters Section in Physics Today, November 1994, pp. 11-15 and 115-117). Quite recently the statistical physics and thermodynamics of nonlinear nonequilibrium systems has been discussed in a relevant set of articles published in the namesake book [111], to which we call the attention of the reader: the present section may be considered as a complement to this book by partially touching upon the question of the statistical foundations of irreversible thermodynamics on the basis of a Gibbs-like ensemble approach for nonequilibrium (and then dissipative) systems.

Consider the question of kinetic and statistical theories for nonequilibrium processes. Presently several approaches are being pursued, which have been classified by R. Zwanzig [15]. Among them we do have NESEF described in the preceding section, which is considered to have an appealing structure and offering a very effective technique to deal with a large class of experimental situations [15]. Such NESEF appears as a quite appropriate formalism to provide microscopic (mechanical-statistical) foundations to phenomenological irreversible thermodynamics [46, 112, 113], and nonclassical thermo-hydrodynamics [114].

NESEF appears to be an appropriate formalism to yield, as already noticed, statistical-mechanical foundations to phenomenological irreversible thermodynamics, in particular the construction of IST (also referred-to as Informational-Theoretic Thermodynamics). It was pioneered by Hobson [110, 115] a few years after the publication of Jaynes' seminal papers [116,117] on the foundations of statistical mechanics based on information theory. A brief review is given in Refs. [46,112,113], the diversity of extremum principles in the field of nonequilibrium theories is reviewed in Ref. [118], and further material is present in Ref. [119]. We notice that Thermostatics, Classical Irreversible Thermodynamics and Extended Irreversible Thermodynamics are encompassed in Informational Statistical Thermodynamics, which gives them a microscopic foundation. Moreover, Generalized Nonequilibrium Thermodynamics (that is, the extension of Classical Irreversible Thermodynamics to the nonlinear domain) is also contained within the informational-statistical theory [120]. Recent attempts to improve on the construction of IST are reported in Refs. [46,121-134].

The present development of theories for the thermodynamics of irreversible processes contained, one way or another, within the list of four levels presented above, and IST is one of them, brings to the fore a fundamental question in nonequilibrium thermodynamics, namely, which is the origin of irreversibility (or the origin of the so-called time-arrow problem [50, 135, 136]) and the definition of an entropy and entropy production functions, and the sign of the latter. This is a quite difficult, however engaging, problem which, as noted, has associated a considerable amount of controversy. The question has been subsumed by Leon Rosenfeld as "to express in a precise formalism [the] complementarity between the thermodynamic or macroscopic aspect and the atomic one" [137-139]. Several approaches, seemingly different at first sight, have been produced, beginning with the great contributions of Ludwig Boltzmann [54]. Some Schools set irreversibility at the level of probability distributions but together with methods for either discarding microscopic information that is unnecessary for predicting the behavior of the macroscopic state of the system (on the basis of information theory), or introducing a dynamic of correlations; they are compared in refs. [140, 142]. More recently some approaches have relied upon a description in terms of a dynamic origin of irreversibility as associated to ergodic properties of chaotic-like systems [143,144]. In Mackey's line of thought the concept of irreversibility appears hidden behind a rather abstract mathematical formalism, and no connection is made with the concept of entropy production. On the other hand, Hasegawa and Driebe's work deals with irreversibility for a particular class of chaotic systems; how it can be extended to quite general thermodynamic situations is an open matter. As pointed out by J. L. Lebowitz [55] all these approaches contain interesting and useful ideas and can be illuminating when properly applied.

We here deal with the question strictly within the framework of Informational Statistical Thermodynamics. Therefore, it must be understood that the functions that in what follows are referred to as entropy and entropy production are those which such theory defines. J. Meixner, over twenty years ago in papers that did not obtain a deserved diffusion [145,146], gave some convincing arguments to show that it is very unlikely that a nonequilibrium state function playing the role that the entropy has in equilibrium may be uniquely defined. Summarizing his ideas one may assert that the conclusion reached by him is that such a function either cannot be defined, or it may be done so in an infinite number of ways. A softened form of this idea was advanced by Grad over forty year ago [147]. Exploring recent literature on this question these conjectures seem to hold true in a more restricted sense (this literature is quite broad; see for example [148,149] and references therein).

We call the attention, and emphasize, the fact that any theory to have physical meaning needs be convalidated by comparison of its predictions with experimental results. In the particular case of NESEF, which provides statistical foundations to IST, as noticed in Section 2, it yields a nonlinear quantum transport theory of large scope [56], which consist of a far-reaching generalization of Mori's theory [19], together with an accompanying response function theory for far-from-equilibrium systems [13,32,84], and a generalized Boltzmann transport theory [33]. As already noticed, NESEF has been applied to the study of ultrafast relaxation processes in the so-called photoinjected plasma in semiconductors with particular success, in the sense of obtaining very good agreement between theory and experiment [66-80] and see Chapter 6 in the book of the Ref. [13]. Such kind of experiments can be used to satisfactorily allow for the characterization and measurement of nonequilibrium temperature, chemical potentials, etc., which are concepts derived from the entropy-like function that the theory defines in a similar way to equilibrium and local equilibrium theories [81]. Since they depend on such entropy-like function they are usually referred to as quasi-temperature, quasi-chemical potentials, etc. Moreover, without attempting a rigorous approach, we simply call the attention to the fact that the formalism here presented appears as providing a kind of partial unification of several apparently differentiated approaches to the subject: First, the formalism begins with a derivation within the framework of Jaynes-style informational approach, and, therefore, the informational entropy that the method introduces is dependent on a restricted set of variables. This is the result that this entropy is a projection on the space of such contracted set of variables of the fine-grained Gibbs entropy (as later on described and depicted in Fig. 1). The latter is obtained, as shown in next section, on the basis of a memory-dependent MaxEnt construction. Second, the connection with the approach of the Brussels-Austin School (subdynamics of correlations) appears partially with the introduction in this particular MaxEnt approach of an ad hoc hypothesis that introduces irreversibility from the outset, consisting in a mimic of Prigogine's dynamical condition for dissipativity [50, 51, 150, 151]. Additional discussions on the equivalence of both approaches have been provided by several authors [27, 140]. We return to a consideration of these questions in last section.

Beginning in next section we describe the construction of the Informational-Statistical Thermodynamics (IST) based on the NESEF (we call the attention to the fact that throughout the review is used Zubarev's approach in NESEF, a concise, elegant, and quite practical formalism). The attention is concentrated on the state function called informational-statistical entropy. After its introduction and an accompanying general discussion, several properties of it are considered, namely: (1) The nonequilibrium equations of state, that is, the differential coefficients of this IST-entropy (meaning the one defined in the context of IST), which are the Lagrange multipliers that the formalism introduces; (2) Derivation of a -type theorem and a, so-called, weak principle of increase of informational-entropy production; (3) Criteria for evolution and (in)stability analysis; (4) A kind of generalized Clausius-Carnot and Gibbs relations; (5) A brief study of fluctuations and generalized Maxwell relations; and (6) a Boltzmann-like formula, relating the informational entropy with the extension in phase space (or number of states at the quantum level) compatible with the macroscopic information available.

IV. PROPERTIES OF IST-ENTROPY

In its original formulation Classical (Onsagerian) Irreversible Thermodynamics starts with a system in conditions of local equilibrium and introduces as basic macrovariables a set of quasi-conserved quantities, namely the fields of energy and mass densities. This theory introduces a state functional of these variables satisfying a Pffafian differential form identical, however locally, to Gibbs relation for entropy in equilibrium. A more general approach is that of Extended Irreversible Thermodynamics, which introduces a state functional dependent on the basic variables of Classical Irreversible Thermodynamics plus all dissipative fluxes elevated to the category of basic variables. We consider now the case of Irreversible Statistical Thermodynamics based on the state space consisting, within the tenets of NESEF, of the set of basic variables {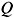_j(x,t)} which can be scalars, vectors, or tensor fields of any rank, chosen in the way described in the Section 2: We recall, and stress, that they are the statistical average values of well defined mechanical quantities. Within this approach, we look next for the definition of a functional of these variables playing the role of a state functional - to be called the IST-entropy-like function or informational-statistical entropy - that is meaningful and pertinent to the class of physical situations and accompanying experiments under analysis within NESEF in each case. Particular care needs be exercised with the use of the word entropy. Entropy has a very special status in Physics, being a fundamental state function in the case of Thermostatics. It is a well established concept in equilibrium, but an elusive one in nonequilibrium conditions when it requires an extended definition allowing for the treatment of open systems and far-from-equilibrium conditions. Clearly, such definition must contain as limiting cases the particular and restricted ones of equilibrium and local equilibrium. In arbitrary nonequilibrium conditions it appears to hold that there is not any possibility to define a unique state function playing the role of a nonequilibrium entropy, as forceful argued by Meixner [145,146] - a point we agree with and the Informational Statistical Thermodynamics in continuation described, seems to reinforce. Hence, it must be kept in mind that in what follows we are introducing this quasi-entropy function in the context of the Informational Statistical Thermodynamics, namely, the based on NESEF, and therefore dependent on the description to be used in each case following Bogoliubov's principle mentioned in Section 2. Nevertheless, it needs be emphasized that this quasi-entropy function goes over the thermodynamic one in equilibrium (thus recovering Clausius' result as shown by Jaynes [152]), as well as over the local equilibrium one of classical irreversible thermodynamics, when the proper restrictive limits are taken. Alternatives for a nonequilibrium quasi-entropy have been proposed by several authors, we may mention the one in extended irreversible thermodynamics [104,105] and the concept of calortropy [103,153], with both of them seemingly encompassed in Informational Statistical Thermodynamics. We return to this point of the introduction of a nonequilibrium entropy-like state function in different approaches, along with further commentaries, in the last section.

A. The IST-informational entropy or quasientropy

Gibbs' entropy, the straightforward generalization of equilibrium and Classical Irreversible Thermodynamics and the one used in the variational approach to NESEF containing memory, namely

cannot represent an appropriate entropy since it is conserved, that is dS_G(t) /dt = 0. This is the result that r_e satisfies a modified Liouville equation with sources [cf. Eq. (27)], the latter going to zero with e going to zero after the calculation of the regular average has been performed, and is a manifestation of the fact that it is a fine-grained entropy which preserves information. The latter is the information provided at the initial time of preparation of the system as given by Eq. (21), i.e. the one given in terms of the initial values of the basic variables, namely 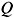_j(t_o) . Hence, for any subsequent time t > t_o we introduce a coarse-grained NESEF-based informational entropy such that, according to the foundations of the formalism, is dependent on the information provided by the constraints of Eq. (11) at each given time and only on this information. We introduce the IST-informational entropy (t), which can also be called quasientropy, given by

In this Eq. (37), is the informational-entropy operator of Eq. (17) [45], and 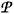_e(t) is a time-dependent projection operator, defined in Eq. (23) [32], which projects over the subspace spanned by the basic set of dynamical variables to be called the informational subspace (or relevant subspace) as illustrated in Fig. 1. Moreover, the last equality in Eq. (37) is a consequence of the coarse-graining condition consisting in that [13,31]

For simplicity we are considering the case when the basic dynamical variables are local densities, i.e. they depend only on the field variable r, the generalization to an extended set of field variables is straightforward.

Consequently, the difference between the IST-informational entropy of Eq. (37) and Gibbs' entropy of Eq. (36), is

which can be interpreted as a kind of measurement of the information lost when the macroscopic state of the system is described in terms of the reduced set of basic variables, i.e., as already noticed, in terms of projection of ln r_e(t) over what we have called the informational subspace of "relevant " variables, (illustrated in Fig. 1, and as already noticed the geometrical-topological aspects of this process are discussed in [47]). The coarse-grained auxiliary operator (the instantaneously "frozen" quasiequilibrium) 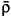(t,0) has the important property that, at any time t, it maximizes the IST-informational entropy of Eq. (37) for the given values of the constraints of Eq. (11), at fixed time t, and the condition of normalization which, we recall, is ensured by the properties of the weight function eexp{e(t' - t)} and the coarse-graining condition of Eq. (38). Furthermore, from Eq. (37) and the definition of 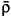we can write that

where (r,t) defines a local informational entropy density. We recall that the variables F and 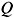can be scalars, vectors or tensors, and so the product F 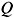in Eq. (40) must be understood as being algebraic product of scalars, scalar product of vectors, and fully contracted product of tensors, respectively, so that the scalar is rendered.

Since

once we take into account that

where d stands for functional differentiation in the sense defined in [154], we find that

and hence

Equation (43) stands for a generalized Gibbs relation in the context of Informational Statistical Thermodynamics, which goes over the well known expressions which follow in the limit of the restricted cases of equilibrium and local equilibrium in Thermostatics and Classical (Linear or Onsagerian) Irreversible Thermodynamics. Equations (42) and (44) tell us that variables F and 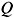are conjugated in the sense of nonequilibrium thermodynamics (these expressions are the generalization of the corresponding relations in equilibrium), what is a consequence of the properties of the weight function eexp{e(t' - t)} and of the coarse-graining property of Eq. (38). Equations (42) and (44) can be considered as nonequilibrium equations of state, and Eqs. (41) and (42) define f(t) as a kind of a logarithm of a nonequilibrium partition function in the nonequilibrium statistical ensemble formalism based on NESEF. Furthermore, (t) has the important property of being a convex function of the variables 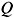_j, what is a result of application of MaxEnt as shown in [13].

We are now in condition to introduce the important thermodynamic function which is the MaxEnt-entropy production (or informational-entropy production), namely

where we have taken into account Eq. (41). In Eq. (45) the evolution of the basic variables is governed by Eqs. (29), meaning that the right-hand side of this Eq. (45) contains the three contributions present in Eqs. (30). But, it can be shown only the collision integrals of Eq. (32) contribute to the informational-entropy production, i.e.

which clearly indicates that the informational-entropy production follows from the fact that 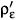is the contribution to the statistical operator in Eq. (22) associated to relaxation effects, while the auxiliar ensemble characterized by 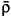is relaxation free. This is a manifestation of the projection procedure used in the definition of the IST-entropy: relaxation processes are associated to the influence of the dynamic effects (collisional processes) generated by H', that acting on the initial condition at time t_o of Eq. (21) drives r_e outside the chosen informational subspace. This is illustrated in Fig. 1.

Taking into account Eq. (45) and the definition of the local informational entropy density of Eq. (40), there follows a generalized local in space Gibbs relation, that is, it is satisfied the relation

for the informational-entropy density of Eqs. (40) and (45). Moreover, we recall that the equations of irreversible evolution for the basic variables consistently follow from the method [23, 24, 56]: for the space-dependent variables

_j(r,t) these equations take the general form [13] [cf. Eqs. (29) and (34)]

where the first term on the right is the divergence of the flux density

_j associated to the density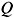 _j(r,t) [13, 14, 24]. Also, let us recall that 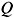_j can be a scalar, a vector, or a rank-r (> 2) tensor (and so is 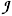_j), then 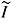_j must be interpreted, respectively, as a vector, a rank two tensor, and rank r (> 3) tensors (see [13]). Moreover, in the equations of evolution for the macrovariables 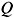_j(x,t) , Eq. (48), for simplicity (the general case can be straightforwardly handled) we consider that 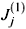vanishes. For better accompanying of the following results we introduce the nomenclature 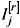to indicate a flux of tensorial rank r = 1,2,3,..., or r-th order flux of a given density.

Using these Eqs. (48), we can write a continuity equation for the IST-entropy density given by

In this Eq. (49), I_s is the flux of the IST-informational-entropy given by

where on the right F Ä I stands for contracted tensorial product (F being a tensor of rank r = 0,1,2,..., and I is a tensor of rank r = 1,2,3,..., respectively) to produce the vector I_s, and s_s is an associated entropy-production density given by

where Grad is the gradient operator in tensorial calculus and (r,t) is given by Eq. (46). Using the definition of Eq. (50), one recovers the limiting case of Classical Irreversible Thermodynamics, and therefore may be considered the straightforward generalization for the entropy flux density to arbitrary nonequilibrium conditions. It is worth recalling that Eq. (48) is the average over the nonequilibrium ensemble, characterized by the distribution in Eq. (16), of the corresponding Hamiltonian equations of evolution in the classical level and Heisenberg equations of evolution in the quantum level, for the local-in-space-dependent dynamical variables. When one introduces the equations for the density of mass and of energy in the case of a fluid, there follows the equations for a nonclassical hydrodynamics, and the classical one is recovered as a limiting restrictive case together with the use of a barycentric frame of reference [14,33].

Integrating in space Eq. (49), we obtain an expression for the global informational-entropy production, namely

But, using Gauss theorem in the last integral of Eq. (52), we can rewrite it as

where the last term is a surface integral over the system boundaries. Equation (53) allows us to separate the entropy production into two contributions (as is usually done, cf. [94] and [99]): one is the internal production of informational entropy

and the other is the exchange of informational entropy with the surroundings, or flux term

Furthermore, using Eq. (41), Eq. (54) becomes

and then taking into account that

use of Eqs. (55) and (56) implies in that

This is just a consequence that the quantities (which gave origin to the divergence of the flux) do not contribute to the informational-entropy production, that is, as already noticed, there is no dissipation in the nonequilibrium macroscopic description associated to the auxiliary operator 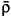(t,0) , but the irreversible processes are fully accounted for by 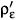(t) [cf. Eqs. (22), (32), and (46), and Fig. 1].

Summarizing these results, the informational-entropy production density s_s(r,t) accounts for the local internal production of informational entropy. Moreover, using Eqs. (54) and (55), together with Eq. (57) we can make the identifications

Accordingly, Eq.(59) stands for internal production of informational-entropy and the contribution in Eq. (60) is associated to informational-entropy exchange with the surroundings. The informational-entropy production (t) can then be interpreted as corresponding in the appropriate limit to the entropy production function of Classical Irreversible Thermodynamics.

B. The nonequilibrium equations of state

Let us next proceed to analyze the differential coefficients of the informational entropy [cf. Eq. (44)]. Consider a system composed of s subsystems. Let e_l(r,t) be the locally-defined energy densities and n_l(r,t) the number densities in each l (= 1,2,...,s) subsystem, which are taken as basic variables in NESEF (some of the subsystems belong to the description of the reservoirs, but we do not separate them at this point). We call b_(r,t) and z_(r,t) their associated intensive variables [the Lagrange multipliers F in Eq. (17) that the formalism introduces]. But, as shown elsewhere [13], it is required the introduction of the fluxes of these quantities as basic variables, and with them all the other higher order fluxes (of tensorial rank r > 2). Consequently, the statistical operator depends on all the densities and their fluxes, and Eq. (44) tells us that the Lagrange multipliers associated to them depend, each one, on all these basic variables, namely, the densities e_(r,t) , n_(r,t) , their vectorial fluxes I_el(r,t) , I_nl(r,t) , and rank r > 2 tensorial fluxes (r,t) , (r,t).

As noticed before, this particular choice of the basic variables implies in a description which can be considered as a far-reaching generalization of a grand-canonical distribution in arbitrary nonequilibrium conditions. The corresponding auxiliary coarse-grained ("instantaneously frozen") distribution is then

where the upper triangular hat stands for the dynamical operator of the corresponding quantity: the energy density , the particle density 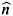, and their fluxes of all orders r > 1 [r is also the corresponding tensorial rank, with r = 1 standing for the vectorial fluxes, which have been explicitly separated out in Eq. (51)]. Moreover, b, z, and the a's are the corresponding Lagrange multipliers (intensive nonequilibrium thermodynamic variables in IST). We further recall that the proper nonequilibrium statistical operator that describes the dissipative irreversible macrostate of the system is r_e(t) of Eq. (16), built on the basis of the auxiliary one of Eq. (61).

Thus, the quantities that are the differential coefficients of the quasientropy in IST, which, as already noted, are in this sense nonequilibrium thermodynamics variables conjugated to the basic ones, are for the densities

where d, we recall, stands for functional differential [154]. The IST-quasientropy of Eqs. (20), appropriately given in terms of e_l, n_l, and their fluxes of all order [cf. Eqs. (5) to (6)], goes over the corresponding one of local equilibrium in Classical Irreversible Thermodynamics, when all variables b_l become identical for all subsystems and equal to the reciprocal of the local equilibrium temperature, while the z_l become equal to -bm_l, where µ_l are the local chemical potentials for the different chemical species in the material. All the other variables associated to the fluxes are null in such limit. Of course, when the complete equilibrium is achieved b and µ go over the corresponding values in equilibrium.

Consequently, in NESEF we can introduce the space and time dependent nonequilibrium temperature-like variables Q_l(,t) , which we call quasitemperature for each subsystem l = 1 to s, namely

where then

with Boltzmann constant taken as unit. This Eq. (65) tells us that the Lagrange multiplier b represents in the MaxEnt approach to the NESEF a reciprocal quasitemperature (nonequilibrium temperature-like variable) of each subsystem, and which is dependent on the space and time coordinates. Evidently, as we have intended to indicate between the curly brackets in Eq. (65), it depends not only on the energies e_l and densities n_l(l = 1,2,...,s) but on all the other basic variables which are appropriate for the description of the macroscopic state of the system, that is, the vectorial and tensorial fluxes. The definition of Eq. (65) properly recovers as particular limiting cases the local-equilibrium temperature of classical irreversible thermodynamics and the usual absolute temperature in equilibrium; in both cases there follows a unique temperature for all subsystems as it should.

A quite important aspect of the question needs be stressed at this point: Equation (64) is the formal definition of the so-called quasitemperature in IST, a very convenient one because of the analogy with local-equilibrium and equilibrium theories, which are recovered in the appropriate asymptotic limits: for a general discussion on nonequilibrium temperature definitions see [155]. But we recall that it is a Lagrange multiplier that the method introduces from the outset being a functional of the basic set of macrovariables. Therefore, its evolution in time, and then its local and instantaneous value, follows from the solution of the generalized transport equations, namely Eqs. (29), for the densities and all their fluxes. Thus, in IST, the quasitemperature of each subsystem is, as already emphasized, a functional of all the basic variables, which are, we recall, the densities and their fluxes of, in principle, all orders. This question is extensively dealt with in references [76, 81], where it is also described how to measure quantities like the quasi-temperature, quasi-chemical potentials, and drift velocities, and comparison with experiment is given: theoretical results and experimental data shows very good agreement.

C. A generalized -theorem

One point that is presently missing is the attempt to extract from this Informational Statistical Thermodynamics (and thus to also provide for a reasonable criterion in phenomenological irreversible thermodynamics) the sign of the entropy production function. This is defined as non-negative in Extended Irreversible Thermodynamics, but such property does not follows immediately from of Eq. (45) [or Eq. (46)]. The collision integral 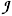on which depends has an extremely complicated expression, even in its alternative form given by Eq. (32). There is only one manageable case, the quasi-linear theory of relaxation near equilibrium, when is definite positive, as for example proved in [24].

However, we can show that for this informational nonequilibrium statistical thermodynamics there follows a generalized -theorem, in the sense of Jancel [156], which we call a weak principle of increasing of informational-entropy production. For that purpose we take into account the definition of the IST-quasientropy, and resorting, for simplicity, to a classical mechanical description, we can write

where G is a point in classical phase space.

But, because of the initial condition of Eq. (21) we have that ln 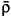(G|t_o,0) = lnr_e(G|t_o) and, further, since Gibbs entropy, namely

is conserved, that is, it is constant in time [then S_G(t) = S_G(t_o) and we recall that S_G(t_o) = (t_o,0) ], it follows that

where

_e is the projection operator of Eq. (38) and then

Recalling that the coarse-graining condition of Eq. (38) ensures, besides the definition of the Lagrange multipliers F_j which according to Eq. (44) are differential coefficients of the entropy and the simultaneous normalization of r_e and 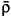, we can write Eq. (66) in the form

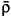since the last integral is null. This quantity D cancels for r_e = [i.e. for null 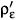of Eq. (22)], and its change when introducing the variation r_e ® r_e + dr_e is

where we used the separation of r_e given by Eq.(22).

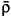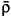The variation in Eq. (71) vanishes for r_e = , when, as shown, also vanishes D(t) , so it follows that D(t) is a minimum for r_e = , when it is zero, and positive otherwise, namely

which defines for the NESOM the equivalent of Jancel's generalized -theorem [156]. It should be noticed that the inequality of Eq. (72) can be interpreted as the fact that, as the system evolves in time from the initial condition of preparation under the governing action of the nonlinear generalized transport equations (29), the informational entropy cannot decrease, or, because of Eq. (72), the IST-informational-entropy is always larger than Gibbs statistical entropy. These results reproduce for the MaxEnt-NESOM described in section 2, those obtained by del Rio and Garcia-Colin [149] in an alternative way.

Using the definition for the informational entropy production function we can rewrite Eq. (72) as

Equation (73) does not prove that (r,t) is a monotonically increasing function of time, as required by phenomenological irreversible thermodynamic theories. We have only proved the weak condition that as the system evolves is predominantly definite positive. We also insist on the fact that this result is a consequence of the presence of the contribution 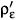to r_e, which is then, as stated previously, the part that accounts for - in the description of the macroscopic state of the system - the processes which generate dissipation. Furthermore, the informational entropy with the evolution property of Eq. (72) is the coarse-grained entropy of Eq. (37), the coarse-graining being performed by the action of the projection operator 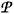_e of Eq. (38): This projection operation extracts from the Gibbs entropy the contribution associated to the constraints [cf. Eq. (11)] imposed on the system, by projecting it onto the subspace spanned by the basic dynamical quantities, what is graphically illustrated in Fig. 1 (see also [47]). Hence, the informational entropy thus defined depends on the choice of the basic set of macroscopic variables, whose completeness in a purely thermodynamic sense cannot be indubitably asserted. We restate that in each particular problem under consideration the information lost as a result of the particular truncation of the set of basic variables must be carefully evaluated [157]. Retaking the question of the signal of (, t) , we conjecture that it is always non-negative, since it can not be intuitively understood how information can be gained in some time intervals along the irreversible evolution of the system. However, this is expected to be valid as long as we are using an, in a sense, complete description of the system meaning that the closure condition is fully satisfied (in the case of the nonequilibrium grand-canonical ensemble when taking densities and fluxes of all orders). Once a truncation procedure is introduced, that is, the closure condition is violated, then the local density of informational entropy production is no longer monotonously increasing in time; this has been illustrated by Criado-Sancho and Llebot [158] in the realm of Extended Irreversible Thermodynamics. The reason is, as pointed out by Balian et al.[47] that the truncation procedure introduces some kind of additional (spurious) information at the step when the said truncation is imposed.

Two other properties of the IST-informational-entropy function are that, first, it is a maximum compatible with the constraints of Eq. (11) when they are given at the specific time t, that is, 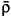maximizes (t) when subjected to normalization and such constraints, and second one recovers the proper values in equilibrium. This particular property of vinculated maximization, which ensures that (t) is a convex function in the space of thermodynamic states, is the one that concomitantly ensures that in the framework of Informational Statistical Thermodynamics are contained generalized forms of Prigogine's theorem of minimum entropy production in the linear regime around equilibrium, and Glansdorff-Prigogine's thermodynamic principles of evolution and (in)stability in nonlinear conditions. Let us see these points next.

D. Evolution and (in)stability criteria

In this subsection we summarize three additional properties of the informational-entropy production, namely the criterion of evolution and the (in)stability criterion - generalizations of those of Glansdorff-Prigogine in nonlinear classical Nonequilibrium Thermodynamics [94], and a criterion for minimum production of informational entropy also a generalization of the one due to Prigogine [91]. Details of the demonstrations are given elsewhere [46].

The time derivative of (t) of Eq. (45) can be split into two terms, namely

where

and

that is, the change in time of the informational-entropy production due to that of the variables F and that of the variables 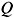, respectively. Recalling that the 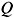_j stand for the thermodynamic variables in Informational Statistical Thermodynamics [cf. Eq. (11)], while the F_j stand for the Lagrange multipliers introduced by the method [cf. Eq. (14)], which are the differential coefficients of the informational entropy [cf. Eq. (44)], Eqs. (75) and (76) are related to what, in the limiting case of classical (linear or Onsagerian) Thermodynamics, are the contributions due to the change in time of the thermodynamic fluxes and forces respectively, as will be better clarified in continuation. First we notice that using Eq. (44) we can write that

and then

which is non-positive because of the convexity of , that is

Inequality (79) can be considered as a generalized Glansdorff-Prigogine thermodynamic criterion for evolution, which in our approach is a consequence of the use of MaxEnt in the construction of IST within the framework of the NESEF of section 2.

Also, an alternative criterion can be derived in terms of the generating functional f(t) , as given by Zubarev [24]. Defining

it follows that

where

and

But (t) / dt is then -d_F(t) / dt, and because of Eq. (79)

during the irreversible evolution of the system, hence it follows an alternative criterion given in terms of the variation in time of the rate of change of the logarithm of the nonequilibrium partition-like function.

Consider next an isolated system composed of a given open system in interaction with the rest acting as sources and reservoirs. These sources and reservoirs are assumed to be ideal, that is, its statistical distribution, denoted by r_SR, is taken as constantly stationary, in order words as unaltered by the interaction with the much smaller open system. The nonequilibrium statistical operator, r_S(t) , for the whole system to be used in the equation of evolution is then written as

where r_e(t) is the statistical operator of the open system constructed in the MaxEnt-NESEF.

If the open system is in a steady state [to be denoted hereafter by an upper index (ss)], then the production of global informational entropy is null, that is, = + = 0, where the two contributions are the internal and external production of informational entropy, as given by Eqs. (59) and (60). Hence, = -, meaning that the increase of the global internal entropy production is compensated by the pumping of entropy to the external world.

Let us consider now a small deviation from the steady state which is assumed to be near equilibrium, and we write

where DF F^(eq), and index (eq) indicates the value of the corresponding quantity in the equilibrium state. The internal production of informational entropy, (_i) = P(t) of Eqs. (59) and (56), in the condition of departure from equilibrium defined by Eq. (86), satisfies in this immediate neighborhood of the steady state near equilibrium, which we call the strictly linear regime (SLR), that

where L^SLR is the symmetric matrix of Onsager-like kinetic coefficients, around the equilibrium state, given by

where

and

with

' the part of the Hamiltonian containing the interactions, and use was made of the fact that

i.e., there is no production of informational entropy in equilibrium. Moreover, in the neighborhood of the equilibrium state the internal production of entropy is nonnegative, that is (see for example [24])

Taking into account that for a system subject to time-independent external constraints, so as to produce a steady state, it is verified that dP_S / dt = 0, we obtain that

and

where

_j are the fluxes [cf. Eqs. (48) and (50)]. But, according to Onsager's relations in the linear domain around equilibrium (see for example [24]), it follows that

where the matrix of kinetic coefficients is symmetric, i.e. (r,r₁) = (r,r₁) . Using Eq. (94) and recalling that the matrix of coefficients is also symmetric [46], we can verify that the expressions in Eqs. (92) and (93) are identical and, therefore,

The results of Eqs. (59), (60), (90) and (95) are of relevance in proving a generalization in IST of Prigogine's theorem of minimum internal production of entropy. In fact, in the SLR regime, taking the time derivative of Eq. (54), it follows from Eq. (95) that

as a consequence that in the steady state the fluxes

_j in Eq. (56) are time independent on the boundaries, i.e. dP_S / dt = 0. Hence, the inequality in Eq. (96) is a consequence for this particular case of the theorem of Eq. (79). Therefore, on account of Eqs. (91) and (96), according to Lyapunov's theorem there follows the generalization in IST of Prigogine's theorem. This theorem proves that in the linear regime near equilibrium, that is in the strictly linear regime,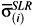 is a nonequilibrium state function with an associated variational principle, and that steady states near equilibrium are attractors characterized by producing the least dissipation (least loss of information in our theory) under the given constraints. We stress that this result is a consequence of the fact that the matrix of kinetic coefficients L_jk is symmetric in the strictly linear regime and this result implies that d_F 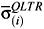near equilibrium is one half the exact differential of the entropy production. Outside the strictly linear regime the antisymmetric part of the matrix of kinetic coefficients may be present and, therefore, there is no variational principle that could ensure the stability of the steady state. The latter may become unstable once a certain distance from equilibrium is attained, giving rise to the emergence of a selforganized dissipative structure [98, 99, 159, 160].

Consequently, outside the strictly linear domain, essentially for systems far-away-from equilibrium, other stability criterion needs be determined. We look for it first noting that, because of the convexity of the MaxEnt-NESEF entropy as is demonstrated in [46] for states around any arbitrary steady state, let it be near or far away from equilibrium, the following result holds, namely

where

Time derivation of Eq. (97) leads to the expression

a quantity called the excess entropy production. In deriving the previous to the last term in Eq. (99) we used the calculation of C in the steady state which is thus time independent, and it was used the fact that C is a symmetric matrix (what is a manifestation of the existence of Maxwell-type relations in IST, as will be shown later on).

Consequently, taking into account Eqs. (97) and (99), Lyapunov stability theorem (see for example [99]) allows us to establish a generalized Glansdorff-Prigogine-like (in)stability criterion in the realm of the Informational Statistical Thermodynamics: For given constraints, if D_Fs is positive, the reference steady state is stable for all fluctuations compatible with the equation of evolution (which are provided in MaxEnt-NESEF by the nonlinear transport theory briefly summarized in Sec. 2). Stability of the equilibrium and steady states in the linear regime around equilibrium are recovered as particular limiting and restricted cases of the general theory. Therefore, given a dynamical open system in a certain steady state, it can be driven away from it by changing one or more control parameters on which its macrostate depends. At some critical value of one or more of these control parameters (for example the intensities of external fields) the sign of the excess entropy production function may change from positive to negative, meaning that the steady state looses its stability and a new macrostate becomes stabilized characterizing some kind of, in general, patterned structure, the so-called Prigogine's dissipative structure. The character of the emerging structure is connected with the type of fluctuation arising in the system that instead of regressing, as should be the case in the linear (or Onsagerian) regime, increases to create the new macrostate. The instability corresponds to a branching point of solutions of the non-linear equations of evolution, and to maintain such non-equilibrium structures a continuous exchange of energy and/or matter with external reservoirs is necessary, i.e. entropy must be pumped out of the open system. We again stress that this kind of self-organized ordered behavior is ruled out in the strictly linear regime as a result of the previously demonstrated generalized Prigogine's minimum entropy production theorem. Thus, nonlinearity is required for these structural transitions to occur at a sufficiently far distance from equilibrium. The new nonequilibrium branch of solution (the dissipative structure) may present one of the following three characteristics: (a) time organization, (b) space organization, (c) functional organization [99, 160]. Finally, we stress the fact that in the nonlinear domain the criteria for evolution and stability are decoupled - differently to the linear domain - and this fact allows for the occurrence of new types of behavior when the dynamical system is driven far away from equilibrium: order may arise out of thermal chaos [161,162] and the system displays complex behavior. As noted before, we restate that IST, built within the framework of MaxEnt-NESEF, can provide solid microscopic and macroscopic basis to deal with selforganization, or the sometimes called Thermodynamics of Complex Systems [163, 164].

E. Generalized Clausius relation in IST

The informational entropy in IST also satisfies a kind of generalized Clausius relation. In fact, consider the modification of the informational entropy as a consequence of the modification of external constraints imposed on the system. Let us call l_l (l = 1,2,...s) a set of parameters that characterize such constraints (e.g., the volume, external fields, etc.). Introducing infinitesimal modifications of them, say dl_l, the corresponding variation in the informational entropy is given by

where

_j are the nonexact differentials

with ád

_j(r)|tñ = Tr{d

_j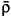(t,0)} . In these expressions the nonexact differentials are the difference between the exact differentials

and

the latter being the average value of the change in the corresponding dynamical quantity due to the modification of the control parameters. This follows from the fact that

and that

Consequently, using Eqs. (104) and (105), we obtain Eq. (100). It is worth noticing that if we take the system in equilibrium at temperature T, described by the canonical distribution, and perform an infinitesimal change in volume, say dV, then

and then follows the form of the first law given by

Equation (100) tells us that the MaxEnt-NESEF Lagrange multipliers are integrating factors for the nonexact differentials

_j.

Let us take as the energy density one of the variables

_j, say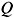 ₁(r,t) = e(r,t) , and in analogy with equilibrium we define the intensive non-equilibrium thermodynamic variable we call quasitemperature, or better to say its reciprocal

After introducing the additional redefinitions of the Lagrange multipliers in the form

using Eq. (40) allows us to introduce a kind of generalized space-dependent Clausius expression for a system in arbitrary nonequilibrium conditions, namely

where we have introduced the nonexact differential for a generalized heat function q(r,t) given by

In Eq. (110) is to be understood that the integration in time extends , in the time interval that goes from t_o to t, along the trajectory of evolution of the system, governed by the kinetic equations (48).

Moreover, using the redefinitions given in Eqs. (109), we may noticed that the generalized space and time dependent Gibbs relation of Eq. (47) becomes

where on the left side it has been put into evidence the quasitemperature Q (we stress that in Eq. (101) indicates the nonexact differential resulting from modifications in the constraints, while in Eq. (112) is present the differential d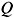 on the variables on which the function depends). This is the case of a single nonequilibrium system; we have already call the attention to the fact that, in the general case, there exist different quasitemperatures for different subsets of degrees of freedom of a given sample in nonequilibrium conditions. The case of the photoinjected highly excited plasma in semiconductors is an excellent example: Coulomb interaction between carriers produces their internal thermalization (in nonequilibrium conditions) resulting in a unique quasitemperature which is attained in the ten-fold femtosecond time scale, while the optical phonons are driven away from equilibrium as a result of the interaction with the nonequilibrium carriers and acquire different quasitemperatures in each mode. Only in the ten-fold picosecond time scale there follows mutual thermalization of carriers and all the phonon modes, when all acquire a unique quasitemperature, and in the long run carriers' and optical-phonons' systems attain final equilibrium with the heat reservoir with which they are in contact; then the quasitemperature goes over the temperature of equilibrium with the reservoir [77,165].

Integrating in space Eq. (111), and taking into account the results that led to the -theorem of subsection IV.C, we can write

This Eq. (113) suggests an interpretation of it, in analogy with equilibrium, as resulting from a kind of pseudo-Carnot principle for arbitrary nonequilibrium systems, in the sense of taking the contribution of the integrand as a local reversible exchange of a heat-like quantity between the system and a pseudo-reservoir at local and instantaneous temperature Q(r,t) . Some considerations on Carnot's principle and its connection with MaxEnt, as a general principle of reasoning, has been advanced by Jaynes [166]. He described the evolution of Carnot's principle, via Kelvin's perception that it defines a universal temperature scale, Clausius' discovery that it implied the existence of the entropy function, Gibbs' perception of its logical status, and Boltzmann's interpretation of entropy in terms of phase volume, into the general formalism of statistical mechanics. The equivalent in IST of Boltzmann's results is provided in subsection IV.G.

F. Fluctuations and Maxwell-like relations

As already shown, the average value of any dynamical quantity P_j(G) of the basic set in MaxEnt-NESEF (the classical mechanical level of description is used for simplicity) is given by

that is, by minus the functional derivative of the generating functional f with respect to the associated Lagrange multiplier F_j(t) [and we recall that this function can be related to a kind of non-equilibrium partition function through the expression f(t) = ln (t)]. Moreover, from a straight calculation it follows that

where

and Eq. (115) defines the matrix of correlations (t). The diagonal elements of are the mean square deviations, or fluctuations, of quantities P_j(G), namely

and the matrix is symmetrical, that is,

what is a manifestation in IST of the known Maxwell relations in equilibrium.

Let us next scale the informational entropy and Lagrange multipliers in terms of Boltzmann constant, k_B, that is, we introduce

and then, because of Eq. (44),

Moreover, we find that

that is, the second order functional derivatives of the IST-informational-entropy are the components of minus the inverse of the matrix of correlations

^(-1) , with elements to be denoted by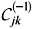 (t) . Moreover, the fluctuation of the IST-informational-entropy is given by

and that of the intensive variables

_j are

therefore

where

and then

The quantities 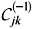are the matrix elements of the inverse of the matrix of correlations, and if the variables are uncorrelated G_jj(t) = 1. Equation (126) has the likeness of an uncertainty principle connecting the variables _j and 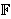_j(t) , which are thermodynamically conjugated in the sense of Eqs. (42) and (44), with Boltzmann constant being the atomistic parameter playing a role resembling that of the quantum of action in mechanics. This leads to the possibility to relate the results of IST with the idea of complementarity between the microscopic and macroscopic descriptions of many-body systems advanced by Rosenfeld and Prigogine [50, 137-139]; this is discussed elsewhere [167].

Care must be exercised in referring to fluctuations of the intensive variables F_j. In the statistical description fluctuations are associated to the specific variables 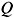_j, but the F's are Lagrange multipliers fixed by the average values of the P's, and so D² is not a proper fluctuation of but a second order deviation interpreted as being a result of the fluctuations of the variables 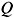on which it depends, in a generalization of the usual results in statistical mechanics in equilibrium [168]. These brief considerations point to the desirability to develop a complete theory of fluctuations in the context of MaxEnt-NESEF; one relevant application of it would be the study of the kinetics of transition between dissipative structures in complex systems, of which is presently available a phenomenological approach [99].

G. A Boltzmann-like relation:

(t) = k_B lnW (t)

According to the results of the previous subsection, quite similarly to the case of equilibrium it follows that the quotient between the root mean square of a given quantity and its average value is of the order of the reciprocal of the square root of the number of particles, that is

Consequently, again quite in analogy with the case of equilibrium, the number of states contributing for the quantity P_j to have the given average value, is overwhelmingly enormous. Therefore, we can write that

where the integration is over the manifold (t) in phase space composed of the phase points G Î (t) such that

where D

_j is of the order of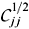 (t) . Hence

after using Eq. (119), and then

where

with extension meaning the measure of the hypervolume in phase space occupied by (t) and changing in time as it proceeds the evolution of the nonequilibrium macroscopic state of the system. We recall that this is an approximate result, with an error of the order of the reciprocal of the square root of the number of degrees of freedom of the system, and therefore exact only in the thermodynamic limit.

Equation (131) represents the equivalent in IST of Boltzmann expression for the thermodynamic entropy in terms of the logarithm of the number of complexions compatible with the macroscopic constraints imposed on the system. It should be noticed that in IST they are given by the so-called informational set, the one used as constraints in the variational process in MaxEnt, that is, the {

_j(t)} , which are the average values of the set of mechanical variables {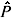_j(t)}. Moreover, they are univocally related to the Lagrange multipliers (or set of intensive nonequilibrium thermodynamical variables) that also completely describe the macroscopic state of the system in IST, namely the set {k_BF_j(t) = 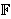_j(t)}.

The expression of Eq. (131) in the quantum level of description follows similarly, when we derive that

where ñ is the set of quantum numbers which characterize the quantum mechanical state of the system, and contains the set of states |ññ, such that

where we have used the usual notations of bracs and kets and matrix elements between those states.

In terms of these results we can look again at the -theorem of subsection 4.3 and write

where ext means extension of the manifold in the classical approach and number of states in the quantum approach fixed by the informational constraints. Evidently, Eq. (135) tells us that the extension of increases in time, what can be interpreted in the following way: Consider the system in an initially highly excited nonequilibrium state (to fix ideas let us think in terms of the photoinjected plasma in semiconductors; see section 7 in Chapter 3 of the book of Ref. [13]), from which it evolves towards final equilibrium, an evolution governed by the kinetic equations of subsection 2. With elapsing time, as pointed out by Bogoliubov, subsets of correlations die down (in the case of photoinjected plasma implies the situation of increasing processes of internal thermalization, nullification (decay) of fluxes, etc.) and a decreasing number of variables are necessary to describe the macroscopic state of the system. In IST this corresponds to a diminishing informational space, meaning of course a diminishing information, and, therefore, a situation less constrained with the consequent increase of the extension of and increase in informational entropy.

Citing Jaynes, it is this property of the entropy - measuring our degree of information about the microstate, which is conveyed by data on the macroscopic thermodynamic variables - that made information theory such a powerful tool in showing us how to generalize Gibbs' equilibrium ensembles to nonequilibrium ones. The generalization could never have been found by those who thought that entropy was, like energy, a physical property of the microstate [166]. Also following Jaynes, W(t) measures the degree of control of the experimenter over the microstate, when the only parameters the experimenter can manipulate are the usual macroscopic ones. At time t, when a measurement is performed, the state is characterized by the set {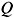_j(t)} , and the corresponding phase volume is W(t), containing all conceivable ways in which the final macrostate can be realized. But, since the experiment is to be reproducible, the region with volume W(t) should contain at least the phase points originating in the region of volume W(t_o) , and then W(t) > W(t_o). Because phase volume is conserved in the micro-dynamical evolution, it is a fundamental requirement on any reproducible process that the phase volume W(t) compatible with the final state cannot be less than the phase volume W(t_o) which describes our ability to reproduce the initial state [152].

V. CONCLUDING REMARKS

We have considered in Section II the construction of a Nonequilibrium Statistical Ensemble Formalism Gibbs' style. On this we stress the point that to derive the behavior of the macroscopic state of the system from partial knowledge has been already present in the original work of Gibbs. This is at the roots of the well established, fully accepted, and exceedingly successful statistical mechanics in equilibrium: the statistical distribution which should depend on all constants of motion is built, in any of the canonical ensembles, in terms of the available information we do have, namely, the preparation of the sample in the given experimental conditions in equilibrium with a given (and quite reduced) set of reservoirs. Werner Heisenberg wrote [169], "Gibbs was the first to introduce a physical concept which can only be applied to an object when our knowledge of the object is incomplete".

Returning to the question of the Bayesian approach in statistical mechanics, Sklar [4] has summarized that Jaynes firstly suggested that equilibrium statistical mechanics can be viewed as a special case of the general program of systematic inductive reasoning, and that, from this point of view, the probability distributions introduced into statistical mechanics have their bases not so much in an empirical investigation of occurrences in the world, but, instead in a general procedure for determining appropriate a priori subjective probabilities in a systematic way. Also, Jaynes' prescription was to choose the probability distribution which maximizes the statistical entropy (now thought in the information-theoretic vein) relative to the known macroscopic constraints, using the standard measure over the phase space to characterize the space of possibilities. This probability assignment is a generalization of the probabilities determined by the Principle of Indifference in Logic specifying one's rational choice of a priori probabilities. In equilibrium this is connected with ergodic theory, as known from classical textbooks. Of course it is implied to accept the justification of identifying averages with measured quantities using the time in the interval of duration of the experiment. This cannot be extended to nonequilibrium conditions involving ultrafast relaxation processes. Therefore, there remains the explanatory question: Why do our probabilistic assumptions work so well in giving us equilibrium values? [4].

The Bayesian approach attempts an answer which, apparently, works quite well in equilibrium, and then it is tempting to extend it to nonequilibrium conditions. Jaynes rationale for it is, again, that the choice of probabilities, being determined by a Principle of Indifference, should represent maximum uncertainty relative to our knowledge as exhausted by our knowledged of the macroscopic constraints with which we start [11]. This has been described in previous sections.

At this point, it can be raised the question that in the study of certain physico-chemical systems we may face difficulties when handling situations involving fractal-like structures, correlations (spatial and temporal) with some type of scaling, turbulent or chaotic motion, finite size (nanometer scale) systems with eventually a low number of degrees of freedom, etc. These difficulties consist, as a rule, in that the researcher is unable to satisfy Fisher's Criterion of Sufficiency [170] in the conventional, well established, physically and logically sound Boltzmann-Gibbs statistics, meaning an impairment to include the relevant and proper characterization of the system. To mend these difficulties, and to be able to make predictions (providing an understanding, even partial, of the physics of the system but of interest in, for example, analyzing the technological characteristics of a device), consists into resorting to statistics other than the Boltzmann-Gibbs one which are not at all extensions of the latter but, as said, introduce a patching method. To mend these difficulties, and to be able to make prediction (an understanding, even partial, of the physics of the system but of interest in, for example, analyzing the technological characteristics of a device), consists into resorting to statistics other than the Boltzmann-Gibbs one (which are not at all extensions of it but, as said, introduce a patching approach).

Several approaches do exist and we can mention Generalized Statistical Mechanics (see for example P. T. Landsberg, in Ref. [171]), Superstatistics (see for example E. G. D. Cohen, C. Beck in Refs. [172, 173]), Nonextensive Statistics (see for example the Conference Proceedings in Ref. [174]), and some particular cases are statistical mechanics based on Renyi Statistics (see for example I. Procaccia in Ref. [175] and T. Arimitzu in Refs. [176, 177]), Kappa (sometimes called Deformational) statistics (see for example G. Kaniadakis in Ref. [178]). A systematization of the subject, accompanied of a description of a large number of different possibilities, are described in what we have dubbed as Unconventional Statistical Mechanics, whose general theory, discussion and applications are presented in Refs. [179-181].

Another point of contention is the long standing question about macroscopic irreversibility in nature. As discussed in section 2, it is introduced in the formalism via the generalization of Kirkwood's time-smoothing procedure, after a specific initial condition [cf. Eq. (21)] - implying in a kind of generalized Stosszahlanzatz - has been defined. This is a working proposal that goes in the direction which was essentially suggested by Boltzmann, as quoted in Ref. [182]: "Since in the differential equations of mechanics themselves there is absolutely nothing analogous to the second law of thermodynamics, the latter can be mechanically represented only by means of assumptions regarding initial conditions". Or, in other words [182], that the laws of physics are always of the form: given some initial conditions, here is the result after some time. But they never tell us how the world is or evolves. In order to account for that, one always needs to assume something, first on the initial conditions and, second, on the distinction of the description being macroscopic and the system never isolated (damping of correlations). In this vein Hawkings [135] has manifested that "It is normally assumed that a system in a pure quantum state evolves in a unitary way through a succession of [such] states. But if there is loss of information through the appearance and disappearance of black holes, there can't be a unitary evolution. Instead, the [...] final state [...] will be what is called a mixed quantum state. This can be regarded as an ensemble of different pure quantum states, each with its own probability".

Needless to say that this question of Eddington's time-arrow problem has produced a very extensive literature, and lively controversies. We do not attempt here to add any considerations to this difficult and, as said, controversial subject. We simply list in the references [50, 54, 55, 135, 135, 136, 161, 183-195] some works on the matter which we have selected. As commented by Sklar [4], Nicolai S. Krylov (the Russian scientist unfortunately prematurely deceased) was developing an extremely insightful and careful foundational study of nonequilibrium statistical mechanics [29]. Krylov held the opinion that he could show that in a certain sense, neither classical nor quantum mechanics provide an adequate foundation for statistical mechanics. Krylov's most important critical contribution is precisely his emphasis on the importance of initial ensembles. Also, that we may be utterly unable to demonstrate that the correct statistical description of the evolution of the system will have an appropriate finite relaxation time, much less the appropriate exact evolution of our statistical correlates of macroscopic parameters, unless our statistical approach includes an appropriate constraint on the initial ensemble with which we choose to represent the initial nonequilibrium condition of the system in question. Moreover, it is thought that the interaction with the system from the outside at the single moment of preparation, rather than the interventionists ongoing interaction, is what grounds the asymmetric evolution of many-body systems. It is the ineluctable interfering perturbation of the system by the mechanism that sets it up in the first place that guarantees that the appropriate statistical description of the system will be a collection of initial states sufficiently large, sufficiently simple in shape, and with a uniform probability distribution over it. Clearly, a question immediately arises, namely: Exactly how does this initial interference lead to an initial ensemble of just the kind we need? [4] We have seen in section 2 how MaxEnt-NESEF, mainly in Zubarev's approach, tries to heuristically address the question. Also something akin to these ideas seems to be in the earlier work of the Russian-Belgian Nobel Prize Ilya Prigogine [50, 150, 161], and also in the considerations in Refs. [4, 190-192, 196, 197]. Certain kind of equivalence - at least partial - seems to exists between Prigogine's approach and MaxEnt-NESEF, as pointed out by Dougherty [141, 142], and we side with Dougherty's view. More recently, Prigogine and his School have extended those ideas incorporating concepts, at the quantum level, related to dynamical instability and chaos (see for example Refs. [198, 199]). In this direction, some attempts try to incorporate time-symmetry breaking, extending quantum mechanics to a general space state, a "rigged" (or "structured") Hilbert space or Gelfand space, with characteristics (superstructure) mirroring the internal structure of collective and cooperative macroscopic systems [200-202]. This formulation of dynamics constitutes an effort towards including the second law of thermodynamics, as displayed explicitly by a -function of the Boltzmann type, which decreases monotonically and takes its minimum value when unstable systems have decayed or when the system reaches equilibrium [203, 204].

Finally, and in connection with the considerations presented so far, we stress that in the formalism described in previous sections, no attempt is made to establish any direct relation with thermodynamic entropy in, say, the classical Clausius-Carnot style, with its increase between initial and final equilibrium states defining irreversibility. Rather, it has been introduced a statistical-informational entropy with an evolution as given by the laws of motion of the macrovariables, as provided by the MaxEnt-NESEF-based kinetic theory. Irreversible transport phenomena are described by the fluxes of energy, mass, etc..., which can be observed, but we do not see entropy flowing. We have already stressed in subsection IV.C that the increase of IST-entropy amounts to a -like theorem, that is, a manifestation on the irreversible character of the transport equations, in close analogy with Boltzmann's -theorem which does so for Boltzmann equation. Moreover, as stated elsewhere (see for example Ref. [13]), we side with Meixner's point of view [53, 205] in that, differently to equilibrium, does not exists a unique and precisely defined concept of thermodynamic entropy out of equilibrium. The one of subsection IV.A, is the one peculiar to IST, and depending on the nonequilibrium thermodynamic state defined by Zubarev-Peletminskii selection law altogether with the use of Bogoliubov's principle of correlation weakening. The IST-informational-entropy, we recall, has several properties listed in subsection IV.B, and one is that it takes (in the thermodynamic limit) a typical Boltzmann-like expression [cf. Eq. (40)], implying that the macroscopic constraints imposed on the system (the informational bases) determine the vast majority of microscopic configurations that are compatible with them and the initial conditions. It is worth noticing that then, according to the weak principle of increase of the IST-informational-entropy, as the dissipative system evolves, such number of microscopic configurations keeps increasing up to a maximum when final full equilibrium is achieved. Further, MaxEnt-NESEF recovers in the appropriate limit the distribution in equilibrium, and in IST one recovers the traditional Clausius-Carnot results for increase of thermodynamics entropy between an initial and a final equilibrium states, as shown in Ref. [13, 166].

Ending this considerations, it can be further noticed that in the preceding sections we have described, in terms of a general overview, a theory that attempts a particular answer to the long-standing sought-after question about the existence of a Gibbs-style statistical ensemble formalism for nonequilibrium systems. Such formalism, providing microscopic (mechanical-statistical) bases for the study of dissipative processes, heavily rests on the fundamental ideas and concepts devised by Gibbs and Boltzmann. It consists into the so-called MaxEnt-NESEF formalism, which appears to be covered under the theoretical umbrella provided by Jaynes' Predictive Statistical Mechanics. We have already called the attention to the fact that it is grounded on a kind of scientific inference approach, Jeffrey's style, based on Bayesian probability and information theory in Shannon-Brillouin's sense [36, 37]. It has been improved and systematized mainly by the Russian School of Statistical Physics, and the different approaches have been brought under a unified description based on a variational procedure. It consists in the use of the principle of maximization of the informational entropy, meaning to rely exclusively on the available information and avoiding to introduce any spurious one. The aim is to make predictions on the behavior of the dynamics of the many-body system on the basis of only that information. On this, Jeffreys, at the beginning of Chapter I in the book of reference [37], states that: "The fundamental problem of scientific progress, and the fundamental of everyday life, is that of learning from experience. Knowledge obtained in this way is partly merely description of what we have already observed, but part consists of making inferences from past experience to predict future experience. This may be called generalization of induction. It is the most important part." Jeffreys also quotes J. C. Maxwell who stated that the true logic for this world is the Calculus of Probability which takes account of the magnitude of the probability that is, or ought to be, in a reasonable man's mind.

Some authors conjecture that this may be the revolutionary thought in modern science (see for example Refs. [36, 37, 161, 206]): It replaces the concept of inevitable effects (trajectories in a mechanicist point of view of many-body (large) systems) by that of the probable trend (in a generalized theory of dynamical systems). Thus, the different branches of science that seem to be far apart, may, within such new paradigm, grow and be hold together organically [207]. These points of view are the subject of controversy, mainly on the part of the adepts of the mechanicist-reductionist school. We call the attention to the subject but we do not take any particular position, simply adhering to the topic here presented from a pragmatical point of view. In that sense, we take a position coincident with the one clearly stated by Stephen Hawkings [208]: "I do not demand that a theory corresponds to reality. But that does not bother me. I do not demand that a theory correspond to reality because I do not know what reality is. Reality is not a quality you can test with litmus paper. All I am concerned with is that the Theory should predict the results of measurement" [emphasis is ours].

MaxEnt-NESEF is the constructive criterion for deriving the probability assignment for the problem of dissipative processes in many-body systems, on the bases of the available information (provided, as Zwanzig pointed out [209], on the knowledge of measured properties, the expectation on the characteristics of the kinetic equations and of sound theoretical considerations). The fact that a certain probability distribution maximizes the informational entropy, subject to certain constraints representing our incomplete information, is the fundamental property which justifies the use of that distribution for inference; it agrees with everything that is known, but carefully avoids assuming anything that is not known. In that way it enforces - or gives a logico-mathematical viewpoint - to the principle of economy in logic, known as Occam's Razor, namely "Entities are not to be multiplied except of necessity". Particularly, in what concerns Statistical Thermodynamics (see Section III), MaxEnt-NESEF, in the context of Jaynes' Predictive Statistical Mechanics, allows to derive laws of thermodynamics, not on the usual viewpoint of mechanical trajectories and ergodicity of classical deductive reasoning, but by the goal of using inference from incomplete information rather than deduction: the MaxEnt-NESEF distribution represents the best prediction we are able to make from the information we have [7-12].

As ending considerations, we stress that, in this review we have given a brief descriptional presentation of MaxEnt-NESEF, which is an approach to a nonequilibrium statistical ensemble algorithm in Gibbs' style, seemingly as a very powerful, concise, soundly based, and elegant formalism of a broad scope apt to deal with systems arbitrarily away from equilibrium, and its application to the construction of a statistical thermodynamics of irreversible processes.

ACKNOWLEDGMENTS

We acknowledge financial support to our group provided in different opportunities by the São Paulo State Research Foundation (FAPESP), the Brazilian National Research Council (CNPq), the Ministry of Planning (Finep), the Ministry of Education (CAPES), Unicamp Foundation (FAEP), IBM Brasil, and the John Simon Guggenheim Memorial Foundation (New York, USA).

[65] D. Zubarev, in reference [24], see Chapter IV, Section 22 .

[114] A. R. Vasconcellos, J. G. Ramos, and R. Luzzi, IFGW-Unicamp Internal Report and future publications XX, xxx (2005), e-Print arXiv.org/abs/cond-mat/0412227 (2004).

[172] C. Beck and E. G. D. Cohen, arXiv.org/abs/cond-mat/0205097 (2002).

[173] C. Beck, arXiv.org/abs/cond-mat/0303288 (2003).

[177] P. Jizba and T. Arimitzu, arXiv.org/abs/cond-mat/0307698 (2003).

[179] R. Luzzi, A. R. Vasconcellos, and J. G. Ramos, arXiv.org/abs/cond-mat/0306217 (2003).

[180] A. R. Vasconcellos, J. G. Ramos, and R. Luzzi, arXiv.org/abs/cond-mat/0306247 (2003).

[181] R. Luzzi, A. R. Vasconcellos, and J. G. Ramos, arXiv.org/abs/cond-mat/0307325 (2003).

Received on 26 July, 2005

• [1] N. Oreskes, H. Shrader-Frechette, and K. Beltz, Science 263, 641 (1994).
• [2] O. Penrose, Rep. Prog. Phys. 42, 1938 (1979).
• [3] R. Kubo, Prog. Theor. Phys. (Japan) Suppl. 64, 1 (1978).
• [4] L. Sklar, Physics and Chance: Philosophical Issues in the Foundations of Statistical Mechanics (Cambridge Univ. Press, Cambridge, UK, 1993).
• [5] H. G. B. Casimir, Rev. Mod. Phys. 17, 343 (1945).
• [6] J. Semura, Am. J. Phys. 64, 526 (1996).
• [7] E. T. Jaynes, in Frontiers of Nonequilibrium Statistical Physics, edited by G. T. Moore and M. O. Scully (Plenum, New York, USA, 1986), pp. 33-55.
• [8] E. T. Jaynes, in The Maximum Entropy Formalism, edited by M. Tribus and R. D. Levine (MIT Press, Cambridge, MA, USA, 1978), pp. 15-118.
• [9] E. T. Jaynes, in Complex Systems: Operational Approaches, edited by H. Haken (Springer, Berlin, Germany, 1985).
• [10] E. T. Jaynes, in E. T. Jaynes Papers on Probability, Statistics, and Statistical Physics, edited by R. D. Rosenkrantz (Reidel-Kluwer Academic, Dordrecht, The Netherlands, 1983).
• [11] E. T. Jaynes, Proc. IEEE 70, 939 (1982).
• [12] E. T. Jaynes, in Maximum Entropy and Bayesian Methods, edited by J. Skilling (Kluwer Academic, Dordrecht, The Netherlands, 1989), pp. 1-27.
• [13] R. Luzzi, A. R. Vasconcellos, and J. G. Ramos, Predictive Statistical Mechanics : A Nonequilibrium Ensemble Formalism (Kluwer Academic, Dordrecht, The Netherlands, 2002).
• [14] R. Luzzi, A. R. Vasconcellos, and J. G. Ramos, The Theory of Irreversible Processes: A Nonequilibrium Ensemble Formalism. IFGW-Unicamp Internal Report (2005), and future publication.
• [15] R. Zwanzig, in Perspectives in Statistical Physics, edited by H. J. Ravechč (North Holland, Amsterdam, The Netherlands, 1981), pp. 123-124.
• [16] J. G. Kirkwood, J. Chem. Phys. 14, 180 (1946).
• [17] M. S. Green, J. Chem. Phys. 20, 1281 (1952).
• [18] H. Mori, I. Oppenheim, and J. Ross, in Studies in Statistical Mechanics I, edited by J. de Boer and G. E. Uhlenbeck (North Holland, Amsterdam, The Netherlands, 1962), pp. 217-298.
• [19] H. Mori, Progr. Theor. Phys. (Japan) 33, 423 (1965).
• [20] R. Zwanzig, in Lectures in Theoretical Physics, edited by W. E. Brittin, B. W. Downs, and J. Downs (Wiley-Interscience, New York, USA, 1961).
• [21] J. A. McLennan, Advances in Chemical Physics (Academic, New York, USA, 1963), Vol. 5, pp. 261-317.
• [22] S. V. Peletminskii and A. A. Yatsenko, Soviet Phys. JETP 26, 773 (1968), Zh. Ekps. Teor. Fiz. 53, 1327 (1967).
• [23] A. I. Akhiezer and S. V. Peletminskii, Methods of Statistical Physics (Pergamon, Oxford, UK, 1981).
• [24] D. N. Zubarev, Nonequilibrium Statistical Thermodynamics (Consultants Bureau, New York, USA, 1974), [Neravnovesnaia Statisticheskaia Termodinamika (Izd. Nauka, Moscow, Russia, 1971)].
• [25] B. Robertson, Phys. Rev. 144, 151 (1966).
• [26] H. Grabert, Projection Operators Techniques in Nonequilibrium Statistics (Springer, Berlin, Germany, 1981).
• [27] D. N. Zubarev and V. P. Kalashnikov, Physica 56, 345 (1971).
• [28] A. Salam, V. Vladimorov, and A. Logunov, Theor. Math. Phys. 92, 817 (1993), [Teor. Mat. Fiz. 92, 179 (1992)].
• [29] N. S. Krylov, Works on the Foundations of Statistical Mechanics (Princeton Univ. Press, Princeton, USA, 1979).
• [30] D. N. Zubarev, V. N. Morozov, and G. Röpke, Statistical Mechanics of Nonequilibrium Processes: Basic Concepts, Kinetic Theory (Akademie Wiley-VHC, Berlin, Germany, 1996).
• [31] D. N. Zubarev and V. P. Kalashnikov, Theor. Math. Phys. 1, 108 (1970), [Teor. Mat. Fiz. 1, 137 - (1969)].
• [32] R. Luzzi and A. R. Vasconcellos, Fortschr. Phys./Prog. Phys. 38, 887 (1990).
• [33] J. G. Ramos, A. R. Vasconcellos, and R. Luzzi, Fortschr. Phys./Prog. Phys. 43, 265 (1995).
• [34] J. T. Alvarez-Romero and L. S. Garcia-Colin, Physica A 232, 207 (1996).
• [35] R. Baierlein, Am. J. Phys. 63, 108 (1995).
• [36] H. Jeffreys, Scientific Inference (Cambridge Univ. Press, Cambridge, UK, 1973).
• [37] H. Jeffreys, Probability Theory (Clarendon, Oxford, UK, 1961).
• [38] P. W. Anderson, Phys. Today 45 (1), 9 (1992).
• [39] A. J. Garret, Contemp. Phys. 33, 271 (1992).
• [40] C. E. Shannon and W. Weaver, The Mathematical Theory of Communication. (Univ. Illinois Press, Urbana, USA, 1948).
• [41] L. Brillouin, Science and Information Theory (Academic Press, New York, USA, 1962).
• [42] N. N. Bogoliubov, in Studies in Statistical Mechanics I, edited by J. de Boer and G. E. Uhlenbeck (North Holland, Amsterdam, The Netherlands, 1962).
• [43] U. Fano, Rev. Mod. Phys. 29, 74 (1957).
• [44] R. Peierls, Lecture Notes in Physics (Springer, Berlin, Germany, 1974), Vol. 31.
• [45] S. A. Hassan, A. R. Vasconcellos, and R. Luzzi, Physica A 262, 359 (1999).
• [46] R. Luzzi, A. R. Vasconcellos, and J. G. Ramos, Statistical Foundations of Irreversible Thermodynamics (Teubner-BertelsmannSpringer, Stuttgart, Germany, 2000).
• [47] R. Balian, Y. Alhassid, and H. Reinhardt, Phys. Rep. 131, 1 (1986).
• [48] N. B. Jr, A Method for Studying Model Hamiltonians (Pergamon, Oxford, UK, 1972).
• [49] M. Gell-Mann and M. L. Goldberger, Phys. Rev. 91, 398 (1953).
• [50] I. Prigogine, From Being to Becoming (Freeman, San Francisco, USA, 1980).
• [51] I. Prigogine, Nature 246, 67 (1975).
• [52] C. Truesdell, Rational Thermodynamics (McGraw-Hill, New York, USA, 1985), [second enlarged edition (Springer, Berlin, Germany, 1988)].
• [53] J. Meixner, in Irreversible Processes of Continuum Mechanics, edited by H. Parkus and L. Sedov (Springer, Wien, Austria, 1968).
• [54] J. L. Lebowitz, Phys. Today 46, 32 (1993), see also Letters Section in Physics Today 47 (11), pp. 13-15 and 115-116 (1994).
• [55] J. L. Lebowitz, Phys. Today (Letters) 47, 115 (1994).
• [56] L. Lauck, A. R. Vasconcellos, and R. Luzzi, Physica A 168, 789 (1990).
• [57] N. G. V. Kampen, in Perspectives in Statistical Physics, edited by H. Ravechč (North Holland, Amsterdam, The Netherlands, 1981), p. 91.
• [58] N. V. Kampen, in Fundamental Problems in Statistical Mechanics, edited by E. Cohen (North Holland, Amsterdan, The Netherlands, 1962), p. 173.
• [59] J. D. Rio and L. G. Colin, Phys. Rev. E 54, 950 (1996).
• [60] J. Madureira, A. Vasconcellos, R. Luzzi, and L. Lauck, Phys. Rev. E 57, 3637 (1998).
• [61] D. Forster, Hydrodynamic Fluctuations, Broken Symmetry, and Correlation Functions (Benjamin, Readings, USA, 1975).
• [62] J. G. Ramos, A. R. Vasconcellos, and R. Luzzi, Physica A 284, 140 (2000).
• [63] J. Madureira, A. Vasconcellos, and R. Luzzi, J. Chem. Phys. 109, 2099 (1998).
• [64] S. V. Peletminskii and A. I. Sokolovskii, Theor. Math. Phys. 18, 85 (1974).
• [66] D. K. Ferry, H. L. Grubin, and G. J. Giafrate, in Semiconductors Probed by Ultrafast Laser Spectroscopy, edited by R. R. Alfano (Academic Press, New York, USA, 1984), Vol. 1, pp. 413-447.
• [67] D. Y. Xing, P. Hiu, and C. S. Ting, Phys. Rev. B 35, 6379 (1987).
• [68] V. N. Freire, A. R. Vasconcellos, and R. Luzzi, Phys. Rev. B 39, 13264 (1988).
• [69] R. Luzzi and L. C. Miranda, Physics Reports Reprint Books Series (North Hollland, Amsterdam, The Netherlands, 1978), Vol. 3, pp. 423-453.
• [70] R. Luzzi and A. R. Vasconcellos, in Semiconductor Processes Probed by Ultrafast Laser Spectroscopy, edited by R. R. Alfano (Academic, New York, USA, 1984), Vol. 1, pp. 135-169.
• [71] R. Luzzi, in High Excitation and Short Pulse Phenomena, edited by M. H. Pilkuhn (North Holland, Amsterdam, The Netherlands, 1985), pp. 318-332.
• [72] A. C. Algarte and R. Luzzi, Phys. Rev. B 27, 7563 (1983).
• [73] A. C. Algarte, Phys. Rev. B 38, 2162 (1988).
• [74] A. R. Vasconcellos and R. Luzzi, Complexity 2, 42 (1997).
• [75] A. C. Algarte, A. R. Vasconcellos, and R. Luzzi, Braz. J. Phys. 26, 543 (1996).
• [76] A. R. Vasconcellos, R. Luzzi, D. Jou, and J. Casas-Vázquez, J. Chem. Phys. 107, 7383 (1998).
• [77] A. C. Algarte, A. R. Vasconcellos, and R. Luzzi, Phys. Stat. Sol. (b) 173, 487 (1992).
• [78] A. C. Algarte, Phys. Rev. B 43, 2408 (1991).
• [79] A. C. Algarte, A. R. Vasconcellos, and R. Luzzi, Solid State Commun 87, 299 (1993).
• [80] A. R. Vasconcellos, A. C. Algarte, and R. Luzzi, Phys. Rev. B 48, 10873 (1993).
• [81] R. Luzzi, A. R. Vasconcellos, J. Casas-Vázquez, and D. Jou, Physica A 248, 111 (1997).
• [82] P. C. Martin, in Many-Body Physics, edited by C. D. Witt and R. Balian (Gordon and Breach, New York, USA, 1968), pp. 37-136.
• [83] H. J. Kreuzer, Nonequilibrium Thermodynamics and its Statistical Foundations (Clarendon, Oxford, UK, 1981).
• [84] R. Luzzi and A. R. Vasconcellos, J. Stat. Phys. 23, 539 (1980).
• [85] A. R. Vasconcellos, J. G. Ramos, M. V. Mesquita, and R. Luzzi, Response Function Theory and a Fluctuation-Dissipation Theorem in a Nonequilibrium Ensemble Formalism. IFGW-Unicamp Internal Report (2005) and future publication.
• [86] A. R. Vasconcellos, J. G. Ramos, M. V. Mesquita, and R. Luzzi, Theory of Scattering in a Nonequilibrium Ensemble Formalism. IFGW-Unicamp Internal Report (2005) and future publication.
• [87] V. P. Kalashnikov, Theor. Math. Phys. 35, 362 (1978), Teor. Mat. Fiz. 35, 127-138 (1978).
• [88] R. Luzzi, A. R. Vasconcellos, and J. G. Ramos, La Rivista del Nuovo Cimento 24, 1 (2001).
• [89] T. D. Donder, L'Affinité (Gauthier-Villars, Paris, France, 1936).
• [90] L. Onsager, Phys. Rev. 37, 405 (1931).
• [91] I. Prigogine, Étude Thermodinamique des Phénomčnes Irreversibles (Desoer, Ličge, Belgium, 1947).
• [92] L. Onsager and S. Machlup, Phys. Rev. 9, 1505 (1953).
• [93] S. de Groot and P. Mazur, Nonequilibrium Thermodynamics (North Holland, Amsterdam, The Netherlands, 1962).
• [94] P. Glansdorff and I. Prigogine, Thermodynamic Theory of Structure, Stability, and Fluctuations (Wiley-Interscience, New York, USA, 1971).
• [95] P. W. Anderson, Science 117, 393 (1972).
• [96] P. W. Anderson, Phys. Today 44 (7), 9 (1991).
• [97] M. Gell-Mann, Complexity 1, 16 (1995).
• [98] I. Prigogine, in From Theoretical Physics to Biology, edited by M. Marois (North Holland, Amsterdam, The Netherlands, 1969).
• [99] G. Nicolis and I. Prigogine, Self-organization in Nonequilibrium Systems (Wiley-Interscience, New York, USA, 1977).
• [100] L. Tisza, in Thermodynamics: History and Philosophy, edited by K. Martinas, L. Ropolyi, and P. Szegedi (World Scientific, Singapore, 1991), pp. pp 515-522.
• [101] A. Drago, in Thermodynamics: History and Philosophy, edited by K. Martinas, L. Ropolyi, and P. Szegedi (World Scientific, Singapore, 1991), pp. 329-345.
• [102] K. Martinas, in Thermodynamics: History and Philosophy, edited by K. Martinas, L. Ropolyi, and P. Szegedi (World Scientific, Singapore, 1991), pp. 285-303.
• [103] B. C. Eu, Kinetic Theory of Irreversible Thermodynamics (Wiley, New York, USA, 1992).
• [104] D. Jou, J. Casas-Vazquez, and G. Lebon, Extended Irreversible Thermodynamics (Springer, Berlin, Germany, 1993), (second edition, Springer, Berlin, Germany, 1996; third enlarged edition Springer, Berlin, Germany 2000).
• [105] I. Müller and T. Ruggeri, Extended Thermodynamics (Springer, Berlin, Germany, 1993).
• [106] R. V. Velasco and L. S. García-Colín, J. Non-Equilib. Thermodyn. 18, 157 (1993).
• [107] I. Gyarmati, J. Non-Equil. Thermodyn. 2, 233 (1977).
• [108] M. Grmela, J. Chem. Phys. 56, 6620 (1997).
• [109] N. Bernardes, Physica A 260, 186 (1998).
• [110] A. Hobson, J. Chem. Phys. 45, 1352 (1966).
• [111] W. Ebeling and W. M. (Editors), Statistical Physics and Thermodynamics of Nonlinear Nonequilibrium Systems (World Scientific, Singapore, 1993).
• [112] L. S. Garcia-Colin, A. R. Vasconcellos, and R. Luzzi, J. Non-Equilib. Thermodyn. 19, 24 (1994).
• [113] R. Luzzi and A. R. Vasconcellos, Physica A 241, 677 (1997).
• [115] A. Hobson, Am. J. Phys. 34, 411 (1966).
• [116] E. T. Jaynes, Phys. Rev. 106, 620 (1957).
• [117] E. T. Jaynes, Phys. Rev. 108, 171 (1957).
• [118] S. Sieniutycz and P. Salamon, in Nonequilibrium Theory and Extremum Principles, edited by S. Sieniutycz and P. Salamon (Taylor and Francis, New York, USA, 1990), pp. 1-38.
• [119] R. E. Nettleton and S. L. Sobolev, J. Non-Equilib. Thermodyn. 19, 205 (1995).
• [120] M. A. Tenan, A. R. Vasconcellos, and R. Luzzi, Forstchr. Phys./Prog. Phys. 45, 1 (1997).
• [121] R. Nettleton, J. Phys. A 21, 3939 (1988).
• [122] R. E. Nettleton, J. Phys. A 22, 5281 (1989).
• [123] R. E. Nettleton, J. Chem. Phys. 93, 8247 (1990).
• [124] R. E. Nettleton, J. Chem. Phys. 99, 3059 (1993).
• [125] E. S. Freidkin and R. E. Nettleton, Nuovo Cimento B 104, 597 (1989).
• [126] R. E. Nettleton, Open Systems and Information Dynamics, Vol. 2 (Copernicus Univ. Press, Varsovia, Poland, 1993), pp. 41-47.
• [127] A. R. Vasconcellos, R. Luzzi, and L. S. Garcia-Colin, Phys. Rev. A 43, 6622 (1991).
• [128] A. R. Vasconcellos, R. Luzzi, and L. S. Garcia-Colin, Phys. Rev. A 43, 6633 (1991).
• [129] A. R. Vasconcellos, R. Luzzi, and L. S. Garcia-Colin, J. Non-Equilib. Thermodyn. 20, 103 (1995).
• [130] A. R. Vasconcellos, R. Luzzi, and L. S. Garcia-Colin, J. Non-Equilib. Thermodyn. 20, 119 (1995).
• [131] A. R. Vasconcellos, R. Luzzi, and L. S. Garcia-Colin, J. Mod. Phys. 9, 1933 (1995).
• [132] A. R. Vasconcellos, R. Luzzi, and L. S. Garcia-Colin, J. Mod. Phys. 9, 1945 (1995).
• [133] A. R. Vasconcellos, R. Luzzi, and L. S. Garcia-Colin, Physica A 221, 478 (1995).
• [134] A. R. Vasconcellos, R. Luzzi, and L. S. Garcia-Colin, Physica A 221, 495 (1995).
• [135] S. Hawkings, 1990 - Yearbook of Science and the Future (Encyclopaedia Britannica, Chicago, USA, 1989).
• [136] H. Price, Time's Arrow and Archimedes' Point (Oxford Univ. Press, Oxford, UK, 1995).
• [137] L. Rosenfeld, in Conversations in Physics and Biology, edited by P. Buckley and D. Peat (Univ. Toronto Press, Toronto, Canada, 1979).
• [138] L. Rosenfeld, in Proceedins of the Int. School Phys.Ënrico Fermi", Course XIV, edited by P. Caldirola (Academic, New York, USA, 1960), pp. 1-20.
• [139] L. Rosenfeld, Acta Phys. Polonica 14, 3 (1955).
• [140] J. P. Dougherty, in Maximum Entropy and Bayesian Method, edited by J. Skilling (Kluwer, Dordrecht, The Netherlands, 1989), pp. 131-136.
• [141] J. P. Dougherty, Stud. Phil. Sci. 24, 843 (1993).
• [142] J. P. Dougherty, Phil. Trans. R. Soc. Lond. A 346, 259 (1994).
• [143] M. C. Makey, Rev. Mod. Phys. 61, 981 (1989).
• [144] H. H. Hasegawa and D. J. Driebe, Phys. Rev. E 50, 1781 (1994).
• [145] J. Meixner, Rheol. Acta 12, 465 (1973).
• [146] J. Meixner, in Foundations of Continuum Thermodynamics, edited by J. J. Delgado, M. N. R. Nina, and J. H. Whitelaw (McMillan, London, UK, 1974), pp. 129-141.
• [147] H. Grad, in Handbuch der Physik XII, edited by S. Flügge (Springer, Berlin, Germany, 1958), pp. 205-294.
• [148] M. C. Mackey, Time's Arrow (Springer, Berlin, Germany, 1992).
• [149] J. L. D. Rio and L. S. Garcia-Colin, Phys. Rev. E 48, 819 (1993).
• [150] I. Prigogine, Acta Physica Austríaca Suppl. X, 401 (1973).
• [151] I. Prigogine, Int. J. Quantum Chem. 9, 443 (1975).
• [152] E. T. Jaynes, Am. J. Phys. 33, 391 (1965).
• [153] B. C. Eu and L. S. Garcia-Colin, Phys. Rev E 54, 2501 (1996).
• [154] R. Courant and D. Hilbert, Methods of Mathematical Physics (Wiley-Interscience, New York, USA, 1953).
• [155] D. Jou and J. Casas-Vazquez, Rep. Prog. Phys. 66, 1937 (2003).
• [156] R. Jancel, Foundations of Classical and Quantum Satistical Mechanics (Pergamon, Oxford, UK, 1963).
• [157] J. G. Ramos, A. R. Vasconcellos, and R. Luzzi, J. Chem. Phys. 112, 2692 (2000).
• [158] M. Criado-Sancho and J. E. Llebot, Phys. Rev. E 47, 4104 (1993).
• [159] G. Nicolis, in The New Physics, edited by P. Davies (Cambridge Univ. Press, Cambridge, UK, 1989), pp. 316-347.
• [160] G. Nicolis and I. Prigogine, Exploring Complexity (Freeman, New York,USA, 1989).
• [161] I. Prigogine and I. Stengers, Order out of the Chaos: Man's New Dialogue with Nature (Bantam, New York, USA, 1984).
• [162] G. Careri, Order and Disorder in Matter (Benjamin/Cummings, New York, USA, 1984).
• [163] G. Nicolis, Physica A 213, 1 (1995).
• [164] A. F. Fonseca, M. V. Mesquita, A. R. Vasconcellos, and R. Luzzi, J. Chem. Phys. 112, 3967 (2000).
• [165] A. R. Vasconcellos, A. C. Algarte, and R. Luzzi, Braz. J. Phys 26, 543 (1996).
• [166] E. T. Jaynes, in Maximum Entropy And Bayesian Methods in Science and Engineering, edited by G. J. Erickson and C. R. Smith (Kluwer, Amsterdam, The Netherlands, 1988), pp. 267-281.
• [167] R. Luzzi, J. G. Ramos, and A. R. Vasconcellos, Phys. Rev. E 57, 244 (1998).
• [168] C. Kittel, Physics Today 41 (5), 93 (1988).
• [169] W. Heisenberg, The Physical Conception of Nature (Hutchinson, London, UK, 1958).
• [170] R. A. Fisher, Phil. Trans. Roy. Soc. London A 222, 309 (1922).
• [171] P. T. Landsberg and V. Vedral, Phys. Lett. A 247, 211 (1998).
• [174] S. Abe and Y. Okamoto, in Nonextensive Statistical Mechanics and its Applications, edited by S. Abe and Y. Okamoto (Springer, Berlin, Germany, 2001).
• [175] H. G. Hentschel and I. Procaccia, Physica D 8, 435 (1983).
• [176] P. Jizba and T. Arimitzu, Ann. Phys. 312, 17 (2004), and arXiv.org/abs/cond-mat/0207707 (2002).
• [178] G. Kaniadakis, Phys. Rev. E 66, 56125 (2002).
• [182] J. Bricmont, The Flight from Science and Reason (The New York Academy of Science, New York, USA, 1996), annals of the New York Academy of Science, Vol 775.
• [183] P. V. Coveney and R. Highfield, The Arrow of Time (Fawcett Columbine, New York, USA, 1990).
• [184] J. Lebowitz, Physics Today 50, 68 (1997).
• [185] S. Savitt, Time's Arrows Today: Recent Physical and Philosophical Work on the Direction of Time (Cambridge Univ. Press, Cambridge, USA, 1995).
• [186] I. Prigogine, La Nascita del Tempo (Theoria, Roma, Italy, 1988).
• [187] J. Brans, I. Stengers, and P. Vincke, Temps et Devenir (Patino, Genčve, Swiss, 1988).
• [188] I. Prigogine and I. Stengers, Entre le Temps et l'Eternité (Fayard, Paris, France, 1988).
• [189] I. Prigogine, La Fin des Certitudes (Jacob, Paris, France, 1996).
• [190] P. Engel, The Sciences (NYAS) 24 (5), 50 (1984).
• [191] T. Rothman, The Sciences (NYAS) 37 (4), 26 (1997).
• [192] H. R. Pagels, Phys. Today 38 (1), 97 (1985).
• [193] R. Penrose, The Emperor's New Mind (Vikings, New York, USA, 1991).
• [194] R. Lestiene, Scientia 113, 313 (1980).
• [195] M. Shinbrot, The Sciences (NYAS) 27 (3), 32 (1987).
• [196] G. Bocchi, Scientia 117, 21 (1982).
• [197] M. Paty, Scientia 117, 51 (1982).
• [198] I. Prigogine, Phys. Rep. 219, 93 (1992).
• [199] T. Petrovky and I. Prigogine, Advances in Chemical Physics (Academic, New York, USA, 1997), Vol. 99.
• [200] A. Böhm, J. Math. Phys. 21, 1040 (1980).
• [201] G. Parravicini, V. Gorini, and E. Sudarshan, J. Math. Phys. 21, 2208 (1980).
• [202] A. Böhm and M. Gadella, Springer Lecture Notes on Physics (Springer, Berlin, Germany, 1989), Vol. 348.
• [203] T. Petrovsky and M. Rosenberg, Found. Phys. 27, 239 (1997).
• [204] I. Antoniou and I. Prigogine, Physica A 192, 443 (1993).
• [205] J. Meixner and H. G. Reik, in Thermodynamik der Irreversiblen Prozesse: Handbuch der Physik, edited by S. Flügge (Springer, Berlin, Germany, 1959), Vol. 112/2.
• [206] J. Bronowski, The Common Sense of Science (Harvard Univ. Press, Cambridge, USA, 1978).
• [207] W. Heisenberg, in Across the Frontiers, edited by R. N. Anshen (Harper and Row, New York, USA, 1975), pp. 184-191.
• [208] S. Hawking, The Nature of Space and Time (Princeton Univ. Press, Princeton, USA, 1996).
• [209] R. Zwanzig, Annual Review of Physical Chemistry (Academic Press, New York, USA, 1965), Vol. 16, pp. 67-102.

Publication Dates

• Publication in this collection
  17 Oct 2005
• Date of issue
  Sept 2005

History

• Received
  26 July 2005