Abstract
We have studied the collective magneto-optical response of layers of semiconductor quantum dots and nano-rings. Expressions for both the polarizability of the individual nano-objects have been used to determine the magneto-optical response on square two-dimensional lattices on those nano-objects as a function on frequency, magnetic field and angle of incidence. The magnetic field dependence of the response for layers of rings gives rise to the Aharonov-Bohm type oscillatory behavior in the reflectance and absorbance that can be measurable. Layers of dots do not display any remarkable magnetic field dependence.
Magneto-optical response; Semiconductor quantum dots; Nano-rings
NANOSTRUCTURES
Magneto-optics of layers of semiconductor quantum dots and nano-rings
O. VoskoboynikovI; C. M. J. WijersII; J. L. LiuI; C. P. LeeI
INational Chiao Tung University,1001 Ta Hsueh Rd., Hsinchu 300, Taiwan
IITwente University, P. O. Box 217, 7500 AE Enschede, The Netherlands
ABSTRACT
We have studied the collective magneto-optical response of layers of semiconductor quantum dots and nano-rings. Expressions for both the polarizability of the individual nano-objects have been used to determine the magneto-optical response on square two-dimensional lattices on those nano-objects as a function on frequency, magnetic field and angle of incidence. The magnetic field dependence of the response for layers of rings gives rise to the Aharonov-Bohm type oscillatory behavior in the reflectance and absorbance that can be measurable. Layers of dots do not display any remarkable magnetic field dependence.
Keywords: Magneto-optical response; Semiconductor quantum dots; Nano-rings
I. INTRODUCTION
Quantum dots and nano-rings are nanosized semiconductor structures resembling artificial atoms. They are expected to play an important role in several urgent areas of modern technology, like optics, optoelectronics, optical computing and quantum cryptography and computing. Semiconductor nano-rings [1] are about the newest not-simply connected quantum nano-objects with unusual magnetic and magnetic-optical properties [2-4]. Like self-assembled semiconductor quantum dots, nano-rings are free of decoherence problems caused by scattering. But topologically the nano-rings are very different from quantum dots. A further consequence of the unusual topology is that the center hole enables trapping of a single magnetic flux and offers the exciting possibility to observe electronic wave-function phases [5] in magneto-optical experiments. This leads to a new so-called öptical" Aharonov-Bohm (AB) effect, which can occur only in semiconductor nano-rings [6-9].
Most of the work done already in the field of the optical AB effect in nano-rings has been about far-infrared (FIR) spectroscopy or magneto-photoluminescence (MP). Far-infrared spectroscopy enabled the investigation of transitions between the split levels directly and revealed level crossings for the rings with varying magnetic field, unknown from dots [10]. MP spectroscopy has been used to demonstrate neutral and charged excitons in nano-rings [8]. Apart from the thorough theoretical analysis in [9], no studies are known about the direct optical observation of the AB effect, involving interband transitions. This effect has been studied experimentally in [11] but the information provided there is very limited.
For a quantitative characterization of the magneto-optical properties of layers of quantum dots and nano-rings based meta-materials a highly developed optical spectroscopy, like ellipsometry, and an advanced theoretical description are indispensable. Proper understanding and modeling of the collective electromagnetic response of nano-object layers requires a correct approach, taking into account their composite and discrete character [12,13]. In addition, comparison of the collective magneto-optical response of structures of semiconductor quantum dots and nano-rings can provide important information about the basic physical distinctions between these two types of systems.
In this paper study theoretically the collective (beyond the single nano-ring picture) electromagnetic properties of layers of semiconductor quantum dots and nano-rings in the optical range (see Fig. 1). We show that the interband magneto-optical response (absorbance) of a layer of InAs/GaAs nano-rings demonstrates AB oscillations in contrast to a layer of quantum dots. It will turn out that, as a result, the magnitude of these effects is within the range of a modern ellipsometric setup.
II. THEORY AND RESULTS
The systems to be investigated in this paper are two dimensional square lattices (lattice parameter aL) of InAs/GaAs quantum dots and nano-rings shown in Fig. 1 (a). Previously we have treated theoretically torus (cut-torus) shaped nano-scale rings in external magnetic fields, using an effective Hamiltonian with position dependent electronic and hole effective masses [4,14]. It was found that experimentally relevant simulations of the behavior of nano-rings can only be obtained with three-dimensional models using the experimentally determined shape, strain and composition of the rings [9].
Recent experiments [4] have shown that the rings, as will be studied here, have the "eye" type cross-section as presented in upper insert in the panel (a) of Fig. 1. The same computational technique we apply for semiconductor quantum dots with cylindrically symmetrical shapes (lower insert in the panel (b) of Fig. 1). Here we calculate electron and hole energies/envelope wave functions, adjacent to the energy gap, for these "eye" shaped dots and rings as a function of a magnetic field in the z-direction. Details of the method of calculation can be found in [4,14]. For frequencies w close to the energy gap of the nano-objects, the size of the object is small as compared to the wavelength and the dipole approximation can be used. Therefore it is possible to use the Kramers-Heisenberg expression [15,16] for the polarizability tensor:
where
S ( w) is the static part of the polarizability (to be discussed letter), and G is the damping factor chosen to be independent on frequency. The possible transition energies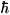 wfi =
wfi = 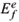 -
- 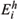 determined by the energies
determined by the energies 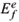 and
and 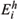 for the excited (electron) and ground (hole) states, respectively. The dynamic part of the polarizability is determined by the optical matrix elements á i| r |f ñ , the expectation value of the position vector r = (x,y,z). The sum over states in (1) is limited to transitions from hole states with i º { nh = 1,mh = 0, - 1 } to electronic states with f º { ne = 1,me = 0, - 1 }, where nh,e is the spectroscopic notation for the radial hole (electron) quantum number, and mh,e is the azimuthal quantum number for holes (electrons). Those states determine the transitions with the lowest
for the excited (electron) and ground (hole) states, respectively. The dynamic part of the polarizability is determined by the optical matrix elements á i| r |f ñ , the expectation value of the position vector r = (x,y,z). The sum over states in (1) is limited to transitions from hole states with i º { nh = 1,mh = 0, - 1 } to electronic states with f º { ne = 1,me = 0, - 1 }, where nh,e is the spectroscopic notation for the radial hole (electron) quantum number, and mh,e is the azimuthal quantum number for holes (electrons). Those states determine the transitions with the lowest 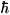 w near the edge of absorption. Excitonic and Faraday/Kerr- or Cotton/Mouton-type magneto-optical effects are not taken into account here.
w near the edge of absorption. Excitonic and Faraday/Kerr- or Cotton/Mouton-type magneto-optical effects are not taken into account here.
Using the description proposed in [9] and following the selection rules me = mh enables us to consider near absorption edge only the optical transitions for dots and rings shown in Fig 1 (b). Those inserts show the lowest allowed optical transition energies as a function of a magnetic field in the z-direction. The crossing between the two transition energies in the case of rings gives rise to the optical AB effect for (w).
(w).
Taking into account the cylindrical symmetry of the nano-objects and both spin polarizations, we obtain for the optical transition matrix elements [17]
where Imn = òrdrdz (r,z)
(r,z) (r,z) is the electron-hole overlap integral for the envelope wave-functions and r = (x,y). The matrix element áS|x|Xñ can be presented in the conventional notation of the Kane parameter P
(r,z) is the electron-hole overlap integral for the envelope wave-functions and r = (x,y). The matrix element áS|x|Xñ can be presented in the conventional notation of the Kane parameter P
This important value one can also take from direct experimental results available for InAs/GaAs nano-structures [18].
The separate addition of the static polarizability tensor
S (w) is necessary to compensate the losses in the real part when the subsequent sum over states in (1) is limited to a small number of levels. We approximate this static polarizability by the polarizability of a homogeneous dielectric ellipsoid of rotation, for which an analytical expression has been given in [19].
where u = x,y,z, V is the volume of the ellipsoid, e is the semiconductor material dielectric constant, and g = b/a, the aspect ratio with a the long and b the short, z-oriented, axis of rotation of the ellipsoid. For reasons of symmetry the relation 2Nx + Nz = 1 can be used to determine Nx.
The polarizability tensor determines the reflection (rss, rpp) and transmission (tss, tpp) coefficients of a layer of dots or rings. For a square lattice Vlieger has shown that these coefficients are given by [12]:
Here subscripts "s" and "p" refer to light polarization perpendicular and parallel to the plane of incidence, respectively, qi is the angle of incidence (see Fig. 1), k = c - 1w is the wave vector, c is the speed of light. In (3) we have made use of the following definitions:
with u as defined before. The values for the diagonal part of the intraplanar transfer tensor  depend on the type of layer lattice. The scaling factor a0 = 4pe0
depend on the type of layer lattice. The scaling factor a0 = 4pe0 is commonly used in discrete dipole calculations [12]. For the two dimensional square lattice of rings we investigate here, we have to use: fS,xx = fS,yy= -4.51681, fS,zz = 2fS,xx.
is commonly used in discrete dipole calculations [12]. For the two dimensional square lattice of rings we investigate here, we have to use: fS,xx = fS,yy= -4.51681, fS,zz = 2fS,xx.
We analyze the dependency of the calculated magneto-optical response on magnetic field and frequency near the absorption edge of the nano-objects for a lattice of InAs/GaAs dots/rings as shown in Fig. 1 (note that axx = ayy due to the cylindrical symmetry). The lattice parameter is aL0 = 80 nm and yields a0 = 5.7 * 10 - 32Fm2. For the calculation of the static polarizability tensor we have used the dielectric constant e = 12.2 and an aspect ratio of g = 0.081. The requirement that the volume of the ellipsoid has to be the same as that of the real object yields a long axis of a = 18.46 nm. The components of the static polarizability tensor are then aS,xx = aS,yy = 2.26 * 10 - 3a0 and aS,zz = 3.4 * 10 - 4a0. Further we use for the uniform damping parameter G= 2 meV, material parameters from [17], and for the matrix element áS|x|Xñ = 0.6 nm [18].
The interesting behavior of the polarization tensor of a nano-ring in a magnetic field (distinct from that of a quantum dot) is a result of the crossing of the transition energies, which produces oscillations in the real and imaginary part of the polarizability. The polarizability reflects directly the optical AB effect for nano-rings and it is related to the magnetic field dependence of the energy levels belonging to the ground state Hamiltonian of the nano-rings. It dominates in the magnetic field dependence of the optical response and has to be distinguished from the weaker Faraday/Kerr and Cotton/Mouton effects.
For layers of rings one can expect to observe the AB effect in the optical reflection, transmission and absorbance of the layers. The last one is defined as
Fig. 2 shows the absorbance of layers of dots and rings as function of energy E = 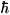 w, magnetic field B, and angle of incidence qi for a two dimensional square lattice with lattice parameter aL0.
w, magnetic field B, and angle of incidence qi for a two dimensional square lattice with lattice parameter aL0.
The absorbance plots display a quite monotonous ridge like patterns for dots (Fig. 2(a)) but a clear "hill/valley" pattern for rings (Fig. 2(b)). This more remarked dependence of the rings upon changes in the magnetic field strength B inherits the oscillatory behavior from the ground state energy levels of electrons and holes. This represents a typical manifestation of the optical AB effect. Obviously, if we enhance the magnetic field range and number of levels involved (|me,h| > 1) the absorbance of the ring system oscillates as many times as transition energies will be crossing. The overall picture is that the absorbance in the ring system is stronger than for the dot system. This is the consequence of the enlargement at resonance of the imaginary part of the polarizability due to the crossing of energy levels in the ring system.
An interesting feature of the absorbance (both for dots and rings) is the large difference in the dependence of Ass and App on the angle of incidence (Fig. 2(c,d)). Since this difference almost disappears when we do a reference calculation with axx = azz, the difference can only be attributed to the cylindrical symmetry of the nano-objects. It is definitely not a Brewster minimum related feature.
More surprisingly, the size of the effect is within the detection range of modern ellipsometry [17,20]. We stress that the magnitude of the AB oscillations depends strongly on the average concentration of the dots and rings. Hence to demonstrate unambiguously the optical AB effect ellipsometrically, the highest possible lattice density should be used.
III. CONCLUSION
In conclusion, we studied theoretically the magneto-optical response functions (like polarizability and absorbance) for semiconductor quantum dots and nano-rings, when they are arranged in a square lattice. The calculations clearly show that rings are more effective to exploit the response from magnetic fields than dots. Despite a lower volume fraction ring structures have stronger variation of absorbance when the magnetic field changes than the dots. We have shown that layers of InAs/GaAs self-assembled nano-rings exhibit the optical AB effect particularly in reflectance mode. While AB effects are discussed in the literature for the cases of infrared absorption and photoluminescent emission, we can expect this behavior to be observable in ellipsometric measurements with good resolution. The calculated results suggest large polarization anisotropy for absorbance at large angles of incidence. This can be measured and should display the new optical AB effects for low temperature and moderate magnetic field regimes. Actual magnitude of the effect should be verified both by experiment and by more sophisticated calculations.
Acknowledgement
This work is supported by the National Science Council of the Republic of China under Contracts No. NSC-94-2811-M-009-020 and NSC-94-2112-M-009-037.
[1] J. M. Garcia, G. Medeiros-Ribeiro et al., Appl. Phys. Lett. 71, 2014 (1997).
[2] A. Lorke and R. J. Luyken, Physica B 256-258, 424 (1998); A. Lorke, R. J. Luyken, A. O. Govorov et al., Phys. Rev. Lett. 84, 2223 (2000).
[3] J. Planelles, W. Jaskolski, and J. I. Aliaga, Phys. Rev. B 65, 033306 (2001).
[4] O. Voskoboynikov, Y. M. Li et al., Phys. Rev. B 66, 155306 (2002); O. Voskoboynikov and C. P. Lee, Physica E 20, 278 (2004).
[5] Y. Aharonov and D. Bohm, Phys. Rev. 115, 485 (1959).
[6] H. Hu, J. L. Zhu, and J. J. Xiong, Phys. Rev. B 62, 16777 (2000); H. Hu, J.-L. Zhu et al., Phys. Rev. B 63, 195307 (2001).
[7] A. O. Govorov, S. E. Ulloa, K. Karrai, and R. J. Waburton, Phys. Rev. B 66, 081309 (2002).
[8] M. Bayer, M. Korkusinski et al., Phys. Rev. Lett. 90, 186801 (2003).
[9] J. I. Climente, J. Planelles, and W Jaskolski, Phys. Rev. B 68, 075307 (2003); J. Climente, J. Planelles, W. Jaskolski et al., J. Phys. C 15, 3593 (2003).
[10] A. Emperador, M. Pi et al., Phys. Rev. B 62, 4573 (2000).
[11] H. Petterson, R.J. Warburton et al., Physica E 6, 510 (2000).
[12] J. Vlieger, Physica 64, 63 (1973).
[13] G. Y. Slepyan, S.A. Maksimenko, V. P. Kalosha, A. Hoffmann, and D. Bimberg, Phys. Rev. B 64, 125326 (2001).
[14] Y. M. Li, H. M. Lu, O. Voskoboynikov at al., Surf. Sci. 532-535, 811 (2003).
[15] H. A. Kramers and W. Heisenberg, Z. Phys. 31, 681 (1925).
[16] C. M. J. Wijers, Phys. Rev. A 70, 063807 (2004).
[17] S. L. Chuang, Physics of Optoelectronics Devices (Wiley Interscience, New York, 1995).
[18] P. G. Eliseev, H. Liet et al., Appl. Phys. Lett. 77, 262 (2000).
[19] J. Avelin, PhD Thesis, Helsinki University of Technology, Report 414 (2003).
[20] H. G. Tompkins and W. A. McGahan, Spectroscopic Ellipsometry and Reflectometry: a User's Guide, (Wiley Interscience, New York, 1999).
Received on 4 April, 2005
- [1] J. M. Garcia, G. Medeiros-Ribeiro et al., Appl. Phys. Lett. 71, 2014 (1997).
- [2] A. Lorke and R. J. Luyken, Physica B 256-258, 424 (1998);
- A. Lorke, R. J. Luyken, A. O. Govorov et al., Phys. Rev. Lett. 84, 2223 (2000).
- [3] J. Planelles, W. Jaskolski, and J. I. Aliaga, Phys. Rev. B 65, 033306 (2001).
- [4] O. Voskoboynikov, Y. M. Li et al., Phys. Rev. B 66, 155306 (2002);
- O. Voskoboynikov and C. P. Lee, Physica E 20, 278 (2004).
- [5] Y. Aharonov and D. Bohm, Phys. Rev. 115, 485 (1959).
- [6] H. Hu, J. L. Zhu, and J. J. Xiong, Phys. Rev. B 62, 16777 (2000);
- H. Hu, J.-L. Zhu et al., Phys. Rev. B 63, 195307 (2001).
- [7] A. O. Govorov, S. E. Ulloa, K. Karrai, and R. J. Waburton, Phys. Rev. B 66, 081309 (2002).
- [8] M. Bayer, M. Korkusinski et al., Phys. Rev. Lett. 90, 186801 (2003).
- [9] J. I. Climente, J. Planelles, and W Jaskolski, Phys. Rev. B 68, 075307 (2003);
- J. Climente, J. Planelles, W. Jaskolski et al., J. Phys. C 15, 3593 (2003).
- [10] A. Emperador, M. Pi et al., Phys. Rev. B 62, 4573 (2000).
- [11] H. Petterson, R.J. Warburton et al., Physica E 6, 510 (2000).
- [12] J. Vlieger, Physica 64, 63 (1973).
- [13] G. Y. Slepyan, S.A. Maksimenko, V. P. Kalosha, A. Hoffmann, and D. Bimberg, Phys. Rev. B 64, 125326 (2001).
- [14] Y. M. Li, H. M. Lu, O. Voskoboynikov at al., Surf. Sci. 532-535, 811 (2003).
- [15] H. A. Kramers and W. Heisenberg, Z. Phys. 31, 681 (1925).
- [16] C. M. J. Wijers, Phys. Rev. A 70, 063807 (2004).
- [17] S. L. Chuang, Physics of Optoelectronics Devices (Wiley Interscience, New York, 1995).
- [18] P. G. Eliseev, H. Liet et al., Appl. Phys. Lett. 77, 262 (2000).
- [19] J. Avelin, PhD Thesis, Helsinki University of Technology, Report 414 (2003).
- [20] H. G. Tompkins and W. A. McGahan, Spectroscopic Ellipsometry and Reflectometry: a User's Guide, (Wiley Interscience, New York, 1999).
Publication Dates
-
Publication in this collection
06 July 2006 -
Date of issue
June 2006
History
-
Received
04 Apr 2005










