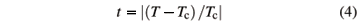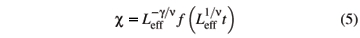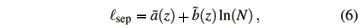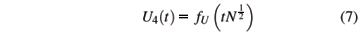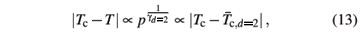Abstract
The critical scaling behavior of Ising models with long range interactions is studied. These long-range interactions, when imposed in addition to interactions on a regular lattice, lead to small world graphs. Large-scale Monte Carlo simulations, together with finite-size scaling, is used to obtain the critical behavior of a number of different models. These include the z-model introduced by Scalettar, standard small-world bonds superimposed on a square lattice, and physical small-world bonds superimposed on a square lattice. These scaling results provide further evidence to support the existence of physical (quasi-) small-world nanomaterials.
Monte Carlo; Nanomaterials; Small world
Critical behavior of ising models with random long-range (small-world) interactions
X. Zhang; M. A. Novotny
Dept. of Physics and Astronomy, Center for Computational Sciences, P.O. Box 5167, Mississippi State University, Mississippi State, MS 39762-5167, USA
ABSTRACT
The critical scaling behavior of Ising models with long range interactions is studied. These long-range interactions, when imposed in addition to interactions on a regular lattice, lead to small world graphs. Large-scale Monte Carlo simulations, together with finite-size scaling, is used to obtain the critical behavior of a number of different models. These include the z-model introduced by Scalettar, standard small-world bonds superimposed on a square lattice, and physical small-world bonds superimposed on a square lattice. These scaling results provide further evidence to support the existence of physical (quasi-) small-world nanomaterials.
Keywords: Monte Carlo; Nanomaterials; Small world
I. INTRODUCTION
The critical behavior, as well as the transport properties, of a particular material depend on a number of factors, in particular the effective dimensionality of the system. Thus one-dimensional (or quasi-one-dimesional) materials [1] behave differently than thin films, both of which have different properties than bulk (three dimensional) materials. In general, constraining the geometry of a system leads to effective dimensions [2, 3] less than the bulk dimension. In the two-body interaction approximation, all materials reduce to a ball-and-stick' model, with atoms as the balls' and the bonds between atoms as the sticks'. This leads from a particular material to a given graph [4], with atoms at the nodes and chemical bonds (two-body interactions) along the edges.
Recently there has been a great deal of interest in graphs which are neither regular graphs (as are the graphs of materials with perfect crystal structures) nor random graphs. One type of such graph is the small-world (SW) graph [5]. Such graphs have been used, for example, to improve scalability of parallel computer algorithms [6-10]. Furthermore, the critical behavior of models of materials, such as the Ising model, Heisenberg model, and random-walker models have been studied on SW graphs [11-21]. The result of these studies is that models on SW graphs exhibit mean-field scaling, namely they have an effective dimension at or above the upper critical dimension of the model (which for the Ising model without disorder is d = 4).
Unfortunately, the study of such materials models on SW networks is not of interest to experimental researchers in materials. The reason is that certain constraints due to the fixed size of atoms and atomic bonds, as well as the necessity of embedding the ball-and-stick' graph in three dimensional space, restricts the types of SW graphs that are of interest to materials researchers. SW graphs with such constraints are called physical SW graphs [22-24], and the critical behavior of Ising models on physical SW graphs has been studied. This study started with a linear graph, with added SW bonds. In this article, a study of Ising critical behavior on graphs starting with a square lattice and with added SW bonds, is reported.
II. MODEL AND METHODS
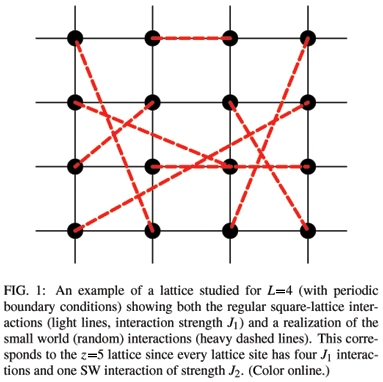
The models studied here are Ising models with N = L2 Ising spins with si = ±1 on a L×L square lattice with periodic boundary conditions, and with a nearest-neighbor ferromagnetic interaction of strength J1. A fixed number of SW bonds with interaction strength J2 are added to the square-lattice (see Fig. 1), by randomly picking pairs of atoms and connecting them with a bond. Note that once the pair of atoms is picked, these atoms are not allowed to be picked again until all atoms have been picked. In other words, every node will have a coordination number z between zmax and zmax-1. The Ising Hamiltonian is given by
We use either normal' SW bonds of strength J2, or else given a SW bond of length  between the randomly chosen atoms we string a chain of
between the randomly chosen atoms we string a chain of  +1 atoms with interaction strength J3 between these chosen square-lattice atoms. We always set either J2 or J3 equal to zero.
+1 atoms with interaction strength J3 between these chosen square-lattice atoms. We always set either J2 or J3 equal to zero.
We will first study here in detail scaling of a model with z SW bonds per atom with J2 = 1 and J1 = J3 = 0. We will call this model the z-model. It was first introduced by Scalettar [25] in 1991, before the introduction of SW networks. Nevertheless, it corresponds to a particular SW lattice. In particular, it can be mapped onto a one-dimesional lattice with z-2 SW interactions. This model is studied to determine whether the scaling for it is that of [25] or of another form predicted by Brézin and Zinn-Justin [26] and utilized to study Ising systems with long-range interactions [27-30].
We utilized standard Monte Carlo (MC) simulations [31], with the site for an attempted update chosen at random. We utilized a Glauber flip probability and the SPRNG [32] random number generator. In particular, if the next random number is r the spin is flipped if
where Eold is the current energy and Enew is the energy if the chosen spin is flipped. The temperature is T and kB is Boltzmann's constant (in our units kB = 1). For a system with N Ising spins, the units of time are Monte Carlo Steps per Spin (MCSS), which corresponds to N spin flip attempts. We measured a number of quantities, and report here on the order parameter  , as well as the integer moments of the magnetization
, as well as the integer moments of the magnetization  . The summation index j runs over the K different configurations generated in the Monte Carlo simulation. From these moments the susceptibility cT =
. The summation index j runs over the K different configurations generated in the Monte Carlo simulation. From these moments the susceptibility cT =  ( á M2ñ- |M|2) and the Binder fourth-order cumulant U4 = 1-
( á M2ñ- |M|2) and the Binder fourth-order cumulant U4 = 1- were calculated. Simulations were performed using up to 128 processing elements using trivial parallelization. Obtaining points for the z-model for the largest system size N = 2562 took about 52 hours per data run. Averages for all runs used between K = 106 and 108 MCSS per point. The crossings for different N values for U4 give the critical temperature Tc for each model [31]. These values are listed in Table I.
were calculated. Simulations were performed using up to 128 processing elements using trivial parallelization. Obtaining points for the z-model for the largest system size N = 2562 took about 52 hours per data run. Averages for all runs used between K = 106 and 108 MCSS per point. The crossings for different N values for U4 give the critical temperature Tc for each model [31]. These values are listed in Table I.
III. RESULTS AND SCALING: z-MODEL
In this section we present results for the z-model (J1 = J3 = 0, J2 = 1) where every node has z random links. There are no square-lattice interactions, and consequently this model maps onto a linear chain with every spin having one random (small-world) link if z = 3. This model also corresponds to the model introduced by Scalettar [25]. We studied the model for z values between 3 and 8, and simulated system sizes up to N = 2562 = 65536 (although the starting square-lattice structure is unimportant for the z-model, we will still report the system size as N = L2).
Fig. 2 shows the values for U4 and cT for the z-model. These figures also allow one to read off the value for Tc. The order parameter for the z-model is shown in Fig. 3 for various values of z. Also shown is the mean-field (mf) value given by the solution of the equation
Note that as z increases the curves for |M| approach that of the mean-field result.
The general form for scaling at a second order phase transition as a function of the reduced temperature
is given by [31]
with g the critical exponent for c and n the critical exponent for the correlation length. Here the effective length that enters scaling, Leff, depends on the dimension of the system. For a regular d-dimesional lattice Leff =  . However, this type of scaling does not hold for systems at or above the upper critical dimension. These systems behave in a mean-field fashion, such as the z-model. Scalettar showed that the average separation of spins in the z-model is
. However, this type of scaling does not hold for systems at or above the upper critical dimension. These systems behave in a mean-field fashion, such as the z-model. Scalettar showed that the average separation of spins in the z-model is
and suggested that scaling for the z-model should scale as in Eq. 5 with Leff ~ sep ~ ln(N). His fit parameters (compare Fig. 5 of ref. [25]) used Tc = 1.87 and fits of a = 2 and b = 1.887 in plots of c/[ln(N)]a versus (T-Tc) [ln(N)]b. Our data for the same parameters are shown in Fig. 4(a). Note that the crossing of U4 with different system sizes actually gives a lower value for Tc (Table 1). Using the best fit parameters a and b for data collapse scaling of our data for z = 3 and the value of Tc from the U4 crossings gives the fit shown in Fig. 4(b). In neither case in Fig. 4 does the scaling look very good. Note that with the additional computer power available today, our system sizes and statistics are much greater than that of ref. [25]. In summary, the z-model does not scale as was proposed in 1991 in ref. [25]. To ensure that these results were accurate, each author developed independently a code for the z = 3 model using different random number generators. Both codes gave comparable results, leading to a belief that our Monte Carlo data are indeed correct for this model.
sep ~ ln(N). His fit parameters (compare Fig. 5 of ref. [25]) used Tc = 1.87 and fits of a = 2 and b = 1.887 in plots of c/[ln(N)]a versus (T-Tc) [ln(N)]b. Our data for the same parameters are shown in Fig. 4(a). Note that the crossing of U4 with different system sizes actually gives a lower value for Tc (Table 1). Using the best fit parameters a and b for data collapse scaling of our data for z = 3 and the value of Tc from the U4 crossings gives the fit shown in Fig. 4(b). In neither case in Fig. 4 does the scaling look very good. Note that with the additional computer power available today, our system sizes and statistics are much greater than that of ref. [25]. In summary, the z-model does not scale as was proposed in 1991 in ref. [25]. To ensure that these results were accurate, each author developed independently a code for the z = 3 model using different random number generators. Both codes gave comparable results, leading to a belief that our Monte Carlo data are indeed correct for this model.
At and above the upper critical dimension, Brézin and Zinn-Justin in 1985 [26] predicted that the Ising model should scale such that for infinite system sizes the value of the Binder cumulant at Tc should be equal to  » 0.2705. As expected, this value is different from the d = 2 Ising result of
» 0.2705. As expected, this value is different from the d = 2 Ising result of  » 0.615 [31]. Furthermore, Brézin and Zinn-Justin predicted that the mean-field systems should exhibit finite size scaling for small values of the reduced temperature t with
» 0.615 [31]. Furthermore, Brézin and Zinn-Justin predicted that the mean-field systems should exhibit finite size scaling for small values of the reduced temperature t with
and taking derivatives with respect to t gives
They also predicted for small t the finite-size scaling form
Although not stated explicitly in their paper, their scaling form for the order parameter is
for T < Tc. The predicted scaling for U4 and its derivative with respect to t works extremely nicely for all values of z from z = 3 to our largest studied value z = 8, as shown in Fig. 5. It should be stressed that this scaling plot has no adjustable parameters , since the value for Tc is obtained by the crossings of U4 for various values of N. Similarly, The exact mean-field (mf) value for U4 for the infinite lattice [26] is shown as the horizontal lines. Fig. 6 shows the predicted scaling for various values of N and z from Eq. 9 for cT and from Eq. 10 for |M|, again with no adjustable parameters since Tc is taken from the crossings of U4. Again the scaling is very good. The asymptotic slopes for small t and large N with large tN for |M| in Fig. 6(a) is
for |M| in Fig. 6(a) is  . This value can be seen since the scaling function gives
. This value can be seen since the scaling function gives
with the mean field value for this exponent is b =  . Similarly, since the mean field value of the susceptibility exponent is g = 1 the asymptotic slope in Fig. 6(b) should be -1. Most of the spread in the scaling in Fig. 6 is a vertical shift of the curves for various values of z. This may be due to one or more of several reasons. One possibility would be slight errors in the values of Tc, perhaps caused by different convergence rates with different z to the infinite lattice values. Another possibility would be that the prefactor for |M| and cT at Tc for finite N is slightly different. Our data at this point is not of a sufficient quality to decide among these possible alternatives. Nevertheless, the scaling predicted by Brézin and Zinn-Justin [26] is seen to hold.
. Similarly, since the mean field value of the susceptibility exponent is g = 1 the asymptotic slope in Fig. 6(b) should be -1. Most of the spread in the scaling in Fig. 6 is a vertical shift of the curves for various values of z. This may be due to one or more of several reasons. One possibility would be slight errors in the values of Tc, perhaps caused by different convergence rates with different z to the infinite lattice values. Another possibility would be that the prefactor for |M| and cT at Tc for finite N is slightly different. Our data at this point is not of a sufficient quality to decide among these possible alternatives. Nevertheless, the scaling predicted by Brézin and Zinn-Justin [26] is seen to hold.
IV. RESULTS AND SCALING: SW-MODEL
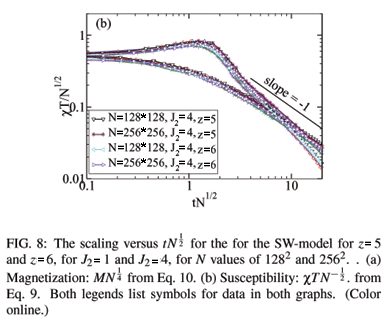
This section presents results for scaling for the normal small-world model (SW-model). This has J1 = 1, J3 = 0, and a non-zero positive value for J2. Every spin has four nearest-neighbor ferromagnetic interactions J1 due to the underlying square-lattice structure. We will study the case where every spin has one SW bond and hence z = 5, and the case where every spin has two SW bonds and hence z = 6. From the crossings of U4 for various values of N we obtain the values of the critical temperature listed in Table 1. Fig. 7 shows that the anticipated form for the scaling of U4 from Eq. 7 and of the derivative of U4 with respect to t from Eq. 8 provides excellent data collapse scaling for various values of z and N and for both the studied values of J2: J2 = 1 and J2 = 4. The thickness of the region of data collapse seems to be more from the statistical properties of the data, or from small errors in Tc, than from a lack of scaling or of corrections to scaling. Fig. 8(a) shows the scaling predicted from Eq. 10 for the order parameter |M|, and Fig. 8(b) shows the data collapse scaling for cT from Eq. 9. In both cases the data collapse is very good for both values of J2, for both z = 5 and z = 6, and for both system sizes shown of N = 1282 and N = 2562. The scaling for smaller system sizes demonstrates corrections to scaling, and consequently only our largest two system sizes are shown in these scaling figures. Again, it must be emphasized that since the value for Tc is taken from the crossings of U4 the curves in Fig. 7 and Fig. 8 have no adjustable parameters .
The underlying scaling behavior of the SW model with z = 5 and z = 6 is consistent with other studies of Ising models with SW interactions (usually starting from d = 1) models [11-13, 15, 16, 18, 20, 22-27]. Consequently, these models have a critical behavior with mean-field critical exponents g = 1, b =  , a = 0, and n =
, a = 0, and n =  (but as in the comment to Ref. [13] with
(but as in the comment to Ref. [13] with  = 2-a = 2).
= 2-a = 2).
There is also a prediction [17] that in the N®¥ limit the order parameter should scale for T < Tc as
with the mean field amplitude à µ p diverging as the strength of the SW couplings p approaches zero. In [17] it is argued that this behavior will also be seen as the number of SW bonds becomes small, i.e. when z = 4+p®4 for our square-lattice model. We have simulated our square-lattice model for z = 5 with weak J2 = 0.01, 0.05 , 0.1, 0.5 for system sizes up to N = 3842. However, we were not able to obtain the predicted scaling. To see this scaling requires that the width of the mean field region, which is [17] within
diverging as the strength of the SW couplings p approaches zero. In [17] it is argued that this behavior will also be seen as the number of SW bonds becomes small, i.e. when z = 4+p®4 for our square-lattice model. We have simulated our square-lattice model for z = 5 with weak J2 = 0.01, 0.05 , 0.1, 0.5 for system sizes up to N = 3842. However, we were not able to obtain the predicted scaling. To see this scaling requires that the width of the mean field region, which is [17] within
be sufficiently probed by the system size that finite size effects are negligible. It would be interesting to have a prediction for how finite N would manifest itself in this scaling. Computer simulations for SW systems with varying strengths J2 have also recently been reported [20].
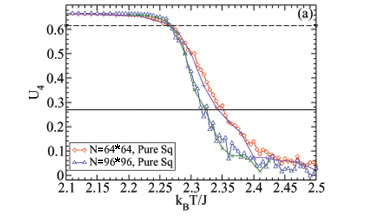
We have also investigated the case where the number of SW connections goes to zero as N increases. This study is motivated by physical small-world networks [22-24] where the number of short-cut bonds (which are SW bonds) cannot grow as fast as N. In [22, 23] it was shown that the properties of such systems for small N can nevertheless show some of the mean field properties of a full small-world system. Fig. 9 shows U4 for both the pure square-lattice Ising model (z = 4) and the SW model with z = 4+ . For the SW model with z = 4+
. For the SW model with z = 4+ as N®¥ the pure square lattice results with Tc = Tc,d = 2 must be recovered. As seen in Fig. 9 even for 256 SW bonds of strength J2 = 4 for N = 2562 = 65536 spins the temperature value where U4 changes from about
as N®¥ the pure square lattice results with Tc = Tc,d = 2 must be recovered. As seen in Fig. 9 even for 256 SW bonds of strength J2 = 4 for N = 2562 = 65536 spins the temperature value where U4 changes from about  to zero is shifted by about 5%. This indicates that even a vanishing fraction of SW bonds can have effects on the behavior of the system. This is demonstrated in the scaling of |M| in [23].
to zero is shifted by about 5%. This indicates that even a vanishing fraction of SW bonds can have effects on the behavior of the system. This is demonstrated in the scaling of |M| in [23].
V. RESULTS AND SCALING: PHYSICAL SW-MODEL
There are two ways to obtain physical SW networks [22-24] to study the effect of SW bonds that can be built from physical building blocks. These physical SW networks must satisfy certain constraints so that they can be built from physical building blocks. These building blocks may be atoms, beads necklaces [23], or ball-and-stick models of atoms. One way to obtain physical SW networks is to have a vanishing number of SW bonds (short-cuts) as N increases. This was discussed in the previous section. The second way to obtain a physical SW network is to build the SW bonds from the underlying building blocks. This was done in [22] starting from a d = 1 chain. Each SW bond is then composed of a string of spins with ferromagnetic coupling constant J3, with the number of spins along the chain equal to the Euclidean distance between the randomly chosen sites. In [23] it was shown that the total number of spins in the d = 1 case starting with N0 spins goes as Ntotµ  . For a d = 2 model on a L2 lattice the total number of spins needed for every initial spin to also have a SW bond is expected to be Ntotµ L3. This severely limits the system size that can be simulated. We studied only system sizes up to L2 = 962 = 9216 in this section, which corresponds to Ntot = 185635 total Ising spins.
. For a d = 2 model on a L2 lattice the total number of spins needed for every initial spin to also have a SW bond is expected to be Ntotµ L3. This severely limits the system size that can be simulated. We studied only system sizes up to L2 = 962 = 9216 in this section, which corresponds to Ntot = 185635 total Ising spins.
Here we present results for the physical SW model with J2 = 0 and J1 = J3 = 1. Fig. 10 shows U4 and the scaling of U4. The SW bonds are built from linear chains of Ising spins. The linear Ising model does not have a finite temperature critical point. Consequently, one expects from renormalization group arguments that the critical exponents should be those of the d = 2 Ising model. Furthermore, one expects that the critical temperature should be the same as for the square lattice Ising model, Tc =  » 2.269 J1. Fig. 10(a) shows that indeed the SW bonds built from linear chains of spins do not significantly affect the behavior of the system. This is also evident in the scaling of U4 shown in Fig. 10(b). The scaling uses the d = 2 Ising exponent n = 1.
» 2.269 J1. Fig. 10(a) shows that indeed the SW bonds built from linear chains of spins do not significantly affect the behavior of the system. This is also evident in the scaling of U4 shown in Fig. 10(b). The scaling uses the d = 2 Ising exponent n = 1.
VI. DISCUSSION AND CONCLUSION
The Ising ferromagnet on models starting from the square lattice Ising model has been studied. The first conclusion, which has also been reached by other researchers, is that the Ising model with normal' small world (SW) bonds exhibits mean field scaling [Fig. 7 and Fig. 8].
We have investigated in detail the z-model of ref. [25], and found that the scaling form for cT is given by Eq. 9 from [26] [Fig. 6(b)] rather than Eq. 5 with Leff = ln(N) postulated in [25] [Fig. 4]. The scaling of ref. [26] [Eq. 7 through Eq. 10] also works without any adjustable parameters for the z-model for other quantities such as the Binder cumulant U4 [Fig. 5] and the order parameter |M| [Fig. 6(a)]. Scaling as predicted for N®¥ predicted in ref. [17] for a low density or for weak SW bonds could not be seen in our data. This most likely is because the finite size effects for the N values we studied obscured the predicted scaling.
We have also investigated the Ising model on physical SW networks starting from an underlying N = L2 square lattice. The physical SW networks either have a number of SW bonds that vanish as N®¥ (here z = 4+ ), or are constructed from a linear chain of spins with the number of spins along the chain equal to the Euclidean distance between the randomly chosen spins on the square lattice. The study here can be compared to physical SW studies in [22-24], as well as the study with power-law SW bond strengths [18]. The summary is twofold. First, physical SW bonds do not change the critical properties of the model as N®¥. Second, the physical SW bonds have some effect on the scaling properties. They lead to much slower approaches to the N®¥ results. They also show a regime near the effective Tc,N, given by the temperature where for finite N the value of U4 quickly changes between
), or are constructed from a linear chain of spins with the number of spins along the chain equal to the Euclidean distance between the randomly chosen spins on the square lattice. The study here can be compared to physical SW studies in [22-24], as well as the study with power-law SW bond strengths [18]. The summary is twofold. First, physical SW bonds do not change the critical properties of the model as N®¥. Second, the physical SW bonds have some effect on the scaling properties. They lead to much slower approaches to the N®¥ results. They also show a regime near the effective Tc,N, given by the temperature where for finite N the value of U4 quickly changes between  and zero, which shows some properties of mean field behavior. This is illustrated in [Fig. 9 and Fig. 10] and seen in [22, 23]. These type of SW connections have been used as models of liquid and amorphous selenium [33]. Consequently, the current study provides further evidence that physical (quasi-) SW nanomaterials may exhibit mean field properties in both their critical behavior and in their transport properties.
and zero, which shows some properties of mean field behavior. This is illustrated in [Fig. 9 and Fig. 10] and seen in [22, 23]. These type of SW connections have been used as models of liquid and amorphous selenium [33]. Consequently, the current study provides further evidence that physical (quasi-) SW nanomaterials may exhibit mean field properties in both their critical behavior and in their transport properties.
VII. ACKOWLEDGEMENTS
We acknowledge useful discussions with a number of people, particularly Gyorgy Korniss, Per Arne Rikvold, and Zoltan Toroczkai. Supported in part by NSF grants DMR-0120310, DMR-0113049, DMR-0426488, and DMR-0444051. Computer time from the Mississippi State University High Performance Computing Collaboratory (HPC2) was critical to this study.
[1] Low Dimensional Conductors and Superconductors , NATO ASI Series B, Phys. Vol. 155, editor D. Jerome and L.G. Caron (Plenum, New York, 1987).
[2] M.A. Novotny, Phys. Rev. B 46, 2939 (1992).
[3] M.A. Novotny, Phys. Rev. Lett. 70, 109 (1993).
[4] G. Chartrand, Introductory Graph Theory , (Dover, New York, 1985).
[5] R. Albert and A.-L. Barabási, Rev. Mod. Phys. 74, 47 (2002).
[6] G. Korniss, M.A. Novotny, H. Guclu, Z. Toroczkai, and P.A. Rikvold, Science 299, 677 (2003).
[7] G. Korniss, M.A. Novotny, and P.A. Rikvold, J. Comp. Phys. 153, 488 (1999).
[8] G. Korniss, Z. Toroczkai, M.A. Novotny, and P.A. Rikvold, Phys. Rev. Lett. 84, 1351 (2000).
[9] A. Kolakowska, M.A. Novotny, and G. Korniss, Phys. Rev. E 67, 046703 (2003).
[10] G. Korniss, M.A. Novotny, P.A. Rikvold, H. Guclu, and Z. Toroczkai, Materials Research Society Symposium Proceedings Series Vol. 700, p. 297 (2002).
[11] M. Gitterman, J. Phys. A: Math. Gen. 33, 8373 (2000).
[12] A. Barrat and M. Weigt, Eur. Phys. J. B 13, 547 (2000).
[13] A. Pekalski, Phys. Rev. E 64, 057104 (2001); comment H. Hong, B.J. Kim, and M.Y. Choi, Phys. Rev. E 66, 018101 (2002).
[14] B.J. Kim, H. Hong, P. Holme, G.S. Jeon, P. Minnhagen, and M.Y. Choi, Phys. Rev. E 64, 056135 (2001).
[15] H. Hong, B.J. Kim, and M.Y. Choi, Phys. Rev. E 66, 018101 (2002).
[16] C.P. Herrero, Phys. Rev. E 65, 066110 (2002).
[17] M.B. Hastings, Phys. Rev. Lett. 91, 098701 (2003).
[18] D. Jeong, H. Hong, B.J. Kim, and M.Y. Choi, Phys. Rev. E 68, 027101 (2003).
[19] B. Kozma, M.B. Hastings, and G. Korniss, Phys. Rev. Lett. 92, 108701 (2004).
[20] D. Jeong, M.Y. Choi, and H. Park, Phys. Rev. E 71, 036103 (2005).
[21] B. Kozma, M.B. Hastings, and G. Korniss, Phys. Rev. Lett. 95, 018701 (2005).
[22] M.A. Novotny and S.M. Wheeler, Braz. J. Phys. 34, 395 (2004).
[23] A.M. Novotny, X. Zhang, T. Dubreus, M.L. Cook, S.G. Gill, I.T. Norwood, and G. Korniss, J. Appl. Phys. 97, 10B309 (2005).
[24] M.A. Novotny, in Computer Simulation Studies in Condensed Matter Physics XVII , editors D.P. Landau, S.P. Lewis, and H.-B. Schüttler, (Springer, Berlin), in press.
[25] R.T. Scalettar, Physica A170, 282 (1991).
[26] E. Brézin and J. Zinn-Justin, Nucl. Phys. B 257, 867 (1985).
[27] E. Luijten and H.W.J. Blöte, Phys. Rev. Lett. 76, 1557 (1996).
[28] M. Laradji, D.P. Landau, and B. Dünweg, Phys. Rev. B 51, 4894 (1995).
[29] E. Luijten and K. Binder, Phys. Rev. E 58, R4060 (1998).
[30] E. Luijten, Phys. Rev. E 60, 7558 (1999).
[31] D.P. Landau and K. Binder, A Guide to Monte Carlo Simulations in Statistical Physics (Cambridge University Press, Cambridge, UK, 2000).
[32] See http://sprng.cs.fsu.edu
[33] T. Koslowski, M. Koblischke, and A. Blumen, Phys. Rev. B 66, 064205 (2002).
Received on 23 September, 2005
- [1] Low Dimensional Conductors and Superconductors , NATO ASI Series B, Phys. Vol. 155, editor D. Jerome and L.G. Caron (Plenum, New York, 1987).
- [2] M.A. Novotny, Phys. Rev. B 46, 2939 (1992).
- [3] M.A. Novotny, Phys. Rev. Lett. 70, 109 (1993).
- [4] G. Chartrand, Introductory Graph Theory , (Dover, New York, 1985).
- [5] R. Albert and A.-L. Barabási, Rev. Mod. Phys. 74, 47 (2002).
- [6] G. Korniss, M.A. Novotny, H. Guclu, Z. Toroczkai, and P.A. Rikvold, Science 299, 677 (2003).
- [7] G. Korniss, M.A. Novotny, and P.A. Rikvold, J. Comp. Phys. 153, 488 (1999).
- [8] G. Korniss, Z. Toroczkai, M.A. Novotny, and P.A. Rikvold, Phys. Rev. Lett. 84, 1351 (2000).
- [9] A. Kolakowska, M.A. Novotny, and G. Korniss, Phys. Rev. E 67, 046703 (2003).
- [10] G. Korniss, M.A. Novotny, P.A. Rikvold, H. Guclu, and Z. Toroczkai, Materials Research Society Symposium Proceedings Series Vol. 700, p. 297 (2002).
- [11] M. Gitterman, J. Phys. A: Math. Gen. 33, 8373 (2000).
- [12] A. Barrat and M. Weigt, Eur. Phys. J. B 13, 547 (2000).
- [13] A. Pekalski, Phys. Rev. E 64, 057104 (2001);
- comment H. Hong, B.J. Kim, and M.Y. Choi, Phys. Rev. E 66, 018101 (2002).
- [14] B.J. Kim, H. Hong, P. Holme, G.S. Jeon, P. Minnhagen, and M.Y. Choi, Phys. Rev. E 64, 056135 (2001).
- [15] H. Hong, B.J. Kim, and M.Y. Choi, Phys. Rev. E 66, 018101 (2002).
- [16] C.P. Herrero, Phys. Rev. E 65, 066110 (2002).
- [17] M.B. Hastings, Phys. Rev. Lett. 91, 098701 (2003).
- [18] D. Jeong, H. Hong, B.J. Kim, and M.Y. Choi, Phys. Rev. E 68, 027101 (2003).
- [19] B. Kozma, M.B. Hastings, and G. Korniss, Phys. Rev. Lett. 92, 108701 (2004).
- [20] D. Jeong, M.Y. Choi, and H. Park, Phys. Rev. E 71, 036103 (2005).
- [21] B. Kozma, M.B. Hastings, and G. Korniss, Phys. Rev. Lett. 95, 018701 (2005).
- [22] M.A. Novotny and S.M. Wheeler, Braz. J. Phys. 34, 395 (2004).
- [23] A.M. Novotny, X. Zhang, T. Dubreus, M.L. Cook, S.G. Gill, I.T. Norwood, and G. Korniss, J. Appl. Phys. 97, 10B309 (2005).
- [24] M.A. Novotny, in Computer Simulation Studies in Condensed Matter Physics XVII , editors D.P. Landau, S.P. Lewis, and H.-B. Schüttler, (Springer, Berlin), in press.
- [25] R.T. Scalettar, Physica A170, 282 (1991).
- [26] E. Brézin and J. Zinn-Justin, Nucl. Phys. B 257, 867 (1985).
- [27] E. Luijten and H.W.J. Blöte, Phys. Rev. Lett. 76, 1557 (1996).
- [28] M. Laradji, D.P. Landau, and B. Dünweg, Phys. Rev. B 51, 4894 (1995).
- [29] E. Luijten and K. Binder, Phys. Rev. E 58, R4060 (1998).
- [30] E. Luijten, Phys. Rev. E 60, 7558 (1999).
- [31] D.P. Landau and K. Binder, A Guide to Monte Carlo Simulations in Statistical Physics (Cambridge University Press, Cambridge, UK, 2000).
- [32] See http://sprng.cs.fsu.edu
- [33] T. Koslowski, M. Koblischke, and A. Blumen, Phys. Rev. B 66, 064205 (2002).
Publication Dates
-
Publication in this collection
16 Oct 2006 -
Date of issue
Sept 2006
History
-
Received
23 Sept 2005