Thermal behavior of the compactified 3-D gross-neveu model

Thermal behavior of the compactified 3-D gross-neveu model

A. P. C. Malbouisson^I; F. C. Khanna^II; J. M. C. Malbouisson^III; A. E. Santana^IV

^ICentro Brasileiro de pesquisas Físicas/MCT, 22290-180, Rio de Janeiro, RJ, Brazil

^IITheoretical Physics Institute, University of Alberta, Edmonton, AB T6G 2J1, Canada

^IIIIntituto de Física, Universidade Federal da Bahia, 40210-340, Salvador, BA, Brazil

^IVInstituto de Física, Universidade de Brasília, 70910-900, Brasília, DF, Brazil

ABSTRACT

We consider the N-component tri-dimensional massive Gross-Neveu model at finite temperature and with compactified spatial coordinates. We study the behavior of the renormalized large-N effective coupling constant, investigating its dependence on the compactification length and the temperature. We show that spatial confinement exists for the model at T = 0, which is destroyed by raising the temperature.

Keywords: Four-fermions interactions; Spatial confinement; Thermal deconfinement

I. INTRODUCTION

In the most commonly accepted scenario for the early evolution of the universe, the hadronic matter emerges in a confining phase transition where the quark-gluon plasma condenses into material "droplets,'' the hadrons, as the universe cooled down. In the context of the standard model, the quantum chromodynamics (QCD) should then be able to predict color and spatial confinement, since hadrons are colorless and their constituents, quarks and gluons, are confined in a region having a linear size of order 1 fm (fossil quarks have never been observed). Also, quarks are asymptotically free, the interaction between them being very weak, at very high energies as probed by deep inelastic scattering processes. QCD should also account for the fact that the hadronization transition occurred in the early universe at a finite temperature, estimated of the order of 200 MeV.

Nevertheless, although lattice calculations have given clear indications, up to present day, no fully analytical treatment with the standard model has been constructed capable of taking into account simultaneously all these different aspects of hadronic matter. This is mainly due to the intricate field theoretical structure of non-Abelian QCD and, for this reason, effective theories and phenomenological approaches have been developed over the last decades. The simplest effective theory is the celebrated Gross-Neveu (GN) model [1], which considers direct four-fermions interaction.

In this spirit, we shall investigate the tri-dimensional Gross-Neveu model, in the large-N limit, at finite temperature and with one or two compactified spatial dimensions. Our aim is to study analytically the simultaneous occurrence of spatial confinement and asymptotic freedom, and investigate the thermal deconfining transition. For that we will determine the dependence of the renormalized effective coupling on the compactification length and the temperature.

In this work, we first review our results for the 3-D GN model with one compactified spatial coordinate, both at zero and finite temperature, presented earlier [2,3]. Then, we extend the analysis to the case where all spatial dimensions are compactified.

II. COMPACTIFIED GROSS-NEVEU MODEL

Our starting point is the Wick-ordered massive Gross-Neveu Lagrangian in a D-dimensional Euclidean space,

where m is the mass, u is the coupling constant, x is a point of R^D and the g's are Dirac matrices. The quantity y(x) is a spin field having N (flavor) components, y^a(x), a = 1,2,...,N. Summation over flavor and spin indexes is understood. Here we consider the large-N limit (N ® ¥), which permits considerable simplification. We use natural units, = c = k_B = 1.

The compactification is engendered via a generalized Matsubara prescription, which corresponds to considering the system in a topology , thus treating spatial and imaginary-time compactifications on the same footing. To describe the model with d ( < D) compactified Euclidean coordinates, that is with x_i restricted to segments of length L_i (i = 1,2,....d) and the field y(x) satisfying anti-periodic (bag model) boundary conditions, the Feynman rules should be modified following the Matsubara replacements

Then the L_i-dependent four-point function at leading order in 1/N and at zero external momenta, from which we will define the effective coupling constant between the fermions, has the formal expression

where L_i-dependent Feynman one-loop (bubble) diagram is given by

and n_i = 2p(n_i+)/L_i.

In order to simplify the use of regularization techniques, we introduce the following dimensionless quantities: q_j' = q_j/2pm (j = d+1,... ,D) and b_i = (m L_i)^-2 (i = 1,2,... ,d). To proceed, we extend the method developed in Refs. [2,3] to calculate the one-loop subdiagram, accounting for the compactification of d ( < D) Cartesian coordinates. We use a modified minimal subtraction scheme, employing concurrently dimensional and analytical regularizations, where the counterterms are poles of the Epstein-Hurwitz zeta-functions [2]. The calculations go through the following steps.

First, using dimensional regularization techniques to perform the integral over q', Eq. (4) becomes

with

where n = µ-.

Secondly, transforming the summations over half-integers into sums over integers, Eq. (6) can be written as

where h = p^-1 and

is the multiple-variable (d-dimensional) Epstein-Hurwitz zeta-function. The function (n,{a_i}) can be analytically extended to the whole complex n-plane [4], through a generalization of the procedure presented in Refs. [5,6]; one finds

where K_n(x) is the Bessel function of the third kind.

Thirdly, we notice that the first term in the square bracket of Eq. (9) leads to the following, b_i-independent, contribution to S_Dd(s;{b_i}):

When we take s = 2, for even dimensions D > 2, this term diverges due to the poles of the G-functions; therefore, it should be subtracted in order to obtain a finite, renormalized, S. For the sake of uniformity, this term should also be suppressed for odd dimensions D, when no poles of the G-functions are present; in such cases, we perform a finite renormalization. The renormalized one-loop (bubble) diagram, which arises from the regular part of the analytical continuation of the Epstein-Hurwitz zeta-function, is then given by

Inserting ({b_i}) into Eq. (3) and taking the limit N ® ¥, with Nu = l fixed as usual, we find the large-N effective ({b_i}-dependent) renormalized coupling constant, for d ( < D) compactified dimensions, as

This is the basic result for subsequent analysis. But, instead of pursuing the problem for general dimension D, we shall restrict our discussion to the D = 3 case considering, initially, the case where only one spatial dimension is compactified.

III. THE 3-D GROSS-NEVEU MODEL WITH ONE COMPACTIFIED SPATIAL DIMENSION

Taking D = 3 and d = 1 in the preceding formulas, and fixing b₁ = L^-2 (thus measuring L in units of m^-1, as it will be done from now on), we find

Using the expression for the Bessel function of order ,

and performing the resulting geometric series, Eq. (13) becomes

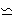The behavior of as a function of L is illustrated in Fig. 1. We find from Eq. (15) that (L) diverges (® +¥) when L ® 0 and tends to 0, through negative values, as L ® ¥. Numerically, we find that (L) vanishes for L = L_min 1.14 m^-1, being negative for L > ; it also assumes a minimum (negative) value, 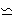-0.0091 m, for L = L_max 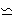1.84 m^-1. This dependence of on L, in particular the fact that (L) is negative for L > L_min, has remarkable influence on the behavior of the renormalized effective coupling constant.

In the present case, Eq. (12) becomes

We first note that, due to the divergence of , g₂₁(L,l) approaches 0 as L ® 0, independently of the value of l; therefore, the system presents a kind of asymptotic-freedom behavior for short distances. On the other hand, starting from a low value of L (within this region of asymptotic freedom) and increasing the size of the system, g₃₁ will present a divergence at a finite value of L (L_c), if the value of the fixed coupling constant (l) is high enough. In fact, this will happen for all values of l above the "critical value" l_c = (- )^-1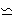 110.0 m^-1. The behavior of the effective coupling as a function of L is illustrated in Fig. 2 for some values of the fixed coupling constant l. We interpret this result by stating that, in the strong-coupling regime (l > l_c) the system gets spatially confined in a segment of length L_c(l). We find also that

with L_max corresponding to the confining length when l = l_c while L_min is associated with l ® ¥. The value of L_c(l), for an arbitrary value of l > l_c, can be found by searching for the smallest solution of the equation 1 + l(L) = 0.

We now consider the GN model, with one compactified spatial dimension, at finite temperature. To do so, we have to compactify the imaginary (Euclidean) time in a length b = 1/T, where T represents the temperature. Taking b₁ = L^-2 and b₂ = b^-2 in the formulas of Sec. II, we obtain

where the function G₂(x,y) is defined by

Notice that the numerical computation of (L,b) is greatly facilitated by the fact that the double series defining the function G₂(y,z) is rapidly convergent.

As a first remark, observe that (L,b) reduces to the expression (15) for the T = 0 case, if we take b ® ¥. On the other hand, (L,b) ® ¥ when b ® 0. This implies that, independently of the value of l, the effective renormalized coupling constant,

vanishes when b ® 0 and, so, the system gets asymptotically free at very high temperatures, as expected. Therefore, if we start with the confined system (l > l_c) at T = 0 and raise the temperature, at some value T = T_d(l), the divergence of g₃₂(L,b,l) is suppressed, the system becoming unconfined.

For a fixed value of l ( > l_c), the determination of the deconfining temperature, T_d(l), can be implemented by examining of the minimum value of (L,b,l) for various values of b; the value of b, b_d(l), for which the minimum vanishes gives the deconfining temperature. In Fig. 3, we plot (L,b,120) as a function of L, for some values of b, to illustrate the process. 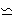In this example with l = 120 m^-1, the minimum of vanishes for b = b_d 1.56 m^-1 and is positive for b > b_d; thus, the deconfining temperature is T_d = 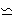0.64 m when l = 120 m^-1. For an arbitrary value of l ( > l_c), we have

where

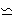0.6 m is the deconfining temperature when l = l_c and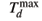 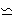0.87 m is the upper bound, which would be only reached when l ® ¥.

IV. THE 3-D GROSS-NEVEU MODEL WITH BOTH SPATIAL DIMENSIONS COMPACTIFIED

We now consider the 3-dimensional GN model at T = 0, where both spatial coordinates x₁ and x₂ have been compactified. Naturally, the expression for (L₁,L₂) can be obtained from Eq. (18) replacing L and b by L₁ and L₂. But, instead of considering the general situation, we shall restrict our analysis to the case where both compactification lengths L₁ and L₂ are equal to L. We then obtain

with the function G₂(x,y) given by Eq. (19).

The function (L) has a behavior similar to that of (L), but the numbers are distinct: it vanishes at L = L_min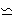 1.3 m^-1 and assumes the minimum value, 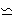-0.0099 m, for L = L_max 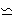2.1 m^-1. Also, (L) diverges when L ® 0 and tends to 0, as L ® ¥. The plot of (L)/m is shown in Fig. 4.

Thus, in the present case, the effective renormalized coupling constant,

maintains the same characteristics as before; it vanishes as L ® 0, irrespective to the value of l, and for l > l_c = (-)^-1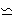 101.0 m^-1, it presents a divergence at a finite value of L, L_c(l) Î ( L_min,L_max ]. Therefore, in the fully compactified 3-D model, we still have a behavior that is quite similar to the asymptotic freedom for small distances and spatial confinement in the strong-coupling regime, l > l_c. Now, it remains to investigate the effect of finite temperature on the effective renormalized coupling constant.

To consider temperature effects, we have to compactifiy the imaginary time in a length b = 1/T. In this case, taking L₁ = L₂ = L and L₃ = b in the formulas of Sec. II, we find the following expression for the L-b dependent renormalized bubble diagram:

where G₂(x,y) is given by Eq. (19) and the function G₃(x,y,z) is defined by

Note that, making b ® ¥, Eq. (24) reduces to (L), given by Eq. (22).

As before, the increase of the temperature destroys the spatial confinement that exists for l > l_c at T = 0. We can determine the deconfining temperature by searching for the value of b(l) for which the minimum of the inverse of the effective renormalized coupling constant, (L,b,l) = (1 + l(L,b))/l, vanishes. For example, taking the specific case of l = 150 m^-1, we find b_d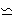1.41 m^-1 which corresponds to the deconfining temperature T_d 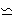0.71 m; this result could be illustrated in a figure with the same pattern as that appearing in Fig. 2 for the case where only one spatial coordinate is compactified. Again, the relation (21) holds with 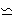0.54 m, the deconfining temperature when l = l_c, and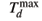 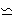0.87 m being the upper bound, achieved when l ® ¥.

Note that , for the fully compactified model, is smaller than the value when only one spatial dimension is compactified. This is because, in the present case, the modulus of the absolute minimum of (L₁,L₂) (which occurs for L₁ = L₂ = L_max) is larger than that of (L), leading to a smaller critical value l_c when both spatial coordinates are compactified. On the other hand, 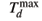is the same for both cases of one or two spatial dimensions compactified. This is not a mere coincidence but reflects the fact that, in the extremely strong-coupling regime, the deconfining temperature is independent of the number of compactified spatial dimensions.

V. CONCLUDING REMARKS

We have analyzed the N-component 3-D massive Gross-Neveu model with compactified spatial dimensions, both at zero and finite temperatures. The large-N effective coupling constant g, for T = 0, shows a kind of asymptotic freedom behavior, vanishing when the compactification length tends to zero, irrespective the value of the fixed coupling constant l. In the strong coupling regime, where the fixed coupling constant is greater than some critical value, starting from small compactification lengths and increasing the size of the system, a divergence of the renormalized effective coupling constant appears at a given length, L_c(l), signaling that the system gets spatially confined. When the temperature is raised, a deconfining transition occurs at a temperature T_d(l), as the minimum of the inverse of the renormalized effective coupling constant reaches zero.

It should be emphasized that these results are intrinsic of the model and do not emerge from any adjustment. The limit values of L_c(l) and T_d(l) depend only on the fermion mass. Thus, to get an estimate of these values we have to fix the parameter m. To do so, we consider the Gross-Neveu model as an effective theory for the strong interaction (in which the gluon propagators have been shrunk, similarly to the Fermi treatment of the weak force) and take m to be the constituent quark mass, m » 350 MeV 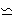1.75 fm^-1 [7]. With such a choice, for the model with both spatial coordinates compactified, we find 0.74 fm < L_c(l) < 1.20 fm and, correspondingly, 305 MeV > T_d(l) > 189 MeV. These values should be compared with the experimentally measured proton charge diameter ( » 1.74 fm) [8] and the estimated deconfining temperature ( » 200 MeV) for hadronic matter [9]. A detailed analysis of such a comparison, for arbitrary dimensions and in particular for D = 4, will be presented elsewhere.

This work was partially supported by CNPq (Brazil) and NSERC (Canada).

Received on 10 August, 2006

• [1] D. J. Gross and A. Neveu, Phys. Rev. D 10, 3235 (1974).
• [2] A. P. C. Malbouisson, J. M. C. Malbouisson, A. E. Santana, and J. C. Silva, Phys. Lett. B 583, 373 (2004).
• [3] F. C. Khanna, A. P. C. Malbouisson, J. M. C. Malbouisson, H. Queiroz, T. M. Rocha-Filho, A. E. Santana, and J. C. Silva, Phys. Lett. B 624, 316 (2005).
• [4] A. P. C. Malbouisson, J. M. C. Malbouisson, and A. E. Santana, Nucl. Phys. B 631, 83 (2002).
• [5] A. Elizalde and E. Romeo, J. Math. Phys. 30, 1133 (1989).
• [6] K. Kirsten, J. Math. Phys. 35, 459 (1994).
• [7] Particle Data Group, Phys. Lett. B 592, 1 (2004); see page 475.
• [8] S. G. Karshenboim, Can. J. Phys. 77, 241 (1999).
• [9] A. Smilga, Lectures on QCD (World Scientific, Singapore, 2001) p. 279.

Publication Dates

• Publication in this collection
  21 June 2007
• Date of issue
  Dec 2006

History

• Received
  10 Aug 2006