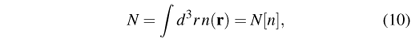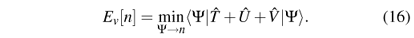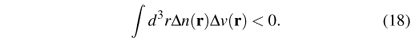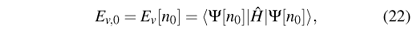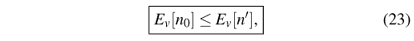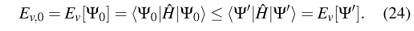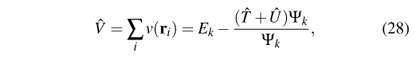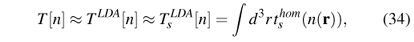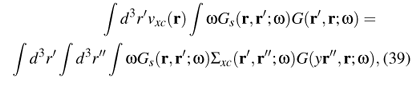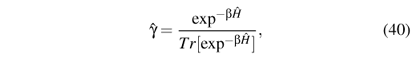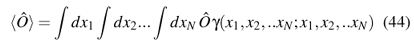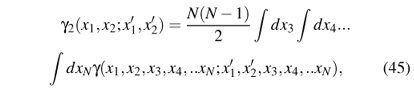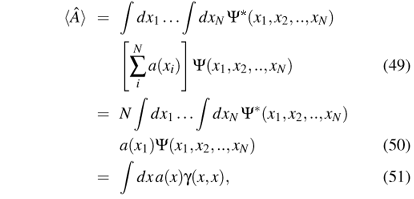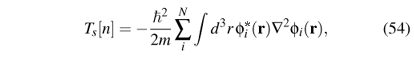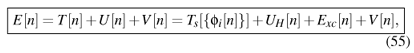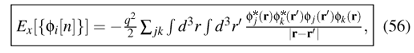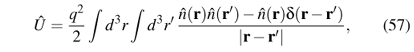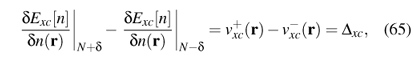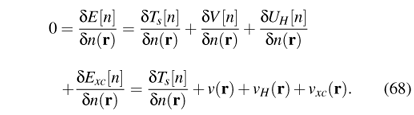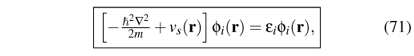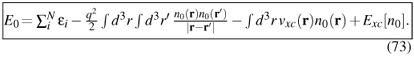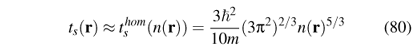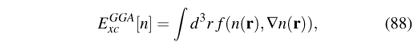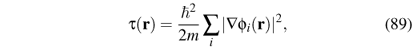Abstract
This paper is the outgrowth of lectures the author gave at the Physics Institute and the Chemistry Institute of the University of São Paulo at São Carlos, Brazil, and at the VIII'th Summer School on Electronic Structure of the Brazilian Physical Society. It is an attempt to introduce density-functional theory (DFT) in a language accessible for students entering the field or researchers from other fields. It is not meant to be a scholarly review of DFT, but rather an informal guide to its conceptual basis and some recent developments and advances. The Hohenberg-Kohn theorem and the Kohn-Sham equations are discussed in some detail. Approximate density functionals, selected aspects of applications of DFT, and a variety of extensions of standard DFT are also discussed, albeit in less detail. Throughout it is attempted to provide a balanced treatment of aspects that are relevant for chemistry and aspects relevant for physics, but with a strong bias towards conceptual foundations. The paper is intended to be read before (or in parallel with) one of the many excellent more technical reviews available in the literature.
Density-functional theory; Electronic-structure theory; Electron correlation; Many-body theory; Local-density approximation
REVIEW ARTICLES
A bird's-eye view of density-functional theory
Klaus Capelle
Departamento de Física e Informática, Instituto de Física de São Carlos, Universidade de São Paulo, Caixa Postal 369, São Carlos, 13560-970 SP, Brazil
ABSTRACT
This paper is the outgrowth of lectures the author gave at the Physics Institute and the Chemistry Institute of the University of São Paulo at São Carlos, Brazil, and at the VIII'th Summer School on Electronic Structure of the Brazilian Physical Society. It is an attempt to introduce density-functional theory (DFT) in a language accessible for students entering the field or researchers from other fields. It is not meant to be a scholarly review of DFT, but rather an informal guide to its conceptual basis and some recent developments and advances. The Hohenberg-Kohn theorem and the Kohn-Sham equations are discussed in some detail. Approximate density functionals, selected aspects of applications of DFT, and a variety of extensions of standard DFT are also discussed, albeit in less detail. Throughout it is attempted to provide a balanced treatment of aspects that are relevant for chemistry and aspects relevant for physics, but with a strong bias towards conceptual foundations. The paper is intended to be read before (or in parallel with) one of the many excellent more technical reviews available in the literature.
Keywords: Density-functional theory; Electronic-structure theory; Electron correlation; Many-body theory; Local-density approximation
I. PREFACE
This paper is the outgrowth of lectures the author gave at the Physics Institute and the Chemistry Institute of the University of São Paulo at São Carlos, Brazil, and at the VIII'th Summer School on Electronic Structure of the Brazilian Physical Society [1]. The main text is a description of density-functional theory (DFT) at a level that should be accessible for students entering the field or researchers from other fields. A large number of footnotes provides additional comments and explanations, often at a slightly higher level than the main text. A reader not familiar with DFT is advised to skip most of the footnotes, but a reader familiar with it may find some of them useful.
The paper is not meant to be a scholarly review of DFT, but rather an informal guide to its conceptual basis and some recent developments and advances. The Hohenberg-Kohn theorem and the Kohn-Sham equations are discussed in some detail. Approximate density functionals, selected aspects of applications of DFT, and a variety of extensions of standard DFT are also discussed, albeit in less detail. Throughout it is attempted to provide a balanced treatment of aspects that are relevant for chemistry and aspects relevant for physics, but with a strong bias towards conceptual foundations. The text is intended to be read before (or in parallel with) one of the many excellent more technical reviews available in the literature. The author apologizes to all researchers whose work has not received proper consideration. The limits of the author's knowledge, as well as the limits of the available space and the nature of the intended audience, have from the outset prohibited any attempt at comprehensiveness.1 1 A first version of this text was published in 2002 as a chapter in the proceedings of the VIII'th Summer School on Electronic Structure of the Brazilian Physical Society [1]. The text was unexpectedly well received, and repeated requests from users prompted the author to electronically publish revised, updated and extended versions in the preprint archive http://arxiv.org/archive/cond-mat, where the second (2003), third (2004) and fourth (2005) versions were deposited under the reference number cond-mat/0211443. The present fifth (2006) version of this text, published in the Brazilian Journal of Physics, is approximately 50% longer than the first. Although during the consecutive revisions many embarrassing mistakes have been removed, and unclear passages improved upon, many other doubtlessly remain, and much beautiful and important work has not been mentioned even in passing. The return from electronic publishing to printed publishing, however, marks the completion of a cycle, and is intended to also mark the end of the author's work on the Bird's-Eye View of Density-Functional Theory.
II. WHAT IS DENSITY-FUNCTIONAL THEORY?
Density-functional theory is one of the most popular and successful quantum mechanical approaches to matter. It is nowadays routinely applied for calculating, e.g., the binding energy of molecules in chemistry and the band structure of solids in physics. First applications relevant for fields traditionally considered more distant from quantum mechanics, such as biology and mineralogy are beginning to appear. Superconductivity, atoms in the focus of strong laser pulses, relativistic effects in heavy elements and in atomic nuclei, classical liquids, and magnetic properties of alloys have all been studied with DFT.
DFT owes this versatility to the generality of its fundamental concepts and the flexibility one has in implementing them. In spite of this flexibility and generality, DFT is based on quite a rigid conceptual framework. This section introduces some aspects of this framework in general terms. The following two sections, and , then deal in detail with two core elements of DFT, the Hohenberg-Kohn theorem and the Kohn-Sham equations. The final two sections, and , contain a (necessarily less detailed) description of approximations typically made in practical DFT calculations, and of some extensions and generalizations of DFT.
To get a first idea of what density-functional theory is about, it is useful to take a step back and recall some elementary quantum mechanics. In quantum mechanics we learn that all information we can possibly have about a given system is contained in the system's wave function, Y. Here we will exclusively be concerned with the electronic structure of atoms, molecules and solids. The nuclear degrees of freedom (e.g., the crystal lattice in a solid) appear only in the form of a potential v(r) acting on the electrons, so that the wave function depends only on the electronic coordinates.2 2 This is the so-called Born-Oppenheimer approximation. It is common to call v( r) a 'potential' although it is, strictly speaking, a potential energy. Nonrelativistically, this wave function is calculated from Schrödinger's equation, which for a single electron moving in a potential v(r) reads
If there is more than one electron (i.e., one has a many-body problem) Schrödinger's equation becomes
where N is the number of electrons and U(ri,rj) is the electron-electron interaction. For a Coulomb system (the only type of system we consider here) one has
Note that this is the same operator for any system of particles interacting via the Coulomb interaction, just as the kinetic energy operator
is the same for any nonrelativistic system.3 3 For materials containing atoms with large atomic number Z, accelerating the electrons to relativistic velocities, one must include relativistic effects by solving Dirac's equation or an approximation to it. In this case the kinetic energy operator takes a different form. Whether our system is an atom, a molecule, or a solid thus depends only on the potential v(ri). For an atom, e.g.,
where Q is the nuclear charge4 4 In terms of the elementary charge e > 0 and the atomic number Z, the nuclear charge is Q = Ze and the charge on the electron is q = -e. and R the nuclear position. When dealing with a single atom, R is usually taken to be the zero of the coordinate system. For a molecule or a solid one has
where the sum on k extends over all nuclei in the system, each with charge Qk = Zke and position Rk. It is only the spatial arrangement of the Rk (together with the corresponding boundary conditions) that distinguishes, fundamentally, a molecule from a solid.5 5 One sometimes says that and Û are 'universal', while is system-dependent, or 'nonuniversal'. We will come back to this terminology. Similarly, it is only through the term Û that the (essentially simple) single-body quantum mechanics of Eq. (1) differs from the extremely complex many-body problem posed by Eq. (2). These properties are built into DFT in a very fundamental way.
The usual quantum-mechanical approach to Schrödinger's equation (SE) can be summarized by the following sequence
i.e., one specifies the system by choosing v(r), plugs it into Schrödinger's equation, solves that equation for the wave function Y, and then calculates observables by taking expectation values of operators with this wave function. One among the observables that are calculated in this way is the particle density
Many powerful methods for solving Schrödinger's equation have been developed during decades of struggling with the many-body problem. In physics, for example, one has diagrammatic perturbation theory (based on Feynman diagrams and Green's functions), while in chemistry one often uses configuration interaction (CI) methods, which are based on systematic expansion in Slater determinants. A host of more special techniques also exists. The problem with these methods is the great demand they place on one's computational resources: it is simply impossible to apply them efficiently to large and complex systems. Nobody has ever calculated the chemical properties of a 100-atom molecule with full CI, or the electronic structure of a real semiconductor using nothing but Green's functions.6 6 A simple estimate of the computational complexity of this task is to imagine a real-space representation of Y on a mesh, in which each coordinate is discretized by using 20 mesh points (which is not very much). For N electrons, Y becomes a function of 3 N coordinates (ignoring spin, and taking Y to be real), and 20 3N values are required to describe Y on the mesh. The density n( r) is a function of three coordinates, and requires 20 3 values on the same mesh. CI and the Kohn-Sham formulation of DFT additionally employ sets of single-particle orbitals. N such orbitals, used to build the density, require 20 3 N values on the same mesh. (A CI calculation employs also unoccupied orbitals, and requires more values.) For N = 10 electrons, the many-body wave function thus requires 20 30/20 3» 10 35 times more storage space than the density, and 20 30/(10 × 20 3) » 10 34 times more than sets of single-particle orbitals. Clever use of symmetries can reduce these ratios, but the full many-body wave function remains unaccessible for real systems with more than a few electrons.
It is here where DFT provides a viable alternative, less accurate perhaps,7
7
Accuracy is a relative term. As a theory, DFT is formally exact. Its performance in actual applications depends on the quality of the approximate density functionals employed. For small numbers of particles, or systems with special symmetries, essentially exact solutions of Schrödinger's equation can be obtained, and no approximate functional can compete with exact solutions. For more realistic systems, modern (2005) sophisticated density functionals attain rather high accuracy. Data on atoms are collected in
Table I in Sec. V B. Bond-lengths of molecules can be predicted with an average error of less than 0.001nm, lattice constants of solids with an average error of less than 0.005nm, and molecular energies to within less than 0.2eV [2]. (For comparison: already a small molecule, such as water, has a total energy of 2081.1eV). On the other hand, energy gaps in solids can be wrong by 100%!
but much more versatile. DFT explicitly recognizes that nonrelativistic Coulomb systems differ only by their potential v(r), and supplies a prescription for dealing with the universal operators  and Û once and for all.8
8
We will see that in practice this prescription can be implemented only approximately. Still, these approximations retain a high degree of universality in the sense that they often work well for more than one type of system.
Furthermore, DFT provides a way to systematically map the many-body problem, with Û, onto a single-body problem, without Û. All this is done by promoting the particle density n(r) from just one among many observables to the status of key variable, on which the calculation of all other observables can be based. This approach forms the basis of the large majority of electronic-structure calculations in physics and chemistry. Much of what we know about the electrical, magnetic, and structural properties of materials has been calculated using DFT, and the extent to which DFT has contributed to the science of molecules is reflected by the 1998 Nobel Prize in Chemistry, which was awarded to Walter Kohn [3], the founding father of DFT, and John Pople [4], who was instrumental in implementing DFT in computational chemistry.
and Û once and for all.8
8
We will see that in practice this prescription can be implemented only approximately. Still, these approximations retain a high degree of universality in the sense that they often work well for more than one type of system.
Furthermore, DFT provides a way to systematically map the many-body problem, with Û, onto a single-body problem, without Û. All this is done by promoting the particle density n(r) from just one among many observables to the status of key variable, on which the calculation of all other observables can be based. This approach forms the basis of the large majority of electronic-structure calculations in physics and chemistry. Much of what we know about the electrical, magnetic, and structural properties of materials has been calculated using DFT, and the extent to which DFT has contributed to the science of molecules is reflected by the 1998 Nobel Prize in Chemistry, which was awarded to Walter Kohn [3], the founding father of DFT, and John Pople [4], who was instrumental in implementing DFT in computational chemistry.
The density-functional approach can be summarized by the sequence
i.e., knowledge of n(r) implies knowledge of the wave function and the potential, and hence of all other observables. Although this sequence describes the conceptual structure of DFT, it does not really represent what is done in actual applications of it, which typically proceed along rather different lines, and do not make explicit use of many-body wave functions. The following chapters attempt to explain both the conceptual structure and some of the many possible shapes and disguises under which this structure appears in applications.
The literature on DFT is large, and rich in excellent reviews and overviews. Some representative examples of full reviews and systematic collections of research papers are Refs. [5-19]. The present overview of DFT is much less detailed and advanced than these treatments. Introductions to DFT that are more similar in spirit to the present one (but differ in emphasis and selection of topics) are the contribution of Levy in Ref. [9], the one of Kurth and Perdew in Refs. [15] and [16], and Ref. [20] by Makov and Argaman. My aim in the present text is to give a bird's-eye view of DFT in a language that should be accessible to an advanced undergraduate student who has completed a first course in quantum mechanics, in either chemistry or physics. Many interesting details, proofs of theorems, illustrative applications, and exciting developments had to be left out, just as any discussion of issues that are specific to only certain subfields of either physics or chemistry. All of this, and much more, can be found in the references cited above, to which the present little text may perhaps serve as a prelude.
III. DFT AS A MANY-BODY THEORY
A. Functionals and their derivatives
Before we discuss density-functional theory more carefully, let us introduce a useful mathematical tool. Since according to the above sequence the wave function is determined by the density, we can write it as Y = Y[n](r1,r2,...rN), which indicates that Y is a function of its N spatial variables, but a functional of n(r).
Functionals. More generally, a functional F[n] can be defined (in an admittedly mathematically sloppy way) as a rule for going from a function to a number, just as a function y = f(x) is a rule (f) for going from a number (x) to a number (y). A simple example of a functional is the particle number,
which is a rule for obtaining the number N, given the function n(r). Note that the name given to the argument of n is completely irrelevant, since the functional depends on the function itself, not on its variable. Hence we do not need to distinguish F[n(r)] from, e.g., F[n(r')]. Another important case is that in which the functional depends on a parameter, such as in
which is a rule that for any value of the parameter r associates a value vH[n](r) with the function n(r'). This term is the so-called Hartree potential, which we will repeatedly encounter below.
Functional variation. Given a function of one variable, y = f(x), one can think of two types of variations of y, one associated with x, the other with f. For a fixed functional dependence f(x), the ordinary differential dy measures how y changes as a result of a variation x ® x + dx of the variable x. This is the variation studied in ordinary calculus. Similarly, for a fixed point x, the functional variation dy measures how the value y at this point changes as a result of a variation in the functional form f(x). This is the variation studied in variational calculus.
Functional derivative. The derivative formed in terms of the ordinary differential, df/dx, measures the first-order change of y = f(x) upon changes of x, i.e., the slope of the function f(x) at x:
The functional derivative measures, similarly, the first-order change in a functional upon a functional variation of its argument:
where the integral arises because the variation in the functional F is determined by variations in the function at all points in space. The first-order coefficient (or 'functional slope') s(x) is defined to be the functional derivative dF[f]/df(x).
The functional derivative allows us to study how a functional changes upon changes in the form of the function it depends on. Detailed rules for calculating functional derivatives are described in Appendix A of Ref. [6]. A general expression for obtaining functional derivatives with respect to n(x) of a functional F[n] = òf(n,n',n'',n''',...;x)dx, where primes indicate ordinary derivatives of n(x) with respect to x, is [6]
This expression is frequently used in DFT to obtain xc potentials from xc energies.9 9 The use of functionals and their derivatives is not limited to density-functional theory, or even to quantum mechanics. In classical mechanics, e.g., one expresses the Lagrangian in terms of of generalized coordinates q( x,t) and their temporal derivatives ( x,t), and obtains the equations of motion from extremizing the action functional [ q] = ò ( q, ; t) dt. The resulting equations of motion are the well-known Euler-Lagrange equations 0 = , which are a special case of Eq. (14).
B. The Hohenberg-Kohn theorem
At the heart of DFT is the Hohenberg-Kohn (HK) theorem. This theorem states that for ground states Eq. (8) can be inverted: given a ground-state density n0(r) it is possible, in principle, to calculate the corresponding ground-state wave function Y0(r1,r2 ..., rN). This means that Y0 is a functional of n0. Consequently, all ground-state observables are functionals of n0, too. If Y0 can be calculated from n0 and vice versa, both functions are equivalent and contain exactly the same information. At first sight this seems impossible: how can a function of one (vectorial) variable r be equivalent to a function of N (vectorial) variables r1 ...rN? How can one arbitrary variable contain the same information as N arbitrary variables?
The crucial fact which makes this possible is that knowledge of n0(r) implies implicit knowledge of much more than that of an arbitrary function f(r). The ground-state wave function Y0 must not only reproduce the ground-state density, but also minimize the energy. For a given ground-state density n0(r), we can write this requirement as
where Ev,0 denotes the ground-state energy in potential v(r). The preceding equation tells us that for a given density n0(r) the ground-state wave function Y0 is that which reproduces this n0(r) and minimizes the energy.
For an arbitrary density n(r), we define the functional
If n is a density different from the ground-state density n0 in potential v(r), then the Y that produce this n are different from the ground-state wave function Y0, and according to the variational principle the minimum obtained from Ev[n] is higher than (or equal to) the ground-state energy Ev,0 = Ev[n0]. Thus, the functional Ev[n] is minimized by the ground-state density n0, and its value at the minimum is Ev,0.
The total-energy functional can be written as
where the internal-energy functional F[n] = minY ® náY| + Û|Yñ is independent of the potential v(r), and thus determined only by the structure of the operators Û and
+ Û|Yñ is independent of the potential v(r), and thus determined only by the structure of the operators Û and  . This universality of the internal-energy functional allows us to define the ground-state wave function Y0 as that antisymmetric N-particle function that delivers the minimum of F[n] and reproduces n0. If the ground state is nondegenerate (for the case of degeneracy see footnote 12), this double requirement uniquely determines Y0 in terms of n0(r), without having to specify v(r) explicitly.10
10
Note that this is exactly the opposite of the conventional prescription to specify the Hamiltonian via
v(
r), and obtain Y
0 from solving Schrödinger's equation, without having to specify
n(
r) explicitly.
. This universality of the internal-energy functional allows us to define the ground-state wave function Y0 as that antisymmetric N-particle function that delivers the minimum of F[n] and reproduces n0. If the ground state is nondegenerate (for the case of degeneracy see footnote 12), this double requirement uniquely determines Y0 in terms of n0(r), without having to specify v(r) explicitly.10
10
Note that this is exactly the opposite of the conventional prescription to specify the Hamiltonian via
v(
r), and obtain Y
0 from solving Schrödinger's equation, without having to specify
n(
r) explicitly.
Equations (15) to (17) constitute the constrained-search proof of the Hohenberg-Kohn theorem, given independently by M. Levy [22] and E. Lieb [23]. The original proof by Hohenberg and Kohn [24] proceeded by assuming that Y0 was not determined uniquely by n0 and showed that this produced a contradiction to the variational principle. Both proofs, by constrained search and by contradiction, are elegant and simple. In fact, it is a bit surprising that it took 38 years from Schrödinger's first papers on quantum mechanics [25] to Hohenberg and Kohn's 1964 paper containing their famous theorem [24].
Since 1964, the HK theorem has been thoroughly scrutinized, and several alternative proofs have been found. One of these is the so-called 'strong form of the Hohenberg-Kohn theorem', based on the inequality [26-28]
Here Dv(r) is a change in the potential, and Dn(r) is the resulting change in the density. We see immediately that if Dv ¹ 0 we cannot have Dn(r) º 0, i.e., a change in the potential must also change the density. This observation implies again the HK theorem for a single density variable: there cannot be two local potentials with the same ground-state charge density. A given N-particle ground-state density thus determines uniquely the corresponding potential, and hence also the wave function. Moreover, (18) establishes a relation between the signs of Dn(r) and Dv(r): if Dv is mostly positive, Dn(r) must be mostly negative, so that their integral over all space is negative. This additional information is not immediately available from the two classic proofs, and is the reason why this is called the 'strong' form of the HK theorem. Equation (18) can be obtained along the lines of the standard HK proof [26,27], but it can be turned into an independent proof of the HK theorem because it can also be derived perturbatively (see section 10.10 of Ref. [28]).
Another alternative argument is valid only for Coulomb potentials. It is based on Kato's theorem, which states [29,30] that for such potentials the electron density has a cusp at the position of the nuclei, where it satisfies
Here Rk denotes the positions of the nuclei, Zk their atomic number, and a0 =  2/me2 is the Bohr radius. For a Coulomb system one can thus, in principle, read off all information necessary for completely specifying the Hamiltonian directly from examining the density distribution: the integral over n(r) yields N, the total particle number; the position of the cusps of n(r) are the positions of the nuclei, Rk; and the derivative of n(r) at these positions yields Zk by means of Eq. (19). This is all one needs to specify the complete Hamiltonian of Eq. (2) (and thus implicitly all its eigenstates). In practice one almost never knows the density distribution sufficiently well to implement the search for the cusps and calculate the local derivatives. Still, Kato's theorem provides a vivid illustration of how the density can indeed contain sufficient information to completely specify a nontrivial Hamiltonian.11
11
Note that, unlike the full Hohenberg-Kohn theorem, Kato's theorem does apply only to superpositions of Coulomb potentials, and can therefore not be applied directly to the effective Kohn-Sham potential.
2/me2 is the Bohr radius. For a Coulomb system one can thus, in principle, read off all information necessary for completely specifying the Hamiltonian directly from examining the density distribution: the integral over n(r) yields N, the total particle number; the position of the cusps of n(r) are the positions of the nuclei, Rk; and the derivative of n(r) at these positions yields Zk by means of Eq. (19). This is all one needs to specify the complete Hamiltonian of Eq. (2) (and thus implicitly all its eigenstates). In practice one almost never knows the density distribution sufficiently well to implement the search for the cusps and calculate the local derivatives. Still, Kato's theorem provides a vivid illustration of how the density can indeed contain sufficient information to completely specify a nontrivial Hamiltonian.11
11
Note that, unlike the full Hohenberg-Kohn theorem, Kato's theorem does apply only to superpositions of Coulomb potentials, and can therefore not be applied directly to the effective Kohn-Sham potential.
For future reference we now provide a commented summary of the content of the HK theorem. This summary consists of four statements:
(1) The nondegenerate ground-state (GS) wave function is a unique functional of the GS density:12 12 If the ground state is degenerate, several of the degenerate ground-state wave functions may produce the same density, so that a unique functional Y[ n] does not exist, but by definition these wave functions all yield the same energy, so that the functional Ev[ n] continues to exist and to be minimized by n 0. A universal functional F[ n] can also still be defined [5].
This is the essence of the HK theorem. As a consequence, the GS expectation value of any observable Ô is a functional of n0(r), too:
(2) Perhaps the most important observable is the GS energy. This energy
where  =
=  + Û +
+ Û +  , has the variational property13
13
The minimum of
E[
n] is thus attained for the ground-state density. All other extrema of this functional correspond to densities of excited states, but the excited states obtained in this way do not necessarily cover the entire spectrum of the many-body Hamiltonian [31].
, has the variational property13
13
The minimum of
E[
n] is thus attained for the ground-state density. All other extrema of this functional correspond to densities of excited states, but the excited states obtained in this way do not necessarily cover the entire spectrum of the many-body Hamiltonian [31].
where n0 is GS density in potential  and n' is some other density. This is very similar to the usual variational principle for wave functions. ¿From a calculation of the expectation value of a Hamiltonian with a trial wave function Y' that is not its GS wave function Y0 one can never obtain an energy below the true GS energy,
and n' is some other density. This is very similar to the usual variational principle for wave functions. ¿From a calculation of the expectation value of a Hamiltonian with a trial wave function Y' that is not its GS wave function Y0 one can never obtain an energy below the true GS energy,
Similarly, in exact DFT, if E[n] for fixed vext is evaluated for a density that is not the GS density of the system in potential vext, one never finds a result below the true GS energy. This is what Eq. (23) says, and it is so important for practical applications of DFT that it is sometimes called the second Hohenberg-Kohn theorem (Eq. (21) is the first one, then).
In performing the minimization of Ev[n] the constraint that the total particle number N is an integer is taken into account by means of a Lagrange multiplier, replacing the constrained minimization of Ev[n] by an unconstrained one of Ev[n]-µN. Since N = òd3rn(r), this leads to
where µ is the chemical potential.
(3) Recalling that the kinetic and interaction energies of a nonrelativistic Coulomb system are described by universal operators, we can also write Ev as
where T[n] and U[n] are universal functionals [defined as expectation values of the type (21) of  and Û], independent of v(r). On the other hand, the potential energy in a given potential v(r) is the expectation value of Eq. (6),
and Û], independent of v(r). On the other hand, the potential energy in a given potential v(r) is the expectation value of Eq. (6),
and obviously nonuniversal (it depends on v(r), i.e., on the system under study), but very simple: once the system is specified, i.e., v(r) is known, the functional V[n] is known explicitly.
(4) There is a fourth substatement to the HK theorem, which shows that if v(r) is not hold fixed, the functional V[n] becomes universal: the GS density determines not only the GS wave function Y0, but, up to an additive constant, also the potential V = V[n0]. This is simply proven by writing Schrödinger's equation as
which shows that any eigenstate Yk (and thus in particular the ground state Y0 = Y[n0]) determines the potential operator  up to an additive constant, the corresponding eigenenergy. As a consequence, the explicit reference to the potential v in the energy functional Ev[n] is not necessary, and one can rewrite the ground-state energy as
up to an additive constant, the corresponding eigenenergy. As a consequence, the explicit reference to the potential v in the energy functional Ev[n] is not necessary, and one can rewrite the ground-state energy as
Another consequence is that n0 now does determine not only the GS wave function but the complete Hamiltonian (the operators  and Û are fixed), and thus all excited states, too:
and Û are fixed), and thus all excited states, too:
where k labels the entire spectrum of the many-body Hamiltonian  .
.
C. Complications: N and v-representability of densities, and nonuniqueness of potentials
Originally the fourth statement was considered to be as sound as the other three. However, it has become clear very recently, as a consequence of work of H. Eschrig and W. Pickett [32] and, independently, of the author with G. Vignale [33,34], that there are significant exceptions to it. In fact, the fourth substatement holds only when one formulates DFT exclusively in terms of the charge density, as we have done up to this point. It does not hold when one works with spin densities (spin-DFT) or current densities (current-DFT).14 14 In Section VI we will briefly discuss these formulations of DFT. In these (and some other) cases the densities still determine the wave function, but they do not uniquely determine the corresponding potentials. This so-called nonuniqueness problem has been discovered only recently, and its consequences are now beginning to be explored [27,32-38]. It is clear, however, that the fourth substatement is, from a practical point of view, the least important of the four, and most applications of DFT do not have to be reconsidered as a consequence of its eventual failure. (But some do: see Refs. [33,34] for examples.)
Another conceptual problem with the HK theorem, much better known and more studied than nonuniqueness, is representability. To understand what representability is about, consider the following two questions: (i) How does one know, given an arbitrary function n(r), that this function can be represented in the form (8), i.e., that it is a density arising from an antisymmetric N-body wave function Y(r1...rN)? (ii) How does one know, given a function that can be written in the form (8), that this density is a ground-state density of a local potential v(r)? The first of these questions is known as the N-representability problem, the second is called v-representability. Note that these are quite important questions: if one should find, for example, in a numerical calculation, a minimum of Ev[n] that is not N-representable, then this minimum is not the physically acceptable solution to the problem at hand. Luckily, the N-representability problem of the single-particle density has been solved: any nonnegative function can be written in terms of some antisymmetric Y(r1,r2 ..., rN) in the form (8) [39,40].
No similarly general solution is known for the v-representability problem. (The HK theorem only guarantees that there cannot be more than one potential for each density, but does not exclude the possibility that there is less than one, i.e., zero, potentials capable of producing that density.) It is known that in discretized systems every density is ensemble v-representable, which means that a local potential with a degenerate ground state can always be found, such that the density n(r) can be written as linear combination of the densities arising from each of the degenerate ground states [41-43]. It is not known if one of the two restrictions ('discretized systems', and 'ensemble') can be relaxed in general (yielding 'in continuum systems' and 'pure-state' respectively), but it is known that one may not relax both: there are densities in continuum systems that are not representable by a single nondegenerate antisymmetric function that is ground state of a local potential v(r) [5,41-43]. In any case, the constrained search algorithm of Levy and Lieb shows that v-representability in an interacting system is not required for the proof of the HK theorem. For the related question of simultaneous v-representability in a noninteracting system, which appears in the context of the Kohn-Sham formulation of DFT, see footnotes 34 and 35.
D. A preview of practical DFT
After these abstract considerations let us now consider one way in which one can make practical use of DFT. Assume we have specified our system (i.e., v(r) is known). Assume further that we have reliable approximations for U[n] and T[n]. In principle, all one has to do then is to minimize the sum of kinetic, interaction and potential energies
with respect to n(r). The minimizing function n0(r) is the system's GS charge density and the value Ev,0 = Ev[n0] is the GS energy. Assume now that v(r) depends on a parameter a. This can be, for example, the lattice constant in a solid or the angle between two atoms in a molecule. Calculation of Ev,0 for many values of a allows one to plot the curve Ev,0(a) and to find the value of a that minimizes it. This value, a0, is the GS lattice constant or angle. In this way one can calculate quantities like molecular geometries and sizes, lattice constants, unit cell volumes, charge distributions, total energies, etc. By looking at the change of Ev,0(a) with a one can, moreover, calculate compressibilities, phonon spectra and bulk moduli (in solids) and vibrational frequencies (in molecules). By comparing the total energy of a composite system (e.g., a molecule) with that of its constituent systems (e.g., individual atoms) one obtains dissociation energies. By calculating the total energy for systems with one electron more or less one obtains electron affinities and ionization energies.15 15 Electron affinities are typically harder to obtain than ionization energies, because within the local-density and generalized-gradient approximations the N + 1'st electron is too weakly bound or even unbound: the asymptotic effective potential obtained from these approximations decays exponentially, and not as 1/ r, i.e., it approaches zero so fast that binding of negative ions is strongly suppressed. Self-interaction corrections or other fully nonlocal functionals are needed to improve this behaviour. By appealing to the Hellman-Feynman theorem one can calculate forces on atoms from the derivative of the total energy with respect to the nuclear coordinates. All this follows from DFT without having to solve the many-body Schrödinger equation and without having to make a single-particle approximation. For brief comments on the most useful additional possibility to also calculate single-particle band structures see Secs. IV B and IV B3.
In theory it should be possible to calculate all observables, since the HK theorem guarantees that they are all functionals of n0(r). In practice, one does not know how to do this explicitly. Another problem is that the minimization of Ev[n] is, in general, a tough numerical problem on its own. And, moreover, one needs reliable approximations for T[n] and U[n] to begin with. In the next section, on the Kohn-Sham equations, we will see one widely used method for solving these problems. Before looking at that, however, it is worthwhile to recall an older, but still occasionally useful, alternative: the Thomas-Fermi approximation.
In this approximation one sets
i.e., approximates the full interaction energy by the Hartree energy, the electrostatic interaction energy of the charge distribution n(r). One further approximates, initially,
where thom(n) is the kinetic-energy density of a homogeneous interacting system with (constant) density n. Since it refers to interacting electrons thom(n) is not known explicitly, and further approximations are called for. As it stands, however, this formula is already a first example of a local-density approximation (LDA). In this type of approximation one imagines the real inhomogeneous system (with density n(r) in potential v(r)) to be decomposed in small cells in each of which n(r) and v(r) are approximately constant. In each cell (i.e., locally) one can then use the per-volume energy of a homogeneous system to approximate the contribution of the cell to the real inhomogeneous one. Making the cells infinitesimally small and summing over all of them yields Eq. (33).
For a noninteracting system (specified by subscript s, for 'single-particle') the function  (n) is known explicitly,
(n) is known explicitly,  (n) = 3
(n) = 3 2 (3p2)2/3n5/3/(10m) (see also Sec. V A). This is exploited to further approximate
2 (3p2)2/3n5/3/(10m) (see also Sec. V A). This is exploited to further approximate
where  [n] is the local-density approximation to Ts[n], the kinetic energy of noninteracting electrons of density n. Equivalently, it may be considered the noninteracting version of TLDA[n]. (The quantity Ts[n] will reappear below, in discussing the Kohn-Sham equations.) The Thomas-Fermi approximation16
16
The Thomas-Fermi approximation for screening, discussed in many books on solid-state physics, is obtained by minimizing
ETF[
n] with respect to n and linearizing the resulting relation between
v(
r) and
n(
r). It thus involves one more approximation (the linearization) compared to what is called the Thomas-Fermi approximation in DFT [44]. In two dimensions no linearization is required and both become equivalent [44].
then consists in combining (32) and (34) and writing
[n] is the local-density approximation to Ts[n], the kinetic energy of noninteracting electrons of density n. Equivalently, it may be considered the noninteracting version of TLDA[n]. (The quantity Ts[n] will reappear below, in discussing the Kohn-Sham equations.) The Thomas-Fermi approximation16
16
The Thomas-Fermi approximation for screening, discussed in many books on solid-state physics, is obtained by minimizing
ETF[
n] with respect to n and linearizing the resulting relation between
v(
r) and
n(
r). It thus involves one more approximation (the linearization) compared to what is called the Thomas-Fermi approximation in DFT [44]. In two dimensions no linearization is required and both become equivalent [44].
then consists in combining (32) and (34) and writing
A major defect of the Thomas-Fermi approximation is that within it molecules are unstable: the energy of a set of isolated atoms is lower than that of the bound molecule. This fundamental deficiency, and the lack of accuracy resulting from neglect of correlations in (32) and from using the local approximation (34) for the kinetic energy, limit the practical use of the Thomas-Fermi approximation in its own right. However, it is found a most useful starting point for a large body of work on improved approximations in chemistry and physics [12,30]. More recent approximations for T[n] can be found, e.g., in Refs. [45-47], in the context of orbital-free DFT. The extension of the local-density concept to the exchange-correlation energy is at the heart of many modern density functionals (see Sec. V A).
E. From wave functions to density functionals via Green's functions and density matrices
It is a fundamental postulate of quantum mechanics that the wave function contains all possible information about a system in a pure state at zero temperature, whereas at nonzero temperature this information is contained in the density matrix of quantum statistical mechanics. Normally, this is much more information that one can handle: for a system with N = 100 particles the many-body wave function is an extremely complicated function of 300 spatial and 100 spin17 17 To keep the notation simple, spin labels are either ignored or condensed into a common variable x := ( r s) in most of this text. They will only be put back explicitly in discussing spin-density-functional theory, in Sec. VI. variables that would be impossible to manipulate algebraically or to extract any information from, even if it were possible to calculate it in the first place. For this reason one searches for less complicated objects to formulate the theory. Such objects should contain the experimentally relevant information, such as energies, densities, etc., but do not need to contain explicit information about the coordinates of every single particle. One class of such objects are Green's functions, which are described in the next subsection, and another are reduced density matrices, described in the subsection III E2. Their relation to the wave function and the density is summarized in Fig. 1.
1. Green's functions
Readers with no prior knowledge of (or no interest in) Green's functions should skip this subsection, which is not necessary for understanding the following sections.
In mathematics one usually defines the Green's function of a linear operator  via [z -
via [z -  (r)]G(x,x';z) = d(x - x'), where d(x - x') is Dirac's delta function. For a single quantum particle in potential v(r) one has, for example,
(r)]G(x,x';z) = d(x - x'), where d(x - x') is Dirac's delta function. For a single quantum particle in potential v(r) one has, for example,
Many applications of such single-particle Green's functions are discussed in Ref. [21]. In many-body physics it is useful to also introduce more complicated Green's functions. In an interacting system the single-particle Green's function is modified by the presence of the interaction between the particles.18 18 Note that expressions like 'two-particle operator' and 'single-particle Green's function' refer to the number of particles involved in the definition of the operator (two in the case of an interaction, one for a potential energy, etc.), not to the total number of particles present in the system. In general it now satisfies the equation19 19 When energy is conserved, i.e., the Hamiltonian does not depend on time, G( r, t; r', t') depends on time only via the difference t - t' and can be written as G( r, r'; t - t'). By Fourier transformation with respect to t - t' one then passes from G( r, r'; t - t') to G( r, r'; E) of Eq. (36).
where G(2)(rt,xt;r't',xt+) is the two-particle Green's function [21,48]. Only for noninteracting systems (U = 0) is G(r,t;r',t') a Green's function in the mathematical sense of the word. In terms of G(r,t;r',t') one can explicitly express the expectation value of any single-body operator (such as the potential, the kinetic energy, the particle density, etc.), and also that of certain two-particle operators, such as the Hamiltonian in the presence of particle-particle interactions.20 20 For arbitrary two-particle operators one needs the full two-particle Green's function G (2).
One way to obtain the single-particle Green's function is via solution of what is called Dyson's equation [21,48,49],
where S is known as the irreducible self energy [21,48,49] and G(0) is the Green's function in the absence of any interaction. This equation (which we will not attempt to solve here) has a characteristic property that we will meet again when we study the (much simpler) Kohn-Sham and Hartree-Fock equations, in Sec. IV: the integral on the right-hand side, which determines G on the left-hand side, depends on G itself. The mathematical problem posed by this equation is thus nonlinear. We will return to such nonlinearity when we discuss self-consistent solution of the Kohn-Sham equation. The quantity S will appear again in Sec. IV B3 when we discuss the meaning of the eigenvalues of the Kohn-Sham equation.
The single-particle Green's function is related to the irreducible self energy by Dyson's equation (38) and to the two-particle Green's function by the equation of motion (37). It can also be related to the xc potential of DFT by the Sham-Schlüter equation [50]
where Gs is the Green's function of noninteracting particles with density n(r) (i.e., the Green's function of the Kohn-Sham equation, see Sec. IV B), and Sxc(r',r'';w) = S(r',r'';w) -d(r' - r'')vH(r') represents all contributions to the full irreducible self energy beyond the Hartree potential.
A proper discussion of S and G requires a formalism known as second quantization [21,48] and usually proceeds via introduction of Feynman diagrams. These developments are beyond the scope of the present overview. A related concept, density matrices, on the other hand, can be discussed easily. The next section is devoted to a brief description of some important density matrices.
2. Density matrices
For a general quantum system at temperature T, the density operator in a canonical ensemble is defined as
where Tr[·] is the trace and b = 1/(kBT). Standard textbooks on statistical physics show how this operator is obtained in other ensembles, and how it is used to calculate thermal and quantum expectation values. Here we focus on the relation to density-functional theory. To this end we write  in the energy representation as
in the energy representation as
where |Yiñ is eigenfunction of  , and the sum is over the entire spectrum of the system, each state being weighted by its Boltzmann weight
, and the sum is over the entire spectrum of the system, each state being weighted by its Boltzmann weight  . At zero temperature only the ground-state contributes to the sums, so that
. At zero temperature only the ground-state contributes to the sums, so that
The coordinate-space matrix element of this operator for an N-particle system is
which shows the connection between the density matrix and the wave function. (We use the usual abbreviation x = rs for space and spin coordinates.) The expectation value of a general N-particle operator Ô is obtained from O = áÔñ = òdx1òdx2...òdxN Y(x1,x2,..xN)* ÔY(x1,x2,..xN), which for multiplicative operators becomes
and involves only the function g (x1,x2,..xN;x1,x2,..xN), which is the diagonal element of the matrix g. Most operators we encounter in quantum mechanics are one or two-particle operators and can be calculated from reduced density matrices, that depend on less than 2N variables.21 21 Just as for Green's functions, expressions like 'two-particle operator' and 'two-particle density matrix' refer to the number of particles involved in the definition of the operator (two in the case of an interaction, one for a potential energy, etc.), not to the total number of particles present in the system. The reduced two-particle density matrix is defined as
where N(N - 1)/2 is a convenient normalization factor. This density matrix determines the expectation value of the particle-particle interaction, of static correlation and response functions, of the xc hole, and some related quantities. The pair-correlation function g(x,x'), e.g., is obtained from the diagonal element of g2(x1,x2;x1',x2') according to g2(x1,x2; x1,x2) =: n(x1)n(x2)g(x,x').
Similarly, the single-particle density matrix is defined as
The structure of reduced density matrices is quite simple: all coordinates that g does not depend upon are set equal in Y and Y*, and integrated over. The single-particle density matrix can also be considered the time-independent form of the single-particle Green's function, since it can alternatively be obtained from
In the special case that the wave function Y is a Slater determinant, i.e., the wave function of N noninteracting fermions, the single-particle density matrix can be written in terms of the orbitals comprising the determinant, as
which is known as the Dirac (or Dirac-Fock) density matrix.
The usefulness of the single-particle density matrix becomes apparent when we consider how one would calculate the expectation value of a multiplicative single-particle operator  =  a(ri) (such as the potential
a(ri) (such as the potential  =
=  v(ri)):
v(ri)):
which is a special case of Eq. (44). The second line follows from the first by exploiting that the fermionic wave function Y changes sign upon interchange of two of its arguments. The last equation implies that if one knows g(x,x) one can calculate the expectation value of any multiplicative single-particle operator in terms of it, regardless of the number of particles present in the system.22 22 For nonmultiplicative single-particle operators (such as the kinetic energy, which contains a derivative) one requires the full single-particle matrix g( x,x') and not only g( x,x). The simplification is enormous, and reduced density matrices are very popular in, e.g., computational chemistry for precisely this reason. More details are given in, e.g., Ref. [6]. The full density operator, Eq. (40), on the other hand, is the central quantity of quantum statistical mechanics.
It is not possible to express expectation values of two-particle operators, such as the interaction itself, or the full Hamiltonian (i.e., the total energy), explicitly in terms of the single-particle density matrix g(r,r'). For this purpose one requires the two-particle density matrix. This situation is to be contrasted with that of the single-particle Green's function, for which one knows how to express the expectation values of Û and  [21,48]. Apparently, some information has gotten lost in passing from G to g. This can also be seen very clearly from Eq. (47), which shows that information on the dynamics of the system, which is contained in G, is erased in the definition of g(r,r'). Explicit information on the static properties of the system is contained in the N-particle density matrix, but as seen from (45) and (46), a large part of this information is also lost ('integrated out') in passing from the N-particle density matrix to the reduced two- or one-particle density matrices.
[21,48]. Apparently, some information has gotten lost in passing from G to g. This can also be seen very clearly from Eq. (47), which shows that information on the dynamics of the system, which is contained in G, is erased in the definition of g(r,r'). Explicit information on the static properties of the system is contained in the N-particle density matrix, but as seen from (45) and (46), a large part of this information is also lost ('integrated out') in passing from the N-particle density matrix to the reduced two- or one-particle density matrices.
Apparently even less information is contained in the particle density23 23 A quantitative estimate of how much less information is apparently contained in the density than in the wave function is given in footnote 6. n(r), which is obtained by summing the diagonal element of g(x,x') over the spin variable,
This equation follows immediately from comparing (8) with (46). We can define an alternative density operator,  , by requiring that the same equation must also be obtained by substituting
, by requiring that the same equation must also be obtained by substituting  (r) into Eq. (51), which holds for any single-particle operator. This requirement implies that
(r) into Eq. (51), which holds for any single-particle operator. This requirement implies that  (r) =
(r) =  d (r-ri).24
24
The expectation value of
is the particle density, and therefore
is often also called the density operator. This concept must not be confused with any of the various density matrices or the density operator of statistical physics, Eq. (40).
d (r-ri).24
24
The expectation value of
is the particle density, and therefore
is often also called the density operator. This concept must not be confused with any of the various density matrices or the density operator of statistical physics, Eq. (40).
The particle density is an even simpler function than g(x,x'): it depends on one set of coordinates x only, it can easily be visualized as a three-dimensional charge distribution, and it is directly accessible in experiments. These advantages, however, seem to be more than compensated by the fact that one has integrated out an enormous amount of specific information about the system in going from wave functions to Green's functions, and on to density matrices and finally the density itself. This process is illustrated in Fig. 1.
The great surprise of density-functional theory is that in fact no information has been lost at all, at least as long as one considers the system only in its ground state: according to the Hohenberg-Kohn theorem the ground-state density n0(x) completely determines the ground-state wave function Y0(x1,x2 ..., xN).25 25 The Runge-Gross theorem, which forms the basis of time-dependent DFT [51], similarly guarantees that the time-dependent density contains the same information as the time-dependent wave function.
Hence, in the ground state, a function of one variable is equivalent to a function of N variables! This property shows that we have only integrated out explicit information on our way from wave functions via Green's functions and density matrices to densities. Implicitly all the information that was contained in the ground-state wave function is still contained in the ground-state density. Part of the art of practical DFT is how to get this implicit information out, once one has obtained the density!
IV. DFT AS AN EFFECTIVE SINGLE-BODY THEORY: THE KOHN-SHAM EQUATIONS
Density-functional theory can be implemented in many ways. The minimization of an explicit energy functional, discussed up to this point, is not normally the most efficient among them. Much more widely used is the Kohn-Sham approach. Interestingly, this approach owes its success and popularity partly to the fact that it does not exclusively work in terms of the particle (or charge) density, but brings a special kind of wave functions (single-particle orbitals) back into the game. As a consequence DFT then looks formally like a single-particle theory, although many-body effects are still included via the so-called exchange-correlation functional. We will now see in some detail how this is done.
A. Exchange-correlation energy: definition, interpretation and exact properties
1. Exchange-correlation energy
The Thomas-Fermi approximation (34) for T[n] is not very good. A more accurate scheme for treating the kinetic-energy functional of interacting electrons, T[n], is based on decomposing it into one part that represents the kinetic energy of noninteracting particles of density n, i.e., the quantity called above Ts[n], and one that represents the remainder, denoted Tc[n] (the subscripts s and c stand for 'single-particle' and 'correlation', respectively).26 26 Ts is defined as the expectation value of the kinetic-energy operator with the Slater determinant arising from density n, i.e., Ts[ n] = áF[ n]| | F[ n]ñ. Similarly, the full kinetic energy is defined as T[ n] = áY[ n] |Y[ n] ñ. All consequences of antisymmetrization (i.e., exchange) are described by employing a determinantal wave function in defining Ts. Hence, Tc, the difference between Ts and T is a pure correlation effect.
Ts[n] is not known exactly as a functional of n [and using the LDA to approximate it leads one back to the Thomas-Fermi approximation (34)], but it is easily expressed in terms of the single-particle orbitals fi(r) of a noninteracting system with density n, as
because for noninteracting particles the total kinetic energy is just the sum of the individual kinetic energies. Since all fi(r) are functionals of n, this expression for Ts is an explicit orbital functional but an implicit density functional, Ts[n] = Ts[{fi[n]}], where the notation indicates that Tsdepends on the full set of occupied orbitals fi, each of which is a functional of n. Other such orbital functionals will be discussed in Sec. V.
We now rewrite the exact energy functional as
where by definition Exc contains the differences T - Ts (i.e. Tc) and U - UH. This definition shows that a significant part of the correlation energy Ec is due to the difference Tc between the noninteracting and the interacting kinetic energies. Unlike Eq. (35), Eq. (55) is formally exact, but of course Exc is unknown although the HK theorem guarantees that it is a density functional. This functional, Exc[n], is called the exchange-correlation (xc) energy. It is often decomposed as Exc = Ex + Ec, where Ex is due to the Pauli principle (exchange energy) and Ec is due to correlations. (Tc is then a part of Ec.) The exchange energy can be written explicitly in terms of the single-particle orbitals as27 27 This differs from the exchange energy used in Hartree-Fock theory only in the substitution of Hartree-Fock orbitals ( r) by Kohn-Sham orbitals f i( r).
which is known as the Fock term, but no general exact expression in terms of the density is known.
2. Different perspectives on the correlation energy
For the correlation energy no general explicit expression is known, neither in terms of orbitals nor densities. Different ways to understand correlations are described below.
Correlation energy: variational approach. A simple way to understand the origin of correlation is to recall that the Hartree energy is obtained in a variational calculation in which the many-body wave function is approximated as a product of single-particle orbitals. Use of an antisymmetrized product (a Slater determinant) produces the Hartree and the exchange energy [48,49]. The correlation energy is then defined as the difference between the full ground-state energy (obtained with the correct many-body wave function) and the one obtained from the (Hartree-Fock or Kohn-Sham28 28 The Hartree-Fock and the Kohn-Sham Slater determinants are not identical, since they are composed of different single-particle orbitals, and thus the definition of exchange and correlation energy in DFT and in conventional quantum chemistry is slightly different [52]. ) Slater determinant. Since it arises from a more general trial wave function than a single Slater determinant, correlation cannot raise the total energy, and Ec[n] < 0. Since a Slater determinant is itself more general than a simple product we also have Ex < 0, and thus the upper bound29 29 A lower bound is provided by the Lieb-Oxford formula, given in Eq. (64). Exc[n] < 0.
Correlation energy: probabilistic approach. Recalling the quantum mechanical interpretation of the wave function as a probability amplitude, we see that a product form of the many-body wave function corresponds to treating the probability amplitude of the many-electron system as a product of the probability amplitudes of individual electrons (the orbitals). Mathematically, the probability of a composed event is only equal to the probability of the individual events if the individual events are independent (i.e., uncorrelated). Physically, this means that the electrons described by the product wave function are independent.30 30 Correlation is a mathematical concept describing the fact that certain events are not independent. It can be defined also in classical physics, and in applications of statistics to other fields than physics. Exchange is due to the indistinguishability of particles, and a true quantum phenomenon, without any analogue in classical physics. Such wave functions thus neglect the fact that, as a consequence of the Coulomb interaction, the electrons try to avoid each other. The correlation energy is simply the additional energy lowering obtained in a real system due to the mutual avoidance of the interacting electrons. One way to characterize a strongly correlated system is to define correlations as strong when Ec is comparable in magnitude to, or larger than, other energy contributions, such as EH or Ts. (In weakly correlated systems Ec normally is several orders of magnitude smaller.)31 31 Other characterizations of strongly correlated systems are to compare the width of the conduction band in a solid with the kinetic energy (if the band width is smaller, correlations are strong), or the quasiparticle energies with the Kohn-Sham eigenvalues e i (if both are similar, correlations are weak, see footnote 37), or the derivative discontinuity D xc, defined in Eq. (65), with the Kohn-Sham energy gap (if the former is comparable to or larger than the latter, correlations are strong). (The meaning of , e i and D xc is explained below.) No universally applicable definition of 'strong correlations' seems to exist.
Correlation energy: beyond mean-field approach. A rather different (but equivalent) way to understand correlation is to consider the following alternative form of the operator representing the Coulomb interaction, equivalent to Eq. (3),
in which the operator character is carried only by the density operators  (in occupation number representation), and the term with the delta function subtracts out the interaction of a charge with itself (cf., e.g., the appendix of Ref. [53] for a simple derivation of this form of Û). The expectation value of this operator, U = áY|Û|Yñ, involves the expectation value of a product of density operators, áY|
(in occupation number representation), and the term with the delta function subtracts out the interaction of a charge with itself (cf., e.g., the appendix of Ref. [53] for a simple derivation of this form of Û). The expectation value of this operator, U = áY|Û|Yñ, involves the expectation value of a product of density operators, áY|  (r)
(r)  (r')|Yñ. In the Hartree term (32), on the other hand, this expectation value of a product is replaced by a product of expectation values, each of the form n(r) = áY|
(r')|Yñ. In the Hartree term (32), on the other hand, this expectation value of a product is replaced by a product of expectation values, each of the form n(r) = áY| (r) |Yñ. This replacement amounts to a mean-field approximation, which neglects quantum fluctuations32
32
At finite temperature there are also thermal fluctuations. To properly include these one must use a finite-temperature formulation of DFT [54]. See also the contribution of B. L. Gyorffy et al. in Ref. [19] for DFT treatment of various types of fluctuations.
about the expectation values: by writing
(r) |Yñ. This replacement amounts to a mean-field approximation, which neglects quantum fluctuations32
32
At finite temperature there are also thermal fluctuations. To properly include these one must use a finite-temperature formulation of DFT [54]. See also the contribution of B. L. Gyorffy et al. in Ref. [19] for DFT treatment of various types of fluctuations.
about the expectation values: by writing  = n + d
= n + d  fluc and substituting in Eq. (57) we see that the difference between áY|Û| Yñ and the Hartree term (32) is entirely due to the fluctuations d
fluc and substituting in Eq. (57) we see that the difference between áY|Û| Yñ and the Hartree term (32) is entirely due to the fluctuations d fluc and the self-interaction correction to the Hartree term. Quantum fluctuations about the expectation value are thus at the origin of quantum correlations between interacting particles.
fluc and the self-interaction correction to the Hartree term. Quantum fluctuations about the expectation value are thus at the origin of quantum correlations between interacting particles.
Correlation energy: holes. The fact that both exchange and correlation tend to keep electrons apart, has given rise to the concept of an xc hole, nxc(r,r'), describing the reduction of probability for encountering an electron at r', given one at r. The xc energy can be written as a Hartree-like interaction between the charge distribution n(r) and the xc hole nxc(r,r') = nx(r,r') + nc(r,r'),
which defines nxc. The exchange component Ex[n] of the exact exchange-correlation functional describes the energy lowering due to antisymmetrization (i.e., the tendency of like-spin electrons to avoid each other). It gives rise to the exchange hole nx(r,r'), which obeys the sum rule òd3r' nx(r,r') = -1. The correlation component Ec[n] accounts for the additional energy lowering arising because electrons with opposite spins also avoid each other. The resulting correlation hole integrates to zero, so that the total xc hole satisfies òd3r' nxc(r,r') = -1. The xc hole can also be written as nxc(r,r') = n(r') ( [n](r,r') - 1), where
[n](r,r') - 1), where  is the average of the pair-correlation function g(r,r'), mentioned in Sec. III E2, over all values of the particle-particle interaction, from zero (KS system) to áÛñ (interacting system). This average is simply expressed in terms of the coupling constant a as
is the average of the pair-correlation function g(r,r'), mentioned in Sec. III E2, over all values of the particle-particle interaction, from zero (KS system) to áÛñ (interacting system). This average is simply expressed in terms of the coupling constant a as  (r,r') =
(r,r') =  ga(r,r')da. For the Coulomb interaction, a = e2, i.e., the square of the electron charge [5,6].
ga(r,r')da. For the Coulomb interaction, a = e2, i.e., the square of the electron charge [5,6].
3. Exact properties
Clearly Ec is an enormously complex object, and DFT would be of little use if one had to know it exactly for making calculations. The practical advantage of writing E[n] in the form Eq. (55) is that the unknown functional Exc[n] is typically much smaller than the known terms Ts, UH and V. One can thus hope that reasonably simple approximations for Exc[n] provide useful results for E[n]. Some successful approximations are discussed in Sec. V. Exact properties, such as the sum rule òd3r' nxc(r,r') = -1, described in the preceding section, are most valuable guides in the construction of approximations to Exc[n].
Among the known properties of this functional are the coordinate scaling conditions first obtained by Levy and Perdew [55]
where nl(r) = l3n(lr) is a scaled density integrating to total particle number N.
Another important property of the exact functional is the one-electron limit
where n(1) is a one-electron density. These latter two conditions, which are satisfied within the Hartree-Fock approximation, but not by standard local-density and gradient-dependent functionals, ensure that there is no artificial self-interaction of one electron with itself.
The Lieb-Oxford bound [56,57],
establishes a lower bound on the xc energy, and is satisfied by LDA and many (but not all) GGAs.
One of the most intriguing properties of the exact functional, which has resisted all attempts of describing it in local or semilocal approximations, is the derivative discontinuity of the xc functional with respect to the total particle number [50,58,59],
where d is an infinitesimal shift of the electron number N, and Dxc is a system-dependent, but r-independent shift of the xc potential vxc(r) as it passes from the electron-poor to the electron-rich side of integer N. The noninteracting kinetic-energy functional has a similar discontinuity, given by
where eN and eN+1 are the Kohn-Sham (KS) single-particle energies of the highest occupied and lowest unoccupied eigenstate. The meaning of these KS eigenvalues is discussed in the paragraphs following Eq. (75) and illustrated in Fig. 2. In the chemistry literature these are called the HOMO (highest occupied molecular orbital) and LUMO (lowest unoccupied molecular orbital), respectively. The kinetic-energy discontinuity is thus simply the KS single-particle gap DKS, or HOMO-LUMO gap, whereas the xc discontinuity Dxc is a many-body effect. The true fundamental gap D = E(N + 1) + E(N - 1) - 2E(N) is the discontinuity of the total ground-state energy functional [5,50,58,59],
Since all terms in E other than Exc and Ts are continuous functionals of n(r), the fundamental gap is the sum of the KS gap and the xc discontinuity. Standard density functionals (LDA and GGA) predict Dxc = 0, and thus often underestimate the fundamental gap. The fundamental and KS gaps are also illustrated in Fig. 2.
All these properties serve as constraints or guides in the construction of approximations for the functionals Ex[n] and Ec[n]. Many other similar properties are known. A useful overview of scaling properties is the contribution of M. Levy in Ref. [19].
B. Kohn-Sham equations
1. Derivation of the Kohn-Sham equations
Since Ts is now written as an orbital functional one cannot directly minimize Eq. (55) with respect to n. Instead, one commonly employs a scheme suggested by Kohn and Sham [60] for performing the minimization indirectly. This scheme starts by writing the minimization as
As a consequence of Eq. (27), dV/ dn = v(r), the 'external' potential the electrons move in.33 33 This potential is called 'external' because it is external to the electron system and not generated self-consistently from the electron-electron interaction, as vH and vxc. It comprises the lattice potential and any additional truly external field applied to the system as a whole. The term dUH/dn simply yields the Hartree potential, introduced in Eq. (11). For the term dExc/dn, which can only be calculated explicitly once an approximation for Exc has been chosen, one commonly writes vxc. By means of the Sham-Schlüter equation (39), vxc is related to the irreducible self energy S, introduced in Eq. (38) [50].
Consider now a system of noninteracting particles moving in the potential vs(r). For this system the minimization condition is simply
since there are no Hartree and xc terms in the absence of interactions. The density solving this Euler equation is ns(r). Comparing this with Eq. (68) we find that both minimizations have the same solution ns(r) º n(r), if vs is chosen to be
Consequently, one can calculate the density of the interacting (many-body) system in potential v(r), described by a many-body Schrödinger equation of the form (2), by solving the equations of a noninteracting (single-body) system in potential vs(r). 34 34 The question whether such a potential vs( r) always exists in the mathematical sense is called the noninteracting v-representability problem. It is known that every interacting ensemble v-representable density is also noninteracting ensemble v-representable, but, as mentioned in Sec. III B, only in discretized systems has it been proven that all densities are interacting ensemble v-representable. It is not known if interacting ensemble-representable densities may be noninteracting pure-state representable (i.e, by a single determinant), which would be convenient (but is not necessary) for Kohn-Sham calculations.
In particular, the Schrödinger equation of this auxiliary system,
yields orbitals that reproduce the density n(r) of the original system (these are the same orbitals employed in Eq. (54)),
where fi is the occupation of the i'th orbital.35 35 Normally, the occupation numbers fi follows an Aufbau principle (Fermi statistics) with fi = 1 for i < N, fi = 0 for i > N, and 0 < fi < 1 for i = N (i.e., at most the highest occupied orbital can have fractional occupation). Some densities that are not noninteracting v-representable by a single ground-state Slater determinant, may still be obtained from a single determinant if one uses occupation numbers fi that leave holes below the HOMO (the Fermi energy in a metal), so that fi ¹ 1 even for some i < N [31], but this is not guaranteed to describe all possible densities. Alternatively (see Sec. III B and footnote 34) a Kohn-Sham equation may be set up in terms of ensembles of determinants. This guarantees noninteracting v-representability for all densities that are interacting ensemble v-representable. For practical KS calculations, the most important consequence of the fact that not every arbitrary density is guaranteed to be noninteracting v-representable is that the Kohn-Sham selfconsistency cycle is not guaranteed to converge. Eqs. (70) to (72) are the celebrated Kohn-Sham (KS) equations. They replace the problem of minimizing E[n] by that of solving a noninteracting Schrödinger equation. (Recall that the minimization of E[n] originally replaced the problem of solving the many-body Schrödinger equation!)
Since both vH and vxc depend on n, which depends on the fi, which in turn depend on vs, the problem of solving the KS equations is a nonlinear one, just as is the one of solving the (much more complicated) Dyson equation (38). The usual way of solving such problems is to start with an initial guess for n(r), calculate the corresponding vs(r), and then solve the differential equation (71) for the fi. ¿From these one calculates a new density, using (72), and starts again. The process is repeated until it converges. The technical name for this procedure is 'self-consistency cycle'. Different convergence criteria (such as convergence in the energy, the density, or some observable calculated from these) and various convergence-accelerating algorithms (such as mixing of old and new effective potentials) are in common use. Only rarely it requires more than a few dozen iterations to achieve convergence, and even rarer are cases where convergence seems unattainable, i.e., a self-consistent solution of the KS equation cannot be found.
Once one has a converged solution n0, one can calculate the total energy from Eq. (55) or, equivalently and more conveniently, from36 36 All terms on the right-hand side of (73) except for the first, involving the sum of the single-particle energies, are sometimes known as double-counting corrections, in analogy to a similar equation valid within Hartree-Fock theory.
Equation (73) follows from writing V[n] in (55) by means of (70) as
and identifying the energy of the noninteracting (Kohn-Sham) system as Es =  ei = Ts + Vs.
ei = Ts + Vs.
2. The eigenvalues of the Kohn-Sham equation
Equation (73) shows that E0 is not simply the sum37 37 The difference between E 0 and e i is due to particle-particle interactions. The additional terms on the right-hand side of (73) give mathematical meaning to the common statement that the whole is more than the sum of its parts. If E 0 can be written approximately as (where the are not the same as the KS eigenvalues e i) the system can be described in terms of N weakly interacting quasiparticles, each with energy . Fermi-liquid theory in metals and effective-mass theory in semiconductors are examples of this type of approach. of all ei. In fact, it should be clear from our derivation of Eq. (71) that the ei are introduced as completely artificial objects: they are the eigenvalues of an auxiliary single-body equation whose eigenfunctions (orbitals) yield the correct density. It is only this density that has strict physical meaning in the KS equations. The KS eigenvalues, on the other hand, in general bear only a semiquantitative resemblance with the true energy spectrum [61], but are not to be trusted quantitatively.
The main exception to this rule is the highest occupied KS eigenvalue. Denoting by eN(M) the N'th eigenvalue of a system with M electrons, one can show rigorously that eN(N) = -I, the negative of the first ionization energy of the N-body system, and eN+1(N + 1) = -A, the negative of the electron affinity of the same N-body system [58,62,63]. These relations hold for the exact functional only. When calculated with an approximate functional of the LDA or GGA type, the highest eigenvalues usually do not provide good approximations to the experimental I and A. Better results for these observables are obtained by calculating them as total-energy differences, according to I = E0(N - 1) - E0(N) and A = E0(N) - E0(N + 1), where E0(N) is the ground-state energy of the N-body system. Alternatively, self-interaction corrections can be used to obtain improved ionization energies and electron affinities from Kohn-Sham eigenvalues [64].
Figure 2 illustrates the role played by the highest occupied and lowest unoccupied KS eigenvalues, and their relation to observables. For molecules, HOMO(N) is the highest-occupied molecular orbital of the N-electron system, HOMO(N+1) that of the N + 1-electron system, and LUMO(N) the lowest unoccupied orbital of the N-electron system. In solids with a gap, the HOMO and LUMO become the top of the valence band and the bottom of the conduction band, respectively, whereas in metals they are both identical to the Fermi level. The vertical lines indicate the Kohn-Sham (single-particle) gap DKS, the fundamental (many-body) gap D, the derivative discontinuity of the xc functional, Dxc, the ionization energy of the interacting N-electron system I(N) = -eN(N) (which is also the ionization energy of the Kohn-Sham system IKS(N)), the electron affinity of the interacting N-electron system A(N) = -eN+1(N + 1) and the Kohn-Sham electron affinity AKS(N) = -eN+1(N).
Given the auxiliary nature of the other Kohn-Sham eigenvalues, it comes as a great (and welcome) surprise that in many situations (typically characterized by the presence of fermionic quasiparticles and absence of strong correlations) the Kohn-Sham eigenvalues ei do, empirically, provide a reasonable first approximation to the actual energy levels of extended systems. This approximation is behind most band-structure calculations in solid-state physics, and often gives results that agree well with experimental photoemission and inverse photoemission data [65], but much research remains to be done before it is clear to what extent such conclusions can be generalized, and how situations in which the KS eigenvalues are good starting points for approximating the true excitation spectrum are to be characterized microscopically [66,67].38 38 Several more rigorous approaches to excited states in DFT, which do not require the KS eigenvalues to have physical meaning, are mentioned in Sec. IV.
Most band-structure calculations in solid-state physics are actually calculations of the KS eigenvalues ei.39 39 A computationally more expensive, but more reliable, alternative is provided by the GW approximation [68-70]. This simplification has proved enormously successful, but when one uses it one must be aware of the fact that one is taking the auxiliary single-body equation (71) literally as an approximation to the many-body Schrödinger equation. DFT, practiced in this mode, is not a rigorous many-body theory anymore, but a mean-field theory (albeit one with a very sophisticated mean field vs(r)).
The energy gap obtained in such band-structure calculations is the one called HOMO-LUMO gap in molecular calculations, i.e., the difference between the energies of the highest occupied and the lowest unoccupied single-particle states. Neglect of the derivative discontinuity Dxc, defined in Eq. (65), by standard local and semilocal xc functionals leads to an underestimate of the gap (the so-called 'band-gap problem'), which is most severe in transition-metal oxides and other strongly correlated systems. Self-interaction corrections provide a partial remedy for this problem [71-74].
3. Hartree, Hartree-Fock and Dyson equations
A partial justification for the interpretation of the KS eigenvalues as starting point for approximations to quasi-particle energies, common in band-structure calculations, can be given by comparing the KS equation with other self-consistent equations of many-body physics. Among the simplest such equations are the Hartree equation
and the Hartree-Fock (HF) equation
where g(r,r') is the density matrix of Eq. (46). It is a fact known as Koopman's theorem [49] that the HF eigenvalues  can be interpreted as unrelaxed electron-removal energies (i.e., ionization energies of the i'th electron, neglecting reorganization of the remaining electrons after removal). As mentioned above, in DFT only the highest occupied eigenvalue corresponds to an ionization energy, but unlike in HF this energy includes relaxation effects.
can be interpreted as unrelaxed electron-removal energies (i.e., ionization energies of the i'th electron, neglecting reorganization of the remaining electrons after removal). As mentioned above, in DFT only the highest occupied eigenvalue corresponds to an ionization energy, but unlike in HF this energy includes relaxation effects.
The KS equation (71) includes both exchange and correlation via the multiplicative operator vxc. Both exchange and correlation are normally approximated in DFT,40 40 A possibility to treat exchange exactly in DFT is offered by the OEP method discussed in Sec. V C. whereas HF accounts for exchange exactly, through the integral operator containing g(r,r'), but neglects correlation completely. In practise DFT results are typically at least as good as HF ones and often comparable to much more sophisticated correlated methods and the KS equations are much easier to solve than the HF equations.41 41 This is due to the integral operator in the HF equations.
All three single-particle equations, Hartree, Hartree-Fock and Kohn-Sham can also be interpreted as approximations to Dyson's equation (38), which can be rewritten as [48]
where S is the irreducible self energy introduced in Eq. (38). The Ek appearing in this equation are the true (quasi-)electron addition and removal energies of the many-body system. Needless to say, it is much more complicated to solve this equation than the HF or KS equations. It is also much harder to find useful approximations for S than for vxc.42 42 The GW approximation [68-70], mentioned in footnote 39, is one such approximation for S, but in actual implementations of it one usually takes DFT-KS results as an input. Obviously, the KS equation employs a local, energy-independent potential vs in place of the nonlocal, energy-dependent operator S. Whenever this is a good approximation, the ei are also a good approximation to the Ek.
The interpretation of the KS equation (71) as an approximation to Eq. (78) is suggestive and useful, but certainly not necessary for DFT to work: if the KS equations are only used to obtain the density, and all other observables, such as total energies, are calculated from this density, then the KS equations in themselves are not an approximation at all, but simply a very useful mathematical tool.
C. Basis functions
In practice, numerical solution of the KS differential equation (71) typically proceeds by expanding the KS orbitals in a suitable set of basis functions and solving the resulting secular equation for the coefficients in this expansion and/or for the eigenvalues for which it has a solution. The construction of suitable basis functions is a major enterprise within electronic-structure theory (with relevance far beyond DFT), and the following lines do little more than explaining some acronyms often used in this field.
In physics much is known about the construction of basis functions for solids due to decades of experience with band-structure calculations. This includes many calculations that predate the widespread use of DFT in physics. There is a fundamental dichotomy between methods that work with fixed basis functions that do not depend on energy, and methods that employ energy-dependent basis functions. Fixed basis functions are used e.g., in plane-wave expansions, tight-binding or LCAO (linear combination of atomic orbitals) approximations, or the OPW (orthogonalized plane wave) method. Examples for methods using energy-dependent functions are the APW (augmented plane wave) or KKR (Korringa-Kohn-Rostoker) approaches. This distinction became less clear-cut with the introduction of 'linear methods' [75], in which energy-dependent basis functions are linearized (Taylor expanded) around some fixed reference energy. The most widely used methods for solving the Kohn-Sham equation in solid-state physics, LMTO (linear muffin tin orbitals) and LAPW (linear augmented plane waves), are of this latter type [76]. Development of better basis functions is an ongoing enterprise [77,78].
The situation is quite similar in chemistry. Due to decades of experience with Hartree-Fock and CI calculations much is known about the construction of basis functions that are suitable for molecules. Almost all of this continues to hold in DFT a fact that has greatly contributed to the recent popularity of DFT in chemistry. Chemical basis functions are classified with respect to their behaviour as a function of the radial coordinate into Slater type orbitals (STOs), which decay exponentially far from the origin, and Gaussian type orbitals (GTOs), which have a gaussian behaviour. STOs more closely resemble the true behaviour of atomic wave functions [in particular the cusp condition of Eq. (19)], but GTOs are easier to handle numerically because the product of two GTOs located at different atoms is another GTO located in between, whereas the product of two STOs is not an STO. The so-called 'contracted basis functions', in which STO basis functions are reexpanded in a small number of GTOs, represent a compromise between the accuracy of STOs and the convenience of GTOs. The most common methods for solving the Kohn-Sham equations in quantum chemistry are of this type [4,49]. Very accurate basis functions for chemical purposes have been constructed by Dunning [79] and, more recently, by da Silva and collaborators [80,81]. More details on the development of suitable basis functions can be found, e.g., in these references and Ref. [49].
A very popular approach to larger systems in DFT, in particular solids, is based on the concept of a pseudopotential (PP). The idea behind the PP is that chemical binding in molecules and solids is dominated by the outer (valence) electrons of each atom. The inner (core) electrons retain, to a good approximation, an atomic-like configuration, and their orbitals do not change much if the atom is put in a different environment. Hence, it is possible to approximately account for the core electrons in a solid or a large molecule by means of an atomic calculation, leaving only the valence density to be determined self-consistently for the system of interest.
In the original Kohn-Sham equation the effective potential vs[n] = vext + vH[n] + vxc[n] is determined by the full electronic density n(r), and the self-consistent solutions are single-particle orbitals reproducing this density. In the PP approach the Hartree and xc terms in vs[n] are evaluated only for the valence density nv, and the core electrons are accounted for by replacing the external potential vext by a pseudopotential  . Hence
. Hence  [nv] =
[nv] =  + vH[nv] + vxc[nv]. 43
43
Note that the
effective potential
vs is a way to deal with the electron-electron interaction. The
pseudopotential is a way to deal with the density of the core electrons. Both potentials can be profitably used together, but are conceptually different.
The PP
+ vH[nv] + vxc[nv]. 43
43
Note that the
effective potential
vs is a way to deal with the electron-electron interaction. The
pseudopotential is a way to deal with the density of the core electrons. Both potentials can be profitably used together, but are conceptually different.
The PP  is determined in two steps. First, one determines, in an auxiliary atomic calculation, an effective PP,
is determined in two steps. First, one determines, in an auxiliary atomic calculation, an effective PP,  , such that for a suitably chosen atomic reference configuration the single-particle orbitals resulting from
, such that for a suitably chosen atomic reference configuration the single-particle orbitals resulting from  agree outside a cut-off radius rc separating the core from the valence region with the valence orbitals obtained from the all-electron KS equation for the same atom. As a consequence, the valence densities
agree outside a cut-off radius rc separating the core from the valence region with the valence orbitals obtained from the all-electron KS equation for the same atom. As a consequence, the valence densities  obtained from the atomic KS and the atomic PP equation are the same. Next, one subtracts the atomic valence contributions vH[
obtained from the atomic KS and the atomic PP equation are the same. Next, one subtracts the atomic valence contributions vH[ ] and vxc[
] and vxc[ ] from
] from  [
[ ] to obtain the external PP
] to obtain the external PP  , 44
44
This external PP is also called the unscreened PP, and the subtraction of
vH[
] and
vxc[
] from
[
] is called the 'unscreening of the atomic PP'. It can only be done exactly for the Hartree term, because the contributions of valence and core densities are not additive in the
xc potential (which is a nonlinear functional of the total density).
which is then used in the molecular or solid-state calculation, together with vH[nv] and vxc[nv] taken at the proper valence densities for these systems.
, 44
44
This external PP is also called the unscreened PP, and the subtraction of
vH[
] and
vxc[
] from
[
] is called the 'unscreening of the atomic PP'. It can only be done exactly for the Hartree term, because the contributions of valence and core densities are not additive in the
xc potential (which is a nonlinear functional of the total density).
which is then used in the molecular or solid-state calculation, together with vH[nv] and vxc[nv] taken at the proper valence densities for these systems.
The way  is generated from the atomic calculation is not unique. Common pseudopotentials are generated following the prescription of, e.g., Bachelet, Hamann and Schlüter [82], Kleinman and Bylander [83], Vanderbilt [84] or Troullier and Martins [85]. Useful reviews are Refs. [86-88]. The pseudopotential approach is very convenient because it reduces the number of electrons treated explicitly, making it possible to perform density-functional calculations on systems with tens of thousands of electrons. Moreover, the pseudopotentials
is generated from the atomic calculation is not unique. Common pseudopotentials are generated following the prescription of, e.g., Bachelet, Hamann and Schlüter [82], Kleinman and Bylander [83], Vanderbilt [84] or Troullier and Martins [85]. Useful reviews are Refs. [86-88]. The pseudopotential approach is very convenient because it reduces the number of electrons treated explicitly, making it possible to perform density-functional calculations on systems with tens of thousands of electrons. Moreover, the pseudopotentials  are much smoother than the bare nuclear potentials vext. The remaining valence electrons are thus well described by plane-wave basis sets.
are much smoother than the bare nuclear potentials vext. The remaining valence electrons are thus well described by plane-wave basis sets.
Some of the choices one has to make in a practical Kohn-Sham calculation are illustrated schematically in Fig. 3.
V. MAKING DFT PRACTICAL: APPROXIMATIONS
There are basically three distinct types of approximations involved in a DFT calculation. One is conceptual, and concerns the interpretation of KS eigenvalues and orbitals as physical energies and wave functions. This approximation is optional if one does not want to make it one simply does not attach meaning to the eigenvalues of Eq. (71). The pros and cons of this procedure were discussed in Secs. IV B2 and IV B3. The second type of approximation is numerical, and concerns methods for actually solving the differential equation (71). A main aspect here is the selection of suitable basis functions, briefly discussed in Sec. IV C. The third type of approximation involves constructing an expression for the unknown xc functional Exc[n], which contains all many-body aspects of the problem [cf. Eq. (55)]. It is with this type of approximation that we are concerned in the present section.
This chapter is intended to give the reader an idea of what types of functionals exist, and to describe what their main features are, separately for local functionals (TF, LDA and Xa; Sec. V A), semilocal, or gradient-dependent, functionals (GEA and GGA; Sec. V B), and nonlocal functionals (hybrids, orbital functionals such as meta-GGAs, EXX and SIC, and integral-dependent functionals such as ADA; Sec. V C). This chapter does deal only most superficially with the actual construction of these functionals. For more details on functional construction and testing the reader is referred to the reviews [5-19] or to the original papers cited below. Sticking to the bird's-eye philosophy of this overview I have also refrained from including numerical data on the performance of each functional extensive comparisons of a wide variety of functionals can be found in Refs. [5-19] and in the original literature cited below.
A. Local functionals: LDA
Historically (and in many applications also practically) the most important type of approximation is the local-density approximation (LDA). To understand the concept of an LDA recall first how the noninteracting kinetic energy Ts[n] is treated in the Thomas-Fermi approximation: In a homogeneous system one knows that, per volume45 45 The change from a capital T to a lower-case t is commonly used to indicate quantities per volume.
where n = const. In an inhomogeneous system, with n = n(r), one approximates locally
and obtains the full kinetic energy by integration over all space
For the kinetic energy the approximation Ts[n] »  [n] is much inferior to the exact treatment of Ts in terms of orbitals, offered by the Kohn-Sham equations, but the LDA concept turned out to be highly useful for another component of the total energy (55), the exchange-correlation energy Exc[n]. For the exchange energy Ex[n] the procedure is very simple, since the per-volume exchange energy of the homogeneous electron liquid is known exactly [5,6],
[n] is much inferior to the exact treatment of Ts in terms of orbitals, offered by the Kohn-Sham equations, but the LDA concept turned out to be highly useful for another component of the total energy (55), the exchange-correlation energy Exc[n]. For the exchange energy Ex[n] the procedure is very simple, since the per-volume exchange energy of the homogeneous electron liquid is known exactly [5,6],
so that
This is the LDA for Ex.46 46 If one adds this term to the Thomas-Fermi expression (35) one obtains the so-called Thomas-Fermi-Dirac approximation to E[ n]. It one multiplies it with an adjustable parameter a one obtains the so-called Xa approximation to Exc[ n]. These approximations are not much used today in DFT.
For the correlation energy Ec[n] the situation is more complicated since  (n) is not known exactly: the determination of the correlation energy of a homogeneous interacting electron system (an electron liquid) is already a difficult many-body problem on its own! Early approximate expressions for
(n) is not known exactly: the determination of the correlation energy of a homogeneous interacting electron system (an electron liquid) is already a difficult many-body problem on its own! Early approximate expressions for  (n) were based on applying perturbation theory (e.g. the random-phase approximation) to this problem [89,90]. These approximations became outdated with the advent of highly precise Quantum Monte Carlo (QMC) calculations for the electron liquid, by Ceperley and Alder [91]. Modern expressions for
(n) were based on applying perturbation theory (e.g. the random-phase approximation) to this problem [89,90]. These approximations became outdated with the advent of highly precise Quantum Monte Carlo (QMC) calculations for the electron liquid, by Ceperley and Alder [91]. Modern expressions for  (n) [92-94] are parametrizations of these data. These expressions are implemented in most standard DFT program packages and in typical applications give almost identical results. On the other hand, the earlier parametrizations of the LDA, based on perturbation theory [89,90], can occasionally deviate substantially from the QMC ones, and are better avoided.
(n) [92-94] are parametrizations of these data. These expressions are implemented in most standard DFT program packages and in typical applications give almost identical results. On the other hand, the earlier parametrizations of the LDA, based on perturbation theory [89,90], can occasionally deviate substantially from the QMC ones, and are better avoided.
Independently of the parametrization, the LDA for Exc[n] formally consists in47 47 Sometimes one uses the per-particle instead of the per-volume energy of the homogeneous system in writing the LDA. Since the conversion factor between both is the number of particles per volume, i.e., the density, an additional n( r) then appears under the integrals in (84) and also contributes to (85).
where  . The corresponding xc potential is simply
. The corresponding xc potential is simply
This approximation for Exc[n] has proved amazingly successful, even when applied to systems that are quite different from the electron liquid that forms the reference system for the LDA. A partial explanation for this success of the LDA is systematic error cancellation: typically, LDA underestimates Ec but overestimates Ex, resulting in unexpectedly good values of Exc. This error cancellation is not accidental, but systematic, and caused by the fact that for any density the LDA xc hole satisfies the correct sum rule òd3r'  (r,r') = -1 (see Sec. IV A2), which is only possible if integrated errors in
(r,r') = -1 (see Sec. IV A2), which is only possible if integrated errors in  cancel with those of
cancel with those of  .
.
For many decades the LDA has been applied in, e.g., calculations of band structures and total energies in solid-state physics. In quantum chemistry it is much less popular, because it fails to provide results that are accurate enough to permit a quantitative discussion of the chemical bond in molecules (so-called 'chemical accuracy' requires calculations with an error of not more than about 1 kcal/mol = 0.04336 eV/particle).
At this stage it may be worthwhile to recapitulate what practical DFT does, and where the LDA enters its conceptual structure: What real systems, such as atoms, molecules, clusters and solids, have in common, is that they are simultaneously inhomogeneous (the electrons are exposed to spatially varying electric fields produced by the nuclei) and interacting (the electrons interact via the Coulomb interaction). The way density-functional theory, in the local-density approximation, deals with this inhomogeneous many-body problem is by decomposing it into two simpler (but still highly nontrivial) problems: the solution of a spatially homogeneous interacting problem (the homogeneous electron liquid) yields the uniform xc energy  (n), and the solution of a spatially inhomogeneous noninteracting problem (the inhomogeneous electron gas described by the KS equations) yields the particle density. Both steps are connected by the local-density potential (85), which shows how the xc energy of the uniform interacting system enters the equations for the inhomogeneous noninteracting system.
(n), and the solution of a spatially inhomogeneous noninteracting problem (the inhomogeneous electron gas described by the KS equations) yields the particle density. Both steps are connected by the local-density potential (85), which shows how the xc energy of the uniform interacting system enters the equations for the inhomogeneous noninteracting system.
The particular way in which the inhomogeneous many-body problem is decomposed, and the various possible improvements on the LDA, are behind the success of DFT in practical applications of quantum mechanics to real materials. Some such improvements on the LDA are discussed in the next two sections.
B. Semilocal functionals: GEA, GGA and beyond
In the LDA one exploits knowledge of the density at point r. Any real system is spatially inhomogeneous, i.e., it has a spatially varying density n(r), and it would clearly be useful to also include information on the rate of this variation in the functional. A first attempt at doing this were the so-called 'gradient-expansion approximations' (GEA). In this class of approximation one tries to systematically calculate gradient-corrections of the form |Ñn(r)|, |Ñn(r)|2, Ñ2n(r), etc., to the LDA. A famous example is the lowest-order gradient correction to the Thomas-Fermi approximation for Ts[n],
This second term on the right-hand side is called the Weizsäcker term.48 48 If one adds this term to the Thomas-Fermi expression (35) one obtains the so-called Thomas-Fermi-Weizsäcker approximation to E[ n]. In a systematic gradient expansion the 8 in the denominator is replaced by a 72 [5,6]. Similarly, in
the second term on the right-hand side is the lowest-order gradient correction49
49
Remarkably, the form of this term is fully determined already by dimensional analysis: In
=
q
2ò
d
3
r f(
n,| Ñ
n|
2) the function
f must have dimensions (length)
-4. Since the dimensions of
n and |Ñ
n|
2 are (length)
-3 and (length)
-8, respectively, and to second order no higher powers or higher derivatives of n are allowed, the only possible combination is
f µ |Ñ
n(
r)|
2/
n
4/3.
to  [n]. In practice, the inclusion of low-order gradient corrections almost never improves on the LDA, and often even worsens it. Higher-order corrections (e.g., µ |Ñn(r)|a or µ Ñbn(r) with a,b > 2), on the other hand, are exceedingly difficult to calculate, and little is known about them.
[n]. In practice, the inclusion of low-order gradient corrections almost never improves on the LDA, and often even worsens it. Higher-order corrections (e.g., µ |Ñn(r)|a or µ Ñbn(r) with a,b > 2), on the other hand, are exceedingly difficult to calculate, and little is known about them.
In this situation it was a major breakthrough when it was realized, in the early eighties, that instead of power-series-like systematic gradient expansions one could experiment with more general functions of n(r) and Ñ n(r), which need not proceed order by order. Such functionals, of the general form
have become known as generalized-gradient approximations (GGAs) [95].
Different GGAs differ in the choice of the function f(n,Ñn). Note that this makes different GGAs much more different from each other than the different parametrizations of the LDA: essentially there is only one correct expression for  (n), and the various parametrizations of the LDA [89,90,92-94] are merely different ways of writing it. On the other hand, depending on the method of construction employed for obtaining f(n,Ñn) one can obtain very different GGAs. In particular, GGAs used in quantum chemistry typically proceed by fitting parameters to test sets of selected molecules. On the other hand, GGAs used in physics tend to emphasize exact constraints. Nowadays the most popular (and most reliable) GGAs are PBE (denoting the functional proposed in 1996 by Perdew, Burke and Ernzerhof [96]) in physics, and BLYP (denoting the combination of Becke's 1988 exchange functional [97] with the 1988 correlation functional of Lee, Yang and Parr [98]) in chemistry. Many other GGA-type functionals are also available, and new ones continue to appear.
(n), and the various parametrizations of the LDA [89,90,92-94] are merely different ways of writing it. On the other hand, depending on the method of construction employed for obtaining f(n,Ñn) one can obtain very different GGAs. In particular, GGAs used in quantum chemistry typically proceed by fitting parameters to test sets of selected molecules. On the other hand, GGAs used in physics tend to emphasize exact constraints. Nowadays the most popular (and most reliable) GGAs are PBE (denoting the functional proposed in 1996 by Perdew, Burke and Ernzerhof [96]) in physics, and BLYP (denoting the combination of Becke's 1988 exchange functional [97] with the 1988 correlation functional of Lee, Yang and Parr [98]) in chemistry. Many other GGA-type functionals are also available, and new ones continue to appear.
Quite generally, current GGAs seem to give reliable results for all main types of chemical bonds (covalent, ionic, metallic and hydrogen bridge). For van der Waals interactions, however, common GGAs and LDA fail.50 50 The PBE GGA [96] and the TPSS MGGA [2] (see below) may be partial exceptions [99,100] because they work reasonably well near the equilibrium distance of the van der Waals bond, but they recover only the short-range behaviour and do not describe correctly the long-range asymptotic regime of the van der Waals interaction. To describe these very weak interactions several more specialized approaches have been developed within DFT [101-105]. Both in physics and in chemistry the widespread use of GGAs has lead to major improvements as compared to LDA. 'Chemical accuracy', as defined above, has not yet been attained, but is not too far away either. A useful collection of explicit expressions for some GGAs can be found in the appendix of Ref. [106], and more detailed discussion of some selected GGAs and their performance is given in Ref. [107] and in the chapter of Kurth and Perdew in Refs. [15,16].
No systematic attempt at comparing explicit functionals can be made here, but many detailed comparisons are available in the literature. For pure illustrative purposes only, Table I contains ground-state energies of the Ar atom, obtained with several of the methods discussed previously in this chapter. Footnote 7 contains additional information on the performance of DFT for larger systems.
C. Orbital functionals and other nonlocal approximations: hybrids, Meta-GGA, SIC, OEP, etc.
In spite of these advances, the quest for more accurate functionals goes ever on, and both in chemistry and physics various beyond-GGA functionals have appeared. Perhaps the most popular functional in quantum chemistry51 51 This was written in early 2002, but at the time of revision of this text in 2006 it is still correct. is B3LYP. This is a combination of the LYP GGA for correlation [98] with Becke's three-parameter hybrid functional B3 for exchange [108]. Common hybrid functionals, such as B3, mix a fraction of Hartree-Fock exchange into the DFT exchange functional (other mixtures are also possible). The construction of hybrid functional involves a certain amount of empiricism in the choice of functionals that are mixed and in the optimization of the weight factors given to the HF and DFT terms. Formally, this might be considered a drawback, but in practice B3 has proven to be the most successful exchange functional for chemical applications, in particular when combined with the LYP GGA functional for Ec. More extreme examples of this semiempirical mode of construction of functionals are Becke's 1997 hybrid functional [109], which contains 10 adjustable parameters, and the functionals of Refs. [110] and [111], each of which contains 21 parameters.
Another recent beyond-GGA development is the emergence of so-called Meta-GGAs, which depend, in addition to the density and its derivatives, also on the Kohn-Sham kinetic-energy density t(r) [2,112,113]
so that Exc can be written as Exc[n(r),Ñn(r),t(r)]. The additional degree of freedom provided by t is used to satisfy additional constraints on Exc, such as a self-interaction-corrected correlation functional, recovery of the fourth-order gradient expansion for exchange in the limit of slowly varying densities, and a finite exchange potential at the nucleus [2]. In several recent tests [2,100,114-116] Meta-GGAs have given favorable results, even when compared to the best GGAs, but the full potential of this type of approximation is only beginning to be explored systematically.
As we have seen in the case of Ts, it can be much easier to represent a functional in terms of single-particle orbitals than directly in terms of the density. Such functionals are known as orbital functionals, and Eq. (54) constitutes a simple example. Another important orbital-dependent functional is the exchange energy (Fock term) of Eq. (56). The Meta-GGAs and hybrid functionals mentioned above are also orbital functionals, because they depend on the kinetic energy density (89), and on a combination of the orbital functional (56) with ordinary GGAs, respectively.
Still another type of orbital functional is the self-interaction correction (SIC). Most implementations of SIC make use of the expressions proposed in Ref. [93] (PZ-SIC),
which subtracts, orbital by orbital, the contribution the Hartree and the xc functionals would make if there was only one electron in the system. This correction can be applied on top of any approximate density functional, and ensures that the resulting corrected functional satisfies  [n(1),0] = -EH[n(1)] for a one-electron system. The LDA is exact for a completely uniform system, and thus is self-interaction free in this limit, but neither it nor common GGAs satisfy the requirement of freedom from self-interaction in general, and even Meta-GGAs have a remaining self-interaction error in their exchange part [2,112]. This self-interaction is particularly critical for localized states, such as the d states in transition-metal oxides. For such systems PZ-SIC has been shown to greatly improve the uncorrected LDA [71,72], but for thermochemistry PZ-SIC does not seem to be significant [117].
[n(1),0] = -EH[n(1)] for a one-electron system. The LDA is exact for a completely uniform system, and thus is self-interaction free in this limit, but neither it nor common GGAs satisfy the requirement of freedom from self-interaction in general, and even Meta-GGAs have a remaining self-interaction error in their exchange part [2,112]. This self-interaction is particularly critical for localized states, such as the d states in transition-metal oxides. For such systems PZ-SIC has been shown to greatly improve the uncorrected LDA [71,72], but for thermochemistry PZ-SIC does not seem to be significant [117].
Unfortunately the PZ-SIC approach, which minimizes the corrected energy functional with respect to the orbitals, does not lead to Kohn-Sham equations of the usual form, because the resulting effective potential is different for each orbital. As a consequence, various specialized algorithms for minimizing the PZ-SIC energy functional have been developed. For more details on these algorithms and some interesting applications in solid-state physics see Refs. [71-73]. For finite systems, PZ-SIC has also been implemented by means of the OEP [64,74], which produces a common local potential for all orbitals, and is discussed in the next paragraph. A detailed review of implementations and applications of PZ-SIC can be found in the contribution of Temmerman et al. in Ref. [17]. Alternatives to the PZ-SIC formulation of Ref. [93] have recently been analysed in [118,119], with a view on either improving results obtained with PZ-SIC, or simplifying the implementation of the correction.
Since hybrid functionals, Meta-GGAs, SIC, the Fock term and all other orbital functionals depend on the density only implicitly, via the orbitals fi[n], it is not possible to directly calculate the functional derivative vxc = dExc/dn. Instead one must use indirect approaches to minimize E[n] and obtain vxc. In the case of the kinetic-energy functional Ts[{fi[n]}] this indirect approach is simply the Kohn-Sham scheme, described in Sec. IV. In the case of orbital expressions for Exc the corresponding indirect scheme is known as the optimized effective potential (OEP) [120] or, equivalently, the optimized-potential model (OPM) [121]. The minimization of the orbital functional with respect to the density is achieved by repeated application of the chain rule for functional derivatives,
where  is the orbital functional (e.g., the Fock term) and vs the KS effective potential. Further evaluation of Eq. (91) gives rise to an integral equation that determines the vxc[n] belonging to the chosen orbital functional Exc[{fi[n]}] [120,122]. As an alternative to solving the full OEP integral equation, Krieger, Li and Iafrate (KLI) have proposed a simple but surprisingly accurate approximation that greatly facilitates implementation of the OEP [120].
is the orbital functional (e.g., the Fock term) and vs the KS effective potential. Further evaluation of Eq. (91) gives rise to an integral equation that determines the vxc[n] belonging to the chosen orbital functional Exc[{fi[n]}] [120,122]. As an alternative to solving the full OEP integral equation, Krieger, Li and Iafrate (KLI) have proposed a simple but surprisingly accurate approximation that greatly facilitates implementation of the OEP [120].
The application of the OEP methodology to the Fock term (56), either with or without the KLI approximation, is also known as the exact-exchange method (EXX). The OEP-EXX equations have been solved for atoms [120,121,123] and solids [124,125], with very encouraging results. Other orbital-dependent functionals that have been treated within the OEP scheme are the PZ self-interaction correction [64,74] and the Colle-Salvetti functional []. A detailed review of the OEP and its KLI approximation is Ref. [122].
The high accuracy attained by complex orbital functionals implemented via the OEP, and the fact that it is easier to devise orbital functionals than explicit density functionals, makes the OEP concept attractive, but the computational cost of solving the OEP integral equation is a major drawback. However, this computational cost is significantly reduced by the KLI approximation [120] and other recently proposed simplifications [126-128]. In the context of the EXX method (i.e., using the Fock exchange term as orbital functional) the OEP is a viable way to proceed. For more complex orbital functionals, additional simplifications may be necessary [120,126-128].
A further reduction of computational complexity is achieved by not evaluating the orbital functional self-consistently, via Eq. (91), but only once, using the orbitals and densities of a converged self-consistent LDA or GGA calculation. This 'post-GGA' or 'post-LDA' strategy completely avoids the OEP and has been used both for hybrid functionals and Meta-GGAs [108,109,112,113]. A drawback of post methods is that they provide only approximations to the selfconsistent total energies, not to eigenvalues, effective potentials, orbitals or densities.
In the case of hybrid functionals, still another mode of implementation has become popular. This alternative, which also avoids solution of Eq. (91), is to calculate the derivative of the hybrid functional with respect to the single-particle orbitals, and not with respect to the density as in (91). The resulting single-particle equation is of Hartree-Fock form, with a nonlocal potential, and with a weight factor in front of the Fock term. Strictly speaking, the orbital derivative is not what the HK theorem demands, but rather a Hartree-Fock like procedure, but in practice it is a convenient and successful approach. This scheme, in which self-consistency is obtained with respect to the single-particle orbitals, can be considered an evolution of the Hartree-Fock Kohn-Sham method [6], and is how hybrids are commonly implemented. Recently, it has also been used for Meta-GGAs [2]. For occupied orbitals, results obtained from orbital selfconsistency differ little from those obtained from the OEP.
Apart from orbital functionals, which are implicit nonlocal density functionals because the orbitals depend on the density in a nonlocal way, there is also a class of explicit nonlocal density functionals. Such nonlocal density functionals take into account, at any point r, not only the density at that point, n(r), and its derivatives, Ñn(r) etc., but also the behaviour of the density at different points r' ¹ r, by means of integration over physically relevant regions of space. A typical example is
where  is the per-particle xc energy of the homogeneous electron liquid (see footnote 47). In the LDA one would have
is the per-particle xc energy of the homogeneous electron liquid (see footnote 47). In the LDA one would have  (r) º n(r), but in the average-density approximation (ADA) one takes [129]
(r) º n(r), but in the average-density approximation (ADA) one takes [129]
where w[n](|r-r'|) is a weight function that samples the density not only semilocally, as do the GGAs, but over a volume determined by the range of w. Conceptually similar to the ADA is the weighted-density approximation (WDA) [129]. In terms of the pair-correlation function (see Secs. III E2 and IV A2) the LDA, ADA and WDA functionals can be written as
where in each case
hom(r-r') is the pair-correlation function of the homogeneous electron liquid, averaged over the coupling constant e2 [5,6]. The dependence of these functionals on  (r), the integral over n(r), instead of on derivatives, as in the GGAs, is the reason why such functionals are called nonlocal. In practice, this integral turns the functionals computationally expensive, and in spite of their great promise they are much less used than GGAs. However, recent comparisons of ADA and WDA with LDA and GGAs for low-dimensional systems [114,130] and for bulk silicon [131] show that nonlocal integral-dependent density functionals can outperform local and semilocal approximations.
(r), the integral over n(r), instead of on derivatives, as in the GGAs, is the reason why such functionals are called nonlocal. In practice, this integral turns the functionals computationally expensive, and in spite of their great promise they are much less used than GGAs. However, recent comparisons of ADA and WDA with LDA and GGAs for low-dimensional systems [114,130] and for bulk silicon [131] show that nonlocal integral-dependent density functionals can outperform local and semilocal approximations.
IV. EXTENSIONS OF DFT: NEW FRONTIERS AND OLD PROBLEMS
Up to this point we have discussed DFT in terms of the charge (or particle) density n(r) as fundamental variable. In order to reproduce the correct charge density of the interacting system in the noninteracting (Kohn-Sham) system, one must apply to the latter the effective KS potential vs = v + vH + vxc, in which the last two terms simulate the effect of the electron-electron interaction on the charge density. This form of DFT, which is the one proposed originally [24], could also be called 'charge-only' DFT. It is not the most widely used DFT in practical applications. Much more common is a formulation that employs one density for each spin,  (r) and
(r) and  (r), i.e, works with two fundamental variables. In order to reproduce both of these in the noninteracting system one must now apply two effective potentials,
(r), i.e, works with two fundamental variables. In order to reproduce both of these in the noninteracting system one must now apply two effective potentials,  (r) and
(r) and  (r).52
52
More generally, one requires one effective potential for each density-like quantity to be reproduced in the KS system. Such potentials and corresponding densities are called conjugate variables.
This formulation of DFT is known as spin-DFT (SDFT) [89,90]. Its fundamental variables
(r).52
52
More generally, one requires one effective potential for each density-like quantity to be reproduced in the KS system. Such potentials and corresponding densities are called conjugate variables.
This formulation of DFT is known as spin-DFT (SDFT) [89,90]. Its fundamental variables  (r) and
(r) and  (r) can be used to calculate the charge density n(r) and the spin-magnetization density m(r) from
(r) can be used to calculate the charge density n(r) and the spin-magnetization density m(r) from
where µ0 = q /2mc is the Bohr magneton. More generally, the Hohenberg-Kohn theorem of SDFT states that in the presence of a magnetic field B(r) that couples only to the electron spin [via the familiar Zeeman term òd3r m(r)B(r)] the ground-state wave function and all ground-state observables are unique functionals of n and m or, equivalently, of
/2mc is the Bohr magneton. More generally, the Hohenberg-Kohn theorem of SDFT states that in the presence of a magnetic field B(r) that couples only to the electron spin [via the familiar Zeeman term òd3r m(r)B(r)] the ground-state wave function and all ground-state observables are unique functionals of n and m or, equivalently, of  and
and  .53
53
In the particular case
B = 0 the SDFT HK theorem still holds and continues to be useful, e.g., for systems with spontaneous polarization. In principle one could also use 'charge-only' DFT to study such systems, but then
(
r) and
(
r) become functionals of
n(
r) and nobody knows how to determine these functionals.
Almost the entire further development of the HK theorem and the KS equations can be immediately rephrased for SDFT, just by attaching a suitable spin index to the densities. For this reason we could afford the luxury of exclusively discussing 'charge-only' DFT in the preceding sections, without missing any essential aspects of SDFT.
.53
53
In the particular case
B = 0 the SDFT HK theorem still holds and continues to be useful, e.g., for systems with spontaneous polarization. In principle one could also use 'charge-only' DFT to study such systems, but then
(
r) and
(
r) become functionals of
n(
r) and nobody knows how to determine these functionals.
Almost the entire further development of the HK theorem and the KS equations can be immediately rephrased for SDFT, just by attaching a suitable spin index to the densities. For this reason we could afford the luxury of exclusively discussing 'charge-only' DFT in the preceding sections, without missing any essential aspects of SDFT.
There are, however, some exceptions to this simple rule. One is the fourth statement of the HK theorem, as discussed in Sec. III B. Another is the construction of functionals. For the exchange energy it is known, e.g., that [132]
In analogy to the coordinate scaling of Eqs. (59) - (61), this property is often called 'spin-scaling', and it can be used to construct an SDFT exchange functional from a given DFT exchange functional. In the context of the LSDA, von Barth and Hedin [89] wrote the exchange functional in terms of an interpolation between the unpolarized and fully polarized electron gas which by construction satisfies Eq. (99). Alternative interpolation procedures can be found in Ref. [92]. GGA exchange functionals also satisfy Eq. (99) by construction. For the correlation energy no scaling relation of the type (99) holds, so that in practice correlation functionals are either directly constructed in terms of the spin densities or written by using, without formal justification, the same interpolation already used in the exchange functional. In the case of the LSDA this latter procedure was introduced in Ref. [89], and further analysed and improved in Ref. [92].
The Kohn-Sham equations of SDFT are
where vss(r) = vs(r) + vH(r)+ vxc,s(r). In a nonrelativistic calculation the Hartree term does not depend on the spin label,54 54 Spin-spin dipolar interactions are a relativistic effect of order (1/ c) 2, as are current-current interactions. but in the presence of an externally applied magnetic field vs(r) = v(r)- sm0B (where s = ±1). Finally,
In the presence of an internal magnetic field Bxc (i.e., in spin-polarized systems)  = µ0Bxc. This field is the origin of, e.g., ferromagnetism in transition metals. References to recent work with SDFT include almost all practical DFT calculation: SDFT is by far the most widely used form of DFT.55
55
SDFT has become synonymous with DFT to such an extent that often no distinction is made between the two, i.e., a calculation referred to as a DFT one is most of the time really an SDFT one.
Some recent work on SDFT is described in Ref. [133]. A more detailed discussion of SDFT can be found in Refs. [5,6,90], and a particularly clear exposition of the construction of xc functionals for SDFT is the contribution of Kurth and Perdew in Refs. [15,16].
= µ0Bxc. This field is the origin of, e.g., ferromagnetism in transition metals. References to recent work with SDFT include almost all practical DFT calculation: SDFT is by far the most widely used form of DFT.55
55
SDFT has become synonymous with DFT to such an extent that often no distinction is made between the two, i.e., a calculation referred to as a DFT one is most of the time really an SDFT one.
Some recent work on SDFT is described in Ref. [133]. A more detailed discussion of SDFT can be found in Refs. [5,6,90], and a particularly clear exposition of the construction of xc functionals for SDFT is the contribution of Kurth and Perdew in Refs. [15,16].
If the direction of the spins is not uniform in space56 56 Such 'noncollinear magnetism' appears, e.g., as canted or helical spin configurations in rare-earth compounds, or as domain walls in ferromagnets. one requires a formulation of SDFT in which the spin magnetization is not a scalar, as above, but a three-component vector m(r). Different proposals for extending SDFT to this situation are available [134-136]. One mechanism that can give rise to noncollinear magnetism is spin-orbit coupling. This is another relativistic effect [28], and as such it is not consistently treated in either DFT or SDFT. A generalization of DFT that does account for spin-orbit coupling and other relativistic effects is relativistic DFT (RDFT) [137,138]. Here the fundamental variable is the relativistic four-component current jm. RDFT requires a more drastic reformulation of DFT than does SDFT. In particular, the KS equation of RDFT is now of the form of the single-particle Dirac equation, instead of the Schrödinger equation. There are also many subtle questions involving renormalizability and the use of the variational principle in the presence of negative energy states. For details on these problems and their eventual solution the reader is referred to the chapters by Engel et al. in Refs. [10] and [19], and to the book by Eschrig [18]. A didactical exposition of RDFT, together with representative applications in atomic and condensed-matter physics, can be found in the book by Strange [28], and a recent numerical implementation is presented in Ref. [139].
To study the magnetic properties of matter one would often like to be able to obtain information on the currents in the system and their coupling to possible external magnetic fields. Important classes of experiments for which this information is relevant are nuclear magnetic resonance and the quantum Hall effects. SDFT does not provide explicit information on the currents. RDFT in principle does, but standard implementations of it are formulated in a spin-only version, which prohibits extraction of information on the currents. Furthermore, the formalism of RDFT is considerably more complicated than that of SDFT. In this situation the formulation of nonrelativistic current-DFT (CDFT), accomplished by Vignale and Rasolt [140,141], was a major step forward. CDFT is formulated explicitly in terms of the (spin) density and the nonrelativistic paramagnetic current density vector jp(r). Some recent applications of CDFT are Refs. [142-145]. E. K. U. Gross and the author have shown that the existence of spin currents implies the existence of a link between the xc functionals of SDFT and those of CDFT [146]. Conceptually, this link is similar to the one of Eq. (99) between functionals of DFT and SDFT, but the details are quite different. Some approximations for xc functionals of CDFT are discussed in Refs. [146-148].
In addition to SDFT, RDFT and CDFT, there exist many other generalizations of DFT that were designed for one or other special purpose. As examples we mention superconductivity [149-152] and spin-density waves [136,153], but there are many more [5-19]. For reasons of space we cannot discuss these extensions here. Instead, let us take a brief look at a problem that requires more radical departures from the framework of conventional DFT: excited states. DFT is formulated in terms of ground-state densities, and it is not immediately obvious how one could extract information on excited states from them (although at least in the case of 'charge-only' DFT the fourth substatement of the HK theorem guarantees that this must be possible).
Apart from the ad hoc identification of the KS eigenvalues with true excitation energies, there exists a considerable variety of more sound approaches to excited states in DFT that have met with some success. The early suggestion of Gunnarsson and Lundqvist [90] to use a symmetry-dependent xc functional to calculate the lowest-energy excited state of each symmetry class has been implemented approximately by von Barth [154], but suffers from lack of knowledge on the symmetry dependence of the functional. More recent work on this dependence is Ref. [155]. An alternative approach to excited states, not restricted to the lowest energy state of a given symmetry, is ensemble DFT, developed by Theophilou [26] and further elaborated by Oliveira, Gross and Kohn [156]. In this formalism the functional depends on the particular choice for the ensemble, and a simple approximation for this dependence is available [156]. Some applications of this method have been worked out by Nagy [157].
Other DFT approaches to excited states can be found in Refs. [158], [159], [160] and [31], but the most widely used method today is time-dependent DFT (TD-DFT). The time-dependent generalization of the HK theorem, the Runge-Gross theorem, cannot be proven along the lines of the original HK theorem, but requires a different approach [51,161]. For recent reviews of TD-DFT see Ref. [162]. Excited states have first been extracted from TD-DFT in Refs. [163,164]. This approach is now implemented in standard quantum-chemical DFT program packages [165,166] and is increasingly applied also in solid-state physics [70]. Another important application of TD-DFT is to systems in external time-dependent fields, such as atoms in strong laser fields [167,168]. First steps towards studying dynamical magnetic phenomena with TD-SDFT have been taken very recently [169].
All these extensions of DFT to time-dependent, magnetic, relativistic and a multitude of other situations involve more complicated Hamiltonians than the basic ab initio many-electron Hamiltonian defined by Eqs. (2) to (6). Instead of attempting to achieve a more complete description of the many-body system under study by adding additional terms to the Hamiltonian, it is often advantageous to employ the opposite strategy, and reduce the complexity of the ab initio Hamiltonian by replacing it by simpler models, which focalize on specific aspects of the full many-body problem. Density-functional theory can be applied to such model Hamiltonians, too, once a suitable density-like quantity has been identified as basic variable. Following pioneering work by Gunnarsson and Schönhammer [170], LDA-type approximations have, e.g., recently been formulated and exploited for the Hubbard [171], the delta-interaction [172] and the Heisenberg [173] models. Common aspects and potential uses of DFT for model Hamiltonians are described in [174].
Still another way of using DFT, which does not depend directly on approximate solution of Kohn-Sham equations, is the quantification and clarification of traditional chemical concepts, such as electronegativity [6], hardness, softness, Fukui functions, and other reactivity indices [6,175], or aromaticity [176]. The true potential of DFT for this kind of investigation is only beginning to be explored, but holds much promise.
All extensions of DFT face the same formal questions (e.g., simultaneous interacting and noninteracting v-representability of the densities, nonuniqueness of the KS potentials, meaning of the KS eigenvalues) and practical problems (e.g., how to efficiently solve the KS equations, how to construct accurate approximations to Exc, how to treat systems with very strong correlations) as do the more widely used formulations 'charge-only' DFT and SDFT. These questions and problems, however, have never stopped DFT from advancing, and at present DFT emerges as the method of choice for solving a wide variety of quantum mechanical problems in chemistry and physics and in many situations, such as large and inhomogeneous systems, it is the only applicable first-principles method at all.
The future of DFT is bright [3,61,177] but to be able to contribute to it, the reader must now leave the present superficial overview behind, and turn to the more advanced treatments available in the literature [5-19].
Acknowledgments
The author has learned density-functional theory from E. K. U. Gross, and then practiced it in collaborations with B. L. Györffy, L. N. Oliveira, and G. Vignale. These scholars are in no way responsible for the content of this work, but the author's intellectual debt to them is enormous. Useful comments by J. Quintanilla, H. J. P. Freire, T. Marcasso, E. Orestes, N. A. Lima, N. Argaman, V. L. Líbero, V. V. França, M. Odashima, J. M. Morbec, A. P. Fávaro, A. J. R. da Silva and L. N. Oliveira on earlier versions of this manuscript are gratefully acknowledged. This work was supported financially by FAPESP and CNPq.
[1] Proceedings of the VIII'th Brazilian Summer School on Electronic Structure (2002), eds. H. F. Santos, P. Z. Coura, S. O. Dantas and P. M. V. B. Barone.
[2] J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett. 91, 146401 (2003); J. Chem. Phys. 119, 12129 (2003); J. Chem. Phys. 120, 6898 (2004); Phys. Rev. B 69, 075102 (2004).
[3] W. Kohn, Rev. Mod. Phys. 71, 1253 (1999).
[4] J. A. Pople, Rev. Mod. Phys. 71, 1267 (1999).
[5] R. M. Dreizler and E. K. U. Gross, Density Functional Theory (Springer, Berlin, 1990).
[6] R. G. Parr and W. Yang, Density-Functional Theory of Atoms and Molecules (Oxford University Press, Oxford, 1989).
[7] W. Koch and M. C. Holthausen, A Chemist's Guide to Density Functional Theory (John Wiley & Sons, New York, 2001).
[8] R. O. Jones and O. Gunnarsson, Rev. Mod. Phys. 61, 689 (1989).
[9] J. M. Seminario (Ed.), Recent Developments and Applications of Modern DFT (Elsevier, Amsterdam, 1996).
[10] R. F. Nalewajski (Ed.), Density Functional Theory I -IV (Springer, Topics in Current Chemistry Vols. 180-183, 1996).
[11] V. I. Anisimov (Ed.), Strong Coulomb Correlations in Electronic Structure Calculations: Beyond the Local Density Approximation (Gordon & Breach, 1999).
[12] N. H. March, Electron Density Theory of Atoms and Molecules (Academic Press, London, 1992).
[13] B. B. Laird, R. B. Ross and T. Ziegler (Eds.), Chemical Applications of Density Functional Theory, (American Chemical Society, 1996).
[14] D. P. Chong (Ed.), Recent Advances in Density Functional Methods (Singapore, World Scientific, 1995).
[15] D. Joulbert (Ed.), Density Functionals: Theory and Applications (Springer Lecture Notes in Physics Vol. 500, 1998)
[16] C. Fiolhais, F. Nogueira and M. Marques (Eds.), A Primer in Density Functional Theory (Springer Lecture Notes in Physics Vol. 620, 2003).
[17] J. F. Dobson, G. Vignale and M. P. Das (Eds.), Density Functional Theory: Recent Progress and New Directions (Plenum, New York, 1998).
[18] H. Eschrig, The Fundamentals of Density Functional Theory (Teubner, Leipzig, 1996).
[19] E. K. U. Gross and R. M. Dreizler (Eds.), Density Functional Theory (Plenum, New York, 1995).
[20] N. Argaman and G. Makov, Am. J. Phys. 68, 69 (2000).
[21] E. N. Economou, Green's Functions in Quantum Physics (Springer, New York, 1979).
[22] M. Levy, Phys. Rev. A 26, 1200 (1982).
[23] E. H. Lieb in Density Functional Methods in Physics, edited by R. M. Dreizler and J. da Providencia, (Plenum, New York, 1985).
[24] P. Hohenberg and W. Kohn, Phys. Rev. 136, B864 (1964).
[25] E. Schrödinger, Ann. Physik 79, 361, 489, 734 (1926); 80, 437 (1926); 81, 109 (1926).
[26] A. K. Theophilou, J. Phys. C 12, 5419 (1979).
[27] O. Gritsenko and E. J. Baerends, J. Chem. Phys. 120, 8364 (2004).
[28] P. Strange, Relativistic Quantum Mechanics with Applications in Condensed Matter and Atomic Physics (Cambridge University Press, Cambridge, 1998).
[29] T. Kato, Commun. Pure Appl. Math. 10, 151 (1957).
[30] N. H. March, Self-consistent fields in atoms (Pergamon Press, Oxford, 1975).
[31] J. P. Perdew and M. Levy, Phys. Rev. B 31, 6264 (1985).
[32] H. Eschrig and W. E. Pickett, Solid State Commun. 118, 123 (2001).
[33] K. Capelle and G. Vignale, Phys. Rev. Lett. 86, 5546 (2001).
[34] K. Capelle and G. Vignale, Phys. Rev. B 65, 113106 (2002).
[35] N. Argaman and G. Makov, Phys. Rev. B 66, 052413 (2002).
[36] N. Gidopolous in The fundamentals of density matrix and density functional theory in atoms, molecules and solids, N. Gidopoulos and S. Wilson eds. (Kluwer Series 'Progress in Theoretical Chemistry and Physics', 2003); and cond-mat/0510199.
[37] W. Kohn, A. Savin and C. A. Ullrich, Int. J. Quantum Chem. 100, 20 (2004).
[38] C. A. Ullrich, Phys. Rev. B 72, 073102 (2005).
[39] T. L. Gilbert, Phys. Rev. B 12, 2111 (1975).
[40] J. E. Harriman, Phys. Rev. A 24, 680 (1981).
[41] J. T. Chayes, L. Chayes and M. B. Ruskai, J. Stat. Phys. 38, 497 (1985).
[42] C. A. Ullrich and W. Kohn, Phys. Rev. Lett. 89, 156401 (2002); ibid 87, 093001 (2001).
[43] P. E. Lammert, J. Chem. Phys. 125, 074114 (2006).
[44] A. P. Favaro, J. V. Batista Ferreira and K. Capelle, Phys. Rev. B 73, 045133 (2006).
[45] L. W. Wang and M. P. Teter, Phys. Rev. B 45, 13196 (1992).
[46] M. Foley and P. A. Madden, Phys. Rev. B 53, 10589 (1996).
[47] B. J. Zhou, V. L. Ligneres and E. A. Carter, J. Chem. Phys. 122, 044103 (2005).
[48] E. K. U. Gross, E. Runge and O. Heinonen, Many Particle Theory (Adam Hilger, 1992).
[49] A. Szabo and N. S. Ostlund, Modern Quantum Chemistry (McGraw-Hill, New York, 1989).
[50] L. J. Sham and M. Schlüter, Phys. Rev. Lett. 51, 1888 (1983).
[51] E. Runge and E. K. U. Gross, Phys. Rev. Lett. 52, 997 (1984).
[52] E. K. U. Gross, M. Petersilka and T. Grabo in Ref. [13].
[53] P. Nozieres and D. Pines, The Theory of Quantum Liquids (Addison Wesley, New York, revised printing 1989).
[54] N. D. Mermin, Phys. Rev. 137, 1441 (1965).
[55] M. Levy and J. P. Perdew, Phys. Rev. A 32, 2010 (1985).
[56] E. H. Lieb and S. Oxford, Int. J. Quantum Chem. 19, 427 (1981).
[57] G. K.-L. Chan and N. C. Handy, Phys. Rev. A 59, 3075 (1999).
[58] J. P. Perdew, R. G. Parr, M. Levy and J. L. Balduz, Phys. Rev. Lett. 49, 1691 (1982).
[59] J. P. Perdew and M. Levy, Phys. Rev. Lett. 51, 1884 (1983).
[60] W. Kohn and L. J. Sham, Phys. Rev. 140, A1133 (1965).
[61] W. Kohn, A. D. Becke and R. G. Parr, J. Phys. Chem. 100, 12974 (1996).
[62] C. O. Almbladh and U. v. Barth, Phys. Rev. B 31, 3231 (1985).
[63] M. Levy, J. P. Perdew and V. Sahni, Phys. Rev. A 30, 2745 (1984).
[64] J. Chen, J. B. Krieger, Y. Li and G. J. Iafrate, Phys. Rev. A 54, 3939 (1996).
[65] M. Lüders, A. Ernst, W. M. Temmerman, Z. Szotek and P. J. Durham, J. Phys. Cond. Mat. 13, 8587 (2001).
[66] J. Muskat, A. Wander, and N. M. Harrison, Chem. Phys. Lett. 342, 397 (2001).
[67] A. Savin, C. J. Umrigar and X. Gonze, Chem. Phys. Lett. 288, 391 (1998).
[68] W. G. Aulbur, L. Jönsson and J. W. Wilkins, Solid State Phys. 54, 1 (1999).
[69] F. Aryasetiawan and O. Gunnarsson, Rep. Prog. Phys. 61, 237 (1998).
[70] G. Onida, L. Reining and A. Rubio, Rev. Mod. Phys. 74, 601 (2002).
[71] A. Svane and O. Gunnarsson, Phys. Rev. Lett. 65, 1148 (1990); ibid 72, 1248 (1994).
[72] Z. Szotek, W. M. Temmermann and H. Winter, Phys. Rev. Lett. 72, 1244 (1994).
[73] P. Strange, A. Svane, W. M. Temmermann, Z. Szotek and H. Winter, Nature 399, 756 (1999).
[74] M. R. Norman and D. D. Koelling, Phys. Rev. B 30, 5530 (1984).
[75] O. K. Andersen, Phys. Rev. B 12, 3060 (1975).
[76] O. K. Andersen, O. Jepsen and D. Glötzel in Highlights of Condensed Matter Theory, F. Bassani, F. Funi and M. P. Tosi, eds. (North Holland, Amsterdam, 1985).
[77] O. K. Andersen and T. Saha-Dasgupta, Phys. Rev. B 62, 16219 (2000).
[78] E. Zurek, O. Jepsen and O. K. Andersen, Chem.Phys.Chem. 6, 1934 (2005).
[79] T. H. Dunning Jr., J. Chem. Phys. 90, 1007 (1989).
[80] A. B. F. da Silva, H. F. M. da Costa and M. Trsic, Mol. Phys. 68, 433 (1989).
[81] F. E. Jorge, E. V. R. de Castro and A. B. F. da Silva, J. Comp. Chem. 18, 1565 (1997).
[82] G. B. Bachelet, D. R. Hamann and M. Schlüter, Phys. Rev. B 25, 2103 (1982).
[83] L. Kleinman and D. M. Bylander, Phys. Rev. Lett. 48, 1425 (1982).
[84] D. Vanderbilt, Phys. Rev. B 41, 7892 (1990).
[85] N. Troullier and J. L. Martins, Phys. Rev. B 43, 1993 (1991).
[86] W. E. Pickett, Comp. Phys. Rep. 9, 116 (1989).
[87] D. Porezag, M. R. Pederson and A. Y. Liu, Phys. Stat. Sol. (b) 217, 219 (2000)
[88] M. C. Payne, M. P. Teter, D. C. Allan, T. A. Arias and J. D. Joannopoulos, Rev. Mod. Phys. 64, 1045 (1992).
[89] U. von Barth and L. Hedin, J. Phys. C 5, 1629 (1972).
[90] O. Gunnarsson and B. Lundqvist, Phys. Rev. B 13, 4274 (1976).
[91] D. M. Ceperley and B. J. Alder, Phys. Rev. Lett. 45, 566 (1980).
[92] S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys. 58, 1200 (1980).
[93] J. P. Perdew and A. Zunger, Phys. Rev. B 23, 5048 (1981).
[94] J. P. Perdew and Y. Wang, Phys. Rev. B 45, 13244 (1992).
[95] J. P. Perdew and Y. Wang, Phys. Rev. B 33, 8800 (1986).
[96] J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett. 77, 3865 (1996); ibid 78, 1396(E) (1997). See also V. Staroverov et al., Phys. Rev. A 74, 044501 (2006).
[97] A. D. Becke, Phys. Rev. A 38, 3098 (1988).
[98] C. Lee, W. Yang and R. G. Parr, Phys. Rev. B 37, 785 (1988).
[99] D. C. Patton and M. R. Pederson, Phys. Rev. A 56, 2495 (1997).
[100] J. Tao and J. P. Perdew, J. Chem. Phys. 122, 114102 (2005).
[101] W. Kohn, Y. Meir and D. E. Makarov, Phys. Rev. Lett. 80, 4153 (1998).
[102] M. Lein, J. F. Dobson and E. K. U. Gross, J. Comp. Chem. 20, 12 (1999).
[103] J. F. Dobson and B. P. Dinte, Phys. Rev. Lett. 76, 1780 (1996).
[104] Y. Andersson, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett. 76, 102 (1996).
[105] E. R. Johnson and A. D. Becke, J. Chem. Phys. 123, 024101 (2005).
[106] C. Filippi, C. J. Umrigar and M. Taut, J. Chem. Phys. 100, 1290 (1994).
[107] P. Ziesche, S. Kurth and J. P. Perdew, Comp. Mat. Sci. 11, 122 (1998).
[108] A. D. Becke, J. Chem. Phys. 98, 5648 (1993).
[109] A. D. Becke, J. Chem. Phys. 107, 8554 (1997). See also A. D. Becke, J. Comp. Chem. 20, 63 (1999).
[110] D. J. Tozer and N. C. Handy, J. Chem. Phys. 108, 2545 (1998).
[111] T. van Voorhis and G. E. Scuseria, J. Chem. Phys. 109, 400 (1998).
[112] J. P. Perdew, S. Kurth, A. Zupan and P. Blaha, Phys. Rev. Lett. 82, 2544 (1999).
[113] A. D. Becke, J. Chem. Phys. 104, 1040 (1996).
[114] Y. H. Ki, I. H. Lee, S. Nagaraja, J. P. Leburton, R. Q. Hood, and R. M. Martin, Phys. Rev. B 61, 5202 (2000).
[115] S. Kurth, J. P. Perdew and P. Blaha, Int. J. Quantum Chem. 75, 889 (1999).
[116] C. Adamo, M. Ernzerhof and G. E. Scuseria, J. Chem. Phys. 112, 2643 (2000).
[117] O. A. Vydrow and G. E. Scuseria, J. Chem. Phys. 121, 8187 (2004).
[118] U. Lundin and O. Eriksson, Int. J. Quantum. Chem. 81, 247 (2001).
[119] C. Legrand, E. Suraud and P.-G. Reinhard, J. Phys. B 35, 1115 (2002).
[120] J. B. Krieger, Y. Li and G. J. Iafrate, Phys. Rev. A 45, 101 (1992); ibid 46, 5453 (1992); ibid 47 165 (1993).
[121] E. Engel and S. H. Vosko, Phys. Rev. A 47, 2800 (1993).
[122] T. Grabo, T. Kreibich, S. Kurth and E. K. U. Gross, in Ref. [11].
[123] T. Grabo and E. K. U. Gross, Int. J. Quantum Chem. 64, 95 (1997). T. Grabo and E. K. U. Gross, Chem. Phys. Lett. 240, 141 (1995).
[124] T. Kotani, Phys. Rev. Lett. 74, 2989 (1995).
[125] M. Stadele, J. A. Majewski, P. Vogl and A. Görling, Phys. Rev. Lett. 79, 2089 (1997). M. Stadele, M. Moukara, J. A. Majewski, P. Vogl and A. Görling, Phys. Rev. B 59, 10031 (1999). Y.-H. Kim, M. Stadele and R. M. Martin, Phys. Rev. A 60, 3633 (1999).
[126] S. Kümmel and J. P. Perdew, Phys. Rev. B 68, 035103 (2003).
[127] W. Yang and Q. Qu, Phys. Rev. Lett. 89, 143002 (2002).
[128] V. N. Staroverov, G. E. Scuseria and E. R. Davidson, J. Chem. Phys. 125, 081104 (2006).
[129] O. Gunnarsson, M. Jonson and B. I. Lundqvist, Phys. Rev. B 20, 3136 (1979).
[130] A. Cancio, M. Y. Chou and R. O. Hood, Phys. Rev. B 64, 115112 (2002).
[131] P. Garcia-Gonzalez, Phys. Rev. B 62, 2321 (2000).
[132] G. L. Oliver and J. P. Perdew, Phys. Rev. A 20, 397 (1979).
[133] K. Capelle and V. L. Libero, Int. J. Quantum Chem. 105, 679 (2005).
[134] L. M. Sandratskii, Adv. Phys. 47, 91 (1998).
[135] L. Nordström and D. Singh, Phys. Rev. Lett. 76, 4420 (1996).
[136] K. Capelle and L. N. Oliveira, Phys. Rev. B 61, 15228 (2000).
[137] A. K. Rajagopal and J. Callaway, Phys. Rev. B 7, 1912 (1973).
[138] A. H. Mac Donald and S. H. Vosko, J. Phys. C 12, 2977 (1979).
[139] E. Engel, T. Auth and R. M. Dreizler, Phys. Rev. B 64, 235126 (2001).
[140] G. Vignale and M. Rasolt, Phys. Rev. Lett. 59, 2360 (1987).
[141] G. Vignale and M. Rasolt, Phys. Rev. B 37, 10685 (1988).
[142] M. Ferconi and G. Vignale, Phys. Rev. B 50, 14722 (1997).
[143] M. Battocletti, H. Ebert and E. K. U. Gross, Europhys. Lett. 40, 545 (1997).
[144] A. M. Lee, N. C. Handy and S. M. Colwell, J. Chem. Phys. 103, 10095 (1996).
[145] K. Capelle, Phys. Rev. B 65, 100515 (2002).
[146] K. Capelle and E. K. U. Gross, Phys. Rev. Lett. 78, 1872 (1997).
[147] P. Skudlarski and G. Vignale, Phys. Rev. B 48, 8547 (1993).
[148] E. Orestes, T. Marcasso and K. Capelle, Phys. Rev. A 68, 022105 (2003).
[149] L. N. Oliveira, E. K. U. Gross and W. Kohn, Phys. Rev. Lett. 60, 2430 (1988).
[150] W. Kohn, E. K. U. Gross and L. N. Oliveira, J. de Physique 50, 2601 (1989).
[151] W. M. Temmermann, Z. Szotek, B. L. Gyorffy, O. K. Andersen, and O. Jepsen, Phys. Rev. Lett. 76, 307 (1996).
[152] S. Kurth, M. Marques, M. Lüders and E. K. U. Gross, Phys. Rev. Lett. 83, 2628 (1999).
[153] K. Capelle and L. N. Oliveira, Europhys. Lett. 49, 376 (2000).
[154] U. von Barth, Phys. Rev. A 20, 1693 (1979).
[155] A. Görling, Phys. Rev. Lett. 85, 4229 (2000).
[156] E. K. U. Gross, L. N. Oliveira and W. Kohn, Phys. Rev. A 37, 2805; ibid 2809; ibid 2821 (1988).
[157] A. Nagy, Phys. Rev. A 49, 3074 (1994); ibid 42, 4388 (1990).
[158] A. Görling, Phys. Rev A 59, 3359 (1999). A. Görling, Phys. Rev A 54, 3912 (1996).
[159] A. Nagy, Chem. Phys. Lett. 296, 489 (1998). M. Levy and A. Nagy, Phys. Rev. Lett. 83, 4361 (1999).
[160] K. Capelle, J. Chem. Phys. 119, 1285 (2003).
[161] R. van Leeuwen, Phys. Rev. Lett. 82, 3863 (1999).
[162] E. K. U. Gross, J. F. Dobson and M. Petersilka in Ref. [10]. K. Burke and E. K. U. Gross in Ref. [15].
[163] M. Petersilka, U. J. Gossmann and E. K. U. Gross, Phys. Rev. Lett. 76, 1212 (1996). See also T. Grabo, M. Petersilka and E. K. U. Gross, J. Mol. Struc. (Theochem) 501, 353 (2000).
[164] M. E. Casida, in Ref. [14]. J. Jamorski, M. E. Casida and D. R. Salahub, J. Chem. Phys. 104, 5134 (1996).
[165] S. J. A. van Gisbergen, J. G. Snijders, G. te Velde and E. J. Baerends, Comp. Phys. Comm. 118, 119 (1999).
[166] R. E. Stratmann, G. E. Scuseria and M. J. Frisch, J. Chem. Phys. 109, 8218 (1998).
[167] M. Lein, E. K. U. Gross and V. Engel, Phys. Rev. Lett. 85, 4707 (2000).
[168] C. A. Ullrich and E. K. U. Gross, Comm. At. Mol. Phys. 33, 211 (1997).
[169] K. Capelle, G. Vignale and B. L. Gyorffy, Phys. Rev. Lett. 87, 206403 (2001). K. Capelle and B. L. Gyorffy, Europhys. Lett. 61, 354 (2003).
[170] O. Gunnarsson and K. Schönhammer, Phys. Rev. Lett. 56, 1968 (1986).
[171] N. A. Lima, M. F. Silva, L. N. Oliveira and K. Capelle, Phys. Rev. Lett. 90, 146402 (2003). N. A. Lima, L. N. Oliveira and K. Capelle, Europhys. Lett. 60, 601 (2002). M. F. Silva, N. A. Lima, A. L. Malvezzi and K. Capelle, Phys. Rev. B 71, 125130 (2005). G. Xianlong et al., Phys. Rev. B 73, 165120 (2006).
[172] R. J. Magyar and K. Burke, Phys. Rev. A 70, 032508 (2004).
[173] V. L. Líbero and K. Capelle, Phys. Rev. B 68, 024423 (2003) and Phys. B 384, 179 (2006). P. E. G. Assis, V. L. Libero and K. Capelle, Phys. Rev. B 71, 052402 (2005). See also Ref. [133].
[174] V. L. Libero and K. Capelle, cond-mat/0506206.
[175] H. Chermette, J. Comp. Chem. 20, 129 (1999).
[176] F. De Proft and P. Geerlings, Chem. Rev. 101, 1451 (2001).
[177] A. E. Mattsson, Science 298, 759 (2002).
Received on 4 October, 2006
- [1] Proceedings of the VIII'th Brazilian Summer School on Electronic Structure (2002), eds. H. F. Santos, P. Z. Coura, S. O. Dantas and P. M. V. B. Barone.
- [2] J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett. 91, 146401 (2003);
- J. Chem. Phys. 119, 12129 (2003);
- J. Chem. Phys. 120, 6898 (2004);
- Phys. Rev. B 69, 075102 (2004).
- [3] W. Kohn, Rev. Mod. Phys. 71, 1253 (1999).
- [4] J. A. Pople, Rev. Mod. Phys. 71, 1267 (1999).
- [5] R. M. Dreizler and E. K. U. Gross, Density Functional Theory (Springer, Berlin, 1990).
- [6] R. G. Parr and W. Yang, Density-Functional Theory of Atoms and Molecules (Oxford University Press, Oxford, 1989).
- [7] W. Koch and M. C. Holthausen, A Chemist's Guide to Density Functional Theory (John Wiley & Sons, New York, 2001).
- [8] R. O. Jones and O. Gunnarsson, Rev. Mod. Phys. 61, 689 (1989).
- [9] J. M. Seminario (Ed.), Recent Developments and Applications of Modern DFT (Elsevier, Amsterdam, 1996).
- [10] R. F. Nalewajski (Ed.), Density Functional Theory I -IV (Springer, Topics in Current Chemistry Vols. 180-183, 1996).
- [11] V. I. Anisimov (Ed.), Strong Coulomb Correlations in Electronic Structure Calculations: Beyond the Local Density Approximation (Gordon & Breach, 1999).
- [12] N. H. March, Electron Density Theory of Atoms and Molecules (Academic Press, London, 1992).
- [13] B. B. Laird, R. B. Ross and T. Ziegler (Eds.), Chemical Applications of Density Functional Theory, (American Chemical Society, 1996).
- [14] D. P. Chong (Ed.), Recent Advances in Density Functional Methods (Singapore, World Scientific, 1995).
- [15] D. Joulbert (Ed.), Density Functionals: Theory and Applications (Springer Lecture Notes in Physics Vol. 500, 1998)
- [16] C. Fiolhais, F. Nogueira and M. Marques (Eds.), A Primer in Density Functional Theory (Springer Lecture Notes in Physics Vol. 620, 2003).
- [17] J. F. Dobson, G. Vignale and M. P. Das (Eds.), Density Functional Theory: Recent Progress and New Directions (Plenum, New York, 1998).
- [18] H. Eschrig, The Fundamentals of Density Functional Theory (Teubner, Leipzig, 1996).
- [19] E. K. U. Gross and R. M. Dreizler (Eds.), Density Functional Theory (Plenum, New York, 1995).
- [20] N. Argaman and G. Makov, Am. J. Phys. 68, 69 (2000).
- [21] E. N. Economou, Green's Functions in Quantum Physics (Springer, New York, 1979).
- [22] M. Levy, Phys. Rev. A 26, 1200 (1982).
- [23] E. H. Lieb in Density Functional Methods in Physics, edited by R. M. Dreizler and J. da Providencia, (Plenum, New York, 1985).
- [24] P. Hohenberg and W. Kohn, Phys. Rev. 136, B864 (1964).
- [25] E. Schrödinger, Ann. Physik 79, 361, 489, 734 (1926); 80, 437 (1926); 81, 109 (1926).
- [26] A. K. Theophilou, J. Phys. C 12, 5419 (1979).
- [27] O. Gritsenko and E. J. Baerends, J. Chem. Phys. 120, 8364 (2004).
- [28] P. Strange, Relativistic Quantum Mechanics with Applications in Condensed Matter and Atomic Physics (Cambridge University Press, Cambridge, 1998).
- [29] T. Kato, Commun. Pure Appl. Math. 10, 151 (1957).
- [30] N. H. March, Self-consistent fields in atoms (Pergamon Press, Oxford, 1975).
- [31] J. P. Perdew and M. Levy, Phys. Rev. B 31, 6264 (1985).
- [32] H. Eschrig and W. E. Pickett, Solid State Commun. 118, 123 (2001).
- [33] K. Capelle and G. Vignale, Phys. Rev. Lett. 86, 5546 (2001).
- [34] K. Capelle and G. Vignale, Phys. Rev. B 65, 113106 (2002).
- [35] N. Argaman and G. Makov, Phys. Rev. B 66, 052413 (2002).
- [36] N. Gidopolous in The fundamentals of density matrix and density functional theory in atoms, molecules and solids, N. Gidopoulos and S. Wilson eds. (Kluwer Series 'Progress in Theoretical Chemistry and Physics', 2003);
- and cond-mat/0510199.
- [37] W. Kohn, A. Savin and C. A. Ullrich, Int. J. Quantum Chem. 100, 20 (2004).
- [38] C. A. Ullrich, Phys. Rev. B 72, 073102 (2005).
- [39] T. L. Gilbert, Phys. Rev. B 12, 2111 (1975).
- [40] J. E. Harriman, Phys. Rev. A 24, 680 (1981).
- [41] J. T. Chayes, L. Chayes and M. B. Ruskai, J. Stat. Phys. 38, 497 (1985).
- [42] C. A. Ullrich and W. Kohn, Phys. Rev. Lett. 89, 156401 (2002); ibid 87, 093001 (2001).
- [43] P. E. Lammert, J. Chem. Phys. 125, 074114 (2006).
- [44] A. P. Favaro, J. V. Batista Ferreira and K. Capelle, Phys. Rev. B 73, 045133 (2006).
- [45] L. W. Wang and M. P. Teter, Phys. Rev. B 45, 13196 (1992).
- [46] M. Foley and P. A. Madden, Phys. Rev. B 53, 10589 (1996).
- [47] B. J. Zhou, V. L. Ligneres and E. A. Carter, J. Chem. Phys. 122, 044103 (2005).
- [48] E. K. U. Gross, E. Runge and O. Heinonen, Many Particle Theory (Adam Hilger, 1992).
- [49] A. Szabo and N. S. Ostlund, Modern Quantum Chemistry (McGraw-Hill, New York, 1989).
- [50] L. J. Sham and M. Schlüter, Phys. Rev. Lett. 51, 1888 (1983).
- [51] E. Runge and E. K. U. Gross, Phys. Rev. Lett. 52, 997 (1984).
- [53] P. Nozieres and D. Pines, The Theory of Quantum Liquids (Addison Wesley, New York, revised printing 1989).
- [54] N. D. Mermin, Phys. Rev. 137, 1441 (1965).
- [55] M. Levy and J. P. Perdew, Phys. Rev. A 32, 2010 (1985).
- [56] E. H. Lieb and S. Oxford, Int. J. Quantum Chem. 19, 427 (1981).
- [57] G. K.-L. Chan and N. C. Handy, Phys. Rev. A 59, 3075 (1999).
- [58] J. P. Perdew, R. G. Parr, M. Levy and J. L. Balduz, Phys. Rev. Lett. 49, 1691 (1982).
- [59] J. P. Perdew and M. Levy, Phys. Rev. Lett. 51, 1884 (1983).
- [60] W. Kohn and L. J. Sham, Phys. Rev. 140, A1133 (1965).
- [61] W. Kohn, A. D. Becke and R. G. Parr, J. Phys. Chem. 100, 12974 (1996).
- [62] C. O. Almbladh and U. v. Barth, Phys. Rev. B 31, 3231 (1985).
- [63] M. Levy, J. P. Perdew and V. Sahni, Phys. Rev. A 30, 2745 (1984).
- [64] J. Chen, J. B. Krieger, Y. Li and G. J. Iafrate, Phys. Rev. A 54, 3939 (1996).
- [65] M. Lüders, A. Ernst, W. M. Temmerman, Z. Szotek and P. J. Durham, J. Phys. Cond. Mat. 13, 8587 (2001).
- [66] J. Muskat, A. Wander, and N. M. Harrison, Chem. Phys. Lett. 342, 397 (2001).
- [67] A. Savin, C. J. Umrigar and X. Gonze, Chem. Phys. Lett. 288, 391 (1998).
- [68] W. G. Aulbur, L. Jönsson and J. W. Wilkins, Solid State Phys. 54, 1 (1999).
- [69] F. Aryasetiawan and O. Gunnarsson, Rep. Prog. Phys. 61, 237 (1998).
- [70] G. Onida, L. Reining and A. Rubio, Rev. Mod. Phys. 74, 601 (2002).
- [71] A. Svane and O. Gunnarsson, Phys. Rev. Lett. 65, 1148 (1990); ibid 72, 1248 (1994).
- [72] Z. Szotek, W. M. Temmermann and H. Winter, Phys. Rev. Lett. 72, 1244 (1994).
- [73] P. Strange, A. Svane, W. M. Temmermann, Z. Szotek and H. Winter, Nature 399, 756 (1999).
- [74] M. R. Norman and D. D. Koelling, Phys. Rev. B 30, 5530 (1984).
- [75] O. K. Andersen, Phys. Rev. B 12, 3060 (1975).
- [76] O. K. Andersen, O. Jepsen and D. Glötzel in Highlights of Condensed Matter Theory, F. Bassani, F. Funi and M. P. Tosi, eds. (North Holland, Amsterdam, 1985).
- [77] O. K. Andersen and T. Saha-Dasgupta, Phys. Rev. B 62, 16219 (2000).
- [78] E. Zurek, O. Jepsen and O. K. Andersen, Chem.Phys.Chem. 6, 1934 (2005).
- [79] T. H. Dunning Jr., J. Chem. Phys. 90, 1007 (1989).
- [80] A. B. F. da Silva, H. F. M. da Costa and M. Trsic, Mol. Phys. 68, 433 (1989).
- [81] F. E. Jorge, E. V. R. de Castro and A. B. F. da Silva, J. Comp. Chem. 18, 1565 (1997).
- [82] G. B. Bachelet, D. R. Hamann and M. Schlüter, Phys. Rev. B 25, 2103 (1982).
- [83] L. Kleinman and D. M. Bylander, Phys. Rev. Lett. 48, 1425 (1982).
- [84] D. Vanderbilt, Phys. Rev. B 41, 7892 (1990).
- [85] N. Troullier and J. L. Martins, Phys. Rev. B 43, 1993 (1991).
- [86] W. E. Pickett, Comp. Phys. Rep. 9, 116 (1989).
- [87] D. Porezag, M. R. Pederson and A. Y. Liu, Phys. Stat. Sol. (b) 217, 219 (2000)
- [88] M. C. Payne, M. P. Teter, D. C. Allan, T. A. Arias and J. D. Joannopoulos, Rev. Mod. Phys. 64, 1045 (1992).
- [89] U. von Barth and L. Hedin, J. Phys. C 5, 1629 (1972).
- [90] O. Gunnarsson and B. Lundqvist, Phys. Rev. B 13, 4274 (1976).
- [91] D. M. Ceperley and B. J. Alder, Phys. Rev. Lett. 45, 566 (1980).
- [92] S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys. 58, 1200 (1980).
- [93] J. P. Perdew and A. Zunger, Phys. Rev. B 23, 5048 (1981).
- [94] J. P. Perdew and Y. Wang, Phys. Rev. B 45, 13244 (1992).
- [95] J. P. Perdew and Y. Wang, Phys. Rev. B 33, 8800 (1986).
- [96] J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett. 77, 3865 (1996); ibid 78, 1396(E) (1997).
- See also V. Staroverov et al., Phys. Rev. A 74, 044501 (2006).
- [97] A. D. Becke, Phys. Rev. A 38, 3098 (1988).
- [98] C. Lee, W. Yang and R. G. Parr, Phys. Rev. B 37, 785 (1988).
- [99] D. C. Patton and M. R. Pederson, Phys. Rev. A 56, 2495 (1997).
- [100] J. Tao and J. P. Perdew, J. Chem. Phys. 122, 114102 (2005).
- [101] W. Kohn, Y. Meir and D. E. Makarov, Phys. Rev. Lett. 80, 4153 (1998).
- [102] M. Lein, J. F. Dobson and E. K. U. Gross, J. Comp. Chem. 20, 12 (1999).
- [103] J. F. Dobson and B. P. Dinte, Phys. Rev. Lett. 76, 1780 (1996).
- [104] Y. Andersson, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett. 76, 102 (1996).
- [105] E. R. Johnson and A. D. Becke, J. Chem. Phys. 123, 024101 (2005).
- [106] C. Filippi, C. J. Umrigar and M. Taut, J. Chem. Phys. 100, 1290 (1994).
- [107] P. Ziesche, S. Kurth and J. P. Perdew, Comp. Mat. Sci. 11, 122 (1998).
- [108] A. D. Becke, J. Chem. Phys. 98, 5648 (1993).
- [109] A. D. Becke, J. Chem. Phys. 107, 8554 (1997).
- See also A. D. Becke, J. Comp. Chem. 20, 63 (1999).
- [110] D. J. Tozer and N. C. Handy, J. Chem. Phys. 108, 2545 (1998).
- [111] T. van Voorhis and G. E. Scuseria, J. Chem. Phys. 109, 400 (1998).
- [112] J. P. Perdew, S. Kurth, A. Zupan and P. Blaha, Phys. Rev. Lett. 82, 2544 (1999).
- [113] A. D. Becke, J. Chem. Phys. 104, 1040 (1996).
- [114] Y. H. Ki, I. H. Lee, S. Nagaraja, J. P. Leburton, R. Q. Hood, and R. M. Martin, Phys. Rev. B 61, 5202 (2000).
- [115] S. Kurth, J. P. Perdew and P. Blaha, Int. J. Quantum Chem. 75, 889 (1999).
- [116] C. Adamo, M. Ernzerhof and G. E. Scuseria, J. Chem. Phys. 112, 2643 (2000).
- [117] O. A. Vydrow and G. E. Scuseria, J. Chem. Phys. 121, 8187 (2004).
- [118] U. Lundin and O. Eriksson, Int. J. Quantum. Chem. 81, 247 (2001).
- [119] C. Legrand, E. Suraud and P.-G. Reinhard, J. Phys. B 35, 1115 (2002).
- [120] J. B. Krieger, Y. Li and G. J. Iafrate, Phys. Rev. A 45, 101 (1992); ibid 46, 5453 (1992); ibid 47 165 (1993).
- [121] E. Engel and S. H. Vosko, Phys. Rev. A 47, 2800 (1993).
- [123] T. Grabo and E. K. U. Gross, Int. J. Quantum Chem. 64, 95 (1997).
- [124] T. Kotani, Phys. Rev. Lett. 74, 2989 (1995).
- [125] M. Stadele, J. A. Majewski, P. Vogl and A. Görling, Phys. Rev. Lett. 79, 2089 (1997).
- M. Stadele, M. Moukara, J. A. Majewski, P. Vogl and A. Görling, Phys. Rev. B 59, 10031 (1999).
- Y.-H. Kim, M. Stadele and R. M. Martin, Phys. Rev. A 60, 3633 (1999).
- [126] S. Kümmel and J. P. Perdew, Phys. Rev. B 68, 035103 (2003).
- [127] W. Yang and Q. Qu, Phys. Rev. Lett. 89, 143002 (2002).
- [128] V. N. Staroverov, G. E. Scuseria and E. R. Davidson, J. Chem. Phys. 125, 081104 (2006).
- [129] O. Gunnarsson, M. Jonson and B. I. Lundqvist, Phys. Rev. B 20, 3136 (1979).
- [130] A. Cancio, M. Y. Chou and R. O. Hood, Phys. Rev. B 64, 115112 (2002).
- [131] P. Garcia-Gonzalez, Phys. Rev. B 62, 2321 (2000).
- [132] G. L. Oliver and J. P. Perdew, Phys. Rev. A 20, 397 (1979).
- [133] K. Capelle and V. L. Libero, Int. J. Quantum Chem. 105, 679 (2005).
- [134] L. M. Sandratskii, Adv. Phys. 47, 91 (1998).
- [135] L. Nordström and D. Singh, Phys. Rev. Lett. 76, 4420 (1996).
- [136] K. Capelle and L. N. Oliveira, Phys. Rev. B 61, 15228 (2000).
- [137] A. K. Rajagopal and J. Callaway, Phys. Rev. B 7, 1912 (1973).
- [138] A. H. Mac Donald and S. H. Vosko, J. Phys. C 12, 2977 (1979).
- [139] E. Engel, T. Auth and R. M. Dreizler, Phys. Rev. B 64, 235126 (2001).
- [140] G. Vignale and M. Rasolt, Phys. Rev. Lett. 59, 2360 (1987).
- [141] G. Vignale and M. Rasolt, Phys. Rev. B 37, 10685 (1988).
- [142] M. Ferconi and G. Vignale, Phys. Rev. B 50, 14722 (1997).
- [143] M. Battocletti, H. Ebert and E. K. U. Gross, Europhys. Lett. 40, 545 (1997).
- [144] A. M. Lee, N. C. Handy and S. M. Colwell, J. Chem. Phys. 103, 10095 (1996).
- [145] K. Capelle, Phys. Rev. B 65, 100515 (2002).
- [146] K. Capelle and E. K. U. Gross, Phys. Rev. Lett. 78, 1872 (1997).
- [147] P. Skudlarski and G. Vignale, Phys. Rev. B 48, 8547 (1993).
- [148] E. Orestes, T. Marcasso and K. Capelle, Phys. Rev. A 68, 022105 (2003).
- [149] L. N. Oliveira, E. K. U. Gross and W. Kohn, Phys. Rev. Lett. 60, 2430 (1988).
- [150] W. Kohn, E. K. U. Gross and L. N. Oliveira, J. de Physique 50, 2601 (1989).
- [151] W. M. Temmermann, Z. Szotek, B. L. Gyorffy, O. K. Andersen, and O. Jepsen, Phys. Rev. Lett. 76, 307 (1996).
- [152] S. Kurth, M. Marques, M. Lüders and E. K. U. Gross, Phys. Rev. Lett. 83, 2628 (1999).
- [153] K. Capelle and L. N. Oliveira, Europhys. Lett. 49, 376 (2000).
- [154] U. von Barth, Phys. Rev. A 20, 1693 (1979).
- [155] A. Görling, Phys. Rev. Lett. 85, 4229 (2000).
- [156] E. K. U. Gross, L. N. Oliveira and W. Kohn, Phys. Rev. A 37, 2805; ibid 2809; ibid 2821 (1988).
- [157] A. Nagy, Phys. Rev. A 49, 3074 (1994); ibid 42, 4388 (1990).
- [158] A. Görling, Phys. Rev A 59, 3359 (1999).
- A. Görling, Phys. Rev A 54, 3912 (1996).
- [159] A. Nagy, Chem. Phys. Lett. 296, 489 (1998).
- M. Levy and A. Nagy, Phys. Rev. Lett. 83, 4361 (1999).
- [160] K. Capelle, J. Chem. Phys. 119, 1285 (2003).
- [161] R. van Leeuwen, Phys. Rev. Lett. 82, 3863 (1999).
- [163] M. Petersilka, U. J. Gossmann and E. K. U. Gross, Phys. Rev. Lett. 76, 1212 (1996).
- See also T. Grabo, M. Petersilka and E. K. U. Gross, J. Mol. Struc. (Theochem) 501, 353 (2000).
- [164] M. E. Casida, in Ref. [14]. J. Jamorski, M. E. Casida and D. R. Salahub, J. Chem. Phys. 104, 5134 (1996).
- [165] S. J. A. van Gisbergen, J. G. Snijders, G. te Velde and E. J. Baerends, Comp. Phys. Comm. 118, 119 (1999).
- [166] R. E. Stratmann, G. E. Scuseria and M. J. Frisch, J. Chem. Phys. 109, 8218 (1998).
- [167] M. Lein, E. K. U. Gross and V. Engel, Phys. Rev. Lett. 85, 4707 (2000).
- [168] C. A. Ullrich and E. K. U. Gross, Comm. At. Mol. Phys. 33, 211 (1997).
- [169] K. Capelle, G. Vignale and B. L. Gyorffy, Phys. Rev. Lett. 87, 206403 (2001).
- K. Capelle and B. L. Gyorffy, Europhys. Lett. 61, 354 (2003).
- [170] O. Gunnarsson and K. Schönhammer, Phys. Rev. Lett. 56, 1968 (1986).
- [171] N. A. Lima, M. F. Silva, L. N. Oliveira and K. Capelle, Phys. Rev. Lett. 90, 146402 (2003).
- N. A. Lima, L. N. Oliveira and K. Capelle, Europhys. Lett. 60, 601 (2002).
- M. F. Silva, N. A. Lima, A. L. Malvezzi and K. Capelle, Phys. Rev. B 71, 125130 (2005).
- G. Xianlong et al., Phys. Rev. B 73, 165120 (2006).
- [172] R. J. Magyar and K. Burke, Phys. Rev. A 70, 032508 (2004).
- [173] V. L. Líbero and K. Capelle, Phys. Rev. B 68, 024423 (2003)
- and Phys. B 384, 179 (2006).
- P. E. G. Assis, V. L. Libero and K. Capelle, Phys. Rev. B 71, 052402 (2005). See also Ref. [133].
- [174] V. L. Libero and K. Capelle, cond-mat/0506206.
- [175] H. Chermette, J. Comp. Chem. 20, 129 (1999).
- [176] F. De Proft and P. Geerlings, Chem. Rev. 101, 1451 (2001).
- [177] A. E. Mattsson, Science 298, 759 (2002).
 and
and  is system-dependent, or 'nonuniversal'. We will come back to this terminology.
is system-dependent, or 'nonuniversal'. We will come back to this terminology.  in terms of of generalized coordinates
in terms of of generalized coordinates  (
( [
[ (
( ;
; , which are a special case of Eq. (14).
, which are a special case of Eq. (14).  is the particle density, and therefore
is the particle density, and therefore  is often also called the density operator. This concept must not be confused with any of the various density matrices or the density operator of statistical physics, Eq. (40).
is often also called the density operator. This concept must not be confused with any of the various density matrices or the density operator of statistical physics, Eq. (40).  with the Slater determinant arising from density
with the Slater determinant arising from density  | F[
| F[ |Y[
|Y[ (
( with the Kohn-Sham eigenvalues e
with the Kohn-Sham eigenvalues e , e
, e e
e (where the
(where the  are not the same as the KS eigenvalues e
are not the same as the KS eigenvalues e . Fermi-liquid theory in metals and effective-mass theory in semiconductors are examples of this type of approach.
. Fermi-liquid theory in metals and effective-mass theory in semiconductors are examples of this type of approach.  ] and
] and  ] from
] from  [
[ ] is called the 'unscreening of the atomic PP'. It can only be done exactly for the Hartree term, because the contributions of valence and core densities are not additive in the
] is called the 'unscreening of the atomic PP'. It can only be done exactly for the Hartree term, because the contributions of valence and core densities are not additive in the  =
=  (
( (
(Publication Dates
-
Publication in this collection
21 June 2007 -
Date of issue
Dec 2006
History
-
Received
04 Oct 2006