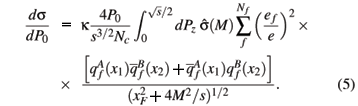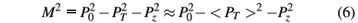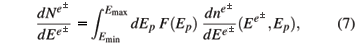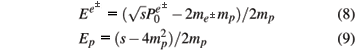Abstract
The recent discovery of a new and intense solar flare radiation spectral component with a maximum in the terahertz range has raised a great deal of interest. The origin of this component is still unknown, constituting a problem that goes beyond the application of canonical models used to describe the well-known microwave spectrum. In this work, we present preliminary results on the investigation of a possible contribution from electron-positron pairs produced in a Drell-Yan process to the emission of the terahertz component observed in solar flares.
Drell-Yan processes; Solar emission spectrum; Terahertz component
Contribution from Drell-Yan processes to the emission spectrum in solar flares
S. SzpigelI; F. O. DurãesI, II; F. M. SteffensI
ICentro de Ciências e Humanidades, Universidade Presbiteriana Mackenzie Rua da Consolacão 930, 01302-907 São Paulo, Brasil
IIInstituto de Física, Universidade de São Paulo, C.P. 66318, 05389-970 São Paulo, SP, Brazil
ABSTRACT
The recent discovery of a new and intense solar flare radiation spectral component with a maximum in the terahertz range has raised a great deal of interest. The origin of this component is still unknown, constituting a problem that goes beyond the application of canonical models used to describe the well-known microwave spectrum. In this work, we present preliminary results on the investigation of a possible contribution from electron-positron pairs produced in a Drell-Yan process to the emission of the terahertz component observed in solar flares.
Keywords: Drell-Yan processes; Solar emission spectrum; Terahertz component
I. INTRODUCTION
Solar flares are sudden and rapid releases of enormous amounts of energy in the solar atmosphere, involving acceleration of particles, plasma heating and bulk mass motions. It is a general believe that they occur when the energy stored in magnetic loops that have built up in the active regions around sunspots is suddenly released, in a process called magnetic reconnection [1]. During the restructuring of the magnetic fields in such a process both electrons and ions are accelerated to high energies and radiation is emitted covering virtually the entire electromagnetic spectrum, from radio-waves to gamma-rays [2].
The recent discovery of a new and intense solar flare radiation component with a maximum in the shorter submillimeter to far infrared range has raised a great deal of interest, confirming theoretical suggestions and experimental evidences proposed for more than twenty years. This new component, which in the frequency domain has a peak in the terahertz range (0.1-100 THz), was identified by Kaufmann et al. [3] during the observation of the 2003 November 4 large solar flare.
The origin of the terahertz component observed during this solar flare is still unknown, constituting a problem that goes beyond the application of canonical models used to describe the well-known microwave spectrum observed at frequencies below 100 GHz. In such canonical models, the processes of energy generation during the flare impulsive phase are generally attributed to a population of relativistic electrons producing microwaves by synchrotron emission and X-rays by collisions in denser regions of the solar atmosphere [4].
Nevertheless, a few early models were proposed to explain solar flare radio emission at frequencies higher than 100 GHz considering electrons with energies much larger than the energies assumed to explain the usual microwaves ( > 10 MeV), such as free-free thermal bremsstrahlung [5] and synchrotron emission by ultra-relativistic electrons [6].
In this work we investigate the contribution from Drell-Yan processes to the emission spectrum in solar flares. We present preliminary results on the calculation of the energy spectrum for electron-positron pairs produced in a Drell-Yan process from proton-proton collisions in the solar atmosphere and discuss its possible contribution to the terahertz component observed in solar flares.
II. THE OBSERVATION OF THE NEW TERAHERTZ SOLAR FLARE COMPONENT
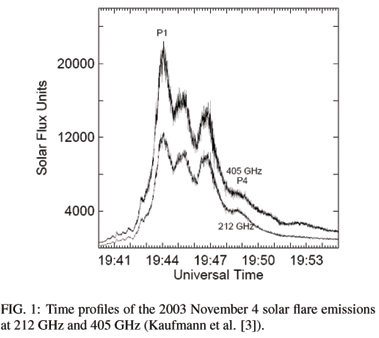
The new terahertz component was detected during the observation of the 2003 November 4 solar flare using the Solar Submillimeter Telescope (SST) at the Leoncito Observatory in Argentina, built to extend the range of solar flare observations to frequencies above 100 GHz [7]. The SST detected this new component with flux increasing between 212 and 405 GHz, along with the well-known microwave component, but distinguished from it. In Fig. 1 (Kaufmann et al. [3]), we show the time profiles of emissions at 212 and 405 GHz, in solar flux units.
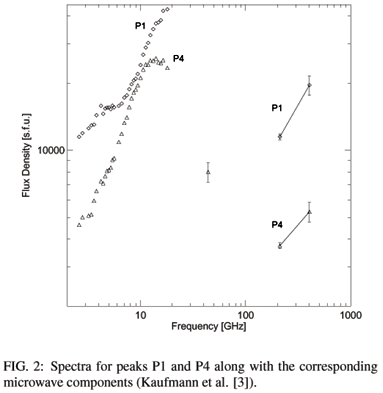
In Fig. 2 (Kaufmann et al. [3]) we show the spectra for the major peak P1 and the smaller peak P4, along with the corresponding well-known gyrosynchrotron microwave components at 15.6 GHz for comparison. As can be seen from the figure, the flux density is much larger at 405 than at 212 GHz for both peaks, indicating a maximum spectral emission lying within the terahertz range.
Recently, Kaufmann and Raulin [8] proposed a mechanism to explain the new terahertz component in which beams of ultra-relativistic electrons produce incoherent synchrotron radiation (ISR) with maximum in the terahertz range, further undergoing density modulations that may generate microbunching instabilities producing the intense broadband coherent synchrotron (CSR) observed at microwaves. This process is similar to what happens in laboratory accelerators with high energy electrons beams in storage rings [9].
In another recent work, Sakai et al. [10] proposed an interpretation for the terahertz component in terms of a plasma emission mechanism in which Langmuir waves, generated when relativistic electron beams propagate into the high density region corresponding to the solar photosphere, are converted in electromagnetic waves.
III. SYNCHROTRON EMISSION FROM POSITRONS IN SOLAR FLARES
A possibility that has also been considered to explain the terahertz component is the synchrotron emission by high-energy positrons [11], whose presence during solar flares is confirmed by the observation of the 511 keV gamma-ray positron-electron annihilation line [12].
The main mechanism for positron production in solar flares is the decay of pions produced by nuclear interactions of flare-accelerated protons with protons or alpha-particles in the ambient solar atmosphere [13], such as in the following mode:
Another contribution is due to the decay of radioactive positron-emitter isotopes such as 10C, 11C, 12N, 13N and 15O which are produced in nuclear interactions of flare-accelerated protons and alpha-particles with ambient heavy nuclei [14]. The importance of these processes for positron production depends on the cross sections and the assumed elemental and isotopic abundances.
In a comparative study of different emission mechanisms that could explain the terahertz component, Valio et al. [11] estimated the synchrotron emission from 1 to 1000 MeV positrons. A fitting for the observed terahertz spectrum shown in Fig. 2 was calculated using a simplified version of an energy spectrum for positrons produced from pion decay evaluated by Murphy et al. [13].
Although a good fit was obtained for the 212 GHz and 405 GHz data points, a total number of positrons had to be assumed which was approximately 200 times larger than the 1030 positrons inferred from measurements of the 511 keV annihilation line. This result gives the main motivation of this work. Electron-positron pairs, produced in a Drell-Yan process at high energies, can carry large momenta and, in principle, could provide an extra contribution to the mechanism of synchrotron emission by positrons in the terahertz range.
IV. SPECTRUM OF POSITRONS PRODUCED IN A DRELL-YAN PROCESS
The Drell-Yan process is a high-energy reaction in which a dilepton pair l+l- is produced from quark-antiquark annihilation in a nucleon-nucleon (nucleus-nucleus) collision [15]. The differential cross-section for dilepton pair production in a Drell-Yan process is a standard calculation in perturbative QCD. In terms of the dilepton pair invariant mass M and the Feynman scaling variable xF for the l+l- pair, if one considers only the lowest order diagram (i.e. quark-antiquark annihilation going to a virtual photon which subsequently decays into an l+l- pair), the cross-section for the process at Leading Order (LO) can be written as:
where Nc( = 3) is the number of colors, ef is the charge of quark with flavor f (= u,d), s is the square of the total energy in the nucleon-nucleon collision center-of-mass frame,  (M) is the elementary cross-section for the
(M) is the elementary cross-section for the  annihilation process and
annihilation process and  are the quark (antiquark) distribution functions for the nucleons A and B.
are the quark (antiquark) distribution functions for the nucleons A and B.
The factor k accounts for the higher-order QCD corrections that enter the process and its value is typically 1-2. In what follows we shall assume k = 1 and use the (LO) proton parton distribution functions, at a fixed scale Q2 = 1 GeV2, taken from [16] (GRV98 LO).
The quantities x1 and x2 are the nucleon momentum fractions carried respectively by partons in the projectile and target. They are related to M2 and xF by:
We consider the production of a positron-electron pair e+e- from a proton-proton collision and integrate over the total longitudinal momentum of the positron-electron pair in the center-of-mass frame Pz = xF  /2 for a fixed s to obtain the e+/e- energy distribution, given by:
/2 for a fixed s to obtain the e+/e- energy distribution, given by:
where  (s) is the total cross-section for inelastic proton-proton collision which we shall take from Ref. [17],
(s) is the total cross-section for inelastic proton-proton collision which we shall take from Ref. [17],  is the e+/e- energy in the proton-proton collision center-of-mass frame, P0 is the total energy of the positron-electron pair and
is the e+/e- energy in the proton-proton collision center-of-mass frame, P0 is the total energy of the positron-electron pair and
In the calculation of the energy distribution we make the assumption P0 = 2 and take an average value for the total transverse momentum of the positron-electron pair PT such that
and take an average value for the total transverse momentum of the positron-electron pair PT such that
with < PT > » 0.3-0.5 GeV.
We calculate the spectrum of e+/e- produced in the Drell-Yan process by considering collisions between flare-accelerated protons (projectile) and protons from the ambient solar atmosphere (fixed target) in the laboratory frame:
where  and Ep are respectively the kinetic energies of the e+/e- and the accelerated proton in the laboratory frame, given by
and Ep are respectively the kinetic energies of the e+/e- and the accelerated proton in the laboratory frame, given by
Following Ref. [18] we use a power-law energy distribution function for the accelerated protons given by
where A is a normalization constant picked so that the protons with energies in the range Emin < Ep < Emax equals 1 and a is chosen in the interval 2-3.
V. PRELIMINARY RESULTS AND DISCUSSION
In Fig. 3 we show the energy spectra for positrons produced in a Drell-Yan process obtained using Eq. 7 for two different average values for the total transverse momentum of the positron-electron pair: < PT > = 0.5 GeV (solid line) and < PT > = 0.3 GeV (dashed line). In both cases we have chosen a = 2, Emin = 1 GeV and Emax = 100 GeV. As can be noted, the energy spectra have a maximum at the threshold positron kinetic energy ( ) and decrease as the energy grows. Such threshold is determined by the condition that the square of the dilepton pair invariant mass M2 in Eq. 6 must be greater than 4
) and decrease as the energy grows. Such threshold is determined by the condition that the square of the dilepton pair invariant mass M2 in Eq. 6 must be greater than 4  . Thus, for smaller values of < PT > the energy spectrum starts at lower values of
. Thus, for smaller values of < PT > the energy spectrum starts at lower values of  .
.
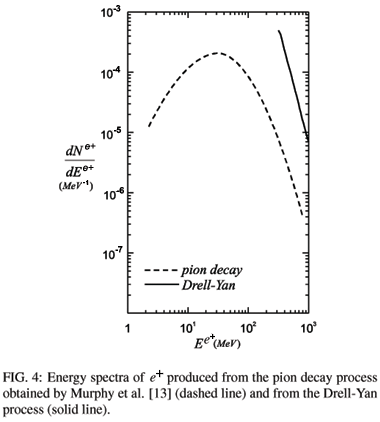
In Fig. 4 we show a comparison between our result for the positron energy spectrum obtained with < PT > = 0.5 GeV (solid line) and the spectrum evaluated by Murphy et al. [13] for positrons produced from pion decay. As can be seen from the figure, for energies above » 0.5 GeV a significant number of positrons can be produced from the Drell-Yan process in comparison to the number of positrons produced from the pion decay process, indicating a possible extra contribution to the synchrotron emission mechanism.
Although preliminary, these results are promising. We are currently refining the numerical calculations and testing for the sensitivity of the results on the parameters a, < PT > , Emin and Emax. Our next step will be the evaluation of the synchrotron emission flux density in solar flares using a positron energy spectrum which takes into account the positrons produced both from the Drell-Yan process and the pion decay process.
By including the Drell-Yan contribution, we believe that the total number of positrons needed to fit the terahertz spectrum shown in Fig. 2 will be smaller than the number used by Valio et al. [11], yielding a result more compatible with the expected number of positrons inferred from the 511 keV annihilation line measurements.
Acknowledgments
The authors wish to thank P. Kaufmann, A. V. R. da Silva and C. G. G. Castro, from Centro de Radio-Astronomia e Astrofísica Mackenzie (CRAAM), for the collaboration and fruitful discussions. This work has been supported by CNPq, FAPESP and Instituto Presbiteriano Mackenzie, educational entity for scientific and technological development, through MACKPESQUISA.
[1] M. J. Aschwanden, Space Sci. Rev. 101, 1 (2002).
[2] T. S. Bastian, A. O. Benz, and D. E. Gary, Annu. Rev. Astron. Astrophys. 36, 131 (1998).
[3] P. Kaufmann, J.-P. Raulin, C. G. Gimenez de Castro, H. Levato, D. E. Gary, J. E. R. Costa, A. Marun, P. Pereyra, A. V. R. Silva, and E. Correia, Ap. J. (Letters) 603, L121 (2004).
[4] M. R. Kundu, in Radio Physics of the Sun, IAU Symp. 86, ed. M. R. Kundu and E. Gergely, 157 (1980); G. A. Dulk and B. R. Dennis, Ap. J. 260, 875 (1982).
[5] K. Ohki and H. S. Hudson, Sol. Phys 43, 405 (1975).
[6] W. A. Stein and E. P. Ney, J. Geophys. Res. 68, 65 (1963); J. Shlovsky, Nature 202, 275 (1964); P. Kaufmann, E. Correia, J. E. R. Costa, and A. M. Zodi Vaz, A&A 157, 11 (1986).
[7] P. Kaufmann et al., in Proc. SBMO/IEEE MTT-S Int. Microwave and Optoelectronics Conf., ed. J. T. Pinho, G. P. Santos, and L. A. H. G. Oliveira (Piscataway:IEEE), 439 (2001).
[8] P. Kaufmann and J.-P. Raulin, Eos. Trans. AGU 86 (18), Jt. Assemb Suppl. Abstract SH54A-06 (2005).
[9] J. M. Byrd, W. P. Leemans, A. Loftsdottir, B. Marcelis, M. C.Martin, W. R. McKinney, F. Sannibale, T. Scarvie, and C. Steier, Phys. Rev. Lett. 89, 224801 (2002).
[10] J. I. Sakai, Y. Nagasugi, S. Saito, and P. Kaufmann, A&A preprint doi http://dx.doi.org/10.1051/0004-6361:20065368 (2006).
[11] A. V. R. Silva, C. G. G. Castro, and P. Kaufmann, in Proc. of the V RHESSI Workshop, v. 1, 10 (2005); A. V. R. Silva, J.E.R. Costa, C. G. Gimenez de Castro, J.-P. Raulin, P. Kaufmann, G. H. Share, and R. J. Murphy, in Proc. of the SCOSTEP's 11th Quadrennial STP Symposium, 1, 1 (2006).
[12] G. H. Share and R. J. Murphy, in Stars as Suns: Activity, Evolution and Planets, ASP Conf. Series 219, ed. A. Benz and A. Dupree, 133 (2004); G. H. Share, R. J. Murphy, D. M. Smith, R. A. Schwartz, and R. P. Lin, Ap. J. (Letters) 615, L169 (2004).
[13] R. J. Murphy, C. D. Dermer, and R. Ramaty, Ap. J. (Supplement) 63, 721 (1987).
[14] R. E. Lingenfelter and R. Ramaty, Planet. Space Sci. 15, 1303 (1967); R. Ramaty, B. Koslovsky, and R. E. Lingenfelter, Space Science Reviews 18, 341 (1975); B. Koslovsky, R. E. Lingenfelter, and R. Ramaty, Ap. J. 316, 801-818 (1987).
[15] S. D. Drell and T. M. Yan, Phys. Rev. Lett. 25, 316 (1970); C. Crosso-Pilcher and M. J. Shochet, Ann. Rev. Nucl. Part. Sci. 36, 1 (1986).
[16] M. Glück and E. Reya and A. Vogt, Eur. Phys. J. C 5, 461 (1998).
[17] A. Donnachie and P. V. Landshoff, Phys. Lett. B 296, 227 (1992).
[18] N. Vilmer, A. L. MacKinnon, G. Trotter, and C. Barat, A&A 412, 865 (2003).
Received on 29 September, 2006
- [1] M. J. Aschwanden, Space Sci. Rev. 101, 1 (2002).
- [2] T. S. Bastian, A. O. Benz, and D. E. Gary, Annu. Rev. Astron. Astrophys. 36, 131 (1998).
- [3] P. Kaufmann, J.-P. Raulin, C. G. Gimenez de Castro, H. Levato, D. E. Gary, J. E. R. Costa, A. Marun, P. Pereyra, A. V. R. Silva, and E. Correia, Ap. J. (Letters) 603, L121 (2004).
- [4] M. R. Kundu, in Radio Physics of the Sun, IAU Symp. 86, ed. M. R. Kundu and E. Gergely, 157 (1980);
- G. A. Dulk and B. R. Dennis, Ap. J. 260, 875 (1982).
- [5] K. Ohki and H. S. Hudson, Sol. Phys 43, 405 (1975).
- [6] W. A. Stein and E. P. Ney, J. Geophys. Res. 68, 65 (1963);
- J. Shlovsky, Nature 202, 275 (1964);
- P. Kaufmann, E. Correia, J. E. R. Costa, and A. M. Zodi Vaz, A&A 157, 11 (1986).
- [7] P. Kaufmann et al., in Proc. SBMO/IEEE MTT-S Int. Microwave and Optoelectronics Conf., ed. J. T. Pinho, G. P. Santos, and L. A. H. G. Oliveira (Piscataway:IEEE), 439 (2001).
- [8] P. Kaufmann and J.-P. Raulin, Eos. Trans. AGU 86 (18), Jt. Assemb Suppl. Abstract SH54A-06 (2005).
- [9] J. M. Byrd, W. P. Leemans, A. Loftsdottir, B. Marcelis, M. C.Martin, W. R. McKinney, F. Sannibale, T. Scarvie, and C. Steier, Phys. Rev. Lett. 89, 224801 (2002).
- [10] J. I. Sakai, Y. Nagasugi, S. Saito, and P. Kaufmann, A&A preprint doi http://dx.doi.org/10.1051/0004-6361:20065368 (2006).
- [11] A. V. R. Silva, C. G. G. Castro, and P. Kaufmann, in Proc. of the V RHESSI Workshop, v. 1, 10 (2005);
- A. V. R. Silva, J.E.R. Costa, C. G. Gimenez de Castro, J.-P. Raulin, P. Kaufmann, G. H. Share, and R. J. Murphy, in Proc. of the SCOSTEP's 11th Quadrennial STP Symposium, 1, 1 (2006).
- [12] G. H. Share and R. J. Murphy, in Stars as Suns: Activity, Evolution and Planets, ASP Conf. Series 219, ed. A. Benz and A. Dupree, 133 (2004);
- G. H. Share, R. J. Murphy, D. M. Smith, R. A. Schwartz, and R. P. Lin, Ap. J. (Letters) 615, L169 (2004).
- [13] R. J. Murphy, C. D. Dermer, and R. Ramaty, Ap. J. (Supplement) 63, 721 (1987).
- [14] R. E. Lingenfelter and R. Ramaty, Planet. Space Sci. 15, 1303 (1967);
- R. Ramaty, B. Koslovsky, and R. E. Lingenfelter, Space Science Reviews 18, 341 (1975);
- B. Koslovsky, R. E. Lingenfelter, and R. Ramaty, Ap. J. 316, 801-818 (1987).
- [15] S. D. Drell and T. M. Yan, Phys. Rev. Lett. 25, 316 (1970);
- C. Crosso-Pilcher and M. J. Shochet, Ann. Rev. Nucl. Part. Sci. 36, 1 (1986).
- [16] M. Glück and E. Reya and A. Vogt, Eur. Phys. J. C 5, 461 (1998).
- [17] A. Donnachie and P. V. Landshoff, Phys. Lett. B 296, 227 (1992).
- [18] N. Vilmer, A. L. MacKinnon, G. Trotter, and C. Barat, A&A 412, 865 (2003).
Publication Dates
-
Publication in this collection
24 Apr 2007 -
Date of issue
Mar 2007
History
-
Received
29 Sept 2006