Abstract
In this work, we evaluate the D+sJ(2317), D(0)0(2308), D(0)0(2407) and D+0(2403) masses. These are scalar mesons recently discovered in the BABAR, BELLE and FOCUS Collaborations. The nature of these particles is intensely discussed nowadays. We treat them as a diquark-antidiquark configuration and treat the problem using the QCD sum rules (QCDSR) approach.
Charmed scalar mesons; QCD Sum Rules
Charmed scalar mesons masses within the QCD sum rules framework
A. LozéaI; M. E. BraccoII; R. D. MatheusIII; M. NielsenIII
IUniversidade Federal do Rio de Janeiro, C.P. 68528, 21945-970, Rio de Janeiro, RJ, Brazil
IIInstituto de Física, Universidade do Estado do Rio de Janeiro, Rua São Francisco Xavier 524, 20559-900, Rio de Janeiro, RJ, Brazil
IIIInstituto de Física, Universidade de São Paulo, C.P. 66318, 05389-970 São Paulo, SP, Brazil
ABSTRACT
In this work, we evaluate the D+sJ(2317), D00(2308), D00(2407) and D+0(2403) masses. These are scalar mesons recently discovered in the BABAR, BELLE and FOCUS Collaborations. The nature of these particles is intensely discussed nowadays. We treat them as a diquark-antidiquark configuration and treat the problem using the QCD sum rules (QCDSR) approach.
Keywords: Charmed scalar mesons; QCD Sum Rules
The detailed study of charmed scalar meson spectroscopy has provided many informations about the properties of q systems. However, our knowledge is still not enough to understand all the meson states known nowadays.
systems. However, our knowledge is still not enough to understand all the meson states known nowadays.
In 1977, R. L. Jaffe proposed a diquark (qq) antidiquark (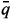
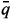 ) bound state structure and he explained the light scalar meson spectroscopy with JP = 0+ quantum numbers [1] using the MIT bag model. Surprisingly, Jaffe has shown that this description (qq
) bound state structure and he explained the light scalar meson spectroscopy with JP = 0+ quantum numbers [1] using the MIT bag model. Surprisingly, Jaffe has shown that this description (qq
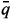 ) was able to accomodate the experimental masses of these mesons. In a recent work, [2] a QCDSR study of these light scalar mesons was carried out, in which they were treated as qq
) was able to accomodate the experimental masses of these mesons. In a recent work, [2] a QCDSR study of these light scalar mesons was carried out, in which they were treated as qq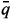
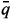 states. In that work the decay constants of these mesons were found and the result was consistent with the existing experimental data.
states. In that work the decay constants of these mesons were found and the result was consistent with the existing experimental data.
The discovery of the 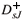 (2317) state reported by the BABAR Collaboration [3] and confirmed by the CLEO [4], BELLE [5] e FOCUS [6] Collaborations, renewed the interest on the subject. This particle is a new possible diquark-antidiquark candidate [7]. Others particles may be non-conventional states in the channel JP = 0+, such as
(2317) state reported by the BABAR Collaboration [3] and confirmed by the CLEO [4], BELLE [5] e FOCUS [6] Collaborations, renewed the interest on the subject. This particle is a new possible diquark-antidiquark candidate [7]. Others particles may be non-conventional states in the channel JP = 0+, such as  (2308), also reported by BELLE Collaboration [8], the neutral state
(2308), also reported by BELLE Collaboration [8], the neutral state  (2407) and the charged state
(2407) and the charged state  (2403), both detected by FOCUS Collaboration [9].
(2403), both detected by FOCUS Collaboration [9].
There is a lively theoretical debate on the masses of these mesons. For 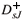 (2317), the result using quark models [10], is 160 MeV above the mass observed experimentally by BABAR [3]. Theoretical models involving c
(2317), the result using quark models [10], is 160 MeV above the mass observed experimentally by BABAR [3]. Theoretical models involving c states [7, 11-14], D - K meson mixing [15], non-conventional structures such as meson molecules [16, 17] or four quarks states [18] also present discrepancies with experimental values. This is specially so in [7], where the authors make use of QCDSR and predict the
states [7, 11-14], D - K meson mixing [15], non-conventional structures such as meson molecules [16, 17] or four quarks states [18] also present discrepancies with experimental values. This is specially so in [7], where the authors make use of QCDSR and predict the 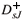 (2317) mass as a c
(2317) mass as a c system. Their result overestimated the data by 163 MeV. In the case of
system. Their result overestimated the data by 163 MeV. In the case of  (2308), the theoretical mass [10] is 100 MeV above of the result measured by BELLE [8]. In the cases of
(2308), the theoretical mass [10] is 100 MeV above of the result measured by BELLE [8]. In the cases of  (2407) and
(2407) and  (2403), the experimental masses [9] are in agreement with the quark model [10] and with the QCDSR calculation [7] for a c
(2403), the experimental masses [9] are in agreement with the quark model [10] and with the QCDSR calculation [7] for a c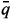 pair.
pair.
Because of the discrepancies between theoretical models and the experimental data, we propose that 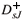 (2317),
(2317),  (2308),
(2308),  (2407) and
(2407) and  (2403) are four quarks states. In order to implement this proposal we use a diquark-antidiquark interpolating current [2] with the quantum numbers of these states.
(2403) are four quarks states. In order to implement this proposal we use a diquark-antidiquark interpolating current [2] with the quantum numbers of these states.
Our group worked with QCDSR several times before [19-24] and there are many others references about this subject. The QCDSR formalism is based on writing the 2-point correlation function
and perform an operator product expansion (OPE). The operators are quark and gluon condensates that appear in this expansion due to the non-trivial nature of the QCD vacuum. We can write the correlation function as a dispersion relation. In the OPE side, this correlation function is given by:
where the spectral density rOPE(s) contains both perturbative and non-perturbative contribuitions to the QCDSR.
In the phenomenological side, the spectral density (a pole state plus resonances) is given by the imaginary part of the correlation function:
where N depends on the decay constant fG and on the mass mG. Thus, we have the phenomenological side of QCDSR given by:
We can identify (2) and (4) and apply on both sides a Borel transformation defined as:
where the ratio Q2/n = M2 is kept finite when Q2, n ® ¥. The parameter M is called Borel mass. Applying this transformation to the correlation functions above we have:
We can see that Borel transformation suppresses exponentially the high momentum component. This does not eliminate the resonance and continuum contributions in Eq. (4) and it favors the low momentum contributions.
It is reasonable to say that the spectral density rOPE(s) contributes to the resonant states in (6) starting from a certain value s0 in the energy spectrum. Therefore, we can cut this contribution imposing a finite value for the upper limit in the energy integration. In this way, the QCDSR for the pole assumes a new form:
where the continuum threshold is given by  ~ mG. With this result, we should find the perturbative and non-perturbative parts of rOPE(s) for all cases studied in this work.
~ mG. With this result, we should find the perturbative and non-perturbative parts of rOPE(s) for all cases studied in this work.
We will find the scalar meson masses using the 2-point function given by the Eq. (1). As suggested in [2], the interpolanting currents with quantum numbers JP = 0+ for  +,
+, 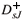 and
and  are given respectively by:
are given respectively by:
where a,..., e are color indices and C is the conjugation charge matrix. After some manipulations in Eq. (7), the QCDSR result for these meson masses is:
In the
+ case, we should calculate the spectral density using (8). An expression for this spectral density is given by:
where we can identify the perturbative and non-perturbative contributions given by the quark, mixed and gluon condensates, which are represented in Fig. (1).
With Eq. (11), the behavior of  can be studied as function of M2. First, we make an analysis of the
can be studied as function of M2. First, we make an analysis of the  Borel stability under small variations of mc. We can see in Fig. 2 the QCDSR results for small variations of mc (1,1 GeV < mc < 1,3 GeV) and continuum threshold given by
Borel stability under small variations of mc. We can see in Fig. 2 the QCDSR results for small variations of mc (1,1 GeV < mc < 1,3 GeV) and continuum threshold given by  = 2,6 GeV. Fig. 2, shows a relatively large interval in M2. To reduce this interval, we analyse the stability and also the relative weight of the pole and the continuum contributions in Eq. (6). We must define an adequate Borel window in order to favor the pole over the continuum and also ensure the convergence of the OPE. We can make this comparison between pole and continuum in relation to total contribution defining the following equations:
= 2,6 GeV. Fig. 2, shows a relatively large interval in M2. To reduce this interval, we analyse the stability and also the relative weight of the pole and the continuum contributions in Eq. (6). We must define an adequate Borel window in order to favor the pole over the continuum and also ensure the convergence of the OPE. We can make this comparison between pole and continuum in relation to total contribution defining the following equations:
where apolo + acont = 1. In Fig. 3 we observe the comparison between the relative contributions due to the pole and to the continuum given respectively by Eqs. (13) (solid curve) and (14) (dashed curve). Looking at Fig. 3, we choose a Borel window where the pole contribution is between 20% and 80% of the QCDSR total contribution what Thus we choose the interval 1 GeV2< M2< 2 GeV2.
Fig. 4 shows the QCDSR result for the  + mass as a function of the Borel parameter, where the values used for the quark mass and the condensates are: mc = 1,2 GeV, á
+ mass as a function of the Borel parameter, where the values used for the quark mass and the condensates are: mc = 1,2 GeV, á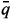 qñ = -(0,23)3 GeV3, ágs
qñ = -(0,23)3 GeV3, ágs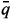 s.Gqñ =
s.Gqñ =  á
á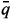 qñ,
qñ,  = 0,8 GeV2, á
= 0,8 GeV2, á G2ñ = 0,5 GeV4 e á
G2ñ = 0,5 GeV4 e á G3ñ = 0,045 GeV6. In the same figure, we use
G3ñ = 0,045 GeV6. In the same figure, we use  = 2,6 GeV (solid curve),
= 2,6 GeV (solid curve),  = 2,7 GeV (dashed curve) and
= 2,7 GeV (dashed curve) and  = 2,8 GeV (dotted curve) as the usual values for the continuum thresholds of the scalar mesons, as suggested in Ref. [7]. Considering the variations the in continuum threshold previously discussed and the Borel mass interval chosen here, the
= 2,8 GeV (dotted curve) as the usual values for the continuum thresholds of the scalar mesons, as suggested in Ref. [7]. Considering the variations the in continuum threshold previously discussed and the Borel mass interval chosen here, the  +(2405) mass found was:
+(2405) mass found was:
where the error is the standard deviation of  due to continuum threshold uncertainties. The result of mD0+0 is approximately 200 MeV smaller than the experimental value. This can be an indication that this hadron is not a diquark-antidiquark state. The QCDSR result for the current (8), at the begining associated with
due to continuum threshold uncertainties. The result of mD0+0 is approximately 200 MeV smaller than the experimental value. This can be an indication that this hadron is not a diquark-antidiquark state. The QCDSR result for the current (8), at the begining associated with  +, can indicate the existence of a scalar resonance in the charm channel with mass around 2,2 GeV, not yet observed experimentally.
+, can indicate the existence of a scalar resonance in the charm channel with mass around 2,2 GeV, not yet observed experimentally.
Proceeding in the same way for the 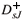 meson current given by Eq. (9), we find some spectral densities that are equal to the
meson current given by Eq. (9), we find some spectral densities that are equal to the  + case. These spectral densities correspond to the diagrams (a), (b), (d) - (i) in Fig. 1. The other possible diagrams are results of non-perturbative corrections due to the s quark mass in the quark propagator. These corrections correspond to the diagrams (a) - (f) of Fig. 5.
+ case. These spectral densities correspond to the diagrams (a), (b), (d) - (i) in Fig. 1. The other possible diagrams are results of non-perturbative corrections due to the s quark mass in the quark propagator. These corrections correspond to the diagrams (a) - (f) of Fig. 5.
In Fig. 6, we see the QCDSR results of 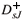 mass in the interval 1 GeV2< M2< 2 GeV2. In these curves, we use the continuum threshold values:
mass in the interval 1 GeV2< M2< 2 GeV2. In these curves, we use the continuum threshold values:  = 2,6 GeV (solid curve),
= 2,6 GeV (solid curve),  = 2,7 GeV (dashed curve) e
= 2,7 GeV (dashed curve) e  = 2,8 GeV (dotted curve). Considering variations in the continuum threshold and in the Borel window , the average value of the
= 2,8 GeV (dotted curve). Considering variations in the continuum threshold and in the Borel window , the average value of the 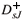 (2317) mass can be estimated as:
(2317) mass can be estimated as:
In this case, we see that the mass associated to the current (9) is in agreement with the experimental value. Therefore, it is an indication that the meson 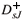 can be considered a four quark state and the scalar current (9) was the best choice to represent it.
can be considered a four quark state and the scalar current (9) was the best choice to represent it.
The spectral densities of  are found proceeding in a similar way. We have found some spectral densities that are equal to
are found proceeding in a similar way. We have found some spectral densities that are equal to  + and
+ and 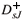 cases given by the diagrams (a), (d)-(g) on the Fig. 1 and (a)-(f) in Fig. 5. It is possible to add corrections due to the s quark propagator given by the diagrames (a)-(f) in Fig. 7. In the Fig. 8, we see the QCDSR results of
cases given by the diagrams (a), (d)-(g) on the Fig. 1 and (a)-(f) in Fig. 5. It is possible to add corrections due to the s quark propagator given by the diagrames (a)-(f) in Fig. 7. In the Fig. 8, we see the QCDSR results of  (2308) mass. Considering the variations in the continuum threshold and the Borel window, the value of
(2308) mass. Considering the variations in the continuum threshold and the Borel window, the value of  (2308) mass can be estimated as:
(2308) mass can be estimated as:
In this case, we also have the mass associated to the current given by (10) in agreement with the experimental value. This result suggests that  (2308) can be considered a four quark state.
(2308) can be considered a four quark state.
To summarize, the
+,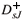 and
and  masses have been calculated using the QCDSR with quark and gluon condensate corrections up to dimension six. Our results are summarized in Table 1. The errors found come from the natural uncertainties due to variations in continuum threshold and the chosen Borel window.
masses have been calculated using the QCDSR with quark and gluon condensate corrections up to dimension six. Our results are summarized in Table 1. The errors found come from the natural uncertainties due to variations in continuum threshold and the chosen Borel window.
Comparing the values in Table 1 with experimental masses [9], [3] and [8], we conclude that  +(2405) can not be associated with a diquark-antidiquark state because the result we have obtained in this work is approximately 200 MeV smaller than experimental data. Therefore, this meson probably corresponds to a
+(2405) can not be associated with a diquark-antidiquark state because the result we have obtained in this work is approximately 200 MeV smaller than experimental data. Therefore, this meson probably corresponds to a  q state, what is in accordance with predictions of the quark model [10] and with the QCDSR calculation [7]. Our result for the current (8), in principle associated with
q state, what is in accordance with predictions of the quark model [10] and with the QCDSR calculation [7]. Our result for the current (8), in principle associated with  +(2405), can indicate the existence of a charmed scalar resonance with mass around 2,2 GeV, not yet observed experimentally. As for
+(2405), can indicate the existence of a charmed scalar resonance with mass around 2,2 GeV, not yet observed experimentally. As for 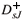 (2317) and
(2317) and  (2308), we conclude that these mesons can be interpreted as four quark states. The other theoretical calculations of these masses using quark models for a quark-antiquark pair [10], are not compatible with the experimental values. In a recent work [25], H. Kim and Y. Oh tested four different tetraquark currents with quantum numbers JP = 0+ in QCDSR for
(2308), we conclude that these mesons can be interpreted as four quark states. The other theoretical calculations of these masses using quark models for a quark-antiquark pair [10], are not compatible with the experimental values. In a recent work [25], H. Kim and Y. Oh tested four different tetraquark currents with quantum numbers JP = 0+ in QCDSR for 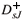 (2317). In that work, the authors conclude that the best current to reproduce this meson mass is the same one chosen here, the diquark-antidiquark state with scalar structure. This gives support to our results.
(2317). In that work, the authors conclude that the best current to reproduce this meson mass is the same one chosen here, the diquark-antidiquark state with scalar structure. This gives support to our results.
[2] T. V. Brito, F. S. Navarra, M. Nielsen, and M. E. Bracco, Phys. Lett. B 608, 69 (2005).
[3] BABAR Coll., B. Aubert et al., Phys. Rev. Lett. 90, 242001 (2003).
[4] CLEO Coll., D. Besson et al., Phys. Rev. D 68, 032002 (2003).
[5] BELLE Coll., P. Krokovny et al., Phys. Rev. Lett. 91, 262002 (2003).
[6] FOCUS Coll., E. W. Vaandering, hep-ex/0406044.
[7] A. Hayashigaki and K. Terasaki, hep-ph/0411285.
[8] BELLE Coll., K. Abe et al., Phys. Rev. D 69, 112002 (2004).
[9] FOCUS Coll., J. M. Link et al., Phys. Lett. B 586, 11 (2004).
[10] S. Godfrey and N. Isgur, Phys. Rev. D 32, 189 (1985); S. Godfrey and R. Kokoski, Phys. Rev. D 43, 1679 (1991).
[11] Y.-B. Dai, C.-S. Huang, C. Liu, and S.-L. Zhu, Phys. Rev. D 68, 114011 (2003).
[12] G. S. Bali, Phys. Rev. D 68, 071501(R) (2003).
[13] A. Dougall et al., Phys. Lett. B 569, 41 (2003).
[14] S. Narison, Phys. Lett. B 605, 319 (2005).
[15] E. van Beveren and G. Rupp, Phys. Rev. Lett. 91, 012003 (2003).
[16] T. Barnes, F. E. Close, and H.J. Lipkin, Phys. Rev. D 68, 054006 (2003).
[17] A. P. Szczepaniak, Phys. Lett. B 567, 23 (2003).
[18] T. Browder, S. Pakvasa, and A. A. Petrov, Phys. Lett. B 578, 365 (2004).
[19] F. S. Navarra, M. Nielsen, M. E. Bracco, M. Chiapparini, and C. L. Schat, Phys. Lett. B 489, 319 (2000).
[20] M. E. Bracco, M. Chiapparini, A. Lozéa, F. S. Navarra, and M. Nielsen, Phys. Lett. B 521, 1 (2001).
[21] F. S. Navarra, M. Nielsen, and M. E. Bracco, Phys. Rev. D 65, 037502 (2002).
[22] F. Carvalho, F. O. Durães, F. S. Navarra, and M. Nielsen, Phys. Rev. C 72, 024902 (2005).
[23] M. E. Bracco, M. Chiapparini, F. S. Navarra, and M. Nielsen, Phys. Lett. B 605, 326 (2005).
[24] R. D. Matheus, F. S. Navarra, M. Nielsen, and R. Rodrigues da Silva, Braz. J. Phys. 34, 236 (2004); Phys. Lett. B 541, 265 (2002).
[25] H. Kim and Y. Oh, Phys. Rev. D 72, 074012 (2005).
Received on 29 September, 2006
- [1] R. L. Jaffe, Phys. Rev. D 15, 267 (1977).
- [2] T. V. Brito, F. S. Navarra, M. Nielsen, and M. E. Bracco, Phys. Lett. B 608, 69 (2005).
- [3] BABAR Coll., B. Aubert et al., Phys. Rev. Lett. 90, 242001 (2003).
- [4] CLEO Coll., D. Besson et al., Phys. Rev. D 68, 032002 (2003).
- [5] BELLE Coll., P. Krokovny et al., Phys. Rev. Lett. 91, 262002 (2003).
- [6] FOCUS Coll., E. W. Vaandering, hep-ex/0406044.
- [7] A. Hayashigaki and K. Terasaki, hep-ph/0411285.
- [8] BELLE Coll., K. Abe et al., Phys. Rev. D 69, 112002 (2004).
- [9] FOCUS Coll., J. M. Link et al., Phys. Lett. B 586, 11 (2004).
- [10] S. Godfrey and N. Isgur, Phys. Rev. D 32, 189 (1985);
- S. Godfrey and R. Kokoski, Phys. Rev. D 43, 1679 (1991).
- [11] Y.-B. Dai, C.-S. Huang, C. Liu, and S.-L. Zhu, Phys. Rev. D 68, 114011 (2003).
- [12] G. S. Bali, Phys. Rev. D 68, 071501(R) (2003).
- [13] A. Dougall et al., Phys. Lett. B 569, 41 (2003).
- [14] S. Narison, Phys. Lett. B 605, 319 (2005).
- [15] E. van Beveren and G. Rupp, Phys. Rev. Lett. 91, 012003 (2003).
- [16] T. Barnes, F. E. Close, and H.J. Lipkin, Phys. Rev. D 68, 054006 (2003).
- [17] A. P. Szczepaniak, Phys. Lett. B 567, 23 (2003).
- [18] T. Browder, S. Pakvasa, and A. A. Petrov, Phys. Lett. B 578, 365 (2004).
- [19] F. S. Navarra, M. Nielsen, M. E. Bracco, M. Chiapparini, and C. L. Schat, Phys. Lett. B 489, 319 (2000).
- [20] M. E. Bracco, M. Chiapparini, A. Lozéa, F. S. Navarra, and M. Nielsen, Phys. Lett. B 521, 1 (2001).
- [21] F. S. Navarra, M. Nielsen, and M. E. Bracco, Phys. Rev. D 65, 037502 (2002).
- [22] F. Carvalho, F. O. Durăes, F. S. Navarra, and M. Nielsen, Phys. Rev. C 72, 024902 (2005).
- [23] M. E. Bracco, M. Chiapparini, F. S. Navarra, and M. Nielsen, Phys. Lett. B 605, 326 (2005).
- [24] R. D. Matheus, F. S. Navarra, M. Nielsen, and R. Rodrigues da Silva, Braz. J. Phys. 34, 236 (2004);
- Phys. Lett. B 541, 265 (2002).
- [25] H. Kim and Y. Oh, Phys. Rev. D 72, 074012 (2005).
Publication Dates
-
Publication in this collection
24 Apr 2007 -
Date of issue
Mar 2007
History
-
Received
29 Sept 2006
























