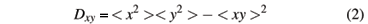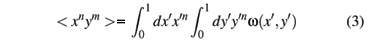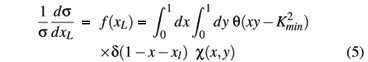Gluon saturation and leading particle spectra in pp collisions

Abstract

In this work we use the IGM, a model that describes well the energy flux in hadronic collisions, to study the leading particle spectrum when saturation effects on the gluon distribution function are included. The leading particle spectrum is calculated for several center of mass energies (<FONT FACE=Symbol>Ö</FONT>s). In the very high energy limit we compare our results with the predictions made in a recent paper, which also addresses the same problem.

Gluon saturation; Leading particle spectra; Hadronic collisions

Gluon saturation and leading particle spectra in pp collisions

F. O. Durães^I; V. P. Gonçalves^II; F. S. Navarra^III; A. L. V. R. dos Reis^III; G. Wilk^IV

^IUniversidade Presbiteriana Mackenzie, C.P. 01302-907, São Paulo, SP, Brazil

^IIUniversidade Federal de Pelotas C.P. 354, CEP 96010-900, Pelotas, RS, Brazil

^IIIInstituto de Física, Universidade de São Paulo, C.P. 66318, 05315-970 São Paulo, SP, Brazil

^VISoltan Institute for Nuclear Studies, Nuclear Theory Department, ul. Hoza 69, 00-681 Warsaw, Poland

ABSTRACT

In this work we use the IGM, a model that describes well the energy flux in hadronic collisions, to study the leading particle spectrum when saturation effects on the gluon distribution function are included. The leading particle spectrum is calculated for several center of mass energies (Ös). In the very high energy limit we compare our results with the predictions made in a recent paper, which also addresses the same problem.

Keywords: Gluon saturation; Leading particle spectra; Hadronic collisions

I. INTRODUCTION

Nowadays there are enough reasons to believe that when hadrons or nuclei suffer scattering at asymptotically high energies, they behave in a qualitatively different way. This high energy limit of QCD is called the Color Glass Condensate (CGC) [1]. It is not yet very clear at which energies we will unambiguously observe the CGC and which are the best observables to look for it.

Many observables have been considered as possible signatures of the CGC. In deep inelastic scattering, for example, there have been many attempts to understand HERA data [2] in the context of gluon saturation. In p-A collisions, going to forward rapidities corresponds to probing the nuclear wavefunction at smaller x, which should exhibit saturation at some low value of x. Thus, this is one of the best places to search for the CGC or the effects of quantum evolution [3]. Such effects should be measured in the nuclear modification factor, and this was indeed done by the BRAHMS experiment in deuteron-Au collisions at RHIC [4]. The experimental data show enhancement of the ratio at mid-rapidity (the Cronin effect) and suppression at forward rapidities. Such global behavior is qualitatively consistent with the predictions made by the CGC [5, 6]. Quantitative results are also available. Kharzeev, Kovchegov, and Tuchin have computed the nuclear modification factor within the framework of the CGC [7], and found rather good agreement with the BRAHMS data.

So far, we have understood many things within the framework of the CGC but, in fact, there are several other approaches which can describe the Cronin effect, high p_T suppression and other proposed CGC signals. Thus, in order to be convinced enough, it is necessary to perform more detailed investigation in the future.

II. LEADING PARTICLES

In high energy hadron-hadron collisions the momentum spectra of outgoing particles which have the same quantum numbers as the incoming particles, also called leading particle (LP) spectra, have been measured already some time ago [8, 14]. More recently data on leading protons produced in electron-proton reactions at HERA with a c.m.s. energy one order of magnitude higher than in the other above mentioned hadronic experiments became available [9]. These measurements of LP spectra both in hadron-hadron and in electron-proton collisions have renewed the interest on the subject, especially because the latter are measured at higher energies and therefore the energy dependence of the LP spectra can be determined.

Until recently gluon saturation effects were never included in the study of leading hadron production. This was done in [10] where it was argued that the inclusive distribution of leading hadrons may be computed with weak coupling methods for very high energy collisions when the target approaches the ''black body'' limit. The main conclusion of [10] was that leading hadron production is strongly suppressed. According to the authors, this should happen because for a dense target all incident proton constituents scatter and experience a large momentum transfer (which is set by the saturation scale of the target). Thus, the coherence of the projectile is destroyed completely, and the scattered quarks and gluons fragment independently. As a consequence, the proton decays predominantly into a beam of leading mesons, with the baryon number shifted to small light-cone momentum fraction (< 0.1). In simple terms, the onset of saturation would be indicated by the onset of quark independent fragmentation for LP production. Moreover, this mechanism of LP production implies a strong energy loss by the valence quarks and the consequent strong enhancement of the energy used to produce secondary particles, the so called inelasticity [11].

III. THE INTERACTING GLUON MODEL

Our model is based on the following assumptions [12, 13]:

(i) The two colliding hadrons are represented by their valence quarks plus the gluon clouds (which include also q - pairs).

(ii) During the collision, the clouds interact strongly and fractions x of the projectile initial 4-momentum and y of the target initial 4-momentum are deposited in the central region, forming a cluster called "central fireball", or CF.

(iii) The valence quarks interact less, "fly through", recombine and form the final leading particles in the fragmentation regions. This happens mainly because s_qq « s_qg « s_gg.

The leading particles carry momentum fracions x_L = 1-x (projectile) and y_L = 1-y (target). The probability that a CF is formed with momentum fractions x and y of the two colliding hadrons is given by the function c(x,y):

where

and

c₀ is a normalization constant. The function w(x¢,y¢) represents the average number of gluon-gluon collisions with x' e y'. This function is a sum of soft (w_S) and semi-hard (w_H) components and hence the quantities <xⁿ y^m> (the so-called ''moments'' of the function w) will be also split into soft and semi-hard parts:

The leading particle spectrum in the IGM is given by:

where K_min = m₀ / , is the minimal inelasticity of the model. Due to the symmetry of proton - proton collisions there are only three independent soft momenta: < x >_S ( = < y > _S) , < x² > _S ( = < y² > _S) and < x y >_S. These three numbers will be adjusted so that (5) reproduces the experimental data [14] taken at lower energies, @ 10 - 20 GeV². In this energy region neither semi-hard nor saturation physics is active.

IV. THE IGM WITH GLUON SATURATION

As it was seen in the previous sections, the IGM contains a non-perturbative (soft) and a perturbative (semi-hard) component. When we move to higher energies the perturbative part becomes dominant. When we reach the energy region where gluon saturation becomes important, there is a change in the reaction dynamics. The gluon density must be computed with a non-linear evolution equation and also the elementary cross sections must include the resummation over a large number of rescatterings. In [15], gluon production in the saturation regime was studied in a simple, analytical approach hereafter called the KLN model. In particular, KLN calculated the rapidity distribution of gluons, produced through gluon-gluon fusion, in proton-proton collisions finding:

where

In the above expression G(x, ) are the gluon distribution function, N_c is the number of colors, S is the area of the projectile or target, a_s is the coupling constant given by pertubative QCD and s_pp is the total proton-proton cross section. k₀ is a constant parameter. Q_s is the saturation scale given by: .

where = 0.34 GeV², x₀ = 3 ×10^-4 and l = 0.29. From (6) it is easy to compute the number of gluon - gluon collisions per unit of rapidity and transverse momentum, , and then change variables obtaining which we indentify with w_H (x,y), the function to be inserted in (4). Thus, we have:

In (7), the exponent D is taken from the GRV94 gluon distribution [16] and is given by D = 2.792 + 2.215 U + 0.422 U² - 0.104 U³ where U µ ln ( ln () ). We were obliged to change D because in our calculation we are integrating over all values of x, for the target and the projectile, whereas in [15], the values of the corresponding x (and y) were fixed at small values. The change in D improves the behavior of G(x,) at large x (x @ 1), which is relevant for us. Finally, imposing the gluon momentum sum rule:

we fix the parameter k₀.

V. NUMERICAL RESULTS

We have fixed the free parameters of the model (the three soft momenta) by fitting lower energy data [14]: < x >_S = 0.6, < x² >_S = 0.5 and < x y >_S = 0.0. We then have varied the c.m.s. energy obtaining the results shown in Fig. 1, where we see that, increasing the energy, the LP spectrum becomes peaked at smaller values of x_L. This softening is though very mild. An interesting question now would be: what would happen to these spectra if there would be no saturation? The answer is obtained by switching off the first line of (7), since when > we are in the linear regine with no saturation effects. The so obtained spectra are shown in Fig. 2. The curves show a similar softening trend, much like in Fig. 1, but at the highest energies this softening is much more pronounced than when saturation is included. In order to make this difference more evident we plot, in Fig. 3 the ratio f(x_L)_sat/f(x_L)_no-sat. This ratio is very flat and almost always close to one. However at the highest energy it shows a departure from one indicating that the effect of saturation is to slow down the softening trend and to generate an excess of fast leading particles. Of course, this result depends on the parton densities used and also on some other numbers used here. However, qualitatively, it is very stable. We can conclude that, for this observable, the onset of saturation tames the softening of LP spectra, as it tames the growth of the total hadron-hadron cross section, the growth of the produced particle densities in the central region of heavy ion collisions.

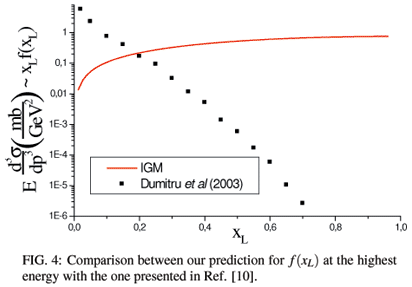
All conclusions above rely, more than on any numerical input, on the assumption that valence quarks go through the target and, after loosing their gluon clouds and loosing some energy due to scattering off the target partons, recombine to form the final leading baryons. This mechanism works very well at low energies [17, 18] and it is not clear that it will no longer work at higher energies. If this happens, then the individual valence quarks will undergo independent fragmentation and originate the leading baryons. In this case there is a very strong softening. In [10], assuming independent fragmentation the authors computed the LP spectrum at very high energies, which we compare with ours in Fig. 4. The discrepancy is very large. Although the authors of [10] did a fine work in calculating the energy loss of a valence quark hitting the color glass condensate in the target, this energy loss remains only a small effect in comparison to the convolution with the fragmentation function, the real ''leading particle killer''.

VI. CONCLUSION

In this work we have studied leading particle (LP) production at high and very high energies. In these processes the non-perturbative component is important, especially at lower energies, and must be modeled. The perturbative component becomes dominant at very high energies and can be calculated with perturbative QCD. On the other hand, at these energies we expect to see the effects of gluon saturation. Using the Interacting Gluon Model, we have fitted the LP spectra at low energies and then, including the effects of parton saturation, we have made predictions for LP spectra at very high energies comparing them with the extrapolation of the usual linear pQCD. This comparison revealed that the behavior of LP spectra with the energy is not a good signature of the color glass condensate (CGC). We have seen that, at least in the context of the IGM, gluon saturation slows down the softening trend of LP spectra with increasing energies. It is however a very modest effect. We conclude then that the LP spectrum is not a good place to search for parton saturation effects. This conclusion depends strongly on the choice of the LP formation mechanism. At low energies this process is dominated by valence quark recombination. We assume that this continues to be the case at very high energies. If, on the other hand, the leading particles are formed through independent quark fragmentation, then saturation effects might become more visible.

Acknowledgements: We are grateful to FAPESP (contract number 2004/08960-4) and to CAPES for financial support.

[1] E. Iancu e R. Venugopalan, hep-ph/0303204, QGP3, Eds. R.C. Hwa and X.N.Wang, World Scientific; E. Iancu, A. Leonidov, and L. McLerran, hep-ph/0202270, Eds. J.-P. Blaizot and E. Iancu, NATO Science Series, Kluwer, 2002; E. Iancu and R, Venugopalan, hep-ph/0303104; J. Jalilian-Marian, J. Phys. G30, 751 (2004); J. Jalilian-Marian and Y. V. Kovchegov, Prog. Part. Nucl. Phys. 56, 104 (2006).

[2] J. Breitweg et al. (ZEUS), Phys. Lett. B 487, 53 (2000); S. Chekanov et al. (ZEUS), Eur. Phys. J. C 21, 443 (2001); C. Adloff et al. (H1), Eur. Phys. J. C 21, 33 (2001).

[3] A. Dumitru and J. Jalilian-Marian, Phys. Rev. Lett. 89, 022301 (2002).

[4] I. Arsene et al. (BRAHMS Collab.), Phys. Rev. Lett. 93, 242303 (2004).

[5] D. Kharzeev, Y. Kovchegov, and K. Tuchin Phys. Rev. D 68, 094013 (2003).

[6] J. Albacete, N. Armesto, A. Kovner, C. Salgado, and U. Wiedemann, Phys. Rev. Lett. 92, 082001 (2004).

[7] D. Kharzeev, Y. V. Kovchegov, and K. Tuchin, Phys. Lett. B 599, 23 (2004).

[8] EHS/NA22 Collaboration, N.M. Agababyan et al., Z. Phys. C 75, 229 (1996).

[9] N. Cartiglia, Leading Baryons at Low x_L in DIS and Photoproduction at ZEUS, hep-ph/9706416.

[10] A. Dumitru, L. Gerland, and M. Strikman, Phys. Rev. Lett. 90, 092301 (2003); Erratum-ibid. 91, 259901 (2003).

[11] F. S. Navarra, O. V. Utyuzh, G. Wilk, and Z. Wlodarczyk, Phys. Rev. D 67, 114002 (2003); H. M. Portella, L. C. Santos de Oliveira, and C. E. Campos Lima, Int. J. Mod. Phys. A 19, 3583 (2004).

[12] G. N. Fowler, F. S. Navarra, M. Plumer, A. Vourdas, R. M. Weiner, and G. Wilk, Phys. Rev. C 40, 1219 (1989).

[13] F. O. Durães, F. S. Navarra, and G. Wilk, Phys. Rev. D 47, 3049 (1993); Braz. J. Phys. 35, 3 (2005).

[14] D.S. Barton et al., Phys. Rev. D 27, 2580 (1983); A.E. Brenner et al., Phys. Rev. D 26, 1497 (1982).

[15] D. Kharzeev and M. Nardi, Phys. Lett. B 507, 121 (2001); D. Kharzeev, E. Levin, and M. Nardi, Nucl. Phys. A 730, 448 (2004); Erratum-ibid A 743, 329 (2004); Phys. Rev. C 71, 054903 (2005); Nucl. Phys. A 747, 609 (2005). ; D. Kharzeev, E. Levin, and L. McLerran, Phys. Lett. B 507, 121 (2001). ; D. Kharzeev and E. Levin, Phys. Lett. B 523, 79 (2001).

[16] M. Gluck, E. Reya, and A. Vogt, Z. Phys. C 67, 433 (1995).

[17] R. Rapp and E. V. Shuryak, Phys. Rev. D 67, 074036 (2003).

[18] E. Braaten, Y. Jia, and T. Mehen, Phys. Rev. Lett. 89, 122022 (2002); E. Braaten and Y. Jia, Phys. Rev. D 66, 014003 (2002); E. Braaten, M. Kusunoki, Y. Jia, and T. Mehen, Phys. Rev. D 70, 054021 (2004).

Received on 29 September, 2006

Publication Dates

• Publication in this collection
  24 Apr 2007
• Date of issue
  Mar 2007

History

• Received
  29 Sept 2006