Abstract
We consider a local, renormalizable, BRST-invariant action for QCD in Coulomb gauge that contains auxiliary bose and fermi ghost fields. It possess a non-perturbative vacuum that spontaneously breaks BRST-invariance. The vacuum condition leads to a gap equation that introduces a mass scale. Calculations are done to one-loop order in a perturbative expansion about this vacuum. They are free of the finite-T infrared divergences found by Lindé and which occur in the order g6 corrections to the Stefan-Boltzmann equation of state. We obtain a finite result for these corrections. Renormalization and renormalization-group flow are described. We calculate the ghost propagator and color-Coulomb potential to one-loop and find that they are long range, whereas the 3-dimensionally transverse would-be physical gluon propagator is suppressed like k² at small |k|. These one-loop results accord with the Gribov scenario in Coulomb gauge and with recent numerical determinations of these quantities. When the auxiliary fields are integrated out, one obtains the standard Coulomb gauge action with a cut-off at the Gribov horizon.
QCD; Gluon plasma; Spontaneous breaking of BRST
Equation of state of gluon plasma and renormalization of local action
Daniel Zwanziger
New York University
ABSTRACT
We consider a local, renormalizable, BRST-invariant action for QCD in Coulomb gauge that contains auxiliary bose and fermi ghost fields. It possess a non-perturbative vacuum that spontaneously breaks BRST-invariance. The vacuum condition leads to a gap equation that introduces a mass scale. Calculations are done to one-loop order in a perturbative expansion about this vacuum. They are free of the finite-T infrared divergences found by Lindé and which occur in the order g6 corrections to the Stefan-Boltzmann equation of state. We obtain a finite result for these corrections. Renormalization and renormalization-group flow are described. We calculate the ghost propagator and color-Coulomb potential to one-loop and find that they are long range, whereas the 3-dimensionally transverse would-be physical gluon propagator is suppressed like k2 at small |k|. These one-loop results accord with the Gribov scenario in Coulomb gauge and with recent numerical determinations of these quantities. When the auxiliary fields are integrated out, one obtains the standard Coulomb gauge action with a cut-off at the Gribov horizon.
Keywords: QCD; Gluon plasma; Spontaneous breaking of BRST
I. INTRODUCTION
A. Overview
There exists a well articulated scenario for confinement in Coulomb gauge that was originally developed by Gribov [1], and which has been confirmed by recent numerical studies that are reviewed below. In the present article we shall show that this scenario may be derived from a local renormalizable, BRST-invariant action. This action possesses a non-perturbative vacuum, and the features of the gluon and ghost propagators foreseen by Gribov are obtained in zeroth and first order of a systematic perturbative expansion in g about this vacuum.
The local, renormalizable, BRST-invariant action differs from the standard action in Coulomb gauge in that it contains auxiliary fermi and bose ghost fields. This action possesses a non-perturbative vacuum that is obtained by a c-number shift of the bose ghost fields which then mix with the gluon field, and the vacuum is determined by a gap equation that introduces a mass into the theory. This is in close analogy to electro-weak theory in which a shift of the Higgs field gives the W and Z bosons a mass. However in electroweak theory the vacuum spontaneously breaks global gauge invariance, whereas in the present case it is BRST invariance that is spontaneously broken. Another difference is that, in electroweak theory, global gauge symmetry is restored at high temperature whereas, in the present approach, the spontaneous breaking of BRST invariance occurs at all temperatures. This allows us to calculate finite corrections to the Stefan-Boltzmann equation of state at high temperature.
In 1980 Lindé [2] showed that standard finite-temperature perturbation theory suffers from infrared divergences. Since then no solution has been found, although the infrared divergences may be avoided by introducing a magnetic mass for the gluon in an ad hoc manner. Some time ago it was suggested that these divergences arise because the suppression of infrared gluons by the proximity of the Gribov horizon in infrared directions is neglected in standard perturbation theory [3]. It appears that the infrared divergences do not arise in the expansion in g presented here, because the free propagator (in the non-perturbative vacuum) of 3-dimensionally transverse, would-be physical gluons is strongly suppressed in the infrared.
Calculations are done in a perturbative expansion in g about the non-perturbative vacuum. Results for the ghost and gluon propagator in zero- and one-loop calculations are in accord with the numerical results described below, and with the Gribov scenario. The issue of Gribov copies is not raised for this action. However when the auxiliary fields are integrated out, one obtains a non-local action and a gap equation that, remarkably, had been obtained previously from the standard Coulomb-gauge action by imposing a cut-off at the Gribov horizon [4].
In general the present review follows [5] closely, but the discussion of renormalization and renormalization-group flow have not been presented before.
B. Confinement scenario in Coulomb gauge and recent numerical results
One would like to explain the presence of a long-range force that confines colored objects. At the same time one is faced by the apparently contradictory requirement that the massless gluons that are supposed to transmit this force are absent from the physical spectrum.
This seeming paradox is addressed in a scenario in Coulomb gauge that was originally developed by Gribov [1]. It relies on the fact that manifest Lorentz invariance does not hold in Coulomb gauge, so space-space and time-time components of the gluon propagator are independent. In this scenario, the 3-dimensionally transverse, would-be physical gluon propagator,  (k, k0), is suppressed at small k because of the proximity of the Gribov horizon in infrared directions, so physical gluons are absent from the physical spectrum. At tree level in the non-perturbative vacuum, the 3-dimensionally transverse propagator is found to be
(k, k0), is suppressed at small k because of the proximity of the Gribov horizon in infrared directions, so physical gluons are absent from the physical spectrum. At tree level in the non-perturbative vacuum, the 3-dimensionally transverse propagator is found to be
which has poles at
in agreement with the Coulomb-gauge energy obtained by Gribov. This propagator is strongly suppressed in the infrared, vanishing like k2. On the other hand confinement of quarks, or any colored object, is explained by the long range of the instantaneous part, Vcoul(R), of the time-time component of the gluon propagator,
that couples universally to color charge. Here P(x,t) is a non-instantaneous vacuum polarization term that is screening, whereas the color-Coulomb potential, Vcoul(R), is anti-screening [6]. Gribov found that the concentration of probability at the Gribov horizon causes Vcoul(R) to have the long-range, confining property limR® ¥Vcoul(R) = ¥. The local, renormalizable theory presented here yields results in agreement with Gribov's predictions to zeroth or first order in an expansion in g about the non-perturbative vacuum.
Numerical studies provide a valuable laboratory for testing various confinement scenarios. In accord with the Gribov scenario, it was found [7] that the equal-time would-be physical gluon propagator  (k)|t = 0 is indeed suppressed at small k, while the fourier transform
(k)|t = 0 is indeed suppressed at small k, while the fourier transform  coul(k) is enhanced at small k. This enhancement corresponds to a long-range, color-Coulomb potential Vcoul(R). It was subsequently found numerically [8] that the long-distance behavior of the color-Coulomb potential is consistent with a linear increase at large R,
coul(k) is enhanced at small k. This enhancement corresponds to a long-range, color-Coulomb potential Vcoul(R). It was subsequently found numerically [8] that the long-distance behavior of the color-Coulomb potential is consistent with a linear increase at large R,
with the Coulomb string tension given approximately by scoul ~ 3s. Here s is the physical string tension between a pair of external quarks as determined from a large Wilson loop. Other studies provided additional support for the confinement scenario in Coulomb gauge, including in particular the consistency of Coulomb-gauge and center-vortex scenarios [9,10]. These numerical studies were certainly encouraging for the confinement scenario in Coulomb gauge.
However, as in the old tale of the sorcerer's apprentice, it was unexpectedly discovered that this "confinement scenario" works also in the deconfined phase. Indeed it was found numerically that the long-distance behavior of Vcoul(R) is consistent with a linear increase, scoul > 0, at temperatures T above the phase transition, T > Tc, where the physical string tension vanishes, s = 0 [9]. Investigation of the temperature dependence of scoul revealed that at high T in the deconfined phase, the Coulomb string tension increases with T, consistent with a magnetic mass [11],
Thus, from the numerical evidence, what has been called the Gribov "confinement" scenario works as well in the deconfined phase of QCD as in the confined phase.
Although this came as a surprise, it was a surprise that could have been predicted. Recall that temperature determines the extent, b = T1, of Euclidean space-time in the time direction, 0 < t < b. On the other hand the Coulomb gauge condition,
holds at each time t, and gauge fixing to the minimal Coulomb gauge is done at each time t, independently of the extent b = T1 in the time direction. [For each t, one minimizes the 3-dimensional norm-square ò d3x|gA(x,t)|2 of the 3-vector potential, A(x,t), with respect to 3-dimensional gauge transformations gt(x) = g(x,t), where gAi = g1Aig + g1¶ig. The minimal Coulomb gauge leaves unfixed space-independent but time-dependent gauge transformations g(t).] Likewise the cut-off at the Gribov horizon is applied to 3-dimensional configurations A(x,t) at each time, t, independently of the extent b in the time direction. So the arguments which lead to these propagators should, and apparently do, apply for all temperatures T, including in the deconfined phase. We shall in fact obtain the temperature dependence (5), and the propagators (1) and (4), modulo a logarithm, at all temperatures T, from a local, renormalizable action with a non-perturbative vacuum.
It thus appears, from both numerical and analytic evidence, that what originated as a scenario for confinement provides a more general framework for QCD that holds both in the confined and deconfined phases. Although this is surprising at first, there is no paradox. For the unbounded increase of the color-Coulomb potential, limR ® ¥ Vcoul(R) = ¥, is a necessary condition for confinement, but it is not a sufficient condition [12]. Indeed at large R, Vcoul(R) provides an upper bound on the physical, gauge-invariant potential V(R) between a pair of external quarks,
provided that V(R) is confining, limR ® ¥V(R) = ¥. Thus there is no confinement without Coulomb confinement.
But the converse is false. To see why this is so, it is sufficient to consider the case of QED, which is simpler than QCD, but manifests screening of the electric field by the plasma. In QED the free energy V(x) of a pair of static electric charges, at a temperature T = b1 and separation x, is obtained from
By periodicity  (x,t + b) =
(x,t + b) =  (x,t), we find that the free energy is given by
(x,t), we find that the free energy is given by
The point is that this is the zero-frequency part of e2D00(x,t), which is not the same as the instantaneous part Vcoul(|x|) of e2D00(x,t), defined in (3). Indeed, in QED the instantaneous part is given by Vcoul(0) =  , which is of infinite range, whereas the free energy is given by the screened potential,
, which is of infinite range, whereas the free energy is given by the screened potential,
where [13], and [14] p. 93,
This QED example provides an instance where the bound V(R) < Vcoul(R) holds for all R.
C. Relation to other approaches
Equal-time correlators in Coulomb gauge may be calculated using the Schwinger-Dyson equations of the Hamiltonian formulation [15-19]. The gluon energy obtained by variational calculation accords at both high and low momentum with the Gribov energy (2), provided that the Faddeev-Popov determinant is properly accounted for [17,18]. Indeed the Faddev-Popov determinant dominates the low-energy dynamics. The same Gribov energy (2) will be obtained here by a quite different method. A systematic study of the infrared limits of propagators and vertices has been reported recently in [19], which includes earlier results [20,21]. The gluon and ghost propagators obtained in the present article from low-order perturbation theory about the non-perturbative vacuum are in qualitative agreement with those of [19] although the infrared critical exponents are not identical. We note that the Schwinger-Dyson equations in Coulomb and Landau gauge should be quite reliable in the infrared limit because the weight in the infrared limit is precisely given by the Faddeev-Popov determinant, det(Di¶i) with negligible contribution from the gluon wave-functional or action [22], a phenomenon known as ghost dominance [23,24]. This is used to advantage with the horizon condition and non-renormalization of ghost-gluon vertices. As a result the infrared limit of the Schwinger-Dyson equations in Coulomb and Landau gauges decouples from finite-momentum correlators. Moreover errors from truncation of 3-vertices have been controlled [19,25,26]. Thus it would appear that the infrared exponents at zero temperature reported in [19] are more accurate than those reported in the present article that are obtained by an expansion in g about the non-perturbative vacuum to one-loop order. Nevertheless both methods have their advantages. In particular the field-theoretic method described here also gives the correlators in Coulomb gauge at unequal times and finite temperature, and does not rely on a variational Ansatz for the wave-functional that would be needed to go beyond the infrared limit. It relies on the familiar methods of local, renormalizable perturbation theory.
The instantaneous color-Coulomb potential has recently been used in Dyson-Schwinger and Bethe-Salpeter equations to find solutions for pseudoscalar and vector mesons [27]. Cancellation of the energy divergences of Coulomb gauge has been demonstrated at the two-loop level [28], and renormalization and cancellation of energy divergences to all orders in perturbation theory in Coulomb gauge has been elucidated recently, [29,30].
Equivalence of a cut-off at the Gribov horizon to a modified local action with auxiliary fields was first established in Landau gauge some time ago [31]. It was then shown that the horizon condition renormalizes consistently, and that the ghost propagator in Landau gauge has a  or dipole singularity [32]. The symmetries of the local theory in Landau gauge were exhibited and algebraic renormalizability established [33,34], and it was shown that the horizon condition coincides with the defining condition for a non-perturbative vacuum that spontaneously breaks the BRST symmetry of a local, renormalizable, BRST-invariant Landau-gauge action [33]. More recently, using this local action in Landau gauge, the gap equation was determined to two-loop order, and it was verified at the two-loop level that the ghost propagator has a dipole singularity in the infrared [35]. It has also been found to one-loop order that the gluon propagator in Landau gauge vanishes like k2, and that the renormalization-group invariant coupling as(k) appropriate to the Landau gauge is finite at k = 0 [36]. Thus the elements of Gribov's scenario in Landau gauge [1] have been derived from a local, renormalizable, BRST-invariant action. The Landau gauge case has been reviewed in [37].
or dipole singularity [32]. The symmetries of the local theory in Landau gauge were exhibited and algebraic renormalizability established [33,34], and it was shown that the horizon condition coincides with the defining condition for a non-perturbative vacuum that spontaneously breaks the BRST symmetry of a local, renormalizable, BRST-invariant Landau-gauge action [33]. More recently, using this local action in Landau gauge, the gap equation was determined to two-loop order, and it was verified at the two-loop level that the ghost propagator has a dipole singularity in the infrared [35]. It has also been found to one-loop order that the gluon propagator in Landau gauge vanishes like k2, and that the renormalization-group invariant coupling as(k) appropriate to the Landau gauge is finite at k = 0 [36]. Thus the elements of Gribov's scenario in Landau gauge [1] have been derived from a local, renormalizable, BRST-invariant action. The Landau gauge case has been reviewed in [37].
The Coulomb gauge provides a more straightforward confinement scenario than the Landau gauge (but see [38]), and for this reason Gribov and others turned to the Coulomb gauge. The Coulomb gauge is also well suited to finite-temperature calculations because the heat-bath provides a preferred Lorentz frame, so symmetries of the Coulomb gauge, which breaks manifest Lorentz invariance, are the physical symmetries of the system. Unitarity and Lorentz invariance in the present approach are discussed in the concluding section and the Appendices. In the Appendices we show that, if one integrates out the unphysical degrees of freedom, one obtains a canonical Hamiltonian system and as such is it formally unitary. Note also that, because the Coulomb gauge condition holds at a fixed time, it is the same in both Euclidean and Minkowski formulations, unlike the Landau gauge condition. In the Appendices we also show the equivalence of the local renormalizable, BRST-invariant action containing auxiliary fermi and bose ghost fields to the usual Coulomb-gauge action with a cut-off at the Gribov horizon.
D. Organization of paper
The local, renormalizable, BRST-invariant action is introduced in sec. II. The nonperturbative vacuum is found in sec. III by a translation of the auxiliary bose fields. The free propagators of the non-perturbative vacuum are found in sec. IV. The gap equation is calculated to one-loop approximation in sec. V. Renormalization and renormalization-group flow are described in sec. VI. The one-loop gap equation is solved in sec. VII. The free energy is derived in sec. VIII, and the correction to the equation of state due to the non-perturbative vacuum is evaluated at high temperature in sec. IX. The ghost propagator is evaluated to one-loop in sec. X. A softly broken Slavnov-Taylor identity is derived in sec. XI that is used in sec. XII to find the color-Coulomb potential to one-loop. Unitarity and Lorentz invariance are briefly discussed in the concluding sec. XIII. The auxiliary fields are integrated out in Appendix AAPPENDIX A: ACTION IN TERMS OF HORIZON FUNCTION but none with w. These cross terms are cancelled by an appropriate shift of w. We next integrate out the quartet that appears in the action in the expression , and the action is expressed in terms of the "horizon function" that is non-local in space but local in time. In Appendix BAPPENDIX B: CANONICAL COULOMB-GAUGE HAMILTONIAN and its canonical momentum . the partition function is expressed in canonical Hamiltonian form in Coulomb gauge, with a cut-off at the Gribov horizon.
II. LOCAL BRST-INVARIANT ACTION IN COULOMB GAUGE
We shall be interested in pure SU(N) gauge theory at temperature T. Finite T is described by a Euclidean action which, for pure SU(N) gauge theory is of the form
where SYM = ò dDx  YM, with
YM, with
is the Yang-Mills action, and
Here g is the coupling constant, and we use the notation for the Lie bracket (A × B)ª º fabc Ab Bc, where fabc are the fully anti-symmetric structure constants of the SU(N) group. The color index is taken in the adjoint representation, a = 1,..., N2 1. We shall generally suppress the color index, and leave summation over it implicit. Configurations are periodic in x0,
with period b = 1/T, where T is the temperature. The integral over x0 always extends over one cycle, ò dx0º  dx0. We are in D Euclidean dimensions. Lower case Latin indices take values, i = 1, 2, ..., D 1, while lower case Greek indices take values µ = 0, 1, ..., D 1.
dx0. We are in D Euclidean dimensions. Lower case Latin indices take values, i = 1, 2, ..., D 1, while lower case Greek indices take values µ = 0, 1, ..., D 1.
In the BRST formulation there are, in addition to Aµ, a pair of Faddeev-Popov ghost fields c and  and a Lagrange multiplier field, b, on which the BRST operator acts according to
and a Lagrange multiplier field, b, on which the BRST operator acts according to
It is nil-potent, s2 = 0. Here Dm is the gauge-covariant derivative in the adjoint representation, Dµc º ¶mc + gAm × c.
The choice of X is the choice of gauge. Physics is independent of X, provided that it provides a well-defined calculational scheme. For finite T, this is a crucial proviso, because the standard gauge choice leads to infrared divergences [2]. The standard Coulomb gauge is defined by the choice
Here the Lagrange-multiplier field b imposes the Coulomb gauge condition ¶iAi = 0. To avoid the infrared divergences of the standard gauge choice we shall modify this gauge choice by adding an s-exact term in the action that involves auxiliary ghost fields.
Recall that observables O are in the cohomology of s (namely s-invariant operators sO = 0, modulo s-exact operators, O ~ O + sX.) One may introduce additional quartets of auxiliary ghost fields on which s acts trivially, because such fields cannot appear in the cohomology of s. We introduce them in the form
The fields  and
and  are a pair of bose ghosts, while
are a pair of bose ghosts, while  and
and  are fermi ghost and anti-ghost. The indices a and b label components in the adjoint representation of the global gauge group, a, b = 1,..., N2 1, and µ is a Lorentz index.
are fermi ghost and anti-ghost. The indices a and b label components in the adjoint representation of the global gauge group, a, b = 1,..., N2 1, and µ is a Lorentz index.
The BRST method insures that physics is unchanged if we add to the action the s-exact term
where we stipulate that the gauge covariant derivative acts on the first color index only,
etc. [More generally we may take the gauge-fixing term to be s ò dDx ¶k akl Al and the auxiliary action to be s ò dDx ¶k
akl Al and the auxiliary action to be s ò dDx ¶k akl (Dlfm)ab, where akl is a positive symmetric matrix that may be chosen to be diagonal.] So far, the pair of indices B º (b,µ) is mute, where b is the second color index and µ is the Lorentz index, and B could run over any index set. We take for the gauge-fixing term
akl (Dlfm)ab, where akl is a positive symmetric matrix that may be chosen to be diagonal.] So far, the pair of indices B º (b,µ) is mute, where b is the second color index and µ is the Lorentz index, and B could run over any index set. We take for the gauge-fixing term
where
The complete action and Lagrangian density are given by
Introduction of the auxiliary ghost fields and of the auxiliary s-exact action (19) is legitimate in the BRST approach [39], although the reason for doing so is not yet apparent.
III. NON-PERTURBATIVE VACUUM
A. Maggiore-Schaden shift
We make a change of variable whereby the bose ghosts are translated by a c-number term linear in the spatial coordinate xm [33],
Note that f and j designate distinct fields. [The shift term x0 is not periodic with finite period b = T1. We shall require periodicity only for the new fields  and
and  . The same remark applies for quantization in a periodic spatial box.] Here g is a parameter with dimensions of (mass)4 that will be determined by the condition
. The same remark applies for quantization in a periodic spatial box.] Here g is a parameter with dimensions of (mass)4 that will be determined by the condition  = 0, where W is the free energy. We also translate b and
= 0, where W is the free energy. We also translate b and  by compensating terms,
by compensating terms,
which are chosen to cancel explicit x-dependence in the new action. The BRST operator s acts on the new variables according to
Despite the x-dependent shift, remarkably, neither the gauge-density (22) nor the Lagrangian density acquire any explicit x-dependence when expressed in terms of the new variables. Indeed from (22) we obtain
where
As before, it is understood that the gauge-covariant derivative acts on the first index only, (Di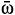 µ)ab = ¶i
µ)ab = ¶i + gfacd
+ gfacd .
.
After the shift, the complete action is given by
where the Lagrangian density has the explicit form
where
i = sxi,
and (Dic × jm)ab º facd(Dic)cjdb acts on the first color index, etc. For purposes of expansion in powers of g we shall change independent parameter from g to m according to
where m has dimensions of mass, and m is taken to be of order g0.
B. Gap equation
Henceforth we shall be concerned with the action S, regarded as a function of the new fields. The partition function is given by
where dF represents integration over all fields, and F º (Am, c,  , b, j,
, b, j,  , w,
, w, 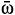 ) is the set of all (new) fields. We have made the substitutions
) is the set of all (new) fields. We have made the substitutions  ®
®  and
and  ® b. The field
® b. The field  is real while
is real while  is pure imaginary. The classical vacuum occurs where all these fields vanish
is pure imaginary. The classical vacuum occurs where all these fields vanish
Finally the value of g is determined by the condition that the free energy W = lnZ be stationary,
or
There is a non-perturbative vacuum if this equation has a solution with g ¹ 0. We do not require that W be a maximum because there are non-physical fields present. By (30) to (33) the last equation reads
The second term vanishes,
because there is no  w term in the action. Moreover the new action (30) to (33) is invariant under space-time translation of the new fields, F(x) ® F(x + a), and the vacuum just found, at F = 0, is also. [This vacuum is not invariant under space-time translation of the old fields,
w term in the action. Moreover the new action (30) to (33) is invariant under space-time translation of the new fields, F(x) ® F(x + a), and the vacuum just found, at F = 0, is also. [This vacuum is not invariant under space-time translation of the old fields,  and
and  , because of the explicit xm dependence in the shift (24).] Translation invariance implies that the terms ¶ij and ¶i
, because of the explicit xm dependence in the shift (24).] Translation invariance implies that the terms ¶ij and ¶i do not contribute to (39), and we obtain
do not contribute to (39), and we obtain
This gap equation determines m = m(g,T). Invariance under scale transformation is spontaneously broken for m ¹ 0.
C. Spontaneous breaking of BRST symmetry
The gap equation expresses the condition  = 0. Here m is the analog of the vacuum expectation-value v of the Higgs field F that appears in spontaneous symmetry breaking of global gauge invariance. For in the Higgs mechanism one makes the translation Fª =
= 0. Here m is the analog of the vacuum expectation-value v of the Higgs field F that appears in spontaneous symmetry breaking of global gauge invariance. For in the Higgs mechanism one makes the translation Fª =  , and the vacuum expectation-value v is determined by the condition that the free-energy be stationary with respect to v, ¶W/¶v = 0. In the present case, BRST invariance is spontaneously broken rather than global gauge invariance, because the expectation-value of s-exact quantities is non-zero, for example
, and the vacuum expectation-value v is determined by the condition that the free-energy be stationary with respect to v, ¶W/¶v = 0. In the present case, BRST invariance is spontaneously broken rather than global gauge invariance, because the expectation-value of s-exact quantities is non-zero, for example
As in the Higgs case, the spontaneously broken theory inherits renormalizability from the unbroken theory. But (42) shows that we cannot identify observables with equivalence classes of s-invariant objects, modulo s-exact quantities, as in the standard BRST approach. However, as shown in the Appendices, the present method is formally equivalent to the canonical formulation of Coulomb gauge, with a cut-off at the Gribov horizon. This allows us to identify observables, such as the energy-momentum tensor Tmn, with the corresponding quantities in the canonical formulation so, for example,
D. Automatic cut-off at Gribov horizon
Recall that b is a Lagrange multiplier field, and integration over b produces a functional d-function that imposes the gauge constraint ¶iAi = 0. Suppose this integration is done, so Ai is identically transverse. The auxiliary field  , which is pure imaginary, is also a Lagrange multiplier. Integration over
, which is pure imaginary, is also a Lagrange multiplier. Integration over  yields a functional d-function that imposes the constraint
yields a functional d-function that imposes the constraint
Suppose that quantization is done in a periodic box of finite spatial volume V. Integration of the last equation over V at fixed t kills the first term, which is a divergence, and yields a new constraint satisfied by Ai,
namely that the zero-momentum component of Ai vanishes. This is an additional gauge condition that expresses a confining property: it is impossible to have a gluon with zero momentum. In accordance with this condition, the propagator,  (k, k0), vanishes with k2, as we shall see.
(k, k0), vanishes with k2, as we shall see.
The last equation results from the trivial zero-eigenvalue of the Faddeev-Popov operator M(A) º ¶iDi(A) = Di(A)¶i, with eigenfunction satisfying ¶iu = 0. By definition, the interior of the Gribov region W is the set of all 3-dimensionally transverse configurations Ai(x) such that all non-trivial eigenvalues of M(A) are strictly positive. The boundary ¶W consists of those configurations A such that the lowest non-trivial eigenvalue l0 = l0(A) vanishes,
Here it is stipulated that u0(x) ¹ const., to assure that this is not the trivial zero eigenvalue. Now, for fixed t, let Ai(x,t) Î ¶W be a point on the boundary of the Gribov region. Upon contraction of (44) with the corresponding non-trivial eigenfunction  (x), we obtain a new constraint (one for each j and c) that should hold at every boundary point Ai(x,t),
(x), we obtain a new constraint (one for each j and c) that should hold at every boundary point Ai(x,t),
However this additional condition is not satisfied at a generic point on ¶W. This implies that the functional integral automatically cuts off at the boundary ¶W. Indeed, after the auxiliary fields are integrated out, the functional weight contains the factor ~ exp(c/l0), where the lowest eigenvalue l0 = l0(A) vanishes as A approaches the boundary (see Appendix AAPPENDIX A: ACTION IN TERMS OF HORIZON FUNCTION but none with w. These cross terms are cancelled by an appropriate shift of w. We next integrate out the quartet that appears in the action in the expression ). This cut off is non-analytic in l0. If now we expand about the interior point A = 0, the expansion is determined by the interior of the Gribov region only.
IV. FREE PROPAGATORS
We now develop a perturbative expansion about the new (non-perturbative) vacuum. For this purpose we treat m as an independent parameter of order g0, and calculate perturbatively all quantities, including the gap equation, to a given order in g. Then m = m(g,T) is determined by solving the the gap equation (41) non-perturbatively.
The first step is to expand the action (29) in powers of g,
The leading term is of order g2,
where the spatial quantization volume is V = L3, and the time extent b = T1. Although this term is independent of the fields, it should not be ignored because, when the gap equation is solved for m = m(T), it gives a T-dependent contribution to the free energy. The terms in the action of order g0,
are all quadratic in the fields and determine the "free" propagators,
The term S0,3 causes a mixing of the zero-order transverse gluon and bose-ghost propagators.
To calculate the free propagators, we define the field that mixes with  ,
,
The orthogonal component  and other components of j and
and other components of j and  do not mix with Ai. Moreover because of the Lagrange-multiplier term i¶jbAj, only the 3-dimensionally transverse part
do not mix with Ai. Moreover because of the Lagrange-multiplier term i¶jbAj, only the 3-dimensionally transverse part  of Aj contributes to propagators, and it mixes only with the transverse part
of Aj contributes to propagators, and it mixes only with the transverse part  of yj. Consequently, the free propagators of the fields Aj and yj are determined by the mixed action
of yj. Consequently, the free propagators of the fields Aj and yj are determined by the mixed action
which corresponds to the matrix in momentum space,
with determinant
The free propagators are given by
Here k0 = 2pn/b are the Matsubara frequencies, where n is any integer, and T = 1/b. The transverse projector is given by Pij(k) = dij  i
i
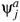 , the gap equation (41) reads
, the gap equation (41) reads
V. GAP EQUATION IN ONE-LOOP APPROXIMATION
When the left-hand side of the gap equation is evaluated to zeroth order in g, using the mixed propagator (59), it reads
where we used Pii(k) = D 2.
To evaluate the sum over Matsubara frequencies,
where E º (k2 +  )1/2, we use the identity
)1/2, we use the identity
or
This gives upon differentiation
We thus obtain for the sum over Matsubara frequencies
The first term in parentheses gives the value of Q at T = 0 and, with b = 1/T, the second term is a Planck-type finite-temperature correction. This gives for the gap equation
which holds in D Euclidean space-time dimensions.
For D < 4 the integral is convergent. We take the limit D ® 4. The first term one the left, which is the zero-temperature contribution, has the limiting form
where e º (4 D)/2, and µ = µ(T) is, in general, a temperature-dependent renormalization mass. There is a pole at D = 4 which results from the familiar ultraviolet divergences of quantum field theory. The second term in (68), which is the finite-temperature contribution, is finite at D = 4. We subtract the pole term, as will be discussed shortly, and the gap equation reads
where u º (x2 +  )1/2. The left-hand side is a function of the single variable mb =
)1/2. The left-hand side is a function of the single variable mb =  .
.
VI. RENORMALIZATION
A. Exact properties
We present a brief sketch of the salient features of the renormalization of the present local theory in Coulomb gauge with auxiliary ghosts. This is done following the method used in Landau gauge [32-34].
We consider the local action defined in eq. (30) and below. Renormalization is done perturbatively in g, with m an arbitrary parameter. The gap equation for m is imposed after renormalization. The action has obvious symmetries and (and supersymmetries at m = 0) that act on the indices (µ,b) of  and
and  , and of
, and of  and
and  . A less obvious symmetry transformation of the action (30), introduced in [33], is defined, for fixed µ and b by
. A less obvious symmetry transformation of the action (30), introduced in [33], is defined, for fixed µ and b by
all other fields being invariant. As a consequence of this symmetry, the auxiliary fermi ghosts have the same propagator as the Faddeev-Popov ghosts,
where µ and b are fixed.
Because of the symmetries, all bose and fermi ghosts renormalize the same way. The number of independent renormalization constants is the same as in the theory at m = 0 (and at T = 0), and they may be evaluated at m = 0 in the Coulomb-gauge theory without auxiliary ghosts. Thus we have
where the subscript r designates renormalized quantities. In Coulomb gauge, the space components Ai of the connection renormalize differently from the time component A0. Because of the symmetries we have
Moreover, in Coulomb gauge, the quantum effective action depends on the combination Ki ¶i , where Ki is the source for sAi = Dic, and ZK =
, where Ki is the source for sAi = Dic, and ZK =  , so it is convenient to choose
, so it is convenient to choose
With this choice, we have in Coulomb (and in Landau) gauge
This follows from the non-renormalization of the ghost-gluon vertex which implies  = 1. An important property in Coulomb gauge is the identity [40]
= 1. An important property in Coulomb gauge is the identity [40]
which implies that gA0 = grA0,r is a renormalization-group invariant, as is g2D00 where D00 is the time-time component of the gluon propagator. It is convenient to choose
The mixed term m2Ai (ji  i) in the action (30) does not introduce any new divergence, so so there is no subtractive renormalization of m, and Zm satisfies
i) in the action (30) does not introduce any new divergence, so so there is no subtractive renormalization of m, and Zm satisfies
Because of these identities, there remain only two independent renormalization constants, which may be chosen to be ZA and Zg.
The gap equation holds for both renormalized and unrenormalized quantities. Indeed, the free energy is a renormalization-group invariant W = Wr, and we have m = Zmmr, which gives
As noted, all renormalization constants Zi are calculated at m = 0. They depend only on the variables
where g0 = g0(L/LQCD). Here L is the ultraviolet cut-off, and LQCD is a physical QCD mass scale. The coupling constant satisfies the familiar RG equation
with solution gr = gr(µ/LQCD), where LQCD is a constant of integration. Likewise, the renormalized mass parameter satisfies
where
is a power series in gr. We change independent variable to t º ln(µ/LQCD), and write gm(t) º gm[gr(t)], so the RG equation for mr reads
with solution
This gives the dependence of mr on the renormalization mass µ. Here M is a constant of integration, whose value is determined by the gap equation. In general M is temperature dependent M = M(T). At T = 0 we have M(0) = cLQCD, where the dimensionless constant c is is determined by the gap equation at T = 0.
The Callan-Symanzik equation,
gives the dependence of all one-particle irreducible correlators Gi on the renormalization mass µ. Here and below we suppress the index r that designates renormalized quantities. By virtue of (80), the gap equation holds for any value of µ, and the Callan-Symanzik equation assures that the solution M(T) of the gap equation is independent of µ. However for approximate correlators there will generally be a dependence of M on µ. One makes an optimal choice of µ to minimize higher corrections which will, in general, be temperature dependent, µ = µ(T). For example, at high T it is convenient to choose µ = 2pT.
B. One-loop calculation
The above equations give for Zm,
As noted, the renormalization constants are calculated at m = 0, where the correlators have the same value as in the ordinary Coulomb gauge without the auxiliary ghosts. From Appendix BAPPENDIX B: CANONICAL COULOMB-GAUGE HAMILTONIAN and its canonical momentum . of [40], we have, in Coulomb gauge, to one-loop order
where
and µ is a renormalization mass. This gives
and, to one-loop order,
To this order we also have  = 24p2 / (11Nt), where t = ln(µ/LQCD), so gm(t) = 7/(44t). Thus the dependence of mr on the renormalization mass µ = µ(T) is given to one-loop order by,
= 24p2 / (11Nt), where t = ln(µ/LQCD), so gm(t) = 7/(44t). Thus the dependence of mr on the renormalization mass µ = µ(T) is given to one-loop order by,
VII. SOLUTION OF ONE-LOOP GAP EQUATION
To solve the gap equation (70) we change unknown from m to m* º m/T so it takes the form
where µ = µ(T), and
is a function of a single variable. The function f(m*) decreases monotonically, f'(m*) < 0, with f(0) = ¥ and f(¥) = ¥, so this equation for m* always has a unique solution
where R = R(T). Moreover, by the inverse function theorem, h(R) is analytic, so in this approximation there is no phase transition, provided that R(T) is analytic.
For each temperature T there is a unique a solution of the one-loop gap equation that defines a non-perturbative vacuum.
We now specialize to high temperature T, and take the renormalization mass to be µ = 2pT. This simplifies the high-T case because of asymptotic freedom. The running coupling is given approximately by
where LQCD is the physical  mass scale, so at high temperature, g(T) is small, and the one-loop gap equation should be a good approximation. According to (94) and (95), high T implies small m*, and for small m* we have
mass scale, so at high temperature, g(T) is small, and the one-loop gap equation should be a good approximation. According to (94) and (95), high T implies small m*, and for small m* we have
so the gap equation at high T simplifies to
To leading order at high T or small m*, the first term on the left is negligible compared to the second, and we obtain, with m* =  ,
,
Thus, in the high-temperature limit, m(T) is proportional to a standard magnetic mass g2(T)T. [This calculation replaces the assumption made in [41] that m is temperature independent.]
VIII. FREE ENERGY
To order g0, the free energy W = lnZ is given by
where S2, given in (49), is field-independent and of order g2, while S0, given in (50), is quadratic in the fields. We obtain
where, for D 1 = 3,
and
To evaluate W0 we observe first that the Faddeev-Popov ghost pair contributes a factor k2 which is cancelled by the two factors of |k|1 that come from the A0 and b integrations. Moreover all auxiliary bose and fermi ghost pairs with the same action give contributions to W0 that cancel. Each single 4-momentum mode of the action S0(A,y), eq. (56), contributes  to expW0, where, by (57), D1 = (k2 +
to expW0, where, by (57), D1 = (k2 +  ) k2 + m4. Corresponding to the bose ghost
) k2 + m4. Corresponding to the bose ghost  that mixes with
that mixes with  is an otherwise unpaired fermi ghost mode that contributes
is an otherwise unpaired fermi ghost mode that contributes  , where D2 = k2. The net result is that for each 4-momentum mode of the
, where D2 = k2. The net result is that for each 4-momentum mode of the  field we obtain a contribution (D1/D2)1/2, where D1/D2 =
field we obtain a contribution (D1/D2)1/2, where D1/D2 =  + E2, and E = (k2 +
+ E2, and E = (k2 +  )1/2. There is an infinite product over all frequencies k0 for each 3-momentum mode of the Ai field. For each 3-momentum k of the
)1/2. There is an infinite product over all frequencies k0 for each 3-momentum mode of the Ai field. For each 3-momentum k of the  field the result of this infinite product is the Planck partition function for a single mode
field the result of this infinite product is the Planck partition function for a single mode
so
The sum over the N2 1 color modes, the 2 degrees of transverse polarization, and over all 3-momentum modes k yields, with åk ® V ò ,
,
where E = E(k) = (k2 +  )1/2. We add the term W2 and obtain to order g0 the free energy per unit volume, w = W/V,
)1/2. We add the term W2 and obtain to order g0 the free energy per unit volume, w = W/V,
The free energy and the equation of state in the non-perturbative vacuum are obtained by substituting into this expression the solution
of the gap equation.
IX. EQUATION OF STATE AT HIGH TEMPERATURE
We now evaluate w in the high-temperature limit, where g(T) is small, and our expansion should be reliable. This will give the leading contribution that comes from the non-perturbative vacuum, namely non-zero m.
From (100) we obtain
where
and
is a small parameter.
The lowest-order expression for K(h) at small h is obtained by setting h = 0,
which gives the Stefan-Boltzmann free energy. To evaluate the leading correction from K(h), we use
We pose y = h1/4x and obtain
where v º (x2 +  )1/2. To leading order in h this gives
)1/2. To leading order in h this gives
From K = K(0) +  , we obtain the leading correction to K(0),
, we obtain the leading correction to K(0),
We substitute this into (110) and obtain
which gives the leading correction to the Stefan-Boltzmann limit from the non-perturbative vacuum. It is of order  .
.
The equation of state of the gluon plasma follows from the thermodynamic formulas for the energy per unit volume and pressure,
and entropy per unit volume, s =  . To calculate the energy density, we use
. To calculate the energy density, we use  = b-function = O(g3), which is of higher order. We thus obtain for the energy density and pressure at high temperature,
= b-function = O(g3), which is of higher order. We thus obtain for the energy density and pressure at high temperature,
with s =  .
.
This is the leading contribution that comes from the non-perturbative vacuum. Numerically it is a small correction, whereas the correction of order g6 is divergent when calculated with the perturbative vacuum [2]. To this must be added the perturbative contributions, including resumations, that have been calculated at m = 0, and that are of lower order in g [14]. Since standard, resummed perturbation theory diverges at order g6, which is precisely the order of the correction we have found, the result obtained here is consistent with standard perturbative calculations.
This completes the calculation of the equation of state at high temperature to one loop, and we turn now to the propagators.
X. (ALMOST) LINEARLY RISING GHOST PROPAGATOR
The complete propagator of the Faddeev-Popov ghost  (x y) = ác(x)
(x y) = ác(x) (y)ñ, is instantaneous,
(y)ñ, is instantaneous,  (x) =
(x) =  (x)d(t), and in momentum space it is independent of p0,
(x)d(t), and in momentum space it is independent of p0,  (p, p0) =
(p, p0) =  (p). This is easily seen because one may follow the ghost line continuously through any graph, and one may route the external ghost momentum p through this line. The free ghost propagator
(p). This is easily seen because one may follow the ghost line continuously through any graph, and one may route the external ghost momentum p through this line. The free ghost propagator  (p) =
(p) =  , is independent of p0, so every graph is independent of p0.
, is independent of p0, so every graph is independent of p0.
We now show that for all finite temperature T, in Euclidean dimension 2 < D < 4, and to one-loop order, the ghost propagator behaves for small p like
where S º D 1 is the number of spatial dimensions. This corresponds to a propagator in position space that is linear rising at large separation,
At D = 4 space-time dimensions there is a logarithmic correction given below. In Landau gauge it has been established to one- and two-loop order by explicit calculation [36] that the ghost propagator is more singular than  , and it has been shown that this is true to every order in g [32]. It is expected in Coulomb gauge also, that the one-loop result, namely that the ghost propagator
, and it has been shown that this is true to every order in g [32]. It is expected in Coulomb gauge also, that the one-loop result, namely that the ghost propagator  (p) is more singular than 1/p2, holds to all orders.
(p) is more singular than 1/p2, holds to all orders.
To one-loop order, the inverse ghost propagator is given by
where  (p + k) =
(p + k) =  is the free fermi-ghost propagator, and
is the free fermi-ghost propagator, and  (k) is the zero-order gluon propagator (58). The trivial color factor dbc has been removed. We are interested in the large x, small p, behavior. For this purpose it is convenient to separate out the p = 0 part of the ghost propagator using the identity,
(k) is the zero-order gluon propagator (58). The trivial color factor dbc has been removed. We are interested in the large x, small p, behavior. For this purpose it is convenient to separate out the p = 0 part of the ghost propagator using the identity,
Corresponding to this separation we have
where
is quadratic in p, and
is of higher order in p.
We first evaluate  (p). By rotational invariance we make the replacement in (127),
(p). By rotational invariance we make the replacement in (127),
This gives
where we have used (58). According to the gap equation (62), this vanishes and we obtain for the quadratic term
Thus, when the gap equation is satisfied, the quadratic part of the one-loop term precisely cancels the tree-level term p2. This gives a maximal enhancement of the ghost propagator, which may be called "maximal anti-screening" of the ghost propagator.
Only the term which is higher-order in p and g survives,  (p) =
(p) =  (p), where
(p), where  (p) is given in (128). The sum over Matsubara frequencies in (128) is done in (63) to (67), with the result
(p) is given in (128). The sum over Matsubara frequencies in (128) is done in (63) to (67), with the result
where
To evaluate this integral for small p, we rescale the integration variable ki according to ki = |p|qi, and observe that, for Euclidean dimension D in the interval 2 < D < 4, the integral remains convergent after this rescaling if p is neglected compared to other quantities. It is not necessary to actually do the rescaling explicitly, because the same result is obtained by neglecting |k| compared to m. Thus we make the substitutions
and obtain
Consequently, for 2 < D < 4 and for all finite T, the asymptotic limit of  at low p is given by
at low p is given by
where
This gives the asymptotic ghost propagator at small p,
With D = S + 1, where S is the number of space dimensions, one sees that this corresponds to a ghost propagator that rises linearly in position space,  (x) ~ |x|, for 2 < D < 4, asymptotically at large |x|.
(x) ~ |x|, for 2 < D < 4, asymptotically at large |x|.
The replacement E(k) = ( k2 +  )1/2®
)1/2®  gave the correct low-momentum asymptotic behavior for 2 < D < 4 , but it introduces a spurious ultraviolet divergence at D = 4 which manifests itself by a pole term
gave the correct low-momentum asymptotic behavior for 2 < D < 4 , but it introduces a spurious ultraviolet divergence at D = 4 which manifests itself by a pole term  in the coefficient C(D). Indeed for small values of e º 4 D we have
in the coefficient C(D). Indeed for small values of e º 4 D we have
In a more accurate evaluation of (132), the divergence gets replaced by a cut-off at |k| = O(m). As is familiar from dimensional regularization of real ultraviolet divergences, we may obtain the leading small p behavior, without actually doing the more accurate evaluation, by expanding the last expression in powers of e = 4 D, which gives
where c is a dimensionless constant. We have replaced the spurious divergent constant  , which is a consequence of the incorrect evaluation at D = 4, by a finite constant. The argument of the logarithm contains the mass m, because that would be the order of the ultraviolet cut-off in a more accurate evaluation at small p. This gives the asymptotic ghost propagator at small p,
, which is a consequence of the incorrect evaluation at D = 4, by a finite constant. The argument of the logarithm contains the mass m, because that would be the order of the ultraviolet cut-off in a more accurate evaluation at small p. This gives the asymptotic ghost propagator at small p,
In position space this is  (x) ~
(x) ~  for D = 4, which is weaker than linear by a logarithmic power.
for D = 4, which is weaker than linear by a logarithmic power.
XI. SOFTLY BROKEN SLAVNOV-TAYLOR IDENTITY
We wish to also calculate the color-Coulomb potential Vcoul(R) to this order. However instead of calculating it directly, it is simpler to derive a softly broken BRST identity that relates Vcoul(R) to the ghost propagator just calculated.
The action (26) of the BRST operator on the shifted fields contains an explicit linear dependence on the spatial coordinate xm. Consequently the Slavnov-Taylor identity that expresses the s-symmetry of the shifted fields breaks manifest invariance under space-time translation. To avoid this inconvenience we introduce instead an operator  that coincides with s, except for the term that breaks translation invariance,
that coincides with s, except for the term that breaks translation invariance,
Although  is not a symmetry, its breaking is soft. It is nil-potent,
is not a symmetry, its breaking is soft. It is nil-potent,  2 = 0, and acts on the Lagrangian density
2 = 0, and acts on the Lagrangian density  according to
according to
This gives
where the  -breaking term,
-breaking term,
It is soft, being proportional to m2.
To obtain a Ward identity, it is convenient to define an extended action,
which includes a term, cB, proportional to the  -breaking term, with a global Grassmannian parameter c that has ghost number 1. Here Km and L are the familiar sources for the
-breaking term, with a global Grassmannian parameter c that has ghost number 1. Here Km and L are the familiar sources for the  -transforms of Am and c that are non-linear in the fields. This extended action is useful because, by
-transforms of Am and c that are non-linear in the fields. This extended action is useful because, by  2 = 0, it satisfies the identity
2 = 0, it satisfies the identity
which reads
The extended action is used to define an (extended) partition function
where F represents the set of all fields, and J the corresponding sources. The quantum effective action G(F, K, L, c) is obtained from the free energy W(J, K, L, c) = lnZ by Legendre transformation. In addition to the usual arguments, G(F, K, L, c) depends on the parameter c. The quantum effective action G satisfies the Slavnov-Taylor identity
where S(G) is the functional
This has the same form as the identity (149) satisfied by the local extended action S.
XII. LONG-RANGE COLOR-COULOMB POTENTIAL
We now use the last identity to calculate the color-Coulomb potential, Vcoul(R), defined in (3). In practice, correlators are calculated in momentum space, and we would like to separate out the instantaneous part Vcoul(R) d(t) directly in momentum space. With reference to (3), we note that the instantaneous term corresponds to a term in momentum space that is independent of p0, whereas the non-instantaneous part, P(x,t), that is more regular in t, vanishes in momentum space at large p0, so
(We use the same symbol for a correlator and its Fourier transform.) More generally, the instantaneous part,  (p), of a generic correlator in momentum space, D'(p,p0), may be separated out by
(p), of a generic correlator in momentum space, D'(p,p0), may be separated out by
The same relation,
holds for the inverse propagators,
Thus the color-Coulomb potential in momentum space is given by
We now use the Slavnov-Taylor identity, S(G) = 0, to express  (p) in terms of
(p) in terms of  (p). This functional identity implies
(p). This functional identity implies
where all sources are set to 0 after differentiation. By (152) this gives
or, in momentum space,
We have separated the contributions from µ = 0 and µ = i.
By rotational invariance we have
for some function f(p). Moreover in Coulomb gauge the quantum effective action satisfies the identity,
(The analogous identity is well known in Landau gauge.) By applying  to this equation we obtain
to this equation we obtain
which yields
This term is purely instantaneous.
In Coulomb gauge  is not subject to radiative corrections,
is not subject to radiative corrections,
Indeed, K0 appears in the local action S only in the term K0D0c = K0¶0c + gK0A0 × c, so radiative corrections to  (p) correspond to graphs where the external K0 line enters the vertex gK0A0 × c. One may continuously follow the ghost c
(p) correspond to graphs where the external K0 line enters the vertex gK0A0 × c. One may continuously follow the ghost c line through the graph from this vertex to its exit point. We route the external momentum p through this ghost line, which consists of instantaneous propagators
line through the graph from this vertex to its exit point. We route the external momentum p through this ghost line, which consists of instantaneous propagators  (p + k). With this routing, the graph is independent of p0. On the other hand by time reversal the amplitude
(p + k). With this routing, the graph is independent of p0. On the other hand by time reversal the amplitude  (p) is proportional to p0. Thus, apart from the tree-level term, every graph that contributes to
(p) is proportional to p0. Thus, apart from the tree-level term, every graph that contributes to  (p) vanishes.
(p) vanishes.
Finally we note that the quantity  (p) is a longitudinal-scalar transition amplitude. It is of the form
(p) is a longitudinal-scalar transition amplitude. It is of the form
where
Putting these results together, we obtain
To obtain an identity satisfied by the instantaneous parts, we divide the last equation by p0 and take the limit p0® ¥. The last term,  (p) is also proportional to p0. However the limit,
(p) is also proportional to p0. However the limit,
holds to one-loop order at least, because the diagrams which contribute to this term, which contains an insertion of B given in (146), contain two transverse propagators which each behave like  at large k0, so the diagram vanishes at large p0. This gives the identity,
at large k0, so the diagram vanishes at large p0. This gives the identity,
To lowest order Linst(p) = 1, which is sufficient for our purposes since, as we have seen,  (p) is of order g2. To one-loop order this gives
(p) is of order g2. To one-loop order this gives
and from (157) we obtain,
The maximal anti-screening of the ghost propagator is transferred to the color-Coulomb potential.
We now use (139) and (142) for  (p) at low momentum. The coupling g2 nicely cancels and we obtain to lowest order at small p,
(p) at low momentum. The coupling g2 nicely cancels and we obtain to lowest order at small p,
where C(D) is given in (138).
In Coulomb gauge, g2D00, and thus also Vcoul(R), are renormalization-group invariants [40]. It follows that Vcoul at T = 0 has the functional dependence indicated by Vcoul = F(p, LQCD). In D = 4 dimensions, m has a renormalization-group flow, but to lowest order in g, m = c1 , where LQCD is a finite physical mass of the order of the QCD mass scale. Comparison with the previous expression which is valid for finite T gives m(0) = c1LQCD, and we obtain, for D = 4 at T = 0,
, where LQCD is a finite physical mass of the order of the QCD mass scale. Comparison with the previous expression which is valid for finite T gives m(0) = c1LQCD, and we obtain, for D = 4 at T = 0,
In position space this gives, asymtotically at large |x|,
The inequality, V(R) < Vcoul(R), holds asymptotically at large R, provided that V(R) is confining, limR® ¥ V(R) = ¥, where V(R) is the physical gauge-invariant interaction energy of an external quark pair [12]. In this case, if the one-loop expression for Vcoul(R) were exact, then inequality
would hold asymptotically at large R for some constant c, and the growth of the external quark-pair potential V(R) at large R would have to be slightly weaker than linear.
XIII. DISCUSSION
We started from a local, renormalizable, BRST-invariant action that contains auxiliary fermi and bose ghost fields. This action possesses a non-perturbative vacuum obtained by a translation of the bose ghost fields. This is in close analogy to the Higgs mechanism in electro-weak theory, although in the present case it is BRST invariance that is spontaneously broken rather than global gauge invariance.
We have calculated the leading correction to the Stefan-Boltzmann equation of state of the gluon plasma at high T that comes from the non-perturbative vacuum, and found it to be of order g6. However we have not attempted to systematically calculate all corrections to the Stefan-Boltzmann law to this order. Indeed there are corrections of lower order than g6(T) that have been obtained from ordinary perturbation theory and resummation of ordinary perturbation theory [14]. Significantly, g6(T) is precisely the order at which resummation of ordinary perturbation theory fails due to infrared divergences, as was first shown by Lindé [2]. Thus our calculation does not contradict the finite results from ordinary perturbation theory and its resummation, but instead gives a finite result precisely where ordinary perturbation theory breaks down.
We also expanded in a power series in g about the non-perturbative vacuum, and calculated the gluon and ghost propagators to low order in g. They have the behavior foreseen by Gribov [1], and which accords with numerical studies, as discussed in the Introduction. This happens because, when the local action is expanded about the non-perturbative vacuum, it provides an automatic cut-off at the Gribov horizon.
The non-perturbative vacuum found here spontaneously breaks both BRST symmetry and (since it is in Coulomb gauge) manifest Lorentz invariance, and one should establish unitarity and Lorentz invariance in the physical sector. One would like to do this within the framework of local, renormalizable quantum field theory that we adopted here, but we are unable to do so at this time. However one may formally establish these properties by integrating out the non-physical degrees of freedom, which yields the canonical Coulomb-gauge Hamiltonian [42], with a cut-off at the Gribov horizon (see Appendices A and B). This Hamiltonian system is unitary and moreover the Coulomb-gauge Hamiltonian admits a representation of the Lorentz group [43]. Consistency of Lorentz invariance and a boundary of the physical configuration space at the Gribov horizon appears to follow in the operator formalism from the fact that Lorentz and gauge transformations commute (see Appendix BAPPENDIX B: CANONICAL COULOMB-GAUGE HAMILTONIAN and its canonical momentum . ). The present approach in Coulomb gauge yields gluon energies (2) that are real and consistent with a unitary spectral representation, whereas in Landau gauge the Gribov propagator  has poles at the unphysical points k2 = ±im2.
has poles at the unphysical points k2 = ±im2.
Acknowledgements
I recall with pleasure stimulating conversations about this work with Reinhard Alkofer, Laurent Baulieu, David Dudal, Andrei Gruzinov, Atsushi Nakamura, Robert Pisarski, Alexander Rutenburg, Martin Schaden, and Silvio Sorella. I am grateful to the organizers, Attilio Cucchieri, Tereza Mendes, and Silvio Sorella, of the meeting Infrared QCD in Rio, Brazil, June 5 - 9, 2006, where part of this work was done.
[5] Daniel Zwanziger, arXiv: hep-th/0610021.
[29] A. Niegawa, [arXiv:hep-th/0604142]
[30] A. Niegawa, M. Inui, and H. Kohyama, [arXiv:hep-th/0607207]
[37] R. F. Sobreiro, S. P. Sorella arXiv:hep-th/0504095
Received on 31 October, 2006
In this Appendix we shall formally integrate out auxiliary fields to express the action in terms of the non-local "horizon function" that effects the cut-off at the Gribov horizon. It is non-local in space, but local in time.
where Mab = ¶i is the Faddeev-Popov operator. This gives
is the Faddeev-Popov operator. This gives
because from the fermi ghost pairs  , we get
, we get  and from the bose ghost pairs
and from the bose ghost pairs  we get 1/
we get 1/ , and these cancel. (This shows that the auxiliary quartet j0, w0,
, and these cancel. (This shows that the auxiliary quartet j0, w0, 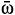 0,
0,  0 plays no role and could have been omitted from the action.)
0 plays no role and could have been omitted from the action.)
We now integrate over the remaining auxiliary fermi ghost pairs and obtain
The remaining auxiliary bose ghost pairs appear only in the action
where we have integrated by parts. The integral over these ghosts is done by completing the square with the result
where
The powers of detM from the fermi- and bose-ghost integrations cancel, so the net result from integrating over all the auxiliary ghost pairs is simply exp(gSh1).
The only remaining dependence on g occurs in the constant term in
3. We combine Sh1 with the constant term and obtain
The integal over the Faddeev-Popov ghosts, c and  , gives detM as usual, and the integral over the Nakanishi-Lautrup field gives Coulomb gauge condition, d(¶iAi). We thus obtain for the partition function
, gives detM as usual, and the integral over the Nakanishi-Lautrup field gives Coulomb gauge condition, d(¶iAi). We thus obtain for the partition function
We recognize this as the Faddeev-Popov weight for Coulomb gauge modified by exp(gSh). The vacuum condition that the free energy W = lnZ be stationary with respect to g now gives
The modified action SYM + gSh and the condition áShñ = 0 were originally obtained by imposing a cut-off at the Gribov horizon appropriate to the minimal Coulomb gauge [4]. The quantity Sh was called the "horizon function" and the last condition was called the "horizon condition". It is remarkable that it also results from a BRST-invariant local action.
Note that although Sh is non-local in space, it is local in time, because the 3-dimensional Faddeev-Popov operator M, and thus also its inverse M1, is local in time. Moreover Sh depends only on Ai but not on its time derivative  i. The latter appears only in SYM = òdDx
i. The latter appears only in SYM = òdDx where
where  and F0i =
and F0i =  i DiA0. This allows us to introduce canonical momenta, which are the color-electric fields
i DiA0. This allows us to introduce canonical momenta, which are the color-electric fields  , by the Gaussian identity
, by the Gaussian identity
Integration over A0 imposes Gauss's law in the form d(Dipi), which gives
We now separate transverse and longitudinal parts, Ai = 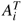 ¶is and pi =
¶is and pi = 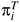 ¶iU, where ¶i
¶iU, where ¶i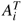 = ¶i
= ¶i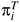 = 0, and U is the color-Coulomb field. This gives
= 0, and U is the color-Coulomb field. This gives
where we have used ò ds d( s) = const. To satisfy Gauss's law we write
s) = const. To satisfy Gauss's law we write
where M(AT) = Di(AT)¶i is the 3-dimensional Faddeev-Popov operator. The Faddeev-Popov determinant now gets absorbed by the identity
where the last d-function that expresses Gauss's law fixes the color-Coulomb potential to its physical value
Here r º  is the color-charge density of the dynamical degrees of freedom. This gives the partition function in canonical form
is the color-charge density of the dynamical degrees of freedom. This gives the partition function in canonical form
where piº 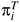 ¶iUphys. This is a canonical system, and thus unitary, for all real g, and stable for g > 0.
¶iUphys. This is a canonical system, and thus unitary, for all real g, and stable for g > 0.
The functional measure ò dAT exp(gSh), supplemented by the horizon condition (A9) that fixes g = gphys, were derived in [31] as a representation of the functional integral restricted to the Gribov region,
This yields the partition function in terms of the standard Coulomb-gauge first-order action
where piº 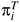 ¶iUphys, and the integral over AT is restricted to the Gribov region W.
¶iUphys, and the integral over AT is restricted to the Gribov region W.
We comment briefly on Lorentz invariance. The boundary ¶W of the Gribov region consists of points where the gauge orbit is tangent to the gauge fixing surface. This provides the boundary condition on wave functionals that holds on the boundary ¶W namely, gauge invariance of the wave functionals in these tangent directions. In the operator formalism in Coulomb gauge [42], the generators of the Poincaré algebra, including the generators of Lorentz transformations, are represented by gauge-invariant operators [43]. As such they commute with the generator of gauge transformations. Thus it appears that the cut-off at the Gribov horizon in Coulomb gauge is consistent with Lorentz invariance. These considerations indicate that unitarity holds for all positive g, whereas Lorentz invariance is regained only for g = gphys.
The Gribov region, W, is the set of local minima with respect to gauge transformations g(x) of the functional FA[g] º ||gA||2. Here ||A|| is the Hilbert norm of A, and gA is the gauge transform of A. The set of relative minima, W, is larger than the set of absolute minima, L, known as the fundamental modular region. The latter provides a true gauge-fixing. However it has been argued [44] that integration over W and over L give the same expectation-value for all n-point functions with finite n.
- [1] V. N. Gribov, Nucl. Phys. B 139, 1 (1978).
- [2] A. D. Lindé, Phys. Lett. 96B, 289 (1980).
- [3] Ismail Zahed and Daniel Zwanziger Phys. Rev. D 61, 037501 (2000) [arXiv:hep-th/9905109].
- [4] Daniel Zwanziger, Nucl. Phys. B 485, 185 (1997) [arXiv: hep-th/9603203].
- [6] Attilio Cucchieri and Daniel Zwanziger, Phys. Rev. D 65, 014002 (2002) [arXiv:hep-th/0008248].
- [7] Attilio Cucchieri and Daniel Zwanziger Phys. Rev. D 65, 014002 (2002) [arXiv:hep-lat/0008026].
- [8] J. Greensite and S. Olejnik, Phys. Rev. D 67, 094503 (2003) [arXiv:hep-lat/0302018].
- [9] Jeff Greensite, Stefan Olejnik, and Daniel Zwanziger Phys. Rev. D 69, 074506 (2004) [arXiv:hep-lat/0401003]
- [10] Jeff Greensite, Stefan Olejnik, and Daniel Zwanziger JHEP 0505, 070 (2005) [arXiv:hep-lat/0407022]
- [11] Y. Nakagawa, A. Nakamura, T. Saito, H. Toki, and D. Zwanziger, Phys. Rev. D 73, 094504 (2006) [arXiv:hep-lat/0603010].
- [12] D. Zwanziger, Phys. Rev. Lett. 90, 102001 (2003) [arXiv: hep-lat/0209105].
- [13] D. J. Gross, R. D. Pisarski, and L. G. Yaffe, Rev. Mod. Phys. 53, 43 (1981).
- [14] Joseph I. Kapusta, Finite-Temperature Field Theory, Cambridge U. Press (1989).
- [15] Adam P. Szczepaniak, Pawel Krupinski Phys. Rev. D 73, 116002 (2006) [arXiv:hep-ph/0604098].
- [16] A. P. Szczepaniak and E. S. Swanson, Phys. Rev. D 65, 025012 (2002) [arXiv:hep-ph/0107078].
- [17] C. Feuchter and H. Reinhardt, Phys. Rev. D 70, 105021 (2004) [arXiv:hep-th/0408236].
- [18] C. Feuchter and H. Reinhardt, Phys. Rev. D 71, 105002 (2005) [arXiv:hep-th/0408237].
- [19] Wolfgang Schleifenbaum, Markus Leder, and Hugo Reinhardt, Phys. Rev. D 73, 125019 (2006) [arXiv:hep-th/0605115].
- [20] D. Zwanziger, Phys. Rev. D 65, 094039 (2002) [arXiv:hep-th/0109224].
- [21] C. Lerche and L. von Smekal, Phys. Rev. D 65, 125006 (2002) [arXiv:hep-ph/0202194].
- [22] D. Zwanziger, Phys. Rev. D 70, 094034 (2004) [arXiv:hep-ph/0312254].
- [23] L. von Smekal, R. Alkofer, and A. Hauck, Phys. Rev. Lett. 79, 3591 (1997) [arXiv:hep-ph/9705242].
- [24] L. von Smekal, A. Hauck, and R. Alkofer, Annals Phys. 267, 1 (1998) [Erratum-ibid. 269, 182 (1998)] [arXiv:hep-ph/9707327].
- [25] W. Schleifenbaum, A. Maas, J. Wambach, and R. Alkofer, Phys. Rev. D 72, 014017 (2005) [arXiv:hep-ph/0411052].
- [26] R. Alkofer, C. S. Fischer, and F. J. Llanes-Estrada, Phys. Lett. B 611, 279 (2005) [arXiv:hep-th/0412330].
- [27] R. Alkofer, M. Kloker, A. Krassnigg, and R. F. Wagenbrunn, Phys. Rev. Lett. 96, 022001 (2006) [arXiv:hep-ph/0510028].
- [28] A. Andrasi, J. C. Taylor, Eur. Phys. J. C 41, 377 (2005) [arXiv:hep-th/0503099]
- [31] D. Zwanziger, Nucl. Phys. B 323, 513 (1989).
- [32] D. Zwanziger, Nucl. Phys. B 399, 477 (1993).
- [33] Nicola Maggiore and Martin Schaden, Phys. Rev. D 50, 6616 (1994).
- [34] D. Dudal, R. F. Sobreiro, S. P. Sorella, and Verschelde, Phys. Rev. D 72, 014016 (2005) [arXiv:hep-th/0502183]
- [35] J. A. Gracey, Phys. Lett. B 632, 282 (2006) [arXiv:hep-ph/0510151].
- [36] J. A. Gracey, JHEP 0605, 052 (2006) [arXiv:hep-ph/0605077].
- [38] Reinhard Alkofer, Christian S. Fischer, and Felipe J. Llanes-Estrada arXiv: hep-ph/0607293.
- [39] Laurent Baulieu, Phys. Reports 129, 1 (1985).
- [40] D. Zwanziger, Nucl. Phys. B 518, 237 (1998).
- [41] Daniel Zwanziger, Phys. Rev. Letts. 94, 182301 (2005) [arXiv:hep-ph/0407103].
- [42] N. H. Christ and T. D. Lee, Phys. Rev. D 22, 939 (1980).
- [43] J. Schwinger, Phys. Rev. 127, 324 (1962) and 130, 406 (1963).
- [44] Daniel Zwanziger, Phys. Rev. D 69, 016002 (2004) [arXiv:hep-ph/0303028].
APPENDIX A: ACTION IN TERMS OF HORIZON FUNCTION
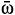 but none with w. These cross terms are cancelled by an appropriate shift of w. We next integrate out the quartet
but none with w. These cross terms are cancelled by an appropriate shift of w. We next integrate out the quartet 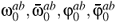 that appears in the action in the expression
that appears in the action in the expression APPENDIX B: CANONICAL COULOMB-GAUGE HAMILTONIAN
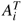 and its canonical momentum
and its canonical momentum 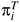 .
. Publication Dates
-
Publication in this collection
11 May 2007 -
Date of issue
Mar 2007



























































































































































































