A new formulation for the dielectric tensor for magnetized dusty plasmas with variable charge on the dust particles

A new formulation for the dielectric tensor for magnetized dusty plasmas with variable charge on the dust particles

L. F. Ziebell^{I, *}; R. S. Schneider^{I, †}; M. C. de Juli^II; R. Gaelzer^III

^IInstituto de Física, Universidade Federal do Rio Grande do Sul, Caixa Postal 15051, CEP: 91501-970, Porto Alegre, RS, Brazil

^IICentro de Rádio-Astronomia e Astrofísica Mackenzie - CRAAM, Universidade Presbiteriana Mackenzie, Rua da Consolação 896, CEP: 01302-907, São Paulo, SP, Brazil

^IIIInstituto de Física e Matemática, Universidade Federal de Pelotas, Caixa Postal 354 - Campus UFPel, CEP: 96010-900, Pelotas, RS, Brazil

ABSTRACT

A kinetic approach to the problem of wave propagation in dusty plasmas, which takes into account the variation of the charge of the dust particles due to inelastic collisions with electrons and ions, is utilized as a starting point for the development of a new formulation, which writes the components of the dielectric tensor in terms of a finite and an infinite series, containing all effects of harmonics and Larmor radius. The formulation is quite general and valid for the whole range of frequencies above the plasma frequency of the dust particles, which were assumed motionless. The formulation is employed to the study of electrostatic waves propagating along the direction of the ambient magnetic field, in the case for which ions and electrons are described by Maxwellian distributions. The results obtained in a numerical analysis corroborate previous analysis, about the important role played by the inelastic collisions between electrons and ions and the dust particles, particularly on the imaginary part of the dispersion relation. The numerical analysis also show that additional terms in the components of the dielectric tensor, which are entirely due these inelastic collisions, play a very minor role in the case of electrostatic waves, under the conditions considered in the present analysis.

Keywords: Langmuir waves; Electrostatic waves; Kinetic theory; Magnetized dusty plasmas; Dust charge fluctuation; Wave propagation

1. INTRODUCTION

The theoretical analysis of waves and instabilities in dusty plasmas have may be traced back to the pioneer work by Bliokh and Yarashenko [1] about waves in Saturn's rings. Most of the published works utilized fluid theory to describe the dusty plasmas, and only a few of them take into account the collisional charging of the dust particles [2, 3], although the importance of this effect to the propagation and damping of the waves is already well known [4, 5].

Although very important studies have been conducted using an hydrodynamical approach, it must be recognized that the fluid formulation has an important limitation: it can not describe purely kinetic effects such as the Landau damping. This consideration, per se, offers motivation for kinetic studies on dusty plasmas. Moreover, it has been shown that the dust charging process must be included in a kinetic approach, for proper derivation of the wave damping [6]. The reason is basically that the charging process is one of the most conspicuous and important dissipative processes to occur in a dusty plasma. As argued in Ref. [7], it is not possible to separate the conventional Landau damping and the damping due to the interaction of ions and electrons with the dust particles, at least for ion-acoustic waves.

The kinetic approach has been used in some investigations, as in the study of instabilities of ion-acoustic waves produced by current in a collisionless dusty plasma, completely ionized, appearing in the paper by Rosenberg [8]. This work has established a critical drift velocity of electrons, relative to the ions, for the occurrence of the instability. However, effects of the variation of the electric charge of the dust particles have not been taken into account. More recently, an approach based on moments of the kinetic equation was utilized for investigation of the effect of dust charge variation on high-frequency electrostatic plasma waves [9], leading to the conclusion that the grain charging contribute to damping of the Langmuir waves.

A kinetic description has been adopted by ourselves in recent publications which analize low-frequency electromagnetic waves in dusty plasmas, taking into account the variation of the dust charges due to inelastic collisions with electrons and ions [10-13]. The same basic kinetic formulation has also been used to the study of electrostatic waves in dusty plasmas [14]. In this kinetic formulation, the components of the dielectric tensor depend on the frequency of inelastic collisions of plasma electrons and ions with the dust particles. They can be connected to other formulations well known and used in the literature. Particularly, as shown in an appendix appearing at the end of Ref. [14], the general expressions for the dielectric tensor appearing in the kinetic formulation which we have been using can be cast in the form which appears in a series of papers of Tsytovich et al. [6, 15, 16], if restrictive assumptions are made.

In the present paper, we resume the use of the same basic kinetic approach, and introduce modifications in the mathematical formulation. We obtain expressions for the components of the dielectric tensor which are written in terms of an infinite and a finite summation, formally incorporating effects of all harmonics and all orders of Larmor radius, keeping effects due to the charging of the dust particles due to inelastic collisions with electrons and ions. The formulation is quite general in terms of frequency range and direction of propagation, and should be very useful for application to the study of wave propagation in dusty plasmas. A preliminary approach to this formulation appeared in the Appendix of Ref. [22], without any details of derivation.

The structure of the paper is the following. In Section we briefly outline the model used to describe the dusty plasma. In Section we present essential features of the kinetic formulation which leads to the dielectric tensor for dusty plasmas, and present the new formulation which leads to components of the dielectric tensor expressed in terms of double summations and a small number of basic integrals. In section we discuss the particular case of electrostatic waves propagating along the direction of the ambient magnetic field, and show the derivation of a dispersion relation assuming Maxwellian distributions for the electrons and ions in the equilibrium. In Sections some numerical results obtained from the dispersion relation are presented and discussed. The conclusions are presented in Section . Appendixes and are included, providing additional details of the derivation of some expressions appearing in the formulation utilized in the present paper. Appendix shows details of the evaluation of the basic integrals appearing in these expressions, for the case of Maxwellian distributions. Appendix presents some useful series of Bessel functions, utilized in the derivation of many expressions in the present formulation.

2. THE DUSTY PLASMA MODEL

In our general kinetic formulation we consider a plasma in a homogeneous external magnetic field B₀ = B₀e_z. In this magnetized plasma we take into account the presence of spherical dust grains with constant radius a and variable charge q_d; this charge originates from inelastic collisions between the dust particles and particles of species β (electrons and ions), with charge q_β and mass m_β. Ions are considered as simply charged, for simplicity.

We consider that the dust grain charging process occurs by the capture of plasma electrons and ions during inelastic collisions between these particles and the dust particles. Since the electron thermal speed is much larger than the ion thermal speed, the dust charge becomes preferentially negative. As a cross-section for the charging process of the dust particles, we use expressions derived from the OML theory (orbital motion limited theory) [17, 18].

Another limiting condition is that we focus our attention on weakly coupled dusty magneto-plasmas, in which the electrostatic energy of the dust particles is much smaller than their kinetic energy. This condition is not very restrictive, since a large variety of natural and laboratory dusty plasmas can be classified as weakly coupled [19].

Dust particles are assumed to be immobile, and consequently the validity of the proposed model will be restricted to waves with frequency much higher than the characteristic dust frequencies. In particular we consider the regime in which |Ω_d|ω_pd < ω, where ω_pd and Ω_d are the plasma frequency and the cyclotron frequency of the dust particles, respectively. This condition therefore excludes the analysis of the modes which can arise from the dust dynamics, as the so-called dust-acoustic wave.

3. THE COMPONENTS OF THE DIELECTRIC TENSOR FOR A HOMOGENEOUS MAGNETIZED DUSTY PLASMA

We assume that the distribution function of particles of species β, in a dusty plasma, satisfies Vlasov's equation appended with a term describing binary inelastic collisions with dust particles,

where f_d0 and f_β0 represent respectively the equilibrium distribution functions of dust particles and of particles of species β, with the subscript β = e,i identifying electrons and ions, respectively. The distribution function for the dust particles, f_d, satisfies the following equation,

where

is the current of electrons and ions which charge the dust particles [6]. The presence of the collisional term in these equations assures the possibility of variation of the electric charge of the dust particles, due to the inelastic collisions with particles of species β.

Upon linearization, the perturbed distribution function satisfies the following equation,

where

and σ_β is the charging cross-section, given by [20]

After use of Fourier-Laplace transform in the system of equations describing the dusty plasmas, the perturbed distribution function can be written as [21]:

where

One notices that has the same formal structure as the perturbed distribution obtained in the evaluation of the dielectric tensor of a conventional homogeneous magnetized plasma, with instead of ω in the argument of the exponential function. This part of the perturbed distribution therefore gives rise to a contribution to the components of the dielectric tensor that corresponds to the usual form of the components obtained for dustless magnetized homogeneous plasma, except for the modifications due to the presence of the inelastic collision frequency , which is related to the equilibrium distribution function of dust particles, as shown by Eq. (3). On the other hand, features an integrand which is proportional to , and which vanishes in the case of dustless plasma. The quantity is the Fourier-Laplace transform of the collision frequency, which is related to inelastic collisions with the fluctuating distribution of dust particles.

Using these two contributions to the perturbed distribution function, the dielectric tensor for a magnetized dusty plasma, homogeneous, fully ionized, with identical immobile dust particles and charge variable in time, could be written in the following way [21, 22]

One notices that the separation in the two terms appearing in Eq. (6) should not be considered arbitrary, since it is motivated by the different nature of the two contributions to the perturbed distribution function depicted by Eq. (5).

The term is formally identical, except for the iz components, to the dielectric tensor of a magnetized homogeneous conventional plasma of electrons and ions, with the resonant denominator modified by the addition of a purely imaginary term which contains the inelastic collision frequency of dust particles with electrons and ions. For the iz components of the dielectric tensor, in addition to the term obtained with the prescription above, there is a term which is proportional to this inelastic collision frequency. Explicit expressions for the components can be found in Refs. [21, 22].

The term is entirely new and arises only due to the process of fluctuation of the charge of the dust particles. Its form is strongly dependent on the model used to describe the charging process of the dust particles. The expression for this term can be found in Refs. [21, 22].

As already mentioned, we assume a homogeneous dusty plasma immersed in a homogeneous magnetic field along z direction, B₀ = B₀e_z. Let us also assume waves propagating in an arbitrary direction relative to the ambient magnetic field, with wave vector k = k_⊥ e₁ + k_||e_z. For the derivation of explicit expressions for the components of the dielectric tensor, we start with the "conventional" part, which in a non-relativistic approximation can be written as follows [21, 22].

where

where the subscript β = e,i identifies electrons and ions respectively, q_d0 = ε_deZ_d is the equilibrium charge of the dust particle (positive, ε_d = +1, or negative, ε_d = -1) and H denotes the Heaviside function.

In the evaluation of the components we need combinations of Bessel functions, as in , and , which can be given by Eqs. (D1) of Appendix D. It must be noticed that these quantities, given by Eqs. (D1), depend on |n| and not on n. However, n appears in other places, as in the resonant denominator. We can write n = s|n|, with s = ±1, and therefore the components of the 'conventional' part of the dielectric tensor may be written as follows,

where we have introduced the definition of the , and introduced N_⊥ as the perpendicular component of N = ck/ω. Correspondingly, N_|| is the parallel component of N. We have also written n instead of |n|, fom simplicity, since n > 1. It is not necessary to write the |n| because here n is positive and the sign s appears explicitly.

Let us define the normalized momentum, u = p/(m_αv_*), where v_* is a characteristic velocity, such that ∫ d³p f(p) = ∫ d³u f(u). For instance, v_* may be the light speed c, or the Alfvén speed v_A, or the ion sound speed c_s. Therefore,

where we have introduced N^* = (v_*/c) N, Y_α = |Ω_α|/ω, s_α = sign(Ω_α), and also the operator L. Eq. (8) can be rewritten in terms of the normalized momentum,

where

For the evaluation of the 'new' contribution, we start from the expression for the in Refs. [21, 22], where it is seen that the "new" contribution contains the product of two terms, which in a non-relativistic approximation can be written as follows,

with

where

Moreover, and σ_β is the charging cross-section, given by (4).

Effects of charge variation of dust particles occurs in the terms with /ω and effects of presence of dust particles, introduced via quasi-neutrality relation (n_i0≠ n_e0), occurs in terms with

Changing variables as in Eq. (8), Eqs. (11), (12), (13), and (14) become

Using the definition of C_β, and q_d = -Z_de,

From Eq. (4), we obtain

from which we obtain

Alternatively, this expression can be written in terms of the inelastic collision frequency,

Using Eq. (15),

Equations (9) and (17)-(20) are quite general. However, they can be rewritten in a different form, which is possibly more useful for the evaluation of the dispersion relation. This new formulation shows explicitly the contribution of harmonics and Larmor radius terms, leading to general expression which depend on a small number of integrals, which have to be evaluated depending on the equilibrium distribution function. The procedure is as follows. The Bessel functions which appear in the R_ij, both in the 'conventional' and in the 'new' contributions, can be expanded using the expressions which appear in Appendix D, and therefore it is possible to write the components of the dielectric tensor in terms of double series which contains some general integrals. For the 'conventional' components,

where we have defined

with the dimensionless variables

The quantities Ω_* and v_* are some characteristic frequency and velocity, respectively. Details on these calculations can be found in Appendix A.

Further development can be made in the particular case of Maxwellian distributions for ions and electrons,

where , and where we have defined u_β = p_β/p_* = v_β/v_*, with . For these distributions, and indeed for any isotropic distribution, it is immediate to show that (f_β0) = 0, with the consequent vanishing of the integral J_ν(n,m,h;f_β0). Therefore

Similar development can be made for the 'new' contribution, with details in Appendix B. For general distributions,

where

with

₁ = ν₁/Ω_* and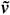 _ch = ν_ch/Ω_* .

For the case of a Maxwellian distribution, the integrals which depend on (f_β0) will vanish, and we obtain

with

_ch and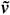 ₁ given by Eqs. (48) and (49), respectively.

4. DISPERSION RELATION FOR THE CASE OF ELECTROSTATIC WAVES AND PARALLEL PROPAGATION

In the case of electrostatic waves (ES waves) and parallel propagation, the dispersion relation is simply given by ε_zz = 0, which can be written as follows,

From Eq. (41),

From Eq. (57), for q_⊥ = 0,

where, from Eq. (48),

and from Eq. (49),

From Eq. (60), for q_⊥ = 0,

After multiplication by z² and use of the previous expressions, the dispersion relation can be written as follows,

In the case of Maxwellian distributions for ions and electrons, and using as an approximation the average value of the collision frequency instead of the actual momentum-dependent value, the J integrals can be evaluated. From Eqs. (C3) and (C6) we obtain

From Eq. (C2),

From Eq. (C5),

Using these results, and using also Eq. (C7), the dispersion relation becomes

where

5. NUMERICAL ANALYSIS

We consider the following parameters, which are in the range of parameters of interest for stellar winds: ion temperature T_i = 1.0×10⁴ K, ion density n_i0 = 1.0×10⁹ cm^-3, ion charge number Z_i = 1.0, and ion mass m_i = m_p, the proton mass. For the radius of the dust particles, we assume a = 1.0×10^-4 cm. For the classical distance of minimum approach, measured in cm, we use the value λ = 1.44×10^-7/T_i(eV), where T_i(eV) means the ion temperature expressed in units of eV.

Initially, we estimate the magnitude of the contribution of the 'new' terms to the dispersion relation of ES waves, and compare it with the 'conventional' contribution. In order to do that we assume the occurrence of weakly damped high-frequency oscillations with ω ~ω_pe. As it is known, waves in this range of frequency are known as Langmuir waves. For normalization purposes, we use v_* = c_s and Ω_* = , where is the equilibrium electron plasma frequency in the absence of dust. For the numerical estimate, we assume that typical Langmuir waves are such that the normalized frequency is z = (1.1, -1×10^-3). For this value of z, and for the parameters considered in the previous paragraph, we plot in Fig. 1 the quantities Λ^C and Λ^N, namely the 'conventional' and the 'new' contributions to the ES dispersion relation, as defined in Eq. (62), versus normalized wavenumber q and normalized dust density ε. The upper panels of Fig. 1 show respectively, from left to right, the real and the imaginary parts of Λ^C, while the bottom panels show from left to right the real and the imaginary parts of Λ^N. It is seen that for most of the interval of q and ε depicted in the figure the real and imaginary contributions of Λ^N are about eight orders of magnitude smaller than the corresponding contributions of Λ^C.

In Fig. 2 we show the quantities Λ^C and Λ^N vs. q and ε, for z = (1×10^-2, -2×10^-4). This value of frequency well below electron plasma frequency was chosen in order to represent ion-sound waves. For this value of z, and for the parameters considered in the previous paragraph, the upper panels of Fig. 2 show respectively, from left to right, the real and the imaginary parts of Λ^C, while the bottom panels show from left to right the real and the imaginary parts of Λ^N. As in the case of the higher frequency Langmuir waves, it is seen that for the interval of q and ε where the values of Λ^C and Λ^N are finite the real and imaginary contributions of Λ^N are much smaller than the corresponding contributions of Λ^C.

We also investigate the relative contributions of the 'conventional' and 'new' terms of the dispersion relation in the frequency range of ion-sound waves for electron temperature higher than ion temperature, case in which ion-sound waves are expected to be much more significant than in the case of equal electron and ion temperatures. Figure 3 is obtained for T_e/T_i = 20, and the other parameters and conditions as in Fig. 2. It shows in the upper panels, from left to right, the real and the imaginary parts of Λ^C, while the bottom panels show from left to right the real and the imaginary parts of Λ^N. As in the case of Fig. 2, for the interval of q and ε where the values of Λ^C and Λ^N are finite the real and imaginary contributions of Λ^N are much smaller than the corresponding contributions of Λ^C.

We further explore the role of the dusty plasma and of the 'new' contribution for the dispersion relation of ES waves, by considering T_e = T_iand numerically solving Eq. (62) for the frequency range of Langmuir waves. The upper left panel of Fig. 4 shows the value of z_r as a function of q and ε, considering ε changing from 0.0 up to 1.0×10^-4. The quantity z_r appears to be quite insensitive to the presence of the dust. In the upper right panel of Fig. 4 we see the corresponding imaginary part. In the scale of the figure, the quantity z_i also appears to be insensitive to the presence of the dust. However, an amplified view of the large wavelength region (small q), where Landau damping is negligible, appears in the bottom panel of Fig. 4 and shows the occurrence of damping due to the presence of the dust particles. The bottom panel of Fig. 4 shows the absolute value of z_i for values of q between 1.0×10^-3 and 4.2×10^-3. It is seen that for ε = 0.0 values of |z_i| due to Landau damping of order 10^-6 starts to appear only above q ~ 0.004. In the region of smaller q (larger wavelengths), the damping rate is zero for ε = 0.0, but it is seen to increase with the increase of the dust density, along the ε axis. The panel shows that the damping due to the dust particles in the large wavelength region (small values of q) increases linearly with the dust density, reaching the maximum of |z_i| ~ 6.0×10^-6 for the maximum value of ε considered in the calculation.

We point out that in Fig. 4 we have plotted the results obtained with the dispersion relation given by Eq. (62) using red color. We have also plotted in the same figure, using blue color, the results obtained from a dispersion relation given by Λ^C = 0, obtained by neglecting the 'new' contribution to the dielectric tensor. The results hardly can be distinguished in the scale of the figure, reflecting the fact that for the range of frequency and for the parameters utilized the effect of the 'new' contribution is negligible in the dispersion relation of ES waves. In a monochromatic version of Fig. 4 the two different results can hardly be distinguished. In a color version of Fig. 4, the two different results appear so close that the curves feature a light purple color, result of the superposition of the results featured with red color and the results featured with blue color.

6. CONCLUSIONS

In the present paper we have addressed the problem of wave propagation in dusty plasmas, starting from a kinetic formulation which takes into account the incorporation of electrons and ions to the dust particles due to inelastic collisions, and used this formulation in order to develop general expressions for the components of the dielectric tensor for magnetized dusty plasmas, valid for general direction of propagation. The dielectric tensor can be divided into two parts, one which is denominated 'conventional' and which is formally similar to the dielectric tensor of dustless plasmas, and another which appears due to occurrence of the inelastic collisions between electrons and ions and the dust particles, and which is denominated as the 'new' contribution. In the formulation developed here, both the 'conventional' and the 'new' contribution were written in terms of double series, formally containing all harmonic and Larmor radius contributions. These general expressions depend on a small number of integrals which depend on the distribution function. We believe that this formulation can be useful for the study of wave propagation in dusty plasmas under a large variety of conditions and parameters.

As further development, we have considered the case of Maxwellian distributions for ions and electrons, and introduced an approximation which uses the average value of the inelastic collision frequencies of electrons and ions with the dust particles, instead of the actual momentum dependent expressions. This approximation was adopted in order to arrive at a relatively simple estimate of the effect of the charging of dust particles due to collisions with electrons and ions, effect which is frequently neglected in analysis of the dispersion relation for waves in dusty plasmas. After the choice of Maxwellian distributions, and after the approximation replacing a fixed average value instead of the momentum dependent collision frequencies, the integrals which appear in the components of the dielectric tensor can be written in terms of the very familiar Z function, whose analytic properties are well known. The formulation therefore becomes specially suitable for numerical analysis.

As an application of the formulation, we have considered the case of electrostatic waves propagating in the direction of the external magnetic field, in a plasma with Maxwellian distributions for electrons and ions. The dispersion relation which has been obtained contains the effects of the charge imbalance due to the capture of charged plasma particles by the dust particles, and also the effect of the inelastic collisions with the dust particles, appearing both in the 'conventional' and in the 'new' contribution to the dielectric tensor. We have made a numerical investigation comparing the magnitudes of the 'conventional' and of the 'new' contributions to the dispersion relation, for frequencies in the range of the Langmuir waves and for frequencies in the range of the ion-sound waves. To our knowledge, it is the first instance of numerical analysis of the effect of the 'new' contribution, which has hitherto only appeared in formal analysis of wave propagation in dusty plasmas [7, 10, 14, 21-23]. For this investigation we have considered parameters which are in the range of parameters typical of stellar winds, and the results obtained have shown that the contribution of the 'new' components is very small compared to the 'conventional' contribution.

We have also numerically solved the dispersion for the case of Langmuir waves, with ω ~ ω_pe. As in previous analysis, the results obtained have shown the appearance of a small damping effect for large wavelength Langmuir waves, where conventional Landau damping is negligible. This damping effect at large wavelengths occurs due to the collisional charging of the dust particles, which contribute to wave absorption because suffer inelastic collisions from ions and electrons, in the dissipative process of dust charging. This damping effect vanishes if the collisional absorption of charged plasma particles by dust particles is neglected.

We conclude with the hope that the formulation developed in the present paper will be useful for further studies on the problem of wave propagation in dusty plasmas.

Acknowledgments

M. C. de Juli was supported by the Brazilian Agency Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP) (process number: 05/60160-5). L. F. Ziebell and R. Gaelzer acknowledge support from Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq). The work was also supported by Fundação de Amparo à Pesquisa do Estado do Rio Grande do Sul (FAPERGS), Programa/Convênio PRONEX/CNPq.

This paper is gratefully dedicated to Dr. Ruth de Souza Schneider, whose unflagging enthusiasm and dedication to teaching and research inspired a whole generation of Physics students at Universidade Federal do Rio Grande do Sul. Dr. Schneider activelly participated in the preparation of this manuscript almost up to her untimely disappearance, at June 17, 2008.

(Received on 11 March, 2008)

APPENDIX A: DETAILS OF THE EVALUATION OF Χ _zz

Here we present some details of the evaluation of the "conventional" part of the zz component of the dielectric tensor, which is necessary for the dispersion relation for electrostatic waves propagating parallel to the ambient magnetic field. From Eq. (9),

For n integer (positive or negative), according to Appendix D,

Using this expansion, and factoring out of the integrals the quantities which don't depend on the integration variable,

where we don't need to use |n| anymore, since n is a positive quantity.

Defining the integrals

we obtain

where we identify e_zz as

with a(0,0) = 1.

Let us introduce small modifications in the evaluation of Eq. (A2). We define m' = m+n, and obtain

We now modify the limits of the summations, and use again the notation m instead of m', for simplicity. We also incorporate again the sign s in the summation index n, such that sn → n, with n assuming positive, negative, and null, values. Moreover, we arrange the expressions in different form, separating the contributions of Χ_zz and e_zz,

where we have defined

We can write the expressions in terms of non-dimensional variables. Let us define

where Ω_* and v_* are some characteristic frequency and velocity, respectively.

For instance, for the study of low-frequency electromagnetic waves we can use:

Ω* = Ω_i; v* = v_A;

where v_A is the Alfvén velocity. For the study of electrostatic waves, we can use:

where c_s is the ion-sound velocity and is the equilibrium electron plasma frequency in the absence of dust.

Using these dimensionless variables, of course,

and

where the J and J_n integrals are defined by Eqs. (31) and (32).

The Maxwellian distributions for ions and electrons are given by

where , we have defined u_β = p_β/p_* = v_β/v_*, with >. For such distributions, and indeed for any isotropic distribution,

(f_β0) = 0, → J_v(n, m, h; f_β0) = 0.

Therefore, we obtain the zz components of the 'conventional' contribution to the dielectric tensor, Eqs. (39) and (41).

APPENDIX B: DETAILS OF THE EVALUATION OF Uz AND Sz

Here we present some details of the evaluation of the "new" part of the zz component of the dielectric tensor, which is necessary for the dispersion relation for electrostatic waves propagating parallel to the ambient magnetic field. From Eqs. (17) and (18),

where we also need

and

Using the series expansion appearing in Appendix D,

Defining m' = m+n,

We can modify the limits of the summations, and use again the notation m instead of m', for simplicity,

We can write these expressions in terms of the dimensionless variables defined given by Eq. (A7),

where the integrals J_U, J_nL, J_nn, J_n0, and J_ch are those defined by Eqs. (50)-(54), and where we have also introduced

Let us assume Maxwellian distributions for ions and electrons, as in Eq. (33). As we have seen, for a Maxwellian distribution, and indeed for any isotropic distribution, (f_β0) = 0. Therefore, we obtain the zz components of the 'new' contribution, as in Eqs. (57), (60), and also obtain Eq. (49).

APPENDIX C: DETAILS OF THE EVALUATION OF INTEGRALS APPEARING IN THE EXPRESSIONS FOR THE COMPONENTS OF THE DIELECTRIC TENSOR

As we have seen, the 'conventional' contributions to the components of the dielectric tensor depend on integrals denoted as J and J_n, defined by Eqs. (31) and (32). The 'new' contribution depends on integrals J_U, J_nL, J_nn, J_n0 and J_ch, defined by Eqs. (50), (51), (52), (53), and (54). In the case of isotropic distributions, we have seen that the integrals which depend of the operator (f_β0) will vanish. It that case, it is only necessary to evaluate integrals J, J_U, J_nL and J_ch, in order to obtain all contributions to the dielectric tensor.

In what follows, we consider the case of Maxwellian distributions for ions and electrons. Moreover, as an approximation we assume that the momentum-dependent collision frequency is replaced by the average value. This approximation is adopted in order to arrive at a relatively simple estimate of the effect of the charging of dust particles due to collisions with electrons and ions, effect which is frequently neglected in analysis of the dispersion relation for waves in dusty plasmas.

1. Evaluation of the integralsJ(n,m,h;f_β0) for the case of Maxwellian distribution, using an average collision frequency

From Eq. (A5),

Let us assume, for simplicity, that the collision frequency is replaced by the average value,

For a Maxwellian distribution,

and therefore

where

Now, let

where

Therefore,

which easily leads to

where . We note that the integral over u⊥ was made assuming that m is integer.

Let us consider the integral appearing at the end of Eq. (C1).

For h = 0,

For h = 1,

For h = 2,

The result is (for integer m),

2. Evaluation of the integralsJ_U(n;m;h; l; f_β0) andJ_nL(n;m;h; f_β0) for the case Maxwellian distribution, using an average collision frequency

From Eq. (50),

Let us assume, for simplicity, that the collision frequency is replaced by the average value,

_β. Let us also neglect the effect of the Heaviside function in the numerator of the integrand. This approximation can be seen from another point of view as follows: The collision frequency (for electrons) already contains a step function, which therefore don't need to be written explicitly in the integrand. Afterwards, we replace the collision frequency by the average value, and obtain

Let us further approximate,

On the other hand, from a few steps before Eq. (C1) we find, for a Maxwellian distribution,

Therefore, we obtain

In other words, the approximated result for the case of a Maxwellian distribution can be written as follows,

From Section 1, we have seen that the J(n;m;h; f_β0) function can be written in terms of the Z function. Particularly, for integer value of m, we have obtained Eq. (C2).

Let us now investigate the case of a half-integer in place of m, namely m - 1/2, required by Eq. (C3). From results appearing before Eq. (C2), we obtain, for a Maxwellian distribution,

Now, using the same variable t defined in Section (1),

where .

Therefore,

As already seen in Section 1, the integral appearing at the end of Eq. (C4) can be written in terms of the Z function. The result is

We also have to evaluate J_nL. From Eq. (51),

using the average value of the collision frequency,

From Eq. (31),

Therefore, for any distribution function, when the collision frequency is approximated by the average value,

Equations (C6) and (C3), together with Eqs. (C5), show that in the case of a Maxwellian distribution, when the dispersion relation is approximated by the average value, the J_U and J_nL integrals can be written as proportional to the J integral, which can be written in terms of the Z function, according to Eqs. (C2) and (C5).

3. Evaluation of the integralsJ_ch( f_β0) for the case of Maxwellian distribution

From Eq. (54),

Let

where

APPENDIX D: USEFUL EXPANSIONS

Useful series expansions for Bessel functions (see Ref. [24])

where

The third equation in Eqs. (D1) is demonstrated as follows,

• [1]P. K. Bliokh and V. V. Yarashenko, Soviet. Astr. Engl. Transl. 29, 330 (1985).
• [2] J. R. Bhatt, Phys. Rev. E 55, 1166 (1997).
• [3] N. D'Angelo, Planet. Space Sci. 42, 507 (1994).
• [4] R. K. Varma, P. K. Shukla, and V. Krishan, Phys. Rev. E 47, 3612 (1993).
• [5] M. R. Jana, A. Sen, and P. K. Kaw, Phys. Rev. E 48, 3930 (1993).
• [6] V. N. Tsytovich and O. Havnes, Comm. Plasma Phys. Contr. Fus. 15, 267 (1993).
• [7] S. I. Popel, S. N. Andreev, A. A. Gisko, A. P. Golub, and T. V. Losseva, Plasma Phys. Rep. 8, 284 (2004).
• [8] M. Rosenberg, Planet. Space Sci. 41, 229 (1993).
• [9] Y. J. Park and Hee J. Lee, Phys. Scripta 71, 213 (2005).
• [10] M. C. de Juli, R. S. Schneider, L. F. Ziebell, and V. Jatenco-Pereira, Phys. Plasmas 12, 052109 (2005).
• [11] L. F. Ziebell, M. C. de Juli, R. S. Schneider, and V. Jatenco-Pereira, Phys. Plasmas 12, 082102 (2005).
• [12] M. C. de Juli, R. S. Schneider, L. F. Ziebell, and R. Gaelzer, Phys. Plasmas 14, 022104 (2007).
• [13] M. C. de Juli, R. S. Schneider, L. F. Ziebell, and R. Gaelzer, J. Geophys. Res. 112, A10105 (2007).
• [14] R. S. Schneider, L. F. Ziebell, M. C. de Juli, and V. Jatenco-Pereira, Braz. J. Phys. 36, 759 (2006).
• [15] V. N. Tsytovich, U. de Angelis, and R. Bingham, Phys. Rev. Lett. 87, 185004 (2001).
• [16] V. N. Tsytovich, U. de Angelis, and R. Bingham, Phys. Plasmas 9, 1079 (2002).
• [17] J. E. Allen, Phys. Scr. 45, 497 (1992).
• [18] V. N. Tsytovich, Sov. Phys. Usp. 40, 53 (1997).
• [19] G. E. Morfill, H. M. Thomas, U. Konopka, and M. Zuzic, Phys. Plasmas 6, 1769 (1999).
• [20] L. J. Spitzer, Physical Processes in the Interstellar Medium (John Wiley, New York, 1978).
• [21] M. C. de Juli and R. S. Schneider, J. Plasma Phys. 60, 243 (1998).
• [22] M. C. de Juli and R. S. Schneider, J. Plasma Phys. 64, 57 (2000).
• [23] M. C. de Juli, R. S. Schneider, D. A. Falceta-Gonçalves, and V. Jatenco-Pereira, IEEE Trans. Plasma Sci. 32, 542 (2004).
• [24] V. Krivenski and A. Orefice, J. Plasma Phys. 30, 125 (1983).

†

In Memoriam

Publication Dates

• Publication in this collection
  22 Sept 2008
• Date of issue
  Sept 2008

History

• Received
  11 Mar 2008