Abstract
We present some essential results for the Hamiltonian of a particle in a box. We discuss the invariance of this operator under time-reversal T, the possibility of choosing real eigenfunctions for it and the degeneracy of its energy eigenvalues. Once these results have been presented, we introduce the usual nondegeneracy theorem and discuss some issues surrounding it. We find that the nondegeneracy theorem is true if the boundary conditions are T-invariant but "confining" (i.e., the particle is in a real impenetrable box). If the boundary conditions are not T-invariant (belonging to a family of so-called "not confining" boundary conditions), the respective eigenfunctions are strictly complex and there is no degeneracy. Consistently, we verify the validity of the theorem also in this case. Finally, if the boundary conditions are also T-invariant, but "not confining", then we can have degeneracy in the energy levels only if the respective eigenfunctions can be specifically written as complex. We find that the nondegeneracy theorem fails in these cases. If the respective eigenfunctions can be written as only real, then we do not have degeneracy and the nondegeneracy theorem is true.
Quantum Mechanics; Particle in a box; Nondegeneracy theorem; Time-reversal invariance
On the nondegeneracy theorem for a particle in a box
Salvatore De Vincenzo
Salvatore De Vincenzo Escuela de Física, Facultad de Ciencias, Universidad Central de Venezuela, A.P. 47145, Caracas 1041-A, Venezuela E-mail: svincenz@fisica.ciens.ucv.ve
ABSTRACT
We present some essential results for the Hamiltonian of a particle in a box. We discuss the invariance of this operator under time-reversal T, the possibility of choosing real eigenfunctions for it and the degeneracy of its energy eigenvalues. Once these results have been presented, we introduce the usual nondegeneracy theorem and discuss some issues surrounding it. We find that the nondegeneracy theorem is true if the boundary conditions are T-invariant but "confining" (i.e., the particle is in a real impenetrable box). If the boundary conditions are not T-invariant (belonging to a family of so-called "not confining" boundary conditions), the respective eigenfunctions are strictly complex and there is no degeneracy. Consistently, we verify the validity of the theorem also in this case. Finally, if the boundary conditions are also T-invariant, but "not confining", then we can have degeneracy in the energy levels only if the respective eigenfunctions can be specifically written as complex. We find that the nondegeneracy theorem fails in these cases. If the respective eigenfunctions can be written as only real, then we do not have degeneracy and the nondegeneracy theorem is true.
Keywords: Quantum Mechanics; Particle in a box; Nondegeneracy theorem; Time-reversal invariance
1. INTRODUCTION
Some time ago, Loudon [1], in studying the one-dimensional model of a hydrogen atom (V(x) = - k/|x|), found that all of the discrete energy levels turn out to be doubly degenerate; that is, two different eigenfunctions have the same energy. Likewise, Loudon himself pointed out that the usual proof that forbids the degeneracy for a one-dimensional system, which seemed to be independent of the shape of the potential did not apply to the case he was treating. A later, more carefully study, gave several arguments that seemed to confirm that these discrete energy levels could not be degenerate [2]. More recently, Cohen and Kuharetz studied another example of a one-dimensional system: An infinite square well with a singular potential (actually proportional to the Dirac delta) with adjustable strength at the center of the well [3]. The solution had doubly degenerate energy eigenvalues. It is worth mentioning that the trouble with the degeneracy in this system had already been mentioned by Oseguera [4]. These aspects have also been considered in the context of supersymmetric quantum mechanics [5]. All of these results apparently prove that the so-called nondegeneracy theorem is not necessarily valid for potentials that have a singular point. In spite of this fact, the proof of this theorem in some books makes no mention of this specific point [6]. We recently found another reference in which the appearance of degeneracy in the presence of certain singular potentials is explored in one-dimensional quantum systems, although the authors of this reference also showed cases of nondegeneracy in the presence of singular potentials [7]. We have also seen a study that found that bound states, degenerate in energy, may exist even if the potential is unbounded from below at infinity [8].
However, there exists another one-dimensional system with real and complex eigenfunctions that is much more simple than any mentioned above and, depending on the boundary conditions, it can present double degeneracy in its energy levels. This is the well known problem of a particle in the closed interval 0 < x < π with a potential of zero inside the box. (Incidentally, as the motion of the particle remains, in this case, limited or restricted to [0,π], we consider the Hilbert space L2([0,π]), where [0,π] ⊂ ℜ. The quantum mechanical treatment of the infinite square well potential with Hilbert space L2(ℜ), with the functions in the respective domain of the Hamiltonian vanishing if x < 0 and x > π, is not equivalent to the problem in L2([0,π]). In such a way that, the usual nondegeneracy theorem does not always work for a particle in a box and, for this reason, it is important to study all of the issues surrounding this result carefully. This is one of the goals of the present paper.
The ordinary differential equation (ODE) for the eigenvalues (and eigenfunctions) in our problem is
u(x) + λu(x) = 0, where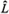 = d2/dx2 is a self-adjoint (hermitian) operator with u(x) satisfying some of the following boundary conditions [9-13]. The Hamiltonian of the system is
= d2/dx2 is a self-adjoint (hermitian) operator with u(x) satisfying some of the following boundary conditions [9-13]. The Hamiltonian of the system is 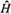 = -
= - 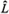 with energy E = λ; moreover ħ2 = 2m = 1:
with energy E = λ; moreover ħ2 = 2m = 1:
The primes denote differentiation with respect to x; the parameter η is inserted for dimensional reasons and the matrix U, belonging to U(2), can be written, in this instance, as [12]:
where ø ∈ [0,π], and the quantities mk ∈ ℜ (k = 0,1,2,3.) satisfy (m0)2 + (m1)2 + (m2)2 + (m3)2 = 1. This matrix is independent of the choice of the function u ∈ D(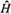 ). It can be shown that for every function u(x) that satisfies one boundary condition included in (1), which is a critical part of the respective domain of the Hamiltonian D(
). It can be shown that for every function u(x) that satisfies one boundary condition included in (1), which is a critical part of the respective domain of the Hamiltonian D(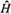 ), the probability current density is:
), the probability current density is:
The bars denote complex conjugation. This satisfies j(0) = j(π), and this condition is equivalent to the self-adjointness of the Hamiltonian. For some of these boundary conditions we have j(0) = j(π) = 0 by necessity, which is the impenetrability condition at the walls of the box (see, for example, [9] and [10]). In fact, we found an expression for the probability current density at the walls of the box:
Notice that, by setting m1 = m2 = 0, we obtain j(0) = j(π) = 0. (See, for example, [9] and [14] for other comments about this fact, although we have a different parameterization for the matrix U in equation (2)). The respective subfamily of ("general" unmixed) confining boundary conditions, which correspond to a particle in a real impenetrable box, can be written (from (1) and (2)) as:
where θ = tan-1(m3/m0). Note that this subfamily of boundary conditions is similar to that studied and termed "separated" by Albeverio et al [15,16] for a free particle on a line with a hole (i.e., a point interaction).
From (3) it is clear that if the eigenfunctions are real functions with m2 = 0 and m1≠ 0, then we also have j(0) = j(π) = 0. Consistently, if the Hamiltonian operator 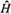 is invariant under time-reversal
is invariant under time-reversal  , we have (
, we have ( -1
-1
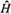 u)(x), so that the operator
u)(x), so that the operator  commutes with
commutes with 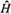 , and the time-reversal transformed function must satisfy (
, and the time-reversal transformed function must satisfy ( u)(x) ∈ D(
u)(x) ∈ D(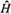 ). If we consider a stationary state of definite energy (in this case,
). If we consider a stationary state of definite energy (in this case,  is also called the complex conjugation operator), this invariance implies that u(x) and (
is also called the complex conjugation operator), this invariance implies that u(x) and (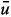 )(x) ≠ (
)(x) ≠ ( u)(x) are two eigenfunctions of
u)(x) are two eigenfunctions of 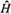 with the same eigenvalue, and that they both comply with the same boundary condition. Thus, the matrix U must satisfy U+ =
with the same eigenvalue, and that they both comply with the same boundary condition. Thus, the matrix U must satisfy U+ = 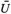 , which implies m2 = 0 [12]. Therefore, the number of the parameters in U is reduced to three, and the eigenfunctions for these
, which implies m2 = 0 [12]. Therefore, the number of the parameters in U is reduced to three, and the eigenfunctions for these  -invariant Hamiltonians can be real functions. This result has also been found for the problem of a particle on a line with a hole; see [17] and references therein. Note that, all of the boundary conditions included in the so-called confining family (4) are automatically
-invariant Hamiltonians can be real functions. This result has also been found for the problem of a particle on a line with a hole; see [17] and references therein. Note that, all of the boundary conditions included in the so-called confining family (4) are automatically  -invariant as well. However, we will prove specifically that they do not lead to degeneracy in the energies. Therefore in this case, we necessarily obtain real eigenfunctions with their respective zero probability currents.
-invariant as well. However, we will prove specifically that they do not lead to degeneracy in the energies. Therefore in this case, we necessarily obtain real eigenfunctions with their respective zero probability currents.
Thus, as u and 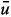 are (different) complex eigenfunctions of
are (different) complex eigenfunctions of 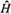 with the same eigenvalue (or Re(u) = (u +
with the same eigenvalue (or Re(u) = (u + 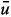 )/2 and Im(u) = (u +
)/2 and Im(u) = (u + 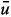 )/2i belonging to ℜ), there is a double degeneracy in the energy levels; therefore, the usual proof that forbids the degeneracy for a one-dimensional system [6] must be re-examined in light of the problem of a particle inside a box. A necessary condition for the existence of degeneracy in the energies in this problem is that the corresponding Hamiltonian be invariant under time-reversal. Hence, there must also exist
)/2i belonging to ℜ), there is a double degeneracy in the energy levels; therefore, the usual proof that forbids the degeneracy for a one-dimensional system [6] must be re-examined in light of the problem of a particle inside a box. A necessary condition for the existence of degeneracy in the energies in this problem is that the corresponding Hamiltonian be invariant under time-reversal. Hence, there must also exist  -invariant boundary conditions which do not lead to degeneracy in the energies; i.e., as u and
-invariant boundary conditions which do not lead to degeneracy in the energies; i.e., as u and 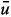 differ only by a constant factor and therefore represent the same state, Re(u) and Im(u) must also represent the same state. In other words, there is only one unique eigensolution for each eigenvalue of the energy, so we can always choose this eigensolution to be real. If the (complex or real) eigenfunctions of the Hamiltonian
differ only by a constant factor and therefore represent the same state, Re(u) and Im(u) must also represent the same state. In other words, there is only one unique eigensolution for each eigenvalue of the energy, so we can always choose this eigensolution to be real. If the (complex or real) eigenfunctions of the Hamiltonian 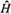 are doubly degenerate, then the respective boundary condition is
are doubly degenerate, then the respective boundary condition is  -symmetric. If the boundary condition is not
-symmetric. If the boundary condition is not  -symmetric, then the eigenfunctions must be necessarily complex and, in addition, they cannot be degenerate.
-symmetric, then the eigenfunctions must be necessarily complex and, in addition, they cannot be degenerate.
When the probability current density is not null at the walls of the box (see relation (3)), we can say that (physically) the walls are transparent to the current. In some of these cases, the underlying classical particle arrives at one wall and then appears at the other (see references in [18] for comments about this point). We can therefore write a second family of boundary conditions; this one may be called, say, "not confining", but only if the respective eigenfunctions are (written as) complex functions and are therefore degenerate, if they are  -invariant; or not degenerate, if they are not
-invariant; or not degenerate, if they are not  -invariant. Note that the probability current is not zero only if the respective functions are complex functions because real functions always lead to zero probability current inside the box. Thus, if the particle is not really confined to the box, the wave function must be complex (we read a very slight comment about this point in [19], page 2, after the equation (7)). Finally, this "not confining" family, together with the family (4) (as well as the general boundary condition (1)) compose the whole family of boundary conditions for the self-adjoint Hamiltonian for a particle in a box (see the article by V. Alonso et al, in [14]):
-invariant. Note that the probability current is not zero only if the respective functions are complex functions because real functions always lead to zero probability current inside the box. Thus, if the particle is not really confined to the box, the wave function must be complex (we read a very slight comment about this point in [19], page 2, after the equation (7)). Finally, this "not confining" family, together with the family (4) (as well as the general boundary condition (1)) compose the whole family of boundary conditions for the self-adjoint Hamiltonian for a particle in a box (see the article by V. Alonso et al, in [14]):
where the matrix M is:
In fact, this matrix can also be written as:
which confirms, due to the relation (m0)2 + (m1)2 + (m2)2 + (m3)2 = 1, that M does belong to the group U(1) × SL(2, ℜ). Moreover, the elements in the matrix M can have only finite values (that is, m1 and m2 cannot be simultaneously null). By the way, the subfamily of boundary conditions (5) is similar to the "connected" subfamily of boundary conditions studied by Albeverio et al [15,16] for a free particle on a line with a point interaction. Lastly, note that all of the coefficients in the matrix M are real for  -invariant boundary conditions (since only m2 = 0).
-invariant boundary conditions (since only m2 = 0).
For examples of boundary conditions included in (1), see Table 1. Within the confining subfamily (4), we have, for example: (a) The usual Dirichlet boundary condition, u(0) = u(π) = 0; (b) the Neumann boundary condition, u'(0) = u'(π) = 0; and the so-called mixed boundary conditions, (c) u(0) = u'(p) = 0 and (d) u'(0) = u(π) = 0. These four  -invariant boundary conditions do not lead to degeneracy in the energies (see Table 2) and satisfy m1 = m2 = 0. Therefore, there is a valid place for the nondegeneracy theorem.
-invariant boundary conditions do not lead to degeneracy in the energies (see Table 2) and satisfy m1 = m2 = 0. Therefore, there is a valid place for the nondegeneracy theorem.
As examples of boundary conditions which are not  -symmetric, we have: (e) one complex condition: u(0) = iu(π), u'(0) = iu'(p); (f) and another odd condition, ηu'(0) = -iu(π), ηu'(π) = -iu(0). (See Table 1). Note that for this pair of boundary conditions, one has m2≠ 0; moreover, all of the respective eigenfunctions are necessarily complex, and none of them are degenerate (see Table 2). Thus, in all these cases, the nondegeneracy is verified.
-symmetric, we have: (e) one complex condition: u(0) = iu(π), u'(0) = iu'(p); (f) and another odd condition, ηu'(0) = -iu(π), ηu'(π) = -iu(0). (See Table 1). Note that for this pair of boundary conditions, one has m2≠ 0; moreover, all of the respective eigenfunctions are necessarily complex, and none of them are degenerate (see Table 2). Thus, in all these cases, the nondegeneracy is verified.
As examples of  -invariant boundary conditions included within the four parameter family (1) and included in subfamily (5) but not within subfamily (4) (see Table 1), which lead to (real and complex) degenerate eigenfunctions, we have: (g) The periodic condition, u(0) = u(π), u'(0) = u'(π); and (η) the antiperiodic condition: u(0) = -u(π), u'(0) = -u(π). With the exception of the ground state eigenfunction of the periodic boundary condition, all the eigenfunctions are doubly degenerate (see Table 2). Note that we have only m2 = 0 and m1≠ 0 for these two boundary conditions, and there is no place, in these two cases, for a valid nondegeneracy theorem. However, within subfamily (5) there also exist
-invariant boundary conditions included within the four parameter family (1) and included in subfamily (5) but not within subfamily (4) (see Table 1), which lead to (real and complex) degenerate eigenfunctions, we have: (g) The periodic condition, u(0) = u(π), u'(0) = u'(π); and (η) the antiperiodic condition: u(0) = -u(π), u'(0) = -u(π). With the exception of the ground state eigenfunction of the periodic boundary condition, all the eigenfunctions are doubly degenerate (see Table 2). Note that we have only m2 = 0 and m1≠ 0 for these two boundary conditions, and there is no place, in these two cases, for a valid nondegeneracy theorem. However, within subfamily (5) there also exist  -invariant boundary conditions that do not lead to degeneracy in the energies. Therefore, these cases always lead to real eigenfunctions and unfortunately they do not represent a particle "not confined" to the box. In fact, as an example we have, (i) the nontrivial condition (the name is due to its nontrivial respective spectrum): ηu'(0) = u(π), ηu'(0) = -u(0) (see Tables 1 and 2).
-invariant boundary conditions that do not lead to degeneracy in the energies. Therefore, these cases always lead to real eigenfunctions and unfortunately they do not represent a particle "not confined" to the box. In fact, as an example we have, (i) the nontrivial condition (the name is due to its nontrivial respective spectrum): ηu'(0) = u(π), ηu'(0) = -u(0) (see Tables 1 and 2).
The plan of this paper is as follows: we have presented in the Introduction the principal results for the Hamiltonian for the problem of a particle in a box, in certain cases confined to the box and, in other cases, not restricted to the box, as well as the invariance of this Hamiltonian under time-inversion ( ) which determines whether the respective eigenfunctions can be written as pure real (and degenerate in some cases). In section 2, we derive the expected nondegeneracy theorem and discuss some issues surrounding this result. Thus, the core of this paper is comprises results about boundary conditions which have consequences with regard to the possibility of having, or not having, two different eigenfunctions with the same energy. Some concluding remarks are given in section 3. Finally, in the AppendixAppendix, we discuss a point that is related with the presence of degeneracy if the boundary condition is
) which determines whether the respective eigenfunctions can be written as pure real (and degenerate in some cases). In section 2, we derive the expected nondegeneracy theorem and discuss some issues surrounding this result. Thus, the core of this paper is comprises results about boundary conditions which have consequences with regard to the possibility of having, or not having, two different eigenfunctions with the same energy. Some concluding remarks are given in section 3. Finally, in the AppendixAppendix, we discuss a point that is related with the presence of degeneracy if the boundary condition is  -invariant (this happens only in certain cases).
-invariant (this happens only in certain cases).
2. THE NONDEGENERACY THEOREM
As is well known, the Sturm-Liouville ODE is
u(x) + λw(x)u(x) = 0 , where the second order, real, and self-adjoint differential operator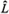 is written as:
is written as:
The eigenvalue is λ and w(x) is a weight function. Since the operator 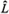 in (7) is in its self-adjoint form, we have
in (7) is in its self-adjoint form, we have  (x) = a1(x). One assumes, as usual, that a0(x) > 0 and w(x) > 0 over the finite interval Ω = [a, b] in which the ODE is to be satisfied. If either vanishes, this will occur on the boundaries. Additionally,
(x) = a1(x). One assumes, as usual, that a0(x) > 0 and w(x) > 0 over the finite interval Ω = [a, b] in which the ODE is to be satisfied. If either vanishes, this will occur on the boundaries. Additionally,  (x), a2(x), and w(x) are integrable over all of Ω [20,21] (that is, we are considering the regular case here). To obtain the corresponding ODE for the problem of a free particle in the interval Ω = [0,π] (see the paragraph above Eq. (1)), we write w(x) = 1, a0(x) = 1 ⇒ a1(x) = 0, -a2(x) = V(x) = 0 (the external potential), λ = E (the energy) and
(x), a2(x), and w(x) are integrable over all of Ω [20,21] (that is, we are considering the regular case here). To obtain the corresponding ODE for the problem of a free particle in the interval Ω = [0,π] (see the paragraph above Eq. (1)), we write w(x) = 1, a0(x) = 1 ⇒ a1(x) = 0, -a2(x) = V(x) = 0 (the external potential), λ = E (the energy) and 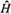 = -
= -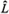 (the Hamiltonian).
(the Hamiltonian).
Let ui(x) and uk(x) be eigenfunctions (real or complex) of 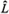 (for a specific boundary condition) corresponding to the eigenvalues λi and λk (of the discrete spectrum). Then:
(for a specific boundary condition) corresponding to the eigenvalues λi and λk (of the discrete spectrum). Then:
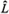 uk(x) + λkw(x) uk(x) = 0.
uk(x) + λkw(x) uk(x) = 0.
If we multiply the equation for ui(x) by uk(x), the equation for uk(x) by ui(x) and then subtract, we obtain:
Note that, there is no distinction from the beginning between real or complex eigenfunctions, as is the procedure followed by textbooks when the nondegeneracy theorem is introduced. By substituting for 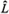 from (7) into this last expression and using the condition λk = λi, we obtain:
from (7) into this last expression and using the condition λk = λi, we obtain:
which is valid for any x ∈ Ω. Note that by specializing to i = k in (9), we automatically have a null constant; likewise, this expression can be written as a0(x)W[uk(x),ui(x)] = const, where W is the Wronskian of the solutions uk(x) and ui(x). If we want to obtain the usual nondegeneracy theorem from relation (9), the constant on the right side of (9) must be zero; if the constant in (9) vanishes at any point in Ω (usually at the ends of Ω), then it vanishes everywhere. If this is so, then we have ui(x) ∝ uk(x). In fact, with a0(x) = 1, we assume that the constant in (9) is zero (const = 0), thus uk(x) (x)-
(x)- (x)ui(x) = 0, and therefore
(x)ui(x) = 0, and therefore  (x)/ui(x) =
(x)/ui(x) =  (x)/uk(x). Integration then gives ui(x) ∝ uk(x), and this relation is valid where ui(x) and uk(x) do not vanish. As we expect, there are several ways to cancel that constant in (9): (a) if the (two) eigenfunctions ui(x) and uk(x) are both zero at some point x0∈ Ω (we usually have x0 = a and/or x0 = b with a0(x0) ≠ 0); (b) if their respective derivatives
(x)/uk(x). Integration then gives ui(x) ∝ uk(x), and this relation is valid where ui(x) and uk(x) do not vanish. As we expect, there are several ways to cancel that constant in (9): (a) if the (two) eigenfunctions ui(x) and uk(x) are both zero at some point x0∈ Ω (we usually have x0 = a and/or x0 = b with a0(x0) ≠ 0); (b) if their respective derivatives  (x) and
(x) and  (x) are both zero in x0 as well; and (c) If we have a condition at x0 such as:
(x) are both zero in x0 as well; and (c) If we have a condition at x0 such as:
where the constant is real. (Incidentally, this type of boundary condition was mentioned in [3] and [22]) It is important to notice that the subfamily of boundary conditions introduced in (4) is precisely of the form given in (10) with x0 = 0 and x0 = π. Moreover, cases (a) and (b) (which were mentioned above) are included in case (c). In principle, the constant in (9) vanishes if the eigenfunctions ui(x) and uk(x), or their derivatives, vanish anywhere in x0∈ Ω or (usually) at both ends or only at one end. The point is that if the eigenfunctions are written as real (i.e., the respective boundary condition is  -invariant), then they always have zeros (i.e., nodes), except for the ground state eigenfunction [23]. It is common to see eigenfunctions with zeros at the ends but, in fact, there are a lot of boundary conditions, for instance, those included in (5) which lead to eigenfunctions with zeros only inside the box (i.e., their respectives nodes). In all of these cases, the constant in (9) is essentially null because there is always a point x0∈ Ω where the real eigenfunctions vanish, and these eigenfunctions lead to a probability current density that vanishes inside the box.
-invariant), then they always have zeros (i.e., nodes), except for the ground state eigenfunction [23]. It is common to see eigenfunctions with zeros at the ends but, in fact, there are a lot of boundary conditions, for instance, those included in (5) which lead to eigenfunctions with zeros only inside the box (i.e., their respectives nodes). In all of these cases, the constant in (9) is essentially null because there is always a point x0∈ Ω where the real eigenfunctions vanish, and these eigenfunctions lead to a probability current density that vanishes inside the box.
Proposition 1: "Boundary conditions included within the confining subfamily (4) verify the nondegeneracy theorem". Demostration: By evaluating (9) for x0 = 0, or x0 = π, or anywhere else, we write uk(x0) (x0)-
(x0)- (x0)ui(x0) = const. Depending on the chosen boundary condition, this constant could be directly zero. We also have a0(x0) ≠ 0, and by using (10) or (4) we can write
(x0)ui(x0) = const. Depending on the chosen boundary condition, this constant could be directly zero. We also have a0(x0) ≠ 0, and by using (10) or (4) we can write  (x0) and
(x0) and  (x0) as functions of ui(x0) and uk(x0), respectively. Finally, we obtain: uk(x0)ui(x0)-uk(x0)ui(x0) = const = 0. Remarkably, note that we did not need any eigenfunction to vanish at x0 to obtain this result. Consequently, uk(x)
(x0) as functions of ui(x0) and uk(x0), respectively. Finally, we obtain: uk(x0)ui(x0)-uk(x0)ui(x0) = const = 0. Remarkably, note that we did not need any eigenfunction to vanish at x0 to obtain this result. Consequently, uk(x)  (x)-
(x)- (x)ui(x) = 0, ∀ x ∈ [0,π], which implies ui(x) ∝ uk(x). Thus, in this case neither of the boundary conditions included in (4) leads to degenerate eigenfunctions, because the eigenfunctions that verify the confining boundary conditions automatically cancel the constant, and the nondegeneracy theorem is verified. (The examples (a)-(d) confirm precisely this conclusion.) As we already know, our subfamily (4) describes a real box, that is, a genuine finite impenetrable region.
(x)ui(x) = 0, ∀ x ∈ [0,π], which implies ui(x) ∝ uk(x). Thus, in this case neither of the boundary conditions included in (4) leads to degenerate eigenfunctions, because the eigenfunctions that verify the confining boundary conditions automatically cancel the constant, and the nondegeneracy theorem is verified. (The examples (a)-(d) confirm precisely this conclusion.) As we already know, our subfamily (4) describes a real box, that is, a genuine finite impenetrable region.
It is clear that relation (9) is valid for real and also for complex eigenfunctions, and if there exist two pure complex eigenfunctions verifying ui(x) ∝ uk(x), then they will cause the constant in (9) to vanish, even when these eigenfunctions do not vanish at any point x0∈ Ω . (We will see below how this situation can occur.) Due to this last aspect (i.e., two complex eigenfunctions, differing only by a scale factor, that are different from zero at x0), we should have some boundary condition not included in the  -symmetric subfamily that also implies that the respective eigenfunctions give a non-zero probability current density. To be more precise, boundary conditions (e) and (f) are not
-symmetric subfamily that also implies that the respective eigenfunctions give a non-zero probability current density. To be more precise, boundary conditions (e) and (f) are not  -symmetric and they should not lead to degeneracy.
-symmetric and they should not lead to degeneracy.
On the other hand, (complex) eigenfuctions (that are degenerate) that satisfy a  -invariant boundary condition for a free particle in a box but not really confined in the box, such as the periodic (g) as well as the antiperiodic (h), could not cancel that constant. Note that we can have real or complex eigenfunctions for these two boundary conditions; nevertheless, only the complex ones correspond to a particle not genuinely restricted to the box. If the eigenfunctions are chosen to be real, then we have a zero probability density current everywhere. See equation 3.
-invariant boundary condition for a free particle in a box but not really confined in the box, such as the periodic (g) as well as the antiperiodic (h), could not cancel that constant. Note that we can have real or complex eigenfunctions for these two boundary conditions; nevertheless, only the complex ones correspond to a particle not genuinely restricted to the box. If the eigenfunctions are chosen to be real, then we have a zero probability density current everywhere. See equation 3.
Proposition 2: "Boundary conditions which are not  -invariant verify the nondegeneracy theorem". Demonstration: Note that relation (9) (with a0(x) = 1) can be written as:
-invariant verify the nondegeneracy theorem". Demonstration: Note that relation (9) (with a0(x) = 1) can be written as:
(which is valid for any x ∈ [0,π]), and by evaluating this relation, for example, at x = x0 = π, we can write
We can now write the row matrix (uk(π) ηu'(π)) and the column matrix  as functions of (uk(0) η
as functions of (uk(0) η (0)) and
(0)) and  respectively, by using the family of boundary conditions (5). Thus, by substituting these two expressions into (12) and by making the product MT
respectively, by using the family of boundary conditions (5). Thus, by substituting these two expressions into (12) and by making the product MT  M, we obtain remarkably:
M, we obtain remarkably:
where MT is the transpose matrix of M. And now, by writing relation (11), which is evaluated at x = 0:
we obtain the following result by comparing (13) with (14):
All of the boundary conditions that are not  -invariant satisfy m2≠ 0. Thus, from (15), we finally obtain const = 0, which implies ui(x) ∝ uk(x); i.e., this kind of boundary conditions does not lead to degenerate eigenfunctions and in particular the complex conditions (e) and (f), do not lead to degenerate eigenfunctions. Besides, in these two examples, we have m1 = 0 and therefore (-1) × const = const. The discussion of the validity of the nondegeneracy theorem in this case (i.e., for boundary conditions which are not
-invariant satisfy m2≠ 0. Thus, from (15), we finally obtain const = 0, which implies ui(x) ∝ uk(x); i.e., this kind of boundary conditions does not lead to degenerate eigenfunctions and in particular the complex conditions (e) and (f), do not lead to degenerate eigenfunctions. Besides, in these two examples, we have m1 = 0 and therefore (-1) × const = const. The discussion of the validity of the nondegeneracy theorem in this case (i.e., for boundary conditions which are not  -invariant), to the best of our knowledge, seems not to have appeared previously as a distinct issue in the physics literature.
-invariant), to the best of our knowledge, seems not to have appeared previously as a distinct issue in the physics literature.
Finally, not all  -invariant boundary conditions (m2 = 0) included within subfamily (5) verify the nondegeneracy theorem. In fact, some
-invariant boundary conditions (m2 = 0) included within subfamily (5) verify the nondegeneracy theorem. In fact, some  -invariant boundary conditions with complex eigenfunctions always lead to degenerate eigenfunctions (for example, the periodic and antiperiodic boundary conditions). Other boundary conditions could lead to a degenerate (non simple) spectrum, as it has been pointed out on page 24 of the second reference in [12]. See the AppendixAppendix for a discussion about this. Note that one obtains from (15) that const = const, and pure complex eigenfunctions do not give zeros anywhere (that is, the constant in (9) is not null). Therefore, the conventional proof of the nondegeneracy theorem fails. However, for the pure real eigenfuctions (i.e., those that we do not need to write as complex) arising from
-invariant boundary conditions with complex eigenfunctions always lead to degenerate eigenfunctions (for example, the periodic and antiperiodic boundary conditions). Other boundary conditions could lead to a degenerate (non simple) spectrum, as it has been pointed out on page 24 of the second reference in [12]. See the AppendixAppendix for a discussion about this. Note that one obtains from (15) that const = const, and pure complex eigenfunctions do not give zeros anywhere (that is, the constant in (9) is not null). Therefore, the conventional proof of the nondegeneracy theorem fails. However, for the pure real eigenfuctions (i.e., those that we do not need to write as complex) arising from  -invariant boundary conditions, there always exists a point inside the box where these eigenfunctions vanish (that is, the constant in (9) is null). Thus, the nondegeneracy theorem is certainly true. Until now, all of these particular aspects of the nondegeneracy theorem had not been sufficiently discussed in the literature (as far as we know).
-invariant boundary conditions, there always exists a point inside the box where these eigenfunctions vanish (that is, the constant in (9) is null). Thus, the nondegeneracy theorem is certainly true. Until now, all of these particular aspects of the nondegeneracy theorem had not been sufficiently discussed in the literature (as far as we know).
As a final comment, note that, if u and 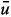 are different complex eigenfunctions of
are different complex eigenfunctions of 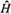 with the same eigenvalue, then the real ones, Re(u) = (u +
with the same eigenvalue, then the real ones, Re(u) = (u + 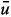 )/2 and Im(u) = (u +
)/2 and Im(u) = (u + 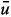 )/2i are also eigenfunctions. Yet are they really physically eigenfunctions corresponding to the given boundary condition? The answer could be certainly not. For example, the real eigenfunctions for the periodic boundary condition are not eigenfunctions of the momentum operator. Moreover, one of them (~ sin(2nx)) verifies the Dirichlet boundary condition! However, the periodic boundary condition must describe a particle that is not really confined to the box. These kind of problems and their relation to the broken symmetry of certain operators have been considered, particularly by considering the antiperiodic boundary condition in [24].
)/2i are also eigenfunctions. Yet are they really physically eigenfunctions corresponding to the given boundary condition? The answer could be certainly not. For example, the real eigenfunctions for the periodic boundary condition are not eigenfunctions of the momentum operator. Moreover, one of them (~ sin(2nx)) verifies the Dirichlet boundary condition! However, the periodic boundary condition must describe a particle that is not really confined to the box. These kind of problems and their relation to the broken symmetry of certain operators have been considered, particularly by considering the antiperiodic boundary condition in [24].
3. CONCLUSIONS
The free particle inside a one-dimensional box (with Hilbert space L2(Ω), where Ω ⊂ ℜ, as usual) is one of the simplest model problems with bound states in quantum mechanics. As is well known, there is an infinite number of boundary conditions and the respective eigenfunctions can be complex and nondegenerate, complex and degenerate, or real and both degenerate or nondegenerate. It is precisely all of this unexpected and interesting variety which makes the problem worth studying. For some of these boundary conditions, the probability current density in effect vanishes at the walls of the box. The respective subfamily of boundary conditions (called "confining") can be obtained from (1) by setting m1 = m2 = 0. Another subfamily is obtained from (1) by setting only m2 = 0 and these boundary conditions are the invariant ones under time-reversal  . As we showed, this last requirement is only a necessary condition for the existence of degeneracy in the energies; therefore, there also exist
. As we showed, this last requirement is only a necessary condition for the existence of degeneracy in the energies; therefore, there also exist  -invariant boundary conditions which do not lead to degeneracy. However, and this is indeed one of the distinguished result of our paper, neither of the boundary conditions included in the "confining subfamily" (which is part of the time-reversal subfamily) leads to degenerate eigenfunctions that is, the nondegeneracy theorem is true in this case. Likewise, we do not find degeneracy if the boundary conditions belonging to subfamily (5) are not pure
-invariant boundary conditions which do not lead to degeneracy. However, and this is indeed one of the distinguished result of our paper, neither of the boundary conditions included in the "confining subfamily" (which is part of the time-reversal subfamily) leads to degenerate eigenfunctions that is, the nondegeneracy theorem is true in this case. Likewise, we do not find degeneracy if the boundary conditions belonging to subfamily (5) are not pure  -invariant (i.e., pure complex eigenfunctions giving a non-zero probability current density). We verified the validity of the nondegeneracy theorem in this case as well. Finally, if the boundary condition is
-invariant (i.e., pure complex eigenfunctions giving a non-zero probability current density). We verified the validity of the nondegeneracy theorem in this case as well. Finally, if the boundary condition is  -invariant but "not confining" (i.e., belonging to (5)), then we can have the following cases: (i) Degeneracy in the energy levels i.e., the nondegeneracy theorem fails in all these cases, as it is in the periodic and antiperiodic boundary conditions whose eigenfunctions can be written as complex. See the final comments in the preceding section. (ii) No degeneracy in the energies, that is, the nondegeneracy theorem does not fail in the cases where the eigenfunctions are inevitably only written as real (as is the case with the so called "nontrivial" boundary condition). We believe that the discussion here complements the standard discussion of the nondegeneracy theorem that we find in some quantum mechanics textbooks and, for this reason, will surely be of interest to physicists working on certain mathematical aspects of quantum model problems.
-invariant but "not confining" (i.e., belonging to (5)), then we can have the following cases: (i) Degeneracy in the energy levels i.e., the nondegeneracy theorem fails in all these cases, as it is in the periodic and antiperiodic boundary conditions whose eigenfunctions can be written as complex. See the final comments in the preceding section. (ii) No degeneracy in the energies, that is, the nondegeneracy theorem does not fail in the cases where the eigenfunctions are inevitably only written as real (as is the case with the so called "nontrivial" boundary condition). We believe that the discussion here complements the standard discussion of the nondegeneracy theorem that we find in some quantum mechanics textbooks and, for this reason, will surely be of interest to physicists working on certain mathematical aspects of quantum model problems.
Acknowledgments
During the time dedicated to this work, financial support was received from CDCH-UCV under Grant No 03-00-6038-2005.
[1] R. Loudon, Am. J. Phys. 27, 649 (1959).
[2] A. N. Gordeyev and S. C. Chhajlany, J. Phys. A: Math. Gen. 30, 6893 (1997).
[3] J. M. Cohen and B. Kuharetz, J. Math. Phys. 34, 12 (1993).
[4] U. Oseguera, Eur. J. Phys. 11, 35 (1990).
[5] J. Goldstein, C. Lebiedzik, and R. W. Robinett, Am. J. Phys. 62, 612 (1994).
[6] J. W. Dettman, Mathematical Methods in Physics and Engineering (Dover, New York, 1988), pp 182-3. R. Shankar Principles of quantum mechanics 2nd edn., (Plenum, New York, 1994), p 176. D. J. Griffiths Introduction to Quantum Mechanics (Prentice-Hall, Upper Saddle River, NJ, 1995), p 69. L. D. Landau and E. M. Lifshitz Quantum Mechanics - Non-relativistic Theory 3rd edn., (Butterworth-Heinemann, New Delhi, 2000), p 60.
[7] K. Bhattacharyya and R. K. Pathak, Int. J. Quantum. Chem. 59, 219 (1996).
[8] S. Kar and R. R. Parwani, Can degenerate bound states occur in one dimensional quantum mechanics? Preprint quant-ph/0706.1135 v1 (2007).
[9] V. Alonso and S. De Vincenzo, J. Phys. A: Math. Gen. 30, 8573 (1997).
[10] T. Fülöp and I. Tsutsui, Phys. Lett. A 264, 366 (2000).
[11] Z. Brzeźniak and B. Jefferies, J. Phys. A: Math. Gen. 34, 2977 (2001).
[12] G. Bonneau, J. Faraut, and G. Valent, Am. J. Phys. 69, 322 (2001). G. Bonneau, J. Faraut and G. Valent, Self-adjoint extensions of operators and the teaching of quantum mechanics, Preprint quant-ph/0103153 (2001). This is an extended version, with mathematical details.
[13] C. Filgueiras and F. Moraes, Extensões auto-adjuntas de operadores em mecânica quântica (in Portuguese), Rev. Bras. Ens. de Fis. 29, 11 (2007).
[14] M. Carreau, E. Farhi, and S. Gutmann, Phys. Rev. D 42, 1194 (1990). V. Alonso, S. De Vincenzo, and L. González-Díaz, Phys. Lett. A 287, 23 (2001).
[15] S. Albeverio and P. Kurasov Singular Perturbations of Differential Operators (University Press, Cambridge, 2000), p 145.
[16] S. Albeverio, L. Dabrowski, and P. Kurasov, Lett. Math. Phys. 45, 33 (1998).
[17] F. A. B. Coutinho, Y. Nogami, and J. Fernando Perez, J. Phys. A: Math. Gen. 32, L133 (1999).
[18] W. A. Atkinson and M. Razavy, Can. J. Phys. 71, 380 (1993). V. S. Araujo, F. A. B. Coutinho, and F. M. Toyama, Braz. J. Phys. 38, 178 (2008).
[19] C. Yuce, Non-hermitian Hamiltonians with real spectra in quantum mechanics, Preprint quant-ph/0702205 v2 (2007).
[20] K. E. Gustafson Introduction to Partial Differential Equations and Hilbert Space Methods 3rd edn., (Dover, New York, 1999), p 175.
[21] G. B. Arfken and H. J. Weber Mathematical Methods for Physicists (Academic Press, Burlington, MA, 2001), p 575.
[22] J. M. Cohen and B. Kuharetz, J. Math. Phys. 34, 4964 (1993).
[23] M. Moriconi, Am. J. Phys. 75, 284 (2007).
[24] A. Z. Capri, Am. J. Phys. 45, 823 (1977).
[25] S. De Vincenzo, Some results for a particle in a box and their supersymmetric partners (2007). Submitted to publication.
Received on 14 July, 2008
The ODE for the eigenvalues and eigenfunctions is: u"(x) + Eu(x) = 0. By considering, for example, only the positive spectra, the eigenfunctions of the Hamiltonian operator have the common form:
where A and B are arbitrary constants. Since we impose some boundary condition on this solution (in this case, one of the  -invariant boundary conditions included in (5)), the constants A and B are related, in general, by two expressions that have the form:
-invariant boundary conditions included in (5)), the constants A and B are related, in general, by two expressions that have the form:
If we obtain f1(η, E)|spectra = g1(η, E)|spectra = 0 and f2(η, E)|spectra = g2(η, E)|spectra = 0, for all of the values of the energy spectrum (which can be obtained from the equations system (17): f2(η, E)g1(η, E)-f1(η, E) g2(η, E) = 0), then we have degenerate eigenfunctions. Therefore, we have to set A = 0 (with B ≠ 0), to obtain a first solution, and then next B = 0 (with A ≠ 0) to obtain a second solution. We were able to check this simple procedure only for the periodic and the antiperiodic boundary conditions, principally because their respective doubly degenerate spectra are very simple. As it has been pointed out and commented on page 24 of the second reference in [12], other boundary conditions could lead to a degenerate spectrum which is not so simple. Generally, in these cases, the spectra are obtained from transcendental equations.
- [1] R. Loudon, Am. J. Phys. 27, 649 (1959).
- [2] A. N. Gordeyev and S. C. Chhajlany, J. Phys. A: Math. Gen. 30, 6893 (1997).
- [3] J. M. Cohen and B. Kuharetz, J. Math. Phys. 34, 12 (1993).
- [4] U. Oseguera, Eur. J. Phys. 11, 35 (1990).
- [5] J. Goldstein, C. Lebiedzik, and R. W. Robinett, Am. J. Phys. 62, 612 (1994).
- [6] J. W. Dettman, Mathematical Methods in Physics and Engineering (Dover, New York, 1988), pp 182-3.
- R. Shankar Principles of quantum mechanics 2nd edn., (Plenum, New York, 1994), p 176.
- D. J. Griffiths Introduction to Quantum Mechanics (Prentice-Hall, Upper Saddle River, NJ, 1995), p 69.
- L. D. Landau and E. M. Lifshitz Quantum Mechanics - Non-relativistic Theory 3rd edn., (Butterworth-Heinemann, New Delhi, 2000), p 60.
- [7] K. Bhattacharyya and R. K. Pathak, Int. J. Quantum. Chem. 59, 219 (1996).
- [8] S. Kar and R. R. Parwani, Can degenerate bound states occur in one dimensional quantum mechanics? Preprint quant-ph/0706.1135 v1 (2007).
- [9] V. Alonso and S. De Vincenzo, J. Phys. A: Math. Gen. 30, 8573 (1997).
- [10] T. Fülöp and I. Tsutsui, Phys. Lett. A 264, 366 (2000).
- [11] Z. Brzeźniak and B. Jefferies, J. Phys. A: Math. Gen. 34, 2977 (2001).
- [12] G. Bonneau, J. Faraut, and G. Valent, Am. J. Phys. 69, 322 (2001).
- G. Bonneau, J. Faraut and G. Valent, Self-adjoint extensions of operators and the teaching of quantum mechanics, Preprint quant-ph/0103153 (2001). This is an extended version, with mathematical details.
- [13] C. Filgueiras and F. Moraes, Extensões auto-adjuntas de operadores em mecânica quântica (in Portuguese), Rev. Bras. Ens. de Fis. 29, 11 (2007).
- [14] M. Carreau, E. Farhi, and S. Gutmann, Phys. Rev. D 42, 1194 (1990).
- V. Alonso, S. De Vincenzo, and L. González-Díaz, Phys. Lett. A 287, 23 (2001).
- [15] S. Albeverio and P. Kurasov Singular Perturbations of Differential Operators (University Press, Cambridge, 2000), p 145.
- [16] S. Albeverio, L. Dabrowski, and P. Kurasov, Lett. Math. Phys. 45, 33 (1998).
- [17] F. A. B. Coutinho, Y. Nogami, and J. Fernando Perez, J. Phys. A: Math. Gen. 32, L133 (1999).
- [18] W. A. Atkinson and M. Razavy, Can. J. Phys. 71, 380 (1993).
- V. S. Araujo, F. A. B. Coutinho, and F. M. Toyama, Braz. J. Phys. 38, 178 (2008).
- [19] C. Yuce, Non-hermitian Hamiltonians with real spectra in quantum mechanics, Preprint quant-ph/0702205 v2 (2007).
- [20] K. E. Gustafson Introduction to Partial Differential Equations and Hilbert Space Methods 3rd edn., (Dover, New York, 1999), p 175.
- [21] G. B. Arfken and H. J. Weber Mathematical Methods for Physicists (Academic Press, Burlington, MA, 2001), p 575.
- [22] J. M. Cohen and B. Kuharetz, J. Math. Phys. 34, 4964 (1993).
- [23] M. Moriconi, Am. J. Phys. 75, 284 (2007).
- [24] A. Z. Capri, Am. J. Phys. 45, 823 (1977).
- [25] S. De Vincenzo, Some results for a particle in a box and their supersymmetric partners (2007). Submitted to publication.
Appendix
Publication Dates
-
Publication in this collection
22 Sept 2008 -
Date of issue
Sept 2008
History
-
Received
14 July 2008






















