Resumos
Apresenta-se neste trabalho a caracterização física e elétrica do elastômero vulcanizado EPDM-ENB (copolímero de etileno-propileno com o dieno de etileno norborneno) carregado com trihidróxido de alumínio (ATH - alumina trihidratada). São determinadas as características do processo de vulcanização, as propriedades mecânicas de rasgamento e de resistência à tração do EPDM com diferentes concentrações de ATH. A dependência da corrente de condução é determinada em função da tensão elétrica aplicada nos compósitos, temperatura e tipos de eletrodos metálicos. Os resultados mostram que a condutividade depende linearmente da raiz quadrada do campo elétrico. A discussão dos processos de condução é feita utilizando os modelos teóricos de Poole-Frenkel e Schottky.
Condutividade elétrica; compósitos; etileno propileno dieno; trihidróxido de alumínio; mecanismos de condução
In this work, electrical and physical properties of vulcanized copolymer EPDM-ENB reinforced with alumina trihydrate, ATH, were investigated. Characteristics of the vulcanizating process, tear resistence, tensile strenght at break are given for different contents of ATH. The dependence of the electric conduction on the applied voltage were measured for the composites. A linear dependence of the logarithm of electric conductivity on the square root of the applied electric field was found. Such results were discussed employing Poole-Frenkel and Schottky theoretical models.
Electrical conductivity; composite; ethylene propylene diene; alumina thrihydrate; conduction mechanism; physical properties
ARTIGO TÉCNICO CIENTÍFICO
Caracterização elétrica e física de compósitos de copolímero EPDM vulcanizado e trihidróxido de alumínio
Electrical and physical characterization of composites of vulcanized EPDM copolymer and aluminium trihydroxide.
Maria Zanin e José A. Giacometti
RESUMO: Apresenta-se neste trabalho a caracterização física e elétrica do elastômero vulcanizado EPDM-ENB (copolímero de etileno-propileno com o dieno de etileno norborneno) carregado com trihidróxido de alumínio (ATH - alumina trihidratada). São determinadas as características do processo de vulcanização, as propriedades mecânicas de rasgamento e de resistência à tração do EPDM com diferentes concentrações de ATH. A dependência da corrente de condução é determinada em função da tensão elétrica aplicada nos compósitos, temperatura e tipos de eletrodos metálicos. Os resultados mostram que a condutividade depende linearmente da raiz quadrada do campo elétrico. A discussão dos processos de condução é feita utilizando os modelos teóricos de Poole-Frenkel e Schottky.
Palavras-chave: Condutividade elétrica, compósitos, etileno propileno dieno, trihidróxido de alumínio, mecanismos de condução.
ABSTRACT: In this work, electrical and physical properties of vulcanized copolymer EPDM-ENB reinforced with alumina trihydrate, ATH, were investigated. Characteristics of the vulcanizating process, tear resistence, tensile strenght at break are given for different contents of ATH. The dependence of the electric conduction on the applied voltage were measured for the composites. A linear dependence of the logarithm of electric conductivity on the square root of the applied electric field was found. Such results were discussed employing Poole-Frenkel and Schottky theoretical models.
Keywords: Electrical conductivity, composite, ethylene propylene diene, alumina thrihydrate, conduction mechanism, physical properties.
Introdução
Componentes, cabos e acessórios isolantes para a indústria eletro-eletrônica têm sido produzidos com materiais poliméricos tais como polietileno de baixa densidade (LDPE), polietileno reticulado (XLPE) e os elastômeros do tipo etileno-propileno (EPRs)1-2. Mais recentemente, o poliéster e resinas epóxi têm sido usados na fabricação de isoladores elétricos para alta tensão3-5. Embora neste tipo de aplicação os materiais poliméricos apresentem muitas vantagens sobre os materiais cerâmicos e vidros (leveza, flexibilidade, facilidade de manutenção e compactação das linhas de distribuição), há ainda limitações no seu uso devido principalmente a sua degradação eletroquímica.
Dos elastômeros empregados em isolação elétrica, os EPDMs possuem qualidades que permitem atenuar alguns problemas devido à sua excelente resistência às ações de intempéries, ozônio e agentes químicos. Além disto, apresentam boa flexibilidade em condições ambientes e mesmo em temperaturas baixas. A adição de trihidróxido de alumínio ou outros tipos de cargas inorgânicas permite melhorar as propriedades mecânicas dos EPDMs, o poder de resistência às chamas e supressão de fumaça, a resistência às descargas elétricas superficiais além de contribuir para a inibição de arborescência elétrica6. O EPDM com carga inorgânica tem sido muito usado na fabricação de isoladores para alta tensão, principalmente em ambientes poluídos e em regiões de risco de vandalismo.
Apesar de ser um material com amplas aplicações, suas características elétricas de condução são relativamente pouco estudadas. Tais propriedades são importantes para se determinar o comportamento do material quando ele for utilizado em condições nas quais é submetido a intensos campos elétricos, envolvendo todo o seu volume.
Outro fator fundamental é a correlação entre as medidas elétricas e propriedades mecânicas como fraturas, espaços vazios, etc. Por exemplo, a formação de pequenos espaços vazios no meio leva ao aparecimento de micro descargas elétricas que acabam prejudicando o desempenho do material como isolante elétrico. A fragilidade ao rasgamento também pode facilitar o aparecimento de micro trincas que desencadeiam descargas elétricas e conseqüentes rupturas elétricas.
Neste trabalho será apresentado o comportamento elétrico do compósito do elastômero vulcanizado EPDM-ENB e trihidróxido de alumínio (ATH). São determinados os parâmetros do processo de vulcanização do elastômero e as características físicas do compósito. Medidas de condução elétrica em amostras com diferentes porcentagens de ATH mostraram que a condutividade elétrica do compósito aumenta com a porcentagem de carga inorgânica. Será também discutida a natureza do processo de condução elétrica que ocorre no material.
Materiais e Procedimentos de Preparação do Compósito
O copolímero empregado é o elastômero EPDM-ENB, cuja estrutura química apresenta o dieno (etileno norborneno) distribuído ao longo da cadeia, o qual fornece a dupla ligação para o processo de vulcanização. A este elastômero, que por simplicidade de notação será simbolizado apenas pela sigla EPDM, acrescentou-se: 2,7 pcp (isto é, partes por cem partes de EPDM) de peróxido de dicumila (agente de cura); 0,3 pcp de enxofre (acelerador da cura), 5,0 pcp de óxido de zinco (carga e ativador) e 4,0 pcp de caulim (agente reforçante)7.
Além dos aditivos acima se acrescentaram ainda alumina trihidratada-ATH (ou trihidróxido de alumínio) em diferentes proporções. Denomina-se F0 as amostras sem ATH e F15, F40, F70 e F100 amostras com 15, 40, 70 e 100 pcp de ATH. O diâmetro médio das partículas da ATH é da ordem de 8,5 mm.
A homogeneização da mistura foi feita utilizando-se um misturador de rolos à temperatura de 45oC durante 40 minutos.
Caracterização do Processo de Vulcanização do Compósito
As características do processo de vulcanização foram determinadas a partir de parâmetros obtidos da curva de vulcanização. Utilizou-se o reômetro Monsanto, modelo 100, acoplado a um registrador gráfico. As medidas foram realizadas de acordo com a norma ASTM D-2084. A mistura EPDM/ATH foi submetida à temperatura de 175oC e pressão de 4,2Kg/cm2. A Tabela 1 mostra os resultados das medidas dos torques de cisalhamento antes, ML, e depois, MH, do processo de vulcanização. Observa-se que ML e MH são linearmente dependentes da quantidade de ATH. O tempo de Scorch, ts2, para se iniciar a vulcanização e o tempo, t90, para se atingir 90% do torque máximo de vulcanização foram ts2 = 1,0 e t90 = 6,3 minutos, sendo ambos independentes da quantidade de ATH.
A taxa de vulcanização definida como 100/(t90 - ts2), obtida para os compósitos, foi de 18,8% e seu valor independe da porcentagem de ATH. Esta independência é comumente esperada nestes tipos de materiais compósitos 6.
Preparação das Amostras
As amostras, de espessuras entre 50 e 200 mm, foram preparadas prensando o material com 10 toneladas, à temperatura de 175 oC durante 8 minutos. Este tempo é ligeiramente maior que o valor encontrado, t90=6,3 min, garantindo a vulcanização completa do material. Após o processo de vulcanização as amostras foram mantidas a temperatura de 45 oC por 24 horas.
Para as medidas elétricas, ouro ou alumínio foi depositado sobre as superfícies das amostras (área A=2,2 cm2) por evaporação a vácuo.
Propriedades Mecânicas dos Compósitos Vulcanizados
Análise Morfológica
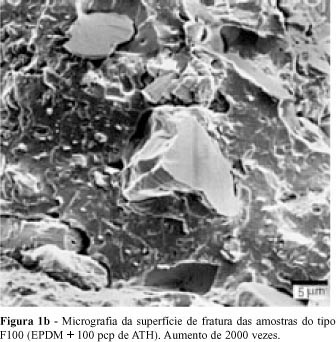
Utilizou-se o microscópio Zeiss, modelo OSM-960, para obter fotografias das superfícies de fraturas das amostras. As superfícies foram obtidas res-friando-se as amostras até a temperatura de nitrogênio líquido e então as fraturando. As fotografias, mostradas na Figura 1, foram obtidas de amostras do tipo F100. A Figura 1a, ampliação de 100 vezes, indica que o EPDM envolve completamente as partículas de ATH. Observa-se na Figura 1b (ampliação de 2000 vezes) que as partículas estão bem distribuídas, não possuem aglomerados, nem espaços vazios e todas as partículas estão envolvidas pela matriz elastomérica. As amostras com menor porcentagem de ATH apresentaram as mesmas características das amostras do tipo F100.
Características de Resistência à Tração e ao Rasgamento do Compósito
Os elastômeros podem apresentar falhas elétricas devidas ao rasgamento do material, um tipo especial de ruptura mecânica, próprio das borrachas. O rasgamento e a resistência à tração são geralmente empregados para a caracterização do desempenho do uso destes materiais em condições de serviço. No caso da aplicação do EPDM em cabos e isoladores elétricos estas características são, portanto, de fundamental importância, uma vez que estes dispositivos elétricos sofrem esforços mecânicos de grande intensidade.
Ensaios de resistência à tração (srup) e rasgamento TS foram realizados em uma máquina Instron, modelo 1127, com corpos de prova padronizados e condições normatizadas de temperatura e velocidade de tração. Utilizou-se a norma ASTM D638-76 para os ensaios à tração8 e a ASTM D624 para os de rasgamento9.
Na Tabela 2 é mostrado que os valores para a resistência à tração independem da porcentagem de ATH até a concentração de 70 pcp aqui empregada, embora para a amostra F100 o valor encontrado seja ligeiramente maior que as demais amostras. Saliente-se que o valor médio determinado para estas formulações, da ordem de 3,5 MPa, se encontra dentro da faixa de EPDMs vulcanizados (0,35 a 25MPa)6.
Nos ensaios de resistência ao rasgamento, observa-se que ocorre fato similar, isto é, com a variação da porcentagem de ATH, a resistência ao rasgamento decresce muito pouco, excluindo aqui o valor de F40. Qualquer decréscimo poderia ser associado ao formato da carga ATH, do tipo particulada e de forma irregular, como mostrado nas micrografias da Figura 1. O uso deste tipo de partícula, sem qualquer tratamento superficial a base de silanos ou titanatos dificulta a adesão à matriz polimérica e pode gerar efeitos de concentração de tensão mecânica que fragilizam o material, facilitando a iniciação e propagação das trincas.
Os resultados para TS e srup indicam que estas propriedades não sofrem grandes alterações com o emprego destas quantidades de ATH nas amostras. Isto mostra que a alumina não produz melhorias nas propriedades mecânicas do elastômero vulcanizado6,10. Como descrito na literatura a alumina é predominantemente um agente supressor de fumaça e retardante de chamas.
Caracterização Elétrica
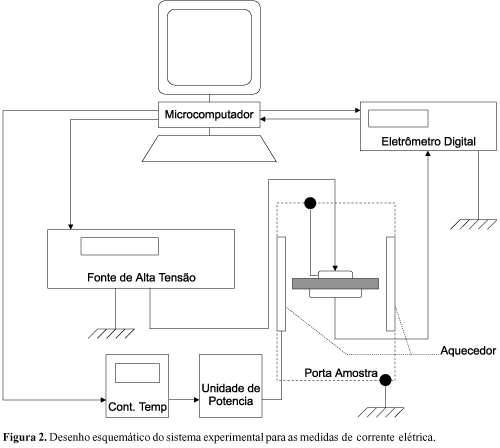
Nas medidas de corrente elétrica em função do tempo utilizou-se a montagem experimental mostrada esquematicamente na Figura 2. Ela é constituída de estufa com temperatura controlada, fonte de tensão contínua Keitlhey, eletrômetro Keithley para se medir a corrente elétrica, I(t), e micro computador para aquisição dos dados e também para controle de temperatura, T, da estufa. A medida é feita aplicando-se uma tensão constante, V, e medindo-se o valor da corrente em função do tempo, t, até atingir o valor estacionário, Ie. Em geral, as medidas foram feitas à temperatura T=30 ºC e eletrodos de ouro. Algumas medidas foram realizadas nas temperaturas de 40, 50, 60, 80 e 100 ºC.
O valor da condutividade elétrica s é calculado pela lei de Ohm, s=IeL/AV, onde L é a espessura da amostra. Apresenta-se os resultados obtidos para uma amostra com diferentes conteúdos de ATH; entretanto saliente-se que os resultados sempre foram reprodutíveis para diferentes amostras.
Medidas da constante dielétrica, no intervalo de freqüência entre 1kHz e 1 MHz, foram realizadas em amostras com eletrodos de ouro, à temperatura ambiente. Utilizou-se um medidor de impedância (Schlumberger) acoplado a um microcomputador para aquisição de dados.
Correntes Elétricas Transientes
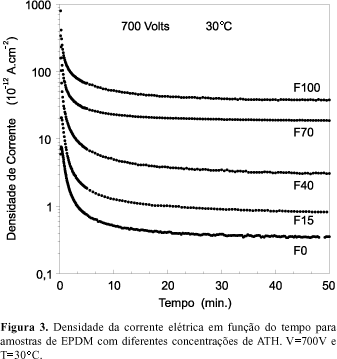
Em geral, ao se submeter dielétricos a uma tensão elétrica, a corrente elétrica decai no tempo (chamadas de corrente de polarização), tendendo a um valor estacionário. Como mostrado na Figura 3, para T=30oC e V=700V, as amostras de EPDM/ATH apresentam este comportamento. Pode-se ver também que as amplitudes das densidades de correntes aumentam com a porcentagem de ATH e, o tempo da ordem de 30 minutos é suficiente para a densidade de corrente atingir o valor estacionário, Je.
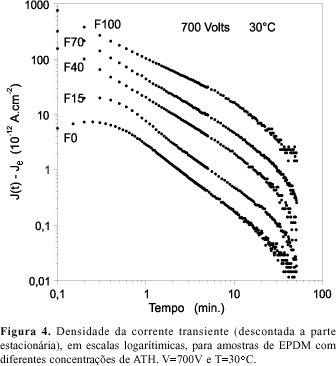
Na Figura 4 mostra-se os transientes da Figura 3 na forma de log(J-Je) versus logt, onde J=I/A. A região linear das curvas indica que a densidade de corrente obedece a dependência do tipo t-n, ou seja,
onde n é uma constante e J0(T) é o valor inicial da densidade de corrente (dependente da temperatura) e Je é a densidade de corrente no estado estacionário.
Medidas da corrente de despolarização, obtidas após colocar a amostra em curto circuito, também obedecem a dependência do tipo t-n. Os resultados mostraram que as curvas de correntes de polarização subtraído o valor estacionário, são coincidentes com as curvas de despolarização. Este resultado indica que a corrente elétrica pode ser atribuída a dois processos: a parte transiente é devida a processos de orientação dipolar (corrente de polarização) enquanto que a parte estacionária é devida à condução elétrica do material (corrente de condução)11.
Na Figura 4, observa-se que a inclinação das curvas, ou seja, o valor de n, diminui ligeiramente com a concentração de ATH incorporada à matriz. Este efeito pode ser observado na Tabela 3, onde são apresentados os valores das constantes J0(T) e n, definidos na Equação 1. Valores de n grandes levam a tempos menores da relaxação da polarização. Do fato de n ser pouco dependente da concentração de ATH (de 1,0 a 1,3), tem-se a indicação de que a matriz polimérica do elastômero EPDM determina os mecanismos associados à corrente de polarização. Além disto, na Figura 3, observa-se um aumento sistemático da amplitude da densidade de corrente em função da concentração de ATH. Conclui-se, portanto, que a alumina é responsável pela condução. Da Figura 3 vê-se que a densidade de corrente estacionária chega a aumentar duas ordens de grandeza das amostras do tipo F0 para as F100.
Corrente Elétrica de Condução
Como foi mostrado no item anterior a corrente de condução pode ser analisada separadamente da corrente de polarização. A densidade de corrente no estado estacionário, em função da tensão aplicada, V, apresenta um comportamento não linear com o campo elétrico, E=V/L. Dos resultados, Figura 5, verifica-se que uma relação linear é obtida, construindo-se gráficos de logs versus . Saliente-se que foram tentadas outras dependências sem tanto sucesso. Como tal dependência parece ser a mais universal possível, os resultados serão apresentados em gráficos de logs versus E1/2.
Devido à dependência linear de logs versus E1/2, os resultados obtidos não podem ser explicados pela existência de uma condutividade intrínseca do tipo ohmico, ou seja, densidade de corrente como J=sE. Outro modelo clássico, corrente limitada por carga espacial, no qual J = (9/8)mV2/L3 12 também não pode ser usado para explicar os resultados. Como será discutido, os processos mais prováveis para a condução no compósito EPDM/ATH seriam então os descritos por modelos do tipo de Poole-Frenkel ou Schottky 11-12.
A Influência dos Eletrodos na Condução
Além das medidas de corrente em amostras com eletrodo de ouro, mediu-se também, veja Figura 6, a densidade de corrente com eletrodos de alumínio para amostras F40 e F100. Observa-se que os resultados seguem o comportamento logs x E1/2 e apresentam maiores correntes para as amostras com eletrodos de alumínio. Uma vez que alterando-se o metal do eletrodo se obtém diferentes valores para a amplitude de corrente, tem-se a indicação que o processo de condução é dependente da injeção de portadores na interface eletrodo-dielétrico12. Nota-se também, que as inclinações das retas para os dois tipos de eletrodos diferem significativamente para amostras do tipo F100. Isto indica que a quantidade de carga ATH na amostra também é importante para a injeção de portadores.
Corrente de Condução versus Porcentagem de ATH
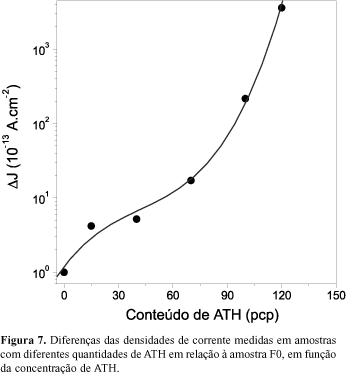
Tomando-se como referência um determinado campo elétrico, por exemplo, o referente a 40KV/cm, determinou-se a diferença, DJ, da corrente elétrica medida em amostras com diferentes quantidades de ATH em relação a corrente na amostra F0. Na Figura 7 é mostrado que DJ cresce com a porcentagem de ATH. Excepcionalmente, incluiu-se, nesta figura, o resultado para amostras com 120 pcp, o qual apresenta uma variação de três ordens de grandeza em relação ao valor das amostras do tipo F0. Isto enfatiza a importância da alumina para o processo de condução.
A Influência da Temperatura na Condução
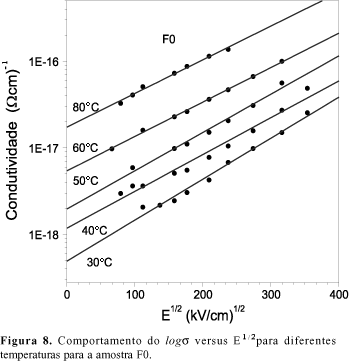
As Figuras 8 e 9 apresentam as curvas logs em função de E1/2, a diferentes temperaturas, para amostras F0 e F100 com eletrodos de ouro. Observa-se que o comportamento linear do logs em função de E1/2 é obtido tanto para amostras F0 como para as amostras F100. Comportamento semelhante também foi encontrado para todas as outras concentrações, independentemente da temperatura. Observou-se também que para a amostra F100, no intervalo de 30 a 80 ºC, as retas de logs versus E1/2 são bastante próximas uma às outras (na figura 9 mostra-se apenas as retas obtidas a 30, 80 e 100oC).
A Figura 10 mostra a dependência de logs em função de (1/T) para a amostra F0. Os resultados são mostrados para diferentes valores de campos elétricos. Os pontos foram obtidos a partir das retas logs versus E1/2 da Figura 8. É interessante notar que a dependência de Arrhenius13, dada por
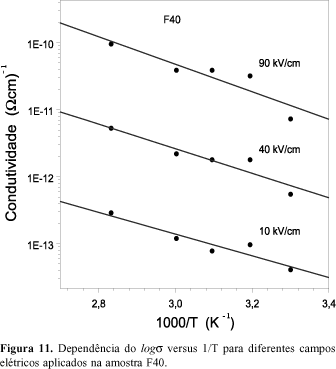
é obedecida para a amostra F0, sendo também encontrada para a amostra F15 (não mostrada aqui). Na expressão, k é a constante de Boltzmann e U é a energia de ativação. Na amostra F40, Figura 11, a dispersão dos resultados experimentais não permite concluir que a relação de Arrhenius seja obedecida. Para as amostras F70 e F100, resultados não mostrados aqui, obteve-se uma dispersão ainda maior. Outros autores sugerem que este fato é devido à possibilidade da existência de várias energias de ativação14-15.
Discussão
A caracterização física das amostras de EPDM/ATH permitiu, numa primeira fase, determinar o tempo de vulcanização para os compósitos, o qual foi encontrado ser independente da porcentagem de ATH dos compósitos. Os resultados das medidas mecânicas de rasgamento e de resistência à tração mostraram que o material aqui usado é compatível com os EPDMs usados em aplicações comerciais. Outro fator importante observado é que as micrografias das superfícies de fratura mostraram que as partículas de ATH são completamente envolvidas pela matriz polimérica, regularmente bem distribuídas mesmo para as amostras F100. Isto é fundamental para o desempenho deste material em aplicações elétricas, pois não contém aglomerados de partículas que formem um caminho contínuo para a corrente elétrica.
Os resultados obtidos de resistência à tração e ao rasgamento (TS e srup) alteraram-se muito pouco em relação ao teor de alumina empregado nas amostras de EPDM. Este fato confirma que o uso da alumina é mais adequado como agente supressor de fumaça e de retardância a chamas do que como agente reforçante6,10 já que as propriedades mecânicas destes compósitos pouco se alteram.
Neste trabalho, apesar de não ser feita nenhuma correlação entre os resultados obtidos para as propriedades mecânicas e as propriedades elétricas, mostrou-se que a adição de ATH causa o aumento da condução elétrica dos compósitos. Das micrografias de varredura conclui-se que as partículas ATH são distribuídas regularmente no volume do polímero não ocorrendo, portanto, a formação de caminhos de percolação.
Nas medidas elétricas a dependência linear de logs versus E1/2, encontradas para todas as formulações de EPDM/ATH, é característica de diversos modelos de condução como o de Poole-Frenkel, Schottky, Calderwood16 e outros17,18. Para distinguir qual o modelo mais satisfatório é feita a seguir uma análise mais aprofundada dos resultados.
No modelo de Poole-Frenkel a corrente elétrica é atribuída a uma condutividade intrínseca do material gerada pela dissociação de pares doadores-elétrons em centros distribuídos no volume do material11. A condutividade elétrica obtida para este modelo é dada por
onde bF=(e3/pee0)1/2 é a constante de Poole-Frenkel, fF é a energia de ionização do doador (sem campo aplicado) e C uma constante.
No modelo de Schottky a corrente elétrica depende do processo de emissão térmica eletrônica que ocorre na interface metal-dielétrico. Neste caso a expressão da densidade de corrente elétrica é dada por:
ou em termos da condutividade elétrica
onde bS=(e3/4pee0) 1/2 é o coeficiente de Schottky, f0 é a função trabalho efetiva (entre o nível de Fermi do metal do eletrodo e a banda de condução do dielétrico) e B é a constante de emissão (120 A/cm2K2 no caso da emissão se dar para o vácuo).
As equações (3) e (5) apresentam, para valores de campo elétrico maiores que 20kV/cm, a dependência linear de logs versus E1/2 (na equação 5 o termo BT2/E não contribui significativamente, não alterando a dependência linear de logs versus E1/2). Do ajuste das curvas da Figura 4, determinou-se os valores das constantes dielétricas eF (Frenkel) e eS (Schottky) a partir dos coeficientes bS e bF, obtendo-se para amostras do tipo F0, eF=eS=1,4; para F15, eF=eS=1,7; para F40, eF=eS=0,6; para F70, eF=eS=0,7 e para F100, eF=eS=0,8. Estes valores são bem diferentes dos valores medidos e mostrados na Tabela IV. A comparação destes resultados mostra claramente que estes modelos não são adequados, pois se obtêm constantes dielétricas muito diferentes daquelas medidas.
Os valores das constantes dielétricas também podem ser comparados com aqueles que se extraem da dependência de s com a temperatura, ou seja, pode-se obter os valores da constante B, f e então o valor de bS da equação (4) de Schottky. Os valores da energia de ativação, f, em função do campo elétrico são mostrados na Tabela V para os compósitos F0 e F15. Desses valores podemos deduzir o valor de f para E=0, isto é, f0 da equação (4) e também bS através de f = f0 - bSE1/2. A Tabela 4 mostra que os valores da constante dielétrica obtidos de bS são inferiores daqueles esperados. Por exemplo, para F0 obtém-se 0,22 comparado com 1,4 antes encontrado, indicando que o modelo de Schottky não é aplicável. Esta discordância tem sido notada ocorrer em outros materiais17-19.
Outros modelos de Poole-Frenkel modificados, como o de Calderwood16 e outros17,18 também podem ser usados. Entretanto, levam a resultados não adequados para as constantes físicas obtidas pelo ajuste dos resultados experimentais. A importância destes resultados, mostrando que estes modelos levam a parâmetros sem valores físicos, é uma das contribuições deste trabalho. Em geral, grande número de publicações omitem este fato e assumem que os modelos de Schottky ou Poole-Frenkel são aplicáveis a partir do argumento de que eles fornecem a correta dependência entre a corrente estacionária e o campo elétrico.
Uma proposta para explicar os resultados nas amostras de EPDM é uma condução elétrica dependente de dois processos: (a) injeção de portadores pelo eletrodo da amostra e (b) condução intrínseca de volume. Tentativas preliminares de ajuste dos resultados, usando a injeção de Schottky e condução de Poole-Frenkel, mostraram que se obtêm constantes físicas mais adequadas. Uma análise mais detalhada com modelos levando mais de um processo terá de ser feita, o que é deixado para um trabalho futuro.
Conclusões
Neste trabalho apresenta-se a caracterização física e elétrica do compósito de EPDM-ENB com alumina trihidratada (ATH). As características físicas encontradas para o material aqui usado são compatíveis com os EPDMs utilizados comercialmente para aplicação em isolação elétrica. Mostrou-se que a adição de até 100 pcp de ATH produz compósitos com as partículas uniformemente distribuídas no material polimérico.
Os resultados das medidas elétricas mostraram claramente que logs depende linearmente de E1/2, independente do metal do eletrodo, temperatura e da porcentagem de ATH. Apesar desta dependência ser a característica principal dos modelos de condução de volume de Poole-Frenkel e injeção de Schottky, conduziram a valores não aceitáveis da constante dielétrica dos compósitos. Saliente-se que estes modelos têm sido utilizados na interpretação de resultados em vários tipos de materiais, mas, em geral, não há análise aprofundada dos parâmetros físicos obtidos.
Embora não tenha sido possível determinar exatamente o modelo que descreve o processo de condução elétrica dos compósitos, fica como sugestão para trabalhos futuros o uso de modelos que levem em conta tanto a dependência dos processos de injeção na interface amostra-metal bem como a condução de volume. Esta análise não é trivial, pois não é possível obter soluções analíticas para o problema e também a análise fica dificultada pelo grande número de parâmetros que serão necessários para equacionar o modelo.
Agradecimentos
Os autores agradecem a valiosa colaboração do Prof. G. F. Leal Ferreira na interpretação dos resultados e à FAPESP projeto no.94/2640-4 e CNPq pelo suporte financeiro.
Maria Zanin, Departamento de Engenharia de Materiais, Universidade Federal de São Carlos, C.P.676, CEP 13565-905, São Carlos, SP; José A. Giacometti, Instituto de Física de São Carlos, Universidade de São Paulo C.P. 369, CEP 13560-970, São Carlos, SP.
- 1. Deschamps,L., Electric Power Research Institute, EPRI, 5c-1, (1990).
- 2. Ieda, M., Ieee Trans. Electr. Insulation, vol. EI-21, n.5, p.793-802, (1986).
- 3. Houlgate, R.C. et alli, Conference Inter. des Grands Réseauxs Electriques a Haute Tension, França, Anais, CIGRE, p.12-18, (1985).
- 4. Starr, W. T., Ieee Trans. Electr. Insulation, Vol 25, no. 1, p.125-131, (1990).
- 5. Sens, M. A., Tan, A.L. e Mason, J.H., Conference Log Term Performance of H.V. Insulating Systems, CIGRE, Berlin, p.46-52, (1985).
-
6The Vanderbilt Rubber Handbook, 1a ed., Los Angeles, R.T. Vanderbilt Company, (1978).
- 7. Mark, H.F. e Gaylord, N.G., Encyclopedia of Polymer Science and Tecnology, N.Y. John Wiley & Sons. Inc. (1972).
-
8Tensile Properties of Plastics, American Society for Testing and Materials, ASTM D638-76.
-
9Rubber Property, Tear Resistence, American Society for Testing and Materials - ASTM D624-84.
- 10. LeRoy D. Hart - Alumina Chemicals: Science and Technology Handbook, Ohio, The American Ceramic Society Inc., 1990.
- 11. Kao, K.C. e Hwang, W., Electrical Transport in solids, International series in the science of the solid state, vol. XIV, Pergamon Press, 1a. ed., USA, 1981.
- 12. Lampert, Mark, Current Injection in solids. 1a ed., Oxford (1969).
- 13. DasGupta, D.K. e Joyner, K., J. Phys. D: Appl. Phys., vol.9, p. 829-839, (1976).
- 14. Khalil, S.M., Conference on Electrical Insulation and Dielectric Phenomena, Annual Report, USA, p.225-230 (1990).
- 15. Martinu, L., Castelli, A. e Bastioli, C., Conf. on Electrical Insulation and Dielectric Phenomena, Annual Report, USA, 172-177 (1990).
- 16. Adamec, V. e Calderwood, J. H., J. Phys. D: Appl. Phys., Vol.8, p. 551-560 (1975).
- 17. Comizzoli, R.B., J. Appl. Phys. 58(2), p. 1032-1033 (15 Jul 1985)
- 18. Taylor, D.M. e Lewis, T.J., J. Phys. D: Appl. Phys., Vol. 4, 1346-1357 (1971).
- 19. Aida, F., Tanimoto, G., Aihara, M. e Hosokawa, E., Conference on Electrical Insulation and Dielectric Phenomena, Annual Report, USA, 465-473 (1990).
Datas de Publicação
-
Publicação nesta coleção
28 Out 2010 -
Data do Fascículo
Jun 1997