Comparação entre duas teorias para a determinação da tensão interfacial pelo método de fibra quebrante

Comparison between two theories for determination of interfacial tension with the breaking thread method

ARTIGO TÉCNICO CIENTÍFICO

Comparação entre duas teorias para a determinação da tensão interfacial pelo método de fibra quebrante

Comparison between two theories for determination of interfacial tension with the breaking thread method

Guillermo Palmer; Nicole R. Demarquette

Departamento de Engenharia Metalúrgica e de Materiais, EPUSP

^{Endereço para correspondência}

RESUMO

A tensão interfacial entre polímeros fundidos é um fator chave para a predição da morfologia de blendas poliméricas. Neste trabalho, as teorias de Tomotika e Tjahjadi et al. para medir tensão interfacial entre polímeros fundidos usando o método de fibra quebrante são avaliadas e comparadas. Em particular, foram testadas ambas as teorias para o par de polímeros PP/PS à temperatura de 200 °C. O valor médio de tensão interfacial calculado usando a teoria de Tomotika foi de 5,88 mN/m, e usando a teoria de Tjahjadi et al. foi de 5,66 mN/m.

Palavras-chave: Blendas poliméricas, tensão interfacial, fibra quebrante.

ABSTRACT

Interfacial tension between molten polymers is a key factor that helps predicting the morphology of polymer blends. In this work, the theories of Tomotika and Tjahjadi et al. to measure interfacial tension between molten polymers using the breaking thread method are evaluated and compared. In particular, both theories were tested for PP/PS polymer pair at temperature of 200 °C. The average values of interfacial tension calculated using Tomotika´s theory and Tjahjadi et al.´s theory are 5.88 mN/m and 5.66 mN/m, respectively.

Keywords: Polymers blends, interfacial tension, breaking thread.

Introdução

A morfologia de uma blenda polimérica depende das propriedades reológicas de seus componentes, condições de processamento e compatibilização entre os componentes poliméricos. A tensão interfacial é o parâmetro mais acessível que descreve as propriedades termodinâmicas e estruturais na interface de uma blenda polimérica e por conseqüência a compatibilidade entre seus componentes^[1-3].

No presente estudo, a tensão interfacial entre dois polímeros é determinada monitorando a evolução da forma de uma fibra longa (método de fibra quebrante) de um polímero fundido inserido em uma matriz de um segundo polímero. Duas teorias diferentes são utilizadas e avaliadas para inferir a tensão interfacial a partir da instabilidade de fibras. Estas duas teorias são apresentadas a seguir.

Teorias

Teoria de Tomotika

No século dezenove, Lord Rayleigh^[4] desenvolveu uma teoria dinâmica para descrever as instabilidades de colunas cilíndricas de fluidos incompressíveis sem considerar o efeito do fluido que as envolve. Em 1935, S. Tomotika^[5,6] estendeu a teoria de Lord Rayleigh considerando a viscosidade do filamento (fibra) e a viscosidade do fluido que envolve o filamento (matriz). Em seu estudo Tomotika considerou uma coluna de um fluido Newtoniano inserida em uma matriz liquida Newtoniana e incompressível (Figura 1). Por causa de movimentos Brownianos, pequenas distorções de comprimento de onda, L, são geradas na superfície da fibra. A amplitude das distorções ao longo do comprimento da fibra cresce exponencialmente com tempo, de acordo com:

onde, b e a são o maior e menor diâmetro da fibra, respectivamente, como é ilustrado na Figura 1; a₀ é a amplitude inicial das distorções senoidais; t é tempo e q é a taxa de crescimento das distorções.

A taxa de crescimento, q, das distorções é uma função da tensão interfacial, g, a viscosidade de cisalhamento zero da matriz, h_m, o raio inicial da fibra, R₀, e da taxa de crescimento adimensional, W(X,l) como pode ser visto na equação (2). A taxa de crescimento adimensional é uma função do número de onda, X (equação 3) e a razão de viscosidade, l (equação 4).

onde, L é o comprimento de onda das distorções e h_f é a viscosidade de cisalhamento zero da fibra.

Como a cresce exponencialmente com o tempo, a plotagem de ln(a/R₀) contra o tempo resulta em uma reta. A inclinação desta reta é a taxa de crescimento, q.

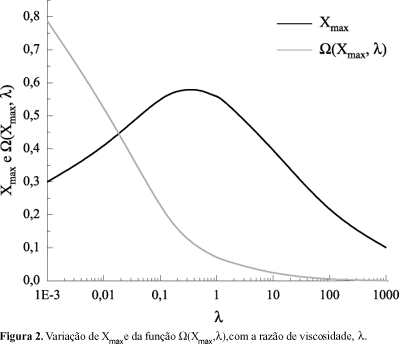
Finalmente, para determinar a tensão interfacial entre dois polímeros usando a equação (2), é necessário conhecer o valor da taxa de crescimento adimensional, W(X,l). Para cada valor de l, a taxa de crescimento adimensional tem um valor máximo, W_max que corresponde a um número de onda dominante X_max. Como as distorções com taxa de crescimento máxima tendem a se desenvolver primeiro, fibras freqüentemente quebram com número de onda dominante e então, W(X,l), corresponde a W_max que pode ser obtido graficamente^[6] utilizando a Figura 2.

Apesar da tendência da evolução da distorção acontecer com o comprimento de onda dominante, foi mostrado que fibras podem quebrar com comprimentos de onda diferentes, dependendo da amplitude inicial das distorções (a₀)^[7]. Para poder inferir a tensão interfacial da dinâmica de instabilidade de fibras quando a fibra não quebra com comprimento de onda dominante, a equação original de Tomotika para inferir W(X,l), deve ser resolvida.

Teoria de Tjahjadi et al.

Tjahajadi et al.^[8] apresentaram uma outra teoria para determinar a tensão interfacial entre dois fluidos Newtonianos a partir do estudo das instabilidades de uma fibra de um polímero fundido inserida em outro. A teoria usa ajustes polinomiais para descrever a dinâmica de crescimento das ampliações. Os valores das curvas polinomiais são calculados a partir de resultados gerados numericamente das formas transitórias que experimenta a fibra até a quebra, usando para o cálculo técnicas de integração de contorno. A dinâmica das amplitudes adimensionais máxima e mínima das distorções senoidais, A_max(t)/R_o e A_min(t)/R_o, é determinada como uma função da razão de viscosidade, l, e o tempo adimensional de acordo com:

onde, A_max e A_min são as amplitudes máximas e mínimas da fibra para um tempo t [µm]; l é a razão de viscosidade definida na equação (4), R_o é o raio da fibra sem deformação para t = 0 [µm]; t é um tempo adimensional computacional:

onde, t é o tempo real do experimento e t_c é um tempo característico de ocorrência dos movimentos provocados pela tensão interfacial dado por:

onde, g é a tensão interfacial.

Os coeficientes k´₀ – k´₃ e k´´₀ – k´´₈ foram apresentados por Tjahjadi et al.^[8] e tabulados para uma gama de razão de viscosidade de 0,01 até 10.

Neste trabalho ambas as teorias Tomotika e Tjahjadi et al. foram testadas e avaliadas para inferir a tensão interfacial através do estudo da dinâmica de uma fibra quebrante.

Experimental

Materiais

Polipropileno comercial (PP) da Polibrasil S.A., e poliestireno (PS) da BASF S.A. foram utilizados neste trabalho. A Tabela 1 mostra as temperaturas de fusão, T_m, e de transição vítrea, T_g, e o índice de fluidez, MFI, dos materiais utilizados. Esses dados são necessários para definir qual material será utilizado como fibra ou matriz nos ensaios.

Cada método que pode ser utilizado para avaliar a tensão interfacial entre dois polímeros fundidos sofre limitações. No caso do método de fibra quebrante a matriz polimérica deve amolecer a uma temperatura mais baixa que a fibra a fim de poder inserir a fibra na matriz sem que a forma dessa se altere. Portanto, em função dos dados apresentados na Tabela 1, PS foi escolhido para fazer os filmes (matriz) e PP para produzir as fibras. Também, quando se avalia a tensão interfacial entre dois polímeros utilizando o método de fibra quebrante é necessário que a viscosidade da fibra seja menor do que a viscosidade da matriz para minimizar o efeito "end pinching" e retração^[9].

A fim de avaliar a tensão interfacial entre dois polímeros utilizando o método da fibra quebrante é necessária a determinação da viscosidade de cisalhamento zero dos polímeros envolvidos. Os valores de viscosidade de cisalhamento zero, h₀, foram obtidos utilizando um reômetro de cisalhamento controlado (modelo SR-5000 da Rheometric Scientific^®) em atmosfera de nitrogênio. Uma configuração de placas paralelas foi utilizada. O diâmetro das placas era de 25,0mm e o gap entre elas de 1,0mm. Ensaios de varredura de tensão e deformação foram conduzidos para definir a região de viscoelasticidade linear dos polímeros.

As fibras de PP foram obtidas por estiramento de grânulos fundidos numa placa aquecida a 220 °C. Os diâmetros das fibras variaram de 30 µm a 110 µm. As fibras foram recozidas durante 12 horas à temperatura de 150 °C baixo vácuo para eliminar tensões residuais. As fibras usadas foram cortadas em pedaços de 1,5 mm antes de ser recozidas. Elas tiveram as extremidades fixadas durante o recozimento para evitar distorções significativas do diâmetro.

Os filmes de PS usados nos experimentos e os discos de PP e PS usados para as medidas reológicas foram obtidos através de moldagem na compressão a uma pressão de 18MPa à temperatura de 200 °C. Os filmes de PS foram obtidos com 0,2mm de espessura, 1,0mm de comprimento e 1,0mm de largura. Os discos foram elaborados com uma espessura de 1,5mm e um diâmetro de 25mm.

A viscosidade de cisalhamento zero (h₀) dos polímeros foi avaliada ajustando o Modelo de Carreau^[10] para o gráfico da viscosidade complexa (h*) vs freqüência. A Figura 3 apresenta um ensaio típico de varredura de freqüência dinâmica para os materiais PP e PS a 200 °C. Pode ser visto que a viscosidade de cisalhamento zero do PP é 10 vezes menor do que a viscosidade de cisalhamento zero do PS. Portanto, o PP foi utilizado como fibra e o PS como matriz, garantindo com isto que a razão de viscosidade seja menor do que 1^[9,11].

Procedimento para a Medição da Tensão Interfacial

As experiências foram feitas colocando fibras de PP entre dois filmes de PS. O "sanduíche" formado foi colocado entre uma lamina de vidro e uma lamínula e aquecido em um estagio a quente (Mettler FP-90). A temperatura foi elevada até 150 °C com uma taxa de 20 °C/sec. O sistema foi mantido a 150 °C até todas as bolhas de ar escaparem. A temperatura foi então elevada ate a temperatura à qual a experiência foi executada (200 °C). Foram feitas observações usando um microscópio óptico e ampliações de 50x ou 100x dependendo do raio da fibra. As imagens do processo de quebra foram registradas utilizando uma câmara CCD.

As imagens foram analisadas utilizando um software de análise de imagens. A Figura 4 apresenta uma seqüência típica de imagens para um ensaio de fibra quebrante.

As imagens registradas correspondem à região central da fibra (L/R₀>40), evitando a influência de outros mecanismos diferentes das instabilidades capilares de Rayleigh^[9,11].

Resultados e Discussão

Os valores de viscosidade de cisalhamento zero dos polímeros PP e PS à temperatura de 200 °C foram 1100 e 9926 Pa.s, respectivamente.

Os valores de tensão interfacial entre o par de polímeros PP/PS à temperatura de 200 °C, determinados pelas teorias de Tomotika e Tjahjadi et al. (método da fibra quebrante), estão resumidos na Tabela 2.

A Tabela 3 apresenta os valores médios e desvios padrões da tensão interfacial, correspondentes aos dados reportados na Tabela 2.

Pode ser visto na Tabela 3, que para ambas as teorias o desvio padrão do valor da tensão interfacial encontra-se acima de 1. Este valor de desvio é alto para valores de tensão interfacial. A media dos valores da tensão interfacial entre os polímeros PP/PS à temperatura de 200 °C, para os ensaios apresentados na Tabela 2, é também reportada na Tabela 3. Estes valores são diferentes daqueles reportados na literatura^[12]. Demarquette et al.,^[12] avaliaram a tensão interfacial para o par de polímeros PP/PS pelo método da gota pendente e reportaram valores de 5,52 mN/m para uma temperatura de 200 °C.

A fim de entender a discrepância entre os resultados apresentados na Tabela 3 e os valores da literatura, os valores da Tabela 2 foram re-analisados.

Comparando os ensaios 5 e 10 da Tabela 2, pode ser visto que, embora para os dois ensaios as fibras possuam o mesmo diâmetro inicial, a fibra correspondente ao ensaio 5 quebrou num intervalo de tempo quase 2000s menor do que no caso da fibra do ensaio 10. Para avaliar a discrepância dos tempos de quebra reportada, o tempo de quebra teórico foi determinado. Ele foi calculado considerando que a quebra de uma fibra é completa quando a amplitude das distorções, a, é igual ao raio médio, R=0,81R_o^[13].

O tempo requerido para a quebra da fibra, t_b, pode ser calculado de acordo com:

onde, t_b é tempo de quebra teórico, q é a taxa de crescimento das distorções, a₀ é a amplitude inicial das distorções senoidais e R₀ é o rádio inicial da fibra.

Kuhn^[14] derivou uma expressão para a amplitude inicial das distorções senoidais, a₀, baseado em movimentos Brownianos:

onde, k é a constante de Boltzmann (1.3807x1023J/K), T é temperatura absoluta (K) e g é a tensão interfacial.

A Figura 5 apresenta os tempos de quebra reais e teóricos para os ensaios da Tabela 2.

Para a determinação do tempo teórico utilizou-se um valor constante de tensão interfacial, 5,52 mN/m. Esse valor foi determinado por Demarquette et al.^[12] utilizando o método da gota pendente.

Pode ser visto na Figura 5 que para os ensaios 2, 5, 6 e 15 a fibra quebrou num intervalo de tempo pelo menos 30% menor do que o tempo previsto pela teoria. Esta discrepância provavelmente se deve a tensões residuais, as quais aceleram a quebra da fibra. Por isto, os ensaios 2, 5, 6, e 15 da Tabela 2 devem ser descartados.

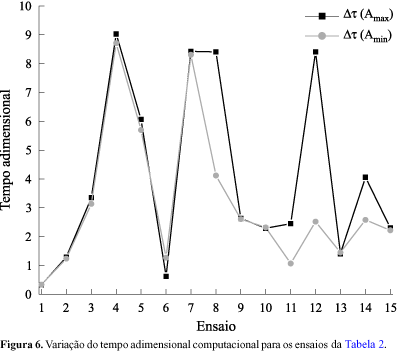
A Figura 6 apresenta o comportamento da variação do tempo adimensional computacional das amplitudes máximas, Dt(A_máx), e mínimas, Dt(A_min), respectivamente, para os ensaios da Tabela 2.

Pode ser visto, que para os ensaios 6, 8, 11, 12 e 14 existe uma diferença de mais de 30% entre os valores de tempo adimensional computacional, Dt, correspondente as amplitudes máximas e mínimas, respectivamente. Isto está devido ao fato de que as instabilidades senoidais máximas e mínimas não surgem de um modo homogêneo ao longo da fibra.

A Figura 7 apresenta as imagens da quebra da fibra do ensaio número 6 da Tabela 2.

Pode ser visto, nessa seqüência de imagens o crescimento irregular das instabilidades. Esta irregularidade no desenvolvimento das instabilidades sugere a presença de tensões residuais não consideradas na teoria do método de fibra quebrante. Em função desse argumento os ensaios 6, 8, 11, 12 e 14 devem ser descartados.

Depois de rejeitados os ensaios 2, 5, 6, 8, 11, 12, 14 e 15 os valores médios da tensão interfacial, assim como os desvios padrões, obtidos para o par de polímeros PP/PS à temperatura de 200 °C usando as teorias de Tomotika e Tjahjadi et al. são apresentados na Tabela 4.

Pode ser visto na Tabela 4 que ambas as teorias conduzem a um resultado semelhante. Os resultados obtidos são também semelhantes aos publicados na literatura, usando o método da gota pendente, g = 5,52 mN/m^[12].

Os dados experimentais foram também comparados a valores obtidos utilizando equações empíricas. Essas equações empíricas correlacionam a tensão interfacial entre dois polímeros com a tensão superficial de ambos os polímeros de acordo com:

equação harmônica:

equação geométrica

onde os sub-índices 1 e 2 referem-se as fases matriz e fibra respectivamente, g^d é a componente de dispersão e g^p é a componente polar da tensão superficial.

Os valores de tensão superficial dos polímeros PP e PS utilizados para a avaliação da tensão interfacial são apresentados na Tabela 5^[15].

Os valores de tensão interfacial, para o par de polímeros PP/PS, determinados pelas equações harmônica e geométrica foram: 5,02 mN/m e 4,84 mN/m, respectivamente. Pode ser visto que os resultados obtidos experimentalmente pelas teorias de Tomotika e Tjahjadi et al., conduzem a valores superiores aos determinados pelas equações empíricas. Esta discrepância já foi vista na literatura^[16].

A diferença entre os valores de tensão interfacial obtidos para o par de polímeros PP/PS, pelos métodos de fibra quebrante, com relação aos valores publicados na literatura^[12] e os determinados pelas equações empíricas, pode ser devida a problemas na determinação do valor da viscosidade de cisalhamento zero.

Analisando a Figura 7, pode-se deduzir também, que as fibras utilizadas nos ensaios de fibra quebrante apresentaram tensões residuais, provavelmente surgidas durante o esticamento realizado no processo de obtenção das fibras. Estas tensões se somam ao valor da tensão interfacial aumentando a magnitude numérica do mesmo.

Conclusão

Neste trabalho as teorias de Tomotika e Tjahjadi et al. correspondentes ao método da fibra quebrante foram utilizadas para inferir a tensão interfacial entre polímeros fundidos. Em particular eles foram testados para o par de polímeros PP/PS à temperatura de 200 ^oC. O valor médio de tensão interfacial calculado usando a teoria de Tomotika foi de 5,88 mN/m e usando a teoria de Tjahjadi et al., foi de 5,66 mN/m. O desvio padrão dos valores obtidos com a teoria de Tjahjadi et al. foi menor que o desvio obtido com a teoria de Tomotika.

A teoria de Tomotika permitiu uma melhor avaliação da taxa de crescimento das instabilidades. Já a teoria de Tjahjadi et al. permitiu uma melhor avaliação da dinâmica dessas instabilidades ao longo do comprimento da fibra durante o processo de quebra. Neste trabalho foi desenvolvido um procedimento, comparando parâmetros de ambas as teorias, para poder avaliar o desenvolvimento das instabilidades e descartar os ensaios cujos resultados não devem ser utilizados para avaliar a tensão interfacial. Entretanto, a determinação da tensão interfacial pela teoria de Tjahjadi et al. é muito complexa.

Agradecimentos

À Polibrasil Resinas S.A. e BASF S.A. pelo suplemento de materiais.

À FAPESP – pelo apoio financeiro (FAPESP 99/02673-3; 97/06071-2 e 00/02744-1).

12. Demarquette, N. R., Martinelli A. C. S., Palmer, G., and Macaúbas H.: "Comparison between five experimental methods to evaluate interfacial tension between molten polymers". Polymer Engineering and Sci., aceito.

14. Kuhn W. Kolloid Z; 132:84 (1953)

Recebido:10/08/01

Aprovado:17/07/02

• 1. Demarquette, N. R. and Kamal, M. R. Polímeros: Ciência e Tecnologia. VI, 3 (1996).
• 2. Demarquette, N. R. and Kamal, M. R. Polímeros: Ciência e Tecnologia VII, 3 (1997).
• 3. Demarquette, N. R. Tese de Livre Docência, EPUSP, (1999).
• 4. Lord Rayleigh. Proc. R. Soc, 29, 71 (1879).
• 5. Tomotika S.. Proc. Roy. Soc, 150, 322 (1936).
• 6. Tomotika, S.. Proc. Roy. Soc., A150, 322 (1935).
• 7. Machiels A. G. C.; Van Dam J.; Posthuma de Boer A. and Norder B. Polymer Engineering and Sci. 37 (9), 1512 (1997).
• 8. M. Tjahjadi; J. M. Ottino and H. A. Stone. AIChE J, 40, 385 (1994).
• 9. Elemans P. H. M.; Hansen J. H. M.; Meijer H. E. H. J. Rheol. 34 (8), 1311 (1990).
• 10. Carreau P. J., De Kee D., Chhabra R. Rheology of Polymeric Systems Principles and Aplic.; Carl Hanser Verlag, Munich Viena New York, (1997).
• 11. Stone H. and Leal L. J. Fluid Mech, 198 (1989).
• 13. Elmendorp J. PhD thesis, Delft U. of Tech., (1986).
• 15. Brandrup Polymer Handbook, 1999 "Surface and Interfacial tension of Polymers, Oligomers, Plasticizers, and Organic Pigments". Pp VI/521
• 16. N. Chapleau; B.D. Favis; P.J. Carreau. Polymer., 41, 6695 (2000).

Datas de Publicação

• Publicação nesta coleção
  28 Mar 2003
• Data do Fascículo
  Jan 2003

Histórico

• Aceito
  17 Jul 2002
• Recebido
  10 Ago 2001