Resumos
Este artigo apresenta um método para a medição de inventário em processo e tempo de atravessamento em um sistema de manufatura. O método consiste em modelar a manufatura por redes de Petri, simular o modelo em computador, alimentando-o com a situação de carga inicial dos processos e com um plano de produção, obtendo os momentos simulados de conclusão de cada ordem do plano. Após este procedimento, com o uso do diagrama de resultados e da fórmula do funil, calcula-se o valor médio simulado de inventário em processo que o plano produzirá na manufatura. Ao fim, faz-se uma discussão na qual explora-se como os resultados do método podem ser úteis em decisões de gestão, envolvendo o inventário admitido, pulmões e restrições da manufatura.
Redes de Petri em manufatura; Filas em manufatura; Medição de inventário em processo; Medição de tempo de atravessamento; Simulação da manufatura
This paper presents a method to measure work-in-process and leadtime in a manufacturing system. The method consists of modeling manufacturing by Petri nets, providing as input for the model the initial load of the process and a production plan, running it and obtaining from the simulation the moments of completion of the orders. Using the throughput diagram and the funnel formula, we then calculate the mean simulated value of the work-in-process that the plan will produce in the manufacturing system. Finally, we discuss how the results can be used to underpin management decisions on issues such as actual work-in-process, buffers and manufacturing constraints.
Petri nets in manufacturing; Queues in manufacturing; Work-in-process measurement; Leadtime measurement; Simulation in manufacturing
Medição do inventário em processo e tempo de atravessamento em manufatura por modelagem em redes de Petri e diagrama de resultados
Measurement of work-in-process and manufacturing leadtime by Petri nets modeling and throughput diagram
Tiago Facchin; Miguel Afonso Sellitto
Universidade do Vale do Rio dos Sinos Unisinos, Programa de Pós-Graduação em Engenharia de Produção e Sistemas, Av. Unisinos 950, CEP 93022-000, São Leopoldo, RS, Brasil, e-mails: tfacchin@terra.com.br; sellitto@unisinos.br
RESUMO
Este artigo apresenta um método para a medição de inventário em processo e tempo de atravessamento em um sistema de manufatura. O método consiste em modelar a manufatura por redes de Petri, simular o modelo em computador, alimentando-o com a situação de carga inicial dos processos e com um plano de produção, obtendo os momentos simulados de conclusão de cada ordem do plano. Após este procedimento, com o uso do diagrama de resultados e da fórmula do funil, calcula-se o valor médio simulado de inventário em processo que o plano produzirá na manufatura. Ao fim, faz-se uma discussão na qual explora-se como os resultados do método podem ser úteis em decisões de gestão, envolvendo o inventário admitido, pulmões e restrições da manufatura.
Palavras-chave: Redes de Petri em manufatura. Filas em manufatura. Medição de inventário em processo. Medição de tempo de atravessamento. Simulação da manufatura.
ABSTRACT
This paper presents a method to measure work-in-process and leadtime in a manufacturing system. The method consists of modeling manufacturing by Petri nets, providing as input for the model the initial load of the process and a production plan, running it and obtaining from the simulation the moments of completion of the orders. Using the throughput diagram and the funnel formula, we then calculate the mean simulated value of the work-in-process that the plan will produce in the manufacturing system. Finally, we discuss how the results can be used to underpin management decisions on issues such as actual work-in-process, buffers and manufacturing constraints.
Keywords: Petri nets in manufacturing. Queues in manufacturing. Work-in-process measurement. Leadtime measurement. Simulation in manufacturing.
1 Introdução
Um correto planejamento e a busca por melhores resultados nos processos produtivos são importantes para a competitividade que a manufatura possa agregar a operações empresariais. No entanto, modificações na manufatura envolvem riscos e incertezas. A modelagem e a simulação da linha de produção podem auxiliar no processo decisório em manufatura, evitando gastos e riscos desnecessários antes da tomada de decisão. Um modelo que possa ser simulado em computador é um mecanismo que transforma parâmetros de entrada, conhecidos e associados às exigências de um processo, em parâmetros de saída e métricas de desempenho que ainda não aconteceram no mundo real (LAW; KELTON, 1991). Assim, um modelo de uma linha de produção, que possa ser usado para simulação computacional, pode ser uma ferramenta de apoio a decisões, pois, antes que os resultados se cristalizem no mundo real da manufatura, podem ser previstos, com uma dada confiabilidade, na virtualidade da simulação.
Inventário em processo e tempos de atravessamento que um plano de produção gerará são grandezas que podem ser úteis em tomadas de decisão em manufatura e podem ser previstas por simulação computacional.
O inventário em processo (work in process ou WIP) também é comumente chamado de estoque em processo e consiste nos materiais que já foram liberados para a manufatura (já saíram do almoxarifado ou já foram recebidos de fornecedores), mas as respectivas ordens ainda não foram concluídas. Tempo de atravessamento é a tradução usada neste artigo para lead time e designa o tempo decorrido entre a liberação da ordem para a manufatura e a disponibilidade do produto para embarque ao cliente (ANTUNES et al., 2007). Algumas decisões em logística interna da manufatura podem estar ligadas a tais grandezas: escolha de alternativas para cumprimento de datas devidas; áreas para armazenagem intermediária de pedidos em processamento; equipamentos para movimentação interna; recursos para trocas de ferramentas e preparação de máquinas. Talvez a decisão mais relevante que possa ser suportada pelo método ora proposto seja a definição do nível de inventário em processo que será admitido na manufatura. Este não deve ser tão baixo a ponto de gerar ociosidade, nem tão alto a ponto de aumentar o tempo de atravessamento.
O objetivo principal do artigo é medir, antecipadamente, o inventário em processo e o tempo de atravessamento em manufatura que um plano de produção gerará. Conhecendo as grandezas antes da liberação do plano, um gestor pode antever e eventualmente prevenir problemas, mudando o plano. Os objetivos específicos foram: i) mapeamento da manufatura; ii) construção de modelo por RP, refino e validação por dados de campo; iii) com os resultados simulados, pelo diagrama de resultados, calcular o inventário em processo e o tempo de atravessamento esperado; e iv) discutir a aplicação. O método de pesquisa é a simulação computacional. A delimitação é que foi feita em uma única aplicação em manufatura calçadista, em um período de duas semanas. O método de trabalho integra duas técnicas de pesquisa operacional, redes de Petri (RP) e o diagrama de resultados (throughput diagram) e foi testado em um plano de produção já executado, cujos resultados serviram para refinar e validar o modelo, que poderá ser usado em planos ainda não liberados para a manufatura.
A principal contribuição do artigo é o método de trabalho, replicável a outras aplicações: simulação por RP, validação por dados de campo e uso do diagrama de resultados para o cálculo de métricas de desempenho. O método pode ser útil em problemas pouco estruturados, como pode ocorrer em manufatura. Como nem sempre há uma definição única de processo, recorre-se a dados agregados de entrada (ordens de fabricação), parâmetros médios de serviço (cronometragem) e métricas globais de desempenho, tais como as duas ora mensuradas.
As RP têm sido usadas para modelagem em manufatura na resolução de problemas específicos. Algumas referências foram consultadas durante a pesquisa e podem ser citadas, pois têm algo a ver com o artigo. Silva (2002) aplica RP para redução de custos em manufatura. Aplicações similares surgem em Dicesare et al. (1993). Jeng (1997) apresenta uma teoria para o uso de RP na modelagem de sistemas de manufatura. Boucher et al. (1989) aplicam RP para controle de células de manufatura. Lee e Dicesare (1994) usam RP em conjunto com heurísticas de busca para programar manufatura flexível. Martinez et al. (1987) usam RP colorida para especificar um sistema de coordenação de produção. Zhou e Dicesare (1991) usam RP em programação de manufatura com compartilhamento de recursos. Proth et al. (1997) e Jeng et al. (2000) propõem classes de RP específicas para modelagem de sistemas de manufatura de alta complexidade. Fung et al. (2002) usam RP em controle adaptativo de manufatura. Wu e Zhou (2001), Xiong e Zhou (1997), Banaszak e Krogh (1990) e Xing et al. (1996) aplicam diferentes métodos baseados em RP para tratar de um problema que pode surgir em manufatura flexível, o deadlock, quando duas tarefas ficam esperando uma pela outra.
Filas também surgem na literatura como apoio à decisão em manufatura. Algumas incidências podem ser citadas. Dallery e Gershwin (1992); Bitran e Dasu (1992); Bitran e Morabito (1995 e 1995A) e Papadopolous e Heavey (1996) apresentam modelos de manufatura baseados na teoria das filas. Govil e Fu (1999) levantaram o uso da teoria em manufatura. Askin e Krisht (1994) e Bitran e Sarkar (1994) otimizam parâmetros de projeto de manufatura, tais como níveis de inventário e taxa de saída. Aplicações e desenvolvimentos avançados surgem em Papadopoulos et al. (1993). Silva e Morabito (2007) usam modelos de filas abertas para estimar inventário em processo e tempo de atravessamento em manufatura. O diagrama de resultado surge em obras ligadas à linha de pesquisa WLC (workload control controle pela carga de trabalho), das quais se destacam Bechte (1994), Wiendahl e Breithaupt (2000) e Breithaupt et al. (2002) e a obra de síntese Wiendahl (1995). O WLC controla a liberação de ordens para manufatura, mantendo o inventário abaixo de um limite que previna ociosidade, mas garanta fluxo rápido, pois o tempo de atravessamento resulta controlado.
O restante do artigo está organizado em: i) descrição de RP e diagrama de resultados; ii) descrição da pesquisa; e iii) discussão dos resultados e sugestões de continuidade.
2 Redes de Petri
As redes de Petri (RP) foram propostas em 1962, por Carl Adam Petri, para representação de sistemas distribuídos discretos. As RP descrevem a estrutura do sistema como um grafo direcionado e podem captar relações de precedência e vínculos estruturais de sistemas reais, com expressividade gráfica para modelar conflitos e filas (PETERSON, 1981).
Uma RP é formada por posições, transições e arcos direcionados que interligam posições e transições, não podendo conectar dois lugares ou duas transições. Uma posição pode armazenar uma ou mais marcas (tokens), que representam quantidades de entidades ou recursos lá disponíveis. A quantidade de marcas na posição é dada por pontos ou por números. Na transição, algumas posições perdem marcas e outras ganham, segundo regras. O estado da RP é representado por um vetor n-dimensional M que indica as quantidades de marcas nas posições (CASTRUCCI; MORAES, 2001). A simbologia é como na Figura 1.
Pode-se definir formalmente uma RP como uma sêxtupla (P, T, A, M0, W, K) na qual: P é o conjunto de posições; T é o conjunto de transições; A é o conjunto de arcos sujeito à restrição de que arcos não ligam duas posições ou transições; m0 é o estado inicial, que informa quantas marcas há em cada posição para o início do processamento; W é um conjunto de pesos de arco, que informa, para cada arco, quantas marcas são requisitadas de uma posição por uma transição ou quantas são colocadas em cada posição após uma transição; e K é o conjunto de restrições de capacidade, que informa, para cada posição, o número máximo de marcas que podem ocupar a posição (CASTRUCCI; MORAES, 2001). Aplicando a definição à RP da Figura 1, P = [p0, p1]; T = [t0]; A = [(p0, t0), (t0, p1)]; W: w (p0, t0) = 1, w (t0, p1) = 1 e M0 = [1; 0]. A marca em p0 habilita a transição t0. Após o disparo, M = [0; 1].
As transições correspondem às mudanças de estado e os lugares correspondem às variáveis de estado do sistema. No disparo de uma transição, as marcas se movimentam pela rede em duas fases: habilitação e disparo de transição. Uma transição tj∈ T é habilitada por uma marcação m se ∀ pi∈ P, m (pi) > w (pi, tj), isto é, a marcação na posição pi é maior ou igual ao peso do arco que liga pi a tj. Quando a transição é disparada, um número de marcas igual ao peso do arco é removido do pré-set e depositado no pós-set. Em posições temporizadas, as marcas só habilitarão novas transições depois de transcorrido este tempo (REISIG, 1998).
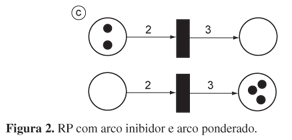
Algumas variantes são admitidas em RP. Se duas transições estiverem em conflito, usam-se arcos inibidores, que só habilitam as transições se não houver marcas no pré-set. Na Figura 2a, a transição t0 está habilitada, pois p1 não está marcada e p0 tem uma marca. Na Figura 2b, a marca em p1 desabilita t0. Na Figura 2c surge uma RP com arcos ponderados. Como o número de marcas na posição p0 é m(p0) = 2 e o peso do arco é w(p0,t0) = 2, a transição t0 está habilitada. Ocorrendo um disparo, em p1 aparecerá um número de marcas m(p1) = 3, pois o peso do arco é w(t0,p1) = 3 (MACIEL et al. 1996; MURATA, 1989).
3 Diagrama de resultados em manufatura
Sistemas de manufatura consistem em máquinas e centros de trabalho, cujas operações ocorrem em itens e submontagens, formando produtos destinados a clientes. Equipamentos de movimentação e estocagem permitem movimentação e abastecimento e permitem que o trabalho parcial seja acumulado até ser requisitado pelo próximo centro. Quando os itens processados são individualizáveis, geralmente organizados em ordens de fabricação, têm-se os sistemas discretos de manufatura. Em manufatura, uma fila surge quando, por variabilidade, em um dado instante, o número de ordens a executar é maior do que o de centros de trabalho disponíveis. A ordem chega ao centro, espera sua vez, é processada e avança. A seqüência está sujeita à troca de prioridades e interrupções por manutenção ou falta de materiais (SILVA; MORABITO, 2007; PAPADOPOULOS et al., 1993). Para este artigo, interessa uma técnica de análise gráfica de filas em manufatura, o diagrama de resultados (throughput diagram), que surge em Wiendahl (1995), obra que sintetiza achados da linha de pesquisa WLC (workload control) do Institut für Fabrikanlagen, de Hannover.
Wiendahl (1995) descreve a origem histórica e a evolução do diagrama. Entre outros, o autor cita Conway et al. (1967), que plotaram no mesmo gráfico o número cumulativo de entradas e de ordens completadas como função do tempo decorrido. Eles observaram que nem sempre a ordem de conclusão era a de chegada, havendo ultrapassagens. Concluíram que, em regime permanente e com muitas ordens, o tempo médio de fluxo através do sistema igualava o número médio de ordens no sistema multiplicado pelo intervalo médio entre chegadas. Os autores referiram-se a Little, que publicou uma prova formal desta relação em sistemas de filas. Ao fim, o autor deu mais ênfase aos trabalhos de Bechte, Erdlenbruch e Lorenz, todos de 1984, para explicar o diagrama.
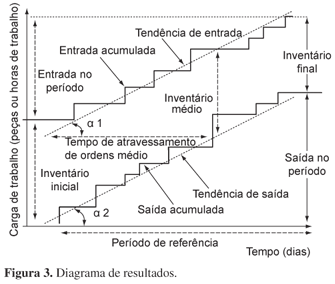
Um centro de trabalho (pode ser uma máquina, uma linha de produto ou uma planta) pode ser comparado a um funil, no qual ordens chegam (entrada), esperam por serviço (inventário) e deixam o sistema (saída). Quando o centro é observado por um período contínuo, o período de referência, os resultados acumulados podem ser plotados. Na Figura 3, é possível observar traçados acumulados de entrada e de saída, medidos em quantidade de trabalho (WIENDAHL, 1995). Esta quantidade pode ser em peças, números de horas ou outra unidade de valor que represente significativamente o esforço de manufatura (SELLITTO, 2005).
Para obter o traçado de entrada, é preciso conhecer a quantidade de trabalho esperando o inventário inicial na fila no início do período de referência. A seguir, plota-se a entrada somando as quantidades de trabalho das novas ordens nas datas em que entram. Plota-se a saída somando o conteúdo de trabalho das ordens que saem, nas datas de saída. Podem ser obtidas ainda as tendências dos traçados. À medida que o período de referência avança, o diagrama se move como se visto através de uma janela. Como os traçados descrevem o resultado do fluxo de ordens pelo sistema de manufatura, (ERDLENBRUCH, 1984 apud WIENDAHL, 1995) estes foram chamados de diagrama de resultados (throughput diagram). Sellitto (2005) acrescentou o cálculo de expressões analíticas para as retas de tendências pelo método dos mínimos quadrados.
Wiendahl (1995) apresenta um desenvolvimento analítico relativo ao diagrama de resultados e calcula diversas grandezas de interesse para o WLC, tais como: tempo de atravessamento de ordens médio e variabilidade, inventário médio, desempenho médio, autonomia e avanços e atrasos na entrega das ordens. Para este artigo, interessa apenas a Equação 1, demonstrada pelo autor e chamada por ele de fórmula do funil.
na qual TLm = tempo de atravessamento de ordens médio (em dias); Im = inventário médio (em peças); e Pm = desempenho médio (em peças por dia).
Para a demonstração, o autor usa a figura e considera regime permanente, ou seja, equilíbrio entre entradas e saídas (α1 = α2) e faz tan α1 = Im/TLm e tan α2 = Pm. Sem equilíbrio, ou o inventário cresce sem limite ou o centro pára por falta de carga, o que na prática é coibido pela gestão (WIENDAHL; BREITHAUPT, 2000). Wiendahl (1995) aponta que a equação pode ser usada para medição e controle de manufatura. Para obter um dado tempo de atravessamento de ordens médio, conhecido o desempenho médio, basta calcular e manter, por uma política de liberação de carga, o inventário médio de ordens em espera.
4 Caracterização da pesquisa
O método de pesquisa foi a simulação computacional. Admitiram-se simplificações na realidade para que o modelo fosse manejável, mas sem perder a replicabilidade. O método de trabalho foi: i) escolha da manufatura, mapeamento do processo e coleta de dados; ii) construção do modelo por RP; iii) alimentação do modelo com a situação inicial de carga e um plano de produção já executado, execução e uso dos resultados no ajuste do modelo; iv) com os resultados simulados, cálculo do inventário em processo e tempo de atravessamento de ordens médios gerados pelo plano; e iv) discussão e refino do método e análise das implicações de seu uso na gestão da manufatura. Não foi objetivo de pesquisa comparar RP com outros métodos de simulação discreta. Usou-se RP por já haver estrutura de recursos humanos e materiais para a técnica, que ainda não havia sido usada em manufatura pelos pesquisadores. A vantagem no uso de RP em relação a outros métodos de simulação surge quando já existe a estrutura, pois não são precisos novos investimentos. Pela disponibilidade e facilidade de acesso, escolheu-se uma manufatura de calçados masculinos.
4.1 Mapeamento do processo de manufatura
A produção consiste em modelagem (ocorre fora), corte, costura, montagem e expedição. Algumas atividades usam mão-de-obra volante, que se desloca entre etapas próximas. Dividiu-se a manufatura em três processos: processo 1 (corte, divisão e chanfração), processo 2 (preparação e costura) e processo 3 (montagem e expedição), a seguir examinados.
O processo 1 inicia no corte, que transforma peças inteiras de couro nas partes que compõem o produto final. Para cada peça, partes diferentes da pele são cortadas, evitando imperfeições, tais como marcas de arame farpado e marcas de identificação (quando o animal é marcado a ferro). É necessário controlar o aproveitamento em relação à forma e direção das fibras. O corte é realizado em balancins e requer moldes (navalhas). Algumas peças, depois de cortadas, passam pela etapa de divisão, em máquina de dividir, que uniformiza a espessura. Segue a chanfração, na qual são desbastadas as bordas das peças de couro, para evitar relevos nas junções, garantindo um melhor acabamento nas peças e no produto final. Os tipos de chanfro são armazenados nas memórias das máquinas de chanfrar, dispensando ajuste manual.
No processo 2, as peças são separadas, preparadas manualmente e costuradas em máquinas, em quatro células de trabalho. No processo 3, na operação de montagem, ocorre a conformação, a passagem em forno quente e frio e a colocação de palmilhas. Por fim, na expedição, os calçados são arrumados e embalados segundo as ordens de fabricação.
4.2 Modelagem do processo 1
A modelagem ocorreu em três partes, referentes aos três processos descritos.
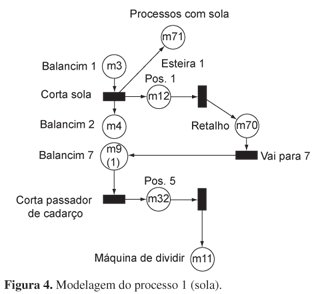
No processo 1, são realizadas as operações de corte dos pré-fabricados (palmilhas e solas) e das peças da parte superior do calçado, o cabedal. Nos pré-fabricados, simplificou-se o modelo, agrupando operações seqüenciais. O corte das peças do cabedal foi detalhado. As peles são cortadas em seqüência, pois para cada peça corta-se a pele em diferentes lugares. Quando a pele chega ao balancim 1, o operador corta a sola. Quando não for mais possível cortar solas, o que resta da pele vai para o balancim 2. As peças cortadas vão para os processos de fabricação da sola, os retalhos são colocados na esteira (posição 1 da esteira 1) e transportadas até o balancim 7, onde serão cortados os passadores de cadarço que irão para a máquina de dividir. Os retalhos do balancim 7 são restos e serão dispostos. O processo é modelado como na Figura 4.
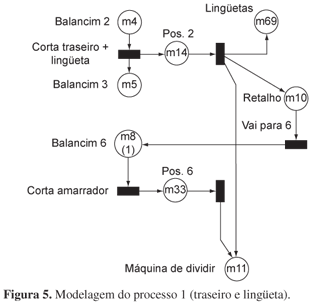
No balancim 2, são cortados o traseiro e a lingüeta, que vão para a esteira, que por sua vez os transporta para a máquina de dividir. Mais pele é cortada no balancim 3. Os retalhos vão para a esteira e são transportados até o balancim 6, onde são cortados os amarradores, que vão para a máquina de dividir. Os retalhos do balancim 6 são dispostos. Para as lingüetas, os processos de dividir, chanfrar e separar são agrupados na posição lingüetas, pois esta peça não entra no processo da Célula 1 da costura junto com as demais. A modelagem é como na Figura 5.
No balancim 3, são cortadas a lateral interna e a lateral externa. A pele é cortada no balancim 4. As peças são colocadas na esteira e vão para as máquinas de chanfrar (chanfradeiras). A modelagem é como na Figura 6. No balancim 4 é cortada a biqueira e a pele passa para ser cortada no balancim 5. As peças são colocadas na esteira e vão para as máquinas de chanfrar (chanfradeiras). A modelagem é como na Figura 7. No balancim 5, são cortados os debruns traseiro e lateral, que são colocados na esteira e vão para as máquinas de chanfrar (chanfradeiras). A modelagem é como na Figura 8. Os retalhos dos balancins são dispostos.
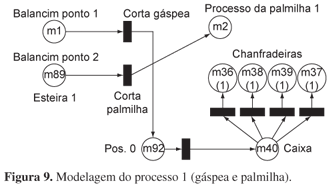
No balancim ponto 1 é cortada a gáspea, e no balancim ponto 2, a palmilha. A gáspea, para a linha de produtos em estudo, é uma tela e não precisa ser dividida, indo direto para a máquina de chanfrar (chanfradeiras). Já a palmilha, depois de cortada, vai para a posição (processo da palmilha 1). A modelagem é como na Figura 9. As peças que passam pela máquina de dividir vão para as máquinas de chanfrar, mas algumas peças vão direto do corte para a chanfração. Após as máquinas de chanfrar, as peças passam para a mesa de separação. A transição "Separa" só estará habilitada quando todas as peças chegarem à mesa de separação, o que é garantido pelas posições auxiliares de Garante 1 a Garante 7.
4.3 Modelagem do processo 2
Neste processo, são coladas, preparadas e costuradas as peças cortadas no processo 1, em quatro células de trabalho. As lingüetas vão para a Célula 3 do processo de costura, onde serão preparadas, forradas e juntadas com o cabedal, que vem da Célula 2. As peças formam conjuntos que vão para a Célula 1.
O cabedal começa a ser produzido na Célula 1. Primeiro, são coladas, preparadas e costuradas as peças laterais (posições: Célula 1 (m42), Mesa de preparação (m44) e Máquina de costura (m45), respectivamente). A seguir, é colado, preparado e costurado o debrum traseiro (posições: Célula 1, Mesa para colar (m34), Mesa de preparação 2 (m48) e Máquina de costura 2 (m49), respectivamente). Por último, é preparado (há duas operações de preparação) e costurado o traseiro (posições Mesa de preparação (m80), Mesa de preparação 2 (m77) e Máquina de costura 2 (m76) ), finalizando as operações da célula.
Algumas operações são realizadas pelos mesmos operadores, o que explica a utilização de arcos inibidores. Por exemplo, nas posições Mesa de preparação (m44 e m80), o mesmo operador prepara as laterais e prepara o traseiro. Quando o produto requerer, ao mesmo tempo, que o operador prepare as laterais e o traseiro, é dada preferência ao último, pois para o mesmo item, para o qual o traseiro será preparado, as laterais já o foram. O mesmo raciocínio é válido para as operações referentes às posições Mesa de preparação 2 (m48 e m77) e Máquina de costura 2 (m49 e m76) (Figura 10).
Na Célula 2, ocorrem três processos em seqüência: prender o forro, colar a espuma e virar o forro. Após estes processos, o cabedal vai para a Célula 3, de onde sairá pronto para receber a sola. Nesta célula, são colados, preparados e costurados o amarrador e o traseiro (costurado novamente, agora com forro). São cortadas as rebarbas e costuradas com a lingüeta, em paralelo na Célula 3. Depois de costurados, são queimados os fios e o cabedal vai para a Célula 4, onde é colocada a ilhose (peça de metal por onde passa o cadarço). A parte superior do calçado está pronta para ser costurada com a sola. Costurados a sola e o cabedal, estes vão para uma máquina de rebater e são desvirados, saindo assim do setor de costura (Figura 11).
4.4 Modelagem do processo 3
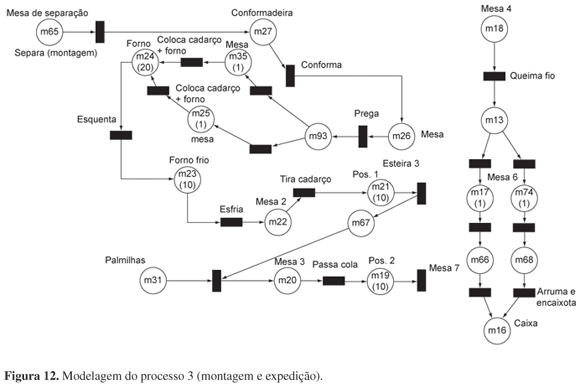
O processo 3 engloba a montagem e a expedição do calçado e, após este processo, o par de calçados estará pronto. Depois que o par sai do setor de costura, vai para uma mesa de separação, onde todos os pares são separados, segundo tamanho e cor. Da mesa de separação, os pares vão para a máquina de conformar, passando para uma mesa onde são pregados na fôrma (para modelar) e os cadarços são colocados (processos realizados por duas pessoas). Passam, então, por um forno quente e depois por um forno frio, os cadarços são tirados e os pares vão para a esteira, onde recebem as palmilhas. A seguir, vão para a esteira e são transportados até um posto de trabalho, em que os pedaços de fios que restaram são queimados, os cadarços são novamente colocados (processo realizado por duas pessoas) e os pares são, finalmente, arrumados e embalados. Neste momento, o processo está finalizado e os pares de calçados estão prontos para embarque. A modelagem é como na Figura 12.
4.5 Atribuição de tempos às transições
Após atribuídos os tempos às transições, chegou-se ao modelo completo da Figura 13.
Para atribuir tempos às transições, os processos foram cronometrados. Com o auxílio do supervisor de produção, foram definidos o início e o fim de cada tarefa. Considerou-se um nível de confiança de 95% e usou-se o modelo de cálculo sugerido por Vaz (1993) e AEP (2003). Como exemplo, na operação de cortar sola, a média dos tempos foi de 18,13 segundos e o desvio padrão foi de 2 segundos. O número mínimo de amostras para garantir o nível de confiança definido foi de 19,5, adotando-se vinte amostras. O tempo de cada transição é a média dos valores coletados. Alguns processos em série foram simplificados e suas médias somadas. Quando mais de um operador faz a mesma tarefa, adotou-se a média das médias dos resultados dos operadores.
No processo 1, foi criada uma posição (Primeiro par) auxiliar que garante que a primeira peça irá levar o tempo total para ser transportada pela esteira (te). As peças seguintes chegam em seqüência, pois são depositadas na esteira após serem processadas (tp). Para isso, calcula-se quanto tempo cada peça leva para chegar na próxima etapa (tpe). Por exemplo, se n = 00 peças, o tempo para transporte pela esteira (te) = 810 segundos e o tempo para processar uma peça tp = 17,39 segundos. Então: tpe = ((tp x n)+ te)/n, perfazendo [(17,39 x 600) + 810)]/600 = 18,74 segundos. Isto significa que, após a chegada da primeira peça, a próxima chegará em 18,74 segundos. Nos demais processos, foram atribuídos às transições os tempos médios.
4.6 Simulação e cálculo do inventário e tempo de atravessamento
Para teste e refino do modelo, foi escolhido um plano já realizado, de duas semanas e nove ordens de produção. Foi informada a carga de cada processo, resultante das ordens anteriores, no momento de liberação do plano. Uma nova ordem encontra ordens anteriores em fila e em processamento, o que explica porque o tempo de atravessamento na manufatura é muito mais alto do que o tempo padrão de fabricação. A disciplina de fila adotada pelo modelo foi FIFO (primeira ordem que chega é a primeira que sai).
Para a simulação, foi usado o software Visual Object Net++ versão 2.0a (DRATH; SCHWUCHOW, 1997; VISUAL OBJECT NET, 2005), desenvolvido na Universidade de Tecnologia de Ilmenau, Alemanha, no Departamento de Controle Automático e Engenharia de Sistemas. É uma ferramenta para modelagem e simulação de RP a eventos discretos, contínuos e híbridos e oferece facilidades equivalentes às dos simuladores discretos, tais como: execução passo a passo, processamento a partir de um instante de tempo, relatórios, animação e gráficos de saídamodleo foi rodadot nufatura). O modelo foi rodado em microcomputador equipado com processador Pentium de 2,8 GHz e 512 Mb de memória RAM. O passo de avanço adotado foi de 1 milissegundo e o tempo aproximado de processamento foi de quatro horas.
Liberaram-se as ordens de fabricação do plano (quantidades e datas) na posição de entrada do sistema (Balancim 1) e obtiveram-se dados simulados na posição de saída do sistema (Caixa). A Tabela 1 traz os dados das nove ordens de fabricação constantes do plano de produção. As datas consideram apenas os dias realmente trabalhados, não os de calendário.
A Tabela 1 apresenta as quantidades das ordens, as datas de liberação e conclusão real, em dias e em segundos (um dia = 8 horas e 40 minutos = 31.200 segundos) e de saída, simuladas, em segundos. Na última coluna, surge o tempo de atravessamento da ordem, calculado pela simulação, e sua média. Wiendahl (1995) apresenta um método que considera o tamanho Qi da ordem. Por este método, TLmédio = Σ[Qi.TLordem i]/[Σ Qi] = 2,73 dias, próximo aos 2,63 dias calculados. A correlação entre as saídas real e simulada (coluna 5 e 6) é de 0,99 e o erro absoluto |real - simulado| médio é de 9.821 segundos (2,27% do maior valor real).
Na Figura 14, comparam-se as informações de saídas reais e simuladas, ordem a ordem.
Observa-se que as curvas de saída real e simulada não se cruzam nas duas semanas simuladas, o que pode indicar viés. Examinando resultados de simulações similares publicados em Wiendahl (1995), observou-se que as curvas de saída e simuladas entrelaçam-se, porém em intervalos de tempo de até 120 dias. Também se observa que, na simulação, as ordens menores terminam mais tarde e as ordens maiores terminam mais cedo do que na produção real. Descobriu-se que supervisores de operação podem tomar decisões locais do tipo: priorizar as ordens menores para reduzir o atraso geral ou antecipar faturamento, ou ainda priorizar as ordens maiores quando há excesso de materiais na área fabril, excesso de setups ou quando falta material em outras ordens. Como estas opções não foram contempladas no modelo, cuja disciplina em filas é FIFO, é possível que expliquem a diferença observada. Por fim, observa-se que a fórmula do funil requer sistema em equilíbrio. A execução considerou as condições iniciais da manufatura, que podia (ou não) estar equilibrada. Para garantir regime permanente, seria desejável simular aum plano maior. Reforça-se que a principal contribuição de pesquisa que se deseja é metodológica: aprendizado e refino do método são desejáveis. A inclusão de alternativas de decisões locais e a execução de um plano maior são remetidas à continuidade.
O desempenho médio simulado é Pm = 31.200 x [7.000/(428.504 - 66.480)] = 583 pares/dia. A base de cálculo é: em (428.504 - 66.480) segundos, foram entregues 7.000 pares. O desempenho real médio é Pm = 31.200 x [7.000/(436.800 - 78.000)] = 608 pares/dia. O intervalo simulado entre saídas é ∆t = [(428.504 - 66.480)/7.000] = 51,7 segundos e o real é ∆t = [(436.800 - 78.000)/7.000] = 51,25 segundos. O inventário médio esperado é Im = Pm.TLm = 583 pares/dia x 2,627 dias = 1.531 pares.
Na Figura 15, tem-se o diagrama de resultados, para chegadas reais e saídas simuladas. A construção do gráfico se dá por acúmulo em intervalos de 25.000 segundos. Este intervalo foi definido de modo arbitrário. Outros intervalos podem produzir outros resultados. Adotaram-se retas médias substitutas, obtidas pelo método dos mínimos quadrados. Os coeficientes de determinação R2, próximos a um, reforçam a substituição. O coeficiente angular de saída é 0,0168 pares por segundo. O recíproco [1/0,0168] = 59,52 segundos por par é próximo ao intervalo calculado entre as saídas de pares. A Tabela 2 mostra as chegadas e saídas acumuladas para as ordens da Tabela 1, nos intervalos de 25.000 segundos. O número instantâneo de pares no sistema é N(t) = [I(t) - O(t)]. A média, um indicativo do inventário médio, calculada por este método, é próxima à calculada pela fórmula do funil (1.546 e 1.531 pares).
5 Implicações do uso do método na gestão da manufatura
A simulação gerou dados referentes a todos os processos, mas discutem-se apenas dois.
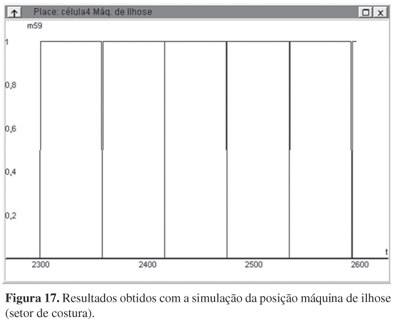
A Figura 16 mostra a tela da posição Mesa de preparação da célula 1 (setor de costura). Observou-se na produção real que o operador desta estava sobrecarregado, o que é confirmado na simulação, pela fila crescente. Uma alternativa seria a redistribuição de tarefas, adotando paralelismos, sem sobrecarregar os postos seguintes. No processo real, já se sabia que a costura é mais lenta. Pouco adiantaria eliminar esta fila, pois mais filas se formam em posições seguintes. Outra situação é a da Figura 17. O tempo que o operador da posição Máquina de ilhose fica ocioso é baixo e, ainda assim, não ocorrem acúmulos de tarefas com o passar do tempo. Isso mostra que, para esta posição, as tarefas estão bem distribuídas.
Outras telas permitem que análises semelhantes sejam feitas em todas as posições de manufatura. Alternativas de gestão, tais como: heurísticas de seqüenciamento de ordens, podem ser simuladas e seus impactos avaliados. Por exemplo, dois dias após a terceira ordem, de 1.500 pares, cuja carga é próxima a três dias de operação, houve nova liberação, provavelmente aumentando a fila e o inventário em processo. As implicações da mudança podem ser testadas a priori. O prazo para a entrega da ordem também pode ser estimado, com reflexos diversos, inclusive nas atividades comerciais da empresa.
O uso do diagrama de resultados também implica possibilidades para a gestão da manufatura.
A curva de saída apresenta declividade constante, o que indica que pode haver uma única restrição ativa na manufatura, cuja capacidade média determina o ritmo médio de saída. Caso houvesse gargalos flutuantes, a declividade da curva de saída variaria de modo mais definido, em segmentos, durante o período, o que não parece ser o caso. Como dito, a restrição é a costura. A contribuição do diagrama de resultados é a visualização, nas duas semanas, que o ritmo de entrada de ordens foi menor do que o ritmo de saída, pois as retas médias estão se aproximando e o coeficiente angular de saída é maior do que o de entrada (0,0168 x 0,0149). Não se sabe se alguma operação parou, mas parece ter havido redução de inventário médio.
Uma indicação de controle para a manufatura seria: aumenta a entrada de ordens, ou diminui a capacidade produtiva, ou ambos, balanceadamente, pois no ritmo atual haverá tendência à interrupção de atividades por falta de tarefas, tal como quase aconteceu entre as datas 300.000 e 350.000 segundos, quando os traçados de entrada e saída se aproximaram. Neste trecho, é possível que tenha havido perda de desempenho local, devido à falta de ordens, o que pode ter sido compensado alhures com horas-extras, para a recuperação do desempenho médio. Também é possível que o desempenho médio pudesse ter sido maior, pois o fato de que não faltou material não garante que o material disponível era o necessário no momento.
Modificações momentâneas na estrutura da manufatura não são captadas individualmente pelo modelo de simulação, pois este simplifica algumas atividades e negligencia algumas contingências. Resta tratá-las de modo agregado, pelo diagrama de resultados, o que pode ser uma contribuição para a resolução de problemas menos estruturados.
Os valores de R2 no diagrama de resultados, de certo modo, validam a substituição por retas dos traçados probabilísticos. Podem ser usadas as expressões analíticas para o cálculo do inventário médio do período, ou seja, a distância entre as retas a 225.000 segundos, que representa o valor médio entre as datas da primeira saída e da última entrada, que são aproximadamente 75.000 e 375.000 segundos.
Aplicando as equações das retas, a distância vertical em 225.000 é de 1.425 pares de calçados, próxima às distâncias anteriores. Ainda, pode-se determinar por quanto tempo o sistema operará sem novas chegadas e com que autonomia. A autonomia média é o inventário médio dividido pelo desempenho médio, ou seja, Rm = 1.531/583 = 2,62 dias e é dimensionalmente igual ao tempo de atravessamento médio. O pulmão, ou o inventário mínimo para que não falte trabalho, é o inventário que será consumido pelo desempenho médio durante o maior intervalo entre chegadas. No período estudado, o maior intervalo entre chegadas foi de 3,2 dias, portanto, um pulmão para o caso em estudo é B = 3,2 x 583 = 1.865 pares.
Um modo de reduzir a necessidade de pulmão é reduzir a variabilidade na liberação de ordens. A política atual de liberação é: recebidos e inspecionados todos os materiais da ordem, estes são transferidos imediatamente do almoxarifado para a manufatura. Um exemplo de política de redução de variabilidade foi citado, quando se mencionou que houve nova liberação dois dias após liberada a terceira ordem, com carga aproximada de três dias de trabalho. Se esta tivesse sido postergada, por exemplo, em meio dia, postergando também as liberações seguintes, o maior intervalo entre chegadas, entre a 6ª e a 7ª ordem, seria menor do que os atuais 3,2 dias. Cai a exigência de pulmão de proteção e, conseqüentemente, o tamanho da fila e o inventário em processo.
Reduzida a variabilidade e calculado um novo pulmão, faz parte da técnica monitorar o tamanho da fila, para que não se afaste do valor mínimo necessário. Fila maior significa perda por espera e antecipação da produção, com custos de armazenagem e guarda de materiais e eventual obsolescência, pois a manufatura estudada tem sazonalidade e é afetada por moda e tendência de consumidores. Por outro lado, fila menor, sob variabilidade, implica risco de perda de desempenho e redução da taxa de retorno do investimento em manufatura, causada pela ociosidade de máquinas e operadores e pela eventual necessidade de recuperação em turnos extraordinários ou com contratação de terceiros. O modelo proposto pode ser útil em decisões sobre qual tamanho de fila admitir, com implicações no controle de estoques, ajuste de carga da manufatura e estimativa de prazos de entrega das ordens.
6 Considerações finais
Foi apresentado e testado um método, baseado em modelagem e simulação por RP e no diagrama de resultados para o cálculo de dois indicadores importantes na gestão da manufatura, o inventário em processo e o tempo de atravessamento. Com os resultados da simulação, o diagrama de resultados ofereceu de forma analítica e gráfica, o inventário, o tempo de atravessamento e a autonomia, e permitiu o cálculo de uma sugestão de pulmão para o sistema produtivo. O método pode apoiar decisões de manufatura, principalmente ligadas ao tamanho do inventário admitido, que não deve ser tão pequeno a ponto de gerar ociosidade, nem tão grande a ponto de aumentar o tempo de atravessamento. Aspectos de logística interna de armazenagem e movimentação também podem ser apoiados pelo método.
O teste e o refino do método apontaram pontos de aprendizado que requerem continuidade de pesquisa. É necessária a simulação por intervalo de tempo maior, buscando o equilíbrio do sistema e verificando se existe ou não viés no modelo. Também é necessária a inclusão de alternativas de decisão locais para inversão de seqüência de ordens. Para novos trabalhos dentro da mesma linha, propõe-se analisar a viabilidade da implantação da automação em alguns processos. Outra possibilidade seria produzir um modelo mais geral para a manufatura estudada, visto que, para outros modelos de calçados, o processo muda e esbarra em uma dificuldade intrínseca das RP: quando é requerida uma modelagem mais detalhada, o modelo tende a crescer em demasia (explosão combinatória de estados). Uma alternativa são as redes de Petri coloridas. Finalmente, sugere-se usar o modelo desenvolvido para a investigação de gargalos flutuantes (shifting bottlenecks), o que requererá ulteriores pesquisas e fundamentação teórica adicional e, possivelmente, testes em outra manufatura, pois a manufatura estudada parece ter um único gargalo estrutural.
Recebido em 18/5/2007
Aceito em 10/4/2008
Agradecimentos: Deseja-se reconhecer a importância da UAPPG da UNISINOS aos esforços de pesquisa do PPGEPS-UNISINOS e o trabalho dos revisores anônimos que contribuíram para a forma final do artigo.
- AEP- Associação Empresarial de Portugal. Métodos e Tempos: Manual Pedagógico. Leça da Palmeira, 2003.
- ANTUNES, J.; ALVAREZ, R.; KLIPPEL, M.; BORTOLOTTO, P.; PELLEGRIN, I. Sistemas de Produção Porto Alegre: Bookman, 2007.
- ASKIN, R.; KRISHT, A. Optimal Operation of Manufacturing Systems with Controlled Work-in-Process Levels. International Journal of Production Research, London, v.32, n.7, p.1637-1653, 1994.
- BANASZAK, Z.; KROGH, B. Deadlock avoidance in flexible manufacturing systems with concurrently competing process flows. IEEE Transactions on Robotics and Automation, v.6, n.6, p.724-734, 1990.
- BECHTE, W. Load-oriented manufacturing control just-in-time production for job shops. Production Planning & Control, London, v.5, n.3, p.292-307, 1994.
- BREITHAUPT, J.; LAND, M.; NYHUIS, P. The workload control concept: theory and practical extensions of Load Oriented Order Release. Production Planning & Control, London, v.13, n.7, p. 625-638, 2002.
- BITRAN, G.; SARKAR, D. Throughput Analysis in Manufacturing Networks. European Journal of Operational Research, v.74, n.3, p.448-465, 1994.
- BITRAN, G.; MORABITO, R. Um exame dos modelos de redes de filas abertas aplicados a sistemas de manufatura discretos: Parte I. Gestão & Produção, São Carlos, v. 2, n.2, p.192-219, 1995.
- BITRAN, G.; MORABITO, R. Um exame dos modelos de redes de filas abertas aplicados a sistemas de manufatura discretos: Parte II. Gestão & Produção, São Carlos, v. 2, n.3, p.297-320, 1995A.
- BITRAN, G.; DASU, S. A review of open queueing network models of manufacturing systems. Queuing Systems, v.12, n.1-2, p. 95-133, 1992.
- CASTRUCCI, P.; MORAES, C. Engenharia de automação industrial. Rio de Janeiro: LTC, 2001.
- BOUCHER, T.; JAFARI, M.; MEREDITH, G. Petri net control of an automated manufacturing cell. Computers and Industrial Engineering, Tarry Town, NY, USA, v. 17, n.1, p.459-463, 1989.
- DALLERY, Y.; GERSHWIN, S. Manufacturing flow line systems: a review of models and analytical results. Queuing Systems, v. 12, n.1-2, p. 3-94, 1992.
- DICESARE, F.; HARHALAKIS, G.; PROTH, J. M.; SILVA, M.; VERNADAT, F. B. Practice of Petri nets in manufacturing London: Chapman & Hall, 1993.
- DRATH, R.; SCHWUCHOW, S. Modellierung diskret-kontinuierlicher Systeme mit Petri-Netzen. In: Schneider, E. (Org.). Entwurf komplexer Automatisierungssyteme Braunschweig: Technische Universität Braunschweig, Institut für Regelungs-und- Automatisierungstechnick, 1997.
- FUNG, R.; JIANG, Z.; ZUO, M.; TU, P. Adaptive production scheduling of virtual production systems using object-oriented Petri nets with changeable structure. International Journal of Production Research, v. 40, n.8, p.1759-1785, 2002.
- GOVIL, M.; FU, M. Queuing theory in manufacturing: a survey. Journal of Manufacturing Systems, v. 18, n.3, p.210-214, 1999.
- JENG, M. A Petri net synthesis theory for modeling flexible manufacturing systems. IEEE Transactions on Systems, Man and Cybernetics Part B, v. 27, n. 2, p.169-183, 1997.
- JENG, M.; XIE, X.; HUANG, Y. Manufacturing modeling using process nets with resources. In: IEEE International Conference on Robotics and Automation. April. 2000, San Francisco, USA. Proceedings San francisco, USA: IEEE, 2000.
- LAW, A.; KELTON, W. Simulation modeling and analysis New York: McGraw-Hill, 1991.
- LEE, D.; DICESARE, F. Scheduling flexible manufacturing systems using Petri nets and heuristic search. IEEE Transactions on Robotics and Automation, New York, NY, v. 10, n.2, p.123-133, 1994.
- MACIEL, P.; LINS, R.; CUNHA, P. Introdução às redes Petri e aplicações. Campinas: Instituto de Computação - UNICAMP, 1996.
- MARTINEZ, J.; MURO, P.; SILVA, M. Modeling, validation and software implementation of production systems using high level Petri nets. IEEE International Conference on Robotics and Automation. Março Abril, 1987, Raleigh, North Carolina. Proceedings Raleigh, North Carolina: I3E Comput. Soc., v.4, p. 1180-1185.
- MURATA, T. Petri Nets: Properties, Analysis and Applications. Proceedings of the IEEE, Chicago, IL, USA, v. 77, n.4, p.541-580, 1989.
- PAPADOPOULOS, H. T.; HEAVEY, C.; BROWNE, J. Queuing theory in manufacturing systems analysis and design. London: Chapman & Hall, 1993.
- PAPADOPOULOS, H.; HEAVEY, C. Queuing theory in manufacturing systems analysis and design: a classification of models for production and transfer olines. European Journal of Operational Research, v.92, n.1, p.1-27, 1996.
- PETERSON, J. Petri Net Theory and the modelling of system. Englewood Cliffs, NJ: Prentice-Hall Editions, 1981.
- PROTH, J.; WANG, L.; XIE, X. A class of Petri nets for manufacturing system integration. IEEE Transactions on Robotics and Automation, Valbonne, v.13, n.3, p.317-326, 1997.
- REISIG, W. Elements of distributed algorithms: modeling and analysis with Petri Nets. Berlim: Springer Verlag, 1998.
- SELLITTO, M. Medição e controle de desempenho em sistemas de manufatura. Porto Alegre, 2005. Tese (Doutorado em Engenharia de Produção), UFRGS.
- SILVA, A. Modelagem de custos em sistemas de manufatura utilizando Redes de Petri. São Carlos, 2002. Dissertação (Mestrado em Engenharia Mecânica), USP São Carlos.
- SILVA, C.; MORABITO, R. Aplicação de modelos de redes de filas abertas no planejamento do sistema job-shop de uma planta metal-mecânica. Gestão & Produção, São Carlos, v.14, n.2, p.393-410, 2007.
- VAZ, A. Cronometragem e a nova realidade. Tecnicouro, Novo Hamburgo, v. 3, n.4, p.34-35, 1993.
- VISUAL OBJECT NET. Software e guia de usuário. Disponível em: http://www.systemtechnik.tu-ilmenau.de/~drath Acesso em: março 2005.
- XING, K.; HU, B.; CHEN, H. Deadlock avoidance policy for Petri-net modeling of flexible manufacturing systems with shared resources. IEEE Transactions on Automatic Control, New York, NY, USA, v.41, n.2, p.289-295, 1996.
- XIONG, H.; ZHOU, M. Deadlock-free scheduling of an automated manufacturing system based on Petri nets. IEEE International Conference on Robotics and Automation, Abril 1997, Albuquerque, New Mexico. Proceedings... Albuquerque, New Mexico: IEEE, v.2, p. 945 950.
- WIENDAHL, H. Load-oriented manufacturing control. Berlim: Springer, 1995.
- WIENDAHL, H.; BREITHAUPT, J. Automatic production control applying control theory. International Journal of Production Economics, Amsterdam, v. 63, n.1, p.33-46, 2000.
- WU, N.; ZHOU, M. Avoiding deadlock and reducing starvation and blocking in automated manufacturing systems. IEEE Transactions on Robotics and Automation, Guang Zhou, v.17, n.5, p.658-669, 2001.
- ZHOU, M.; DICESARE, F. Parallel and sequential mutual exclusions for Petri net modeling of manufacturing systems with shared resources. IEEE Transactions on Robotics and Automation, Newark, NJ, USA, v.7, n.4, p.515-527, 1991.
Datas de Publicação
-
Publicação nesta coleção
17 Set 2008 -
Data do Fascículo
Ago 2008
Histórico
-
Recebido
18 Maio 2007 -
Aceito
10 Abr 2008