Resumos
A maior parte da literatura a respeito de Planejamento e Controle da Produção (PCP) é focada em estudar e desenvolver aplicativos para grandes empresas, principalmente de ambiente repetitivo. Nesse contexto, são as poucas as alternativas para o PCP para pequenas e médias empresas que fabricam sob encomenda, as quais têm papel fundamental na atual economia brasileira. Em resposta a essa demanda, o presente trabalho objetiva apresentar uma abordagem para o PCP denominada Controle de Carga (Workload Control - WLC). Essa abordagem é reconhecidamente um método com potencial para trazer melhorias no lead time, no estoque em processo e na pontualidade de entregas em ambientes que fabricam sob encomenda (Make-To-Order - MTO). Primeiramente, o artigo apresenta a abordagem WLC, revisando e discutindo os principais assuntos tratados pela literatura internacional na área. Após isso, o desempenho do WLC é avaliado por meio de simulação. Os resultados mostram o potencial de melhorias no lead time e nas ordens em atraso que o WLC pode trazer a pequenas e médias empresas que fabricam sob encomenda. Dessa forma, o presente trabalho pretende contribuir tanto para a teoria a respeito de tal abordagem, praticamente introduzindo tal assunto na literatura brasileira, como para a prática, fornecendo e demonstrando, por meio de simulação, aos gerentes de PCP, uma alternativa para suas empresas trabalharem rumo a baixos lead times e de acordo com modernos paradigmas de produção, tais como o Lean Manufacturing e o Quick Response Manufacturing.
Controle de carga; Planejamento e controle da produção; Redução do lead time; Pequenas e médias empresas; Fabricação sob encomenda
The majority of Production Planning and Control (PPC) literature is focused on the study and development of solutions for large companies, especially in repetitive environments. Therefore, there are few specific PPC solutions available in the literature for small and medium sized companies (SMC) operating in a Make -to-Order (MTO) environment. This paper presents the Workload Control (WLC), which is a useful PPC approach designed for small sized Make-to-Order companies. According to the literature, such approach has the potential to reduce lead time, work in process, and to provide a better tardiness performance in MTO companies. Firstly, the paper presents the WLC approach reviewing and discussing the main WLC aspects addressed in the literature. The objective is to introduce the concept and present the recent developments to fellow researchers and practitioners. The performance of WLC is then assessed by simulation. The results underline the potential of WLC to bring major improvements in terms of lead time and tardiness performance supporting small and medium sized MTO companies. Therefore, this study aims at contributing to PPC academic and practical areas by introducing WLC approach concepts to Brazilian researchers and managers showing its benefits and potential to help national companies in their efforts towards lead time reduction and best tardiness performance according to modern manufacturing paradigms such as Lean Manufacturing and Quick Response Manufacturing.
Workload control; Production planning and control; Lead time reduction; Small and medium companies; Make-to-order
Redução do lead time e entregas no prazo em pequenas e médias empresas que fabricam sob encomenda: a abordagem Worload Control (WLC) para o Planejamento e Controle da Produção (PCP)
Lead time reduction and improved tardiness performance in small and medium sized Make-to-Order Companies: the Workload Control (WLC) approach, a solution for Production Planning and Control (PPC)
Matthias Thurer; Moacir Godinho Filho
Departamento de Engenharia da Produção, Centro de Ciências Exatas e de Tecnologia, Universidade Federal de São Carlos UFSCar, Rod. Washington Luiz, Km 235, CP 676, CEP 13565-905, São Carlos, SP, Brasil, e-mail: moacir@dep.ufscar.br
RESUMO
A maior parte da literatura a respeito de Planejamento e Controle da Produção (PCP) é focada em estudar e desenvolver aplicativos para grandes empresas, principalmente de ambiente repetitivo. Nesse contexto, são as poucas as alternativas para o PCP para pequenas e médias empresas que fabricam sob encomenda, as quais têm papel fundamental na atual economia brasileira. Em resposta a essa demanda, o presente trabalho objetiva apresentar uma abordagem para o PCP denominada Controle de Carga (Workload Control WLC). Essa abordagem é reconhecidamente um método com potencial para trazer melhorias no lead time, no estoque em processo e na pontualidade de entregas em ambientes que fabricam sob encomenda (Make-To-Order MTO). Primeiramente, o artigo apresenta a abordagem WLC, revisando e discutindo os principais assuntos tratados pela literatura internacional na área. Após isso, o desempenho do WLC é avaliado por meio de simulação. Os resultados mostram o potencial de melhorias no lead time e nas ordens em atraso que o WLC pode trazer a pequenas e médias empresas que fabricam sob encomenda. Dessa forma, o presente trabalho pretende contribuir tanto para a teoria a respeito de tal abordagem, praticamente introduzindo tal assunto na literatura brasileira, como para a prática, fornecendo e demonstrando, por meio de simulação, aos gerentes de PCP, uma alternativa para suas empresas trabalharem rumo a baixos lead times e de acordo com modernos paradigmas de produção, tais como o Lean Manufacturing e o Quick Response Manufacturing.
Palavras-chave: Controle de carga. Planejamento e controle da produção. Redução do lead time. Pequenas e médias empresas. Fabricação sob encomenda.
ABSTRACT
The majority of Production Planning and Control (PPC) literature is focused on the study and development of solutions for large companies, especially in repetitive environments. Therefore, there are few specific PPC solutions available in the literature for small and medium sized companies (SMC) operating in a Make -to-Order (MTO) environment. This paper presents the Workload Control (WLC), which is a useful PPC approach designed for small sized Make-to-Order companies. According to the literature, such approach has the potential to reduce lead time, work in process, and to provide a better tardiness performance in MTO companies. Firstly, the paper presents the WLC approach reviewing and discussing the main WLC aspects addressed in the literature. The objective is to introduce the concept and present the recent developments to fellow researchers and practitioners. The performance of WLC is then assessed by simulation. The results underline the potential of WLC to bring major improvements in terms of lead time and tardiness performance supporting small and medium sized MTO companies. Therefore, this study aims at contributing to PPC academic and practical areas by introducing WLC approach concepts to Brazilian researchers and managers showing its benefits and potential to help national companies in their efforts towards lead time reduction and best tardiness performance according to modern manufacturing paradigms such as Lean Manufacturing and Quick Response Manufacturing.
Keywords: Workload control. Production planning and control. Lead time reduction. Small and medium companies. Make-to-order.
1 Introdução
De acordo com Fernandes e Godinho Filho (2010), Planejamento e Controle da Produção (PCP) envolvem uma série de decisões com o objetivo de definir o que, quanto e quando produzir, comprar e entregar, além de quem e/ou onde e/ou como produzir. Ainda de acordo com esses autores, o Planejamento da Produção (PP) se ocupa com decisões agregadas em um universo de médio prazo (em geral entre 3 e 18 meses). Já o Controle da Produção (CP) é responsável por regular (planejar, coordenar, dirigir e controlar), no curto prazo (geralmente até 3 meses), o fluxo de materiais em um sistema de produção por meio de informações e decisões para execução. Algumas das principais atividades do PCP, de acordo com um grande número de autores da área (BURBIDGE, 1990; CORREA; GIANESI; CAON, 2008; FERNANDES; GODINHO FILHO, 2010), são as seguintes: i) programar a produção em termos de itens finais, determinando prazos aos clientes (para o caso Make to Order (produção sob encomenda)); ii) programar ou organizar/explodir as necessidades em termos de componentes e materiais; iii) controlar a emissão/liberação das ordens de produção e compra, determinando se as ordens devem ser liberadas e quando; e, iv) programar/sequenciar as operações nas máquinas (na literatura esta atividade é chamada por alguns autores de dispatching e por outros scheduling - para uma discussão sobre estes dois termos ver Melnyk, Vickery e Carter (1986)).
Uma abordagem que se propõe a realizar todas as 4 atividades do CP mencionadas acima em conjunto é o Workload Control (WLC). Ele simultaneamente controla o lead time dos produtos, a capacidade produtiva e o estoque em processo (Work-In-Process WIP), integrando produção e vendas em um sistema hierárquico de cargas de trabalho o qual "protege" a taxa de saída do processo (throughput) de várias formas de variabilidades (e.g., TATSIOPOULOS; KINGSMAN, 1983; KINGSMAN; TATSIOPOULOS; HENDRY, 1989). Por isso, conforme Hopp e Spearman (2004), o WLC é totalmente coerente com modernos modelos de gestão da manufatura, como, por exemplo, a Produção Enxuta (Lean Manufacturing LM) e o Quick Response Manufacturing (SURI, 1998, 2010). Também, pode-se dizer que o WLC é um sistema que guarda forte relação com o heijunka, o qual busca nivelar a produção por tipo e quantidade de produto ao longo de um horizonte de tempo (MARCHWINSKI; SHOOK; SCHROEDER, 2008).
O foco do presente trabalho são pequenas e médias empresas que fabricam sob encomenda (Make To Order MTO). Isso se deve ao fato de que, apesar da maioria dessas empresas saber que devem melhorar seu PCP a fim de obter reduções de lead time e de WIP (e com isso, maior lucratividade), elas simplesmente não sabem como fazer isso, uma vez que a grande maioria de pesquisas e soluções para o PCP é focada em grandes empresas com ambiente repetitivo (MUDA; HENDRY, 2003). Além disso, segundo o Fundo Monetário Internacional (FMI), o Brasil será em 2011 a sétima economia mundial (Folha online, 2010). Nesse contexto, as pequenas e médias empresas ocupam papel de destaque, uma vez que, além de representar importante fatia do PIB (aproximadamente 20%), ainda contribuem de forma contundente na geração de empregos (aproximadamente 70% dos postos de trabalho).
A moderna literatura em Gestão de Operações (incluindo principalmente o PCP) tem clamado por soluções contingenciais, focadas em ambientes e situações específicas e com grande potencial de aplicabilidade prática (SOUSA; VOSS, 2008). Tenhiälä (2010) sugere que o sucesso na implementação de um conceito de PCP é diretamente relacionado ao grau de aderência de tal solução com as características do sistema e do ambiente produtivo. O presente trabalho pretende contribuir nessa direção, apresentando a abordagem WLC como uma alternativa que atenda às necessidades de pequenas e médias empresas que operam em ambiente MTO (ver ZÄPFEL; MISSBAUER, 1993; STEVENSON; HENDRY; KINGSMAN, 2005).
O WLC é uma abordagem para o PCP elaborada primordialmente para ambientes sob encomenda (MTO). Apesar de já estar sendo estudado pela literatura há algum tempo, com atenção especial nos últimos anos (ver LAND; GAALMAN, 2009; FREDENDALL; OJHA; PATTERSON, 2010; THÜRER; SILVA; STEVENSON, 2010), tal tema é praticamente desconhecido e não estudado/pesquisado no Brasil. Dessa forma, tal conceito ainda está longe de ser colocado na prática em empresas brasileiras, apesar de evidências empíricas que mostram os benefícios que o WLC traz para empresas MTO (por exemplo, BECHTE, 1994; HENDRY et al., 2008). É exatamente nesse contexto que o presente trabalho se insere, objetivando apresentar o WLC para a comunidade científica e empresarial brasileira. Para alcançar tal objetivo, o presente trabalho primeiramente define e apresenta uma revisão dos pontos importantes a respeito do WLC atualmente tratados pela literatura internacional na área. A seguir, uma simulação é realizada, objetivando avaliar o desempenho do WLC em um ambiente MTO. Os resultados mostram o potencial do WLC para o PCP de pequenas e médias empresas brasileiras que fabricam sob encomenda.
O restante do artigo é organizado da seguinte forma: a seção 2 apresenta uma revisão dos principais conceitos e tópicos discutidos atualmente sobre o WLC; a seção 3 apresenta o modelo de simulação utilizado; a seção 4 mostra os resultados da simulação realizada e, na seção 5, são apresentadas as conclusões do presente trabalho.
1.1 WLC: conceituação básica e principais tópicos tratados na literatura recente
WLC dá suporte simultaneamente ao controle de estoque, capacidade e lead time produtivo por meio da integração de produção e vendas em um sistema hierárquico de cargas de trabalho (TATSIOPOULOS; KINGSMAN, 1983; KINGSMAN; TATSIOPOULOS; HENDRY, 1989; KINGSMAN et al., 1993; KINGSMAN, 2000). Essa hierarquia de cargas de trabalho é formada por 3 níveis:
i. Carga de trabalho do chão de fábrica ou WIP;
ii. Carga de trabalho planejada: É formada por todas as ordens aceitas; portanto essa carga inclui a carga de trabalho do chão de fábrica (WIP) e a carga de trabalho formada pelas ordens vindas do planejamento de mais alto nível que já foram aceitas (pre-shop pool); e;
iii.Carga de trabalho total: é formada por todas as ordens aceitas somadas a uma porcentagem que reflete a probabilidade da empresa conseguir novos pedidos. Essa probabilidade, baseada no histórico da empresa em ganhar novos pedidos, é chamada na literatura internacional a respeito de WLC de strike rate.
Note que o presente trabalho utiliza a palavra "pedido" quando se trata de ordens não confirmadas, sendo que o termo ordem é usado para ordens já confirmadas.
A Figura 1 representa a estrutura básica do WLC. O WLC é formado por dois níveis de controle, denominados (a) Gestão dos pedidos de clientes (Customer Enquire Management CEM); e (b) Liberação das ordens (Order Release OR).
A carga de trabalho planejada é controlada pelo CEM, o qual dá suporte à determinação das datas de entrega (Due ou Delivery Date DD) e à determinação da probabilidade da empresa em conseguir novos pedidos. É exatamente a explícita consideração dessa probabilidade que adiciona uma dimensão estratégica ao processo de determinação de lead times do WLC (DUENYAS; HOPP, 1995; KINGSMAN; MERCER, 1997), fornecendo à empresa um diferencial competitivo frente aos seus concorrentes. A carga de trabalho do chão de fábrica é controlada por mecanismos de liberação de ordens (OR). Esses mecanismos liberam ordens para o chão de fábrica de modo que a carga de trabalho no chão de fábrica seja mantida em um nível constante e as datas de entrega (DD) sejam cumpridas. Além disso, uma abordagem abrangente de PCP baseado no WLC integra também as funções de gestão de materiais e programação da produção (dispatching).
Para ilustrar a abordagem WLC, imagine o seguinte exemplo: um cliente pede uma cotação de preço e data de entrega para um pedido. O nível 1 do WLC (CEM) determina a data de entrega de acordo com a capacidade disponível no chão de fábrica. Dessa forma, a capacidade produtiva pode ser ajustada em função dos pedidos. O WLC também dá suporte à determinação da taxa de sucesso na obtenção de novos pedidos (strike rate SR). De acordo com a data de entrega e o preço, o cliente aceita ou rejeita o pedido. Caso o pedido seja aceito, os materiais são adquiridos (comprados ou produzidos). Quando os materiais estiverem disponíveis, a ordem passa a estar disponível para liberação. Tal ordem é liberada quando a capacidade do chão da fábrica permitir. Dessa forma, a entrada de uma ordem de produção no chão de fábrica é controlada por regras de liberação. Finalmente, a ordem é produzida e entregue ao cliente.
Para uma revisão da literatura a respeito do WLC, ver Thürer, Stevenson e Silva (2011). A seguir, detalhamos os dois níveis do WLC: CEM e OR.
1.2 Gestão de pedidos de clientes (CEM)
Em empresas MTO, fornecer prazos de entrega é um processo de importância estratégica (KINGSMAN; TATSIOPOULOS; HENDRY, 1989; HOPP; STURGIS, 2000; STEVENSON; HENDRY; KINGSMAN, 2005) que deve ser realizado para cada pedido individualmente, uma vez que os requisitos de cada pedido podem ser bastante diferentes. Em tais situações, a habilidade de fornecer aos clientes datas de entrega ao mesmo tempo curtas e realísticas é fundamental (BERTRAND, 1983a,b; SPEARMAN; ZHANG, 1999). Quando um pedido de cotação é recebido pela empresa, o WLC determina as datas de entrega por meio de uma análise comparativa entre a capacidade existente e a requerida, simulando a entrada do novo pedido dentro da carga total existente de tal forma que tal pedido possa ser produzido de forma lucrativa e na data devida (TATSIOPOULOS; KINGSMAN, 1983; HENDRY; KINGSMAN; CHEUNG, 1998; KINGSMAN, 2000).
Dois tipos de pedidos são considerados dentro do CEM: pedidos com datas de entrega negociáveis e, portanto, proposto pela empresa; e, pedidos com data devida fixa estabelecida pelo cliente. No primeiro caso, uma data de entrega possível é determinada por meio de programação para frente a partir da data de liberação mais cedo do pedido (pedido já confirmado e materiais disponíveis) (KINGSMAN; TATSIOPOULOS; HENDRY, 1989; KINGSMAN, 2000). Quando necessário, a capacidade pode ser aumentada ou pode-se dar prioridade a um pedido de tal forma que a data de entrega fornecida pela empresa seja aceita pelo cliente. Por meio da combinação interativa do controle de capacidade com a probabilidade da empresa fechar novos pedidos, pode-se determinar os preços e as datas devidas de forma a maximizar a probabilidade de ganhar o pedido e manter a lucratividade. No segundo caso, o cálculo da possibilidade de cumprir a data requerida pelo cliente é feito por meio de programação para trás. Dessa forma, encontra-se uma data de início planejada (isto é, a data em que o pedido precisa ser liberado para que esse seja entregue no prazo). As seções 2.1.1 e 2.1.2 a seguir discutem, brevemente, a literatura a respeito da determinação da strike rate e também das regras para determinação das datas de entrega mais utilizadas no ambiente WLC.
1.2.1 Determinação da taxa de sucesso na obtenção de novos pedidos (strike rate SR)
A pesquisa a respeito do CEM dentro do contexto do WLC é focada basicamente em um dos três seguintes assuntos:
i. Determinação dos lead times em função da carga de trabalho e capacidade existente (por exemplo BERTRAND, 1983a,b);
ii. Avaliação de quais pedidos devem ser aceitos (PHILIPOOM; FRY, 1992; CORTI; POZZETTI; ZORZINI, 2006);
iii. Ajuste de capacidade para auxiliar a aceitação de um novo pedido (por exemplo, HENDRY; ELINGS; PEGG, 1993; HENDRY; KINGSMAN; CHEUNG, 1998).
Apesar dos três tópicos serem vitais e cada um deles mostrar efeito positivo no desempenho do WLC, eles devem ser considerados de forma conjunta. Isso pode ser feito por meio do cálculo da taxa de sucesso da empresa em conseguir novos pedidos (KINGSMAN et al., 1996; KINGSMAN; MERCER, 1997). Na prática, a grande maioria das empresas MTO não rejeita um novo pedido dos clientes; ao invés disso, a empresa determina um prazo longo de entrega ou cobra bem mais caro por uma data de entrega mais curta.
Conhecer a relação entre lead time, preço e strike rates fornece uma dimensão estratégica às tarefas de determinação das datas de entrega e precificação. A abordagem WLC fornece uma forma simples para a determinação e atualização da taxa de sucesso da empresa em obter novos pedidos em relação a datas de entrega e preço baseado no histórico de pedidos. A seguir são mostradas ambas as fases:
Fase 1 - Determinação da taxa de sucesso: Primeiramente, deve-se dividir o mercado no qual a empresa compete em segmentos (também denominados clusters). Cada um desses segmentos é escolhido exatamente em função das taxas de sucesso e probabilidades de conseguir novos pedidos (KINGSMAN et al., 1996; KINGSMAN; MERCER, 1997). Dessa forma, estarão agrupados em um mesmo segmento potenciais pedidos com praticamente a mesma probabilidade de se tornarem pedidos reais. Tal segmentação pode considerar, por exemplo, o tamanho do pedido ou a relação da empresa com um cliente;
Fase 2 - Atualização do valor da taxa de sucesso: Depois de os segmentos e as taxas de sucesso terem sido definidos, deve haver um processo para atualização de tais taxas. Operacionalmente, isso é feito por meio da utilização de uma matriz 2 × 2 baseada na relação entre mark up e lead time de entrega (KINGSMAN et al., 1993). Basicamente essa matriz traz os valores absolutos dos pedidos conseguidos (sucesso) pela empresa para cada combinação de mark up e lead time de entrega. Mark up é um índice normalmente utilizado em Economia e Contabilidade, que pode ser calculado conforme a Equação 1 a seguir.
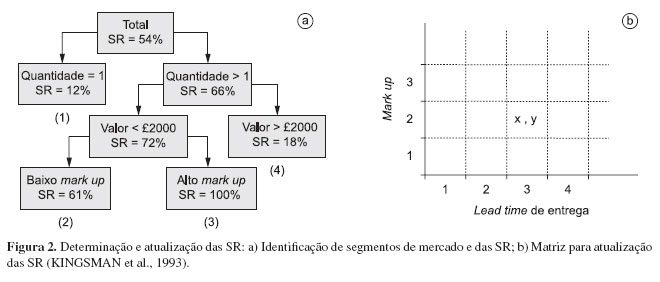
Para ilustrar como é feita a determinação e atualização da taxa de sucesso, vamos usar um exemplo mostrado em Kingsman et al. (1996, 1993). A Figura 2a mostra um exemplo de segmentação de mercado e a Figura 2b mostra um exemplo da matriz para atualização da taxa de sucesso.
Na Figura 2a, vê-se que Kingsman et al. (1996) identificou quatro segmentos de mercado, cada um com uma diferente taxa de sucesso (SR) na obtenção de novos pedidos. Tais SR são determinadas baseadas no histórico de cada segmento em conseguir novos pedidos. Dessa forma, no exemplo dado, pedidos unitários, identificados na Figura 2a, são caracterizados como segmento (1), com SR de 12%. Os pedidos com quantidade maior do que 1 e valor menor do que £2,000 foram divididos em dois segmentos de acordo com a taxa de sucesso: o segmento (2) representa os pedidos com baixo mark-up, tendo SR = 61%; e o segmento (3) abrange os pedidos com alto mark-up. Esse segmento tem SR = 100%. Finalmente, o último segmento é formado pelos pedidos de valor maior do que £2,000 (segmento (4) na Figura 2a). Esse último segmento apresenta SR = 18% independentemente do mark-up.
Uma vez definidos os SR para cada segmento de mercado, utiliza-se uma matriz para se atualizar os valores de SR. Isso é feito da seguinte forma (Figura 2b):
Se um pedido, em um dado segmento de mercado com um mark-up (x) e lead time de entrega (y), é conseguido, então a célula (x,y) da matriz é aumentada em uma unidade, aumentando, em termos absolutos, o número total de pedidos conseguidos pela empresa para a combinação (x,y). Também as células com mark-up e lead time menor do que (x,y) são aumentadas em uma unidade, uma vez que, se a empresa conseguiu um novo pedido para a combinação (x,y), com certeza também o conseguiria para valores de mark up e lead time menores;
Se o pedido não é conseguido, a matriz não é atualizada.
A taxa de sucesso para um pedido com um mark-up (x) e lead time (y) em um dado período de tempo é dado pela divisão entre cada célula (x,y) e o número total de cotações realizadas.
1.2.2 Determinação das datas de entrega (WLC DD setting rules)
As regras do WLC para a determinação das datas de entrega utilizam informações detalhadas a respeito das cargas de trabalho (ver THÜRER et al., 2011). Inicializa-se tal determinação a partir da data de liberação mais cedo do pedido (Earliest Release Date ERD). Essa data corresponde ao momento em que todos os materiais estão disponíveis e o pedido já pode ser liberado no chão de fábrica (OCD0). A data de finalização de uma operação i em um centro de trabalho j (Operation Completion Date OCDi) é dada pela Equação 2.
Vê-se que o cálculo de OCDi é realizado em função de 3 fatores:
O OCD da operação imediatamente anterior (OCDi-1);
O tempo de processamento da operação i (tproc_i);
Uma estimativa do tempo de espera da operação i no centro de trabalho j, dada pelos fatores k e F (Wt,j,Ct,j). O fator k representa o menor tempo de fluxo permitido e o fator F (Wt,j,Ct,j) representa o tempo de espera estimada extra de um pedido na operação i em função da carga de trabalho (Wt,j) e da capacidade (Ct,j) existentes no centro de trabalho j no instante futuro t.
O OCD da última operação de um pedido é a data de entrega desse pedido (DD).
A principal diferença entre as várias abordagens existentes na literatura para a determinação do F (Wt,j,Ct,j) recai sobre dois pontos fundamentais:
O tipo de informação a respeito da carga de trabalho: dois tipos podem ser utilizados - carga não cumulativa e cumulativa (ou acumulada);
A consideração ou não de faltas (backlog).
Regras para determinação das datas de entrega considerando carga não cumulativa são propostas em Bobrowski (1989), Ahmed e Fisher (1992), Kim e Bobrowski (1995), e Cigolini, Perona e Portioli (1998). Já regras para determinação das datas de entrega considerando carga de trabalho cumulativa são apresentadas em Bertrand (1983a,b) e Bechte (1994). Thürer et al. (2011) recentemente avaliaram o desempenho de ambos os tipos de regras, mostrando que regras que consideram faltas têm melhor desempenho com relação a lead time e atraso do que regras que não consideram faltas.
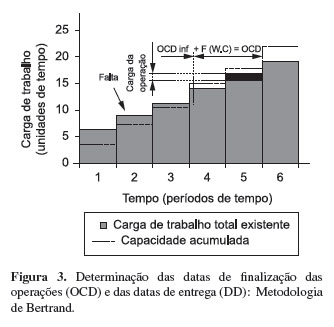
Além disso, Thürer et al. (2011) mostraram que a abordagem proposta por Bertrand (1983a,b) apresentou os melhores resultados. Por isso, é exatamente essa regra que é aplicada na simulação realizada no presente estudo. Essa abordagem utiliza carga cumulativa e considera faltas. A Figura 3 ilustra essa abordagem. A carga acumulada a ser alocada é dada pela carga de trabalho total existente (soma da carga de trabalho do chão de fábrica (WIP), da carga de trabalho formada pelas ordens vindas do planejamento de mais alto nível que já foram aceitas (pre-shop pool) e de uma porcentagem de pedidos não confirmados dados pela taxa de sucesso da empresa em obter novos pedidos - strike rate). Portanto, tem-se que a strike rate está diretamente relacionada ao processo de determinação de datas de entrega. Isso faz com que se estabeleça um loop de controle que permite à carga que está entrando no sistema ser suavizada nos níveis mais altos de planejamento, aplicando, portanto, nesses níveis os princípios do heijunka. Para levar em conta a falta, a carga de uma operação é subtraída da carga acumulada quando a operação é finalizada.
Basicamente, na metodologia de Bertrand, o horizonte de planejamento é dividido em períodos de tempo (time buckets). A partir disso, iniciando em ERD (OCD0), a carga de trabalho total existente é alocada dentro da capacidade acumulada em cada período de tempo da seguinte forma:
i. A data de finalização planejada de uma operação i em um centro de trabalho j é determinada assumindo que a capacidade é infinita. Dessa forma, tal data é denominada Data de Finalização Planejada da Operação com carga infinita (OCDinf). Tal data é dada pela Equação 3;
ii. Se o período de tempo dentro do qual o OCDinf deve ser alocado tem capacidade disponível suficiente para acomodar tal operação sem violar as restrições de capacidade, a operação é alocada a esse período de tempo;
iii. Se não há capacidade suficiente para tal alocação, o próximo período de tempo é utilizado até que a carga total da operação possa ser inteiramente alocada. A carga total alocada é na verdade o resultado da multiplicação da carga total dos pedidos pela strike rate. Somente no momento em que o cliente aceita as condições de prazo e preço é que as cargas passam a contar inteiramente como sendo as cargas dos centros. Dessa forma, durante o período de tempo da cotação, somente uma porcentagem da carga dos pedidos ainda não confirmados (dada pela strike rate) entra no cálculo da carga total dos centros de trabalho. O fator F(Wt,j,Ct,j) representa o tempo de fluxo (espera) extra necessário devido às limitações de carga já alocadas ao centro e a capacidade do centro. Tal fator faz aumentar o valor do OCDinf. Dessa forma, tal fator é dado pelo tempo de finalização obtido (OCDi), menos a data de finalização planejada (OCDinf). Portanto: F(Wt,j,Ct,j) = OCDi - OCDinf;
iv. Esse procedimento é repetido até que todas as operações tenham sido alocadas.
Deve-se atentar ao fato de que as regras para a determinação das datas de entrega fornecem estimativas dos lead times, ou seja, o objetivo é se obter um atraso igual a zero. Como a variabilidade do atraso nunca pode ser zero, um buffer de lead time deve ser adicionado a fim de que o desempenho de entrega não seja comprometido (BERTRAND, 1983a,b). Portanto, por definição, as regras para determinação das datas de entrega dentro do WLC fazem uma distinção entre data de entrega interna e data de entrega externa. A data de entrega interna é o OCD da última operação, já a data de entrega externa acrescenta à data de entrega interna um estoque de tempo para reduzir os efeitos da variabilidade. Para uma discussão a respeito das vantagens dessa distinção entre data de entrega interna e externa e comparação entre tal abordagem e outras abordagens alternativas (por exemplo, assumir k como sendo um fator não relacionado com os lead times reais), ver Enns (1995) e Hopp e Sturgis (2000).
1.3 Liberação de ordens (OR)
Altos níveis de estoque em processo e o resultante "congestionamento" no chão de fábrica aumenta o risco de obsolescência e danos ao produto, influencia negativamente a qualidade e causa altos lead times. Dentro da abordagem WLC, as ordens não são imediatamente liberadas para o chão de fábrica; elas ficam retidas na chamada pre-shop pool, sendo liberadas a partir de níveis pré-determinados de carga existentes no chão de fábrica, níveis esses denominados "limites" ou "normas" (workload norm). Controlar a liberação das ordens "protege" o chão de fábrica contra a variabilidade, reduz o WIP e o lead time, tornando o fluxo produtivo visível, facilitando a identificação dos desperdícios. Dessa forma, o WLC, que integra OR e CEM com uma efetiva programação da produção e gestão de materiais, consegue contribuir mesmo em um ambiente job shop caracterizado pela alta variedade de produtos. Os métodos para OR dentro do WLC são basicamente divididos em dois grupos:
Métodos que liberam as ordens do pre-shop pool de forma periódica; e
Métodos que liberam as ordens do pre-shop pool de forma contínua.
Ambos os grupos são discutidos, respectivamente, nas seções 2.2.1 e 2.2.2. Na seção 2.2.3 é mostrada uma abordagem que combina ambas as formas de liberação. Para outras abordagens e formas de classificação de OR, ver Philipoom, Malhorta e Jensen (1993), Wisner (1995), Bergamaschi et al. (1997), Sabuncuoglu e Karapinar (1999) e Fredendall, Ojha e Patterson (2010).
1.3.1 Métodos de liberação periódica
Tais métodos tomam a decisão de liberar novas ordens para o chão de fábrica em intervalos de tempo periódicos. A grande parte dos métodos de liberação periódica apresenta algumas características comuns (LAND; GAALMAN, 1998):
As ordens na pre-shop pool são consideradas para liberação de acordo com regras tradicionais, como por exemplo, Data de Entrega Mais Cedo (Earliest Due Date EDD), menor folga ou Data de Liberação Planejada (Planned Release Date PRD);
A carga de cada operação de tal ordem é somada à carga já existente em todos os centros de trabalho pertencentes ao roteiro da ordem em questão. Se essa(s) nova(s) carga(s) for(em) menor que o limite pré-determinado (workload norm), a ordem é liberada e a carga das operações da ordem, atribuída à carga dos centros. Se pelo menos um dos limites pré-determinados forem excedidos, então se aguarda o próximo período de liberação. Tal procedimento é repetido até que todas as ordens tenham sido consideradas.
A principal diferença entre os diversos métodos de revisão periódica é como o acréscimo de carga nos centros de trabalho é considerado (LAND; GAALMAN, 1998), ou melhor, como as cargas direta e indireta são tratadas. Carga direta é a carga existente na fila de um centro de trabalho e carga indireta é aquela carga que ainda não chegou ao centro de trabalho. Por exemplo, suponha uma ordem com 3 operações a serem feitas em três centros de trabalho A, B, C, exatamente nessa sequência. Quando o pedido é liberado, sua carga passa a ser contabilizada nos 3 centros de trabalho, porém ele está, num primeiro momento, somente sendo processado no centro de trabalho A (carga direta). A carga dos centros B e C para esse pedido é a chamada carga indireta. Existe uma incerteza a respeito do momento da real chegada de tais cargas nesses centros. Portanto, tal consideração pode levar a não liberação de uma ordem para um centro devido a sua carga indireta, podendo resultar em uma ociosidade no centro de trabalho devido a uma carga que vai chegar em algum momento. Esse fenômeno é denominado por Land e Gaalman (1998) de ociosidade prematura do centro de trabalho. Tal ociosidade pode ser parcialmente evitada. Bechte (1988, 1994) utilizou um fator de depreciação para estimar a carga direta de uma ordem em um centro de trabalho. Tal fator se baseia na seguinte premissa: quanto mais longe do início do roteiro de uma ordem (mais downstream) um centro de trabalho estiver, menos carga (indireta) deve ser atribuída a esse centro de trabalho. Como tal fator de depreciação utiliza dados históricos, tal abordagem é denominada abordagem probabilística. Uma abordagem alternativa é simplesmente somar a carga de uma operação à carga do centro, sem considerar a posição da operação no roteiro da ordem (portanto não diferenciando carga direta e indireta). Tal abordagem é chamada abordagem atemporal ou abordagem da carga agregada clássica. Uma extensão importante de tal abordagem foi apresentada por Land e Gaalman (1996). Essa abordagem é denominada abordagem da carga agregada corrigida. Tal abordagem estima a carga direta de forma similar à abordagem probabilística, mas transformando a carga indireta de forma simplificada: a carga de trabalho atribuída a um centro de trabalho é a carga de trabalho total dividida pela posição do centro de trabalho no roteiro da ordem.
Das abordagens periódicas existentes na literatura, estudos mostrados em Oosterman, Land e Gaalman (2000), mostraram que as abordagens de carga agregada corrigida e probabilística apresentaram melhor desempenho.
1.3.2 Métodos de liberação contínua
Utilizar um método de liberação contínua significa que a decisão sobre a liberação de um novo pedido no chão de fábrica deve ser feito em qualquer momento (ao invés de periodicamente uma vez por dia, por semana, etc.). Normalmente, a liberação é iniciada por um evento no chão de fábrica, tal como: i) a carga de um equipamento gargalo cair abaixo de um determinado nível (GLASSEY; RESENDE, 1988; ENNS; PRONGUE COSTA, 2002); ii) a carga de um centro de trabalho cair abaixo de um determinado nível (MELNYK; RAGATZ, 1989); ou, iii) a carga do chão de fábrica como um todo cair abaixo de um determinado nível (MELNYK; RAGATZ, 1989; QI; SIVAKUMAR; GERSHWIN, 2009).
As ordens que serão liberadas do pre-shop pool são escolhidas por meio de regras, da mesma forma que nos métodos periódicos (por exemplo, EDD, PRD, dentre outras). No caso (iii), a ordem também pode ser liberada segundo a regra denominada Work-In-Next-Queue (WINQ), a qual seleciona para ser liberada a ordem cuja primeira operação do seu roteiro produtivo contém o centro de trabalho com a menor fila (estoque em processo - WIP). As ordens são liberadas até que a carga de trabalho exceda o nível de liberação. Melnyk e Ragatz (1989) comparou vários métodos de liberação contínua e identificou que os métodos de liberação contínua que consideram informações a respeito da carga dos centros de trabalho apresentam melhor desempenho em job shops. Esse resultado foi mais tarde confirmado por Hendry e Wong (1994), e Sabuncuoglu e Karapinar (1999).
1.3.3 LUMS COR - combinando as abordagens de liberação contínua e periódica
De acordo com a revisão da literatura realizada pelos autores do presente trabalho, somente um método combina as liberações periódica e contínua. Essa abordagem, proposta por Hendry e Kingsman (1991), é conhecida como Lancaster University Management School Order Release ou LUMS OR. Nessa abordagem, liberação periódica é combinada com um mecanismo contínuo que tenta evitar que um centro de trabalho fique ocioso (starvation avoidance mechanism) devido a uma possível alta carga indireta (ociosidade prematura, conforme descrito na seção 2.2.1). Dessa forma, tal abordagem libera novos pedidos para o chão de fábrica periodicamente, porém, se em algum momento, a carga de trabalho de qualquer centro de trabalho cair para zero, uma ordem é liberada.
O LUMS OR original inclui a abordagem de carga agregada clássica (ou atemporal). Conforme salientado na seção 2.2.1, tal abordagem é considerada inferior comparativamente com abordagens alternativas em uma série de estudos recentes (e.g., OOSTERMAN; LAND; GAALMAN, 2000; THÜRER; SILVA; STEVENSON, 2011). Dadas essas novas evidências, a abordagem da carga agregada corrigida foi adicionada ao LUMS OR. A partir daí, o LUMS OR passou a ser denominado de LUMS COR (LUMS Corrected Order Release).
O exemplo seguinte ilustra o método de liberação LUMS COR e sua capacidade de balancear a produção e evitar a ociosidade prematura nos centros de trabalho. Vamos supor que o pre-shop pool contenha múltiplas ordens com diferentes roteiros e datas de liberação planejadas. Todas as ordens são consideradas para liberação em intervalos periódicos de tempo (por exemplo, uma vez por dia ou por semana). Vamos assumir que as ordens são selecionadas para liberação segundo a regra PRD. A "ordem J" tem a data de liberação planejada (PRD) mais cedo e por isso é a primeira a ser considerada. Tal ordem deve ser trabalhada em três centros de trabalho A, B e C exatamente nessa sequencia. Ao se considerar a liberação da ordem J, utilizando-se o método da carga agregada corrigida, a carga total da ordem J no centro de trabalho A será adicionada à carga do centro de trabalho. Já com relação aos centros de trabalho B e C, somente metade e um terço das cargas desses centros relativos a essa ordem serão atribuídos a ambos os centros, respectivamente. Se qualquer uma dessas novas cargas de trabalho calculadas forem maiores do que o limite pré-determinado de carga de qualquer um dos centros de trabalho (A, B ou C), a ordem J não é liberada e continua no pre-shop pool. Caso tal violação não ocorra, a ordem J é liberada. Portanto, o método realiza o balanceamento da carga no chão de fábrica. Porém, se em algum momento do tempo, a carga de algum centro de trabalho cai a zero, então uma liberação é feita. Por exemplo, se o centro de trabalho A está sem trabalho, todas as ordens no pre-shop pool cuja primeira operação é no centro de trabalho A passam a ser candidatas à liberação. A ordem selecionada é a que apresenta o PRD mais cedo. A carga de tal ordem é atribuída também por meio da abordagem da carga agregada corrigida.
2 Modelo de simulação
2.1 Características do chão de fábrica simulado
Um modelo de simulação de um job shop puro (MELNYK; RAGATZ, 1989) foi desenvolvido utilizando-se o módulo SimPy© do Python©. O ambiente contém seis centros de trabalho, cada um com uma única máquina. A capacidade dos centros de trabalho é mantida constante. O roteiro produtivo dos pedidos tem entre uma a seis operações. O tamanho do roteiro e os centros de trabalho visitados por cada ordem são selecionados aleatoriamente. Todos os centros de trabalho têm a mesma probabilidade de ser utilizado. Além disso, uma ordem necessita no máximo uma vez de um centro de trabalho qualquer.
2.2 Workload Control
2.2.1 Gestão dos pedidos de clientes (CEM)
Por uma questão de simplificação, assume-se que as taxas de sucesso na obtenção de novos pedidos são constantes e iguais a 1. Dessa forma, todas as datas de entrega propostas pela empresa são aceitas pelos clientes e não há perda de pedidos. A fim de se avaliar o efeito do WLC no desempenho da empresa, são simulados cinco diferentes cenários com relação à determinação das datas de entrega. Basicamente, esses cinco cenários se referem a diferentes combinações percentuais de duas situações possíveis:
Situação A (usando WLC): as datas de entrega são determinadas por meio das regras de determinação de datas de entrega do WLC (ou seja, tais datas são definidas internamente), portanto utilizando-se o CEM, conforme visto nas seções 2.1 (mais especificamente na seção 2.1.2);
Situação B (sem a utilização do WLC): as datas de entrega são determinadas utilizando-se um lead time fixo padrão. Essa situação ocorre quando: (i) um cliente tem uma data de entrega fixa e deve ser atendido (essa situação é chamada de data de entrega definida externamente); (ii) mesmo a empresa podendo participar da determinação da data de entrega requerida, ela não o faz, seguindo um lead time padrão fixo (esse caso é seguido por grande parte das empresas MTO na prática).
Dessa forma, os cinco diferentes cenários simulados são:
1) A data de entrega para todas as ordens (100%) é determinada usando-se o WLC;
2) 25% dos pedidos têm as datas de entrega determinadas utilizando-se lead times fixos (sem WLC) e os outros 75% dos pedidos têm suas datas de entrega calculadas utilizando-se o WLC;
3) 50% das ordens têm suas datas de entrega fixadas sem a ajuda do WLC e as outras 50% têm suas datas de entrega calculadas por meio do WLC;
4) 75% das ordens têm suas datas determinadas sem a ajuda do WLC e as outras 25% das ordens têm suas datas de entrega calculadas por meio do WLC;
5) 100% dos pedidos têm suas datas de entrega determinadas sem o auxílio do WLC.
Para os casos de utilização do WLC, as datas de entrega dos pedidos são calculadas utilizando-se a abordagem de Bertrand, apresentada na seção 2.1.2. Os intervalos de tempo (time buckets) foram definidos de forma arbitrária como sendo iguais a 4 unidades. Algumas simulações preliminares (realizadas utilizando-se liberação imediata e datas de entrega calculadas por meio de lead time fixo) indicaram um lead time médio de um pedido como sendo igual a 28 unidades de tempo. Como o número de operações por ordem é aleatório entre 1 e 6, então tem-se que o número médio de operações de uma ordem é igual a 3,5 operações. Como o tempo de processamento de cada operação é assumido como sendo igual a 1 unidade, tem-se que o tempo médio de processamento de um pedido no chão de fábrica é igual a 3,5 unidades de tempo e o tempo médio de espera igual a 24,5 unidades (28 - 3,5). Assumindo-se que o tempo de espera é igualmente distribuído entre os centros de trabalho (job shop puro), tem-se que o tempo de espera médio em um centro de trabalho é igual a 7 unidades de tempo (24,5/3,5). Entretanto, estimar-se o menor tempo de fluxo k como sendo 7 unidades, não permitiria que a regra de determinação de datas de entrega (F(Wt,j,Ct,j)) pudesse ser efetiva em sua tarefa de suavizar a produção. Portanto, assim como a maioria dos estudos presentes na literatura, o presente trabalho definiu o valor k como tendo um valor inferior ao tempo de espera médio, ou seja, k foi definido como sendo igual a 5 unidades.
O controle da liberação de ordens no chão de fábrica reduz o tempo de atravessamento da ordem no chão de fábrica (tempo de throughput), uma vez que retém as ordens na pre-shop pool. Para programar as operações, o tempo que a ordem espera na pre-shop pool deve ser considerado (BERTRAND, 1983a). Isso significa que a data de liberação mais cedo (ERD) de uma ordem, a partir da qual as operações são programadas, é dada pelo ERD original mais uma estimativa do tempo que a ordem espera para ser liberada. Assume-se que esse tempo é igual a 8 unidades de tempo. Se a liberação for controlada, o menor tempo de fluxo k é assumido como sendo 3 unidades de tempo.
No presente estudo, também distinguimos data de entrega interna e data de entrega externa (ver seção 2.1.2). Portanto, a data de entrega externa (ou lead time de entrega) é dada pela data de entrega interna (ou lead time estimado) mais uma segurança (lead time buffer). Assume-se o valor do lead time buffer como sendo igual a 10 unidades de tempo.
Já para o caso da data de entrega ser calculada a partir de um lead time fixo (sem o uso do WLC), o lead time de entrega segue uma distribuição normal com média de 40 unidades e desvio padrão 10 (σ = 10). A programação para trás segue o método denominado Carregamento Infinito para trás (Backward Infinite Loading BIL). De acordo com tal método, inicia-se a programação a partir da data de entrega determinada menos o lead time buffer (OCD da última operação). A OCD para uma dada operação i no roteiro de um pedido é determinado utilizando-se a Equação 4. A data de liberação planejada (PRD) de uma ordem é dada pela OCD da primeira operação menos a soma do valor k com o tempo de processamento da primeira operação.
O fator k para o método BIL foi definido como sendo igual a 4 unidades de tempo. Portanto, a data de liberação planejada da maioria das ordens ocorre após a data de liberação mais cedo da ordem. Se a data de liberação planejada determinada pela programação BIL ocorrer no passado, automaticamente priorizam-se tais ordens, seguindo-se a regra de despacho OCD, ou seja, colocam-se na frente as ordens com data de finalização planejada mais cedo.
2.2.2 Liberação de ordens
O presente trabalho não considera strike rates. Portanto, o tempo de cotação de um pedido é assumido como sendo igual a zero. Depois das datas de entrega (DDs) e as OCDs terem sido determinadas, as ordens entram na pre-shop pool. Essas ordens são liberadas deixando a pre-shop pool de duas formas: i) ou de forma imediata (Immediate Release - IMM); ii) ou periodicamente (LUMS COR) a cada quatro unidades de tempo, de acordo com as seguintes regras:
1)As ordens na pre-shop pool são escolhidas de acordo com o número de operações no roteiro da ordem e PRD (conforme determinado pela regra de determinação de datas de entrega). Ordens com roteiros mais longos são consideradas para serem liberadas prioritariamente;
2)Dentre as ordens com maior roteiro, inicia-se com as ordens com o menor PRD. Atribui-se a carga de cada operação aos centros de trabalho pertencentes ao roteiro da ordem, seguindo-se a abordagem da carga agregada corrigida (ver Seção 2.2.1). Dessa forma, a carga atribuída a cada centro de trabalho é a carga dividida pela posição do centro de trabalho no roteiro da ordem;
3)Se um ou mais limites pré-determinados de carga forem excedidos pela nova carga originada da ordem, a ordem é mantida na pre-shop pool até a próxima data de liberação. Se os limites não forem violados, a ordem é liberada para o chão de fábrica e suas cargas atribuídas às cargas dos centros de trabalho;
4)Os passos 2 e 3 são repetidos até que todas as ordens na pre-shop pool tenham sido consideradas para alocação.
Adicionalmente, se a carga de algum centro de trabalho se torna zero, uma ordem tendo o referido centro de trabalho como sendo o primeiro em seu roteiro é liberado imediatamente para o chão de fábrica. Caso exista mais de uma ordem a ser liberada, considera-se a ordem com menor PRD. A carga de tal ordem é atribuída também por meio da abordagem da carga agregada corrigida.
Finalmente, é importante salientar que a carga da operação de uma ordem fica alocada a um centro de trabalho até que a operação seja finalizada, ou seja, somente na finalização da operação é que a carga é subtraída da carga total do centro, deixando carga livre para a liberação de outra ordem.
2.2.3 Programação (Dispatching) e gestão de materiais
Para que a regra de determinação das datas de entrega seja efetiva, as regras de programação aplicadas devem estar relacionadas às OCDs determinadas. Isso garante que ocorra o controle de capacidade dos centros de trabalho; em outras palavras: a programação garante que as capacidades sejam utilizadas exatamente nos momentos planejados (ver BERTRAND, 1983a). Portanto, a programação é feita de acordo com as OCDs, isto é, as ordens com datas de finalização planejadas mais cedo são escolhidas. Da mesma forma que em todos os estudos a respeito de WLC (por exemplo, LAND; GAALMAN, 1998; OOSTERMAN; LAND; GAALMAN, 2000; THÜRER; SILVA; STEVENSON, 2010), assume-se que todas as matérias-primas necessárias estão disponíveis. Portanto, nenhuma política especial para gestão de materiais é utilizada.
2.3 Características das ordens
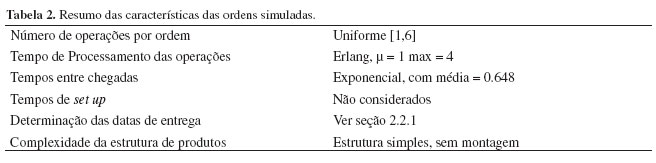
Os tempos de processamento das operações seguem uma distribuição Erlang truncada com média de uma unidade e máximo de 4 unidades. O tempo entre chegadas dos pedidos segue uma distribuição exponencial com média 0,648. O nível de utilização resultante é de 90%. As características gerais do chão de fábrica e das ordens simuladas estão sumarizadas nas Tabelas 1 e 2, respectivamente.
2.4 Projeto de experimentos e medidas de desempenho
Os resultados são obtidos por meio da redução gradual do limite pré-determinado de carga dos centros de trabalho da LUMS COR em uma unidade tempo a partir do tempo 10 até o tempo 4. Esses parâmetros foram identificados como sendo os melhores em experimentos preliminares realizados. Os experimentos são fatoriais completos para LUMS COR, liberação imediata (IMM) e para os diferentes percentuais de determinação de datas de entrega mostradas na seção 3.2.1. A Tabela 3 resume os fatores considerados nos experimentos. Cada experimento foi rodado 50 vezes, sendo que o tempo de simulação de cada "rodada" é 10000 unidades de tempo. O período de aquecimento (warm-up) foi padronizado como sendo de 3000 unidades de tempo. Esses parâmetros permitiram obter a estabilidade nos resultados (steady-state) em um tempo relativamente curto.
As medidas de desempenho consideradas no presente trabalho foram: tempo de throughput ou lead time da manufatura, lead time total, que representa o tempo de throughput somado ao tempo que as ordens esperam na pre-shop pool; e, porcentagem de ordens em atraso.
3 Resultados
Os resultados obtidos para o tempo de throughput e lead time total podem ser visualizados na Figura 4. Em cada curva, os 8 pontos (da direita para a esquerda) representam o seguinte:
O primeiro ponto da direita é o caso de liberação imediata (IMM);
Os outros sete níveis se referem aos 7 limites pré-estabelecidos de carga para o LUMS COR, sendo que, da direita para a esquerda, os pontos representam reduções no limite pré-estabelecido de carga (o último ponto da esquerda em cada linha representa o limite de carga mais apertado).
A partir dos resultados da Figura 4, pode-se ver que ambos, o tempo de throughput e o lead time total, podem ser significantemente reduzidos por meio do uso da abordagem WLC. A grande maioria das empresas job shop que trabalham sob encomenda determina na prática suas datas de entrega por meio da alocação de um lead time fixo ao pedido (situação B no presente trabalho), liberando-os imediatamente para o chão de fábrica, sem controlar tal liberação (liberação imediata). Tal política está representada na Figura 4 como sendo o ponto mais à direita da curva 100% sem WLC (lead time fixo). A comparação entre tal política regularmente utilizada pelas empresas na prática e a utilização do WLC traz os seguintes resultados:
Desempenho: o WLC permitiu aos lead times totais serem reduzidos em até 20% e os tempos de throughput em até 41%, para um mesmo limite pré-estabelecido de carga. Dessa forma nota-se claramente o potencial do WLC frente a políticas tradicionalmente utilizadas em empresas MTO;
CEM e OR: Ambos os estágios de controle do WLC apresentam influência significativa no desempenho da abordagem. Quanto maior a porcentagem de pedidos cujas datas de entrega são definidas por meio do CEM do WLC, menores os valores do lead time e dos tempos de throughput. Isso pode ser notado claramente na Figura 4, uma vez que o melhor desempenho é dado pela política 100% WLC, depois 75, 50, 25% WLC e finalmente 100% sem a determinação de datas de entrega dadas pelo WLC, que obteve o pior desempenho. É interessante salientar o desempenho do CEM de forma isolada (comparações dos pontos extremos à direita de cada curva, como liberação imediata, sem OR): comparando-se tais pontos, nota-se claramente o melhor desempenho conforme a maior parte dos pedidos utiliza o CEM do WLC. Portanto conclui-se que o CEM efetivamente balanceia a carga no chão de fábrica, levando a menores lead times totais e tempos de throughput. Já a liberação controlada de ordens no chão de fábrica (OR) permite a melhoria ainda maior do desempenho por meio do controle de WIP no chão de fábrica.
É interessante observar que o tempo de throughput (bem como o lead time) aumenta conforme o limite pré-estabelecido de carga se torna muito pequeno (pontos mais à esquerda das linhas). Isso aparentemente parece contradizer a famosa Lei de Little (LITTLE, 1961), uma vez que normalmente uma menor carga leva a menores valores de WIP e, por consequência, a menores tempos de throughput. Porém o que se tem aqui é o seguinte: quando o limite pré-estabelecido de capacidade é muito pequeno, a maioria das ordens é liberada por meio do mecanismo que não permite que as máquinas fiquem paradas (starvation avoidance mechanism) do LUMS COR. No presente trabalho, decidiu-se que tal liberação de ordens pelo starvation avoidance não deve levar em conta os tamanhos das ordens, uma vez que priorizar ordens grandes faz com que o desempenho geral do sistema seja melhorado, porém, prejudica o desempenho das ordens pequenas (ver THÜRER; SILVA; STEVENSON, 2010). Tal decisão leva a um pior desempenho nos extremos do gráfico e a um valor ótimo intermediário. Portanto, se o limite de carga é muito apertado, o mecanismo de liberação de ordens se transforma automaticamente em um gatilho de liberação contínua de ordens. Como, nesse caso, a seleção de ordens que deixará o pre-shop pool é feita sem se considerar os tamanhos delas, ordens grandes não são favorizadas, o que aumenta o tempo de throughput. Além disso, se o nível de WIP é muito reduzido, as ordens têm que esperar por mais tempo no pre-shop pool e isso aumenta o lead time. Por outro lado, os resultados também significam que o LUMS COR apresenta desempenho satisfatório mesmo em casos de capacidades demasiado limitadas (para os quais os mecanismos de liberação periódicos levariam a ociosidades grandes no chão de fábrica). Portanto, pode-se concluir que o LUMS COR supera o perigo representado pela determinação de níveis de carga muito pequenos; isso com certeza facilita a implementação do WLC na prática.
Finalmente, na Figura 5, é mostrado o percentual de pedidos em atraso, obtido por meio da simulação realizada.
Conforme pode ser visto na Figura 5, os mecanismos de liberação do WLC não somente resultaram em uma melhoria considerável nos tempos de throughput, mas também nos atrasos, sempre comparando-se os resultados com a política padrão regularmente utilizada pelas empresas. Além disso, também é interessante salientar outros resultados:
Desempenho: O percentual de ordens em atraso pode ser reduzido consideravelmente quando se utiliza o WLC (entre 50 e 100%). Portanto, lead times menores e mais confiáveis podem ser prometidos aos clientes no CEM, utilizando-se o WLC, contribuindo para que a empresa tenha um diferencial competitivo importante frente aos concorrentes;
CEM e OR: CEM e a sua regra de determinação das datas de entrega têm uma importância fundamental no desempenho do WLC. Quanto maior a porcentagem de pedidos que utiliza o CEM do WLC, menor o percentual de ordens em atraso (essa porcentagem chega a ser zero para o caso de 100% de pedidos usando o WLC e liberação imediata). Com relação à liberação de ordens (OR), pode-se ver na Figura 5 que para os casos em que a maioria dos pedidos tem suas datas de entrega determinadas por regras de determinação de datas de entrega (linhas 100 e 75% WLC), um limite pré-estabelecido de carga mais alto favorece o desempenho do CEM e a redução do percentual de atrasos. A influência dos mecanismos de OR para esses casos deve ser menor. Já, conforme se aumenta o percentual de ordens cujas datas de entrega são fixas (linhas 50, 25 e 100% sem WLC), um limite um pouco mais apertado de carga favorece a redução do percentual de pedidos em atraso; nesses casos, a influência do mecanismo de OR deve ser maior.
É importante notar-se na Figura 5 que o aumento da porcentagem de ordens em atraso é devido principalmente ao aumento na variabilidade dos tempos médios de atraso. Isso pode ser visto comparando-se os resultados do lead time com os resultados do percentual de atrasos (ou seja, Figuras 4 e 5). Apesar de o lead time continuar caindo (principalmente no caso de um maior percentual de ordens utilizando o CEM), o percentual de ordens em atraso continua subindo. Esse efeito é maior para liberação contínua (ver LAND; GAALMAN, 1998). Isso explica a alta porcentagem de ordens em atraso apesar do baixo lead time nos casos de 100% das datas de entrega das ordens serem determinadas por meio do WLC e limites pré-estabelecidos de carga bastante restritivos.
4 Conclusões
Os resultados do presente trabalho demonstraram que um PCP efetivo começa com uma eficaz Gestão de pedidos de Clientes (CEM) e continua em direção a uma estratégia adequada de liberação de pedidos no chão de fábrica. O WLC representa uma solução apropriada para o complexo processo decisório do PCP em empresas MTO. Tal abordagem permite lead times curtos e confiáveis, melhorando o nível de serviço ao cliente. Nas simulações realizadas, o WLC superou a política tradicional de determinação de datas de entrega e liberação de ordens utilizadas em empresas MTO para os três indicadores utilizados: lead time total, tempo de throughput e porcentagem de pedidos em atraso. Além disso, conforme esperado, o desempenho do WLC melhorou conforme mais pedidos são controlados pelo CEM de tal abordagem. De uma forma geral, os resultados encontrados dão suporte ao argumento de que para que o WLC obtenha todas as suas vantagens, ele deve ser implementado de uma forma abrangente, englobando CEM e OR. Por meio da análise conjunta das capacidades necessárias e disponíveis, o CEM determina a carga de trabalho total para que a demanda possa ser produzida de forma lucrativa. Já a liberação seletiva de ordens de produção, realizada pelo LUMS COR, fornece ao WLC a habilidade de manter a carga de trabalho no chão de fábrica nivelada. Isso faz com que os princípios do heijunka, advindos do Lean Manufacturing, possam ser implementados mesmo em um ambiente não repetitivo.
O WLC, controlando cargas de trabalho e melhorando a confiabilidade, é, portanto, uma ferramenta do PCP que auxilia as empresas a alcançar os princípios dos modernos modelos de gestão da manufatura, tais como Lean Manufacturing e Quick Response Manufacturing. Por exemplo, o Lean Manufacturing é uma abordagem que protege a taxa de saída do sistema (throughput) contra a variabilidade a um mínimo custo de estoque ou capacidade. Nesse estudo, todas as medidas de desempenho do WLC foram alcançadas em um ambiente com capacidade fixa e sem aumentar o lead time de entrega pedido pelo cliente. Melhorias podem ser realizadas por meio de um melhor uso da capacidade existente, sem aumentos adicionais nos custos. Portanto, o WLC tem o potencial de suportar a melhoria nos sistemas de produção da seguinte forma:
Permite um lead time menor, mais previsível e possível;
Permite que a capacidade possa ser controlada e utilizada de forma mais efetiva;
Controla o WIP, resultando em um chão de fábrica mais enxuto; e,
Seus princípios fundamentais são de fácil entendimento e aplicação na prática.
O presente estudo fornece a base para o uso do WLC na prática. Gerentes que desejem adotar tal abordagem devem, portanto, utilizar uma regra de determinação de datas devidas, dentro do CEM, conforme visto na seção 2.1 e também adotar um mecanismo adequado de liberação de ordens, como, por exemplo, o LUMS COR, não se esquecendo de que, conforme visto nas simulações mostradas, a determinação do limite pré-estabelecido de carga é vital para o desempenho do WLC como um todo.
Recebido em 11/5/2011
Aceito em 12/7/2011
Suporte financeiro: FAPESP.
- AHMED, I.; FISHER, W. W. Due date assignment, job order release and sequencing interaction in job shop scheduling. Decision Sciences, v. 23, p. 633-647, 1992. http://dx.doi.org/10.1111/j.1540-5915.1992.tb00409.x
- BECHTE, W. Theory and practise of load-oriented manufacturing control. International Journal of Production Research, v. 26, n. 3, p. 375-395, 1988. http://dx.doi.org/10.1080/00207548808947871
- BECHTE, W. Load-oriented manufacturing control just-in-time production for job shops. Production Planning and Control, v. 5, n. 3, p. 292-307, 1994. http://dx.doi.org/10.1080/09537289408919499
- BERGAMASCHI, D. et al. Order review and release strategies in a job shop environment: A review and a classification. International Journal of Production Research, v. 35, n. 2, p. 399-420, 1997. http://dx.doi.org/10.1080/002075497195821
- BERTRAND, J. W. M. The use of workload information to control job lateness in controlled and uncontrolled release production systems. Journal of Operations Management, v. 3, n. 2, p. 79-92, 1983a. http://dx.doi.org/10.1016/0272-6963(83)90009-8
- BERTRAND, J. W. M. The effect of workload dependent due-dates on job-shop performance. Management Science, v. 29, n. 7, p. 799-816, 1983b. http://dx.doi.org/10.1287/mnsc.29.7.799
- BOBROWSKI, P. M. Implementing a loading heuristic in a discrete release job shop. International Journal of Production Research, v. 27, n. 11, p. 1935-1948, 1989. http://dx.doi.org/10.1080/00207548908942665
- BURBIDGE, J. L. Production Control: a universal conceptual framework. Production Planning and Control, v. 1, n. 1, p. 3-16, 1990. http://dx.doi.org/10.1080/09537289008919289
- CIGOLIN, R.; PERONA, M.; PORTIOLI, A. Comparison of Order Review and Release techniques in a dynamic and uncertain job shop environment. International Journal of Production Research, v. 36, n. 11, p. 2931-2951, 1998. http://dx.doi.org/10.1080/002075498192210
- CORREA, H. L.; GIANESI, I. G. N.; CAON, M. Planejamento, Programação e Controle da produção. 5. ed. São Paulo: Atlas, 2008.
- CORTI, D.; POZZETTI, A.; ZORZINI, M. A capacity-driven approach to establish reliable due dates in a MTO environment. International Journal of Production Economics, v. 104, p. 536-554, 2006. http://dx.doi.org/10.1016/j.ijpe.2005.03.003
- DUENYAS, I.; HOPP, W. J. Quoting Customer Lead Times. Management Science, v. 41, n. 1, p. 43-57, 1995. http://dx.doi.org/10.1287/mnsc.41.1.43
- ENNS, S. T. A dynamic forecasting model for job shop flowtime prediction and tardiness control. International Journal of Production Research, v. 33, n. 5, p. 1295-1312, 1995. http://dx.doi.org/10.1080/00207549508930210
- ENNS, S. T.; PRONGUE COSTA, M. The effectiveness of input control based on aggregate versus bottleneck workloads. Production Planning and Control, v. 13, n. 7, p. 614-624, 2002. http://dx.doi.org/10.1080/0953728021000026258
- FERNANDES, F. C. F.; GODINHO FILHO, M. Planejamento e Controle da Produção: dos fundamentos ao essencial. São Paulo: Atlas, 2010
- FREDENDALL, L. D.; OJHA, D.; PATTERSON, J. W. Concerning the theory of workload control. European Journal of Operational Research, v. 201, n. 1, p. 99-111, 2010. http://dx.doi.org/10.1016/j.ejor.2009.02.003
- FOLHA ONLINE. Brasil será 7ª economia em 2011-projeta fundo monetário internacional. Correio do Estado, 07 nov. 2010. Disponível em: <http://www.correiodoestado.com.br/noticias/brasil-sera-7-economia-em-2011-projeta-fundo-monetario-inter_83943>. Acesso em: 11 maio 2011.
- GLASSEY, C. R.; RESENDE, M.G. Closed-loop job release control for VLSI circuit manufacturing. IEEE Transactions on Semiconductor Manufacturing, v. 1, p. 36-46, 1988. http://dx.doi.org/10.1109/66.4371
- HENDRY, L. C.; ELINGS, P.; PEGG, D. Production planning for an artists studio-A case study. European Journal of Operational Research, v. 64, p. 12-20, 1993. http://dx.doi.org/10.1016/0377-2217(93)90004-7
- HENDRY, L. C.; KINGSMAN, B. G.; CHEUNG, P. The effect of workload control (WLC) on performance in make-to-order companies. Journal of Operations Management, v. 16, p. 63-75, 1998. http://dx.doi.org/10.1016/S0272-6963(97)00011-9
- HENDRY, L. C.; KINGSMAN, B. G. A decision support system for job release in make to order companies. International Journal of Operations and Production Management, v. 11, p. 6-16, 1991. http://dx.doi.org/10.1108/01443579110144655
- HENDRY, L. C. et al. Investigating implementation issues for workload control (WLC): A comparative case study analysis. International Journal of Production Economics, v. 112, p. 452-469, 2008. http://dx.doi.org/10.1016/j.ijpe.2007.05.012
- HENDRY, L. C.; WONG, S. K. Alternative order release mechanisms: a comparison by simulation. International Journal of Production Research, v. 32, n. 12, p. 2827-2842, 1994. http://dx.doi.org/10.1080/00207549408957103
- HOPP, W. J.; SPEARMAN, M. L. To pull or not to pull: What is the question? Manufacturing and Service Operations Management, v. 6, n. 2, p. 133-148, 2004. http://dx.doi.org/10.1287/msom.1030.0028
- HOPP, W. J.; STURGIS, M. L. R. Quoting manufacturing due dates subject to a service level constraint. IIE Transactions, v. 32, p. 771-784, 2000. http://dx.doi.org/10.1080/07408170008967437
- KIM, S. J.; BOBROWSKI, P. M. Evaluating order release mechanisms in a job shop with sequence-dependent set-up times. Production and Operations Management, v. 4, n. 2, p. 163-180, 1995. http://dx.doi.org/10.1111/j.1937-5956.1995.tb00048.x
- KINGSMAN, B. G. Modelling input-output workload control for dynamic capacity planning in production planning systems. International Journal of Production Economics, v. 68, n. 1, p. 73-93, 2000. http://dx.doi.org/10.1016/S0925-5273(00)00037-2
- KINGSMAN, B. G.; MERCER, A. Strike rat matrices for integrating marketing and production during the tendering process in Make-to-Order subcontractors. International Transactions in Operational Research, v. 4, n. 1, p. 251-257, 1997. http://dx.doi.org/10.1111/j.1475-3995.1997.tb00081.x
- KINGSMAN, B. G. et al. Responding to customer enquiries in make-to-order companies: Problems and solutions. International Journal of Production Economics, v. 46-47, p. 219-231, 1996. http://dx.doi.org/10.1016/0925-5273(95)00199-9
- KINGSMAN, B. G. et al. Integrating marketing and production planning in make-to-order companies. International Journal of Production Economics, v. 30-31, p. 53-66, 1993. http://dx.doi.org/10.1016/0925-5273(93)90081-U
- KINGSMAN, B. G.; TATSIOPOULOS, I. P.; HENDRY, L. C. A structural methodology for managing manufacturing lead times in make-to-order companies. European Journal of Operational Research, v. 40, p. 196-209, 1989. http://dx.doi.org/10.1016/0377-2217(89)90330-5
- LAND, M. J.; GAALMAN, G. J. C. Towards simple and robust workload norms. In: WORKSHOP PRODUCTION PLANNING AND CONTROL, 1996, Mons, Belgium. Proceedings.. Mons, 1996. p. 66-96.
- LAND, M. J., GAALMAN, G. J. C. The performance of workload control concepts in job shops: Improving the release method. International Journal of Production Economics, v. 56-57, p. 347-364, 1998. http://dx.doi.org/10.1016/S0925-5273(98)00052-8
- LAND, M. J.; GAALMAN, G. J. C. Production planning and control in SMEs: Time for change. Production Planning and Control, v. 20, n. 7, p. 548-558, 2009. http://dx.doi.org/10.1080/09537280903034230
- MARCHWINSKI, C.; SHOOK, J.; SCHROEDER, A. (Ed.). Lean lexicon: a graphical glossary for lean thinkers. 4th ed. Cambridge: The Lean Enterprise Institute, 2008.
- LITTLE, J. D. C. A proof of the queuing formula L = λW. Operations Research, v. 9, p. 383-387, 1961. http://dx.doi.org/10.1287/opre.9.3.383
- MELNYK, S. A.; RAGATZ, G.L. Order review/release: research issues and perspectives. International Journal of Production Research, v. 27, n. 7, p. 1081-1096, 1989.
- MELNYK, S. A.; VICKERY, S. K.; CARTER, P. L. Scheduling Sequencing and Dispatching-alternative perspectives. Production and Inventory Management, v. 27, n. 2, p. 58-68, 1986. http://dx.doi.org/10.1080/00207548908942609
- MUDA, M. S.; HENDRY, L. The SHEN model for MTO SMEs: A performance improvement tool. International Journal of Operation and Production Management, v. 23, n. 5, p. 470-486, 2003.
- OOSTERMAN, B.; LAND, M. J.; GAALMAN, G. The influence of shop characteristics on workload control. International Journal of Production Economics, v. 68, n. 1, p. 107-119, 2000. http://dx.doi.org/10.1016/S0925-5273(99)00141-3
- PHILIPOOM, P. R.; FRY, T. D. Capacity-based order review/release strategies to improve manufacturing performance. International Journal of Production Research, v. 30, n. 11, p. 2559-2572, 1992. http://dx.doi.org/10.1080/00207549208948176
- PHILIPOOM, P. R.; MALHORTA, M. K.; JENSEN, J.B. An evaluation of capacity sensitive order review and release procedures in job shops. Decision Sciences, v. 24, n. 6, p. 1109-1133, 1993. http://dx.doi.org/10.1111/j.1540-5915.1993.tb00506.x
- QI, C.; SIVAKUMAR, A. I.; GERSHWIN, S. B. An efficient new job release control methodology. International Journal of Production Research, v. 47, n. 3, p. 703-731, 2009. http://dx.doi.org/10.1080/00207540701455335
- SABUNCUOGLU, I.; KARAPINAR, H. Y. Analysis of order review/release problems in production systems. International Journal of Production Economics, v. 62, p. 259-279, 1999. http://dx.doi.org/10.1016/S0925-5273(98)00248-5
- SOUSA, R.; VOSS, C. A. Contingency research in operations management practices. Journal of Operations Management, v. 26, p. 697-713, 2008. http://dx.doi.org/10.1016/j.jom.2008.06.001
- SPEARMAN, M. L.; ZHANG, R. Q. Optimal Lead Time Policies. Management Science, v. 45, n. 2, p. 290-295, 1999. http://dx.doi.org/10.1287/mnsc.45.2.290
- STEVENSON, M.; HENDRY, L. C.; KINGSMAN, B. G. A review of production planning and control: the applicability of key concepts to the make to order industry. International Journal of Production Research, v. 43, n. 5, p. 869-898, 2005.
- SURI, R. Quick response manufacturing: a companywide approach to reducing lead times. Productive Press, 1998. http://dx.doi.org/10.1201/EBK1439805954
- SURI, R. It's about time: the competitive advantage of quick response manufacturing. Productive Press, 2010.
- TATSIOPOULOS, I. P.; KINGSMAN, B. G. Lead time management. European Journal of Operational Research, v. 14, p. 351-358, 1983. http://dx.doi.org/10.1016/0377-2217(83)90235-7
- TENHIÄLÄ, A. Contingency theory of capacity planning: the link between process types and planning methods. Journal of Operations Management, v. 29, n. 1-2, p. 65-77, 2010. http://dx.doi.org/10.1016/j.jom.2010.05.003
- THÜRER, M.; SILVA, C.; STEVENSON, M. Workload control release mechanisms: from practice back to theory building. International Journal of Production Research, v. 48, n. 12, p. 3593-3617, 2010. http://dx.doi.org/10.1080/00207540902922810
- THÜRER, M. et al. Workload control due date setting rules: the key to short and reliable lead times. In: PRODUCTION AND OPERATIONS MANAGEMENT SOCIETY - POMS Conference, 2011. Proceedings.. POMS, 2011.
- THÜRER, M.; SILVA, C.; STEVENSON, M. Optimising workload norms: the influence of shop floor characteristics on setting workload norms for the workload control concept. International Journal of Production Research, v. 49, n. 4, p. 1151-1171, 2011. http://dx.doi.org/10.1080/00207541003604836
- THÜRER, M.; STEVENSON, M.; SILVA, C. Three decades of workload control research: a systematic review of the literature. International Journal of Production Research, p. 1-31, 2011. http://dx.doi.org/10.1080/00207543.2010.519000
- WISNER, J. D. A review of the order release policy research. International Journal of Operations and Production Management, v. 15, n. 6, p. 25-40, 1995. http://dx.doi.org/10.1108/01443579510090318
- ZÄPFEL, G.; MISSBAUER, H. New concepts for production planning and control. European Journal of Operational Research, v. 67, p. 297-320, 1993. http://dx.doi.org/10.1016/0377-2217(93)90287-W
Datas de Publicação
-
Publicação nesta coleção
28 Mar 2012 -
Data do Fascículo
2012
Histórico
-
Recebido
11 Maio 2011 -
Aceito
12 Jul 2011