Modelo de dinâmica de sistemas para o processo de S&OP ampliado

Systems dynamics model for the expanded S&OP process

Resumo

Apesar de o processo de S&OP (Sales and Operations Planning) não ser uma prática nova nas empresas, principalmente naquelas de grande porte, ainda é tema de estudos nas suas práticas e ferramentas computacionais de apoio. Modelos e ferramentas computacionais focadas para o auxílio no processo de S&OP são utilizadas e podem contribuir para a melhoria da qualidade da sua execução e dos seus resultados. As ferramentas mais comuns são aquelas baseadas em planilhas eletrônicas, e as mais sofisticadas, em técnicas de pesquisa operacional inseridas em sistemas APS (Advanced Planning Systems). A partir da revisão bibliográfica realizada sobre teoria e técnicas computacionais usadas para o auxílio do processo de S&OP, foi identificada a ausência de estudos relacionados ao uso de Dinâmica de Sistemas (System Dynamics). Adicionalmente, a revisão aponta a necessidade de estudos relacionados à integração de análise econômica e financeira durante a elaboração dos planos agregados e o uso de variáveis probabilísticas no processo que possibilitem a análise estatística no sentido de fornecer planos mais confiáveis. Outra questão relevante observada é que os gestores que participam do processo de S&OP nem sempre têm uma visão global de todas as variáveis e restrições envolvidas neste processo, assim observa-se também que as técnicas e ferramentas utilizadas para execução do processo de S&OP não oferecem uma visão holística das atividades e variáveis envolvidas. Com isso, neste trabalho, é proposto um modelo de Simulação de Dinâmica de Sistemas que proporcione uma visão holística para o processo de S&OP e que permita a integração com os processos da área financeira e o uso de variáveis probabilísticas. A avaliação dos resultados das simulações realizadas com o modelo, apoiada por um projeto de experimentos (DoE), mostra que os planos gerados são compatíveis se comparados com a prática empresarial, com a vantagem de tratar a análise econômica e financeira simultaneamente e ainda possibilitar a geração de inúmeros cenários de planos de S&OP.

Palavras-chave:
Planejamento de vendas e operações; Simulação computacional; Dinâmica de sistemas; Visão holística; Integração financeira

Abstract

Despite the S&OP (Sales and Operations Planning) process not being a new procedure in enterprises, especially the large size, it is still a research subject for their practices and computational tools support. Computational models and tools focused to aid the S&OP process are used and can contribute to improve the quality of its implementation and results. The most common tools are those based on spreadsheets; and the most sophisticated ones are based on operational research techniques inserted in Advanced Planning Systems (APS). The literature review on theory and computational techniques used to aid the S&OP process identified a lack of studies related to the use of System Dynamics. Additionally, the review indicates the need for economic and financial analysis integration studies during the preparation of aggregates plans and the use of probabilistic variables in the process enabling the statistical analysis in order to provide more reliable plans. Another relevant issue observed is that managers involved in the S&OP process do not always have a global vision of all variables and constraints involved in the process, therefore, the techniques and tools used to implement the S&OP process do not provide a holistic view of the activities and variables involved. Hence, this paper proposes a System Dynamics Model simulation that provides a holistic vision for the S&OP process, allowing the integration of finance processes and the use of probabilistic variables. The evaluation of the simulations results performed with the model, supported by a design of experiments (DoE), shows that the generated plans are compatible if compared to business procedure, with the advantage of dealing simultaneously with economic and financial analysis and still allows the generation of numerous scenarios of S&OP plans.

Keywords:
Sales and operations planning; Simulation; System dynamics; Holistic vision; Finance integration

1 Introdução

Um dos grandes desafios dos gestores é manter-se atualizado sobre tudo o que acontece em sua organização e compreender como ela age e reage diante do mercado ou das inúmeras mudanças estratégicas, políticas, organizacionais e mercadológicas que ocorrem com o tempo. Esta dificuldade aumenta quanto mais complexa for a organização e o ambiente de negócios em que ela está inserida.

O correto entendimento da organização ocorre a partir do momento em que cada gestor consegue observar como tudo “funciona” ao seu redor, não somente sob sua ótica, mas com uma visão que engloba a dos demais gestores da organização, como cada uma das áreas interage e como são as integrações entre os processos internos com os processos externos da empresa tais como clientes, fornecedores, concorrentes, entre outros.

Geralmente as decisões de nível estratégico e tático relacionadas à capacidade produtiva estão vinculadas a incertezas do ambiente de negócios da organização, pois objetivam o médio/longo prazo e envolvem disponibilizar recursos materiais, humanos e financeiros significativos.

Segundo Wallace (2004), o processo de S&OP visa prover esta “visão de futuro”, pois um de seus principais objetivos é buscar o balanceamento entre a demanda e a oferta de produtos, mostrando, com antecedência, quando e onde as faltas e excessos de capacidade irão ocorrer em um determinado período de tempo.

Grande parte das decisões tomadas no processo de S&OP tem um grande potencial de risco, em que um número razoável de decisões incorretas pode levar as organizações à perda de mercado e a condições financeiras delicadas. Neste ambiente complexo e dinâmico que permeia o processo de S&OP, os gestores devem buscar ferramentas que possam servir de apoio às decisões, com o objetivo de minimizar os riscos e consequentemente os resultados indesejados. As ferramentas mais comuns são aquelas baseadas em planilhas eletrônicas (Silva et al., 2009) e as mais sofisticadas, em técnicas de pesquisa operacional inseridas em sistemas APS (Advanced Planning Systems) (Hahn & Kuhn, 2012; Genin et al., 2007; Chen-Ritzo et al., 2010; Shapiro, 2010; Ivert & Jonsson, 2010; Van Nieuwenhuyse et al., 2011).

Alguns autores afirmam que o futuro do S&OP (Landeghem & Vanmaele, 2002; Schlegel & Murray, 2010) será baseado no planejamento probabilístico, para modelar a variabilidade das incertezas que o mercado apresenta, usando modelos de simulação apoiados por projeto de experimentos de modo a fornecer valores mais apropriados para as variáveis de decisão do processo. Uma revisão da literatura de S&OP publicada na International Journal Production Economics por Thomé et al. (2012), na qual 271 artigos foram revistos, apontou a necessidade de pesquisas para a integração do processo de análise financeira. Portanto, considera-se que o processo de S&OP ainda carece de estudos na academia e nas práticas empresariais.

Uma questão relevante observada nas práticas empresariais é que os gestores que participam do processo de S&OP nem sempre têm uma visão global de todas as variáveis e restrições envolvidas na construção dos planos agregados. A falta desta visão global pode gerar tomada de decisões não assertivas pelos gestores participantes. Observa-se também na revisão da literatura, que as técnicas e ferramentas utilizadas para execução do processo de S&OP não oferecem esta visão holística para o processo, dificultando o compartilhamento de informações e o entendimento de como cada decisão a ser tomada afeta o desempenho global da empresa.

A Dinâmica de Sistemas pode ser usada para definir políticas de médio e longo prazo e regras de negócio nas organizações, bem como fornece elementos que permitem explicitar e compartilhar os modelos mentais dos colaboradores/gestores das organizações como o uso de diagramas de estoque e fluxo (Sterman, 2000).

Considerando características que permitam explicitar e compartilhar modelos mentais e com base na literatura acadêmica, a abordagem de Dinâmica de Sistemas foi escolhida para ser utilizada como ferramenta alternativa para apoiar o processo de S&OP. Este trabalho trata da utilização da teoria da dinâmica de sistema para modelagem do processo de planejamento de vendas e operações (S&OP). A representação deste processo com elementos da teoria da dinâmica de sistemas tem o objetivo de proporcionar aos gestores uma visão holística do processo de S&OP, que permite a compreensão do comportamento do sistema em um horizonte temporal com o auxílio de um recurso de simulação computacional.

Adicionalmente, este trabalho se justifica por não encontrar nenhuma literatura existente sobre o uso da Dinâmica de Sistemas para apoiar o processo de análise e decisão que envolve o S&OP.

Este trabalho está organizado da seguinte forma: a Seção 2 apresenta o método de pesquisa utilizada no desenvolvimento deste trabalho; nas Seções 3 e 4, uma breve revisão da literatura a respeito da Dinâmica de Sistemas e do processo de planejamento de vendas e operações é apresentada; na Seção 5, é detalhado o modelo desenvolvido; na Seção 6, são descritos os experimentos realizados e os resultados; e na Seção 7, são descritas as conclusões.

2 Método de pesquisa

O propósito deste trabalho foi o estudo e o desenvolvimento de um modelo de simulação que descreva adequadamente os relacionamentos causais existentes entre as regras de negócios envolvidas no processo de S&OP e assim conduzir melhor compreensão do processo em si. Com base nesse propósito, este trabalho é classificado como uma pesquisa descritiva, pois busca a identificação da existência de relações entre variáveis e pretende determinar a natureza dessa relação. Quanto à natureza dos resultados, esse trabalho classifica-se como uma pesquisa aplicada, uma vez que está dirigida à solução de um problema específico e busca gerar conhecimento para aplicação prática.

Com relação à caracterização deste trabalho quanto à abordagem do problema, utiliza tanto a abordagem de pesquisa qualitativa quanto a quantitativa. Quantitativa porque utiliza uma modelagem matemática baseada na dinâmica de sistemas e avalia os resultados estatisticamente por meio de um projeto de experimento fatorial. Qualitativa pela característica de observar e coletar dados para o desenvolvimento do modelo a partir de reuniões com gestores do processo de S&OP em empresas com características MTS (Make To Stock).

A abordagem qualitativa contribuiu para reunir as informações e definições de variáveis para o entendimento do processo de S&OP do ponto de vista acadêmico, a partir da revisão bibliográfica, e das práticas empresarias. Com relação às práticas empresariais, ela foi realizada por meio de entrevistas não estruturadas e reuniões com diversos gestores responsáveis pelo processo de S&OP em algumas empresas com características MTS e consultorias listadas a seguir:

• •

  Duas empresas multinacionais fabricantes de componentes e equipamentos da linha branca

• •

  Uma empresa de grande porte fabricante de refrigerantes

• •

  Duas empresas de consultoria, sendo que uma é especializada em implantações de S&OP e outra especializada em estratégia empresarial

• •

  Duas empresas de médio porte fabricantes do setor agrícola

• •

  Uma empresa multinacional produtora de material de escritório.

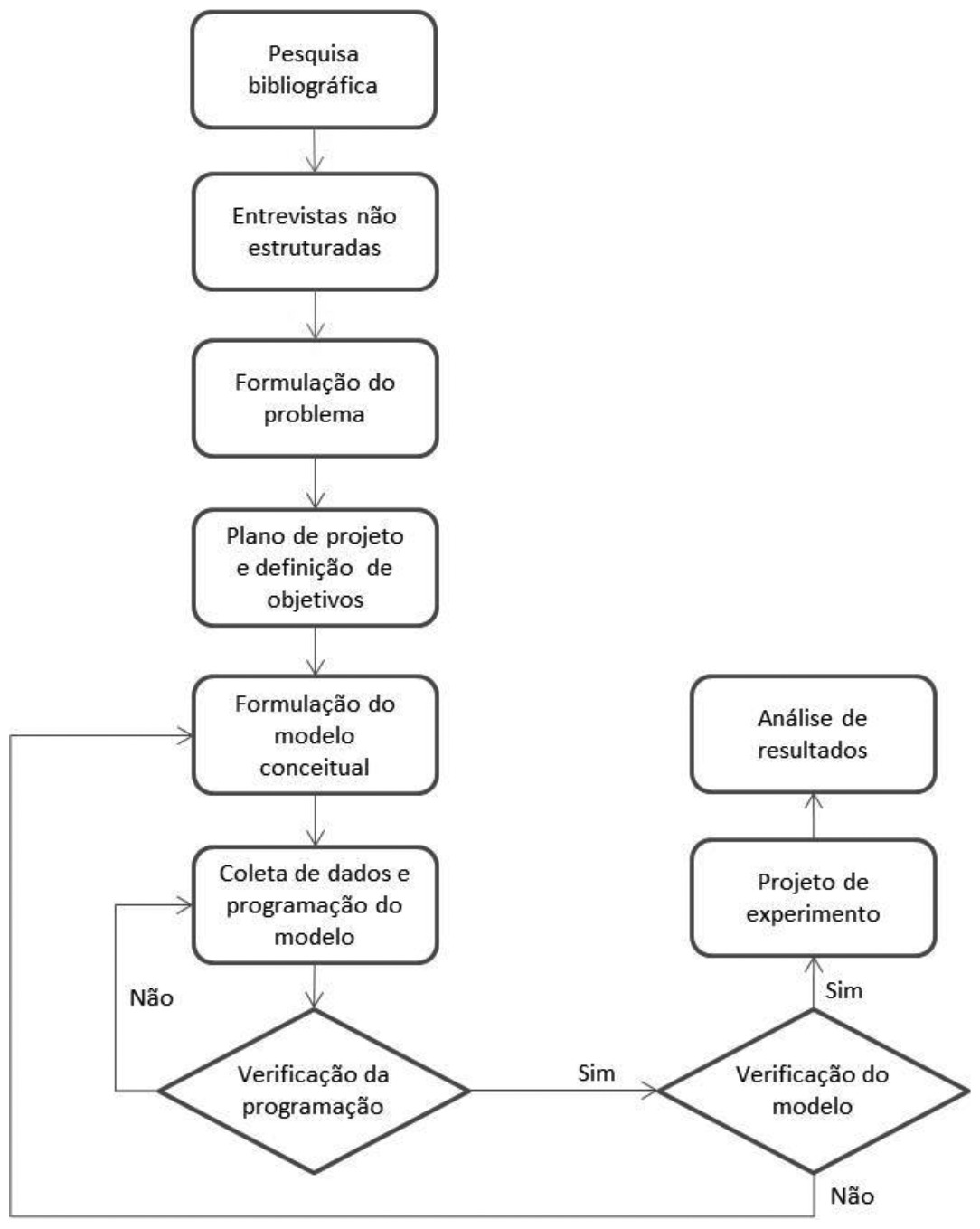
Considerando o propósito desta pesquisa, foi utilizado como método, para conduzir o desenvolvimento deste trabalho, a modelagem e simulação, cujas etapas empregadas neste trabalho são ilustradas na Figura 1.

Figura 1
Método utilizado para o desenvolvimento do Modelo de Dinâmica de Sistemas para S&OP.

A partir da revisão bibliográfica e das entrevistas não estruturadas realizadas nas empresas, construiu-se um primeiro modelo conceitual utilizando como ferramenta para representação desse modelo um diagrama de enlace causal. O modelo conceitual foi então convertido para um primeiro modelo de simulação de Dinâmica de Sistemas para o S&OP. Neste modelo, foram incluídas as variáveis e regras de negócio identificadas na abordagem qualitativa, as quais são utilizadas nas equações matemáticas e regras de produção na Dinâmica de Sistemas. Esse modelo de dinâmica de sistema representa as interações das variáveis envolvidas de todas as áreas participantes do processo de S&OP.

De posse do primeiro modelo, uma sequência de reuniões foi realizada nas empresas relacionadas anteriormente para apresentação e discussão sobre as variáveis e regras de negócios implementadas no modelo de simulação. Em função dessas reuniões, o modelo foi incrementado até o momento em que as principais funções do processo de S&OP, descritas na seção 5, estivessem representadas. Obteve-se um modelo referencial de simulação que representa o processo de S&OP de empresas com características MTS, detalhado na seção 5.

3 Dinâmica de sistemas

Desde o livro Industrial Dynamics, que representa um marco para o início desta área de pesquisa, vários trabalhos vêm sendo desenvolvidos com o uso da Dinâmica de Sistemas em diversas áreas da gestão da produção, tais como os trabalhos modelando vários aspectos da cadeia de suprimentos em Martinez-Olvera (2009), Towill (1996), Kamath & Roy (2007), Cagliano et al. (2011), Sakuramoto (2008), Sasaki et al. (2008), Yimer & Demirli (2010), Olhager (2010), Tako & Robinson (2012), e também propostas de modelos teóricos de planejamento agregado e plano mestre da produção em Pastrana et al. (2010), Venkateswaran & Son (2005), Morecroft & Robinson (2005) e Rabelo et al. (2003).

Outros trabalhos buscam uma solução híbrida com a integração da simulação da Dinâmica de Sistemas com a simulação de eventos discretos (Discrete Event Simulation – DES). Como exemplo, no trabalho de Helal et al. (2007), é proposto um método de simulação híbrida para sistemas de manufatura. Em Pastrana et al. (2010), o modelo teórico de simulação híbrida, proposto por Helal et al. (2007), é aplicado em uma empresa fabricante de lentes para aparelhos a laser. O modelo híbrido mostrou ser capaz de explicar o comportamento das operações do chão de fábrica e das decisões no nível de planejamento de capacidade. Outros trabalhos seguindo a abordagem de simulação híbrida foram propostos em Venkateswaran et al. (2004) e Rabelo et al. (2003), também com o enfoque no planejamento de capacidade e controle da produção.

A aplicação somente da simulação baseada na Dinâmica de Sistemas no planejamento da produção também é tema de discussão em trabalhos como de Orcun et al. (2006), Suryani et al. (2010) e Godinho & Uzsoy (2009), os quais também apresentam propostas para o planejamento de capacidade e controle de produção. Outros trabalhos como de Georgiadis & Michaloudis (2012) utilizam a metodologia de Dinâmica de Sistemas como ferramenta para desenvolvimento de um modelo dinâmico para planejamento e controle da produção (PCP) em tempo real em um job-shop. Esta abordagem em tempo real reflete o processo de monitoramento e ajuste contínuo do estado do sistema para alinhá-lo com um estado desejado, sendo também direcionado ao planejamento de capacidade e controle da produção.

Ausência de aplicação para o S&OP representa uma das motivações para a realização deste trabalho. Além disso, os recentes avanços tecnológicos na modelagem por simulação computacional e o surgimento de novos softwares de modelagem e simulação com Dinâmica de Sistemas permitiram que esta técnica fosse mais utilizada. Isto torna este trabalho também uma contribuição para a prática na área de gestão da produção.

4 Planejamento de vendas e operações (S&OP)

Com os avanços dos recursos computacionais e do estudo da prática e teoria do PCP, os modelos matemáticos tornaram-se uma alternativa para o uso de planilhas eletrônicas, que ainda são encontradas como uma ferramenta de auxílio ao processo de S&OP na maioria das empresas.

Vollmann et al. (2008) descrevem vários modelos matemáticos baseados em formulações de programação linear e programação inteira mista para o problema do planejamento agregado da produção, com o objetivo de otimizar o plano de menor custo para atender à previsão de vendas para famílias de produtos. Apesar de estes modelos matemáticos serem conhecidos e estudados no meio acadêmico, são pouco empregados no meio empresarial. Geralmente, as empresas preferem o uso de métodos gráficos e tabulares.

Assim como Hahn & Kuhn (2012), Genin et al. (2007) e Chen-Ritzo et al. (2010) descrevem técnicas de modelagem matemática baseadas em programação linear, programação linear mista, programação estocástica, entre outros, que são utilizadas para gerar os planos de produção agregados e planos de vendas agregados, considerando restrições de recursos e utilizando funções objetivo para minimizar os custos ou maximizar os lucros.

Com o objetivo de apoiar os processos de decisão estratégico, tático e operacional, sistemas avançados de planejamento (APS - Advanced Planning Systems) vêm sendo desenvolvidos e oferecidos às empresas como módulos integrados aos sistemas de gestão empresarial conhecido como ERP (Shapiro, 2010). Os sistemas APS são ferramentas computacionais que incorporam técnicas da pesquisa operacional que podem simular vários cenários das funções empresariais e que podem gerar planos segundo critérios otimizantes (Ivert & Jonsson, 2010; Jonsson et al., 2007; Stadtler, 2005). Sistemas APS também vêm sendo desenvolvidos por pesquisadores e centros de pesquisas, buscando apresentar novas propostas em termos de novos algoritmos e processos (Van Nieuwenhuyse et al., 2011).

Apesar das funcionalidades inseridas nos APS que visam atender às necessidades das cadeias de suprimentos, a maioria das suas implementações se restringe a uma única organização ou a um único chão de fábrica, visto que são grandes as dificuldades técnicas e organizacionais em gerar planos para todos os parceiros da cadeia (Hvolby & Steger-Jensen, 2010; Ivert & Jonsson, 2011; Rudberg & Cederborg, 2011; Azevedo et al., 2006).

Alguns autores afirmam que o futuro do S&OP (Landeghem & Vanmaele, 2002; Schlegel & Murray, 2010) será baseado no planejamento probabilístico, para modelar a alta variabilidade que o mercado apresenta, usando modelos de simulação que utilizam o projeto de experimentos (DoE – Design of Experiments) para fornecer valores mais apropriados para as variáveis de decisão do processo e possibilitar o gerenciamento dos riscos.

Thomé et al. (2012) apresentaram uma extensa revisão da literatura de S&OP com o estudo e classificação de 271 artigos. Nesse trabalho, foi realizada uma revisão sistemática sobre o processo de S&OP a fim de identificar e analisar o S&OP como um processo de negócio e apresentar evidências do seu impacto sobre o desempenho da empresa. O principal resultado apresentado na maioria dos artigos revistos apontou que existe uma variedade de trabalhos que estudam a integração funcional de planos de S&OP, embora poucos estudos relatassem sobre a integração de planos financeiros em S&OP. Apesar da existência de descrição de processos comuns e definições de S&OP, há falta de uma arquitetura que possa conter modelos de maturidade, sistema de medição de S&OP e os processos que se relacionam com o desempenho da empresa (Pandin et al., 2012). A necessidade de integrar ainda mais a função financeira ao S&OP foram destacadas por vários autores e carece de mais pesquisas.

5 Modelo de dinâmica de sistemas para S&OP

A partir da revisão da literatura e das entrevistas realizadas em empresas, observou-se que as técnicas e ferramentas utilizadas para apoiar o processo de S&OP não oferecem aos gestores do processo uma visão holística das atividades e não apresentam as inter-relações entre as variáveis envolvidas na elaboração dos planos agregados. Estas ausências dificultam o compartilhamento de informações e o entendimento de como as decisões a serem tomadas influenciam o desempenho global da empresa. Essa observação direcionou este trabalho para o desenvolvimento de um modelo de simulação de Dinâmica de Sistemas que representa, além das interações existentes nos processos típicos do ciclo S&OP (planejamento de vendas, planejamento de produção e suprimento), as interações com os demais processos existentes em uma empresa que estão implicitamente envolvidos nas decisões resultantes do S&OP. Assim, o modelo desenvolvido amplia a visão do S&OP quando, concomitantemente aos processos típicos, considera o conjunto de informações e regras de negócios dos processos custeio, faturamento, fluxo de caixa e análise econômica.

Para o desenvolvimento do modelo de simulação, foi inicialmente construído um modelo conceitual de Dinâmica de Sistemas que mostra as relações de causa e efeito das regras de negócios existentes nas diversas áreas funcionais de uma empresa. Este modelo é apresentado na Figura 2 por meio de um diagrama de enlace causal.

Figura 2
Modelo de enlace causal do processo de S&OP.

Este diagrama de enlace causal apresenta o relacionamento entre: Plano de Vendas, Plano de Estoque, Plano de Produção, Suprimentos, Custos de Estoque, Custo Unitário Médio Móvel, Capacidade dos Centros de Trabalho, Faturamento, Contas a Pagar, Contas a Receber e Fluxo de Caixa. Este diagrama mostra a causa e efeito da estrutura do sistema. Cada seta representa um relacionamento de causa e efeito entre duas variáveis. Por exemplo, aumentando-se o volume do estoque de matéria-prima, pode-se reduzir a quantidade de itens da lista de compras, por outro lado, aumentando-se a quantidade de reservas de matéria-prima, pode-se reduzir o volume de estoque de matéria-prima.

O modelo proporciona a visão holística para o processo de S&OP e, dessa forma, permite que as decisões de planejamento sejam tomadas de maneira compartilhada e com a ótica de como os planos resultantes do S&OP são inter-relacionados. O modelo tem o objetivo de apoiar todo o processo de S&OP, desde a organização da coleta de dados à construção e avaliação dos planos agregados.

O modelo conceitual de enlace causal foi convertido em um modelo de estoque e fluxo que permite maior detalhamento da estrutura das regras de negócio do processo e sua implementação computacional.

O modelo construído possibilita aos gestores ajustar as restrições de cada área funcional modelada e por meio da execução da simulação do modelo computacional de estoque e fluxo permite gerar um cenário de planejamento para o horizonte de tempo desejado. Múltiplos cenários de planejamento podem ser criados rapidamente a partir da alteração dos valores de entrada do modelo e execução da simulação, em que cada cenário constitui um conjunto de planos agregados formados por plano de vendas, plano de produção considerando volume de produtos e capacidade, plano de estoque, plano de suprimentos, plano financeiro e previsão do fluxo de caixa.

Neste modelo de Dinâmica de Sistemas, também é considerado o uso de variáveis probabilísticas, o que permite aos gestores definirem qual variável terá comportamento aleatório e qual distribuição probabilística será utilizada. Este recurso permite a elaboração de inúmeros cenários que, em conjunto com uma ferramenta de análise estatística, possibilita aos gestores do processo de S&OP a escolha de planos com maior acuracidade, minimizando os riscos por uma escolha incorreta. Outro recurso importante do modelo é a integração de variáveis econômicas e financeiras como elementos participantes do processo de simulação, o que permite a valorização dos planos de S&OP no tempo de execução e o acompanhamento de índices financeiros de cada cenário simulado. Esses recursos do modelo são também uma contribuição para a área de pesquisa, tendo em vista os trabalhos de revisão da literatura dos autores Thomé et al. (2012) e Schlegel & Murray (2010), que apontam a necessidade de mais pesquisas sobre a integração da função financeira ao S&OP e a necessidade de se ter um planejamento probabilístico.

Assim, o modelo desenvolvido tem como características importantes: a visão sistêmica dos processos que representam as áreas funcionais do S&OP, representada no modelo com regras de negócios modeladas por elementos de estoque, fluxo e variáveis do tipo endógenas e exógenas com características determinísticas e probabilísticas; a geração de múltiplos cenários, podendo-se simular inúmeros cenários, além do tradicional otimista, pessimista e provável, utilizados na prática empresarial; a análise estatística, pois o uso de variáveis probabilísticas permite o tratamento das incertezas no ambiente empresarial; o tempo de execução da simulação realizado em segundos para períodos maiores do que doze meses, o que permite fazer análises no momento da reunião do S&OP; o aprendizado organizacional, pois a metodologia da Dinâmica de Sistemas possui características de aprendizado com o seu uso; a possibilidade de adaptação e ampliação do modelo, na medida em que se aprende mais sobre o processo ou se criam novas regras de negócios; e a documentação do conhecimento do processo de S&OP, além de possibilitar o armazenamento dos processos anteriores para analisar a sua evolução.

O modelo de estoque e fluxo da Dinâmica de Sistemas do S&OP foi construído de forma modular de modo que todas as regras de negócios implementadas foram agrupadas, para melhor organização, em macroprocessos. Cada macroprocesso representa um conjunto de processos relacionado às principais áreas funcionais de uma empresa que estão envolvidas com o ciclo de S&OP, sendo estas áreas vendas, suprimentos, produção, custos, finanças e recursos humanos. Assim, seguindo uma analogia com as principais áreas funcionais, a organização do modelo foi agrupada em sete macroprocessos: suprimentos, produção, capacidade, previsão de vendas, custeio por absorção, faturamento/análise econômica e fluxo de caixa.

O modelo construído é constituído de 216 elementos da Dinâmica de Sistemas classificados em variáveis do tipo estoque, fluxo e auxiliares, os quais são descritos em detalhes, respectivamente, nos Quadro 1A, 2A e 3A do Anexo A deste artigo. Diversas variáveis são tratadas como estrutura de dados do tipo matriz unidimensional e bidimensional, o que dá ao modelo a capacidade de utilizar, a princípio, n famílias de produtos acabados com suas respectivas listas de materiais (Bill of Material – BOM) e roteiros de produção, n famílias de matérias-primas, n recursos de produção e usar n variáveis probabilísticas ou determinísticas, para n períodos de tempo em um horizonte de planejamento. O detalhamento de toda a estrutura do modelo e a relação de todas as equações e variáveis implementadas são apresentadas nos Anexos B e C deste artigo.

Neste estudo, o processo do S&OP com a simulação iniciou-se com atualização do status atual de todas as variáveis do tipo estoque do modelo de Dinâmica de Sistemas e com a entrada de dados referentes à previsão de vendas de cada família de produto acabado. A previsão de vendas é tratada no modelo como uma variável exógena ao sistema, pois atualmente o modelo não executa métodos de previsão e segue a premissa de que a previsão será fornecida já com os devidos tratamentos. Os dados de entrada referentes à previsão de vendas são inseridos no modelo por meio do macroprocesso denominado “previsão de vendas”, apresentado na Figura 3, que tem a função de realizar a inserção dos valores previstos na simulação como valor médio de uma distribuição probabilística, a qual pode ser definida a critério do gestor para cada cenário simulado.

Figura 3
Estrutura modelada em Dinâmica de Sistemas para o macroprocesso “Previsão de Vendas”.

Neste macroprocesso, também é representado um método de suavização exponencial simples que utiliza a variável de estoque “demanda”, a variável de fluxo “EntradaPrev” e as variáveis auxiliares “alfa” e “PlanoVendas”, que tem como objetivo oferecer uma alternativa ao gestor para elaborar o plano de estoque inicial de cada família de produto representado pela variável auxiliar “PlanoEstoque”. Neste caso, um plano inicial de estoque é definido com base na estratégia de utilização de taxas de cobertura de estoque sobre o cálculo da demanda média prevista, realizada com o método de suavização em função da entrada dos dados da previsão. Além deste caso, uma variável exógena (Estq_Desejado) para a entrada de dados referentes a um plano de estoque também é disponibilizada no modelo como uma alternativa para o gestor.

Os dados de entrada referentes à previsão de vendas e plano de estoque são direcionados para o macroprocesso “produção”, detalhado na Figura 4, constituindo-se assim os planos iniciais de vendas e de estoque, definidos para o ciclo de S&OP, que serão submetidos às restrições de recursos. A partir da entrada destes planos, é definido o plano de produção em função da diferença entre os níveis de estoque de família de produto acabado com as necessidades planejadas para vendas e estoque de cada mês no horizonte de planejamento definido.

Figura 4
Estrutura modelada em Dinâmica de Sistemas para o macroprocesso “Produção” e “Compras”.

No macroprocesso “produção”, apresentado na Figura 4, é efetuada a explosão da lista de materiais para as famílias de produto acabado de acordo com os volumes definidos no plano de produção e calculado o volume necessário de matéria-prima para atendimento do plano de produção. Este volume de matéria-prima é encaminhado ao macroprocesso “suprimentos” que realiza a verificação das restrições de matéria-prima e de fluxo de caixa para definir o volume a comprar. Depois da verificação das restrições de matéria-prima, serão definidas as quantidades possíveis de se produzir mediante os níveis de estoque de matéria-prima durante o período de planejamento. Outra verificação do plano de produção é realizada em relação aos níveis de capacidade disponíveis dos centros de trabalho restrito, o qual é calculado no macroprocesso “capacidade”. Depois das etapas de verificação de capacidade e verificação dos estoques de matéria-prima disponíveis, são definidos os volumes das ordens de produção que serão liberadas para entrada na produção, efetivando a transferência da matéria-prima para o Work in Process (WIP) de produção, no qual serão consumidas as horas de mão de obra e matéria-prima necessária. As ordens em processo de produção serão concluídas após os tempos de ciclo de produção definidos por uma distribuição probabilística para cada família de produto acabado. Finalizando o processo de produção, ocorrerá a baixa dos estoques em processos (WIP) e será efetivada a entrada do produto acabado no estoque de produtos acabados, disponibilizando-os para vendas.

O macroprocesso denominado “Suprimentos”, apresentado em conjunto com o macroprocesso produção na Figura 4, recebe, como dados de entrada do macroprocesso “produção”, a lista de famílias de matéria-prima necessária para atender ao plano de produção das famílias de produto acabado. A partir dessa lista, inicia-se o cálculo da quantidade de matéria-prima necessária para se comprar. Neste cálculo, são levados em consideração os níveis de estoque de matéria-prima disponível, a quantidade de compra que se encontra atualmente em processo de aquisição e a cobertura de estoque adotada como estratégia para reposição dos estoques de matéria-prima. Definidas as quantidades a comprar, estas são valorizadas pelo preço unitário de compra, que é definido para cada família de matéria-prima em cada mês do período de planejamento, formando-se assim o plano de suprimentos. Valorizado o plano de suprimentos, esse é submetido a uma restrição de acordo com os limites de caixa financeiro disponível. Depois da definição do plano, serão confirmadas as requisições de compras e transferidas para carteira de compras em que permanecerão até o prazo de suprimento estabelecido para a família de matéria-prima, quando então ocorrem as entradas no estoque em valores de custos e quantidade.

O macroprocesso denominado “Capacidade”, detalhado na Figura 5, tem como dado de entrada principal os volumes definidos para as famílias de produto acabado no plano de produção. O processo inicia-se calculando o total de horas trabalhadas necessárias do centro de trabalho restrito, definido para cada família de produto, considerando a taxa de produtividade especificada para cada centro e o tempo padrão utilizado para a produção de uma unidade de cada família de produto. Tem-se então o total de horas de capacidade planejada do centro restrito para o plano de produção, e o percentual de alocação da capacidade restrita para cada família de produto.

Figura 5
Estrutura modelada em Dinâmica de Sistemas para o macroprocesso “Capacidade”.

As horas planejadas são comparadas às horas de capacidade padrão definida para o centro restrito e, em função da diferença, é definido o volume de horas necessárias para ajustar a capacidade atual à capacidade planejada. Quando esse ajuste é negativo, a capacidade atual dos centros restritos é igualada às horas de capacidade padrão pré-definidas para o modelo. No caso em que o ajuste é positivo, ou seja, é necessário o incremento de capacidade para atender ao plano de produção, será calculado no modelo, considerando as restrições de fluxo caixa do modelo, o volume de horas extras necessárias a serem adicionados na capacidade dos centros restritos e na capacidade total da produção. Esta é uma estratégia adotada para que o modelo reaja às necessidades de capacidade planejada para atender ao plano de produção. De forma geral, neste macroprocesso são avaliadas as restrições existentes para se realizar os ajustes de horas de capacidade necessária, considerando o custo adicional de horas extras e o tempo de atraso para realizar esse ajuste de maneira que os volumes de produção planejados para as famílias de produtos possam ser limitados ou não.

O macroprocesso “custeio por absorção”, apresentado na Figura 6, é responsável pela apuração dos custos de produção, realizada no modelo por meio do método de custeio por absorção (Martins, 2003), um método derivado da aplicação dos princípios de contabilidade geralmente aceitos e seu uso amplamente disseminado, principalmente, pela contabilidade financeira para preparar relatórios destinados ao público externo à empresa. Este método resume-se no critério de se apropriar de todos os custos de produção, quer sejam fixos, variáveis, diretos ou indiretos, e tão somente dos custos de produção aos produtos elaborados. Neste macroprocesso, se concentram todos os dados pertinentes à apuração dos custos de produção incorridos nos demais macroprocessos do modelo.

Figura 6
Estrutura modelada em Dinâmica de Sistemas para o macroprocesso “Custeio por Absorção”.

De maneira integrada aos outros macroprocessos, é simulado o controle dos custos de matéria-prima em estoque, considerando a atualização desses custos pelo método do preço médio móvel em face das entradas por aquisição de compras; são apurados os custos com mão de obra direta, considerando as horas de capacidade padrão e as horas extras disponibilizadas pelo macroprocesso “capacidade”; são apurados os custos fixos e indiretos ocorridos no período, como também os custos dos produtos em processo de produção. A simulação deste macroprocesso “custeio de absorção” é conduzida de maneira a permitir a realização da apuração dos custos dos produtos produzidos no mês e a atualização do custo do estoque de produtos acabados pelo custo médio móvel. A finalidade deste macroprocesso é valorizar os planos de produção gerados pelo modelo desenvolvido, fornecendo métricas financeiras para análise e apuração dos resultados dos cenários de S&OP simulados.

No macroprocesso denominado “faturamento e análise econômica”, detalhado na Figura 7, foram agrupadas a simulação do processo de faturamento referente ao plano de vendas e a análise econômica das operações simuladas durante o período de planejamento do S&OP. Neste macroprocesso, o plano de vendas inicial é submetido às restrições de estoque e de capacidade de produção avaliadas no macroprocesso “produção”, simulando a concretização da venda e a geração de receita financeira auferida pelas vendas concluídas no período de planejamento simulado para o S&OP. As vendas concluídas consistem em um mix de famílias de produto acabado que são atendidas no prazo mediante a disponibilidade do estoque durante o período de simulação. Esse mix totaliza o plano de vendas realizado e é direcionado como input para apuração da receita financeira. A partir da receita financeira gerada pelo plano de vendas e em face dos custos dos produtos vendidos calculados por meio do macroprocesso “custeio por absorção”, é disponibilizado, pelo modelo desenvolvido, um conjunto de métricas financeiras e relatórios de demonstração de resultado (Gitman, 2010) para realização de uma análise econômica do cenário simulado.

Figura 7
Estrutura modelada em Dinâmica de Sistemas para o macroprocesso “Faturamento e análise econômica”.

O macroprocesso “fluxo de caixa” construído no modelo é apresentado na Figura 8, e este tem a função de demonstrar uma projeção de todos os pagamentos e recebimentos esperados para o período de planejamento definido para o S&OP. Neste macroprocesso, são simulados os processos de contas a receber e contas a pagar, os quais são alimentados respectivamente pelo macroprocesso faturamento, por meio das receitas geradas pelo plano de vendas mês a mês, e pelos macroprocessos suprimentos e custos, que fornecem os pagamentos a serem realizados mediante a compra de matéria-prima, salários, despesas com comercialização, despesas administrativas, comissões, despesas financeiras, gastos gerais de produção e impostos. A simulação da operação do fluxo de caixa ocorre a partir dos saldos em contas a pagar e a receber, e mediante os prazos médios de recebimento e pagamento são efetuadas as entradas e saídas do caixa. Dessa forma, é possível obter um planejamento financeiro da empresa por meio da simulação de cenários de S&OP.

Figura 8
Estrutura modelada em Dinâmica de Sistemas para o macroprocesso “Fluxo de caixa”.

6 Resultados

Para a realização de testes e avaliação do modelo de Dinâmica de Sistemas, foi construído pelo autor uma base de dados hipotética de teste com o auxílio de colaboradores responsáveis das áreas de Custos, PCP, Compras, Vendas e Financeiro de algumas das empresas consultadas. Essa base de dados foi definida buscando a similaridade com os dados de empresas com características de produção MTS e manufatura discreta. Depois da definição dos dados hipotéticos, realizou-se um estudo juntamente com as áreas da empresa para a definição de como agregar as informações obtidas de modo a constituir as famílias de produtos acabados, as famílias de matérias-primas, a lista de materiais e os roteiros de fabricação para o processo de S&OP. A agregação desses dados foi conduzida segundo as sugestões de Corrêa et al. (2007). Neste processo, os produtos acabados foram agregados em cinco famílias de produto e os itens de matéria-prima foram agregados em dez famílias de matéria-prima, a partir das quais foram compostas as listas de materiais das famílias de produto acabado. Os tempos de produção dos roteiros de fabricação foram agregados em cinco centros de trabalho e, para cada família de produto acabado, foi identificado e selecionado um dos cinco centros como recurso de capacidade restrita. Esses dados são apresentados no Quadro 1C do Anexo C como variáveis auxiliares de entrada. Adicionalmente a esses dados, outro conjunto de dados, que deve retratar o estado inicial do sistema para a simulação, foi definido como valores iniciais a serem utilizados nas variáveis auxiliares de entrada e variáveis de estoque do modelo.

Outro conjunto de simulações foi realizado para avaliação do modelo de Dinâmica de Sistema, considerando a utilização de variáveis probabilísticas na estrutura do modelo para S&OP. Estas simulações foram conduzidas com base em uma parte da estatística probabilística que estuda o planejamento, execução, análise e interpretação de resultados provenientes de experimentos, denominada de projeto de experimentos (DoE – Design of Experiments) (Montgomery, 1976; Hicks, 1973; Box et al., 1978).

O projeto de experimentos (DoE) denominado fatorial 2k (Montgomery, 1976; Johnson & Leone, 1977; Box et al., 1978; Vieira, 1999; Freitas, 2001) foi utilizado neste trabalho para auxiliar no planejamento de novas simulações do modelo com o uso de variáveis probabilísticas e na análise estatística dos resultados obtidos.

As simulações planejadas com o DoE foram realizadas com os dados da base de teste, e dentre as variáveis de entrada desta base foram selecionadas três variáveis relevantes no processo de S&OP que apresentam comportamento probabilístico para serem representadas no modelo por meio de uma distribuição normal. As variáveis selecionadas foram: prazo médio de entrega de suprimento, tempo de ciclo de produção e previsão de vendas.

O DoE foi analisado com base em seis indicadores de desempenho considerando os valores totais de um período de 12 meses de planejamento. Esses indicadores de desempenho foram selecionados considerando as entrevistas realizadas nas empresas visitadas como sendo as medidas mais utilizadas: Lucro líquido; Percentual de margem de líquida; Percentual de margem de contribuição; Percentual de utilização da capacidade do centro de trabalho restrito; Percentual de atendimento de plano de vendas; Volume de produção.

Neste DoE fatorial, as simulações foram planejadas com o objetivo de analisar os efeitos de três variáveis, que são preponderantes no processo de S&OP, sobre os indicadores de desempenho selecionados para avaliar os planos gerados pela simulação. As três variáveis de entradas selecionadas, tratadas como fatores do projeto fatorial (Montgomery, 1976), são: previsão de vendas, plano de estoque de produto acabado e cobertura do estoque de matéria-prima. Estas variáveis foram observadas como estratégicas para o S&OP pelos gestores das empresas. Visto que cada fator necessita de dois níveis ou alternativas no projeto fatorial 2^k (Montgomery, 1976), foram propostos os seguintes planos como valores para as variáveis do processo de S&OP eleitas como fatores para esse projeto de experimentos:

1. 1

   Dois planos de previsão de vendas foram elaborados e denominados de “previsão de vendas 0” e “previsão de vendas 1” conforme os valores apresentados mensalmente na Tabela 1. Essa variável é inserida no modelo seguindo uma distribuição normal, tendo como valor médio os valores descritos mês a mês na Tabela 1, e um desvio padrão de 10%.

   Tabela 1
   Planos de Previsão de Vendas utilizados nas simulações com o projeto de experimentos.
   

   Previsão de vendas - 0
   Família de produto	Mês 1	Mês 2	Mês 3	Mês 4	Mês 5	Mês 6	Mês 7	Mês 8	Mês 9	Mês 10	Mês 11	Mês 12
   Família Produto A	18	25	13	16	18	37	31	40	40	30	42	23
   Família Produto B	29	12	12	15	9	11	16	28	28	44	36	19
   Família Produto C	17	9	8	9	7	13	13	16	16	18	23	28
   Família Produto D	4	3	2	6	6	22	23	27	20	14	8	4
   Família Produto E	3	2	2	3	6	16	22	14	20	19	11	8
   Previsão de vendas - 1
   Família de produto	Mês 1	Mês 2	Mês 3	Mês 4	Mês 5	Mês 6	Mês 7	Mês 8	Mês 9	Mês 10	Mês 11	Mês 12
   Família Produto A	22	30	16	19	22	44	37	48	48	36	50	28
   Família Produto B	35	14	14	18	11	13	19	34	34	53	43	23
   Família Produto C	20	11	10	11	8	16	16	19	19	22	28	34
   Família Produto D	5	4	2	7	7	26	28	32	24	17	10	5
   Família Produto E	4	2	2	4	7	19	26	17	24	23	13	10

2. 2

   Dois planos de estoque foram sugeridos para o segundo fator, conforme apresentado na Tabela 2 e, analogamente a esses planos, foram denominados de “plano de estoque 0” e “plano de estoque 1”.

   Tabela 2
   Planos de Estoques utilizados nas simulações com o projeto de experimentos.
   

   Plano de Estoque – 0
   Família de produto	Mês 1	Mês 2	Mês 3	Mês 4	Mês 5	Mês 6	Mês 7	Mês 8	Mês 9	Mês 10	Mês 11	Mês 12
   Família Produto A	60	61	75	84	92	84	81	66	50	44	23	26
   Família Produto B	21	31	39	45	57	67	72	65	58	32	14	15
   Família Produto C	11	17	25	31	40	42	44	45	45	43	35	20
   Família Produto D	21	31	39	46	51	49	40	40	27	13	12	15
   Família Produto E	11	20	34	47	58	54	42	38	22	6	3	4
   Plano de Estoque – 1
   Família de produto	Mês 1	Mês 2	Mês 3	Mês 4	Mês 5	Mês 6	Mês 7	Mês 8	Mês 9	Mês 10	Mês 11	Mês 12
   Família Produto A	22	22	19	28	34	43	44	44	45	38	33	26
   Família Produto B	21	16	14	14	14	22	29	40	43	40	34	24
   Família Produto C	14	10	10	12	13	17	18	20	23	28	27	22
   Família Produto D	4	4	6	14	20	29	28	24	17	10	6	4
   Família Produto E	3	3	4	10	18	21	22	21	20	15	9	5

3. 3

   Para o terceiro fator, para o qual foi selecionada a variável de entrada cobertura do estoque de matéria-prima, foram propostas duas alternativas, sendo a primeira um nível de cobertura de estoque desejado de 1 mês e o segundo um nível de 2 meses.

Considerando os fatores e níveis definidos para o projeto fatorial, foram esquematizados oito cenários de planejamento para o S&OP para análise por meio da combinação dos três fatores com os dois níveis, os quais são sumarizados na Tabela 3.

Tabela 3
Cenários gerados para o projeto de experimentos fatorial 2^k.

Fator A = Previsão de Vendas	Fator B = Plano de estoque de produto acabado
	B0		B1
	Fator C = Cobertura do estoque de matéria-prima
	C0	C1	C0	C1
A0	A0 B0 C0	A0 B0 C1	A0 B1 C0	A0 B1 C1
A1	A1 B0 C0	A1 B0 C1	A1 B1 C0	A1 B1 C1

Estes oito cenários de S&OP foram utilizados como dados de entrada para o modelo de simulação de Dinâmica de Sistemas. Por meio da simulação, esses cenários são submetidos à análise de suas restrições de capacidade e de materiais para cada família de produtos, nos quais são gerados para um horizonte de doze meses, pela simulação, planos de produção (considerando volume de produtos e capacidade dos recursos necessários), plano de suprimentos e propostas de ajustes nos planos de vendas e estoques inicialmente planejados. Os planos de vendas e estoque inseridos como dados de entrada são ajustados durante a execução da simulação em função das restrições inseridas no modelo. Com um conjunto de simulações de cada cenário, são obtidos também os resultados de cada indicador de desempenho, necessários para a análise do experimento.

Em um processo de análise de resultados obtidos por meio da simulação de sistema de natureza estocástica, é fundamental a definição do número de replicações do experimento e o nível de confiança desejado aos resultados para determinação do intervalo de confiança das variáveis de interesse (indicadores de desempenho) que medem o desempenho do sistema (Box et al., 1978). Para análise do projeto fatorial, foi fixado um nível de confiança de 95% e foi definido um número de 10 replicações para realização do experimento. Assim, cada cenário de S&OP foi replicado 10 vezes, ou seja, foram realizadas 10 simulações para cada cenário, sendo que nestas simulações o estado inicial do sistema utilizado é sempre o mesmo, alterando-se apenas as sementes dos geradores de números aleatórios em cada simulação.

Neste experimento fatorial, oito cenários de S&OP estão em comparação com o objetivo de se avaliar os efeitos das variáveis de entrada escolhidas do modelo proposto (fatores) sobre os indicadores de desempenho e comparar quais dos cenários planejados possuem o melhor desempenho. Essa análise é realizada com ajuda de um método estatístico denominado análise de variância, que visa, fundamentalmente, verificar se existe uma diferença significativa entre as médias dos resultados obtidos para cada indicador, e se os fatores exercem influência sobre esses resultados (Scheffé, 1959; Vieira, 1999). Em outras palavras, a análise de variância é utilizada quando se quer decidir se as diferenças dos resultados observadas são reais (causadas por diferenças significativas) ou casuais (decorrentes da mera variabilidade amostral). Deste modo, essa análise parte da hipótese de que o acaso só produz pequenos desvios, sendo as grandes diferenças provocadas por causas reais.

Os resultados médios obtidos para os indicadores de desempenho, em cada cenário de S&OP, a partir das simulações realizadas no projeto fatorial, são apresentados na Tabela 4.

Tabela 4
Resultados dos indicadores de desempenho obtidos nas simulações realizadas com cada cenário do experimento fatorial.

Planos	Lucro Líquido Total	% Margem Líquida	% Margem Contribuição	% Utiliz. Cap.Restrita	% Atend. Plano Vendas	Volume Produção
A0 B0 C0	13.739.395,99	6,79	28,30	95,21	100,00	1.006,80
A0 B0 C1	14.691.322,71	7,25	28,70	75,92	100,00	1.012,10
A0 B1 C0	10.816.290,99	5,35	27,68	108,82	99,95	1.028,00
A0 B1 C1	12.645.545,27	6,23	28,71	84,27	100,00	1.029,30
A1 B0 C0	21.843.267,22	8,95	29,53	119,95	100,00	1.217,70
A1 B0 C1	23.259.964,66	9,50	30,03	94,58	100,00	1.228,30
A1 B1 C0	19.901.326,49	8,27	28,77	131,65	99,23	1.227,50
A1 B1 C1	21.923.018,96	8,95	29,89	102,49	100,00	1.239,30

A partir da análise de variância realizada sobre os dados obtidos nas simulações com o experimento, pode-se constatar que para todos os indicadores de desempenho os fatores A, B e C influenciam nos resultados obtidos em um nível de confiança estatístico de 95%. Com relação às interações entre esses fatores, verificou-se que essas interações têm influências diferentes em cada indicador de desempenho, como a interação dos fatores A e B contribuem significantemente com os resultados obtidos no indicador de desempenho “percentual de margem líquida”, mas não tem influência significativa no indicador de desempenho “lucro líquido”. Assim, pode-se concluir, de uma maneira geral, que as variações sofridas pelos indicadores de desempenho são devidas às variáveis de entrada previsão de vendas, plano de estoque e cobertura de estoque de matéria-prima, o que demonstra estar em consenso com as práticas empresariais.

Sabendo-se que os fatores A, B e C são responsáveis pelos resultados obtidos nos indicadores de desempenho, pode-se verificar qual dos níveis destes fatores proporciona o melhor desempenho, ou seja, entre os cenários de S&OP analisados nas simulações, qual obteve melhor resultado nos indicadores de desempenho. Esta análise comparativa foi realizada com a aplicação do teste estatístico de Tukey (Vieira, 1999), utilizado para verificar se os resultados médios obtidos para cada indicador de desempenho são realmente diferentes estatisticamente. Com a aplicação deste teste, constatou-se que os resultados obtidos por cada cenário de S&OP são estatisticamente diferentes, o que permite concluir que o cenário A₁B₀C₁, que se refere ao cenário formado pelos planos “previsão de vendas 1”, “plano de estoque 0” e dois meses de cobertura de estoque de matéria-prima, tem melhor resultado para os indicadores lucro líquido, percentual da margem líquida e percentual da margem de contribuição, como pode ser observado na Tabela 4. No caso dos indicadores percentual de utilização da capacidade do centro de trabalho restritro e volume de produção, o melhor resultado foi obtido com a utilização do cenário de S&OP referenciado por A₁B₁C₁, diferenciando do cenário A₁B₀C₁ pela utilização do plano “plano de estoque 1”. Com relação ao indicador de desempenho percentual de atendimento do plano de vendas, pode-se verificar que em apenas dois cenários existem diferença nos resultados obtidos, e que nos demais nota-se que os planos de vendas foram cumpridos em sua totalidade.

Tomando como base as práticas empresarias, nota-se que a escolha do melhor cenário do S&OP é influenciada fortemente pelos indicadores de desempenho relacionados aos resultados financeiros, considerada no experimento como margem líquida e margem de contribuição. Neste critério, o melhor cenário do experimento realizado foi o que considerou a combinação de variáveis A₁B₀C₁, ou seja, a variável previsão de vendas com a atribuição “previsão de vendas 1”, a variável plano de estoque com a atribuição “plano de estoque 0” e para a variável cobertura de estoque de matéria-prima com a atribuição que representa o período de 2 meses.

7 Conclusão

O processo de S&OP é fundamental para o posicionamento da empresa no mercado em que ela atua. O processo serve como um direcionador de decisões no sentido de equilibrar a demanda e a oferta de produtos ao longo de um determinado horizonte de tempo, considerando o bom uso dos recursos restritivos de suas áreas funcionais para atender a um nível de qualidade de serviço aos clientes e às metas estratégicas da empresa. Busca-se o equilíbrio, pois, caso não ocorra, o resultado é uma operação não eficaz da empresa.

A abordagem da pesquisa deste trabalho considerou que um modelo de simulação baseado em Dinâmica de Sistemas fosse uma alternativa de ferramenta computacional que possibilitasse um entendimento sistêmico e integrado das variáveis envolvidas no processo de S&OP: compartilhar o modelo com todos os tomadores de decisão, bem como o uso de análise estatística das simulações dos cenários para avaliação e seleção de planos de S&OP.

O modelo apresentado neste trabalho contempla a integração dos processos de negócio da área financeira no processo de S&OP, o que possibilita a interação das variáveis financeiras de modo que elas contribuam com a construção dos planos. Além disso, são definidas no modelo variáveis que representam indicadores financeiros com o objetivo de auxiliar na análise financeira dos planos gerados. A integração deste processo ao S&OP é uma dificuldade ainda enfrentada pelas empresas e é um assunto que necessita de pesquisa acadêmica.

O modelo fornece agilidade na execução do processo de S&OP, o que possibilita reduzir o tempo para sua realização, uma vez que com o uso da Dinâmica de Sistemas as atividades envolvidas podem ser realizadas de forma interativa e simultânea.

Como a modelagem de todas as atividades envolvidas no processo de S&OP estão representadas no modelo por meio de elementos da dinâmica de sistema, o conhecimento do processo fica explícito e pode ser compartilhado por todos os participantes. Dessa forma, conforme se utiliza o modelo e analisam-se os resultados das simulações, identificando causas e efeitos, mais se aprende sobre o processo de modo que se possam gerar melhores planos de S&OP, buscando a redução da diferença entre o real e o planejado.

O modelo desenvolvido é um modelo referencial e tem flexibilidade para simular o impacto da entrada de novos produtos, bem como mudanças bruscas na demanda, atrasos na entrega de matéria-prima e mudanças nas taxas cambiais, entre outros. O modelo também pode ser facilmente expandido de modo a adicionar novos elementos que represente novas regras de negócio que não estejam atualmente sendo contempladas. Portanto, é possível gerar inúmeras simulações propiciando a geração de inúmeros cenários para tomada de decisão.

Considerando os métodos estatísticos e a utilização de variáveis probabilísticas, tem-se uma estratégia ou guia para a construção de cenários de S&OP e, com o uso de variáveis probabilísticas, podemos incluir ao modelo as incertezas existentes no processo como a previsão de vendas e prazos de entregas. Com abordagem probabilística, aumenta-se o número de cenários de S&OP gerados e o uso de métodos estatísticos se faz necessário para avaliação dos resultados, garantido uma escolha ou decisão com maior grau de assertividade. Nas empresas consultadas, não foi evidenciado o uso de métodos estatísticos em todo o processo de S&OP, somente algumas utilizam o processo de previsão de vendas. O uso adequado de métodos estatísticos pode melhorar a eficácia dos planos gerados pelo processo de S&OP.

Diferentemente das variáveis utilizadas nas planilhas, a utilização da Dinâmica de Sistemas trata o comportamento dinâmico das variáveis que compõem os planos de S&OP, visto que seus valores são computados durante a simulação segundo a lógica do processo modelado e considerando as realimentações existentes, assim, as variáveis que são de natureza dinâmica são calculadas/obtidas no decorrer da simulação em função do tempo e do estado do sistema.

O objetivo de mostrar que a dinâmica de sistema fornece a visão holística do processo foi apresentado neste trabalho. Além disso, apresentou-se uma abordagem baseada no pensamento sistêmico para a geração de planos de S&OP, que se espera ser uma alternativa de prática para as empresas.

Anexo A. Definições dos termos utilizados no modelo de Dinâmica de Sistemas.

Neste anexo, são apresentadas as descrições explicativas de cada variável presente nos macroprocessos do modelo. As variáveis estão agrupadas segundo seus tipos, variáveis do tipo estoque, variáveis do tipo fluxo e variáveis auxiliares.

Quadro 1A
Variáveis do tipo estoque.

Termo usado no modelo	Definição
CapacidadeRestrita	Representa as horas de capacidade disponível para cada centro restritivo.
CapacidadeTotal	Representa as horas totais de capacidade disponível de todos os centros produtivos.
ContasPagar	Variável que acumula os valores de contas a pagar à vista.
ContasPagar Prazo	Variável que acumula os valores de contas a pagar a prazo.
ContasReceber	Variável que acumula os valores de contas a receber.
CustoEstqMP	Representa os valores totais de custo em estoque das famílias de matéria-prima.
CustoEstqProd	Representa os valores totais de custo em estoque das famílias de produto acabado.
Demanda	Armazena o valor médio da previsão de demanda utilizada para definição do plano de estoque por taxa de cobertura.
Divida Emprestimo	Acumula o montante de capital tomado como empréstimo.
EstoqMat KG	Representa a quantidade em estoque das famílias de matéria-prima.
EstoqProd	Representa a quantidade em estoque das famílias de produto acabado.
Faturamento emProcesso	Acumula os valores de receita em processo de faturamento.
Imobilizado Custo	Representa o valor total ativo imobilizado destinado à produção.
Imobilizado Despesa	Representa o valor total ativo imobilizado destinado a despesas.
Producao	Acumula a quantidade de produto acabado que está em processo de fabricação.
Suprimento	Acumula a quantidade de itens de matéria-prima em processo de compras.
SuprimentoR$	Acumula os valores de custo dos itens de matéria-prima em processo de compras.
WIP GGP	Acumula os valores de custo em processo de produção referente aos gastos gerais de produção.
WIP MO	Acumula os valores de custo de mão de obra em processo de produção.
WIP MP	Acumula os valores de custo de matéria-prima em processo de produção.

Quadro 2A
Variáveis do tipo fluxo.

Termo usado no modelo	Definição
Amortizacao	Taxa de amortização da dívida referente ao empréstimo realizado.
Depreciacao Custo	Taxa de depreciação que é apropriada para o custos de produção.
Depreciacao Despesas	Taxa de depreciação que é apropriada como despesas.
Emprestimo bancario	Taxa de entrada para o empréstimo tomado.
EntGGP	Taxa de entrada dos gastos gerais de produção para WIP.
Termo usado no modelo	Definição
EntMO R$	Taxa de entrada dos custos de mão de obra para WIP.
EntradaPrev	Taxa de entrada dos valores de previsão de venda.
EntradaR$ MP	Taxa de entrada dos valores de custos dos itens de matéria-prima adquirido para o estoque de famílias de matéria-prima.
EntradaR$ MPProcesso	Taxa de entrada dos custos de matéria-prima para WIP.
EntradaR$ Produtos	Taxa de entrada dos custos dos produtos produzidos para o estoque de famílias de produto acabado.
EntradasCaixa	Taxa de saída dos valores de receitas do saldo de contas a receber para entrada no caixa.
EntregaMP	Taxa de entrada de itens de matéria-prima adquirida para o estoque de famílias de matéria-prima.
Faturamento	Taxa de saída dos valores de receitas do saldo de faturamento em processo.
FluxoEntrada	Taxa de entrada de valores de receitas para o caixa.
FluxoSaida	Taxa de saída de valores do caixa para pagamento.
HorasAdicionais	Taxa de horas adicionais para incremento de capacidade nos centros restritos.
HorasAdicTotal	Taxa de horas adicionais para incremento da capacidade total.
MatCompra	Taxa de recebimento de matéria-prima.
MatCompra R$	Taxa de recebimento de matéria-prima em valores de custo.
Ordens	Taxa de entrada de ordens de produção para o processo de fabricação.
PerdasInadimplencia	Taxa de saída do saldo de contas a receber por perdas por inadimplência.
RedHorasTotal	Taxa de saída de horas para redução da capacidade total.
ReducaoHoras	Taxa de saída de horas para redução da capacidade dos centros restritos.
ReqCompras	Taxa de entrada de requisições de compras de matéria-prima para processo de aquisição.
ReqCompras R$	Taxa de entrada de requisições de compras em valores de custo para o processo de aquisição.
SaidaMP KG	Taxa de saída em quantidades de matéria-prima do estoque por transferência para produção.
SaidaR$ MP	Taxa de saída em valores de custo de matéria-prima do estoque por transferência para produção.
SaidaR$ MPProcesso	Taxa de saída em valores de custo de matéria-prima em WIP.
SaidaR$ Produtos	Taxa de saída de produtos vendidos em valores de custos.
SaidasCaixa	Taxa de saída de valores do saldo de contas a pagar à vista.
SaidasCaixa Parcelas	Taxa de saída de valores do saldo de contas a pagar a prazo.
SaiGGP	Taxa de saídas dos gastos gerais da produção em WIP.
SaiMO R$	Taxa de saída dos custos de mão de obra em WIP.
Titulos aPagar	Taxa de entrada dos valores de títulos a pagar à vista.
Titulos aPagarPrazo	Taxa de entrada dos valores de títulos a pagar a prazo.
TxProducao	Taxa de saída de produtos acabados do processo de fabricação.
ValorVendas	Taxa de entrada dos valores de vendas para o processo de faturamento.
Vendas	Taxa de saída das quantidades vendidas de produto acabado.

Quadro 3A
Variáveis do tipo auxiliar.

Termo usado no modelo	Definição
AjusteCpRest	Efetua o cálculo de horas necessárias para ajustar a capacidade do centro restrito à capacidade planejada.
AjusteCpRest LimitCaixa	Efetua o cálculo que limita o ajuste de horas em função das restrições de caixa.
AjusteCpTotal	Efetua o cálculo de horas necessárias para ajustar a capacidade total à capacidade planejada.
Alfa	Coeficiente de ajuste alfa para suavização de média de previsão de vendas.
BaixaMP	Calcula os valores de custo de matéria-prima a serem baixados do WIP.
BOM	Lista de materiais por família de produto.
CobertEstq	Tempo de cobertura de estoque de produto acabado planejado para o horizonte de tempo definido para o S&OP.
CobertEstqMP	Tempo de cobertura de estoque de matéria-prima planejado para o horizonte de tempo definido para o S&OP.
Comissoes	Efetua o cálculo de comissão.
Compras Aprovadas	Calcula o volume de compras de matéria-prima aprovadas pelas restrições de caixa.
ConsumoMP	Calcula o consumo de matéria-prima para as ordens de produção em processo.
CpAdicional	Calcula o total de horas de capacidade adicional para os centros restritos.
Termo usado no modelo	Definição
CpNec	Variável que armazena qual o centro restrito da família e a quantidade total de horas necessárias do centro para a produção das quantidades definidas no plano de produção.
CpNec LimitCaixa	Calcula o total de horas de capacidade adicional que foram aprovadas pela restrição do caixa
CpPadrao	Horas de capacidade padrão para cada centro restrito.
CpRest PorFamilia	Variável que relaciona o centro restrito com a família, ou seja, diz qual é o centro restritivo para a família.
CpTotalNec	Calcula o total de horas planejadas para a capacidade total para atender ao plano de produção
CpTotalPadrao	Horas de capacidade total padrão.
CpUtilizada	Indicador de desempenho que calcula o percentual de utilização da capacidade dos centros restritos.
CustIndHora	Calcula os custos indiretos rateados por hora produzida.
CustoHora	Calcula o custo de mão de obra em função das horas efetivamente consumidas no processo de produção.
CustoMedio MP	Calcula o custo médio de matéria-prima consumida para produção de uma unidade de produto.
CustoMO	Calcula o custo total de mão de obra consumida nas ordens de produção concluída.
CustoMP OP	Calcula o custo médio de matéria-prima consumida nas ordens produção concluída.
CustoProdutos Vendidos	Calcula custo dos produtos vendidos por família de produto acabado.
CustosInd FabVar	Calcula o custo indireto varíavel consumido nas ordens de produção concluída.
CustosProdutos Vendidos Total	Custo total de todos os produtos vendidos.
CustoUnit DiretoVariavel	Calcula o custo direto variável por unidade de família de produto.
CustoUnit MedMovel	Calcula o custo unitário médio móvel do produto acabado.
CustoUnit MP	Calcula o custo unitário médio móvel de cada item matéria-prima.
CustoUnit Variavel	Calcula o custo unitário variável.
CustoUnitario	Calcula o custo unitário do produto produzido no período.
CustoUnitario MaoObra	Calcula o custo unitário de mão de obra apropriada no produto acabado.
DepesasGerais	Realiza o somatório de todas as despesas.
Despesas	Calcula as despesas a pagar.
Despesas Administrativas	Calcula as despesas administrativas.
Despesas Comerciais	Calcula as despesas com comercialização.
Despesas Financeiras	Calcula as despesas financeiras.
EBTIDA	Indicador de desempenho que calcula o índice EBTIDA.
EstoqProd Total	Realiza o somatório de todos os produtos em estoque.
Estq Desejado	Plano de estoque desejado.
Faturamento Total	Realiza o somatório das receitas de vendas.
Fim Embolso	Período de termíno das parcelas de embolso.
Gastos Producao	Gastos de produção a pagar.
GastosFixo Producao	Valor mensal dos gastos fixos de produção.
GastosGerais Producao	Calcula o total dos gastos gerais de produção, considerando custos fixos, depreciação e custos indiretos variáveis.
Giro Estoque	Indicador de desempenho que calcula o giro de estoque de produtos.
HoraRestrita Unid	Horas utilizadas da capacidade restrita para a produção de uma unidade da família de produto.
Horas ConsumidaFam	Total de horas consumida da capacidade total por família para as ordens concluídas.
Horas Utilizadas	Total de horas planejadas para ordens liberadas.
HorasEfetiva	Calcula o total de horas capacidade restrita efetivamente disponível para a execução do plano de produção.
HorasTotal Consumida	Calcula o total de horas de capacidade consumida na execução da produção.
HorasTotal Unid	Total de horas utilizadas da capacidade total para a produção de uma unidade de cada família de produto.
HorasUtiliz CentroFam	Total de horas utilizadas por família em cada centro produtivo.
Impostos IRCSSL	Calcula o valor dos impostos I.R. e C.S.L.L. por família no período.
Impostos SobreVenda	Calcula o valor dos impostos sobre a venda por família no período.
ImpostosIRCSSL Total	Calcula o valor total dos impostos I.R. e C.S.L.L. do período.
ImpostosSobreVenda Total	Calcula o valor total dos impostos sobre a venda no período.
Inicio Embolso	Período de início das parcelas de embolso.
LimitarCapacid	Variável lógica para ativar e desativar a restrição do caixa sobre o incremento de capacidade.
LimitarCompra	Variável lógica para ativar e desativar a restrição do caixa sobre a compra de matéria-prima.
Termo usado no modelo	Definição
LimiteCaixa Capacid	Valor limitante de caixa disponível para incremento de capacidade.
LimiteCaixa Compra	Valor limitante de caixa disponível para aquisição de matéria-prima.
ListaCompras	Calcula a necessidade de compra de matéria-prima para reabastecimento do estoque.
ListaMatOP	Calcula o volume de cada família de matéria-prima necessária para o plano de produção.
LucroBruto	Calcula o lucro bruto por família de produto obtido sobre as receitas de vendas do período.
LucroBruto Total	Calcula o lucro bruto total obtido sobre as receitas de vendas do período.
LucroLiquido	Calcula o lucro líquido por família de produto obtido sobre as receitas de vendas do período.
LucroLiquido Total	Calcula o lucro líquido total obtido sobre as receitas de vendas do período.
MargContrib Total	Calcula o valor total de margem de contribuição obtida no período.
MargContrib TotFamilia	Calcula o valor total de margem de contribuição por família de produto obtida no período.
MargContrib Unitaria	Calcula o valor de margem de contribuição unitária por família de produto.
Margem EBTIDA	Indicador de desempenho que calcula o índice EBTIDA obtido sobre a receita de vendas do período.
Margem Liquida	Indicador de desempenho que calcula a margem líquida por família obtida sobre a receita de vendas do período.
MargemLiquida Total	Indicador de desempenho que calcula a margem líquida total obtida sobre as receitas de vendas.
Markup	Calcula o índice de mark up para cálculo do preço de venda sugerido.
MaterialNec	Realiza o somatório das necessidades por família de matéria-prima.
MatPrima Encomenda	Calcula o volume de matéria-prima necessária que é adquirida por encomenda.
Montante Emprestimo	Montante adquirido como empréstimo.
MpDispOP	Calcula a disponibilidade de matéria-prima a ser fornecida para produção.
OPLiberadas	Calcula o volume de ordens a serem liberadas para produção segundo as restrições de capacidade e de matéria-prima.
OPLibMat	Variável que limita o quanto é possível produzir de uma família de produto pelo estoque de matéria-prima disponível.
OPLibMOB	Variável que limita o quanto é possível produzir de uma família de produto com as horas de capacidade efetivamente disponíveis.
PercAloc CpRest	Calcula a porcentagem de horas planejadas de capacidade do centro restrito por familia de produto.
PercAtend PlanoEstq	Indicador de desempenho que calcula o percentual de atendimento de plano de estoque.
PercAtend PlanoProd	Indicador de desempenho que calcula o percentual de atendimento de plano de produção.
PercAtend PlanoVendas	Indicador de desempenho que calcula o percentual de atendimento de plano de vendas.
PercMargem Contrib	Indicador de desempenho que calcula o percentual de margem de contribuição obtido sobre a receita bruta do período, por família de produto.
PercMargem ContrTotal	Indicador de desempenho que calcula o percentual de margem de contribuição total obtido sobre a receita bruta do período.
PercMP PlanoProd	Calcula a porcentagem de matéria-prima planejada para cada família de produto em relação ao total planejado de cada família de matéria-prima.
PercTempo	Calcula o percentual de tempo de ciclo realizado para os produtos que estão em processo de fabricação.
PercUtil PlanCpRest	Calcula o percentual de utilização dos centros produtivos.
PercVendas	Calcula o percentual de participação de cada família de produto sobre o total de vendas.
PgtoJuros	Calcula o valor de juros a ser pago no período para os casos de utilização de empréstimo.
PlanoEstoque	Plano de estoque do S&OP por família de produto.
PlanoEstoque Total	Realiza o somatório do plano de estoque.
PlanoProducao	Calcula o plano de produção de S&OP.
PlanoProducao Total	Realiza o somatório do plano de produção.
PlanoVendas	Calcula o plano de vendas conforme a distribuição probabilística.
PlanoVendas Total	Realiza o somatório do plano de vendas.
PrazoMedio Pagamento	Prazo médio de pagamento de títulos a pagar.
PrazoMedio Recebimento	Prazo médio de recebimento de títulos a receber.
PrazoSupr	Prazo médio de suprimento em dias.
Preco MedioMP	Preço médio de compra deduzindo-se os impostos recuperados.
PrecoVenda	Preço de venda praticado por unidade vendida de cada família de produto acabado.
PrecoVenda Sugerido	Calcula o preço sugerido em função dos custos e do índice de mark up.
PrevisaoVendas	Variável exógena representa graficamente os valores mensais propostos de previsão de vendas.
Producao Total	Volume de produção total.
Produtividade	Taxa de produtividade de cada centro de trabalho restrito.
Termo usado no modelo	Definição
Provisao IRCSSL	Percentual p/ provisão I.R. e CSSL.
Rateio CustosIndiretos	Calcula o rateio dos custos indiretos.
Rateio DespesasGerais	Calcula o rateio das despesas gerais por família de produto.
ReceitaBruta	Calcula a receita bruta obtida no período por família de produto.
ReceitaBruta Total	Calcula a receita bruta total obtida no período.
ReceitaLiquida	Calcula a receita líquida obtida no período por família de produto.
ReceitaLiquida Total	Calcula a receita líquida total obtida no período.
ReservaMP Producao	Calcula o volume de matéria-prima a ser consumido para ordens liberadas.
Resultado Operacional	Calcula o resulta operacional obtido no período por família de produto.
ResultadoOperacional Total	Calcula o resulta operacional total obtido no período.
Tciclo	Calcula o tempo de ciclo de produção realizado.
TCicloProd	Tempo de ciclo de produção para cada família de produto acabado.
Tempo Amortizacao	Tempo de amortização da dívida de empréstimo.
Tempo IncrementoCap	Tempo de atraso para aumento de capacidade.
TempoFat	Variável para tempo de atraso para realização do faturamento.
TempoProc CentroFam	Total de horas de capacidade utilizada de cada centro produtivo por família de produto.
TempoProcTot CentroFam	Calcula o tempo total de horas planejadas para centro produtivo para realização do plano de produção.
Tomar Emprestimo	Variável lógica que ativa ou desativa a aquisição de empréstimo.
TotalHoras Utilizadas	Realiza o somatório do total de horas utilizadas da capacidade.
TotalPlanej CpRest	Calcula o total de horas planejadas por centro produtivo.
TotComissoes	Realiza o somatório das comissões de vendas do período.
TotCompraR$	Calcula o custo total dos materiais planejados para compra.
TotCpNec PorCpRest	Calcula o total de capacidade necessária para cada centro produtivo.
TotCpPadrao	Realiza o somatório da capacidade padrão de cada centro produtivo.
TotCustos IndFabVar	Realiza o somatório dos custos indiretos variáveis.
TotVendas	Realiza o somatório dos valores de vendas.
TotVendas PorFam	Calcula o valor total das vendas por família de produto.
txCapacid Aprovada	Calcula a taxa de capacidade aprovada mediante a restrição do caixa.
txComiss	Percentual de comissão sobre vendas.
txCustoInd Variavel	Percentual do custo indireto variável sobre o total dos custos diretos (mão de obra direta + matéria-prima).
txDepreciacao	Depreciação mensal do ativo destinado à despesa.
txDepreciacao 2	Depreciação mensal do ativo destinado à apropriação dos custos de produção.
txDespAdm	Despesas administrativas. Pode ser informada uma média percentual do total das despesas administrativas sobre o faturamento ou o valor planejado mensalmente conforme Budget.
txDespComerc	Despesas com comercialização. Pode ser informada uma média percentual do total das despesas com comercialização sobre o faturamento ou o valor planejado mensalmente conforme Budget.
txDespFinan	Despesas financeiras. Pode ser informada uma média percentual do total das despesas financeiras sobre o faturamento ou o valor planejado mensalmente conforme Budget.
txImpostos SobreVenda	Percentual de impostos sobre vendas.
txInadimplencia	Percentual de inadimplência.
txJuros	Taxa de juros para aquisição de empréstimo.
txMargem Desejada	Margem de lucro desejada utilizada para cálculo de preço de venda sugerido.
txMatPrima Encomenda	A quantidade por item da lista de materiais que são comprados por encomenda.
txPercCaixa Capacid	Percentual do valor em caixa definido para restrição de incremento de capacidade.
txPercCaixa Compra	Percentual do valor em caixa definido para restrição de compra de matéria-prima.
txRelacaoCpRestrita	Percentual de utilização da capacidade total em relação à utilização total da capacidade do centro restrito, ou seja, é o percentual de utilização da capacidade total quando o recurso crítico estiver com 100% de utilização.
txVlrHoraExtra	Percentual de acréscimo no valor da mão de obra para hora extra.
ValorEstoque	Calcula o valor total do estoque, considerando produto acabado e matéria-prima.
ValorTotal MaoObra	Calcula o valor total de mão de obra disponível no período.
ValorTotal MOBNec	Calcula o valor total de mão de obra planejado para atendimento do plano de produção.
Vendas Total	Realiza o somatório das quantidades de vendas.
VlrHoraMedioMO	Valor hora média da mão de obra direta, incluindo encargos trabalhistas.

Anexo B. Equações do modelo de Dinâmica de Sistemas.

Este anexo contém as equações do modelo organizadas em ordem alfabética e separadas em equações de estoque e fluxo, e equações de variáveis auxiliares.

Equações de estoques (STOCK) e fluxos (INFLOWS, OUTFLOWS)

1. STOCK:

Caixa(t) = Caixa(t - dt) + (FluxoEntrada - FluxoSaida) * dt

INIT Caixa = 6176500

INFLOWS:

FluxoEntrada = EntradasCaixa+Emprestimo_bancario

OUTFLOWS:

FluxoSaida = SaidasCaixa+Amortizacao+PgtoJuros+SaidasCaixa_Parcelas

2. STOCK:

CapacidadeRestrita[CpRest](t) = CapacidadeRestrita[CpRest](t - dt) + (HorasAdicionais[CpRest] - ReducaoHoras[CpRest]) * dt

INIT CapacidadeRestrita[1] = 4186

INIT CapacidadeRestrita[2] = 6728

INIT CapacidadeRestrita[3] = 648

INIT CapacidadeRestrita[4] = 2316

INIT CapacidadeRestrita[5] = 2702

INFLOWS:

HorasAdicionais[CpRest] =

if (AjusteCpRest_LimitCaixa[CpRest]>0) then

AjusteCpRest_LimitCaixa[CpRest]/Tempo_IncrementoCap

else 0

OUTFLOWS:

ReducaoHoras[CpRest] =

if (AjusteCpRest_LimitCaixa[CpRest]) < 0 then

abs(AjusteCpRest_LimitCaixa[CpRest])

else 0

3. STOCK:

CapacidadeTotal(t) = CapacidadeTotal(t - dt) + (HorasAdicTotal - RedHorasTotal) * dt

INIT CapacidadeTotal = 16580

INFLOWS:

HorasAdicTotal =

if (AjusteCpTotal>0) then

AjusteCpTotal/Tempo_IncrementoCap

else 0

OUTFLOWS:

RedHorasTotal =

if (AjusteCpTotal) < 0 then

abs(AjusteCpTotal)

else 0

4. STOCK:

ContasPagar(t) = ContasPagar(t - dt) + (Titulos_aPagar - SaidasCaixa) * dt

INIT ContasPagar = 0

INFLOWS:

Titulos_aPagar = Despesas + Gastos_Producao + arraysum(Impostos_IRCSSL[*]) + ValorTotal_MaoObra +

arraysum(Impostos_SobreVenda[*])

OUTFLOWS:

SaidasCaixa = delay(Titulos_aPagar,1)

5. STOCK:

ContasPagar_Prazo(t) = ContasPagar_Prazo(t - dt) + (Titulos_aPagarPrazo - SaidasCaixa_Parcelas) * dt

INIT ContasPagar_Prazo = 28975968.78

INFLOWS:

Titulos_aPagarPrazo = arraysum(MatCompra_R$[*])

OUTFLOWS:

SaidasCaixa_Parcelas = ContasPagar_Prazo/PrazoMedio_Pagamento

6. STOCK:

ContasReceber(t) = ContasReceber(t - dt) + (Faturamento[1] + Faturamento[2] + Faturamento[3] + Faturamento[4] + Faturamento[5] + Faturamento[familia] - EntradasCaixa - PerdasInadimplencia) * dt

INIT ContasReceber = 34494437.34

INFLOWS:

Faturamento[familia] = delay(ValorVendas[familia],TempoFat)

OUTFLOWS:

EntradasCaixa = ContasReceber/PrazoMedio_Recebimento

PerdasInadimplencia = arraysum(Faturamento[*])*txInadimplencia

7. STOCK:

CustoEstqMP[matprima](t) = CustoEstqMP[matprima](t - dt) + (EntradaR$_MP[matprima] - SaidaR$_MP[matprima]) * dt

INIT CustoEstqMP[1] = 267707.15

INIT CustoEstqMP[2] = 5004021.18

INIT CustoEstqMP[3] = 64541.13

INIT CustoEstqMP[4] = 452026.26

INIT CustoEstqMP[5] = 414151.65

INIT CustoEstqMP[6] = 297213.11

INIT CustoEstqMP[7] = 200090.25

INIT CustoEstqMP[8] = 478391.39

INIT CustoEstqMP[9] = 312988.14

INIT CustoEstqMP[10] = 1549056.15

INFLOWS:

EntradaR$_MP[matprima] = MatCompra_R$[matprima]

OUTFLOWS:

SaidaR$_MP[matprima] = ARRAYSUM(ReservaMP_Producao[*,matprima]) * CustoUnit_MP[matprima]

8. STOCK:

CustoEstqProd[familia](t) = CustoEstqProd[familia](t - dt) + (EntradaR$_Produtos[familia] - SaidaR$_Produtos[familia]) * dt

INIT CustoEstqProd[1] = 2227057.70

INIT CustoEstqProd[2] = 10778045.72

INIT CustoEstqProd[3] = 440137.78

INIT CustoEstqProd[4] = 262372.60

INIT CustoEstqProd[5] = 77500.15

INFLOWS:

EntradaR$_Produtos[familia] = CustoUnitario[familia]*TxProducao[familia]

OUTFLOWS:

SaidaR$_Produtos[familia] = Vendas[familia]*CustoUnit_MedMovel[familia]

9. STOCK:

Demanda[familia](t) = Demanda[familia](t - dt) + (EntradaPrev[familia]) * dt

INIT Demanda[familia] =$({\sum }_{\mathrm{i}=1}^{\mathrm{N}}\left({\mathrm{P}\mathrm{r}\mathrm{e}\mathrm{v}\mathrm{i}\mathrm{s}\mathrm{a}\mathrm{o}\mathrm{V}\mathrm{e}\mathrm{n}\mathrm{d}\mathrm{a}\mathrm{s}\left[\mathrm{f}\mathrm{a}\mathrm{m}\mathrm{i}\mathrm{l}\mathrm{i}\mathrm{a}\right]}_{\mathrm{i}}\right))/\mathrm{}\mathrm{N}$

INFLOWS:

EntradaPrev[familia] = alfa*(PlanoVendas[familia]-Demanda[familia])

10. STOCK:

Divida_Emprestimo(t) = Divida_Emprestimo(t - dt) + (Emprestimo_bancario - Amortizacao) * dt

INIT Divida_Emprestimo = 0

INFLOWS:

Emprestimo_bancario = step(Montante_Emprestimo*Tomar_Emprestimo/(Fim_Embolso-Inicio_Embolso), Inicio_Embolso) + step(-Montante_Emprestimo*Tomar_Emprestimo/(Fim_Embolso-Inicio_Embolso), Fim_Embolso)

OUTFLOWS:

Amortizacao = step(Montante_Emprestimo*Tomar_Emprestimo/Tempo_Amortizacao, Fim_Embolso) +

step(-Montante_Emprestimo*Tomar_Emprestimo/Tempo_Amortizacao, Fim_Embolso + Tempo_Amortizacao)

11. STOCK:

EstoqMat_KG[matprima](t) = EstoqMat_KG[matprima](t - dt) + (EntregaMP[matprima] - SaidaMP_KG[matprima]) * dt

INIT EstoqMat_KG[1] = 147904.50

INIT EstoqMat_KG[2] = 331831.64

INIT EstoqMat_KG[3] = 3536.50

INIT EstoqMat_KG[4] = 16779

INIT EstoqMat_KG[5] = 9185

INIT EstoqMat_KG[6] = 3974.50

INIT EstoqMat_KG[7] = 1660.50

INIT EstoqMat_KG[8] = 1649

INIT EstoqMat_KG[9] = 346

INIT EstoqMat_KG[10] = 226.50

INFLOWS:

EntregaMP[matprima] = MatCompra[matprima]

OUTFLOWS:

SaidaMP_KG[matprima] = ARRAYSUM(ReservaMP_Producao[*,matprima])

12. STOCK:

EstoqProd[familia](t) = EstoqProd[familia](t - dt) + (TxProducao[familia] - Vendas[familia]) * dt

INIT EstoqProd[1] = 53

INIT EstoqProd[2] = 30

INIT EstoqProd[3] = 13

INIT EstoqProd[4] = 15

INIT EstoqProd[5] = 5

INFLOWS:

TxProducao[familia] = delay(Ordens[familia],TCicloProd[familia])

OUTFLOWS:

Vendas[familia] = min(EstoqProd[familia]/dt,PlanoVendas[familia])

13. STOCK:

Faturamento_emProcesso[familia](t) = Faturamento_emProcesso[familia](t - dt) + (ValorVendas[familia] - Faturamento[familia]) * dt

INIT Faturamento_emProcesso[familia] = 4800000

INFLOWS:

ValorVendas[familia] = TotVendas_PorFam[familia]

OUTFLOWS:

Faturamento[familia] = delay(ValorVendas[familia],TempoFat)

14. STOCK:

Imobilizado_Custo(t) = Imobilizado_Custo(t - dt) + (- Depreciacao_Custo) * dt

INIT Imobilizado_Custo = 52140000

OUTFLOWS:

Depreciacao_Custo = txDepreciacao_2

15. STOCK:

Imobilizado_Despesa(t) = Imobilizado_Despesa(t - dt) + (- Depreciacao_Despesas) * dt

INIT Imobilizado_Despesa = 1200000

OUTFLOWS:

Depreciacao_Despesas = txDepreciacao

16. STOCK:

Producao[familia](t) = Producao[familia](t - dt) + (Ordens[familia] - TxProducao[familia]) * dt

INIT Producao[1] = 0.5

INIT Producao[2] = 4.72

INIT Producao[3] = 2.58

INIT Producao[4] = 0.25

INIT Producao[5] = 0.25

INFLOWS:

Ordens[familia] = OPLiberadas[familia]

TIMESTAMPED

OUTFLOWS:

TxProducao[familia] = delay(Ordens[familia],TCicloProd[familia])

17. STOCK:

Suprimento[matprima](t) = Suprimento[matprima](t - dt)+(ReqCompras[matprima]-MatCompra[matprima])*dt

INIT Suprimento[1] = 4815

INIT Suprimento[2] = 115179

INIT Suprimento[3] = 1625

INIT Suprimento[4] = 6428

INIT Suprimento[5] = 9740

INIT Suprimento[6] = 3797

INIT Suprimento[7] = 1582

INIT Suprimento[8] = 951

INIT Suprimento[9] = 364

INIT Suprimento[10] = 338

INFLOWS:

ReqCompras[matprima] = Compras_Aprovadas[matprima]

OUTFLOWS:

MatCompra[matprima] = Suprimento[matprima]/PrazoSupr[matprima]

18. STOCK:

SuprimentoR$[matprima](t) = SuprimentoR$[matprima](t - dt) + (ReqCompras_R$[matprima] - MatCompra_R$[matprima]) * dt

INIT SuprimentoR$[1] = 8715.15

INIT SuprimentoR$[2] = 1736899.32

INIT SuprimentoR$[3] = 29656.25

INIT SuprimentoR$[4] = 173170.32

INIT SuprimentoR$[5] = 439176.60

INIT SuprimentoR$[6] = 283939.66

INIT SuprimentoR$[7] = 190631.00

INIT SuprimentoR$[8] = 275894.61

INIT SuprimentoR$[9] = 329270.76

INIT SuprimentoR$[10] = 2311615.80

INFLOWS:

ReqCompras_R$[matprima] = Compras_Aprovadas[matprima]*Preco_MedioMP[matprima]

OUTFLOWS:

MatCompra_R$[matprima] = SuprimentoR$[matprima]/PrazoSupr[matprima]

19. STOCK:

WIP_GGP(t) = WIP_GGP(t - dt) + (EntGGP - SaiGGP) * dt

INIT WIP_GGP = 115636.92

INFLOWS:

EntGGP = GastosGerais_Producao

OUTFLOWS:

SaiGGP = CustIndHora*HorasTotal_Consumida

20. STOCK:

WIP_MO(t) = WIP_MO(t - dt) + (EntMO_R$ - SaiMO_R$) * dt

INIT WIP_MO = 85483.42

INFLOWS:

EntMO_R$ = ValorTotal_MaoObra

OUTFLOWS:

SaiMO_R$ = HorasTotal_Consumida*CustoHora

21. STOCK:

WIP_MP[matprima](t) = WIP_MP[matprima](t - dt) + (EntradaR$_MPProcesso[matprima] - SaidaR$_MPProcesso[matprima]) * dt

INIT WIP_MP[1] = 24121.99

INIT WIP_MP[2] = 588237.44

INIT WIP_MP[3] = 7018.02

INIT WIP_MP[4] = 13637.50

INIT WIP_MP[5] = 52293.86

INIT WIP_MP[6] = 21600.45

INIT WIP_MP[7] = 26724.80

INIT WIP_MP[8] = 31137.95

INIT WIP_MP[9] = 52559.63

INIT WIP_MP[10] = 502116.31

INFLOWS:

EntradaR$_MPProcesso[matprima] = ARRAYSUM(ReservaMP_Producao[*,matprima]) * CustoUnit_MP[matprima]

OUTFLOWS:

SaidaR$_MPProcesso[matprima] = ARRAYSUM(BaixaMP[*,matprima])

Equações das variáveis

1. AjusteCpRest[CpRest] =

if (CpPadrao[CpRest] >= TotCpNec_PorCpRest[CpRest]) then

(CpPadrao[CpRest]-CapacidadeRestrita[CpRest])

else (TotCpNec_PorCpRest[CpRest]-CapacidadeRestrita[CpRest])

2. AjusteCpRest_LimitCaixa[CpRest] =

if (CpPadrao[CpRest] >= CpNec_LimitCaixa[CpRest]) then

(CpPadrao[CpRest]-CapacidadeRestrita[CpRest])

else (CpNec_LimitCaixa[CpRest]-CapacidadeRestrita[CpRest])

3. AjusteCpTotal =

if (CpTotalPadrao >= (CpTotalNec*txCapacid_Aprovada)) then

(CpTotalPadrao-CapacidadeTotal)

else ((CpTotalNec*txCapacid_Aprovada)-CapacidadeTotal)

4. BaixaMP[familia,matprima] =

if ARRAYSUM(ConsumoMP[*,matprima]) > 0 then

((WIP_MP[matprima] + EntradaR$_MPProcesso[matprima])/ ARRAYSUM(ConsumoMP[*,matprima])) * (TxProducao[familia]*BOM[familia,matprima])

else 0

5. Comissoes[familia] = Faturamento[familia]*txComiss

6. Compras_Aprovadas[matprima] =

if (LimitarCompra=0) then

ListaCompras[matprima]

else

if LimiteCaixa_Compra >= 1 then

ListaCompras[matprima]

else ListaCompras[matprima]*LimiteCaixa_Compra

7. ConsumoMP[familia,matprima] = (Producao[familia]+Ordens[familia])*BOM[familia,matprima]

8. CpAdicional = ARRAYSUM(CapacidadeRestrita[*]) - ARRAYSUM(CpPadrao[*]) + ARRAYSUM(AjusteCpRest[*])

9. CpNec[familia,percapacid] =

if ARRAYIDX(CpRest_PorFamilia[familia,percapacid],2)=1 then

CpRest_PorFamilia[familia,1]

else (HoraRestrita_Unid[familia]*PlanoProducao[familia]) / ARRAYVALUE(Produtividade[*], CpRest_PorFamilia[familia,1])

10. CpNec_LimitCaixa[CpRest] = (CapacidadeRestrita[CpRest]+AjusteCpRest[CpRest]) * txCapacid_Aprovada

11. CpTotalNec =

if ((1+ (CpAdicional/TotCpPadrao)) > (1/txRelacaoCpRestrita)) then

(1+ (CpAdicional/TotCpPadrao)) * (txRelacaoCpRestrita * CpTotalPadrao)

else CpTotalPadrao+CpAdicional

12. CpUtilizada[CpRest] = arraysum(HorasUtiliz_CentroFam[*,CpRest]) / CapacidadeRestrita[CpRest]

13. CustIndHora =

if TotalHoras_Utilizadas > 0 then

(WIP_GGP + GastosGerais_Producao) / TotalHoras_Utilizadas

else 0

14. CustoHora =

if TotalHoras_Utilizadas > 0 then

(WIP_MO + ValorTotal_MaoObra) / TotalHoras_Utilizadas

else 0

15. CustoMedio_MP[familia] = arraysum(CustoMP_OP[familia,*])

16. CustoMO[familia] = CustoHora*Horas_ConsumidaFam[familia]

17. CustoMP_OP[familia,matprima] =

if TxProducao[familia]>0 then

BaixaMP[familia,matprima] / TxProducao[familia]

else 0

18. CustoProdutos_Vendidos[familia] = SaidaR$_Produtos[familia]

19. CustosInd_FabVar[familia] = (TxProducao[familia]*CustoUnit_DiretoVariavel[familia])*txCustoInd_Variavel

20. CustosProdutos_Vendidos_Total = ARRAYSUM(CustoProdutos_Vendidos[*])

21. CustoUnitario[familia] = CustoUnit_DiretoVariavel[familia]+Rateio_CustosIndiretos[familia]

22. CustoUnitario_MaoObra[familia] =

if (TxProducao[familia]>0) then

(CustoMO[familia]/TxProducao[familia])

else 0

23. CustoUnit_DiretoVariavel[familia] = CustoUnitario_MaoObra[familia]+CustoMedio_MP[familia]

24. CustoUnit_MedMovel[familia] =

if (EstoqProd[familia]>0) then

(CustoEstqProd[familia]+EntradaR$_Produtos[familia])/(EstoqProd[familia]+TxProducao[familia])

else

if (TxProducao[familia]>0) then

EntradaR$_Produtos[familia]/TxProducao[familia]

else 0

25. CustoUnit_MP[matprima] =

if (EstoqMat_KG[matprima]>0) then

(CustoEstqMP[matprima]+EntradaR$_MP[matprima]) / (EstoqMat_KG[matprima] + EntregaMP[matprima])

else (EntradaR$_MP[matprima]/EntregaMP[matprima])

26. CustoUnit_Variavel[familia] =

if arraysum(Horas_ConsumidaFam[*]) >0 then

CustoUnit_DiretoVariavel[familia] + ((TotCustos_IndFabVar / arraysum(Horas_ConsumidaFam[*])) * HorasTotal_Unid[familia])

else

CustoUnit_DiretoVariavel[familia]

27. DepesasGerais = TotComissoes + Despesas_Administrativas + Despesas_Comerciais + Despesas_Financeiras + Depreciacao_Despesas

28. Despesas = DepesasGerais-Depreciacao_Despesas

29. Despesas_Administrativas = txDepAdm*Faturamento_Total

30. Despesas_Comerciais = txDespComerc*Faturamento_Total

31. Despesas_Financeiras = (txDespFinan*Faturamento_Total)+PgtoJuros+Amortizacao

32. EBTIDA = arraysum(Resultado_Operacional[*]) + Despesas_Financeiras + Depreciacao_Custo + Depreciacao_Despesas

33. EstoqProd_Total = ARRAYSUM(EstoqProd[*])

34. Faturamento_Total = ARRAYSUM(Faturamento[*])

35. Fim_Embolso = Inicio_Embolso+1

36. GastosGerais_Producao = GastosFixo_Producao+Depreciacao_Custo+TotCustos_IndFabVar

37. Gastos_Producao = GastosGerais_Producao-Depreciacao_Custo

38. Giro_Estoque =

if (arraysum(CustoProdutos_Vendidos[*])>0) then

ValorEstoque/ARRAYSUM(CustoProdutos_Vendidos[*])

else 0

39. HorasEfetiva[CpRest] = CapacidadeRestrita[CpRest]*Produtividade[CpRest]

40. HorasTotal_Consumida = ARRAYSUM(Horas_ConsumidaFam[*])

41. HorasUtiliz_CentroFam[familia,CpRest] = TempoProc_CentroFam[familia,CpRest]*OPLiberadas[familia]

42. Horas_ConsumidaFam[familia] = (TxProducao[familia]*HorasTotal_Unid[familia])

43. Horas_Utilizadas[familia] = (OPLiberadas[familia]*HorasTotal_Unid[familia]) + (Producao[familia]*HorasTotal_Unid[familia]*PercTempo[familia])

44. ImpostosIRCSSL_Total = ARRAYSUM(Impostos_IRCSSL[*])

45. ImpostosSobreVenda_Total = ARRAYSUM(Impostos_SobreVenda[*])

46. Impostos_IRCSSL[familia] =

if (Resultado_Operacional[familia]>0) then

Resultado_Operacional[familia]*Provisao_IRCSSL

else 0

47. Impostos_SobreVenda[familia] = ReceitaBruta[familia]*txImpostos_SobreVenda

48. LimiteCaixa_Capacid = Caixa*txPercCaixa_Capacid

49. LimiteCaixa_Compra =

if (arraysum(TotCompraR$[*]))>0 then

(Caixa*txPercCaixa_Compra) / (arraysum(TotCompraR$[*]))

else 1

50. ListaCompras[matprima] =

if (((MaterialNec[matprima]-MatPrima_Encomenda[matprima]) * CobertEstqMP) + (MaterialNec[matprima]-MatPrima_Encomenda[matprima]) - (EstoqMat_KG[matprima] + Suprimento[matprima])) >0 then

(((MaterialNec[matprima]-MatPrima_Encomenda[matprima]) * CobertEstqMP) + (MaterialNec[matprima]-MatPrima_Encomenda[matprima])) - (EstoqMat_KG[matprima] + Suprimento[matprima]) + MatPrima_Encomenda[matprima]

else MatPrima_Encomenda[matprima]

51. ListaMatOP[familia,matprima] = BOM[familia,matprima]*PlanoProducao[familia]

52. LucroBruto[familia] = ReceitaLiquida[familia]-CustoProdutos_Vendidos[familia]

53. LucroBruto_Total = ARRAYSUM(LucroBruto[*])

54. LucroLiquido[familia] = Resultado_Operacional[familia]-Impostos_IRCSSL[familia]

55. LucroLiquido_Total = ARRAYSUM(LucroLiquido[*])

56. MargContrib_Total = ARRAYSUM(MargContrib_TotFamilia[*])

57. MargContrib_TotFamilia[familia] = ReceitaLiquida[familia] - Comissoes[familia] - (CustoUnit_Variavel[familia]*Vendas[familia])

58. MargContrib_Unitaria[familia] =

if Vendas[familia] > 0 then

MargContrib_TotFamilia[familia]/Vendas[familia]

else 0

59. MargemLiquida_Total =

if arraysum(ReceitaLiquida[*])>0 then

(arraysum(LucroLiquido[*])/arraysum(ReceitaLiquida[*]))*100

else 0

60. Margem_EBTIDA =

if (arraysum(ReceitaLiquida[*])>0) then

(EBTIDA/arraysum(ReceitaLiquida[*]))*100

else 0

61. Margem_Liquida[familia] =

if ReceitaLiquida[familia]>0 then

(LucroLiquido[familia]/ReceitaLiquida[familia])*100

else 0

62. Markup = txComiss+txDepAdm+txDespComerc+txDespFinan+txMargem_Desejada+txImpostos_SobreVenda

63. MaterialNec[matprima] = ARRAYSUM(ListaMatOP[*,matprima])

64. MatPrima_Encomenda[matprima] = MaterialNec[matprima]*txMatPrima_Encomenda[matprima]

65. MpDispOP[familia,matprima] =

if BOM[familia,matprima] > 0 then

(EstoqMat_KG[matprima]*PercMP_PlanoProd[familia,matprima]) / BOM[familia,matprima]

else 999999999

66. OPLiberadas[familia] = min(OPLibMat[familia],OPLibMOB[familia],PlanoProducao[familia])

67. OPLibMat[familia] = ARRAYMIN(MpDispOP[familia,*])

68. OPLibMOB[familia] =

if (CpRest_PorFamilia[familia,2] =1) then

int((ARRAYVALUE(HorasEfetiva[*],CpRest_PorFamilia[familia,1]) * PercAloc_CpRest[familia,2]) / HoraRestrita_Unid[familia])

else int((ARRAYVALUE(HorasEfetiva[*],CpRest_PorFamilia[familia,1]) * CpRest_PorFamilia[familia,2]) / HoraRestrita_Unid[familia])

69. PercAloc_CpRest[familia,percapacid] =

if ARRAYIDX(CpNec[familia,percapacid],2)=1 then

CpNec[familia,1]

else

if ARRAYVALUE(TotCpNec_PorCpRest[*], CpNec[familia,1]) > 0 then

CpNec[familia,2] / ARRAYVALUE(TotCpNec_PorCpRest[*], CpNec[familia,1])

else 0

70. PercAtend_PlanoEstq =

if PlanoEstoque_Total > 0 then

(EstoqProd_Total/PlanoEstoque_Total)*100

else 0

71. PercAtend_PlanoProd =

if PlanoProducao_Total>0 then

(Producao_Total/PlanoProducao_Total)*100

else 0

72. PercAtend_PlanoVendas =

if PlanoVendas_Total > 0 then

(Vendas_Total/PlanoVendas_Total)*100

else 0

73. PercMargem_Contrib[familia] =

if ReceitaBruta[familia]>0 then

(MargContrib_TotFamilia[familia]/ReceitaBruta[familia])*100

else 0

74. PercMargem_ContrTotal =

if ReceitaBruta_Total>0 then

(MargContrib_Total/ReceitaBruta_Total)*100

else -100

75. PercMP_PlanoProd[familia,matprima] =

if MaterialNec[matprima]>0 then

(PlanoProducao[familia]*BOM[familia,matprima]) / MaterialNec[matprima]

else 0

76. PercTempo[familia] = TCiclo[familia]/TCicloProd[familia]

77. PercUtil_PlanCpRest[CpRest] = (TotalPlanej_CpRest[CpRest]/CpPadrao[CpRest])*100

78. PercVendas[familia] =

if(TotVendas>0) then

TotVendas_PorFam[familia]/TotVendas

else 0

79. PgtoJuros = txJuros*Divida_Emprestimo

80. PlanoEstoque[familia] =

if Estq_Desejado[familia] > 0 then

Estq_Desejado[familia]

else int(CobertEstq[familia]*Demanda[familia])

81. PlanoEstoque_Total = ARRAYSUM(PlanoEstoque[*])

82. PlanoProducao[familia] = int(Max(0,PlanoEstoque[familia]-EstoqProd[familia]+PlanoVendas[familia]))

83. PlanoProducao_Total = ARRAYSUM(PlanoProducao[*])

84. PlanoVendas[familia] = max(0, NORMAL(PrevisaoVendas[familia], (0.10*PrevisaoVendas[familia])))

85. PlanoVendas_Total = ARRAYSUM(PlanoVendas[*])

86. PrecoVenda_Sugerido[familia] =

if (Vendas[familia]>0) then

((CustoProdutos_Vendidos[familia]+(Depreciacao_Despesas*PercVendas[familia]))/(1-Markup))/Vendas[familia]

else 0

87. Producao_Total = ARRAYSUM(TxProducao[*])

88. Rateio_CustosIndiretos[familia] =

if TxProducao[familia] > 0 then

(CustIndHora*Horas_ConsumidaFam[familia])/TxProducao[familia]

else 0

89. Rateio_DespesasGerais[familia] = DepesasGerais*PercVendas[familia]

90. ReceitaBruta[familia] = Faturamento[familia]

91. ReceitaBruta_Total = ARRAYSUM(ReceitaBruta[*])

92. ReceitaLiquida[familia] = ReceitaBruta[familia]-Impostos_SobreVenda[familia]

93. ReceitaLiquida_Total = ARRAYSUM(ReceitaLiquida[*])

94. ReservaMP_Producao[familia,matprima] = OPLiberadas[familia]*BOM[familia,matprima]

95. ResultadoOperacional_Total = ARRAYSUM(Resultado_Operacional[*])

96. Resultado_Operacional[familia] = LucroBruto[familia]-Rateio_DespesasGerais[familia]

97. TCiclo[familia] = CYCLETIME(TxProducao[familia])

98. TempoProcTot_CentroFam[familia,CpRest] = TempoProc_CentroFam[familia,CpRest]*PlanoProducao[familia]

99. TotalHoras_Utilizadas = arraysum(Horas_Utilizadas[*])

100. TotalPlanej_CpRest[CpRest] = arraysum(TempoProcTot_CentroFam[*,CpRest])

101. TotComissoes = ARRAYSUM(Comissoes[*])

102. TotCompraR$[matprima] = Preco_MedioMP[matprima]*ListaCompras[matprima]

103. TotCpNec_PorCpRest[CpRest] = (if (CpNec[1,1]=CpRest) then CpNec[1,2] else 0) + (if (CpNec[2,1]= CpRest) then CpNec[2,2] else 0) + (if (CpNec[3,1]= CpRest) then CpNec[3,2] else 0) + (if (CpNec[4,1]= CpRest) then CpNec[4,2] else 0) + (if (CpNec[5,1]= CpRest) then CpNec[5,2] else 0)

104. TotCpPadrao = ARRAYSUM(CpPadrao[*])

105. TotCustos_IndFabVar = ARRAYSUM(CustosInd_FabVar[*])

106. TotVendas = ARRAYSUM(TotVendas_PorFam[*])

107. TotVendas_PorFam[familia] = Vendas[familia]*PrecoVenda[familia]

108. txCapacid_Aprovada =

if (LimitarCapacid=0) then 1

else

if (LimiteCaixa_Capacid >= ValorTotal_MOBNec) then 1

else (LimiteCaixa_Capacid/ValorTotal_MOBNec)

109. ValorEstoque = ARRAYSUM(CustoEstqProd[*])+ARRAYSUM(CustoEstqMP[*])

110. ValorTotal_MaoObra = (CapacidadeTotal*VlrHoraMedioMO)+(((CapacidadeTotal-CpTotalPadrao) * VlrHoraMedioMO)*txVlrHoraExtra)

111. ValorTotal_MOBNec = (CpTotalNec*VlrHoraMedioMO) + (((CpTotalNec-CpTotalPadrao)*VlrHoraMedioMO)* txVlrHoraExtra)

112. Vendas_Total = ARRAYSUM(Vendas[*])

Anexo C. Variáveis e funções gráficas do modelo de Dinâmica de Sistemas.

Este anexo contém as variáveis constantes e variáveis de funções gráficas utilizadas no modelo, ambas organizadas em ordem alfabética.

Quadro 1C
Variáveis constantes.

alfa = 0.2 BOM[1,1] = 470; BOM[1,2] = 1225; BOM[1,3] = 4; BOM[1,4] = 14; BOM[1,5] = 68; BOM[1,6] = 17; BOM[1,7] = 6; BOM[1,8] = 6; BOM[1,9] = 2; BOM[1,10] = 0; BOM[2,1] = 2574; BOM[2,2] = 7673; BOM[2,3] = 75; BOM[2,4] = 90; BOM[2,5] = 223; BOM[2,6] = 57; BOM[2,7] = 44; BOM[2,8] = 21; BOM[2,9] = 11; BOM[2,10] = 15; BOM[3,1] = 263; BOM[3,2] = 776; BOM[3,3] = 11; BOM[3,4] = 12; BOM[3,5] = 24; BOM[3,6] = 2; BOM[3,7] = 3; BOM[3,8] = 2; BOM[3,9] = 2; BOM[3,10] = 1; BOM[4,1] = 668; BOM[4,2] = 394; BOM[4,3] = 0; BOM[4,4] = 87; BOM[4,5] = 22; BOM[4,6] = 16; BOM[4,7] = 0; BOM[4,8] = 0; BOM[4,9] = 0; BOM[4,10] = 0; BOM[5,1] = 364; BOM[5,2] = 238; BOM[5,3] = 0; BOM[5,4] = 86; BOM[5,5] = 21; BOM[5,6] = 8; BOM[5,7] = 13; BOM[5,8] = 0; BOM[5,9] = 0; BOM[5,10] = 0 CobertEstqMP = [1; 2] CpPadrao[1] = 4186 CpPadrao[2] = 6728 CpPadrao[3] = 648 CpPadrao[4] = 2316 CpPadrao[5] = 2702 CpRest = [1; 2; 3; 4; 5] CpRest_PorFamilia[1,1] = 4 CpRest_PorFamilia[1,2] = 1 CpRest_PorFamilia[2,1] = 4 CpRest_PorFamilia[2,2] = 1 CpRest_PorFamilia[3,1] = 4 CpRest_PorFamilia[3,2] = 1 CpRest_PorFamilia[4,1] = 4 CpRest_PorFamilia[4,2] = 1 CpRest_PorFamilia[5,1] = 4 CpRest_PorFamilia[5,2] = 1 CpTotalPadrao = 16580 familia = [1; 2; 3; 4; 5] GastosFixo_Producao = 1200000 HoraRestrita_Unid[1] = 8 HoraRestrita_Unid[2] = 65

HoraRestrita_Unid[3] = 6 HoraRestrita_Unid[4] = 3.5 HoraRestrita_Unid[5] = 3.5 HorasTotal_Unid[1] = 45 HorasTotal_Unid[2] = 284 HorasTotal_Unid[3] = 30 HorasTotal_Unid[4] = 20 HorasTotal_Unid[5] = 21.5 Inicio_Embolso = 4 LimitarCapacid = 0 LimitarCompra = 0 matprima = [1; 2; 3; 4; 5; 6; 7; 8; 9; 10] Montante_Emprestimo = 500000 N = [1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12] PrazoMedio_Pagamento = 3 PrazoMedio_Recebimento = 1 PrazoSupr[1] = NORMAL(0.23,0.06) PrazoSupr[2] = NORMAL(0.67,0.06) PrazoSupr[3] = NORMAL(0.5,0.06) PrazoSupr[4] = NORMAL(0.5,0.06) PrazoSupr[5] = NORMAL(0.5,0.06) PrazoSupr[6] = NORMAL(0.5,0.06) PrazoSupr[7] = NORMAL(0.5,0.06) PrazoSupr[8] = NORMAL(0.5,0.06) PrazoSupr[9] = NORMAL(0.23,0.06) PrazoSupr[10] = NORMAL(0.23,0.06) PrecoVenda[1] = 101500 PrecoVenda[2] = 849000 PrecoVenda[3] = 80200 PrecoVenda[4] = 43960 PrecoVenda[5] = 38900 Produtividade[CpRest] = 0.8 Provisao_IRCSSL = 0.24 TCicloProd[1] = normal(0.5,0.06) TCicloProd[2] = normal(0.66,0.06) TCicloProd[3] = normal(0.5,0.06) TCicloProd[4] = normal(0.23,0.03) TCicloProd[5] = normal(0.23,0.03) TempoFat = 0 TempoProc_CentroFam[1,1] = 5 TempoProc_CentroFam[1,2] = 23 TempoProc_CentroFam[1,3] = 2 TempoProc_CentroFam[1,4] = 8 TempoProc_CentroFam[1,5] = 7 TempoProc_CentroFam[2,1] = 51

TempoProc_CentroFam[2,2] = 122 TempoProc_CentroFam[2,3] = 2 TempoProc_CentroFam[2,4] = 65 TempoProc_CentroFam[2,5] = 44 TempoProc_CentroFam[3,1] = 3 TempoProc_CentroFam[3,2] = 15 TempoProc_CentroFam[3,3] = 1 TempoProc_CentroFam[3,4] = 6 TempoProc_CentroFam[3,5] = 5 TempoProc_CentroFam[4,1] = 3 TempoProc_CentroFam[4,2] = 10 TempoProc_CentroFam[4,3] = 0.5 TempoProc_CentroFam[4,4] = 3.5 TempoProc_CentroFam[4,5] = 3 TempoProc_CentroFam[5,1] = 3.5 TempoProc_CentroFam[5,2] = 10 TempoProc_CentroFam[5,3] = 0.5 TempoProc_CentroFam[5,4] = 3.5 TempoProc_CentroFam[5,5] = 4 Tempo_Amortizacao = 6 Tempo_IncrementoCap = 0.125 Tomar_Emprestimo = 0 txComiss = 0.0266 txCustoInd_Variavel = 0.08 txDepAdm = 0.07 txDepreciacao = 10000 txDepreciacao_2 = 434500 txDespComerc = 0.08 txDespFinan = 0.003 txImpostos_SobreVenda = 0.2725 txInadimplencia = 0.003 txJuros = 1.5/100 txMargem_Desejada = 0.15 txMatPrima_Encomenda[1] = 0 txMatPrima_Encomenda[2] = 0 txMatPrima_Encomenda[3] = 0 txMatPrima_Encomenda[4] = 0 txMatPrima_Encomenda[5] = 0 txMatPrima_Encomenda[6] = 0 txMatPrima_Encomenda[7] = 0 txMatPrima_Encomenda[8] = 0 txMatPrima_Encomenda[9] = 0 txMatPrima_Encomenda[10] = 0 txPercCaixa_Capacid = 0.40 txPercCaixa_Compra = 0.40 txRelacaoCpRestrita = 0.74 txVlrHoraExtra = 0.75 VlrHoraMedioMO = 104.50

Equações de funções gráficas

1. CobertEstq[1..5] = GRAPH(TIME) (0.00, 0.00)

2. Estq_Desejado = GRAPH(TIME) – Valores definido, para cada experimento, conforme Tabela 2 no corpo do texto.

3. Preco_MedioMP[1] = GRAPH(TIME) (1.00, 1.81), (2.00, 1.81), (3.00, 1.81), (4.00, 1.81), (5.00, 1.81), (6.00, 1.81), (7.00, 1.81), (8.00, 1.81), (9.00, 1.81), (10.0, 1.81), (11.0, 1.81), (12.0, 1.81), (13.0, 1.81)

4. Preco_MedioMP[2] = GRAPH(TIME) (1.00, 15.1), (2.00, 15.1), (3.00, 15.1), (4.00, 15.1), (5.00, 15.1), (6.00, 15.1), (7.00, 15.1), (8.00, 15.1), (9.00, 15.1), (10.0, 15.1), (11.0, 15.1), (12.0, 15.1), (13.0, 15.1)

5. Preco_MedioMP[3] = GRAPH(TIME) (1.00, 18.3), (2.00, 18.3), (3.00, 18.3), (4.00, 18.3), (5.00, 18.3), (6.00, 18.3), (7.00, 18.3), (8.00, 18.3), (9.00, 18.3), (10.0, 18.3), (11.0, 18.3), (12.0, 18.3), (13.0, 18.3)

6. Preco_MedioMP[4] = GRAPH(TIME) (1.00, 26.9), (2.00, 26.9), (3.00, 26.9), (4.00, 26.9), (5.00, 26.9), (6.00, 26.9), (7.00, 26.9), (8.00, 26.9), (9.00, 26.9), (10.0, 26.9), (11.0, 26.9), (12.0, 26.9), (13.0, 26.9)

7. Preco_MedioMP[5] = GRAPH(TIME) (1.00, 45.1), (2.00, 45.1), (3.00, 45.1), (4.00, 45.1), (5.00, 45.1), (6.00, 45.1), (7.00, 45.1), (8.00, 45.1), (9.00, 45.1), (10.0, 45.1), (11.0, 45.1), (12.0, 45.1), (13.0, 45.1)

8. Preco_MedioMP[6] = GRAPH(TIME) (1.00, 74.8), (2.00, 74.8), (3.00, 74.8), (4.00, 74.8), (5.00, 74.8), (6.00, 74.8), (7.00, 74.8), (8.00, 74.8), (9.00, 74.8), (10.0, 74.8), (11.0, 74.8), (12.0, 74.8), (13.0, 74.8)

9. Preco_MedioMP[7] = GRAPH(TIME) (1.00, 121), (2.00, 121), (3.00, 121), (4.00, 121), (5.00, 121), (6.00, 121), (7.00, 121), (8.00, 121), (9.00, 121), (10.0, 121), (11.0, 121), (12.0, 121), (13.0, 121)

10. Preco_MedioMP[8] = GRAPH(TIME) (1.00, 290), (2.00, 290), (3.00, 290), (4.00, 290), (5.00, 290), (6.00, 290), (7.00, 290), (8.00, 290), (9.00, 290), (10.0, 290), (11.0, 290), (12.0, 290), (13.0, 290)

11. Preco_MedioMP[9] = GRAPH(TIME) (1.00, 905), (2.00, 905), (3.00, 905), (4.00, 905), (5.00, 905), (6.00, 905), (7.00, 905), (8.00, 905), (9.00, 905), (10.0, 905), (11.0, 905), (12.0, 905), (13.0, 905)

12. Preco_MedioMP[10] = GRAPH(TIME) (1.00, 6839), (2.00, 6839), (3.00, 6839), (4.00, 6839), (5.00, 6839), (6.00, 6839), (7.00, 6839), (8.00, 6839), (9.00, 6839), (10.0, 6839), (11.0, 6839), (12.0, 6839), (13.0, 6839)

13. PrevisaoVendas = GRAPH(TIME) – Valores definidos para cada experimento, conforme Tabela 1 no corpo do texto.

• Suporte financeiro: Nenhum.

Referências

• Azevedo, R. C., Bremer, C. F., Rebelatto, D. A., & Tarallo, F. B. (2006). O uso de ERP e CRM no suporte à gestão da demanda em ambientes de produção Make-to-Stock. Gestão & Produção, 13(2), 179-190.
• Box, G., Hunter, W. G., & Hunter, J. S. (1978). Statistics for experimenters. New York: John Wiley & Sons.
• Cagliano, A. C, DeMarco, A., Rafele, C., & Volpe, S. (2011). Using system dynamics in warehouse management: a fast-fashion case study. Journal of Manufacturing Technology Management, 22(2), 171-188. http://dx.doi.org/10.1108/17410381111102207.
  » http://dx.doi.org/10.1108/17410381111102207
• Chen-Ritzo, C., Ervolina, T., Harrinson, T. P., & Gupta, B. (2010). Sales and operations planning in systems with order configuration uncertain. European Journal of Operational Research, 205(3), 604-614. http://dx.doi.org/10.1016/j.ejor.2010.01.029.
  » http://dx.doi.org/10.1016/j.ejor.2010.01.029
• Corrêa, H. L., Gianesi, I. G. N., & Caon, M. (2007). Planejamento, programação e controle da produção (5. ed.). São Paulo: Atlas.
• Freitas, F. P. J. (2001). Introdução à modelagem e simulação de sistemas: com aplicações em arena. Visual Books.
• Genin, P., Thomas, A., & Lamouri, S. (2007). How to manage robust tactical planning with an APS (Advanced Planning Systems). Journal of Intelligent Manufacturing, 18(2), 209-221. http://dx.doi.org/10.1007/s10845-007-0015-y.
  » http://dx.doi.org/10.1007/s10845-007-0015-y
• Georgiadis, P., & Michaloudis, C. (2012). Real-time production planning and control system for job-shop manufacturing: a system dynamics analysis. European Journal of Operational Research, 216(1), 94-104. http://dx.doi.org/10.1016/j.ejor.2011.07.022.
  » http://dx.doi.org/10.1016/j.ejor.2011.07.022
• Gitman, L. J. (2010). Princípios de administração financeira (12. ed.). São Paulo: Pearson Addison Wesley. 775 p.
• Godinho, M., Fo., & Uzsoy, R. (2009). Efeito da redução do tamanho de lote e de programas de Melhoria Contínua no Estoque em Processo (WIP) e na utilização: estudo utilizando uma abordagem híbrida System Dynamics - Factory Physics. Produção, 19(1), 214-229.
• Hahn, G. J., & Kuhn, H. (2012). Value-based performance and risk management in supply chains: a robust optimization approach. International Journal of Production Economics, 139(1), 135-144.
• Helal, M., Rabelo, L., Veda, J. S., & Jones, A. (2007). A methodology for integrating and synchronizing the system dynamics and discrete event simulation paradigms. In Proceedings of the 25 International Conference of the System Dynamics Society. Boston.
• Hicks, C. R. (1973). Fundamental concepts in the design of experiments. New York: John Wiley and Sons.
• Hvolby, H., & Steger-Jensen, K. (2010). Technical and industrial issues of Advanced Planning and Scheduling (APS) Systems. Computers in Industry, 61(9), 845-851. http://dx.doi.org/10.1016/j.compind.2010.07.009.
  » http://dx.doi.org/10.1016/j.compind.2010.07.009
• Ivert, L. K., & Jonsson, P. (2011). Problems in the onward and upward phase of APS system implementation Why do they occur? International Journal of Physical Distribution & Logistics Management, 41(4), 343-363. http://dx.doi.org/10.1108/09600031111131922.
  » http://dx.doi.org/10.1108/09600031111131922
• Ivert, L. K., & Jonsson, P. (2010). The potential benefits of advanced planning and scheduling systems in sales and operations planning. Industrial Management & Data Systems, 110(5), 659-681. http://dx.doi.org/10.1108/02635571011044713.
  » http://dx.doi.org/10.1108/02635571011044713
• Johnson, N. L., & Leone, F. C. (1977). Statistics and experimental design. New York: John Wiley and Sons.
• Jonsson, P., Kjellsdotter, L., & Rudberg, M. (2007). Applying advanced planning systems for supply chain planning: three case studies. International Journal of Physical Distribution & Logistics Management, 37(10), 816-833. http://dx.doi.org/10.1108/09600030710848932.
  » http://dx.doi.org/10.1108/09600030710848932
• Kamath, N. B., & Roy, R. (2007). Capacity augmentation of a supply chain for a short lifecycle product: a system dynamics framework. European Journal of Operational Research, 179(2), 334-351. http://dx.doi.org/10.1016/j.ejor.2006.03.045.
  » http://dx.doi.org/10.1016/j.ejor.2006.03.045
• Landeghem, H. V., & Vanmaele, H. (2002). Robust planning: a new paradigm for demand chain planning. Journal of Operations Management, 20(6), 769-783. http://dx.doi.org/10.1016/S0272-6963(02)00039-6.
  » http://dx.doi.org/10.1016/S0272-6963(02)00039-6
• Martinez-Olvera, C. (2009). Benefits of using hybrid business models within a supply chain. International Journal of Production Economics, 120(2), 501-511. http://dx.doi.org/10.1016/j.ijpe.2009.04.006.
  » http://dx.doi.org/10.1016/j.ijpe.2009.04.006
• Martins, E. (2003). Contabilidade de custos (9. ed.). São Paulo: Atlas. 370 p.
• Montgomery, D. C. (1976). Design and analysis of experiments. New York: Wiley.
• Morecroft, J., & Robinson, S. (2005). Explaining puzzling dynamics: comparing the use of system dynamics and discrete-event simulation. In Proceedings of the 23th System Dynamics Society International Conference. Boston: System Dynamics Review.
• Olhager, J. (2010). The role of the customer order decoupling point in production and supply chain management. Computers in Industry, 61(9), 863-868. http://dx.doi.org/10.1016/j.compind.2010.07.011.
  » http://dx.doi.org/10.1016/j.compind.2010.07.011
• Orcun, S., Uzsoy, R., & Kempf, K. (2006). Using system dynamics simulations to compare capacity models for production planning. In IEEE Proceedings of the Winter Simulation Conference. Monterey: IEEE.
• Pandin, F. J., Pereira, N. A., & Politano, P. R. (2012). Modelo quantitativo para avaliação e melhoria de desempenho do processo de S&OP baseado no diagnóstico e redução de falhas. Gestão & Produção, 19(2), 361-375. http://dx.doi.org/10.1590/S0104-530X2012000200010.
  » http://dx.doi.org/10.1590/S0104-530X2012000200010
• Pastrana, J., Marin, M., Helal, M., & Mendizabal, C. (2010). Enterprise scheduling: hybrid and hierarchical issues. In Proceedings of the 2010 Winter Simulation Conference (WSC). Baltimore.
• Rabelo, L., Son, Y. J., Helal, M., Jones, A., Min, J., & Deshmukh, A. (2003). A hybrid approach to manufacturing enterprise simulation. In Proceedings of the 2003 Winter Simulation Conference (Vol. 2, pp. 1125-1133).
• Rudberg, M., & Cederborg, O. (2011). APS for tactical planning in a steel processing company. Industrial Management & Data Systems, 111(4), 608-628. http://dx.doi.org/10.1108/02635571111133579.
  » http://dx.doi.org/10.1108/02635571111133579
• Sakuramoto, C. Y. (2008). A influência da conectividade no desempenho de uma cadeia de suprimentos característica do setor automobilístico brasileiro utilizando a dinâmica de sistemas (Tese de doutorado). Escola de Administração de Empresas de São Paulo/FGV, São Paulo.
• Sasaki, F. A., Oliveira, G. H. C., Araujo, H. X., Cardoso, P. A., & Pacheco, E. O. (2008). Gerenciando uma cadeia de suprimentos utilizando a dinâmica de sistemas. In Anais do XXVIII Encontro Nacional de Engenharia de Produção. Rio de Janeiro.
• Scheffé, H. (1959). The analysis of variance. New York: Wiley.
• Schlegel, G. L., & Murray, P. (2010). Next generation of S&OP: scenario planning with predictive analytics & digital Modeling. Journal of Business Forecasting, 29(3), 20-30.
• Shapiro, J. E. (2010). Advanced analytics for sales & operations planning. Analytics, may-june, 20-26. Recuperado em 17 de setembro de 2011, de http://www.analytics-magazine.org
  » http://www.analytics-magazine.org
• Silva, O. S. Fo, Cesarino, W., & Ratto, J. (2009). Planejamento agregado da produção: modelagem e solução via planilha Excel e Solver. Revista Produção On Line, IX(3), 572-599.
• Stadtler, H. (2005). Supply chain management and advanced planning: basics, overview and challenges. European Journal of Operational Research, 163(3), 575-588. http://dx.doi.org/10.1016/j.ejor.2004.03.001.
  » http://dx.doi.org/10.1016/j.ejor.2004.03.001
• Sterman, J. D. (2000). Business dynamics: system thinking and modeling a complex world (1. ed.). USA: McGraw Hill.
• Suryani, E., Chou, S., Hartono, R., & Chen, C. (2010). Demand scenario analysis and planned capacity expansion: a system dynamics framework. Simulation Modelling Practice and Theory, 18(6), 732-751. http://dx.doi.org/10.1016/j.simpat.2010.01.013.
  » http://dx.doi.org/10.1016/j.simpat.2010.01.013
• Tako, A. A., & Robinson, S. (2012). The application of discrete event simulation and system dynamics in the logistics and supply chain context. Journal Decision Support Systems, 52(4), 802-815. http://dx.doi.org/10.1016/j.dss.2011.11.015.
  » http://dx.doi.org/10.1016/j.dss.2011.11.015
• Thomé, A. M. T., Scavarda, L. F., Fernandez, N. S., & Scavarda, A. J. (2012). Sales and operations planning: a research synthesis. International Journal of Production Economics, 138(1), 1-13. http://dx.doi.org/10.1016/j.ijpe.2011.11.027.
  » http://dx.doi.org/10.1016/j.ijpe.2011.11.027
• Towill, D. R. (1996). Industrial dynamics modelling of supply chains. Logistics Information Management, 9(4), 43-56. http://dx.doi.org/10.1108/09576059610116707.
  » http://dx.doi.org/10.1108/09576059610116707
• Van Nieuwenhuyse, I., De Boeck, L., Lambrecht, M., & Vandaele, N. J. (2011). Advanced resource planning as a decision support module for ERP. Computers in Industry, 62(1), 1-8. http://dx.doi.org/10.1016/j.compind.2010.05.017.
  » http://dx.doi.org/10.1016/j.compind.2010.05.017
• Venkateswaran, J., & Son, Y. (2005). Hybrid system dynamic-discrete event simulation-based architecture for hierarchical production planning. International Journal of Production Research, 43(20), 4397-4429. http://dx.doi.org/10.1080/00207540500142472.
  » http://dx.doi.org/10.1080/00207540500142472
• Venkateswaran, J., Son, Y., & Jones, A. (2004). Hierarchical production planning using a hybrid system dynamic-discrete event simulation architecture. In Proceedings of the 2004 Winter Simulation Conference.
• Vieira, S. (1999). Estatística experimental. Rio de Janeiro: Atlas.
• Vollmann, T. E., Berry, W. L., Whybark, D. C., & Jacobs, F. R. (2008). Sistemas de Planejamento e Controle da Produção: o gerenciamento da cadeia de suprimentos (5. ed.). Bookman.
• Wallace, T. F. (2004). Sales & Operations Planning: the how-to handbook (2. ed.). Cincinnati: T. F. Wallace & Company.
• Yimer, A. D., & Demirli, K. (2010). A genetic approach to two-phase optimization of dynamic supply chain scheduling. Computers & Industrial Engineering, 58(3), 411-422. http://dx.doi.org/10.1016/j.cie.2009.01.010.
  » http://dx.doi.org/10.1016/j.cie.2009.01.010

Datas de Publicação

• Publicação nesta coleção
  09 Out 2015
• Data do Fascículo
  Oct-Dec 2015

Histórico

• Recebido
  05 Set 2014
• Aceito
  20 Ago 2015