Resumos
As primeiras pesquisas matemáticas no Brasil foram realizadas por pessoas com formação politécnica, isto é, oriundos das Escolas Politécnicas. Este trabalho apresenta esboços biográficos e as principais contribuições de onze desses(as) pioneiros(as), que atuaram em escolas militares e politécnicas e nas faculdades de filosofia que surgiram a partir da década de 1930, no país. Diferencia-se o grupo dos onze matemáticos(as) entre os simpatizantes e os(as) não-simpatizantes do positivismo.
matemáticos; politécnicos; positivismo; história da matemática
The first mathematics research were realized in Brazil by people with polytechnical formation, that means, coming from Polytechnic . This work presents biographical drafts and the main contributions of elevens from these pioneers. The worked in military Schools and Polytechnic. And also in the faculties of philosophy that started to appear in the country since 1930. In these group of eleven mathematicians one can differentiated between the ones who were sympathetic with positivism and the ones who were not.
mathematicians; polytechnicians; positivism; history of mathematics
ANÁLISE
Politécnicos ou matemáticos?* * Pesquisa financiada pelo CNPq.
Polytechnicians or mathematicians?
Circe Mary da Silva
Professora do Programa de Pós-Graduação em Educação da UFES Rua José Teixeira, 1400/901, Bairro Santa Lucia, 29055-310, Vitória ES Brasil. circe@npd.ufes.br
RESUMO
As primeiras pesquisas matemáticas no Brasil foram realizadas por pessoas com formação politécnica, isto é, oriundos das Escolas Politécnicas. Este trabalho apresenta esboços biográficos e as principais contribuições de onze desses(as) pioneiros(as), que atuaram em escolas militares e politécnicas e nas faculdades de filosofia que surgiram a partir da década de 1930, no país. Diferencia-se o grupo dos onze matemáticos(as) entre os simpatizantes e os(as) não-simpatizantes do positivismo.
Palavras-chave: matemáticos; politécnicos; positivismo; história da matemática.
ABSTRACT
The first mathematics research were realized in Brazil by people with polytechnical formation, that means, coming from Polytechnic . This work presents biographical drafts and the main contributions of elevens from these pioneers. The worked in military Schools and Polytechnic. And also in the faculties of philosophy that started to appear in the country since 1930. In these group of eleven mathematicians one can differentiated between the ones who were sympathetic with positivism and the ones who were not.
Keywords: mathematicians; polytechnicians; positivism; history of mathematics
Procura-se com este trabalho resgatar um pouco da contribuição dos brasileiros para a construção do campo científico matemático. Os onze nomes escolhidos são exemplares de um grupo maior, selecionados pelas ações que exerceram e que favoreceram a consolidação do campo científico. Somente os 'matemáticos' já falecidos foram contemplados na pesquisa. Deseja-se mostrar que a formação dessa comunidade, surgida modestamente no início do século XX, conseguiu gerar bons frutos e que houve uma luta pela conquista de espaço acadêmico, só consolidada no final do século.
O campo científico de matemáticos, no Brasil, passou por um período natural de formação. No início do século XX, com a ausência de faculdades destinadas à formação de matemáticos e sem um programa de fomento à pesquisa, os pesquisadores adquiriam a sua formação em escolas politécnicas e atuavam de forma isolada, levando à frente suas pesquisas motivados pelo interesse apaixonado em resolver problemas tanto na matemática pura quanto na aplicada e em outras afins. Entende-se que a formação do campo científico esteve estreitamente ligada com a organização do sistema universitário do país, e não se pode falar de um e ignorar o outro. Assim, somente na medida em que começa a se estruturar o sistema universitário brasileiro é que efetivamente as estratégias de valorização do campo profissional do pesquisador, das formas de associar-se e organizar-se por meio de sociedades científicas, começam a tomar forma. Isso não poderia ter acontecido no século XIX.
A formação da comunidade científica no Brasil ocorreu de forma diferente da vizinha Argentina, como concluiu Hugo Lovisolo. O curioso é que entre 1900 e 1950 a situação econômica, cultural e educacional da Argentina parecia estar mais adequada à formação de uma comunidade científica, em comparação com a equivalente brasileira, mas, paradoxalmente, é no Brasil que essa comunidade científica iria se fortalecer.
Para a formação da comunidade foram cruciais as ações desses pioneiros. Tais ações ocorreram dentro de um contexto pouco propício para o desenvolvimento de pesquisas matemáticas, ainda pouco valorizadas e compreendidas pela maioria dos leigos. Contribuiu para o fortalecimento da estratégia academicista a participação dos mais sistemática ao Brasil a partir da década de 1930. Eles transmitiram uma visão de ciência e de profissão academicista.
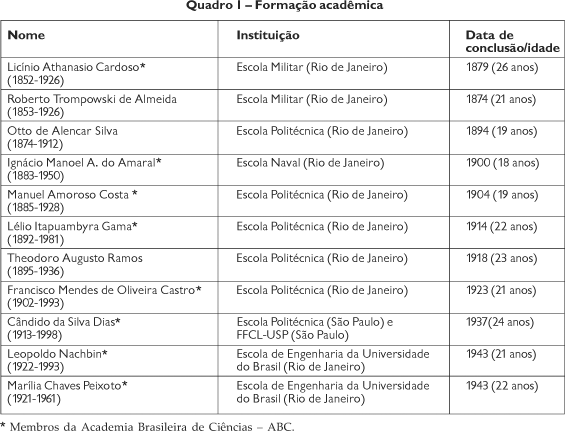
Entre os brasileiros que atuaram principalmente até meados da década de 1970 na área de matemática, vamos dar destaque, neste trabalho, a: Otto de Alencar Silva (1874-1912), Roberto Trompowski Leitão de Almeida (1853-1926), Manoel Amoroso Costa (1885-1928), Ignacio Manoel Azevedo do Amaral (1883-1950), Francisco Mendes de Oliveira Castro (1902-1993), Licinio Athanasio Cardoso (1852-1926), Theodoro Augusto Ramos (1895-1936), Lélio Itapuambyra Gama (1892-1981), Cândido Lima da Silva Dias (1913-1998), Leopoldo Nachbin (1922-1993) e Marília Chaves Peixoto (1921-1961).
Os politécnicos
Até 1930, a matemática desenvolvia-se timidamente no país, graças aos esforços isolados de autodidatas. Algumas mentes brilhantes começaram a despontar, quase como num processo de seleção natural. A maioria dos que vamos mencionar obteve a sua formação acadêmica em escolas politécnicas e não em faculdades especializadas de matemática, que só começaram a surgir a partir dos anos 30. Vamos utilizar a conceituação de Isidoro Alves para explicitar o sentido dessa palavra: o "modelo politécnico configura a formação e reprodução, através do ensino, de uma camada intelectual que se caracterizaria pela competência técnica e científica para atuar no campo das engenharias..." (1996, p. 65-6). Os politécnicos brasileiros eram oriundos das Escolas Militares, da Escola Naval e das Escolas Politécnicas (Rio de Janeiro e São Paulo, por exemplo), Escola de Minas de Ouro Preto e Escolas de Engenharia (ver Quadro 1). É interessante notar que, entre os matemáticos listados, oito deles foram membros da Academia Brasileira de Ciências ABC.
A própria ausência de cursos específicos para as áreas básicas, como a matemática, gerou a necessidade de um trabalho conjunto entre matemáticos, físicos, astrônomos e engenheiros. Essa situação não pode ser entendida como um aspecto negativo; ao contrário, propiciou uma fértil colaboração entre os escassos pesquisadores ativos nas primeiras décadas do século XX. Mas a defesa da pesquisa em ciência pura, independentemente das aplicações, era uma bandeira erguida por vários pesquisadores, entre os quais Manuel Amoroso Costa, que não aceitava a concepção utilitarista de ciência.
Matemáticos simpatizantes do positivismo
Entre as correntes cientificistas que se propagaram no Brasil, na virada do século XIX para o XX, sobressaiu-se o positivismo. A discussão dessas teorias ocorria predominantemente nas instituições científicas, como a Escola Politécnica do Rio de Janeiro, as Faculdades de Medicina e de Direito e as academias militares, entre outras. Como o positivismo de Comte ganhara estatuto de teoria científica, atraía muito os jovens estudantes ligados a essas instituições. Roberto Trompowski Leitão de Almeida, Licínio Cardoso e Ignácio Azevedo do Amaral fizeram parte desse grupo de positivistas. Os demais, começando com Otto de Alencar Silva, romperam com as idéias positivistas e iniciaram um movimento de reação e negação à ideologia comtiana, dominante até a década de 1920 no Brasil.
A influência das idéias de Comte pode ser notada não somente entre os positivistas, mas também em outros cientistas não identificados como positivistas, como o caso de Henrique Morize, presidente da Academia Brasileira de Ciências (ABC) durante os anos de 1916 a 1926. Em discurso proferido na ABC, em 1922, ele afirmava concordar com Comte, quando este reverenciava a ciência pura: "as aplicações mais importantes se derivam de teorias constituídas com vistas simplesmente científicas, cultivadas durante séculos antes de produzirem qualquer resultado prático" (Morize, 1917, p. 3).
Formar as primeiras abstrações, instituir as idéias abstratas é fácil, foi possível desde os primeiros exercícios da razão humana; mas descobrir as relações abstratas, isto é o difícil; porque é constituir a ciência que só lenta e pacientemente tem sido elaborada pelos verdadeiros servidores da humanidade. (Cardoso, 1885, p. x)
Licínio Athanasio Cardoso nasceu em Lavras (RS). Em 1879 concluiu o curso na Escola Militar. Foi aluno de Benjamin Constant Botelho de Magalhães, recebendo dele uma orientação para o positivismo. Em 1887 ingressou como docente de Mecânica Racional na Escola Politécnica do Rio de Janeiro. Em 1889 concluiu o curso de Medicina e começou a interessar-se pela homeopatia. Foi fundador da Escola de Medicina e Cirurgia do Rio de Janeiro e do Hospital Hahnemanniano. Com a fundação da Sociedade Brasileira de Ciências no Rio de Janeiro, em 1916, tornou-se o primeiro presidente da seção de ciências matemáticas, cargo que ocupou até 1925, quando Manoel Amoroso Costa assumiu o posto.
Não foi um positivista ortodoxo da doutrina de Comte, aceitou apenas parte dos princípios, rejeitando aqueles que lhe pareciam contraditórios ou errados. Assim como Comte, formulou uma classificação das ciências, ainda enquanto aluno da Escola Militar, segundo estes princípios: novidade, utilidade e simplicidade das leis a descobrir. Nessa escala hierárquica, a matemática abstrata aparece como a primeira ciência, seguida da matemática concreta, na qual o autor inclui oito ciências: geometria, mecânica, física, química, biologia, frenologia, sociologia e antroponomia.
A obra que tornou Licínio Cardoso conhecido no meio acadêmico foi a sua tese Teoria elementar das funções , publicada em 1885. O texto registra uma forte influência positivista. No capítulo em que trata da classificação das funções percebe-se, novamente, a forte influência da concepção de Comte: "a opinião de Comte tem para nós o peso de um dogma" (p. 7). Após apresentar a classificação comtiana de funções, Cardoso abordou um assunto proibido pelo filósofo francês as funções elípticas. Entre as suas publicações incluem-se trabalhos sobre mecânica, equações diferenciais e críticas à teoria da relatividade.
Mal egressos do tremendo carrascal da geometria elementar de Serrasqueiro, bem me recorda da alegre surpresa que nos assaltou, quando vimos surgir diante de nós, a figura empolgante do então Coronel Trompowsky, duplo gigante na estatura e no saber, a librar-se em vôos condoreioros pelas regiões estratosféricas do cálculo transcendente. (Alfredo Severo, apud Lins, 1967, p.290)
Roberto Trompowski Leitão de Almeida (1853-1926) nasceu em Desterro, hoje Florianópolis (Santa Catarina). Foi aluno de Benjamin Constant Botelho de Magalhães na Escola Militar da Praia Vermelha, onde, mais tarde, por indicação do próprio Benjamin Constant, tornou-se docente. Exerceu nessa escola muitos anos de magistério e tornou-se também seu diretor. Em 1916 foi promovido a general de divisão. A sua obra matemática que, segundo Luis Freire, constitui-se no maior esforço didático realizado até a década de 1950, foi toda ela inspirada no positivismo. Reúne os seguintes livros: Lições de geometria algébrica (1903); Lições de álgebra superior (1904); Lições de geometria diferencial (1904), Lições de geometria integral (1905) e Regras de falsa posição (1923).
Os quatro tratados publicados até 1905 compreendem cerca de quatro mil páginas. Na opinião de Luis Freire, suas exposições não eram meras compilações de outros autores, ele conhecia e estudava os grandes clássicos da matemática, transmitindo a seus alunos uma visão de conjunto útil aos iniciantes. Na obra de geometria integral, Trompowski tratou não apenas das séries de Fourier, como também da teoria das funções elípticas, mostrando muitas aplicações. Dessa maneira, constatamos que Trompowski distanciou-se parcialmente de seu mestre positivista, abordando temas condenados por Comte, como o caso das funções elípticas. A parte mais vasta da obra de Trompowski é sem dúvida a relativa às equações diferenciais, embora, como observou Luis Freire, estudos mais avançados sobre essa teoria, como os desenvolvidos por Picard, Drash, Fuchs e Poincaré, não tenham sido abordados pelo autor. A geometria diferencial, que abrangia os conteúdos de cálculo diferencial e equações diferenciais, é o melhor entre os livros com orientação positivista produzidos por esse autor.
Deixou alguns trabalhos inéditos, como "A inscrição de polígonos regulares em uma circunferência" e sobre a teoria elementar das séries, assim como um tratado de trigonometria retilínea e esférica.
A Universidade é a consciência e o cérebro da nação, a mais elevada expressão sistemática da sua vida espiritual, pois ela reflete o pensamento do Brasil, do passado que ela herdou e do presente que procura formar, para a conquista do futuro. A Universidade não é somente, a depositária da ciência, da cultura e da técnica ... cumpre-lhe, também, aplicar todo esse valioso depósito, para que ele frutifique nos resultados das convenientes soluções de todos os grandes problemas da nação. (Amaral, 1936)
Ignacio Manoel Azevedo do Amaral nasceu no Rio de Janeiro. Concluiu, em 1900, o curso de águas marinhas na Escola Naval. Foi professor dessa escola, bem como da Escola Normal do Distrito Federal, do Colégio Pedro II e da Escola Naval. Em 1912 ingressou para o magistério da Escola Politécnica do Rio de Janeiro, lecionando as disciplinas de Geometria Analítica e Cálculo Infinitesimal. Exerceu muitos cargos públicos e acadêmicos, chegando a reitor da Universidade do Brasil no período de 1945-1946. Considerado o instaurador da autonomia nessa universidade, lançou as bases e planos para a construção da cidade universitária da Universidade do Rio de Janeiro. Foi membro fundador da Academia Brasileira de Ciências e tornou-se presidente no biênio 1939-1941. Publicou trabalhos sobre balística, análise e equações diferenciais, de 1906 até 1942.
A influência do positivismo é bastante visível na tese que apresentou à congregação da Escola Politécnica do Rio de Janeiro, em 1912, como candidato a livre docência. No prefácio, o autor afirma que considerou o desenvolvimento em série de funções exclusivamente sob o ponto de vista algébrico ou analítico, sem levar em conta considerações sobre a convergência das séries. Sua justificativa apoiava-se em Comte, para quem as questões de convergência ou divergência de séries era "algo destituído de sentido" (p. 5). Comte é amplamente citado no prefácio.
Deixou vários trabalhos de natureza técnica ligados a problemas de balística e navegação, descrições biográficas e discursos publicados, em 1958, pelo Ministério da Marinha sob o título Reminiscências..., e outro trabalho publicado postumamente em 1968, intitulado Ensaio sobre a revolução brasileira: 1931-1934. Iria representar a ABC no Congresso de Matemática de Cambridge, em 1950, quando faleceu.
A oposição ao positivismo
Tanto a adesão quanto a oposição ao positivismo pelos politécnicos ocorreu no seio das escolas militares e de engenharia. Como muitos dos alunos da Escola Politécnica do Rio de Janeiro, Otto de Alencar Silva esteve ligado ao positivismo comtiano, no início de sua vida acadêmica, mas mudaria radicalmente de ideologia e se tornaria um defensor das modernas teorias matemáticas dominantes no exterior. Seu discípulo mais destacado foi Manoel Amoroso Costa, que deu continuidade ao movimento iniciado pelo mestre. Mais tarde, dois alunos de Amoroso Costa, Theodoro Augusto Ramos e Lélio Gama, ergueram a mesma bandeira contra as idéias positivistas, inaugurando um período novo na história da matemática no país.
Infelizmente, apesar da autoridade de Auguste Comte, uma proposição de Matemática não se impõe ao espírito como objeto de fé. (Silva, 1898)
Otto de Alencar Silva foi um pioneiro nas pesquisas matemáticas no Brasil. A leitura das obras do matemático português Francisco Gomes Teixeira e os contatos com ele foram decisivos para a sua ruptura total com o positivismo. Em 1898 Otto de Alencar Silva publicou na Revista da Escola Politécnica um trabalho sobre a superfície mínima de Riemann. O matemático Manfredo Perdigão do Carmo, pesquisador em geometria diferencial, identificou esse trabalho como a primeira contribuição brasileira à geometria diferencial. O problema estudado por Otto de Alencar diz respeito a uma superfície gerada pelo movimento de um círculo de modo que, nesse movimento, o plano do círculo se mantém paralelo ao plano inicial. Segundo Carmo, Riemann também estudara esse problema, em texto publicado postumamente, em 1869. Comparando as duas resoluções, ele afirma que o trabalho do brasileiro "é mais elegante e mais simples" (Carmo, 1999, p. 4) que o de Riemann. A solução proposta por Otto de Alencar envolveu o uso de funções elípticas e deu a equação da superfície em termos da função de Jacobi. O trabalho revela que o autor estava bem informado sobre os desenvolvimentos da matemática na época, principalmente considerando que o estudo de funções elípticas (introduzidas em torno de 1830) não era tema muito estudado nas escolas de engenharia. Carmo diz que o trabalho não era original, tratava-se de um exercício sobre funções elípticas, mas mesmo assim não deixa de ser muito interessante, principalmente considerando-se ter sido um trabalho pioneiro na área e resultado do autodidatismo do autor. Uma listagem das obras de Otto de Alencar Silva pode ser encontrada nas publicações de Clóvis Pereira da Silva.
Estou convencido, porém, de que só se aprende com segurança fazendo alguma cousa, não simplesmente ouvindo dizer como se faz: e de que só fazendo alguma cousa é que se sente a cada instante a necessidade imperiosa de possuir uma boa base teórica. Estou convencido da inutilidade de toda e qualquer reforma do ensino que não reforme antes de mais nada, a maneira de ensinar e aprender. (Costa, 1930)
Manuel Amoroso Costa foi o discípulo mais destacado de Otto de Alencar Silva na Escola Politécnica do Rio de Janeiro. Nessa escola ingressou aos quinze anos de idade e bacharelou-se em Engenharia Civil (1905) e em ciências físicas e matemáticas (1906). Diferentemente de seus antecessores, que não tiveram oportunidade de sair do país, Costa conseguiu estudar em Paris. Lá permaneceu de maio a dezembro de 1921 e de agosto de 1923 a fevereiro de 1925, freqüentando a Faculdade de Letras de Paris, onde teve oportunidade de ser aluno de Abel Rey, Leon Brunschwicg e Henry Andoyer. Essa influência o levou a conceber o projeto de escrever a história da filosofia matemática. Interessava-se, particularmente, pelos aspectos teóricos da matemática, por suas fundamentações. Era um defensor ferrenho da ciência pura: "Eu não aceito e nunca aceitei a concepção utilitária da ciência. Nunca me conformei com o modo de ver dos que a consideravam uma serva da técnica, destinada a fornecer-lhe receitas e regras de ação; muito pelo contrário, penso que essas regras e receitas são subprodutos da ciência" (Discurso de posse da cadeira de Astronomia, 1924).
O papel que desempenhou na fundação da Sociedade Brasileira de Ciências e na Associação Brasileira de Educação foi extremamente importante. Fez parte da diretoria da ABC em duas gestões (1917-1920 e 1920-1923), como segundo secretário, e depois da morte de Licínio Cardoso assumiu a direção da seção de Ciências Matemáticas.
Sua obra é variada, abrangendo, além da matemática, a astronomia, a física e a filosofia da matemática. Destacamos seu livro Introdução à teoria da relatividade, primeiro trabalho de divulgação da teoria de Einstein no Brasil, em 1922. Além disso, merece referência o livro publicado postumamente As idéias fundamentais da Matemática (Rio de Janeiro), em 1929, em que o autor mostra os modernos conceitos e teorias matemáticas.
Não se pode pensar em progresso cultural de um país, sem dotá-lo de um corpo de professores capazes de preencher a sua missão intelectual. O nosso país, como muitos outros, tem necessidade de elevar e aperfeiçoar os conhecimentos dos professores de estabelecimentos secundários e superiores." (Ramos, 1934, O Estado de S. Paulo)
Theodoro Augusto Ramos nasceu em São Paulo. Em 1911 ingressou na Escola Politécnica do Rio de Janeiro, onde, em 1918, defendeu a tese intitulada Sobre as funções de variáveis reais. Nesse trabalho, introduziu a recente linguagem formulada por Lebesgue sobre conjuntos fechados e medida de conjuntos. Ingressou, ainda em 1919, na carreira acadêmica, na Escola Politécnica de São Paulo. O artigo "Integrais definidas das funções descontínuas", em originalidade e profundidade, é comparável à sua tese de doutorado e mereceu do matemático Borel um voto de louvor. Da mesma forma, o livro publicado em língua francesa Lições de cálculo vetorial, em 1930, mereceu da crítica européia, particularmente do matemático Levi-Civita, o reconhecimento como uma valiosa obra didática. Segundo Theodoro Ramos, a introdução do cálculo vetorial, no Brasil, aconteceu em 1926, quando foi fundada a disciplina de Teoria dos Vetores. Nos Anais da ABC, n. 3, tomo VI, publicou Theodoro um artigo sobre uma integral hiperelíptica. A demonstração desse resultado foi discutida com o matemático Denjoy, e Theodoro Ramos, finalmente, ao retornar ao Brasil em 1934, conseguiu uma demonstração que foi considerada por Denjoy de extrema simplicidade. Theodoro Ramos era um analista puro, possuía um sadio espírito de generalização, uma visão intelectual direta misturada com uma boa dose de intuição. A partir de 1925, começou a interessar-se pela física teórica, mas só em seus aspectos matemáticos. Um artigo sobre "Reflexões sobre a Teoria da Relatividade" surgiu em O Jornal de 21 de março de 1925 e quatro anos mais tarde, o artigo "A Teoria da Relatividade e as raias espectrais do hidrogênio", nos Anais da ABC, v. 1, n. 1.
Além de professor, trabalhou como engenheiro em São Paulo. Projetou e construiu o serviço de águas do Ipiranga, em 1922, e com Saturnino de Brito trabalhou na retificação do rio Tietê. Em 1930 viajou para Estocolmo e Liège para representar o Brasil nos Congressos de Mecânica e Mecânica aplicada, respectivamente. Mas a grande marca da atuação de Theodoro Augusto Ramos foi o seu papel de liderança na criação da Faculdade de Filosofia, Ciências e Letras da Universidade de São Paulo (USP) em 1934. A escolha acertada de cientistas estrangeiros foi decisiva para o sucesso dos cursos de Matemática e Física, instituídos a partir de então, e que visavam à formação de professores e ao desenvolvimento da pesquisa científica. Theodoro Ramos realizou uma missão política fundamental nesse processo, recrutando cientistas estrangeiros em suas viagens pela Europa.
Lustosa, que coincidências! / Nascemos no mesmo dia, / Cursamos a mesma escola, / No mesmo ano, tiramos / O cobiçado canudo, / E já temos, de existência, / Muito mais do que eu previa. / Chegamos a oitenta e nove / Se atingirmos os noventa / Com saúde, assim espero, / Vamos começar de novo / Pois é (noves fora zero). (Castro apud Marques, 1997)
Francisco Mendes de Oliveira Castro (1902-1993) nasceu em Petropólis (RJ). Sua família, de classe média alta, era ligada à família imperial. Formou-se em engenharia civil (1923) e elétrica pela Escola Politécnica do Rio de Janeiro. Trabalhou em projetos de mineração, de obras civis e ferrovias em diferentes estados brasileiros. Foi assistente de Lélio Gama na Escola Politécnica e, mais tarde, tornou-se catedrático nas disciplinas de Estações Geradoras, Medidas Elétricas e Linhas de Transmissão. Ensinou Análise Matemática de 1935 a 1937 na Escola de Ciências da Universidade do Distrito Federal. Em 1939, surgiu sua primeira publicação internacional no Zeitschrift für Physik, de Berlim, intituladoo "Zur Theorie der dieletrischen Nachwirkung". Nesse trabalho, o modelo matemático estudado é uma equação integral, e as soluções que o autor apresenta são numéricas.
Em 1949, junto com José Leite Lopes e Leopoldo Nachbin, entre outros, ajudou a fundar o Centro Brasileiro de Pesquisas Físicas (CBPF). Teve participação ativa na fundação do periódico Summa Brasiliensis Mathematicae, em 1945, no núcleo matemático da Fundação Getúlio Vargas (FGV), revista dedicada à publicação de artigos matemáticos. Nesse mesmo ano, apresentou à congregação da Escola Nacional de Engenharia da Universidade do Brasil a dissertação Ondas em linha de transmissão. Com a vinda do matemático Laurent Schwartz ao Brasil, em 1950, Francisco de Oliveira Castro aproveitou as recentes teorias criadas por Schwartz sobre a teoria das distribuições para aperfeiçoar métodos de resolução de problemas em física matemática, cujos resultados começou a divulgar nos Anais da Academia Brasileira de Ciências. A capacidade criativa de Castro era um tanto incomum, pois até os 84 anos continuava a publicar trabalhos originais. Segundo o depoimento de Cesar Lattes, aos 90 anos Castro continuava alerta, tendo resolvido a equação de Schrödinger para o oscilador harmônico no caso das diferenças finitas em vez das diferenciais. Francisco de Oliveira Castro gostava de cooperar com seus colegas, e Lattes lembra que a seu pedido o mestre resolveu vários problemas matemáticos relativos a equações de difusão dos raios cósmicos.
O matemático traz em si mesmo o mundo que lhe cabe explorar. Não precisa recorrer a nenhum dos cinco sentidos para entrar em contato com o objeto de investigação... A missão do matemático consiste em extrair esses conceitos de seu subconsciente, da mesma forma que o geológo extrai um diamante da mina que explora. (Gama, 1960, conferência ABC)
Lélio Gama (1892-1981) nasceu no Rio de Janeiro. Diplomou-se em engenharia geográfica, em 1914, e quatro anos depois, em engenharia civil. Nesses cursos, seu interesse e concentração de estudos giravam em torno das disciplinas matemáticas e da astronomia. Sua primeira experiência profissional ocorreu no Observatório Nacional, para o qual foi contratado interinamente, em 1917, como calculador, e onde permaneceu até 1962. Ingressou como docente da Escola Politécnica do Rio de Janeiro em 1925, no cargo de assistente da disciplina de Cálculo das Variações e Mecânica Racional. Nessa mesma instituição, tornou-se livre docente e chegou a catedrático de Mecânica Racional, tendo lecionado no período de 1925 a 1949. Além disso, exerceu atividades de docência na Universidade do Distrito Federal (UDF) no período de 1935 a 1937. Foi catedrático de Análise Matemática e Análise Superior na Faculdade Nacional de Filosofia da Universidade do Rio de Janeiro. Em 1941 publicou o livro Introdução à teoria dos conjuntos. Entre 1945 e 1946 foram publicados dois importantes trabalhos de Lélio Gama: "Notion de proximité et espaces à structure sphéroidale", no American Journal of Mathematics (jan. 1945) e "Limites d'ésembles dans les spaces abstraits", no Summa Brasiliensis Mathematical (ago. 1946). Paralelamente ao seu interesse pela matemática e pela atualização do seu ensino, Lélio Gama se interessava pela ciência aplicada. Ele foi um pioneiro da gravimetria no Brasil, e, em 1955, implantou a primeira estação de gravimetria estudo que iria se expandir pelo país e chegar a cerca de 2 mil estações no ano de 1973. A importância dessa rede reside no fato de constituir a base para o estudo das anomalias da gravidade terrestre no Brasil.
Entre 1956 e 1964 Gama fez parte da comissão de Tempo Astrônomico e de Rotação da Terra da International Astronomical Union (IAU) e também participou do grupo de trabalho da International Association of Geomagnetism and Aeronomy (IAGA). O Conselho Nacional de Pesquisa (CNPq) foi fundado em 1951, e um ano depois surgiu o Instituto Nacional de Matemática Pura e Aplicada (Impa). Lélio foi seu primeiro diretor, ocupando o cargo de 1952 até 1965, e foi membro do conselho deliberativo do CNPq de 1951 até 1973.
Desde pequeno eu brincava com os números. Meu pai era engenheiro e se divertia me estimulando a fazer contas ... As brincadeiras com os números grandes, feitas por meu pai, tornaram a matemática fácil para mim... Quando entrei no grupo escolar, fazer operações matemáticas era coisa banal para mim. (Dias, 1997)
Cândido Lima da Silva Dias nasceu em Mococa (SP) e foi um dos primeiros bacharéis em matemática da Faculdade de Filosofia, Ciências e Letras (FFCL) da Universidade de São Paulo. Recebeu seu diploma em 25 de janeiro de 1937, com grandes festejos e a presença do governador de São Paulo. Nesse mesmo ano, com 23 anos de idade, foi nomeado assistente de Luigi Fantappié. Após o regresso de Fantappié à Itália, permaneceram como docentes na FFCL Giacomo Albanese, Cândido da Silva Dias, Omar Catunda e Fernando Furquim. Em 1942, Cândido tornou-se doutor com uma tese sobre os funcionais analíticos identificados com a teoria dos espaços vetoriais topológicos. Em 1945, tomou parte, juntamente com Omar Catunda, da fundação da Sociedade de Matemática de São Paulo, que mais tarde se transformaria em Sociedade Brasileira de Matemática. Recebeu uma bolsa da Fundação Guggenheim no período de 1948 e 1949 para pesquisar nas Universidades de Harvard e Chicago e no Institute for Advacend Study de Princeton. Em 1951 foi eleito membro da ABC e também nomeado diretor do Setor de Pesquisas Matemáticas do CNPq. Cândido desempenhou um papel importante na criação do Impa, em 1952. Em 1960, tomou a iniciativa de criar o Instituto de Pequisas Matemáticas da USP, posteriormente transformado em Instituto de Matemática dessa universidade.
Suas principais publicações referem-se à área dos funcionais analíticos. Um de seus mais importantes trabalhos foi "Espaços vetoriais topológicos e sua aplicação nos espaços funcionais analíticos", publicado em 1950. Os resultados encontrados por Cândido Dias nesse artigo foram simultaneamente obtidos por G. Kothe, na Alemanha, por A. Grothendieck, na França, e por Sebastião Silva, em Portugal. O trabalho foi provavelmente motivado por investigações de Schwartz e Dieudonné e tem por finalidade mostrar que a topologia considerada nos espaços de funções analíticas, que toma tais espaços como limites indutivos de espaços de Banach, permite obter facilmente as propriedades de dualidade dos espaços de funções analíticas.
Cândido Dias abre com suas pesquisas um novo campo de pesquisas a Análise Funcional.
No Brasil, ainda permanece a impressão de que ... os matemáticos são pessoas que trabalham isoladamente, possuem temperamentos bizarros, maneiras distraídas e cabelereiras desgrenhadas; de que os matemáticos necessitam apenas de lápis, papel, um canto sossegado e, talvez uma biblioteca incompleta..." (Nachbin, 1996, p. 776)
Em 1962, pela primeira vez foi concedido a um matemático brasileiro o Prêmio Moinho Santista. Esse matemático é Leopoldo Nachbin. Esse acontecimento inusitado chamou a atenção da imprensa, que expôs em grandes manchetes o valor monetário do prêmio e o fato de um judeu brasileiro ter sido contemplado. Afinal, não somente jogadores de futebol eram agraciados com grandes quantias, mas também um professor de matemática.
Leopoldo Nachbin iniciou seus estudos universitários na Escola de Engenharia do Rio de Janeiro. Ao saber da criação da Faculdade Nacional de Filosofia da Universidade do Brasil e da presença de matemáticos italianos nessa faculdade, passou a assistir às aulas como aluno ouvinte, e, diante da proibição de freqüentar dois cursos na mesma universidade, concluiu seu curso de engenheiro e não o de bacharel em matemática.
Sua primeira contribuição surgiu aos 19 anos de idade, com o trabalho Sobre a permutabilidade entre as operações de passagem ao limite e de integração de equações diferenciais (1941). No início de sua formação acadêmica, Nachbin sofreu a influência de dois matemáticos italianos: Gabriele Mammana e Luigi Sobrero, professores visitantes estrangeiros da Faculdade Nacional de Filosofia da Universidade do Brasil. Com vinte anos de idade, publicou dois trabalhos em revistas estrangeiras: "Un estensione di un lemma di Dirichlet", Atti Accad. Italia Rend. (1942) e "Sobre as séries de funções quasi-sempre absolutamente divergentes", Rev. Univ. de Tucumán (1942). De 1945 a 1948, com a presença no Brasil dos matemáticos Andre Weil e Jean Dieudonné, do grupo Bourbaki, percebe-se uma outra influência nas investigações de Nachbin a topologia. Em torno de 1947, motivado pela compactificação de Stone-Cech, estudou o completamento de espaços regulares, que ficou conhecido como Espaços Hewitt Nachbin. Esse estudo foi divulgado no Congresso Internacional de Matemática (1950) e intitulado "On the continuity of positive linear transformations". Nesse mesmo ano tornou-se membro titular da Academia Brasileira de Ciências. Nesse frutífero ano de 1950, Nachbin produziu o artigo "A theorema of Hahn-Banach type for linear transformations", que talvez tenha sido um de seus artigos individuais mais citados essa extensão do teorema de Hahn-Banach é referida por Laurent Schwartz como "o teorema de Nachbin". Entre 1948 e 1950, Nachbin recebeu duas bolsas de estudo: uma do USA State Departament e outra da Fundação Guggenheim, por recomendação de Marshall Stone.
Suas atividades de pesquisa e ensino desenvolveram-se, principalmente, em dois países: Brasil e Estados Unidos. Pode-se dizer que Nachbin pesquisou em muitas áreas e que suas principais contribuições foram para a topologia, conjuntos ordenados, análise funcional, teoria da aproximação e holomorfia ou análise complexa. Na opinião do matemático francês Andre Weil, Leopoldo Nachbin foi o mais conhecido e o mais apreciado entre os matemáticos brasileiros, e "é aquele que mais fez para firmar a reputação da matemática brasileira" (Weil, 1974).
Vendo aquela moça calma, de olhos muito grandes e expressivos, era preciso que alguém nos segredasse que se tratava de uma insigne Professora de Cálculo e Mecânica da Escola Nacional de Engenharia, enérgica e, ao mesmo tempo, generosa, além de uma inteligência aguda que se voltava para as pesquisas matemáticas. (Maria Laura Mozinho, em palestra na ABC, em 1961)
As mulheres não estiveram ausentes na construção do campo científico da matemática no Brasil, mas apenas um número reduzido delas teve acesso a uma formação específica. Como o acesso dos brasileiros à matemática se deu pelas Escolas Politécnicas, e esse era um reduto tradicionalmente masculino, foi apenas com o surgimento das faculdades de filosofia, na década de 1930, que as mulheres começaram realmente a ocupar espaços. A presença das mulheres nas escolas de engenharia não era muito comum no início do século, mas em 1939 Marília de Magalhães Chaves estava matriculada na Escola Nacional de Engenharia, tendo como colegas Maurício Peixoto e Leopoldo Nachbin. Ela formou-se em engenharia em 1943. No Rio de Janeiro, na década de 1940, na Faculdade Nacional de Filosofia, aparecem nomes femininos: Maria Laura Mouzinho, Moema Mariani e Maria Yolanda de Mello e Nogueira, entre outros. Segundo Maria Laura Mouzinho, Marília Chaves foi aluna ouvinte no curso de Matemática da Faculdade Nacional de Filosofia, enquanto realizava o curso de engenharia e atuava como monitora na Escola Nacional de Engenharia. Posteriormente, casou-se com o matemático Maurício Peixoto e passou a chamar-se Marília Chaves Peixoto. Segundo depoimento do matemático e pesquisador emérito do Impa, Maurício Peixoto, ele recebeu de Marília um forte estímulo para dedicar-se à matemática: "Ambos [Marília e Nachbin] foram influências importantes no sentido de eu me tornar um matemático. Isso no sentido de procurar viver para e de matemática".1 1 Disponível em www.abc.org.br/org/aca.asp?codigo= peixoto#biog.
Marília Chaves Peixoto desenvolveu trabalhos importantes em equações diferenciais, e em pareceria com Maurício Peixoto publicou nos Anais da Academia Brasileira de Ciências dois artigos: "On the inequalities y'" ³ G(x,y,y',y")", em 1949, e "Structural stability in the plane with enlarged boundary conditions", em 1959. Foi eleita como membro associado da Academia Brasileira de Ciências em 12 de junho de 1951.
A primeira mulher a entrar na ABC foi Marie Curie, em 1926, na categoria de associada estrangeira, mas Marília foi a primeira mulher brasileira a ingressar nessa academia. Atuou como professora de Cálculo e Mecânica na Escola Nacional de Engenharia e em cursos especiais no Centro Brasileiro de Pesquisas Físicas. Publicou pela Escola de Engenharia da Universidade Federal do Rio de Janeiro um livro sobre Cálculo Vetorial. Faleceu ainda jovem, mas sua dedicação à matemática e seu talento não passaram despercebidos da comunidade que começava a se formar.
Considerações finais
No final do século XIX e início do século XX, a matemática feita no Brasil estava restrita a poucas instituições (especialmente as escolas politécnicas e de engenharia), e o grupo de pesquisadores era muito reduzido.
Vários fatores contribuíram decididamente para o desenvolvimento e institucionalização da comunidade matemática no Brasil: a criação da Faculdade de Filosofia, Ciências e Letras da Universidade de São Paulo (FFCL-USP), em 1934, e da Faculdade Nacional de Filosofia da Universidade do Brasil (1939), onde se iniciaram os cursos de formação de professores e pesquisadores de matemática; a criação de alguns departamentos de Matemática em instituições como o Centro Brasileiro de Pesquisas Físicas; a fundação da Sociedade Brasileira de Ciências (SBC), em 1916 (posteriormente transformada em Academia Brasileira de Ciências); a criação do Conselho Nacional de Pesquisas, em 1951; a criação da Coodenação de Aperfeiçoamento de Pessoal de Ensino Superior (Capes), em 1951, e a criação do Instituto Nacional de Matemática Pura e Aplicada (Impa), em 1952. Com a fundação do Conselho Nacional de Pesquisas (CNPq), os recursos para as pesquisas e para a formação de pesquisadores começaram a favorecer a área de matemática; e, finalmente, com a criação do Impa, em 1952, a pesquisa matemática começou a tomar papel de destaque no cenário acadêmico brasileiro. As importantes ações aqui apontadas foram possíveis graças à interferência, ousadia e competência desses brasileiros e de outros tantos nomes que ainda merecem ser pesquisados, ajudando a despontar e a consolidar as investigações matemáticas no país.
É digno de nota que a formação científica de alguns desses pesquisadores sofreu influências da matemática produzida em Portugal, na Itália, na França, e, principalmente, nos Estados Unidos. A divulgação de suas pesquisas logo começa a aparecer em veículos de divulgação internacionais e alguns deles conseguem formar discípulos, como foi o caso de Cândido Dias e Leopoldo Nachbin. Este último, por exemplo, orientou 21 alunos de doutorado, tanto no Brasil como no exterior.
A herança deixada por esses pioneiros, que tiveram de vencer obstáculos enormes para adquirir novos conhecimentos e construir novos saberes, assim como suas ações já mencionadas para a formação do campo científico da Matemática, favoreceram as pesquisas em dois campos a análise funcional e sistemas dinâmicos que podem ser considerados como fortes, entre os desenvolvidos por pesquisadores brasileiros.
Considerando a formação recebida, personagens abordados foram sem dúvida politécnicos. Mas, estamos convictos de que alguns deles foram, em sua época mais do que politécnicos, e, pelos trabalhos desenvolvidos, podem ser denominados de matemáticos brasileiros.
Recebido para publicação em janeiro de 2005.
Aprovado para publicação em junho de 2005.
- Alves, I. M. S. 1996 Modelo politécnico, produção de saberes e a formação do campo científico no Brasil. In: Hamburger, A. et al. (org.) A ciência nas relações Brasil-França (1850-1950) São Paulo: Edusp.
- Amaral, I. A. 1958 Reminiscências Rio de Janeiro: Imprensa Naval.
- Amaral, I. A. 1952 Licínio Athanasio Cardoso: o matemático. Rio de Janeiro: Gráfica Editora Souza.
- Bourdieu, Pierre 1983 O campo científico. In: Ortiz, R. (org.) Sociologia São Paulo: Ática.
- Cardoso, L. 1944 Licínio Cardoso: seu pensamento, sua obra, sua vida. Rio de Janeiro: Zélio Valverde.
- Cardoso, L. 1885 Teoria elementar das funções Rio de Janeiro: Typografia Mont'Alverne.
- Carmo, M. P. 1999 Pesquisa em geometria diferencial no Brasil. Matemática Universitária, n. 26/27, p. 1-27, jun./dez.
- Carmo, M. P. 1994 Entrevista. Matemática Universitária, n. 16, p. 1-18, jul.
- Castro, F. M. O. 1992 A matemática no Brasil Campinas: Ed. Unicamp.
- Catunda, Omar 1952 O Curso de Análise Matemática São Paulo: Bandeirantes.
- Catunda, Omar 1945 Aula Inaugural em 1945. Anuário da Faculdade de Filosofia, Ciências e Letras da USP São Paulo, p. 119-31.
- Chagas Filho, C. 1986 História da Ciência e Tecnologia no Brasil.In: Seminário Nacional sobre História da Ciência e Tecnologia, 1, 1986, Rio de Janeiro. Anais... Rio de Janeiro. p. 6-15.
- Costa, M. A. 1930 O ensino de astronomia na Escola Politécnica. Revista Didática da Escola Politécnica, Rio de Janeiro n. 36, p. 9-14.
- Costa, M. A. 1922 Introdução à teoria da relatividade Rio de Janeiro: Süssekind de Mendonça.
- Dias, C. L. S. 1998 Entrevista. In: Cientistas do Brasil São Paulo: SBPC. p. 693-701. Entrevista concedida a Vera Rita de Costa.
- Dias, C. L. S. 1997 Cândido da Silva Dias. Ciência Hoje, nov. Entrevista concedida a Vera Rita da Costa.
- Dias, C. L. S. 1994 Cândido da Silva Dias: meio século como pesquisador. Estudos Avançados, v. 8, n. 22, p. 97-105.
- Fávero, M. L. 1989 Faculdade Nacional de Filosofia Rio de Janeiro: Ed. UFRJ. v. 4.
- Freire, Luis 1936 A obra mathematica de Theodoro Ramos. Jornal do Comércio, 5 jul. 1936.
- Hönig, C.; Gomide, E. 1979 Instituto de Matemática e Estatística da USP. In: Ferri, M. G.; Motoyama, S. (org.) História das ciências no Brasil São Paulo: Edusp.
- Horváth, J. 1986 The life and works of Leopoldo Nachbin. In: Barroso, J. A. (ed.) Aspects of Mathematics and its applications Elsevier Science Publishers, B. V. p. 1-75.
- IME-USP 1998 Instituto de Matemática e Estatística: história e cotidiano. São Paulo.
- Lins, Ivan 1967 História do positivismo no Brasil São Paulo: Editora Nacional.
- Lovisolo, Hugo 2000 Vizinhos distantes: universidade e ciência na Argentina e no Brasil. Rio de Janeiro: Eduerj.
- Marques, A.; Medeiros, L. A. 1997 Relembrando Oliveira Castro. In: Caruso, F.; Tropper, A. Perfis Rio de Janeiro: CBPF/CNPq. p. 423-59.
- Morettin, P. P. 1998 Omar Catunda. In: História e cotidiano São Paulo: IME-USP.
- Morize, H. 1917 Discurso. Revista da Sociedade Brasileira de Ciências, n. 1, p. 7.
- Motoyama, S.; Nagamini, M. 1996 CNPq e CNRS: duas histórias numa perspectiva comparada. In: Hamburger, A. et al. (org.) A ciência nas relações Brasil-França (1850-1950) São Paulo: Edusp.
- Mouzinho, M. L. 1961 Discurso proferido na ABC. (Não publicado.)
- Nachbin, L. 1996 Ciência e Sociedade Curitiba: Ed. UFPR.
- Nachbin, L. 1961 Etapas do desenvolvimento da matemática no Brasil. Boletim da Sociedade Paranaense de Matemática v. 4, n. 2, p. 22-8.
- Schartzman, S. 1979 Formação da comunidade científica no Brasil São Paulo: Cia. Ed. Nacional.
- Schartzman, S. 1982 (org.) Universidades e instituições científicas no Rio de Janeiro Brasília: CNPq.
- Silva, O. A. 1898 Alguns Erros de Mathematica na Synthese Subjectiva de A. Comte. Revista da Escola Politécnica, Rio de Janeiro, v. 2, n. 9/10,
- Silva, C. M. 2002 Formação de professores e pesquisadores de matemática na Faculdade Nacional de Filosofia. Cadernos de pesquisa, n. 117, p. 103-26.
- Silva, C. M. 2000a A Faculdade de Filosofia, Ciências e Letras da USP e a formação de professores de Matemática. In: Reunião Anual da Anped, 23, 2000. Caxambu. Anais... Caxambu.
- Silva, C. M. 2000b Lélio Itapuambyra Gama e a modernização do ensino da Matemática no Brasil. In: Seminário Nacional de História da Ciência e da tecnologia, 7, 2000. Anais... São Paulo: Edusp, Ed. Unesp, Imprensa Oficial.
- Silva, C. P. 1998 A contribuição de Otto de Alencar Silva para o desenvolvimento da ciência no Brasil. Revista da Sociedade Brasileira de História da Ciência, n. 19, jan.-jun. p. 13-30.
- Venancio Filho, F. 1935 Theodoro Ramos. Revista Brasileira de Engenharia, Tomo xxx, n. 6, dez.
- Weil, A. 1974 Leopoldo Nachbin. Recorte de jornal, 1974. Arquivo Leopoldo Nacbin, Mast/CNPq.
Datas de Publicação
-
Publicação nesta coleção
16 Jan 2007 -
Data do Fascículo
Dez 2006
Histórico
-
Aceito
Jun 2005 -
Recebido
Jan 2005