Resumos
Por que municípios próximos tendem a ter resultados eleitorais semelhantes? Testam-se aqui três possíveis explicações: as interações sociais entre residentes de municípios próximos; a concentração das campanhas eleitorais em determinadas regiões em detrimento de outras; e as similaridades socioeconômicas observadas entre municípios próximos. Com dados das eleições de 2010 e ferramentas de econometria espacial, a primeira hipótese foi rejeitada; a segunda hipótese foi corroborada preliminarmente; e a terceira hipótese foi corroborada inequivocamente. Os dados mostram ainda que Dilma Rousseff "herdou" a base geográfica de Lula e que essa base é bastante diferente da do PT, que continua sobretudo um partido urbano.
geografia eleitoral; econometria espacial; Partido dos Trabalhadores
Why do nearby towns tend to have similar electoral results? We test here three possible explanations: social interactions between inhabitants of nearby towns; the concentration of campaign strategies in some areas to the detriment of other areas; and the socioeconomic similarities of nearby towns. Using data from the 2010 elections and spatial econometrics, we rejected the first hypothesis; we found some preliminary support for the second hypothesis; and we found unequivocal support for the third hypothesis. The data also show that Dilma Rousseff "inherited" Lula's electoral basis of support and that this is quite different from that of the PT, which remains an urban-based party.
electoral geography; spatial econometrics; Workers' Party
A dimensão geográfica das eleições brasileiras
Thiago Marzagão
Doutorando em Ciência Política The Ohio State University. marzagao.1@osu.edu
RESUMO
Por que municípios próximos tendem a ter resultados eleitorais semelhantes? Testam-se aqui três possíveis explicações: as interações sociais entre residentes de municípios próximos; a concentração das campanhas eleitorais em determinadas regiões em detrimento de outras; e as similaridades socioeconômicas observadas entre municípios próximos. Com dados das eleições de 2010 e ferramentas de econometria espacial, a primeira hipótese foi rejeitada; a segunda hipótese foi corroborada preliminarmente; e a terceira hipótese foi corroborada inequivocamente. Os dados mostram ainda que Dilma Rousseff "herdou" a base geográfica de Lula e que essa base é bastante diferente da do PT, que continua sobretudo um partido urbano.
Palavras-chave: geografia eleitoral; econometria espacial; Partido dos Trabalhadores
ABSTRACT
Why do nearby towns tend to have similar electoral results? We test here three possible explanations: social interactions between inhabitants of nearby towns; the concentration of campaign strategies in some areas to the detriment of other areas; and the socioeconomic similarities of nearby towns. Using data from the 2010 elections and spatial econometrics, we rejected the first hypothesis; we found some preliminary support for the second hypothesis; and we found unequivocal support for the third hypothesis. The data also show that Dilma Rousseff "inherited" Lula's electoral basis of support and that this is quite different from that of the PT, which remains an urban-based party.
Keywords: electoral geography; spatial econometrics; Workers' Party
Puzzle, hipóteses e informação contextual1 1 Esta pesquisa foi possível devido aos financiamentos da Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES), da Fundação Fulbright e do Ministério do Planejamento. O autor agradece as críticas e sugestões do (a) parecerista anônimo (a).
Por que eleitores que vivem em municípios próximos tendem a votar nos mesmos candidatos? A literatura existente fornece abundante evidência de que a interação com familiares e amigos afeta a escolha do eleitor (HUCKFELDT & SPRAGUE, 1991; NICKERSON, 2008). Mas familiares e amigos tendem a residir dentro do mesmo município; portanto, esse tipo de interação não explica a similaridade do voto entre municípios. Este artigo testa três hipóteses para a autocorrelação espacial observada entre os resultados eleitorais de municípios próximos. A primeira é que o voto é influenciado não apenas por interações sociais que acontecem dentro de cada município, mas também por interações sociais que acontecem entre municípios. Como mostram os modelos gravitacionais, fluxos de comércio são inversamente proporcionais à distância (TINBERGEN, 1962), de modo que tudo o mais constante municípios próximos devem transacionar mais do que municípios distantes. Essas interações econômicas, por sua vez, ensejam interações sociais -por exemplo, empresas criam cadeias de fornecimento nas quais residentes de diferentes municípios interagem regularmente. Essas interações podem resultar em discussões políticas que influenciam a escolha eleitoral.
A segunda hipótese testada neste artigo é que campanhas eleitorais focam em certas regiões e negligenciam outras, o que aproxima o voto dos eleitores residentes em municípios pertencentes a uma mesma região. Candidatos têm recursos finitos, de modo que eles precisam alocar seus "war chests" estrategicamente. Isso é alcançado quando os candidatos concentram seus recursos naquelas regiões com o maior retorno em termos de votos ou doações de campanha (CHO & GIMPEL, 2007). Na medida em que essa taxa de retorno é semelhante em municípios próximos (devido a fatores históricos), a alocação de recursos de campanha também será espacialmente autocorrelacionada e, a menos que a campanha tenha efeito nulo, o voto também será espacialmente autocorrelacionado.
Por fim, a terceira hipótese é que eleitores de municípios próximos tendem a votar de maneira parecida simplesmente porque são socioeconomicamente semelhantes e, portanto têm preferências políticas semelhantes. Condições socioeconômicas não são distribuídas aleatoriamente pelo território nacional; municípios pobres normalmente estão próximos de outros municípios pobres e vice-versa. Na medida em que condições materiais objetivas influenciam o comportamento eleitoral, o voto deve ser espacialmente autocorrelacionado.
Informação contextual
A dimensão geográfica das eleições brasileiras é discutida em Carraro et al (2007), Nicolau & Peixoto (2007), Soares & Terron (2008), Hunter & Power (2008) e Terron & Soares (2010). Apenas Carraro et al (2007), Soares & Terron (2008) e Terron & Soares (2010) usam econometria espacial; Nicolau & Peixoto (2007) e Hunter & Power (2008) somente discutem a variação do resultado eleitoral entre estados. Três achados principais emergem da literatura existente. Primeiro, enquanto até 2002 a maior parte do voto em Lula estava concentrada nos centros urbano-industriais do sul e do sudeste, após ganhar a Presidência, em 2003, Lula conseguiu estender seu apoio eleitoral para as áreas rurais e subdesenvolvidas do norte e nordeste (SOARES & TERRON, 2008). Essa transformação ficou clara na eleição de 2006 e, segundo a maioria dos pesquisadores, resultou principalmente do Bolsa Família, programa que concede R$ 68 mensais (mais R$ 22 por criança na escola) a famílias pobres. O programa custa cerca de 0,5% do PIB nacional e beneficia cerca de 44 milhões de pessoas, concentradas sobretudo nas áreas rurais do norte e nordeste -precisamente onde o apoio eleitoral de Lula se expandiu entre 2002 e 2006. Carraro et al (2007) são os únicos pesquisadores que apontam o crescimento econômico, e não o Bolsa Família, como a principal explicação para a variação no apoio eleitoral de Lula entre municípios.
O segundo principal achado da literatura existente é que a autocorrelação espacial do voto é geralmente alta. A estatística Moran I (que varia entre -1=correlação negativa perfeita e +1=correlação positiva perfeita) para autocorrelação espacial do voto entre municípios variou entre 0,60 e 0,81 para as eleições ocorridas entre 1994 e 2006 (TERRON & SOARES, 2010). Por fim, o terceiro achado é que as bases eleitorais de Lula e do PT seguiram trajetórias diferentes a partir de 2002. Enquanto Lula conseguiu expandir seu apoio eleitoral para o norte e nordeste, o PT permaneceu principalmente um partido urbano. Soares & Terron (2010) mostram que a correlação espacial bivariada entre os votos em Lula e os votos em deputados do PT declinou de 0,41 em 2002 para -0,04 em 2006. Essa divergência é provavelmente relacionada ao caráter personalista da política brasileira; os eleitores associam o Bolsa Família (ou o crescimento econômico, na interpretação de Carraro et al (2007)) à figura do Presidente, não ao partido.
Em suma, a literatura revela padrões eleitorais interessantes. Erros metodológicos, porém, lançam dúvidas sobre os resultados. Nem todos os autores informam qual método de estimação foi utilizado nas análises multivariadas -mínimos quadrados ordinários (ordinary least squares -OLS), máxima verossimilhança (maximum likelihood -ML) ou o método generalizado dos momentos (generalized method of moments -GMM). Essa omissão é problemática porque regressores espacialmente defasados sempre introduzem endogeneidade (dado que observações próximas influenciam-se mutuamente) e usualmente também heterocedasticidade (ANSELIN, 2006) e esses problemas têm consequências distintas para diferentes métodos de estimação (WARD & GLEDITSCH, 2008; KELEJIAN & PRUCHA, 2010).
Outro problema metodológico é que a interpretação dos coeficientes é na maior parte das vezes equivocada. Considere Soares & Terron (2008), por exemplo. Eles usam um modelo de defasagens espaciais para a diferença na proporção de votos em Lula entre o primeiro e o segundo turnos da eleição de 2006, em cada município. Eles encontram um coeficiente de 0,97 para a razão Bolsa Família/renda e concluem que "Se fosse possível manter constante o efeito da renda domiciliar, cada 1% de acréscimo do BF/renda significaria, em média, 1% de incremento sobre a diferença nos votos percentuais de Lula no município" (SOARES & TERRON, 2008, p. 295). Mas municípios próximos influenciam-se mutuamente, de modo que os coeficientes de uma regressão com defasagens espaciais não podem ser interpretados como em um modelo linear (WARD & GLEDITSCH, 2008). Enquanto as estimativas de um modelo não-espacial são computadas como E[y] = Xβ , no modelo de defasagens espaciais, as estimativas devem ser computadas como E[y] = (I ρP)-1Xβ , onde I é uma matriz identidade (uma matriz com 1s na diagonal principal e 0s nas demais células) e os demais termos são explicados na Seção "Testes de hipóteses", adiante2 2 A fórmula é uma simples derivação do modelo de defasagens espaciais, y = ρ Py + X β+ ε . Movendo todos os termos relacionados a y para o lado esquerdo da equação o resultado é ( I ρ P)y = X β+ ε , o que pode ser rearranjado como y = ( X β+ ε)/( I ρ P) = ( I ρ P) -1( X β+ ε). Dado que E[ ε] = 0, a fórmula reduz-se a E[ y] = ( I ρ P) -1 X β . Vide Seção "Testes de hipóteses" para mais detalhes sobre o modelo de defasagens espaciais. . Como Ward & Gleditsch (2008) observam, o termo (I ρP)-1 é um multiplicador que captura a dinâmica de longo prazo em que alterações na observação i produzem alterações na observação k, que reverberam em novas alterações na observação i e assim por diante, até que o choque se dissipe. O coeficiente de 0,97 encontrado por Soares & Terron (2008) indica apenas o impacto direto de uma alteração em X sobre Y , sem considerar a natureza dinâmica do modelo. O equilíbrio final é o produto do impacto direto e do impacto indireto - e, note-se, o equilíbrio final é diferente para cada observação, visto que cada município tem uma matriz de pesos própria. (Outro problema é que ainda que o modelo fosse estático, um coeficiente de 0,97 implicaria que para cada ponto percentual de acréscimo na razão Bolsa Família/renda a diferença na votação de Lula aumentaria um ponto percentual; ambas as variáveis precisariam estar em forma logarítmica para permitir a interpretação pretendida por Soares & Terron (2008). Terron & Soares (2010) e Carraro et al (2007) cometem os mesmos erros.
Outro problema com a literatura existente é que a escolha da matriz de pesos é por vezes questionável. Carraro et al (2007), por exemplo, consideram como "municípios próximos" todos aqueles cujos centroides estão dentro de um raio de 50 km do centroide do município i; municípios que excedem essa distância são excluídos da matriz de pesos (ou seja, têm peso zero). Como será discutido na Seção "Regularidades espaciais nas eleições brasileiras", essa escolha exclui metade do território brasileiro da estimação, devido às grandes dimensões dos municípios da região norte. Dado que o norte é socioeconomicamente muito distinto do sul e do sudeste (municípios do norte tendem a ser muito mais pobres e menos populosos), as inferências de Carraro et al (2007) são baseadas em estimativas fortemente enviesadas.
Por fim, nenhum dos trabalhos existentes discute a possibilidade de heterogeneidade, i.e., de que os efeitos (inclusive diretos) das variáveis independentes (Bolsa Família, renda, etc.) sejam diferentes de uma região para outra.
Roteiro
A próxima seção mostra que o voto foi espacialmente autocorrelacionado na eleição de 2010 e identifica em quais áreas do país essa autocorrelação foi mais forte. Ela também compara as regularidades observadas na eleição de 2010 com aquelas observadas em eleições anteriores. Embora sem carisma, sem experiência com política eleitoral e pouco conhecida do público antes da campanha, Dilma Rousseff venceu a eleição. Qual foi a distribuição geográfica de seu apoio eleitoral? Foi similar à de Lula em 2006? Como essa distribuição se compara com a do PT? O partido conseguiu "pegar carona" na popularidade de Lula e expandir geograficamente suas bases eleitorais desde 2006? Essas são as perguntas que orientam a próxima seção. A seção seguinte, por seu turno, testa as três hipóteses discutidas anteriormente, discute os resultados e também testa a premissa de homogeneidade (i.e., de que o efeito de cada variável incluída no modelo é o mesmo em todo o território nacional), o que é feito por meio de uma regressão geograficamente ponderada.
Regularidades espaciais nas eleições brasileiras
Esta seção faz uma análise exploratória dos dados, avalia se de fato há autocorrelação espacial nas eleições brasileiras e discute a escolha da matriz de pesos apropriada.
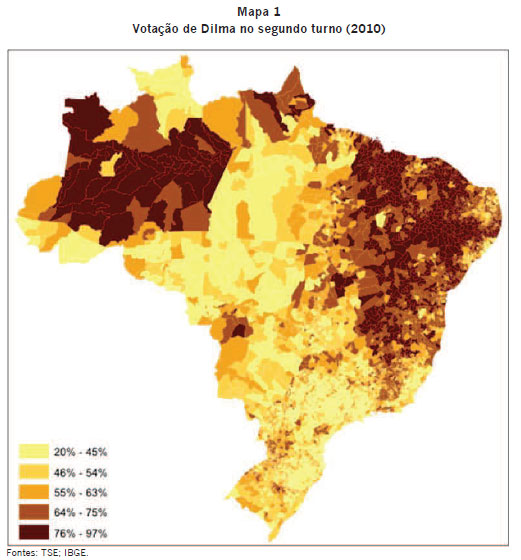
O Mapa 1 mostra a proporção de votos em Dilma Rousseff em cada município no segundo turno da eleição presidencial de 20103 3 A fonte dos dados geocodificados foi o Instituto Brasileiro de Geografia e Estatística (IBGE). A fonte dos dados eleitorais foi o Tribunal Superior Eleitoral (TSE). Maiores detalhes e estatísticas descritivas estão no Apêndice. .
Como o Mapa 1 mostra, os votos em Dilma concentraram-se na região nordeste e nos estados do Amazonas (em cujos municípios Dilma teve entre 76% e 97% dos votos) e Amapá. Esse padrão é bastante similar ao de 2006; diferenças de escala à parte, o Mapa 1 é muito semelhante ao encontrado em Soares & Terron (2008).
O Mapa 1 também sugere autocorrelação espacial: municípios próximos tendem a votar de forma parecida. É preciso porém testar formalmente a existência de autocorrelação espacial. Para tanto, o primeiro passo é definir exatamente o que é um município "próximo". Como discutido na seção anterior, usar um raio de 50 km, como Carraro et al (2007) fazem, é inadequado. Devido a padrões históricos de colonização, os municípios brasileiros tendem a ser pequenos no sul, sudeste e nordeste e grandes no norte e em parte do centro-oeste4 4 Um padrão similar é observado nos Estados Unidos, onde os municípios tendem a ser maiores na costa oeste do que na costa leste. . Por exemplo, um indivíduo no centroide de Altamira (um município paraense de 159.695 km2, maior do que Portugal) precisaria atravessar 198,6 km para chegar até o centroide mais próximo. Portanto adotar um raio de 50 km implica transformar Altamira em um município sem "vizinhos"; em econometria espacial observações sem vizinhos são chamadas de "ilhas" e excluídas da estimação. No total, 334 municípios brasileiros estão na mesma situação de Altamira, i.e., a distância entre o próprio centroide e o centroide mais próximo é superior a 50 km. Pode parecer pouco, mas juntos aqueles 334 municípios representam aproximadamente 50% do território nacional (quase 100% da região norte e mais de 50% da região centro-oeste), como mostra o Mapa 2:
Excluir tamanha fatia do país das estimações seria uma limitação grave: a análise toda seria aplicável apenas às regiões sul e sudeste (e à parte da região nordeste). Um contra-argumento é que, dadas as dimensões dos municípios do norte, talvez eles sejam de fato isolados uns dos outros e, portanto, a ideia de influência recíproca - que fundamenta o modelo de defasagens espaciais - não se lhes aplica e sua exclusão é apropriada. Mas, mesmo municípios grandes fazem comércio - nenhum município produz tudo o que consome e consome tudo o que produz. Altamira e Gurupá (municípios vizinhos no Pará) podem interagir menos que, digamos, Florianópolis e São José (municípios vizinhos em Santa Catarina), mas alguma interação existe e assumir que essa interação é zero é um erro de especificação do modelo.
Aumentar o raio para 80 km elimina muitas das "ilhas" no nordeste mas altera quase nada no norte e no centro-oeste. Aumentar o raio para 110 km elimina praticamente todas as ilhas no nordeste e no centro-oeste mas ainda altera muito pouco no norte. O menor raio necessário para eliminar todas as ilhas é de 374 km. Mas o raio não pode ser aumentado arbitrariamente. Um raio de 374 km não modela adequadamente as dinâmicas no sul e no sudeste: esse raio equivale aproximadamente a distância entre, por exemplo, São Paulo e Ribeirão Preto, mas existem 16 municípios entre os dois. Qualquer influência que Ribeirão Preto poderia ter sobre os resultados eleitorais de São Paulo (e vice-versa) é certamente dissipada ao longo do caminho.
Em suma, não é possível encontrar um raio que seja apropriado para todas as regiões do país. Dessa forma duas alternativas são adotadas neste artigo. A primeira - adotada nesta e na próxima seções - é definir municípios "próximos" como municípios contíguos. Em termos práticos, isso equivale a adotar um vetor de pesos Pi que atribui peso 1 (um) aos municípios contíguos ao município i e peso 0 (zero) a todos os demais municípios5 5 Em particular, a escolha aqui é por "contiguidade rainha" em vez de "contiguidade torre" (os termos derivam dos movimentos da rainha e da torre no jogo de xadrez). Com polígonos muito irregulares (como os municípios brasileiros), a diferença entre ambas é pequena e a "contiguidade rainha" exige menos em termos computacionais. . Essa matriz de contiguidade produz apenas três "ilhas": Fernando de Noronha e Ilhabela (que são ilhas no sentido literal e portanto não têm municípios contíguos) e Brasília (que tecnicamente não é um município). A segunda alternativa, adotada na maior parte da próxima seção, é uma matriz de distâncias inversas. Nessa matriz, cada município relaciona-se com todos os demais municípios do país mas o peso atribuído ao município k é inversamente proporcional à distância entre os municípios i e k (i.e., 1/[distância em km entre o município i e o município k]). A razão pela qual a matriz de distâncias inversas é adotada em parte da próxima seção é técnica e não estatística (o Apêndice fornece maiores detalhes). Em todo caso, como será demonstrado, a matriz de contiguidade e a matriz de distâncias inversas produzem resultados muito semelhantes (embora a dimensão espacial tenha um impacto maior sobre a variável dependente usando-se a matriz de distâncias inversas).
Adotando-se a matriz de contiguidade, a estatística Moran I para a eleição presidencial de 2010 é de 0,783 (p < 0.0001), o que confirma que o voto em Dilma é espacialmente autocorrelacionado. O Mapa 3 mostra quais aglomerados eleitorais são "reais" e não meros artefatos visuais. As áreas em realce representam municípios cuja proporção do voto em Dilma é estatisticamente correlacionada com a proporção do voto em Dilma nos municípios vizinhos. Em termos técnicos, esses são os municípios cujos indicadores locais de associação espacial (LISA -local indicators of spatial association) são estatisticamente significativos. Esses municípios podem ser categorizados em quatro grupos. "High-high" representa os municípios onde a votação de Dilma foi alta e que estão circundados por municípios onde a votação de Dilma também foi alta. "Low-low" representa os municípios onde a votação de Dilma foi baixa e que estão circundados por municípios onde a votação de Dilma também foi alta. "High-low" representa os municípios onde a votação de Dilma foi alta e que estão circundados por municípios onde a votação de Dilma foi baixa. E "low-high" representa os municípios onde a votação de Dilma foi baixa e circundados por municípios onde a votação de Dilma foi alta. Esses últimos dois grupos -"high-low" e "low-high" -são residuais (apenas 50 municípios de um total de 2891 municípios cujos LISAs são estatisticamente significativos), de modo que a análise é focada nos municípios "high-high" e "low-low".
Existem três grandes aglomerados "high-high": a região nordeste; o estado do Amazonas; e a porção nordeste do estado de Minas Gerais. Por outro lado, existem quatro grandes aglomerados "lowlow": o estado de Roraima; a porção norte do estado do Mato Grosso junto com a porção central do estado do Pará; o estado do Mato Grosso do Sul; e o estado de São Paulo junto com as porções oeste de Paraná, Santa Catarina e Rio Grande do Sul. Comparando o Mapa 3 com seu equivalente em Soares & Terron (2008), a única diferença é o estado do Amapá. Em 2006 o Amapá era quase inteiramente um aglomerado "high-high" ao passo que, em 2010, havia apenas um pequeno aglomerado "high-high" no meio do estado. Fora isso, não houve grandes alterações.
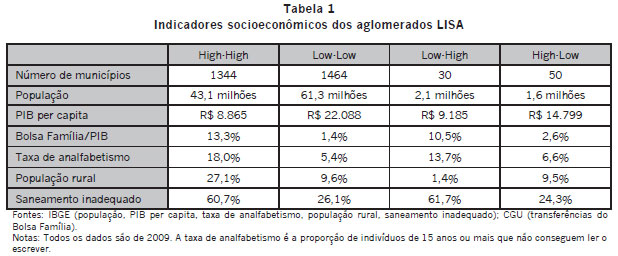
A Tabela 1 compara os indicadores socioeconômicos dos quatro grupos:
Os indicadores mostram uma nítida divisão socioeconômica entre os aglomerados "high-high" e os aglomerados "low-low". No primeiro caso (que compreende 1344 municípios e 43,1 milhões de pessoas), o PIB per capita é de R$ 8.865; 18% são analfabetos; 27,1% vivem na zona rural; 60,7% dos domicílios não têm saneamento apropriado e o Bolsa Família representa 13,3% do PIB. No segundo caso (que compreende 1464 municípios e 61,3 milhões de pessoas), o PIB per capita é quase três vezes maior (R$ 22.088); a taxa de analfabetismo é mais de dez vezes menor (1,4%); a incidência de saneamento inapropriado é de 26,1%; menos de 10% vivem na zona rural e a razão Bolsa Família/PIB é de apenas 1,4%6 6 A fonte de todos os dados socioeconômicos, exceto o Bolsa Família, é o IBGE. A fonte dos dados relativos ao Bolsa Família é a Controladoria-Geral da União (CGU). Detalhes e estatísticas descritivas estão no Apêndice. . A divisão é não apenas socioeconômica mas geográfica: 99,7% dos aglomerados "high-high" estão no norte e nordeste e na porção norte de Minas Gerais, ao passo que 93,2% dos aglomerados "low-low" estão no sul, sudeste, centro-oeste e na porção sul de Minas Gerais.
Em suma, a eleição presidencial de 2010 dividiu o "norte" (numa definição flexível da palavra) e o "sul". Dado que o peso eleitoral dos aglomerados "low-low" (61,3 milhões de pessoas) é muito maior que o dos aglomerados "high-high" (43,1 milhões de pessoas), à primeira vista é surpreendente que Dilma tenha vencido a eleição. Sua vitória é resultado de dois fatores: os municípios não-pertencentes a qualquer aglomerado (2675 no total, com indicadores socioecômicos entre aqueles dos aglomerados "low-low" e aqueles dos aglomerados "high-high") e sua expressiva votação mesmo nos aglomerados "lowlow". Este último ponto merece alguma elaboração. Ao que parece, a votação de Dilma teve um "piso": em nenhum município do país, ela recebeu menos de 19% do voto. Mesmo no município de Capixaba, no Acre, cuja estatística LISA (5,13) é a maior entre todos os municípios "low-low", Dilma conseguiu obter mais de 20% dos votos. No município de São Paulo, histórico reduto tucano, Dilma conseguiu obter 46,8%, quase metade dos votos, e perdeu para Serra por apenas 6,25 pontos percentuais. Portanto mesmo onde ela perdeu Dilma ainda obteve votações substantivas. O mesmo não aconteceu com Serra. Sua votação não teve um "piso": em aglomerados "high-high", ele frequentemente recebeu menos de 10% dos votos; no município de Calumbi (Ceará), por exemplo, ele recebeu apenas 3,49% dos votos.
Os Mapas 1 e 3 mostraram que o apoio eleitoral a Dilma em 2010 seguiu o mesmo padrão geográfico do apoio a Lula em 2006. E quanto ao apoio eleitoral ao PT? Como discutido antes, Lula conseguiu estender sua base geográfica, mas o PT não (TERRON & SOARES, 2010). Isso mudou entre 2006 e 2010? Os Mapas 4 e 5 mostram a votação em deputados estaduais e federais do PT em 2010.
Claramente, a política brasileira continua altamente personalista: a distribuição geográfica da votação no PT não nos ajuda a prever a distribuição geográfica da votação em Dilma. Isso indica que o desacoplamento identificado por Terron & Soares (2010) ainda continua. Ele é especialmente visível no estado do Amazonas e nas regiões sudeste e sul. No Amazonas, Dilma recebeu 81,1% dos votos, mas o PT recebeu apenas 5,2% dos votos para a assembleia estadual. Por outro lado, em São Paulo, Dilma recebeu apenas 44,9% dos votos, enquanto o PT recebeu 17,1% dos votos para a assembleia estadual. Portanto se há alguma correlação entre a votação de Dilma e a do PT, ela é negativa: Dilma tem mais apoio onde o PT tem menos, e vice-versa (de fato, a estatística Moran I bivariada entre as duas votações é de -0,0453). A conclusão é que Lula conseguiu transferir sua base eleitoral para Dilma, mas não para o PT7 7 Também vale notar que, embora a votação do PT para assembleias estaduais mostre autocorrelação espacial, o efeito é muito menos pronunciado do que na eleição presidencial (a estatística Moran I é 0,3733, com p < 0.0001). .
Em resumo, esta seção mostrou haver forte autocorrelação espacial na votação para Presidente em 2010; que a base geográfica de Dilma em 2010 foi essencialmente a mesma que a base geográfica de Lula em 2006; e que as bases geográficas do PT, por um lado, e de Lula e Dilma, por outro, continuam divergentes. A próxima seção testa explicações alternativas para a autocorrelação espacial do voto em Dilma e avalia se essas explicações são igualmente válidas em diferentes regiões do país.
Explicando as regularidades espaciais das eleições brasileiras
Testes de hipóteses
Em termos econométricos, cada hipótese discutida neste artigo implica um modelo espacial diferente. A primeira hipótese (interações sociais entre municípios) implica um modelo de defasagens espaciais: o valor da variável dependente em cada município é determinado por uma média ponderada dos valores da variável dependente em municípios próximos. Formalmente, essa relação pode ser resumida como yi = ρPiyk+εi, onde yi é o valor da variável dependente para o município i (i.e., porcentagem dos votos obtida pelo Partido dos Trabalhadores no município i), yé uma matriz que contém o valor da variável dependente para os municípios próximos, Pi é um vetor que especifica o peso atribuído a cada município próximo (i.e., 1/[distância em km entre o município i e o município k]), ρ é o efeito imediato de Piyk em yi (i.e., a alteração imediata em yi quando Piyk aumenta em uma unidade) εi representa o "erro", i.e., a diferença entre o yi estimado pelo modelo e o yi observado na realidade (essa diferença captura tudo aquilo que influencia yi mas foi deixado de fora do modelo; idealmente a média dos erros, ou "resíduos", é zero, sua variância é constante e o erro de uma observação não tem relação com os erros das demais observações). O modelo pode ser facilmente estendido para o caso em que outras variáveis (além da influência recíproca entre municípios) também determinam a variável dependente: yi=ρPiyk+Xi β+εi onde Xi é um vetor que contém os valores das demais variáveis independentes (i.e., renda média, taxa de analfabetismo) para o município i e β é um vetor de coeficientes. (O termo "defasagem", que pode soar estranho nesse contexto, vem da analogia com modelos temporais, em que se regride o valor atual de y a valores passados -i.e., defasados -de y).
A segunda e terceira hipóteses implicam um modelo de erros espaciais (e não de defasagens espaciais): resultados eleitorais são espacialmente autocorrelacionados não porque municípios próximos influenciam-se reciprocamente, mas apenas porque municípios próximos são influenciados por fatores comuns (campanhas eleitorais ou condições socioeconômicas) e ao menos um desses fatores não pode ser explicitamente incluído no modelo. Formalmente, o modelo é yi= Ciβ1+ Siβ2+εi, onde β1 é o efeito das campanhas eleitorais e β2 é o efeito das condições socioeconômicas. Esse modelo, em si, é apenas um modelo comum de regressão linear. A dimensão espacial surge quando uma das variáveis independentes não pode ser explicitamente incluída. Aqui a dificuldade é com as campanhas eleitorais: não há dados comparáveis e publicamente disponíveis sobre a concentração geográfica das campanhas eleitorais dos partidos brasileiros. Dessa forma o modelo (estimável) passa a ser yi=Siβ2+ζi, onde ζi=λPiξk+εi . Diferentemente do modelo de defasagens espaciais, discutido anteriormente, aqui o termo de erro, ζi, não é aleatório: ele contém um componente sistemático,λPiξk, por meio do qual o erro de uma observação está espacialmente autocorrelacionado com os erros das observações próximas, ponderados pelo vetor de pesos Pi (WARD & GLEDITSCH, 2008). Esse componente sistemático é resultado da exclusão da variável "campanhas eleitorais".
Testar a primeira hipótese implica testar se o modelo contém um termo de defasagem espacial (ρPiyk), o que é feito por meio de testes de Lagrange e por meio da estimação de um modelo de defasagens e erros espaciais (i.e., yi=ρPiyk+ Siβ+ζi, que é uma combinação do modelo de defasagens espaciais e do modelo de erros espaciais). A ideia é que se ρ for estatisticamente significativo a primeira hipótese é aceita (o que, naturalmente, não implica a rejeição das demais hipóteses, visto que elas não são mutuamente excludentes).
Testar a segunda e a terceira hipóteses implica testar se os resíduos do modelo são espacialmente autocorrelacionados, o que também é feito por meio de testes de Lagrange e por meio da estimação de um modelo de defasagens e erros espaciais. A ideia aqui é que como as defasagens espaciais e os indicadores socioeconômicos estão explicitamente incluídos no modelo qualquer autocorrelação espacial observada nos resíduos deve resultar das campanhas eleitorais (i.e., a variável independente omitida e capturada por meio dos resíduos). A lógica é simples. Se o efeito das condições socioeconômicas for estatisticamente significativo e os resíduos não forem espacialmente autocorrelacionados, a segunda hipótese é rejeitada e a terceira hipótese é aceita. Se o efeito das condições socioeconômicas for estatisticamente significativo mas os resíduos ainda mostrarem autocorrelação espacial, tanto a segunda como a terceira hipóteses são aceitas. E se o efeito das condições socioeconômicas não for estatisticamente significativo e os resíduos mostrarem autocorrelação espacial, a segunda hipótese é aceita e a terceira hipótese é rejeitada8 8 O cenário onde o efeito das condições socioeconômicas não é estatisticamente significativo e os resíduos não são espacialmente autocorrelacionados é logicamente inconsistente -variáveis com efeito nulo não podem eliminar a autocorrelação dos resíduos. .
Em suma, a terceira hipótese (condições socioeconômicas) é testada diretamente ao passo que a primeira (influência recíproca) e a segunda (campanhas eleitorais) hipóteses são testadas indiretamente.
O primeiro passo é a escolha do modelo espacial a ser estimado. Para tanto, estima-se um modelo não-espacial por mínimos quadrados e então aplicam-se testes baseados no multiplicador de Lagrange (testes LM). Se o teste LM para a presença de defasagens espaciais for estatisticamente significativo mas o teste LM para a presença de erros espaciais não, conclui-se que o modelo de defasagens espaciais é o adequado, e vice-versa. Se os dois testes forem estatisticamente significativos, apela-se para uma versão modificada do teste LM. Nessa versão modificada, o teste LM para a presença de defasagens espaciais é válido mesmo na presença de erros espaciais e o teste LM para a presença de erros espaciais é válido mesmo na presença de defasagens espaciais. Se os dois testes modificados forem estatisticamente significativos, então: a) escolhe-se o modelo com a maior estatística LM; ou b) conclui-se que o modelo adequado é o de defasagens e erros espaciais (que é uma combinação dos dois modelos).
O modelo escolhido é então estimado por meio de GMM ou ML. OLS geralmente não é uma alternativa. O modelo de defasagens espaciais introduz endogeneidade: a variável dependente aparece tanto do lado direito quanto do lado esquerdo da equação, de modo que os coeficientes estimados por OLS são enviesados e inconsistentes (i.e., o viés não desaparece conforme o número de observações aumenta; Ward & Gleditsch (2008) notam que, em modelos espaciais o viés tende a aumentar, em vez de diminuir com o número de observações). O modelo de erros espaciais, por sua vez, viola a premissa de que os resíduos são independentes uns dos outros. Nesse caso os coeficientes estimados por OLS são não-viesados e consistentes, mas os erros-padrão são subestimados, o que leva a erros tipo I (i.e., rejeita-se a hipótese nula mesmo quando ela não é falsa). Coeficientes e erros-padrão estimados por meio de ML e GMM, por outro lado, são consistentes, i.e., podem ser enviesados, mas o viés tende a desaparecer conforme o número de observações aumenta (LEE, 2004; KELEJIAN & PRUCHA, 2010).
Seguindo o roteiro detalhado anteriormente, a Tabela 2 apresenta estimativas de mínimos quadrados para a votação de Dilma (em porcentagem) em cada município no segundo turno da eleição de 2010. A especificação é simples. O objetivo é "filtrar" o efeito das condições socioeconômicas para que qualquer autocorrelação espacial remanescente possa ser atribuída a influência recíproca (capturada pelo termo de defasagem espacial) e às campanhas eleitorais (capturadas pelo termo de erro espacial). Dessa forma as variáveis independentes incluídas no modelo são a razão Bolsa Família/PIB, o logaritmo natural do PIB per capita, a porcentagem de pessoas vivendo na zona rural, a taxa de analfabetismo e a porcentagem de domicílios com saneamento inadequado. Há ainda uma variável dummy para cada estado exceto o Acre (que serve como referência) e uma variável dummy codificada como 1 se o prefeito em 2009 era do PT e 0 se o prefeito pertencia a outro partido (a ideia é que a votação de Dilma pode ter sido maior nos municípios governados pelo PT)9 9 Fontes e maiores informações são fornecidas no Apêndice. .
Na Tabela 2, a seguir, três diferentes estimações são reportadas: OLS, mínimos quadrados ponderados usando o número de habitantes como peso (WLSH) e mínimos quadrados ponderados usando a variância intra-estado como peso (WLSV). A estimação por OLS é apenas uma referência. Os resíduos são heterocedásticos (i.e., sua variância não é constante), de modo que as estimativas OLS não são confiáveis. As estimações por WLS têm por objetivo reduzir a heterocedasticidade. Na estimação em que a ponderação é feita com base no número de habitantes, a ideia é que a votação em Dilma é apenas uma proxy do "verdadeiro" apoio eleitoral de Dilma em cada município. Essa proxy, por seu turno, é medida com erro (supostamente aleatório) que deve ser maior em municípios menores do que em municípios maiores. Por exemplo, Dilma obteve 46,8% dos votos no município de São Paulo e igualmente 46,8% dos votos no município de Água Limpa. Mas enquanto São Paulo tem 11,3 milhões de habitantes, Água Limpa tem apenas 2,2 mil. De acordo com o teorema do limite central, quanto maior o número de observações, mais próxima a proporção observada estará da "verdadeira" proporção i.e., da proporção prevista pelo modelo dadas as variáveis independentes e seus respectivos coeficientes. Em Água Limpa, um incêndio acidental em uma das zonas eleitorais poderia fazer a votação de Dilma desviar substancialmente da votação prevista. Em São Paulo, porém, um incêndio acidental em uma das zonas eleitorais provavelmente causaria apenas um desvio marginal em relação à votação prevista. Portanto as previsões do modelo são mais confiáveis para municípios com grandes populações do que para municípios com pequenas populações -em outras palavras, os resíduos são negativamente correlacionados com o tamanho da população, o que viola a premissa de que a variância dos resíduos é constante (i.e., homocedástica). A estimação por WLSP enfrenta esse problema ao ponderar cada observação pelo logaritmo natural da população municipal10 10 A forma logarítmica é escolhida para trazer todas as variáveis a uma escala semelhante, dado que diferenças de escala podem elas próprias causar heterocedasticidade. .
A estimação WLSV, por seu turno, enfrenta o problema da heterocedasticidade agrupando por estado os resíduos da estimação OLS e usando as respectivas variâncias como pesos numa estimação subsequente. A ideia é que a variância dos resíduos, embora não seja constante entre os estados, pode ser constante dentro de cada estado. Essa abordagem é conhecida como correção de heterocedasticidade grupo-específica (groupwise heteroskedasticity correction). Infelizmente não há como corrigir os dois "níveis" de heterocedasticidade - municipal e estadual - ao mesmo tempo, de modo que tanto a estimação WLSH quanto a estimação WLSV não resolvem completamente o problema, apenas o amenizam.
A Tabela 2 e todas as demais tabelas omitem as dummies estaduais. A matriz de pesos adotada nos testes LM é a matriz de contiguidade discutida na seção "Regularidades espaciais nas eleições brasileiras".
Os três modelos mostram forte autocorrelação espacial11 11 Ademais, nem a estimação WLS H nem a estimação WLS V eliminaram completamente a heterocedasticidade: o teste Breusch-Pagan rejeita a hipótese nula de homocedasticidade em ambos os casos. . A estatística Moran I rejeita a hipótese nula de aleatoriedade espacial em todos os casos. No que respeita à escolha do modelo espacial mais apropriado, a estimação por OLS sugere um modelo de defasagens e erros espaciais, ao passo que as estimações WLS sugerem um modelo de erros espaciais. Dado que os testes em favor do modelo de defasagens e erros espaciais não são robustos às correções de heterocedasticidade feita nas estimações WLS, o modelo de erros espaciais parece ser o adequado. Não obstante, em favor da completude, os dois modelos serão estimados e comparados. Se o modelo de erros espaciais for de fato o correto, então o termo de defasagem espacial do modelo de defasagens e erros espaciais não será estatisticamente significativo.
Para checar se os resultados são sensíveis à escolha da matriz de pesos, cada modelo será estimado usando-se tanto uma matriz de contiguidade quanto uma matriz de distâncias inversas (vide discussão na seção "Regularidades espaciais nas eleições brasileiras"). No que respeita ao método de estimação, o principal é o estimador GMM desenvolvido por Kelejian & Prucha (2010). A principal vantagem desse estimador é que ele é robusto à heterocedasticidade. Ele é limitado, porém, por não permitir a imposição de restrições no modelo, de modo que não é possível restringir o termo de defasagens ou o termo de erros a zero. Em outras palavras, ele permite a estimação apenas do modelo de defasagens e erros espaciais. Dessa forma, o modelo de erros espaciais é estimado por ML. Lee (2004) mostra que o estimador ML é consistente sob homocedasticidade mas Arraiz et al (2010) mostram que esse não é o caso na presença de heterocedasticidade. Portanto as estimativas ML devem ser vistas com cautela. A Tabela 3 apresenta os resultados:
O termo de defasagem espacial é extremamente próximo de zero ou estatisticamente nãosignificativo no modelo irrestrito. O termo de erro espacial, porém, é estatisticamente significativo em todos os modelos. E os indicadores socioeconômicos são estatisticamente significativos e têm o sinal esperado em todos os modelos (exceto pelo PIB per capita). Os coeficientes e erros-padrão são bastante parecidos nas três estimações12 12 É importante ter em mente, porém, que a interpretação dos coeficientes é diferente em cada modelo: no modelo de defasagens e erros espaciais, os coeficientes capturam apenas o efeito direto de cada variável e negligenciam os efeitos indiretos cada alteração município i influencia o município k, que influencia o município i e assim por diante. . Curiosamente, prefeitos do PT parecem ter um efeito negativo sobre a votação em Dilma. De acordo com Strøm (1990) a incumbência é geralmente um passivo eleitoral, mas soa improvável que os eleitores tenham usado a eleição presidencial para punir prefeitos: como discutido anteriormente, a política brasileira é personalista e as bases eleitorais de Dilma e do PT são diferentes. O efeito negativo encontrado aqui não é uma anomalia porém: nas estimações de Nicolau & Peixoto (2007) e Zucco (2008), os prefeitos do PT também têm um efeito negativo sobre a votação de Lula em 2006. Esse resultado é inesperado e merece maiores investigações (o que está fora do escopo deste artigo). Outro resultado contraintuitivo é que o efeito do PIB per capita não é estatisticamente significativo. Isso provavelmente se deve à desigualdade de renda em certas áreas, o que torna o PIB per capita uma medida imperfeita de prosperidade individual. Todas as outras variáveis têm o sinal esperado e são estatisticamente significativas: quanto mais rural, com mais analfabetos, dependente do Bolsa Família ou carente em saneamento o município, maior a votação em Dilma.
Em termos substantivos, os resultados corroboram a segunda e a terceira hipóteses mas não a primeira, i.e., a autocorrelação espacial da votação de Dilma é devida ao fato de que campanhas eleitorais tendem a privilegiar determinadas regiões em detrimento de outras e ao fato de que municípios próximos são socioeconomicamente similares; a hipótese de influência recíproca não é corroborada pelas estimações. Infelizmente não há dados suficientes para testar a segunda hipótese diretamente. Apenas os gastos totais de campanha são divulgados, sem desagregação por município. Ademais, no Brasil a porcentagem de gastos de campanha não-contabilizados é geralmente alta, de modo que o uso de dados oficiais seria problemático de qualquer forma. Qualquer desenho de pesquisa precisaria basear-se em dados não-financeiros - por exemplo, quantas vezes Dilma visitou o município durante a campanha. Mas esses dados não-financeiros capturariam apenas aspectos pouco importantes da campanha, visto que um candidato só pode visitar um número relativamente pequeno de municípios. De modo que ao fim os resíduos provavelmente ainda seriam espacialmente autocorrelacionados.
Embora não reportado neste artigo, o modelo irrestrito também foi estimado por ML (com uma matriz de contiguidade e com uma matriz de distâncias inversas) e tanto os coeficientes dos indicadores socioeconômicos quanto os termos espaciais são muito semelhantes aos da estimação GMM reportada na Tabela 3. Isso sugere que a heterocedasticidade discutida anteriormente não está causando muito problema nas estimações do modelo de erros espaciais. Outro achado é que embora a escolha da matriz de pesos tenha pouca influência sobre os coeficientes dos indicadores socioeconômicos, ela tem um impacto considerável no termo de erros espaciais. Usando-se uma matriz de distâncias inversas, o termo de erros espaciais aumenta de 0,113 para 0,702. Em termos substantivos, a conclusão é que cada município é afetado não apenas pelos municípios contíguos mas também por outros municípios próximos13 13 É importante não confundir matrizes baseadas em raios com matrizes baseadas em distâncias inversas. No primeiro caso, cada observação dentro do raio recebe peso um e todas as demais recebem peso zero. No segundo caso, cada observação é relacionada a todas as demais observações, mas os pesos são inversamente proporcionais às respectivas distâncias. É possível combinar ambos os tipos, atribuindo pesos inversamente proporcionais às distâncias para todas as observações dentro de um raio pré-estabelecido e zero para todas as demais observações. Isso não é feito neste artigo porque, como discutido na seção "Regularidades espaciais nas eleições brasileiras", nenhum raio seria apropriado para a totalidade do território brasileiro. .
Heterogeneidade
Esta subseção avalia se as estimativas são espacialmente estacionárias, i.e., se o efeito de cada variável é constante ao longo do território nacional. Isso é feito por meio de uma regressão geograficamente ponderada (geographically weighted regression - GWR), que é uma técnica de estimação em que o efeito de cada variável pode ser diferente para observações distintas. A ideia é semelhante à de "quebras estruturais". A diferença é que a GWR explicitamente atribui heterogeneidade à localização geográfica e permite que cada observação (em vez de cada grupo de observações) tenha seus próprios coeficientes14 14 Para uma discussão detalhada de GWR, vide Fotheringham, Brudson & Charlton (2002). . À primeira vista isso pode soar estranho: em qualquer estimação, é preciso ter mais observações do que estimativas, então como é possível que cada observação tenha suas próprias estimativas? A resposta é que as estimativas para cada observação são baseadas em outras observações; especificamente, naquelas consideradas "próximas" (por contiguidade, raio ou distâncias inversas, conforme a matriz de pesos adotada). Dado que cada observação tem seu próprio conjunto de "vizinhos", o resultado é um conjunto diferente de estimativas para cada observação. Formalmente, enquanto o estimador OLS é β= (X' X)-1 X' y , o estimador GWR é βi= (X' PiX)-1 X' Piy , onde P é a matriz de pesos e o subscrito i em β indica que cada observação tem seu próprio coeficiente15 15 Quando a matriz adotada é a de distâncias inversas, uma escolha frequente é calcular os pesos como wik= exp( -dik/ h) 2, onde d é a distância entre as observações i e k e h é uma quantidade chamada de banda ou "kernel". O kernel é um raio além do qual todas as observações recebem peso zero e, portanto, não entram na estimação de β i . O kernel pode ser fixo ou variável de acordo com cada Pi(kernel adaptativo). Como não há um único raio que seja satisfatório para todo o território brasileiro (vide seção "Regularidades espaciais nas eleições brasileiras"), um kernel adaptativo é utilizado aqui. .
A Tabela 4 resume os resultados. Os resultados da estimação GMM usando a matriz de distâncias inversas (1ª coluna da Tabela 3) são incorporados como a 1ª coluna da Tabela 4 para facilitar a comparação:
Embora os resultados sejam visivelmente diferentes entre a estimação GMM e a estimação GWR, as estimativas GWR em si não variam muito. O cálculo de erros-padrão para estimativas GWR é problemático, pois levanta questões de testes conjuntos de hipóteses (FOTHERINGHAM, BRUDSON & CHARLTON, 2002) mas a Tabela 4 sugere que, na maior parte, as estimativas provavelmente não seriam estatisticamente diferentes umas das outras. Fora urbanização, para fins práticos as estimativas da Tabela 4 podem ser consideradas equivalentes.
A conclusão é que as estimativas são espacialmente estacionárias, i.e., o efeito de cada variável é relativamente homogêneo ao longo do território nacional.
Conclusão
Usando dados da eleição presidencial de 2010, este artigo testou três explicações alternativas para o fato de que municípios próximos tendem a ter resultados eleitorais similares: as interações sociais entre residentes de municípios próximos; a concentração das campanhas eleitorais em determinadas regiões em detrimento de outras; e as similaridades socioeconômicas observadas entre municípios próximos. A primeira hipótese não foi corroborada, i.e., não há evidência de que os residentes de um município influenciem a escolha eleitoral dos residentes dos municípios próximos. A segunda hipótese foi corroborada preliminarmente: o termo de erro espacial é estatisticamente significativo, de modo que mesmo considerando o efeito das similaridades socioeconômicas, os resíduos ainda mostram autocorrelação espacial. Dado que esse teste é indireto (a autocorrelação espacial residual sugere, mas não demonstra inequivocamente que as campanhas eleitorais concentram-se em algumas regiões), as conclusões relativas à segunda hipótese são necessariamente preliminares. Por fim, a terceira hipótese foi corroborada inequivocamente: todos os indicadores socioeconômicos (exceto o PIB per capita) são estatisticamente significativos e têm o sinal esperado. O artigo mostrou ainda que Dilma "herdou" a base geográfica de Lula e que essa base é bastante diferente da do PT, que continua sobretudo, um partido urbano.
No que respeita a investigações futuras, três linhas de pesquisa parecem promissoras. A primeira é testar a segunda hipótese diretamente. No momento não há dados disponíveis que permitam isso, mas em tese seria possível coletá-los a partir de documentos não-públicos e entrevistas com estrategistas de campanha. A segunda linha de pesquisa que merece ser considerada é estender a análise a outras eleições -para governador ou para o Legislativo (federal ou estadual), por exemplo. Por fim, a terceira linha é testar todas as três hipóteses usando-se dados eleitorais de outros países em desenvolvimento. Até o momento o uso de econometria espacial em Ciência Política tem se limitado em grande medida a dados de países desenvolvidos (e dos Estados Unidos em particular). Os trabalhos pioneiros de Carraro et al (2007) e Soares & Terron (2008) começaram a alterar esse cenário e seria interessante levar a mesma abordagem a, por exemplo, outros países latino-americanos.
Referências Bibliográficas
ANSELIN, L. Spatial econometrics. In: MILLS, T. & PATTERSON, K. (Eds.). Palgrave Handbook of Econometrics. Basingstoke: Palgrave Macmillan, vol.1, p. 901-941, 2006.
_____.; & FLORAX, R. Introduction. In: ANSELIN, L. & FLORAX, R. (Eds.). New directions in spatial econometrics. Berlin: Springer, p. 3-18, 1995. .
ARRAIZ, I.; DRUKKER, D.; KELEJIAN, H. & PRUCHA, I. "A spatial Cliff-Ord-type model with heteroskedastic innovations: small and large sample results." Journal of Regional Science, vol. 50, nº 2, p. 592-614, 2010. .
CARRARO, A.; ARAÚJO JUNIOR, A.; DAMÉ, O.; MONASTERIO, L. & SHIKIDA, C. 'É a economia companheiro!': uma análise empírica da reeleição de Lula com dados municipais [Online]. IBMEC-MG, 2007. Disponível em: <http://ceaee.ibmecmg.br/wp/wp41.pdf>. Acesso em: 23 mar. 2012. .
CHO, W. & GIMPEL, J. "Rough terrain: spatial variation in campaign contributing and volunteerism." American Journal of Political Science, vol. 54, nº 1, p. 74-89, 2007. .
FOTHERINGHAM, A.; BRUDSON, C. & CHARLTON, M. Geographically weighted regression: the analysis of spatially varying relationships. Chichester: Jon Wiley & Sons, 2002. .
HUCKFELDT, R. & SPRAGUE, J. "Discussant effects on vote choice: intimacy, structure, and interdependence." Journal of Politics, vol. 53, nº 1, p. 122-158, 1991. .
HUNTER, W. & POWER, T. "Rewarding Lula: executive power, social policy, and the Brazilian elections of 2006." Latin American Politics & Society, vol. 49, nº 1, p. 1-30, 2008. .
KELEJIAN, H. & PRUCHA, I. "Specification and estimation of spatial autoregressive models with autoregressive and heteroskedastic disturbances." Journal of Econometrics, vol. 157, p. 53-67, 2010. .
LEE, L. "Asymptotic distributions of quasi-maximum likelihood estimators for spatial autoregressive models." Econometrica, vol. 72, nº 6, p. 1899-1925, 2004. .
NICOLAU, J. & PEIXOTO, V. Uma disputa em três tempos: uma análise das bases municipais das eleições presidenciais de 2006, [Online]. ANPOCS, 2007. Disponível em: <http://jaironicolau.iesp.uerj.br/artigos/NICOLAU%20&%20PEIXOTO%20ANPOCS2007%20ST%2024%20PARTIDOS% 20E%20SISTEMAS%20PARTIDA%C2%A6%C3%BCRIOS.pdf>. Acesso em: 23 mar. 2012. .
NICKERSON, D. "Is voting contagious? Evidence from two field experiments." American Political Science Review, vol. 102, nº 1, p. 49-57, 2008. .
SOARES, G. & TERRON, S. "Dois Lulas: a geografia eleitoral da reeleição (explorando conceitos, métodos e técnicas de análise geoespacial)". Opinião Pública, vol. 14, nº 2, p. 269-301, 2008. .
STRØM, K. Minority government and majority rule. Cambridge: Cambridge University Press, 1990. TERRON, S. & SOARES, G. "As bases eleitorais de Lula e do PT: do distanciamento ao divórcio." Opinião Pública, vol. 16, nº 2, p. 310-337, 2010. .
TINBERGEN, J. An analysis of world trade flows, the Linder hypothesis and exchange risk. In: TINBERGEN, J. (Ed.). Shaping the world economy. New York: The Twentieth Century Fund, 1962. .
WARD, M. & GLEDITSCH, K. Spatial regression models. Los Angeles: Sage, 2008.
ZUCCO, C. "The president's 'new' constituency: Lula and the pragmatic vote in Brazil's 2006 presidential elections". Journal of Latin American Studies, vol. 40, nº 1, p. 29-49, 2008.
Submetido à publicação em março de 2012
Versão final aprovada em setembro de 2012
Apêndice - Fontes, software e estatísticas descritivas
Fontes:
Todos os dados geocodificados foram baixados da página do IBGE e estão disponíveis em: <ftp://geoftp.ibge.gov.br/malhas_digitais/municipio_2007/escala_2500mil/proj_policonica_sirgas2000/>. Eles refletem a malha municipal brasileira em 2007 e são baseados em projeções cônicas (e portanto podem ser usados para cálculos envolvendo distâncias euclidianas). As coordenadas são expressas em quilômetros.
Dados sobre filiação partidária do prefeito, PIB per capita, urbanização, taxa de analfabetismo e saneamento foram extraídos de diferentes pesquisas do IBGE. Dados sobre o Bolsa Família foram extraídos da página da CGU e estão disponíveis em: <http://www.portaltransparencia.gov.br/>. Todos os dados são de 2009 (dados de 2010 não estavam disponíveis para os indicadores sociais).
Um total de 37 municípios tinham uma ou mais variáveis faltando. Em econometria não-espacial, observações com valores omissos podem ser simplesmente deletadas, mas em econometria espacial isso é problemático porque as observações são espacialmente dependentes. Dessa forma, médias estaduais foram imputadas para variáveis contínuas (no caso dos indicadores sociais) e modas estaduais foram imputadas para variáveis binárias (prefeito petista ou não petista).
Software:
Os mapas de votação foram produzidos em ArcGIS 10. O Mapa 2, que mostra a área excluída usandose um raio de 50 km na matriz de pesos, e o Mapa 3, que mostra os aglomerados LISA, foram produzidos em GeoDa 1.0.1. A análise estatística foi dividida entre Stata 12 e R 2.14.2. Os testes estatísticos da seção "Regularidades espaciais nas eleições brasileiras", as regressões de mínimos quadrados e as estimativas GWR foram produzidas principalmente em R, usando-se os pacotes 'spdep' e 'sphet' (as ferramentas do Stata para calcular Moran I, estatísticas LISA e testes LM requerem que a matriz de pesos seja criada por meio da ferramenta 'spatwmat', mas essa ferramenta não funciona bem com bancos de dados grandes; a ferramenta do Stata para GWR não requer o uso de 'spatwmat', mas o algoritmo é menos eficiente do que o do equivalente em R e "falha" após poucas iterações). Por outro lado, todas as estimativas GMM e ML foram produzidas no Stata, usando-se o pacote 'sppack' (aqui o algoritmo ineficiente é o do R, especialmente com as estimativas GMM; ademais, o R não comporta matrizes de pesos baseadas em distâncias inversas).
Estatísticas descritivas:
Clique para ampliar

- ANSELIN, L. Spatial econometrics. In: MILLS, T. & PATTERSON, K. (Eds.). Palgrave Handbook of Econometrics. Basingstoke: Palgrave Macmillan, vol.1, p. 901-941, 2006.
- _____.; & FLORAX, R. Introduction. In: ANSELIN, L. & FLORAX, R. (Eds.). New directions in spatial econometrics Berlin: Springer, p. 3-18, 1995.
- ARRAIZ, I.; DRUKKER, D.; KELEJIAN, H. & PRUCHA, I. "A spatial Cliff-Ord-type model with heteroskedastic innovations: small and large sample results." Journal of Regional Science, vol. 50, nş 2, p. 592-614, 2010.
- CARRARO, A.; ARAÚJO JUNIOR, A.; DAMÉ, O.; MONASTERIO, L. & SHIKIDA, C. 'É a economia companheiro!': uma análise empírica da reeleição de Lula com dados municipais [Online]. IBMEC-MG, 2007. Disponível em: <http://ceaee.ibmecmg.br/wp/wp41.pdf>. Acesso em: 23 mar. 2012.
- CHO, W. & GIMPEL, J. "Rough terrain: spatial variation in campaign contributing and volunteerism." American Journal of Political Science, vol. 54, nş 1, p. 74-89, 2007.
- FOTHERINGHAM, A.; BRUDSON, C. & CHARLTON, M. Geographically weighted regression: the analysis of spatially varying relationships. Chichester: Jon Wiley & Sons, 2002.
- HUCKFELDT, R. & SPRAGUE, J. "Discussant effects on vote choice: intimacy, structure, and interdependence." Journal of Politics, vol. 53, nş 1, p. 122-158, 1991.
- HUNTER, W. & POWER, T. "Rewarding Lula: executive power, social policy, and the Brazilian elections of 2006." Latin American Politics & Society, vol. 49, nş 1, p. 1-30, 2008.
- KELEJIAN, H. & PRUCHA, I. "Specification and estimation of spatial autoregressive models with autoregressive and heteroskedastic disturbances." Journal of Econometrics, vol. 157, p. 53-67, 2010.
- LEE, L. "Asymptotic distributions of quasi-maximum likelihood estimators for spatial autoregressive models." Econometrica, vol. 72, nş 6, p. 1899-1925, 2004.
- NICOLAU, J. & PEIXOTO, V. Uma disputa em três tempos: uma análise das bases municipais das eleições presidenciais de 2006, [Online]. ANPOCS, 2007. Disponível em: <http://jaironicolau.iesp.uerj.br/artigos/NICOLAU%20&%20PEIXOTO%20ANPOCS2007%20ST%2024%20PARTIDOS% 20E%20SISTEMAS%20PARTIDA%C2%A6%C3%BCRIOS.pdf>. Acesso em: 23 mar. 2012.
- NICKERSON, D. "Is voting contagious? Evidence from two field experiments." American Political Science Review, vol. 102, nş 1, p. 49-57, 2008.
- SOARES, G. & TERRON, S. "Dois Lulas: a geografia eleitoral da reeleição (explorando conceitos, métodos e técnicas de análise geoespacial)". Opinião Pública, vol. 14, nş 2, p. 269-301, 2008.
- STRØM, K. Minority government and majority rule Cambridge: Cambridge University Press, 1990.
- TERRON, S. & SOARES, G. "As bases eleitorais de Lula e do PT: do distanciamento ao divórcio." Opinião Pública, vol. 16, nş 2, p. 310-337, 2010.
- TINBERGEN, J. An analysis of world trade flows, the Linder hypothesis and exchange risk. In: TINBERGEN, J. (Ed.). Shaping the world economy New York: The Twentieth Century Fund, 1962.
- WARD, M. & GLEDITSCH, K. Spatial regression models Los Angeles: Sage, 2008.
- ZUCCO, C. "The president's 'new' constituency: Lula and the pragmatic vote in Brazil's 2006 presidential elections". Journal of Latin American Studies, vol. 40, nş 1, p. 29-49, 2008.
Datas de Publicação
-
Publicação nesta coleção
13 Dez 2013 -
Data do Fascículo
Nov 2013
Histórico
-
Recebido
Mar 2012 -
Aceito
Set 2012